Приложение 1 — Примеры решения задач и комментарии
Пример 1
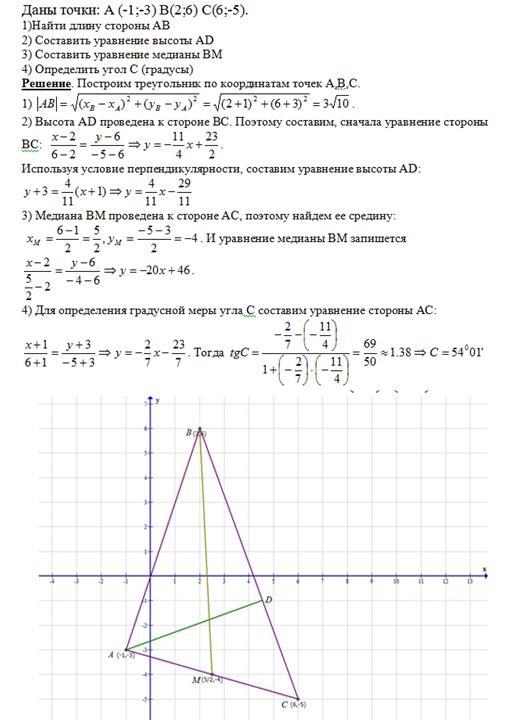
Даны координаты вершин треугольника А(0, –2), В(1, 1), С(3, 0). Написать общее уравнение медианы треугольника, опущенной из вершины В.
Решение. Найдем координаты точки М, середины основания АС.
; .
Напишем теперь уравнение прямой ВМ, проходящей через две точки В и М:
; ; .
После элементарных преобразований имеем:
или –Y – 1 = 4X – 6, отсюда 4X + Y – 5 = 0.
Получили искомое уравнение медианы.
Пример 2
Даны три точки А(3, 1), В(1, –2), С(3, 4). Написать уравнение прямой, проходящей через точку С перпендикулярно прямой АВ.
Решение. Запишем уравнение прямой АВ, проходящей через две точки А и В.
, или –2(Y – 1) = –3(X – 3), отсюда 2Y – 2 = 3X – 9.
Разрешая это уравнение относительно переменной У, найдем уравнение прямой АВ с угловым коэффициентом:
Угловой коэффициент этой прямой равен .
Из условия перпендикулярности двух прямых получим угловой коэффициент К1 прямой, перпендикулярной прямой АВ:
Запишем теперь уравнение прямой с данным угловым коэффициентом К1 и проходящей через точку С. Воспользуемся формулой Y – Yc = K1(X – Xc). Отсюда . После элементарных преобразований получаем требуемое уравнение
Пример 3. Заданы две прямые и .
А. Найти угол между ними.
Б. Провести нормаль к прямой L1 в точке . Образуется треугольник, написать уравнение третьей стороны и указать вершины треугольника.
Решение. а. Угол между прямыми L1 и L2 определяется по формуле ; .
Б. Уравнение нормали к прямой L1, проходящей через точку A, имеет вид , где . Откуда , и уравнение нормали или .
Точка A принадлежит прямым L1 и L3. Надо найти точку пересечения прямых L1 и L2, . Откуда . Обозначим эту точку . А также надо найти точку пересечения прямых L2 и L3. . Имеем . Обозначим эту точку . Таким образом, имеем три вершины треугольника ABC.
Пример 4. Заданы координаты вершин параллелограмма:
.
Написать уравнения всех сторон параллелограмма, определить углы параллелограмма и его площадь.
Решение. Для написания уравнений сторон параллелограмма используем формулу
.
Уравнение стороны AD имеет вид , или .
Уравнение стороны BC имеет вид или .
Уравнение стороны AB имеет вид , или .
Уравнение стороны CD имеет вид , или .
Угол между прямыми L1 и L2 определим по формуле . . Угол между прямыми L3 и L2 . .
Сторона параллелограмма равна . Расстояние от точки B до прямой L1 вычисляется по формуле . . Площадь параллелограмма равна .
Пример 5
Дано уравнение второго порядка
9X2 – 4Y2 – 36X – 8Y – 4 = 0.
Написать каноническое уравнение кривой и определить ее тип. Найти полуоси, координаты центра симметрии и фокусы кривой.
Решение. Задача сводится к тому, чтобы привести данное уравнение к одному из следующих видов:
или
Первое из этих уравнений определяет эллипс, а второе – гиперболу с центром симметрии в точке О(Х0,У0), полуосями A, B (для гиперболы: A – вещественная полуось). Фокусы таких кривых имеют координаты: F1(X0 + C, Y0) и F2(X0 – C, Y0), где C2 = A2 – B2 (для эллипса, если A – большая полуось) и C2 = A2 + B2 (для гиперболы).
Для решения поставленной задачи выделим полные квадраты в следующих выражениях:
9X2 – 36X = 9(X2 — 4X + 4) – 36 = 9(X – 2)2 – 36;
–4Y2 – 8Y = –4(Y2 + 2Y + 1) + 4 = –4(Y + 1)2 + 4.
Подставим теперь полученные выражения в данное уравнение:
9(X – 2)2 – 36 – 4(Y + 1)2 + 4 – 4 = 0 или 9(X – 2)2 – 4(Y + 1)2 = 36.
Поделив обе части уравнения на 36, получим каноническое уравнение гиперболы
Отсюда видно, что центр симметрии гиперболы находится в точке О(2, –1), прямые Х – 2 = 0,
У + 1 = 0 являются ее осями симметрии. Вещественная полуось гиперболы А = 2, мнимая полуось
B = 3,
Получим координаты фокусов .
Пример 6
Дано уравнение кривой в декартовых координатах (
Решение. Воспользуемся формулами ((1.1), гл. 1) X = R × cos j, Y = R × sin j и подставим эти выражения в данное уравнение.
(R2cos2j + R2sin2j)2 = 4R cos j × R2(sin j)2.
Используя формулы тригонометрии cos2j +sin2j = 1, 2sin j × cos j = sin 2j, получим
R4 = 2R3sin 2j sin j.
Поделим обе части на r3 и получим искомое уравнение
R = 2sin 2j × sin j.
| < Предыдущая |
|---|
Даны координаты вершин треугольника авс найти онлайн. Дано координаты вершин треугольника
Пример решения некоторых заданий из типовой работы «Аналитическая геометрия на плоскости»
Даны вершины
,
,
треугольника АВС. Найти:
Уравнения всех сторон треугольника;
Систему линейных неравенств, определяющих треугольник АВС ;
Уравнения высоты, медианы и биссектрисы треугольника, проведенных из вершины А ;
Точку пересечения высот треугольника;
Точку пересечения медиан треугольника;
Длину высоты, опущенной на сторону АВ ;
Угол А ;
Сделать чертеж.
Пусть вершины треугольника имеют координаты: А (1; 4), В (5; 3), С (3; 6). Сразу нарисуем чертеж:
1. Чтобы выписать уравнения всех сторон треугольника, воспользуемся уравнением прямой, проходящей через две заданные точки с координатами (x 0 , y 0 ) и (x 1 , y 1 ):
=
Таким образом, подставляя вместо (x 0 , y 0 ) координаты точки А , а вместо (x 1 , y 1 ) координаты точки В , мы получим уравнение прямой АВ :
 Аналогично
находим уравнение прямой АС :
Аналогично
находим уравнение прямой АС :И так же уравнение прямой ВС :
2. Заметим, что множество точек треугольника АВС представляет собой пересечение трех полуплоскостей, причем каждую полуплоскость можно задать с помощью линейного неравенства. Если мы возьмем уравнение любой из сторон ∆АВС , например АВ , тогда неравенства
и
задают точки, лежащие по разные стороны от прямой АВ . Нам нужно выбрать ту полуплоскость, где лежит точка С. Подставим ее координаты в оба неравенства:
Правильным будет второе неравенство, значит, нужные точки определяются неравенством
.
Аналогично поступаем
с прямой ВС, ее уравнение
.
В качестве пробной используем точку А
(1, 1):
значит, нужное неравенство имеет вид:
.
Если проверим прямую АС (пробная точка В), то получим:
значит, нужное неравенство будет иметь вид
Окончательно получаем систему неравенств:
Знаки «≤», «≥»
означают, что точки, лежащие на сторонах
треугольника, тоже включены во множество
точек, составляющих треугольник АВС .
3. а) Для того, чтобы
найти уравнение высоты, опущенной из
вершины А на
сторону ВС ,
рассмотрим уравнение стороны ВС :
.
Вектор с координатами
перпендикулярен сторонеВС и, значит, параллелен высоте. Запишем
уравнение прямой, проходящей через
точку А параллельно вектору
:
Это уравнение высоты, опущенной из т. А на сторону ВС .
б) Найдем координаты
середины стороны ВС по формулам:
Здесь
– это координаты т.В ,
а
– координаты т.С .
Подставим и получим:
Прямая, проходящая через эту точку и точку А является искомой медианой:
в) Уравнение
биссектрисы мы будем искать, исходя из
того, что в равнобедренном треугольнике
высота, медиана и биссектриса, опущенные
из одной вершины на основание треугольника,
равны. Найдем два вектора
и
и их длины:
Тогда вектор
имеет такое же направление, что и вектор
,
а его длина
Точно так же единичный вектор
совпадает по направлению с вектором
Сумма векторов
есть вектор, который
совпадает по направлению с биссектрисой
угла А . Таким образом, уравнение искомой
биссектрисы можно записать виде:
Таким образом, уравнение искомой
биссектрисы можно записать виде:
4) Уравнение одной
из высот мы уже построили. Построим
уравнение еще одной высоты, например,
из вершины В .
Сторона АС задается уравнением
Значит, вектор
(т. е. перпендикулярноАС ), имеет вид:
Известно, что высоты треугольника пересекаются в одной точке. В частности, эта точка является пересечением найденных высот, т.е. решением системы уравнений:
— координаты этой точки.
5. Середина АВ имеет координаты
.
Запишем уравнение медианы к сторонеАВ. Эта
прямая проходит через точки с координатами
(3, 2) и (3, 6), значит, ее уравнение имеет
вид:
Заметим, что ноль в знаменателе дроби в записи уравнения прямой означает, что эта прямая проходит параллельно оси ординат.
Чтобы найти точку пересечения медиан достаточно решить систему уравнений:
Точка пересечения
медиан треугольника имеет координаты
.
6. Длина высоты, опущенной на сторону
и находится по формуле:
7. Косинус угла А можно найти по формуле косинуса угла между векторами и, который равен отношению скалярного произведения этих векторов к произведению их длин:
.
1. Даны вершины треугольника АВС .А (–9; –2), В (3; 7), С (1; –7).
1) длину стороны АВ ;
2) уравнения сторон АВ и АС и их угловые коэффициенты;
3) угол А в радианах;
4) уравнение высоты С D и ее длину;
5) уравнение окружности, для которой высота С D есть диаметр;
6) систему линейных неравенств, определяющих треугольник АВС .
Решение . Сделаем чертеж.
1. Найдем длину стороны АВ. Расстояние между двумя точками определяется по формуле
2. Найдем уравнения сторон АВ и АС и их угловые коэффициенты.
Запишем уравнение прямой, проходящей через две точки.
Это общее уравнение прямой. Разрешим его относительно у, получим
, угловой коэффициент прямой равен
Аналогично для стороны АС имеем.
угловой коэффициент прямой равен
3. Найдем угол А в радианах . Это угол между двумя векторами
и
. Запишем координаты векторов . Косинус угла между векторами равен
4. Найдем уравнение высоты С D и ее длину .
, следовательно, их угловые коэффициенты связаны соотношением
.
Запишем уравнение высоты через угловой коэффициент
Точка
принадлежит прямой CD, следовательно ее координаты удовлетворяют уравнению прямой, отсюда имеем
Окончательно
или
Длину высоты вычислим, как расстояние от точки С до прямой АВ
5. Найдем уравнение окружности , для которой высота С D есть диаметр.
Координаты точки D найдем, как точку пересечения двух прямых AB и CD, уравнения которых известны.
Найдем координаты точки О – центра окружности. Это середина отрезка CD.
Радиус окружности равен
Запишем уравнение окружности.
6) Определим треугольник АВС системой линейных неравенств.
Найдем уравнение прямой CB.
Система линейных неравенств будет выглядеть так.
2. Решить данную систему уравнений пользуясь формулами Крамера. Сделать проверку полученного решения.
Решение. Вычислим определитель этой системы:
.
Найдем определители
и решим систему:
Проверка:
Ответ:
3. Систему уравнений записать в матричной форме и решить ее с помощью
обратной матрицы. Сделать проверку полученного решения
Решение.
Найдем определитель матрицу А
матрица невырожденная и имеет обратную. Найдем все алгебраические дополнения и составим союзную матрицу.
Обратная матрица имеет вид:
Выполним умножение
и найдем вектор решений.
Проверка
.
Ответ:
Решение.
N = (2, 1). Перпендикулярно вектору нормали проводим линию уровня и перемещаем ее в направлении нормали,
Минимум целевая функция достигает в точке А, а максимум в точке В. Координаты этих точек находим решая совместно уравнения прямых, на пересечении которых они находятся.
5. Туристской фирме требуется не более а трехтонных автобусов и не более в
пятитонных автобусов. Отпускная цена автобусов первой марки 20000 у.е., второй марки
40000 у.е. Туристская фирма может выделить для приобретения автобусов не более с у.е.
Сколько следует приобрести автобусов каждой марки в отдельности, чтобы их общая
(суммарная) грузоподъёмность была максимальной. Решить задачу графическим методом.
а = 20 в = 18 с = 1000000
Решение . Составим математическую модель задачи. Обозначим через
Составим математическую модель задачи. Обозначим через
— количество автобусов каждой тоннажности, которое будет приобретено. Цель закупок – иметь максимальную грузоподъемность приобретенных машин, описывается функцией цели
Ограничения задачи обусловлены количеством приобретенных автобусов и их стоимостью.
Решим задачу графически. . Строим область допустимых решений задачи и нормаль к линиям уровней N = (3, 5). Перпендикулярно вектору нормали проводим линию уровня и перемещаем ее в направлении нормали.
Максимум функция цели достигает в точке
, функция цели при этом принимает значение .
Решение . 1. Областью определения функции является вся числовая ось.
2, Функция не является ни четной, ни нечетной.
3. При х=0, у=20
4. Исследуем функцию на монотонность и экстремумы.
Найдем нули производной
Стационарные точки функции.
Нанесем стационарные точки на ось Ох и проверим знаки производной на каждом участке оси.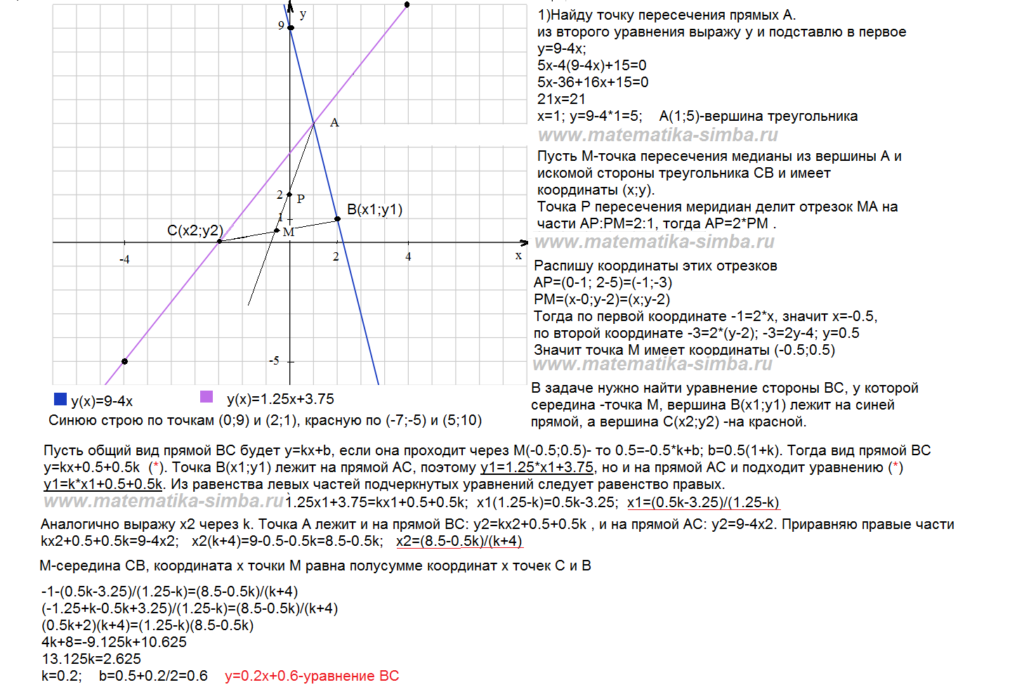
–точка максимума
;
-точка минимума
5. Исследуем график функции на выпуклость и вогнутость. Возьмем 2-ю производную
Точка перегиба графика функции.
При
— функция выпукла; при
— функция вогнута.
Графий функции имеет вид
6. Найдем наибольшее и наименьшее значение функции на отрезке [-1; 4]
Вычислим значение функции на концах отрезка
В точке минимума функция принимает значения , следовательно, наименьшее значение на отрезке [-1; 4] функция принимает в точке минимума , а наибольшее на левой границе интервала.
7. Найти неопределённые интегралы и результаты интегрирования проверить
дифференцированием.
Решение .
Проверка.
Здесь произведение косинусов было заменено суммой, согласно тригонометрическим формулам.
Задача 1 . Даны координаты вершин треугольника АВС: А(4; 3), В(16;-6), С(20; 16). Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) угол В в радианах с точностью до двух знаков; 4) уравнение высоты СD и ее длину; 5) уравнение медианы AE и координаты точки К пересечения этой медианы с высотой CD; 6) уравнение прямой, проходящей через точку К параллельно стороне АВ; 7) координаты точки М, расположенной симметрично точке А относительно прямой СD.
Решение:
1. Расстояние d между точками A(x 1 ,y 1) и B(x 2 ,y 2) определяется по формуле
Применяя (1), находим длину стороны АВ:
2. Уравнение прямой, проходящей через точки A(x 1 ,y 1) и B(x 2 ,y 2) имеет вид
(2)
Подставляя в (2) координаты точек А и В, получим уравнение стороны АВ:
Решив последнее уравнение относительно у, находим уравнение стороны АВ в виде уравнения прямой с угловым коэффициентом:
откуда
Подставив в (2) координаты точек В и С, получим уравнение прямой ВС:
Или
3. Известно, что тангенс угла между двумя прямыми, угловые коэффициенты которых соответственно равны и вычисляется по формуле
(3)
Искомый угол В образован прямыми АВ и ВС, угловые коэффициенты которых найдены: Применяя (3), получим
Или рад.
4. Уравнение прямой, проходящей через данную точку в заданном направлении, имеет вид
(4)
Высота CD перпендикулярна стороне АВ. Чтобы найти угловой коэффициент высоты CD, воспользуемся условием перпендикулярности прямых. Так как то Подставив в (4) координаты точки С и найденный угловой коэффициент высоты, получим
Так как то Подставив в (4) координаты точки С и найденный угловой коэффициент высоты, получим
Чтобы найти длину высоты CD, определим сначала координаты точки D- точки пересечения прямых АВ и CD. Решая совместно систему:
находим т.е. D(8;0).
По формуле (1) находим длину высоты CD:
5. Чтобы найти уравнение медианы АЕ, определим сначала координаты точки Е, которая является серединой стороны ВС, применяя формулы деления отрезка на две равные части:
(5)
Следовательно,
Подставив в (2) координаты точек А и Е, находим уравнение медианы:
Чтобы найти координаты точки пересечения высоты CD и медианы АЕ, решим совместно систему уравнений
Находим .
6. Так как искомая прямая параллельна стороне АВ, то ее угловой коэффициент будет равен угловому коэффициенту прямой АВ. Подставив в (4) координаты найденной точки К и угловой коэффициент получим
3x + 4y – 49 = 0 (KF)
7. Так как прямая АВ перпендикулярна прямой CD, то искомая точка М, расположенная симметрично точке А относительно прямой CD, лежит на прямой АВ. Кроме того, точка D является серединой отрезка AM. Применяя формулы (5), находим координаты искомой точки М:
Кроме того, точка D является серединой отрезка AM. Применяя формулы (5), находим координаты искомой точки М:
Треугольник ABC, высота CD, медиана АЕ, прямая KF и точка М построены в системе координат хОу на рис. 1.
Задача 2. Составить уравнение геометрического места точек, отношение расстояний которых до данной точки А(4; 0) и до данной прямой х=1 равно 2.
Решение :
В системе координат хОу построим точку А(4;0) и прямую х = 1. Пусть М(х;у) – произвольная точка искомого геометрического места точек. Опустим перпендикуляр MB на данную прямую x = 1 и определим координаты точки В. Так как точка В лежит на заданной прямой, то ее абсцисса равна 1. Ордината точки В равна ординате точки М. Следовательно, В(1;у) (рис. 2).
По условию задачи |МА|: |МВ| = 2. Расстояния |МА| и |MB| находим по формуле (1) задачи 1:
Возведя в квадрат левую и правую части, получим
или
Полученное уравнение представляет собой гиперболу, у которой действительная полуось а = 2,а мнимая –
Определим фокусы гиперболы.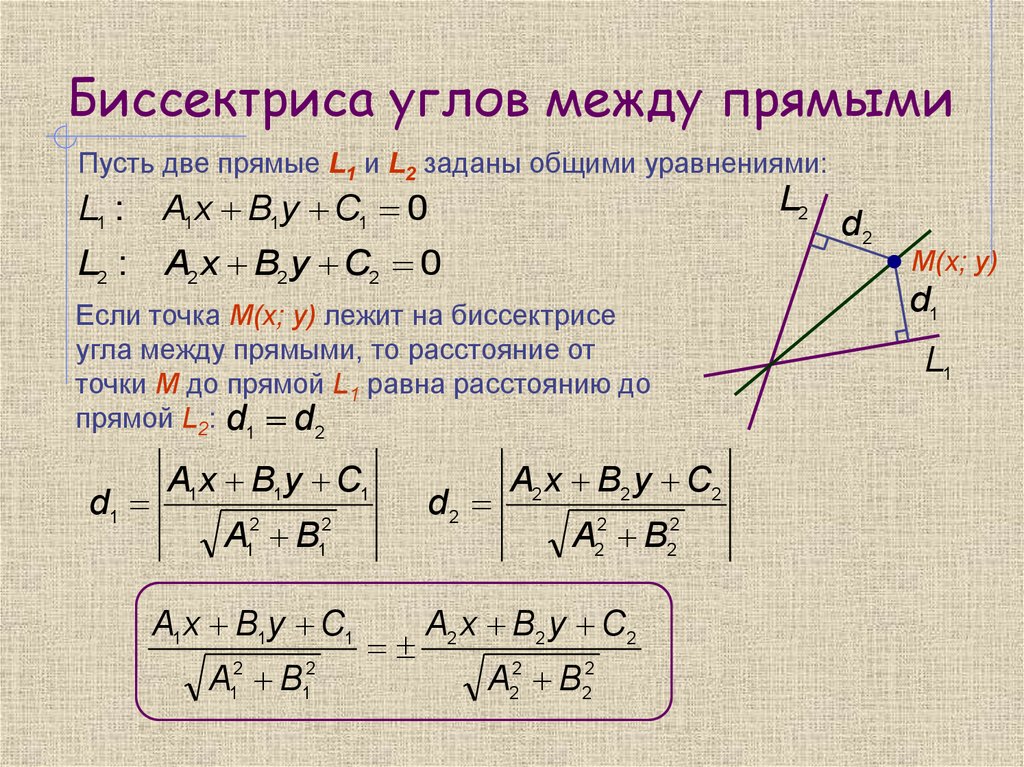 Для гиперболы выполняется равенство Следовательно, и – фокусы гиперболы. Как видно, заданная точка А(4;0) является правым фокусом гиперболы.
Для гиперболы выполняется равенство Следовательно, и – фокусы гиперболы. Как видно, заданная точка А(4;0) является правым фокусом гиперболы.
Определим эксцентриситет полученной гиперболы:
Уравнения асимптот гиперболы имеют вид и . Следовательно, или и – асимптоты гиперболы. Прежде чем построить гиперболу, строим ее асимптоты.
Задача 3 . Составить уравнение геометрического места точек, равноудаленных от точки А(4; 3) и прямой у = 1. Полученное уравнение привести к простейшему виду.
Решение: Пусть М(х; у) — одна из точек искомого геометрического места точек. Опустим из точки М перпендикуляр MB на данную прямую у = 1 (рис. 3). Определим координаты точки В. Очевидно, что абсцисса точки В равна абсциссе точки М, а ордината точки В равна 1, т. е. В(х; 1). По условию задачи |МА|=|МВ|. Следовательно, для любой точки М(х;у), принадлежащей искомому геометрическому месту точек, справедливо равенство:
Полученное уравнение определяет параболу с вершиной в точке Чтобы уравнение параболы привести к простейшему виду, положим и y + 2 = Y тогда уравнение параболы принимает вид:
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Задача Между учениками двух классов разделили поровну 200 учебников . В одном классе 24 ученика , а в другом -26. Сколько учебников получил каждый класс?
В зале 89 стульев. сначала из зала вынесли 2стула потом1.на сколько меньше стульев вынесли, чем их осталось?
На экзамене 20 билетов, Андрей не выучил 1 из них. Найдите вероятность того, что ему попадется выученный билет
Найдите вероятность того, что ему попадется выученный билет
диаметр шара равен 4m. через конец диаметра проведена плоскость под углом 30 градусов к нему. найдите площадь сечения шара этой плоскостью
Прошу решение задачи: между числами 1 2 3 4 5 расставить знаки математических действий так, чтобы в сумме получилось 40 или 80
Пользуйтесь нашим приложением
Значение, примеры, формула и расчет
Предположим, вам нужно разделить последний кусок торта со своим братом. И ни один из вас не хочет получить меньший кусок. Чтобы избежать драки между вами и вашим братом из-за торта, ваша мама отрезает треугольный кусок торта от его медианы , равной , так что вы оба получите торт одинакового размера. Но что это за медиана? Как твоя мама решила, где разрезать торт?
Определим медиану треугольника как отрезок, соединяющий вершину с серединой противоположной стороны. В этой статье мы рассмотрим определение медиана , ее различные свойства, математическая формула и, наконец, работа с несколькими примерами.
В этой статье мы рассмотрим определение медиана , ее различные свойства, математическая формула и, наконец, работа с несколькими примерами.
В конце этой статьи вы сможете:
Определить медиану и связать ее с площадью треугольника.
Определите и начертите медианы в треугольнике.
Вычислить длину медианы по сторонам и координатам треугольника.
Значение медианы
Итак, что именно означает медиана? Представьте, что у вас есть кусок пиццы, который вам нужно разделить между собой и вашим другом. Для простоты назовем эту пиццу \(\bigtriangleup ABC\). Теперь имейте в виду, что вам нужно разделить пиццу поровну между своими друзьями. Здесь может помочь медиана .
Медиана куска пиццы, pexels.com
Выберите сторону пиццы, скажем, сторону \(a\) (то есть сторону \(BC\)), и разрежьте пиццу по отрезку, соединяющему среднюю точку линии и противоположный внутренний угол, как показано на рисунке ниже. Ура! Теперь вы и ваш друг можете наслаждаться пиццей поровну. Воображаемая линия, разрезающая пиццу на две равные части, — это медиана . Поскольку все треугольники имеют \(3\) сторон и \(3\) внутренних углов. У него всегда будут \(3\) медианы.
Ура! Теперь вы и ваш друг можете наслаждаться пиццей поровну. Воображаемая линия, разрезающая пиццу на две равные части, — это медиана . Поскольку все треугольники имеют \(3\) сторон и \(3\) внутренних углов. У него всегда будут \(3\) медианы.
Медиана — построенная линия, соединяющая середину одной стороны с противоположным внутренним углом.
Интересно отметить, что периметр треугольника всегда больше суммы трех его медиан.
Что такое центроид? Теперь, когда мы знаем, что такое медиана, давайте рассмотрим, что такое центроид. Точка пересечения трех медиан называется центроидом . Центроид представляет собой точки параллелизма. Точка параллелизма — это точка, в которой пересекаются две или более линий. Например, точка пересечения медиан, серединных перпендикуляров и высот. Центроид всегда будет лежать внутри треугольника, в отличие от других точек параллелизма.
Точка пересечения трех медиан называется центроидом .
Три медианы с центроидом в качестве точки пересечения, StudySmarter Originals
Центроид обладает несколькими интересными свойствами. Он всегда будет делить медиану на соотношение \(2:1\). Центроид всегда расположен на расстоянии двух третей медианы от внутреннего угла.
Представим себе, как медиана делится на соотношение \(2:1\). Возьмите \(\bigtriangleup ABC\) и проведите \(3\) медианы из каждой вершины. Пусть теперь \(O\) будет центром тяжести треугольника. Если \(AM\) — медиана треугольника из вершины \(A\), то \(2OM = OA\).
Центроид делит медиану на части \(2:1\), StudySmarter Originals
В прямоугольном треугольнике медиана, проведенная из вершины прямого угла, составляет половину длины гипотенузы треугольника. Медиана из прямого угла треугольника делит гипотенузу на две равные части и каждая часть гипотенузы равна длине медианы.
Медиана равна половине гипотенузы, StudySmarter Originals
На приведенном выше рисунке медиана \(AD\) делит гипотенузу на две равные части \(CD\) и \(BD\) таким образом, что \(AD=CD; AD=BD\).
Свойства медианы
Свойства медианы можно описать следующим образом:
Любой треугольник содержит 3 медианы с точкой пересечения, называемой центром тяжести.
Соединительная сторона медианы разделена на две равные части.
Два треугольника одинакового размера и площади образуются путем построения медианы из любой из вершин треугольника.
На самом деле любой треугольник делится на 6 меньших треугольников с одинаковой площадью 3 медианами треугольника.
Медиана и высота треугольника
Различие между медианой и высотой треугольника может немного сбить с толку, но легко принять их за одно и то же. Но медиана и высота треугольника — это два разных элемента треугольника. Медиана треугольника — это отрезок прямой от одной вершины до середины его противоположной стороны. Принимая во внимание, что высота треугольника — это перпендикулярный отрезок прямой от вершины до его противоположной стороны.
Медиана и высота треугольников, StudySmarter Originals
На приведенном выше рисунке \(AD, BE,\) и \(CF\) — медианы треугольника \(\bigtriangleup ABC\), а \(XM, YN,\) и \(ZO\) — высоты треугольника \(\bigtriangleup XYZ\).
Разница между медианой и высотой
Посмотрим разницу между медианой и высотой треугольника.
| Медиана | Высота |
|
|
|
|
|
|
|
где медиана треугольника равна \(m_c\), стороны треугольника равны \(a, b,\) и \(c\), а медиана образована на стороне \ (‘с’\). Но как тогда вычислить длину, используя только координаты треугольника? Сначала мы оцениваем середины стороны с медианой, используя приведенную ниже формулу. Треугольник с серединой и медианой, StudySmarter Originals \[M(x_m, y_m)=\frac{(x_2+x_3)}{2}, \frac{(y_2+y_3)}{2}\] где \(M(x_m,y_m)\) — один из концов медианы. Используя эти координаты и оставшуюся точку, мы можем вычислить длину медианы. Координаты нужно подставить в следующую формулу. Это формула расстояния, и она дает расстояние между любыми двумя координатами на двумерной плоскости. где \(M(x_m, y_m)=\frac{(x_1+x_2)}{2}, \frac{(y_1+y_2)}{2}\). Примеры медианДавайте посмотрим на некоторые примеры медиан и поймем их. Найдите длину медианы данного треугольника \(ABC\), стороны которого заданы следующим образом: \(AB = 10\, единицы\), \(BC = 6\, единицы\) и \(AC = 8\, ед.\) соответственно, в котором АМ — медиана, образованная на стороне \(ВС\). Треугольник с длинами сторон, StudySmarter Originals Решение: 92}{4}} = 8,54\] Следовательно, длина медианы \(AM\) равна \(8,54 \; единиц\). Найдите длину медианы \(AM\), если координаты треугольника \(ABC\) заданы как \(A (2,5), B (6,3), C (-3,0 )\). Треугольник с координатами, StudySmarter Originals Решение: Шаг 1: Рассчитать координаты средней точки \(BC\) \begin{align}M(x,y)&=\frac {(x_1+x_2)}{2}, \frac{(y_1+y_2)}{2} \\&=\frac{(6+(-3))}{2}, \frac{3+0} {2} \\&=(1. Это дает нам длину \(3.53\) единиц. Это подводит нас к концу статьи. Вот основные выводы, которые помогут освежить в памяти то, что мы уже узнали. Медиана — ключевые выводыСоединить медианы треугольникаСоединить медианы треугольникаПРЕДУПРЕЖДЕНИЕ. В вашем браузере отсутствует Javascript или он не включен. Это означает, что вы не увидите уравнений или фильмов. Р. Адам Молнар Первые три исследования по логарифмам и параболам были сосредоточены главным образом на алгебре. Мы построили декартову геометрию с помощью точек и кривых, но основное внимание уделялось символьной математике. Определение треугольника и медианыХотя более серьезные математики, вроде тех, кто работает в Wolfram Mathworld, могут съёжиться при таком определении, мы могли бы назвать геометрию изучением форм. Геометрия имеет долгую историю. Платон и Сократ говорили о геометрии. Чуть позже, в III веке до нашей эры, были написаны «Начала» Евклида. Книги по-прежнему доступны и полезны сегодня. Для сравнения, наши более ранние темы (логарифмы и декартовы координаты) были впервые опубликованы примерно в 1615 году нашей эры. Большинство статистических тем касаются относительных детей за последние 100 лет! Элементы начинаются с некоторых определений. В этой записи мы рассмотрим одну из основных фигур, определяемую тремя прямыми линиями. Мы можем нарисовать много вещей, имея треугольник. В этом задании мы сосредоточимся на отрезках, называемых медианами. Медиана треугольника соединяет одну из угловых точек треугольника, называемую вершиной, с серединой противоположной стороны. Внутри каждого треугольника есть три медианы, по одной из каждой вершины. Построим медианы треугольника. Я продемонстрирую на картинках из бесплатного Java-пакета GeoGebra. Мы начнем с треугольника в системе координат, обозначив вершины A, B и C. У греков, включая Евклида, были правила относительно того, что можно строить. В их конструкциях разрешалось использовать только циркуль и линейку без опознавательных знаков. Если вы хотите увидеть, как они построили медиану, вы можете изучить эту страницу в Math Open Reference. Вместо этого подхода мы будем использовать свойства системы координат. Обозначим координаты точки B как (b_x, b_y). Середина стороны AB находится на полпути между A и B. В горизонтальном направлении x это \frac{0 + b_x}{2} = \frac{b_x}{2}. В вертикальном направлении Y средняя точка будет находиться в точке \frac{0 + b_y}{2} = \frac{b_y}{2}. Точно так же, если координаты точки C равны (c_x, c_y). середина стороны AC равна \left( \frac{c_x}{2}, \frac{c_y}{2} \right) . Середина стороны BC равна \left( \frac{b_x + c_x}{2} , \frac{b_y + c_y}{2} \right) . В GeoGebra мы будем называть эти точки midAB, midAC и midBC соответственно. Трехцветный перекрестокИнтересно, что лиловая, зеленая и черная срединные линии пересекаются в одной и той же точке. Это правда, или они просто рядом? Пройдемся по математике и покажем, не обманывают нас глаза, что все три медианы соединены. На плоскости любые две непараллельные прямые имеют точку пересечения. Нам нужно найти уравнения для срединных линий, а затем найти пересечение. Чтобы найти уравнения линии, мы найдем наклон линии. На основании двух точек (x_1, y_1), (x_2, y_2) наклон m равен изменению y, деленному на изменение x, m = \frac{y_2 — y_1}{x_2 — x_1}. (Есть особый случай, который мы не можем игнорировать. Если линия вертикальная, две координаты x будут одинаковыми, и мы попытаемся разделить на ноль. Поскольку это бесполезно, мы не забудем правильно писать вертикальные линии. y — y_1 = m (x — x_1) ~~ = \frac{y_2 — y_1}{x_2 — x_1} (x — x_1) Так как мы знаем координаты вершин и средних точек, мы подставляем, чтобы найти уравнения прямой. Немного алгебры находит следующие уравнения: \mbox{Фиолетовая медиана от C}: y = \frac{b_y — 2 c_y}{b_x — 2 c_x} (x — c_x) + c_y \mbox{Зеленая медиана от B}: y = \frac{c_y — 2 b_y}{c_x — 2 b_x} (x — b_x) + b_y \mbox{Черная медиана от A}: y = \frac{b_y + c_y}{b_x + c_x} ~ x Чтобы найти пересечение фиолетовой и зеленой медиан, поскольку они у нас есть в форме ( y = something ), мы устанавливаем y = y и находим x. \frac{b_y — 2 c_y}{b_x — 2 c_x} (x — c_x) + c_y ~~ = ~~ \frac{c_y — 2 b_y}{c_x — 2 b_x} (x — b_x) + b_y Цель состоит в том, чтобы изолировать два термина, включающих x, с одной стороны и терминов, не включающих x, с другой стороны, а затем выполнить необходимое деление. х = \ гидроразрыва {b_x + c_x} {3} , а затем подставив это значение x обратно в любую строку, мы получим координату y y = \frac{b_y + c_y}{3} . Точка \left( \frac{b_x + c_x}{3} , \frac{b_y + c_y}{3} \right) лежит на фиолетовом и зеленом сегментах. Он также лежит на третьей медиане? Для проверки попробуем подставить точку в уравнение для черной медианы от A. \left( \frac{b_y + c_y}{3} \right) = \frac{b_y + c_y}{b_x + c_x} ~ \left( \frac{b_x + c_x}{3} \right) \left( \frac{b_y + c_y}{3} \right) = \frac{b_y + c_y}{3} Две стороны совпадают, что означает, что точка действительно лежит на медиане из A. Поскольку мы нашли эту точку как пересечение медиан из B и C, все три медианы имеют общее пересечение. Эта точка имеет специальное название — центроид. На этом рисунке я добавил числовые метки к точкам. Волшебные две трети В предыдущей части мы видели, что в состав дробей входят числа 2 и 3. Расстояние до центроида равно одной трети квадратного корня, а большее второе расстояние равно половине квадратного корня. Отношение \frac{1/3}{1/2} = \frac{2}{3} , как и было заявлено. Я только что показал вычисления для черной медианы от A. Процедура такая же для двух других медиан, просто вычисления немного длиннее. Для экспериментов с манипуляциями я предлагаю перейти на страницу centroid.html для апплета GeoGebra. Вы можете щелкнуть и переместить все три вершины треугольника — A, B и C. Математическая задача: Длины медиан от координатИмеется треугольник ABC: A[-6.6; 1,2], Б [3,4; -5,6], С [2,8; 4.2]. Вычислите длины его медиан. Правильный ответ:T 1 = 9,8843T 2 = 9,8478 T 3 = 7,766699696666.1916669.1796669.179669.1916669.191669.1916669.1916669.1916669.1916669.1916669. 9. 9. 9.8. =(−6.6,1.2) B=(3.4,−5.6)=(3.4,−5.6) C=(2.8,4.2)=(2.8,4.2) Tx=3Ax+Bx+Cx=3( −6,6)+3,4+2,8=−152≐−0,1333Ty=3Ay+By+Cy=31,2+(−5,6)+4,2=−151≐−0,0667 TXAT=2:1 t1=∣AT∣+∣TX∣ AT=(Tx−Ax)2+(Ty−Ay)2 =((−0,1333)−(−6,6))2+((−0,0667)−1,2)2 ≐6,5896 t1=23⋅ AT=23⋅ 6,5896=9,8843 BT=( Tx−Bx)2+(Ty−By)2 =((−0,1333)−3,4)2+((−0,0667)−(−5,6))2 ≐6,5652 t2= 23⋅ BT=23⋅ 6,5652=9,8478 CT=(Tx–Cx)2+(Ty–Cy)2 =((−0,1333)−2,8)2+((−0,0667 )−4,2)2 ≐5,1777 t3=23⋅ CT=23⋅ 5,1777=7,7666 Попробуйте рассчитать с помощью нашего калькулятора треугольников. Нашли ошибку или неточность? Не стесняйтесь напишите нам. Благодарю вас! Советы по использованию связанных онлайн-калькуляторов Нужна помощь в вычислении среднего арифметического? You need to know the following knowledge to solve this word math problem:Grade of the word problem:Предлагаем вам посмотреть обучающее видео по этой математической задаче: видео1 видео2 видео3 |

 НАЙТИ: 1) длину стороны АВ; 2…
НАЙТИ: 1) длину стороны АВ; 2… 02.17
02.17


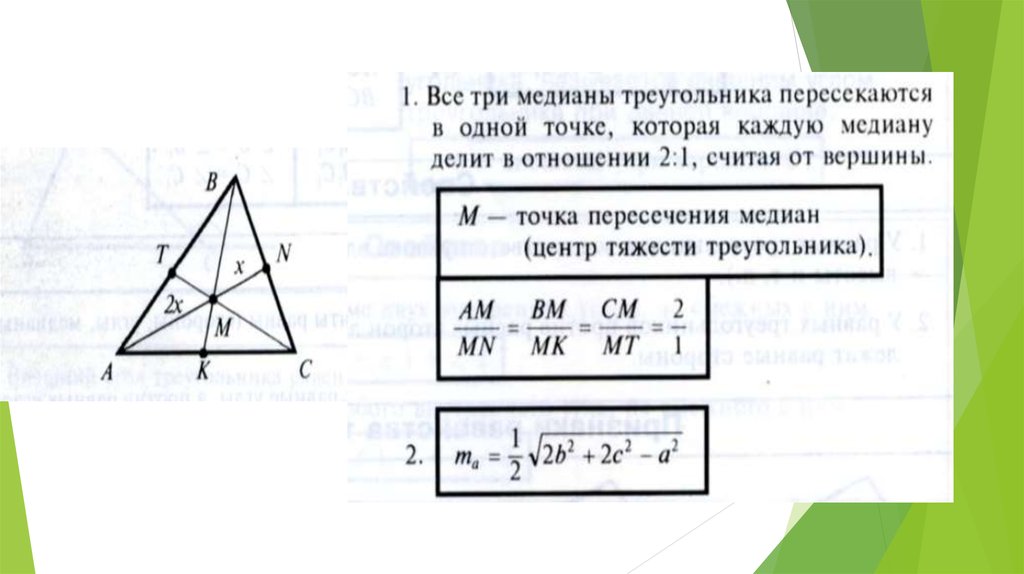
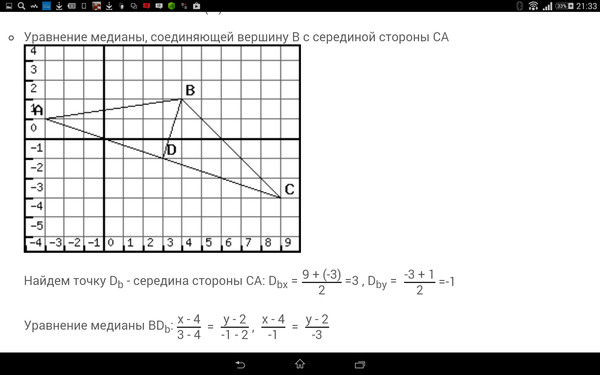 92}\]
92}\]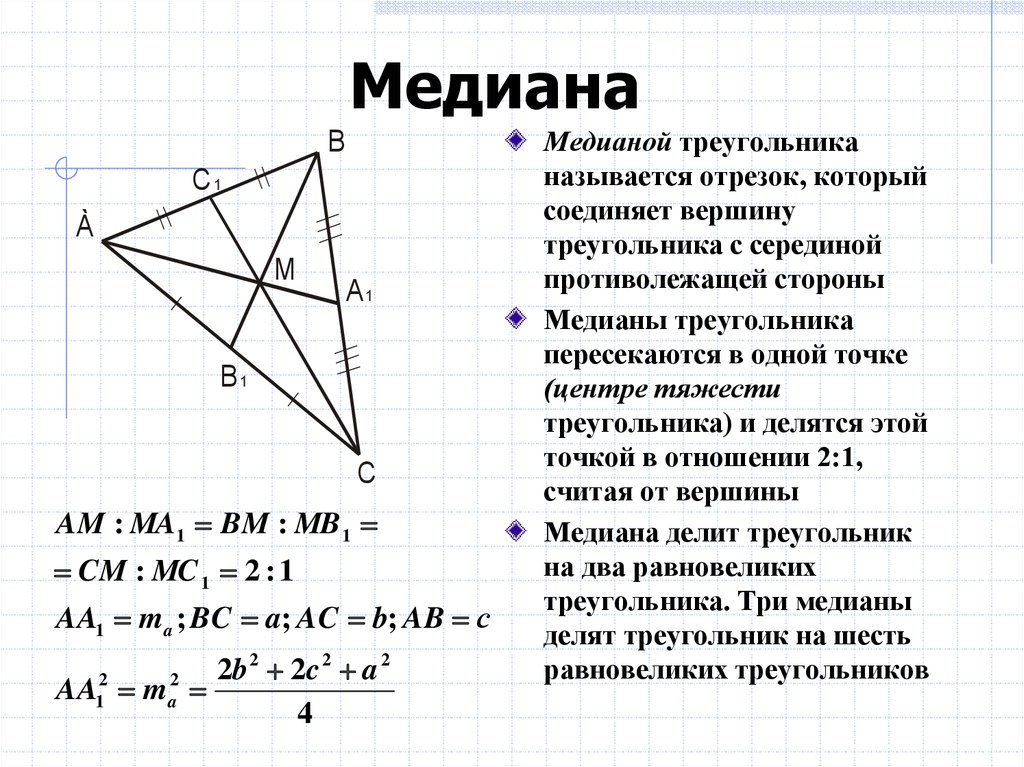 5, 1.5)\end{выравнивание} 92} \\&=\sqrt{12.5} \\&=3.53\end{align}
5, 1.5)\end{выравнивание} 92} \\&=\sqrt{12.5} \\&=3.53\end{align} Это исследование начинает наш переход к геометрии, основанной на фигурах, хотя мы сохраним некоторые алгебраические шаги. Он предназначен для учащихся начальных классов средней школы, таких как Джорджия Математика 1 или начальная геометрия.
Это исследование начинает наш переход к геометрии, основанной на фигурах, хотя мы сохраним некоторые алгебраические шаги. Он предназначен для учащихся начальных классов средней школы, таких как Джорджия Математика 1 или начальная геометрия. Книга I, определение 19 называет это трехугольником по количеству сторон. На современном языке мы называем это треугольником, потому что фигура имеет три внутренних угла. На рисунке ниже показаны некоторые распространенные типы треугольников. В частности, нам нужно помнить, что некоторые треугольники тупоугольные, у которых один угол больше прямого. Иногда они выглядят не так аккуратно, как нетупые остроугольные треугольники (не только потому, что я покрасил этот треугольник в коричневый цвет).
Книга I, определение 19 называет это трехугольником по количеству сторон. На современном языке мы называем это треугольником, потому что фигура имеет три внутренних угла. На рисунке ниже показаны некоторые распространенные типы треугольников. В частности, нам нужно помнить, что некоторые треугольники тупоугольные, у которых один угол больше прямого. Иногда они выглядят не так аккуратно, как нетупые остроугольные треугольники (не только потому, что я покрасил этот треугольник в коричневый цвет).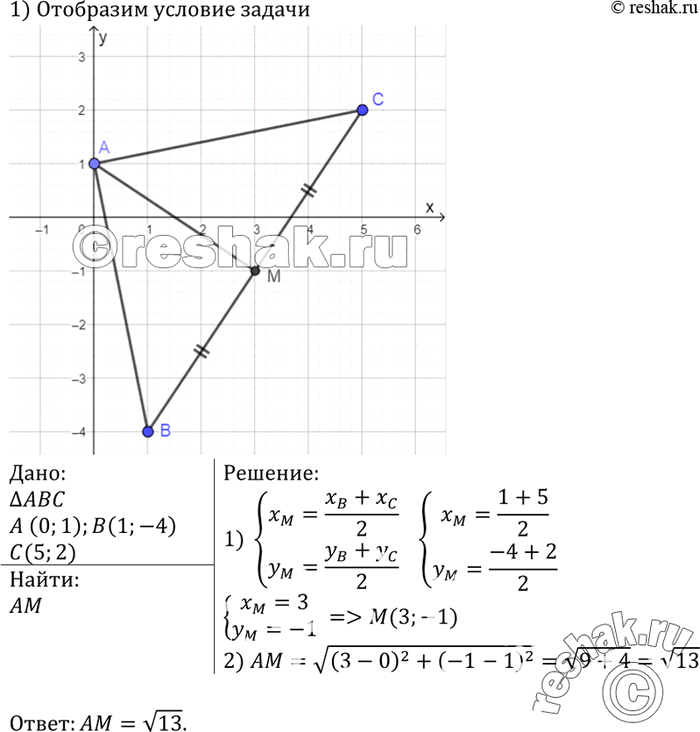 Чтобы упростить задачу, я зафиксирую точку A в начале координат (0, 0). Мы можем составить любой треугольник, перемещая B и C.
Чтобы упростить задачу, я зафиксирую точку A в начале координат (0, 0). Мы можем составить любой треугольник, перемещая B и C.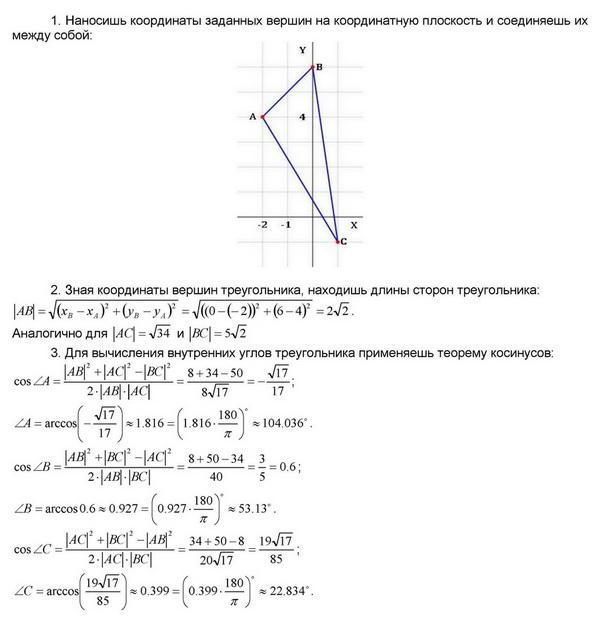 Медианы соединяют эти средние точки с противоположной вершиной, например, от середины АВ до С. На рисунке каждая медиана показана своим цветом — фиолетовым, зеленым и черным.
Медианы соединяют эти средние точки с противоположной вершиной, например, от середины АВ до С. На рисунке каждая медиана показана своим цветом — фиолетовым, зеленым и черным.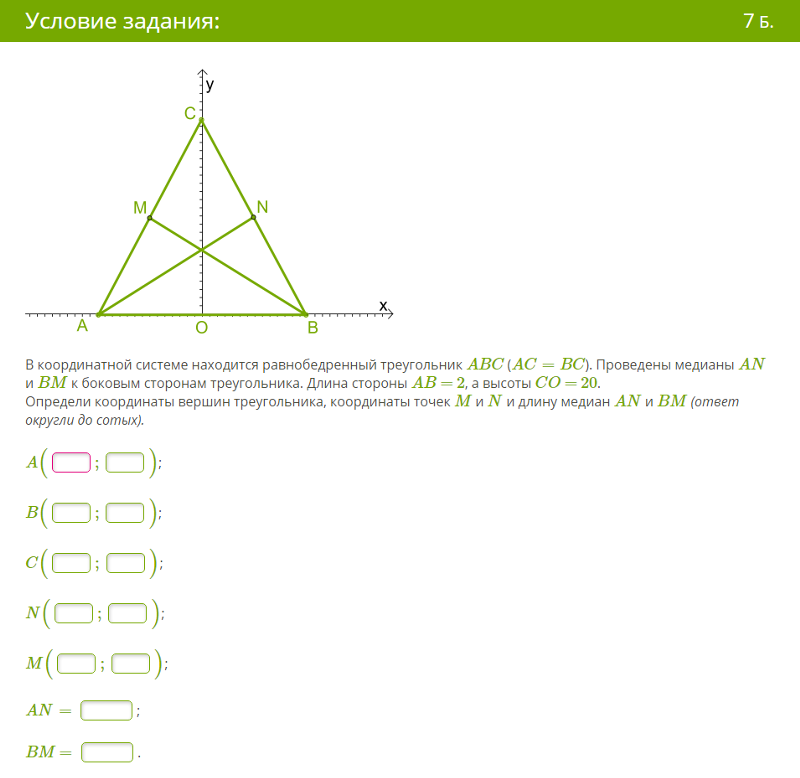 как x = x_1 = x_2, если необходимо.) Учитывая наклон, мы можем указать линию, используя точку и наклон.
как x = x_1 = x_2, если необходимо.) Учитывая наклон, мы можем указать линию, используя точку и наклон. Есть несколько алгебраических шагов, но в итоге мы приходим к результату
Есть несколько алгебраических шагов, но в итоге мы приходим к результату Оказывается, центр тяжести имеет особое положение. Он не только пересекает все три медианы, но и проходит две трети пути от вершины до середины. Например, расстояние от А до центроида в два раза больше расстояния от центроида до середины ВС. Есть несколько способов продемонстрировать это. Невероятная Академия Хана предоставляет Youtube видео двух подходов. Можно использовать подобные треугольники или применить трехмерное расстояние. Чтобы показать что-то другое, я собираюсь применить формулу расстояния в двух измерениях. 9{2} }
Оказывается, центр тяжести имеет особое положение. Он не только пересекает все три медианы, но и проходит две трети пути от вершины до середины. Например, расстояние от А до центроида в два раза больше расстояния от центроида до середины ВС. Есть несколько способов продемонстрировать это. Невероятная Академия Хана предоставляет Youtube видео двух подходов. Можно использовать подобные треугольники или применить трехмерное расстояние. Чтобы показать что-то другое, я собираюсь применить формулу расстояния в двух измерениях. 9{2} } Апплет автоматически обновляет средние точки, медианы и расстояния.
Апплет автоматически обновляет средние точки, медианы и расстояния.
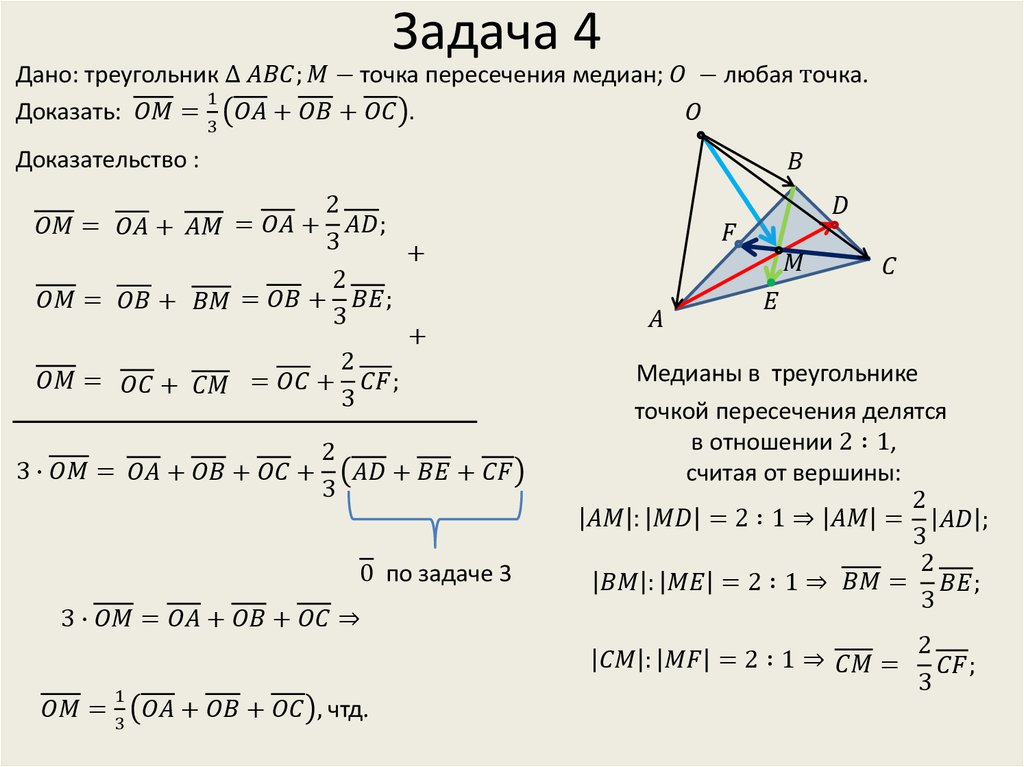 Найдите периметр треугольника АВТ (Т = центр тяжести).
Найдите периметр треугольника АВТ (Т = центр тяжести).