Что такое точка максимума и минимума функции: Найдите точку максимума и точку минимума функции y=f(x),если известно ,что f'(x)=x^2-5x+6

Содержание

4.12. Применение производной функции к нахождению точек экстремума функции

Напомним (см. § 1), что термин «точки экстремума» – это общее название точек максимума и минимума функции. А под ними, в свою очередь, понимаются абсциссы вершин и впадин графика функции (проекции вершин и впадин на ось оХ). Или, если не прибегать к геометрической трактовке, точки экстремума функции – это те значения ее аргумента X, при которых функция принимает экстремальные (пиковые) значения – максимальные или минимальные. Точек экстремума у функции столько, сколько вершин и впадин у ее графика.

Рассмотрим рис. 4.11. На нем изображен график непрерывной функции , имеющей и интервалы возрастания, и интервалы убывания, и точки экстремума:

Интервалы возрастания функции помечены знаком (+), а интервалы убывания – знаком (–). Согласно доказанной выше теореме 1, это заодно и знаки производной функции .

Точками экстремума данной функции являются точки (X1, X2, X3, X4). Причем точки

X1 и X3 – точки максимума, а X2 и X4 – точки минимума. Точки X5 и X6 точками экстремума функции не являются, так как соответствующие им точки графика М5 и М6 – не вершины и не впадины этого графика.

Точки экстремума разделяют интервалы возрастания и убывания функции. В точках максимума совершается переход от возрастания функции (слева от точки максимума) к ее убыванию (справа от точки максимума). То есть в точках максимума знак производной функции меняется с (+) слева на (–) справа. А в точках минимума, наоборот, совершается переход от убывания функции к ее возрастанию. То есть в точках минимума знак производной функции меняется с (–) слева на (+) справа.

Сами же точки экстремума не принадлежат ни к интервалам возрастания, ни к интервалам убывания функции. Потому в точках экстремума производная не может быть ни положительной, ни отрицательной. Значит, в этих точках она или равна нулю, или ее не существует вообще.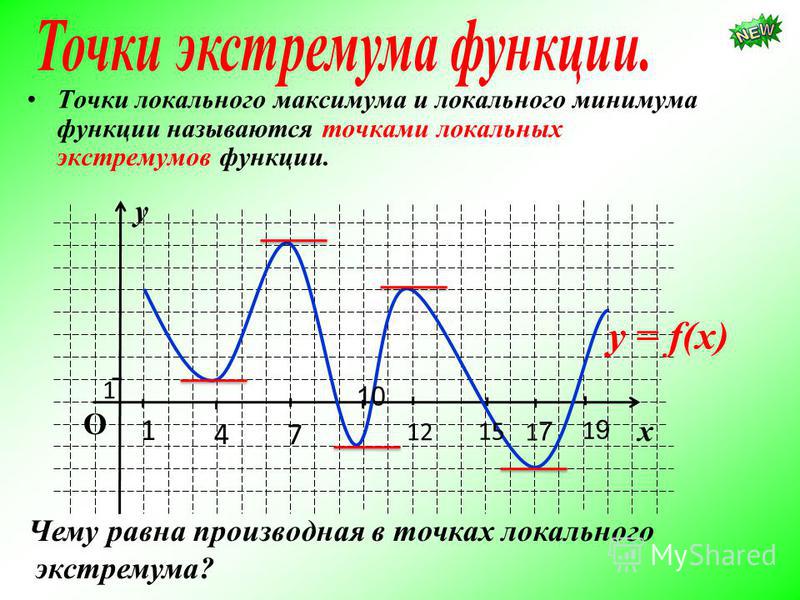

Этот вывод понятен и с геометрической точки зрения. Действительно, производная функции, согласно ее геометрического смысла (1.11) и рис. 4.5, связана с касательной к графику функции. А именно, представляет собой тангенс угла наклона этой касательной к оси Ох. Но точкам экстремума функции соответствуют на ее графике вершины и впадины, в которых касательная к графику или параллельна оси Ох (если вершина или впадина графика округлая), или эта касательная отсутствует вообще (если вершина или впадина острая). В первом случае угол наклона касательной к оси Ох равен нулю. Значит, и , а значит, и производная . Во втором случае угол не существует вообще, а значит, не существует для данной точки экстремума X и производная . В частности, для рис. 4.11 имеем:

; – не сущ.; – не сущ.; .

Однако заметим, что не любая точка X, в которой производная равна нулю или не существует, непременно будет точкой экстремума. В частности, на рис. 4.11 ; не существует, и тем не менее ни точка

X5, ни точка X6 не являются точками экстремума функции .

Все сказанное выше о точках экстремума функции можно оформить в виде теоремы.

Теорема 2. Необходимое условие экстремума.

Для того, чтобы некоторая точка X являлась точкой экстремума функции , необходимо, чтобы в этой точке производная Этой функции или равнялась нулю, или не существовала. Это условие не является достаточным.

Таким образом, лишь те точки (значения X), в которых производная функции равна нулю или не существует, могут быть точками экстремума этой функции. Но еще не факт, что все такие точки будут точками экстремума. Иначе говоря, точки (значения X), в которых или не существует, являются Лишь подозрительными на экстремум

. Чтобы выяснить суть каждой подозрительной точки, нужно посмотреть знак производной слева и справа от неё. Здесь возможны три варианта:

1) Если слева от подозрительной на экстремум точки знак производной (+), а справа (–), то эта подозрительная точка – точка максимума.

2) Если справа от подозрительной на экстремум точки знак производной (–), а справа (+), то эта подозрительная точка – точка минимума.

3) Если слева и справа от подозрительной на экстремум точки знак производной один и тот же, то эта подозрительная точка – не точка экстремума.

Сказанное наглядно иллюстрирует рис. 4.11. Таким образом, становится понятной и очевидной следующая

< Предыдущая		Следующая >

Максимум и минимум (экстремум) функции. Практикум по математическому анализу. Урок 52

Высшая математика / Практикум по математическому анализу

28.09.201728.09.2017

Значение функции в точке называется максимумом (минимумом), если оно является наибольшим (наименьшим) по сравнению с ее значениями во всех достаточно близких точках слева и справа от .
Функция может иметь экстремум (максимум или минимум) только в тех точках, которые лежат внутри области определения функции и где ее производная равна нулю или не существует.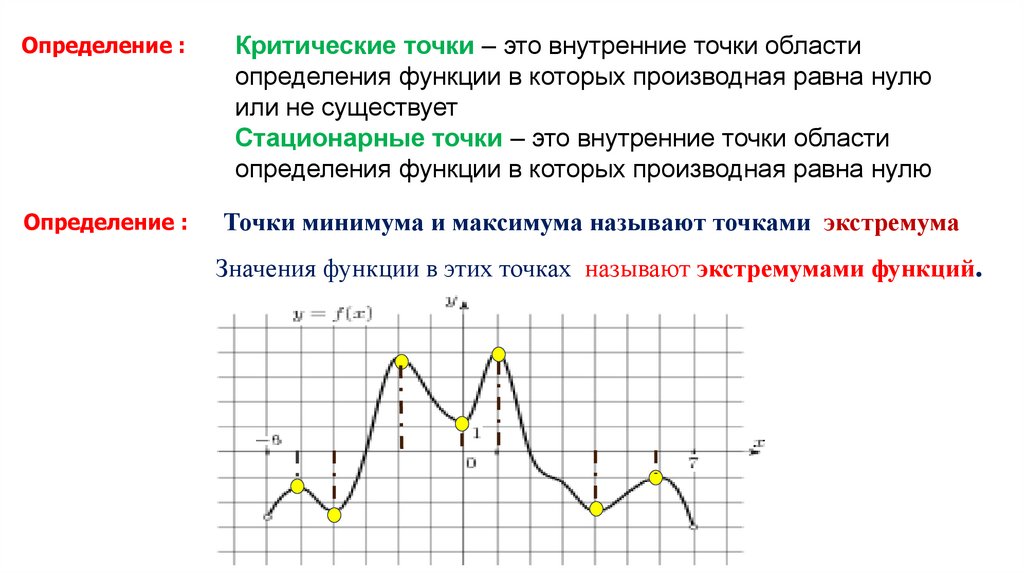 (Это необходимые условия экстремума, но недостаточные; они могут выполняться и в точках, где нет экстремума, например в точках

рис. 44.) Такие точки называются критическими. В соответствующих точках графика функции касательная параллельна оси абсцисс (), или оси ординат () или нет определенной касательной (например, как в угловой точке).

На графике функции (рис. 44) отчетливо видно, что точками экстремума являются все точки, где функция меняет свое направление и непрерывна.
Точки и , при переходе через которые аргумента возрастание функции сменяется на убывание, являются точками максимума, а точки и при переходе через которые аргумента убывание функции сменяется на возрастание, являются точками минимума.
Поскольку поведение функции характеризуется знаком ее производной, то функция будет иметь экстремум в тех точках, где ее производная меняет свой знак, а сама функция непрерывна. Это достаточные условия экстремума (если они выполнены в какой-либо точке, то она обязательно будет точкой экстремума).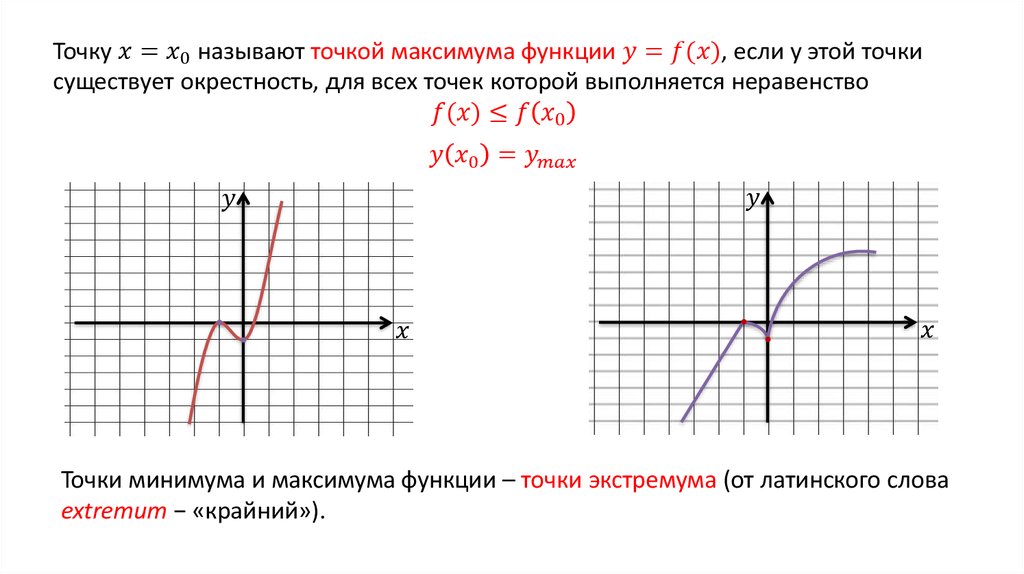
Отсюда вытекает следующее правило исследования функции на экстремум.
Чтобы найти точки экстремума функции , в которых она непрерывна, нужно:
I. Найти производную и критические точки, в которых или не существует, а сама функция непрерывна, и которые лежат внутри области определения функции.
IIа. Определить знак слева и справа от каждой критической точки.
Если при переходе аргумента через критическую точку :
1) меняет знак с + на —, то есть точка максимума;
2) меняет знак с — на +, то есть точка минимума;
3) не меняет знака, то в точке нет экстремума.
Иногда проще исследовать критические точки, где , по знаку второй производной,— вместо правила IIа можно пользоваться следующим правилом:
IIб. Найти вторую производную и определить ее знак в каждой критической точке.
Если в критической точке , где :
1) 0″ />, то есть точка минимума;
2) , то есть точка максимума;
3) , то вопрос о наличии экстремума в точке остается открытым. Такую критическую точку, как и всякую другую, можно исследовать по правилу IIа.
Далее следует найти экстремумы функции, т. е. вычислить значения функции в найденных точках экстремума.
При исследовании на экстремум некоторых типов функций возможны существенные упрощения. Например, если функция представляет дробь с постоянным числителем или корень с целым положительным показателем.
Характер упрощений, возможных при исследовании на экстремум указанных функций, разъясняется в решении задачи №2.

Тегидостаточные условия экстремумакритические точкикритические точки функциимаксимум функцииминимум функциинайдите минимум функции yнайдите точку максимума функциинайдите точку минимума функциинайдите экстремумы функции f xнайти экстремумы функции fсхема исследования функцииточек экстремума функции f xточка максимума функцииточка максимума функции yточка минимума функцииточки экстремума функцииэкстремум функцииэкстремумы графика функцииэкстремумы функции онлайн

Страница не найдена — Фонд Наффилда

Страница, которую вы ищете, не может быть найдена.

Пожалуйста, попробуйте использовать либо главное меню, либо поиск по сайту.

Поиск проектов, новостей, воздействия, событий

Поиск

Образование 654 Когнитивные и некогнитивные навыки 33Curriculum и субъекта. образование и навыки 95primary Education 134Q-шаг 26School Эффективность 45 Сторонного образования 156 Специальные потребности в образовании и инвалидность 56 ВОПРОСЫ ОБРАЗОВАНИЯ. интеллект 3Вспомогательная смерть 1Дополненная реальность 0Преимущества 52Обязанности по уходу 27Сообщества и социальная сплоченность 63Стоимость жизни 21Страна рождения 24COVID-19327Прогнозирование преступности 2Данные для общественного блага 29Цифровой вред и дезинформация 33Цифровая интеграция и исключение 14Цифровые навыки 16Цифровое общество 48Инвалидность 14Экономика, государственные расходы и услуги 182Этническая принадлежность 48Семья и семейная динамика 117Гендер 43Глобальное неравенство в отношении здоровья и нуждающиеся дети 74Психическое здоровье 92Заболевания опорно-двигательного аппарата 18Пенсии 16Физическое здоровье 50Бедность и уровень жизни 109Productivity and innovation 7Public health 150Social media 2Socioeconomics of ageing 25Socioeconomics of early adulthood 42Sports science 1Substance misuse 11Tax 48Trust in democracy 65Valuing data 5

ProjectsNewsEventsImpactOpinionPublicationsSeriesReportsEducation 654Cognitive and non-cognitive skills 33Curriculum and subject choice 31Early years 166Education workforce 75Educational assessment 29Higher education 92Language and literacy 79Lifelong обучение 15Nuffield Research Placement 23Числа 84Воспитание детей 75Педагогика 20Образование и навыки после 16 лет 95primary Education 134Q-шаг 26School Эффективность 45 Сторонного образования 156 Специальные потребности в образовании и инвалидность 56 ВОПРОСЫ ОБРАЗОВАНИЯ.

интеллект 3Вспомогательная смерть 1Дополненная реальность 0Преимущества 52Обязанности по уходу 27Сообщества и социальная сплоченность 63Стоимость жизни 21Страна рождения 24COVID-19327Прогнозирование преступности 2Данные для общественного блага 29Цифровой вред и дезинформация 33Цифровая интеграция и исключение 14Цифровые навыки 16Цифровое общество 48Инвалидность 14Экономика, государственные расходы и услуги 182Этническая принадлежность 48Семья и семейная динамика 117Гендер 43Глобальное неравенство в отношении здоровья и нуждающиеся дети 74Психическое здоровье 92Заболевания опорно-двигательного аппарата 18Пенсии 16Физическое здоровье 50Бедность и уровень жизни 109Производительность и инновации 7Общественное здравоохранение 150Социальные сети 2Социоэкономика старения 25Социоэкономика раннего взросления 42Спортивная наука 1Злоупотребление психоактивными веществами 11Налоги 48Доверие к демократии 65Оценка данных 5

Ознакомьтесь с нашими проектами

Новый

Образование | 2023 – 2025

Посмотреть проект

Сообщено

Образование | 2014 – 2015

The Nuffield Languages Inquiry and Nuffield Languages Program

Посмотреть проект

Увидеть все

Последние

2.

5: Максимумы и минимумы — Mathematics LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 2254

Майкл Коррал
Колледж Скулкрафт

С помощью градиента можно найти крайних точек вещественных функций нескольких переменных, то есть точек, где функция имеет локальных максимумов или локальных минимумов . Мы будем рассматривать только функции двух переменных; функции трех или более переменных требуют методов, использующих линейную алгебру. 92\).

Аналогично, мы говорим, что \(f\) имеет локальных минимумов в точках \((a,b)\text{, если }f (x, y) \gt f (a,b)\text{ для всех }(x, y)\) внутри некоторого круга положительного радиуса с центром в \((a,b)\).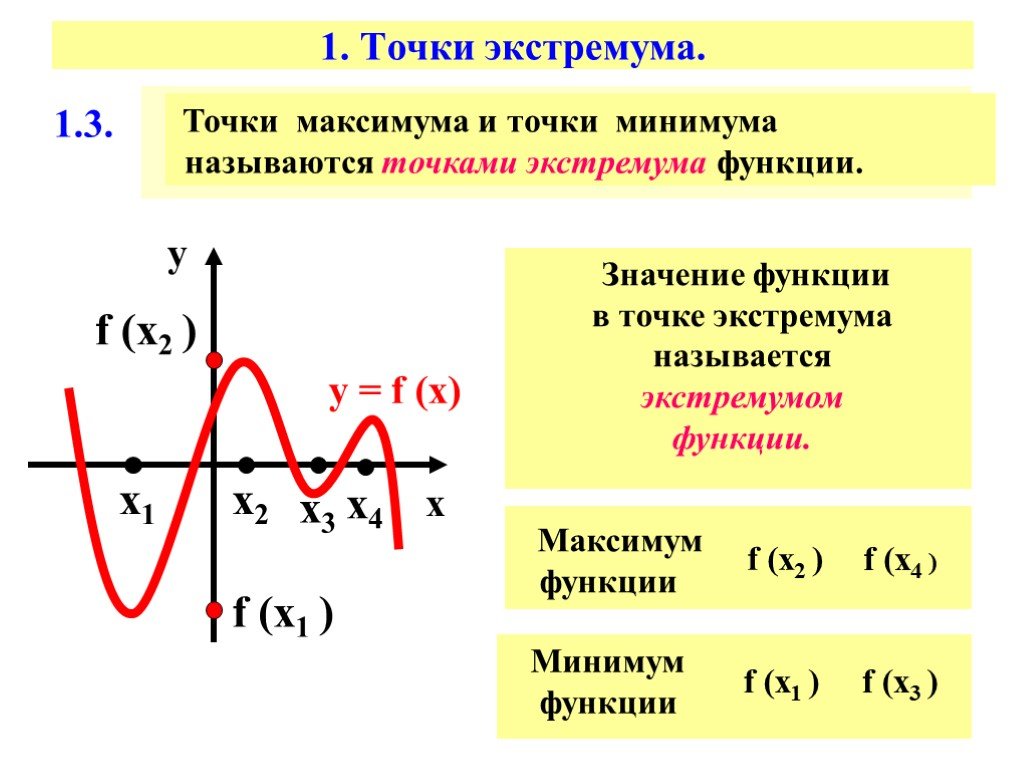

Если \(f (x, y) \le f (a,b)\text{ для всех }(x, y)\) в области определения \(f\), то \(f\) имеет глобальный максимум в \((a,b)\). Если \(f (x, y) \ge f (a,b)\text{ для всех }(x, y)\text{ в области определения }f \text{, то }f\) имеет глобальных минимум в \((a,b)\).

Предположим, что \((a,b)\) является точкой локального максимума для \(f (x, y)\) и что частные производные первого порядка от \(f\) существуют в точке \((a, б)\). Мы знаем, что \(f (a,b)\) является наибольшим значением \(f (x, y)\text{, поскольку }(x, y)\) идет во всех направлениях от точки \((a, б)\) в некотором достаточно малом круге с центром в \((а,Ь)\). В частности, \(f (a,b)\) есть наибольшее значение \(f\) в направлении \(x\) (вокруг точки \((a,b)\)), т.е. функция одной переменной \(g(x) = f (x,b)\) имеет локальный максимум в точке \(x = a\). Итак, мы знаем, что \(g ′ (a) = 0\). Поскольку \(g ′ (x) = \dfrac{∂f}{∂x} (x,b)\text{, то }\dfrac{∂f}{∂x} (a,b) = 0\). Точно так же \(f (a,b)\) является наибольшим значением \(f\) вблизи \((a,b)\) в направлении \(y\), поэтому \(\dfrac{∂f} {∂y} (a,b) = 0\). Таким образом, мы имеем следующую теорему:

Теорема 2.5

Пусть \(f (x, y)\) — вещественнозначная функция такая, что \(\dfrac{∂f}{∂x} (a,b)\) и \(\dfrac{ ∂f}{∂y} (a,b)\) существуют. Тогда необходимое условие для \(f (x, y)\) иметь локальный максимум или минимум в \((a,b)\) состоит в том, что \(\nabla f (a,b) = \textbf{0} \).

Примечание. Теорему 2.5 можно распространить на функции трех и более переменных.

Точка \((a,b)\), где \(\nabla f (a,b) = \textbf{0}\), называется критической точкой для функции \(f (x, y)\ ). Итак, учитывая функцию \(f (x, y)\), чтобы найти критические точки \(f\), вы должны решить уравнения \(\dfrac{∂f}{∂x} (x, y) = 0\text{ и }\dfrac{∂f}{∂y} (x, y) = 0\) одновременно для \((x, y)\). Как и в случае с одной переменной, необходимое условие, что \(\nabla f (a,b) = \textbf{0}\) не всегда достаточно, чтобы гарантировать, что критическая точка является локальным максимумом или минимумом.

Пример 2. 2\), имеющую локальный максимум в точке \((0,0) \). Таким образом, \((0,0)\) является примером седловая точка , т.е. это локальный максимум в одном направлении и локальный минимум в другом направлении. График \(f (x, y)\) показан на рис. 2.5.1 и представляет собой гиперболический параболоид.

Рисунок 2.5.1 \(f (x, y) = x y\), седловая точка (0,0)
Следующая теорема дает достаточные условия для того, чтобы критическая точка была локальным максимумом или минимумом гладкой функции (т. е. функции, частные производные всех порядков которой существуют и непрерывны), которые мы не будем здесь доказывать. 92−3x\).
Решение
Сначала найдите критические точки, т.е. где \(\nabla f = \textbf{0}\). Поскольку
\[\nonumber \dfrac{∂f}{∂x} = 2x+ y−3 \text{ и }\dfrac{∂f}{∂y} = x+2y\]
, то критические точки \ ((x, y)\) являются общими решениями уравнений
\[\nonumber \begin{align} 2x+ y−3 &= 0 \\[4pt] \nonumber x +2y &= 0 \end{align }\]
, имеющее единственное решение \((x, y) = (2,−1)\).
No related posts.

4.12. Применение производной функции к нахождению точек экстремума функции

Максимум и минимум (экстремум) функции. Практикум по математическому анализу. Урок 52

Страница не найдена — Фонд Наффилда

Поиск проектов, новостей, воздействия, событий

Ознакомьтесь с нашими проектами

Целенаправленная и эффективная практическая работа по естествознанию начальных классов

Широкие плечи: повышение налогов в топ-

Подтверждение аутсорсинга оказания социальной помощи в Англии

Оптимизация и осуществимость родительской программы Triple P для дистанционного обучения

Продление трудовой жизни людям с заболеваниями опорно-двигательного аппарата

Ювенильные ревматические заболевания: образование, профессиональная подготовка и трудоустройство

Создание и использование более качественных данных о правосудии

Испытание PAW: осуществимость и приемлемость инструментария Pain-at-Work Toolkit

Приоритеты образования на следующих всеобщих выборах

Кризис стоимости жизни: влияние на школы

Широкие плечи: повышение налогов наверху

Приоритеты образования на следующих всеобщих выборах

Физические наказания и последствия для детей в Великобритании

Оптимизация и осуществимость родительской программы Triple P для дистанционного обучения

Понимание использования прав на дошкольное образование

Переосмысление особых образовательных потребностей

Артрит, работа и благополучие: исследование смешанных методов с рекомендациями по политике

Испытание PAW: осуществимость и приемлемость инструментария Pain-at-Work Toolkit

Региональный индекс регенерации для отслеживания социально-экономического «повышения уровня»

Пути развития после 16 лет: роль сверстников, семейное положение и ожидания

Разработка инклюзивной удаленной и гибридной работы для поддержки работников с ограниченными возможностями

Влияние выявления потребностей в дополнительном обучении в Уэльсе

Изучение расового неравенства при отвлечении от системы ювенальной юстиции

Административная справедливость в цифровом государстве всеобщего благосостояния

Прозрачность и судебный контроль: исследование долга откровенности

Влияние автоматического зачисления на пенсию и COVID-19 на сберегательное поведение

Долгосрочное влияние пособия на содержание образования

Дистанционное наставничество по остеоартриту для малообеспеченных людей

Ювенильные ревматические заболевания: образование, профессиональная подготовка и трудоустройство

Продление трудовой жизни людям с заболеваниями опорно-двигательного аппарата

Изменение выбора школы для более справедливого обучения в Англии

Среднесрочное влияние пандемии COVID-19 на учащихся с SEND

Этические принципы, лежащие в основе совместного производства с молодежью

Могут ли математические приложения повысить ценность обучения?

Реалии COVID: малообеспеченные семьи в период пандемии

Как население Великобритании получает информацию о COVID-19

Влияние заболеваний опорно-двигательного аппарата на исходы других заболеваний

Систематический обзор учебных степеней и путей трудоустройства

Измерение разрыва в уровнях образования в 16-19 лет

«Неуправляемые» школы: может ли решение Ofsted помешать устойчивому улучшению?

The Nuffield Languages ​​Inquiry and Nuffield Languages ​​Program

2.

Добавить комментарий Отменить ответ

The Nuffield Languages Inquiry and Nuffield Languages Program