Президентский фонд культурных инициатив
Сергей Владиленович
Кириенко
Первый заместитель Руководителя Администрации Президента Российской Федерации
(председатель Координационного комитета)
Татьяна Алексеевна
Голикова
Заместитель Председателя Правительства Российской Федерации (заместитель
председателя Координационного комитета)
Сергей Геннадьевич
Новиков
Начальник Управления Президента Российской Федерации по общественным проектам
(ответственный секретарь Координационного комитета)
Дмитрий Игоревич
Азаров
Губернатор Самарской области, председатель комиссии Государственного Совета
Российской Федерации по направлению «Культура»
Ирада Хафизяновна
Аюпова
Министр культуры Республики Татарстан
Светлана Евгеньевна
Баланова
Генеральный директор акционерного общества «Национальная Медиа Группа»
Александр Сергеевич
Галушка
Заместитель секретаря Общественной палаты Российской Федерации, председатель
Координационного совета при Общественной
палате Российской Федерации по национальным проектам и народосбережению
Алексей Сергеевич
Гореславский
Генеральный директор автономной некоммерческой
организации «Институт развития интернета»
Лилия Салаватовна
Гумерова
Председатель Комитета Совета Федерации Федерального Собрания Российской Федерации
по науке, образованию и культуре
Олег Борисович
Добродеев
Генеральный директор Всероссийской государственной телевизионной
и радиовещательной компании (ВГТРК)
Александр Александрович
Жаров
Генеральный директор акционерного общества «Газпром-Медиа Холдинг»
Александр Владимирович
Журавский
Заместитель начальника Управления Президента Российской Федерации
по общественным проектам
Алексей Геннадиевич
Комиссаров
Генеральный директор автономной некоммерческой организации «Россия – страна
возможностей», исполняющий обязанности ректора Российской академии народного хозяйства и государственной службы (РАНХиГС)
Ольга Борисовна
Любимова
Министр культуры Российской Федерации
Денис Владимирович
Молчанов
Директор Департамента культуры, спорта, туризма и национальной политики
Аппарата Правительства Российской Федерации
Борис Михайлович
Пиотровский
Вице-губернатор Санкт-Петербурга
Наталья Алексеевна
Сергунина
Заместитель Мэра Москвы в Правительстве Москвы – руководитель Аппарата
Мэра и Правительства Москвы
Тихон (Георгий
Александрович Шевкунов)
Митрополит Псковский и Порховский, председатель Патриаршего совета
по культуре
Владимир Ильич
Толстой
Советник Президента Российской Федерации
Бэлла Мухарбиевна
Черкесова
Заместитель Министра цифрового развития, связи и массовых коммуникаций
Российской Федерации
Илья Владимирович
Чукалин
Генеральный директор Фонда президентских грантов
Михаил Ефимович
Швыдкой
Специальный представитель Президента Российской Федерации по международному
культурному сотрудничеству
Константин Львович
Эрнст
Генеральный директор акционерного общества «Первый канал»
Елена Александровна
Ямпольская
Председатель Комитета Государственной Думы Федерального Собрания Российской
Федерации по культуре
Максим Алексеевич
Древаль
Генеральный директор общероссийской
общественно-государственной просветительской
организации «Российское общество “Знание”»
Степан Кириллович
Ковальчук
Старший вице-президент по медиастратегии
и развитию сервисов ООО «Компания ВК»
Константин Ильич
Могилевский
Заместитель Министра науки и высшего
образования Российской Федерации
Ксения Денисовна
Разуваева
Руководитель Росмолодежи
Официальная информация о коронавирусе в России на портале – стопкоронавирус.
рф
window.yaContextCb.push(()=>{
Ya.adfoxCode.createAdaptive({
ownerId: 699232,
containerId: ‘adfox_16594540782315496’,
params: {
pp: ‘g’,
ps: ‘fxsi’,
p2: ‘htzo’
}
}, [‘desktop’, ‘tablet’], {
tabletWidth: 1023,
phoneWidth: 767,
isAutoReloads: false
})
})
window.yaContextCb.push(()=>{
Ya.adfoxCode.createAdaptive({
ownerId: 699232,
containerId: ‘adfox_165945411636098147’,
params: {
pp: ‘g’,
ps: ‘fxsi’,
p2: ‘htzq’
}
}, [‘phone’], {
tabletWidth: 1023,
phoneWidth: 767,
isAutoReloads: false
})
})
Новости
09 мая, 11:00 • СТОПКОРОНАВИРУС.
РФВ России за сутки от коронавируса выздоровело 3 152 человека
08 мая, 13:08 • ТАСС
Япония перевела ковид в категорию сезонного гриппа
08 мая, 11:00 • СТОПКОРОНАВИРУС.РФ
В России за сутки от коронавируса выздоровело 3 656 человек
07 мая, 11:00 • СТОПКОРОНАВИРУС.РФ
В России за сутки от коронавируса выздоровело 4 749 человек
- 06 мая, 18:17 • ТАСС
В ВОЗ назвали полную ликвидацию SARS-CoV-2 маловероятной
РФСмотреть все новости
window.yaContextCb.push(()=>{ Ya.
adfoxCode.createAdaptive({
ownerId: 699232,
containerId: ‘adfox_165945424881161083’,
params: {
pp: ‘h’,
ps: ‘fxsi’,
p2: ‘htzo’
}
}, [‘desktop’, ‘tablet’], {
tabletWidth: 1023,
phoneWidth: 767,
isAutoReloads: false
})
})
window.yaContextCb.push(()=>{
Ya.adfoxCode.createAdaptive({
ownerId: 699232,
containerId: ‘adfox_165945416122152949’,
params: {
pp: ‘h’,
ps: ‘fxsi’,
p2: ‘htzq’
}
}, [‘phone’], {
tabletWidth: 1023,
phoneWidth: 767,
isAutoReloads: false
})
})
Узнай больше про коронавирус
COVID–19Психолог Наталья Курдюкова.
Об организации удаленной работы в пандемиюПсихолог Светлана Штукарева. Как побороть чувство тревоги во время пандемии
Психолог Екатерина Приходько. Как поддержать пожилых людей в пандемию
Психолог Константин Лемешко. Как врачи справляются с пандемией
Психолог Татьяна Попова. Как грамотно рассказать ребёнку про пандемию
Вакцинация от коронавируса: ситуация в России и в мире
Гериатр Ольга Ткачёва о вакцинации старшего поколения
Судмедэксперт Алексей Решетун о влиянии COVID-19 на организм
Онколог Игорь Самойленко о вакцинации онкопациентов
Что сделано?
Меры поддержки малых и средних предприятий
ПодробнееЧто предпринять?
Советы психологов
ПодробнееЧто предпринять?
Хочешь помочь?
ПодробнееМировая статистика
Университет Джонса Хопкинса
Карта распространения коронавируса в России и мире на Яндекс.
Картах
- силовая серия
- расширение Тейлора
$\endgroup$
1
$\begingroup$
Я понимаю, что это старая ветка, но я хотел бы расширить приведенные выше ответы о том, как вывести формулу для всех, кто может встретиться. Начав с геометрического ряда и взяв последовательные производные: 9м. \end{выравнивание*}
$\endgroup$
$\begingroup$
Я написал этот ответ, чтобы уменьшить чувство неуверенности в отношении расширения.
$\endgroup$
1
Формулы биномиального разложения — вывод, примеры
Прежде чем изучать формулы биномиального разложения, давайте вспомним, что такое «биномиал».
Биномиал — это алгебраическое выражение с двумя членами. Например, a + b, x — y и т. д. являются биномами. У нас есть набор алгебраических тождеств, чтобы найти разложение, когда двучлен возводится в степени 2 и 3. Например, (a + b) 2 = а 2 + 2ab + b 2 . Но что, если показатели степени больше? Утомительно искать расширение вручную. Формула биномиального расширения упрощает этот процесс. Давайте изучим формулу биномиального расширения вместе с несколькими решенными примерами.
Что такое формулы биномиального разложения?
Как мы обсуждали в предыдущем разделе, формулы биномиального разложения используются для нахождения степеней биномов, которые нельзя разложить с помощью алгебраических тождеств. Формула биномиального расширения включает биномиальные коэффициенты, которые имеют вид \(\left(\begin{array}{l}n \\k\end{array}\right)\) (или) \(n_{C_{k} }\) и рассчитывается по формуле \(\left(\begin{array}{l}n \\k\end{array}\right)\) =n! / [(н — к)! к!].
Формула биномиального разложения также известна как биномиальная теорема. Вот формулы биномиального разложения.
Формула биномиального расширения природных сил
Эта формула биномиального расширения дает расширение (x + y) n где n – натуральное число. Расширение (x + y) n имеет (n + 1) членов. Эта формула говорит:
(x + y) n = n C\(_0\) x n y 0 + n 90 094 С\(_1\) x н — 1 y 1 + n C\(_2\) x n-2 y 2 + n C\(_3\) x n — 3 y 3 + … + n C \(_{n-1}\) x y n — 1 + n C\(_n\) x 0 y n
Здесь мы используем формулу nC\(_k\) для расчета биномиального коэффициента s, который говорит n C\ (_к\) = п! / [(н — к)! к!].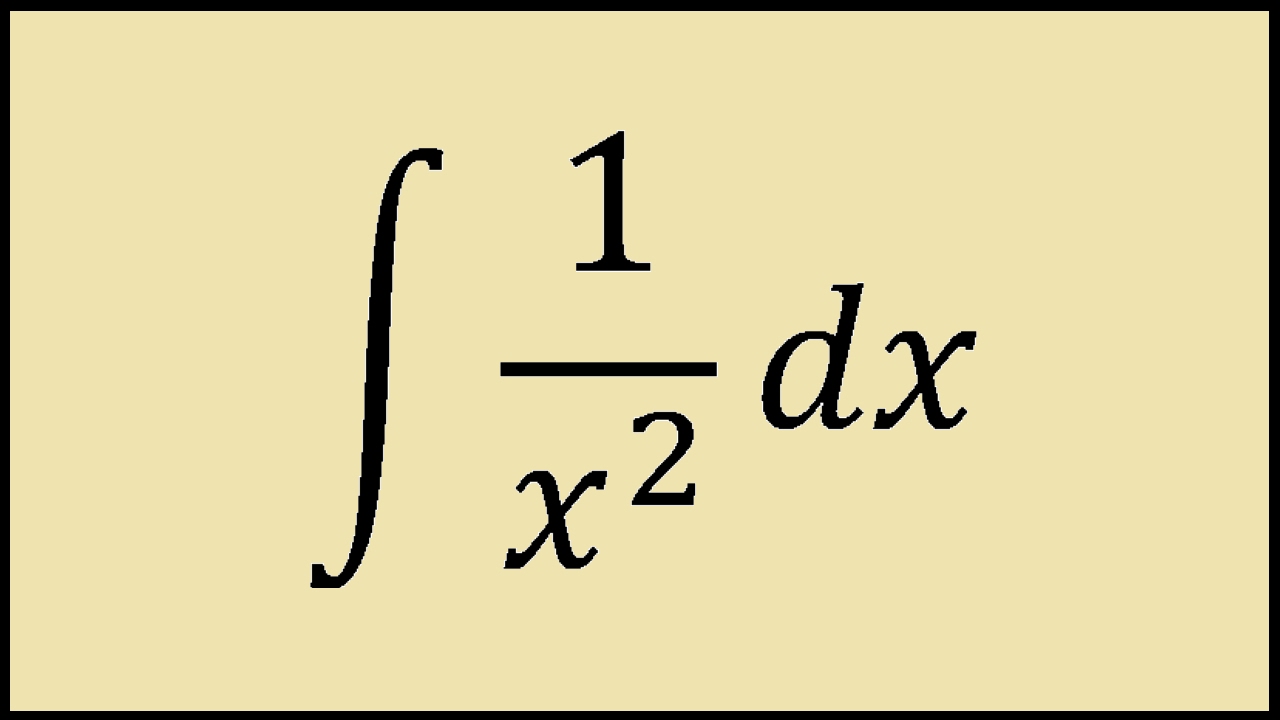
Применяя эту формулу, приведенную выше формулу биномиального расширения также можно записать как
(x + y) n = x n + n x n — 1 y 1 + [n(n — 1)/2!] x n-2 y 2 + [n(n — 1)( n — 2)/3!] x n — 3 y 3 +… + n x y n — 1 + y n
900 99 Примечание: Если мы рассмотрим только коэффициенты, они симметричны относительно среднего члена. т. е. первый коэффициент равен последнему, второй коэффициент равен второму от последнего и т. д.
Формула биномиального разложения рациональных степеней
Эта формула биномиального разложения дает разложение (1 + x) n где n – рациональное число. Это разложение имеет бесконечное число членов.
(1 + x) n = 1 + n x + [n(n — 1)/2!] x 2 + [n(n — 1)(n — 2)/3 !] x 3 +.
..
Примечание. Чтобы применить эту формулу, значение |x| должно быть меньше 1.
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.
Закажите бесплатный пробный урок
Примеры использования формул биномиального расширения
Пример 1: Найдите расширение (a + b) 3 .
Решение:
Чтобы найти: (a + b) 3
Используя формулу биномиального разложения,
(x + y) n = n C\(_0\) x n y 0 + n C\ (_1\) x n — 1 y 1 + n C\(_2\) x n-2 y 2 + n C\(_3\) x 90 093 н — 3 у 3 + .
.. + n C\(_{n-1}\) x y n — 1 + n C\(_n\) x 0 y n 9000 5
(а + б) 3 = 3 С\(_0\) а 3 + 3 С\(_1\) а (3 — 1) б + 3 90 094 С\(_2\) а (3 — 2) b 2 + 3 C\(_3\) a (3 — 3) b 3
= ( 3! / [( 3-0)!0! ] ) a 3 + ( 3! / [(3-1)!1!] ) a (3 — 1) b + ( 3! / [(3-2)!2!] ) a (3 — 2) b 2 + ( 3! / [(3-3)!3!] ) а (3 — 3) б 3
= (1) а 3 + (3) а 2 б + (3) а 1 б 2 + (1) а 0 б 3
= а 3 + 3а 2 б + 3аб 2 + б 3
900 02 Ответ: (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 .
Пример 2: Найти разложение (x + y) 6 .
Решение:
Используя формулу биномиального разложения,
(x + y) n = n C\(_0\) x 900 93 n y 0 + n C\ (_1\) x n — 1 y 1 + n C\(_2\) x n-2 y 2 9 0094 + n C\(_3\) x n — 3 y 3 + … + n C\(_{n-1}\) x y n — 1 + n C\(_n\) x 0 y n
(x + y) 6 = 6 C\(_0\) x 6 + 6 С\( _1\) x 5 y + 6 C\(_2\) x 4 y 2 + 6 C\(_3\) x 3 y 9 0093 3 + 6 С\ (_4\) x 2 y 4 + 6 C\(_5\) xy 5 + 6 C\(_6\) y 6 900 05
= ( 6! / [(6 -0)!0!] ) x 6 + ( 6! / [(6-1)!1!] ) x 5 y + ( 6! / [(6-2)!2!] ) x 4 y 2 + ( 6! / [(6-3)!3!] ) x 3 y 3 + ( 6! / [(6-4)!4!] ) x 2 y 4 + ( 6! / [(6-5)!5!] ) xy 5 + ( 6! / [(6-6)!6!] ) y 6
= x 6 + 6x 5 y + 15x 4 y 2 + 20x 3 y 3 + 15x 2 y 4 + 6x y 5 + y 6
Ответ: (x + y) 6 = x 6 + 6x 5 y + 15x 4 y 2 + 20x 3 y 3 + 15x 2 y 4 + 6x y 5 + y 6 .
Пример 3: Найдите разложение (3x + y) 1/2 до первых трех членов, используя формулу биномиального разложения рациональных показателей, где \(\left|\dfrac y {3x}\right|\ ) < 1.
Решение:
(3x + y) 1/2 = 3x (1 + y/(3x)) 1/2
Сравнивая (1 + y/(3x)) 1/2 с (1 + x) n , мы имеем x = y/ (3x) и n = 1/2.
Расширение (1 + y/(3x)) 1/2 до первых трех членов с использованием формулы биномиального разложения:
1 + n x + [n(n — 1)/2! ] x 2 = 1 + (1/2) (y / (3x)) + [(1/2) ((1/2) — 1)/2!] (y / (3x) ) 2
= 1 + у / (6x) — у 2 / (72x 2 )
Таким образом, разложение 3x (1 + y/(3x)) 1/2 до первых трех членов:
3x [ 1 + y / (6x) — y 2 / (72x 2 ) ] = 3x + y / 2 — y 2 / (24x)
Ответ: (3x + y) 1/2 = 3x + y / 2 — y 9 0093 2 / (24x).
Часто задаваемые вопросы о формулах биномиального расширения
Что такое биномиальное расширение в математике?
Биномиальное расширение заключается в расширении и записи членов, которые равны натуральному показателю суммы или разности двух членов. Для двух терминов x и y биномиальное расширение в степени n равно (x + y) n = n C\(_0\) x n y 0 + 900 93 п С\(_1\) x n — 1 y 1 + n C\(_2\) x n-2 y 2 + n 9009 4 C\(_3\) x n — 3 y 3 + … + n C\(_{n-1}\) x y n — 1 + n C\(_n\) x 0 у н . Здесь в этом разложении количество слагаемых на единицу больше, чем значение n.
Что такое формулы биномиального разложения?
Формулы биномиального расширения используются для нахождения расширения, когда бином возводится в число.
Формулы биномиального расширения:
Как вывести формулу биномиального расширения?
Формула биномиального разложения: (x + y) n = n C\(_0\) x n y 0 + n C\(_1\) x n — 1 y 1 + n C\(_2\) x n-2 y 900 93 2 + n C\(_3\ ) x n — 3 y 3 + … + n C\(_{n-1}\) x y n — 1 + 90 093 н С\(_н\) x 0 y n и его можно вывести с помощью математической индукции. Вот шаги, чтобы сделать это.
- Шаг 1: Докажите формулу для n = 1.
- Шаг 2: Предположим, что формула верна для n = k.
- Шаг 3: Докажите формулу для n = k.
Каковы применения формулы биномиального разложения?
Формула биномиального разложения в основном используется для нахождения степени бинома без многократного умножения бинома на самого себя.