Lg логарифмы: Логарифмы, log, ln, lg

Занятие «Логарифмы и их свойства. Десятичные и натуральные логарифмы»

Материал опубликовала

#ФГОС #Методические разработки #Занятие #Учитель-предметник #Среднее профессиональное образование

ЛОГАРИФМЫ И ИХ СВОЙСТВА. ДЕСЯТИЧНЫЕ И НАТУРАЛЬНЫЕ ЛОГАРИФМЫ. Преподаватель математики : Левенкова Оксана Юрьевна Чебоксарский экономико-технологический колледж

Цели и задачи урока: сформировать понятие логарифма числа, десятичного и натурального логарифма; рассмотреть основные свойства логарифмов; научить применять основное логарифмическое тождество и свойства логарифмов при нахождении значений выражений; развитие математического мышления, умение рационально работать; формирование умений и навыков применять основное логарифмическое тождество и свойства логарифмов; воспитание познавательной активности, уверенности в себе.

Логарифмы Ряд явлений природы помогает описать именно логарифмическая зависимость. Одним из наиболее наглядных примеров является логарифмическая спираль. Хищные птицы кружат над добычей по логарифмической спирали (они лучше видят, если смотрят не прямо на добычу, а чуть в сторону). В сельском хозяйстве, исследовав рождение телят, оказалось, что их вес можно вы- числять с помощью логарифмов.

Логарифмы В шишках сосны, подсолнухе семена расположены по дугам, близким к логарифмической спирали. Спирально закручиваются усики растений. Паук эпейра закручивает нити вокруг центра паутины по логарифмической спирали.

Логарифмы Раковины многих моллюсков, улиток и рога горных козлов закручены по логарифмической спирали. По логарифмической спирали закручена галактика, которой принадлежит Солнечная система. «Величина» звезды определяется как логарифм её физической яркости.

Повторение ранее изученного материала Продолжите формулы: ax ∙ay =…, ax :ay =…, (ax)y =…, a0=…, a –x =…, =… Решите устно примеры:

Логарифм числа Определение. Логарифмом положительного числа b по основанию a (a>0, a≠1) называется показатель степени, в которую нужно возвести основание a, чтобы получить число b. log3 81=4, т.к. 34 =81; log5 125=3, т.к. 53 =125; log2 16= …, т.к. 2… =16; log6 36= …, т.к. 6… =36.

Сравните:

Основное логарифмическое тождество Решить примеры согласно тождеству:

Основные свойства логарифмов При любом a > 0, a ≠ 1 и любых положительных x и y справедливы:

Десятичный и натуральный логарифмы Логарифм положительного числа b по основанию 10 называют десятичным логарифмом числа b и обозначают lg b, т.е. lg b = log10 b Натуральным логарифмом называется логарифм по основанию e (e≈2,7) и обозначается ln b = log e b

Примеры вычисления десятичных логарифмов lg 1 = 0, так как 1 = 100 lg 10 = 1 , так как 10 = 101 lg 100 = 2, так как 100 = 102 lg 0,1 = –1, так как 0,1 = 10–1 lg 0,01 = –2, так как 0,01 = 10–2 lg 0,001 = –3, так как 0,001 = 10–3

Закрепление изученного № 267 (устно), 268–271, 273, 274 (устно), 275–276, 290–294.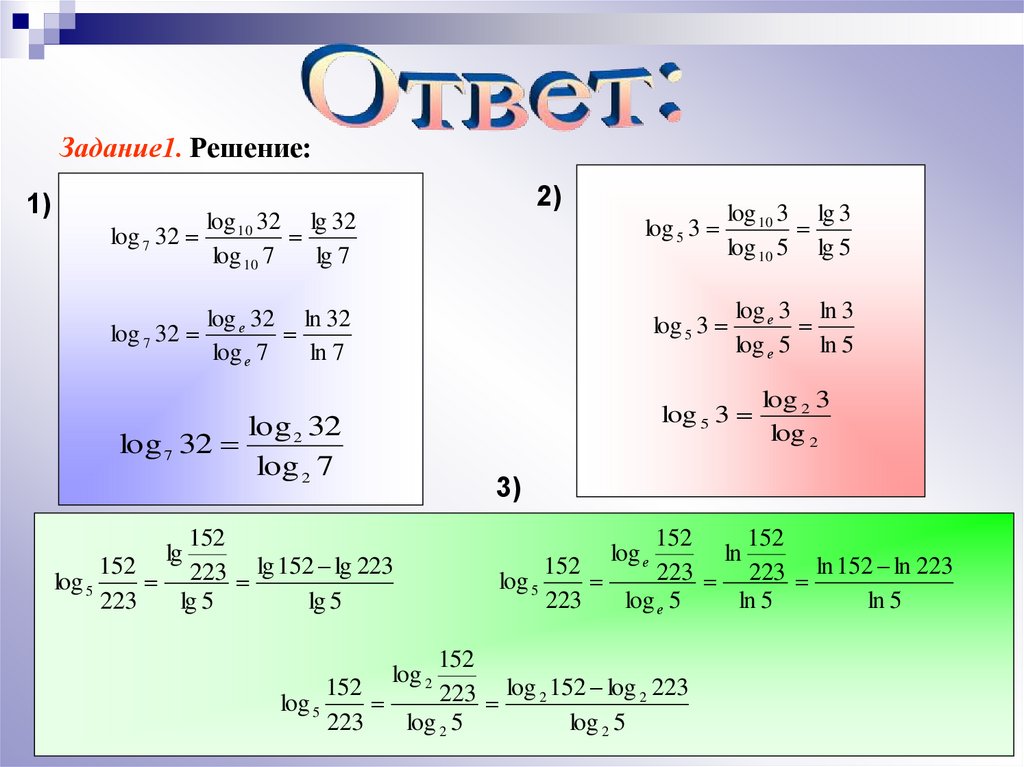 Алимов Ш.А. Алгебра и начала математического анализа. 10–11 кл.

Вычислите и выясните имя изобретателя логарифмов 12 4 3 5 2 10 1 П О Ж Н Д Е Р

Домашнее задание Глава IV §15–§17, № 272, 281, 296.

Использование SymPy в вычислениях / Хабр

Добрый день уважаемые пользователи. Данная статья ориентированна на начинающих программистов. Как вы знаете для Python существует большое множество библиотек которые помогают с вычислениями. И я хотел бы поделиться одной из библиотек, которая может существенно помочь при вычислениях, но использовать ее в коде я не рекомендую. Но она может значительно облегчить вам жизнь, если вы решаете уровнения и занимаетесь их преобразованием, упрощением для дальнейшего использования.

Библиотека SymPy умеет многое, начиная с решения уравнений и заканчивая построениями графиков, но тут я хотел рассмотреть на примерах, как же работают функции «упрощения» в этой библиотеке на примере решения нескольких простых задач.

Приступим!)

Задача. Найдите значение выражения:

Проведем преобразования:

Проверим наше преобразование с помощью SymPy:

from sympy import * # знак звездочки означает, чт омы импортировали все данные из библиотеки

init_printing(use_unicode = False, wrap_line = False, no_global = True) # формат вывода информации

expression = (sqrt(13)+sqrt(7))**2/(10+sqrt(91))
expression

Скопируйте этот код и посмотрите на нывод. Библиотека SymPy не дала нам ответ, а вывел очень красиво нашу формулу:

Предлагаю упростить это выражение, т.е. решить его, но для упрощения я буду использовать функцию simplify:

simplify(expression) # функция simplify выполняет упрощение выражений

И тут мы получаем:

2

Для лучшего понимаю как можно использовать функцию simplify приведем еще пару примеров.

Задача. Найдите значение выражения, если lgb = 5:

Проведем преобразования. Для начала вычислим значение b.

Теперь поставим значение b в наше выражение, которое нужно было вычислить:

Проверим наше преобразование с помощью SymPy:

b = Symbol('b') # введем символ b далее мы сможем его вычислить
expression_b = log(b, 10)
expression_b

Этот код выведет нам следующее сообщение:

После того как мы создадим выражение expression_b давайте вычислим само значение b:

solve_b = solve(expression_b-5, b) # функция slove решает уровнение,тут "-5" эквивалентно "=5"
solve_b = solve_b[0]
solve_b

На выводе получим 100000.

Да, мы уже получили с вами это же числе проводя преобразования в ручную.

Подставим b в выражение:

expression_b_main = log(10 / solve_b**3)
expression_b_main

На выводе получим:

Да, вывод не всегда удобно читать. Но отметим что, В ответе выше содержится 14 нулей, а логарифм по основанию 10 будет равен — 14.

И именно тут я хочу сделать важное замечание, что в SymPy нужно быть очень внимательными с логарифмами и нужно явно указывать основание. Если его не указать, то по умолчанию основание логарифма будет — е.

Задача. Упростите выражение:

Когда перемножаются степени одинаковых чисел, можно просто сложить показатели степеней.

Проверим наше выражение и упростим его с помощью библиотеки.

a = Symbol('a')

expression_a = 2 * a * a**(4/3) * 3 * a**(2/3)
expression_a

Выведет , в красивом виде:

Наша библиотека сразу же дала нам упрощенное выражение, перемножив все слагаемые. Результат верный. Реализуйте функцию на языке Python, принимающую на вход n и возвращающую значение следующей суммы:

Задача. Реализуйте функцию на языке Python, принимающую на вход n и возвращающую значение следующей суммы:

def summa(n):
    summa = 0
    for x in range(1, n+1, 1):
        summa = log(x) + summa
    return summa

Используем нашу функцию:

summa(5)

Получим на выводе:

Обратите внимание что функция работает верно.

Т.е. наша сумма начинается с i = 1, но поскольку натуральный логарифм т 1 будет равен 0, то в вывод 0 не попадает.

Задача. Реализуйте функцию на языке Python, принимающую на вход n и возвращающую значение следующего выражения:

Сразу скажу что не нужно пугаться большой буквы П. В этой записи П оначает что это произведение ряда числе начиная с 1 и до n.

В этом математическом выражении нам необходимо посчитать натуральный логарифм от произведений чисел от 1 до n.

А теперь используем функцию:

multiplication(2)

Получим на вывод:

Задача. Проверьте, что функции из предыдущих двух заданий эквивалентны. Объясните, почему это так.

print('Функция из задния 4:', summa(5))
print('Функция из задния 5:', multiplication(5))

Тут мы вывели значения которые получили от функций суммы и произведения. Полуим на выводе:

Исходя из свойств логарифмов упростим первое выражение. Поскольку у логарифмов везде одинаковое основание, то мы можем перемножить числа в скобках.

summa_expression_simplify = simplify(summa(5))
summa_expression_simplify

На выводе получим:

Как мы видим выражения полностью одинаковы.

Задача. Найдите значение выражения.

Воспользуемся SymPy:

x = Symbol('x')

expression_g = (4*x-x*x)**(1/3)
expression_g = simplify(expression_g)
expression_g

Выведет нам:

Решим данное уравнение:

expression_g_solve = solve(expression_g-0, x) # Найдем корни
expression_g_solve

На выводе получим:

Мы нашли корни уравнения.

Теперь перейдем к решению основного уравнения. На самом деле для решения не нужно было искать корни, это было продемонстрировано для примера.

numerator_g = (4*(2-x)-(2-x)*(2-x))**(1/3)
denominator_g = (4*(2+x)-(2+x)*(2+x))**(1/3)

expr_g_main = numerator_g / denominator_g
expr_g_main

На выводе получим:

Воспользовавшись функцией упрощения, упростим это выражение.

expr_g_main = simplify(expr_g_main)
expr_g_main

На выводе получим:

И так мы получили ответ 1. Посмотрим как это получилось, приведя поэтапные преобразования:

Задача. Найдите значение выражения.

Упростим выражение в ручную:

В ответе мы получили 5. Проверим наши преобразования используя библиотеку sympy.

x = Symbol('x')
Expression = ((2*x**3)**4-(x**2)**6)/(3*x**12)
Expression

На выводе получим:

Наше решение верно. Ответы сошлись.

Задача. Найдите значение выражения при b=2.

Проведем упрощения выражения:

Ответ при b=2 будет -1/2.

Проверим наши вычисления с помощью библиотеки:

b = Symbol('b')
expression_b = (11*a**6*b**3-(3*a**2*b)**3)/(4*a**6*b**6)
expression_b

На выводе получим:

Как видим библиотека сразу сделал упрощение нашего выражения.

expression_g_solve = solve(expression_b+0.5, b)
expression_g_solve[0]

На выводе получим:

Поставив свой ответ который мы получили, мы нашли значение b = 2, значит выражение решено верно.

Надеюсь на нескольких простых примерах вы поняли суть работы с SymPy и применением ее в ваших вычислениях.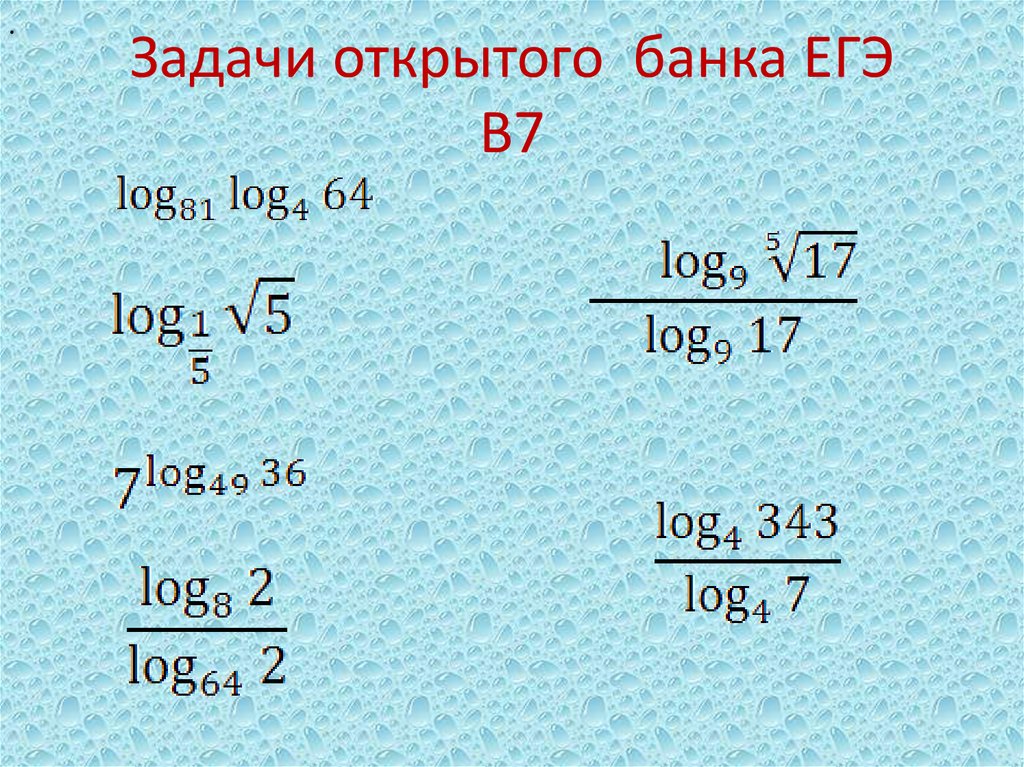 Обращаю внимание, что SymPy не всегда упрошает выражения до самого простого, это было видно по заданиям в этой статье.

Алгоритм

— Значение lg * N в алгоритмическом анализе

спросил 12 лет, 1 месяц назад

Изменено 2 года, 11 месяцев назад

Просмотрено 25 тысяч раз

Я сейчас читаю об алгоритмическом анализе и прочитал, что некий алгоритм (взвешенное быстрое объединение со сжатием пути) имеет порядок N + M lg * N. Очевидно, хотя это линейно, потому что lg * N является константой в этой вселенной. . О какой математической операции здесь идет речь. Я не знаком с обозначением lg*N.

• алгоритм
• время выполнения
• big-o
• анализ
• повторный логарифм

3

Ответы, данные здесь до сих пор, неверны.

lg* n (читается «логарифмическая звезда») — повторный логарифм. Он определяется так же рекурсивно, как

 0, если n <= 1
лг* п =
         1 + lg*(lg n), если n > 1
 

По-другому это можно представить как количество повторений логарифма, прежде чем результат станет меньше или равен 1.

Очень медленно растет. Вы можете прочитать больше в Википедии, где есть несколько примеров алгоритмов, для которых lg* n всплывает при анализе.

1

Я предполагаю, что вы говорите об алгоритме, проанализированном на слайде 44 этой лекции: http://www.cs.princeton.edu/courses/archive/fall05/cos226/lectures/union-find.pdf

Там, где они говорят, что «lg * N является константой в этой вселенной», я считаю, что это не так. совершенно буквально. lg*N, по-видимому, увеличивается с увеличением N согласно их таблице в правой части слайда; просто так получилось, что он растет с такой медленной скоростью, что его нельзя рассматривать как что-то еще (N = 2 ^ 65536 -> log * n = 5). x = n. В анализе сложности Big O база для регистрации не имеет значения. Степени числа 2 появляются в CS, поэтому неудивительно, если нам придется выбирать основание, это будет основание 2. 9h-1 узлов. Если мы позволим n быть количеством узлов, эта связь будет деревом высотой lg n с n узлами. Алгоритму обхода этого дерева требуется не более lg n, чтобы увидеть, сохранено ли значение в дереве.

Как и следовало ожидать, в вики есть отличная дополнительная информация.

2

Логарифм обозначается log или lg. В вашем случае я предполагаю, что правильная интерпретация — N + M * log (N).

РЕДАКТИРОВАТЬ: Основание логарифма не имеет значения при анализе асимптотической сложности.

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

java — Вычисление наибольшего целого меньше, чем основание 2 журнала N

спросил 4 года 3 месяца назад

Изменено 4 года, 3 месяца назад

Просмотрено 2к раз

Я читал Algorithms, 4th Edition, и он определяет вопрос следующим образом:

Напишите статический метод lg() , который принимает значение int N в качестве аргумента и возвращает наибольшее значение int , не превышающее логарифм по основанию 2 числа 9. 0027 N на Яве. Не используйте мат.

Я обнаружил следующее решение:

 public static int lg(int N) {
    интервал х = 0;
    для (int n = N; n > 1; n/= 2) x++;
    вернуть х;
}
 

Мне интересно, почему это решение работает. Почему непрерывное деление на 2 позволяет нам найти наибольшее целое число, меньшее логарифма аргумента по основанию 2? Я понимаю Java, но не знаю, как работает этот конкретный алгоритм.

Спасибо.

• ява
• алгоритм
• математика
• логарифм

5

Это связано со свойствами показателей степени и логарифмов. Главное наблюдение, которое вам нужно, это то, что

2 ^{lg n} = n,

, потому что логарифмы обратны экспонентам. Преобразование этого выражения дает

1 = н / 2 ^{лг н} .

Другими словами, значение lg n — это количество раз, которое вы должны разделить n на два, чтобы уменьшить его до 1. Это, кстати, очень полезная интуиция при изучении алгоритмов, поскольку log термины появляются все время в таких контекстах.

Здесь есть еще несколько нюансов, касающихся работы целочисленного деления, но это основная идея, почему этот код работает.

4

Тривиально следует из логарифмического тождества log(a/b) = log(a) - log(b) .

Вы ищете наибольшее целое число x , чтобы:

 x <= log2(n)
 

Используя приведенное выше тождество и принимая во внимание, что log2(2) = 1 получаем:

 x <= log2(n/2) + log2(2)
х <= log2(n/2) + 1
х <= log2(n/4) + 2
х <= log2(n/8) + 3
...
х <= log2 (1) + к
x <= k (поскольку log2(1) = 0)
 

Таким образом, x — это количество раз, которое вы разделили n на 2 до получения 1 .

Ответ чисто математический,

log₂(n) = ln(n)/ln(2) = x

Применяя экспоненциальные правила:

9{x-x+1}

Последнее также записывается 1 <= N_x < 2

Но N_x является целым числом, поэтому N_x = 1

Следовательно, x - это число деления на 2 числа N, оставшееся больше или равное 1

Вместо того, чтобы начинать с N_1, мы можем начать с N_0 = N и остаться больше 1.