Что значит непрерывная функция: Что такое непрерывная функция в точке. Непрерывность функций – теоремы и свойства

Непрерывная функция — Энциклопедия по экономике

Таким образом, нормативы потребности МТР на ремонтно-профилактические работы также являются функциями суммарно произведенного модулем целевого эффекта. Их можно представить в виде непрерывных функций несмотря на то, что ремонты и обслуживание модуля осуществляются периодически (рис. 19).  [c.50]
Зависимость отдельных составляющих целевой функции от числа пунктов разгрузки, включенных в какой-либо вариант внешнего транспортного обеспечения и условно рассматриваемых как непрерывные функции в области целочисленных величин числа пунктов разгрузки пгв, представлена на рис. 27. Как видно из рисунка, с увеличением числа пунктов разгрузки возрастают суммарные затраты на их организацию и уменьшаются транспортные расходы по доставке труб к месту работ. Следовательно, целевая функция как сумма указанных составляющих имеет экстремум при некотором значении числа пунктов разгрузки. Учитывая нелинейную зависимость функционала и его отдельных составляющих от числа вводимых пунктов разгрузки и искомых переменных, для решения поставленной задачи не могут быть применены классические методы математического программирования (например,. линейного). Как известно из курса высшей математики, математическое программирование — область математики, разрабатывающая теорию и методы решения многомерных экстремальных задач с ограничениями, т. е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных. Само название программирование взято из линейного программирования, где оно обычно обозначает распределение наилучшим образом ограниченных ресурсов для достижения поставленных целей. Следовательно, термин программирование здесь можно заменить термином планирование .  [c.145]
Если предположить непрерывность функций df/dxt (i =1,. .., п.), то границей экономической области будут поверхности, на которых  [c.93]

Что касается первого вопроса, то в качестве примера, по крайней мере, не вполне оправданного применения математики в экономике можно привести известный в анализе хозяйственной деятельности интегральный метод факторного анализа. Его разработчики, безжалостно критикуя простой и наглядный метод цепных подстановок, говорят о том, что интегральный метод «обеспечивает более высокую точность».

Не вдаваясь в комментарий относительно точности в рамках ретроспективного анализа, отмечу только, что обоснованность применения интегрального метода в экономике является исключительно условной, поскольку он требует непрерывности функции, описывающей факторную связь, и бесконечно малого изменения признаков, чего в экономических явлениях часто не может быть в принципе, поскольку многие показатели изменяются дискретно.  [c.315]

Для выявления циклической составляющей динамики валютного курса статистикой также используется выравнивание по ряду Фурье, поскольку циклические колебания являются разновидностью периодических, как и сезонные. Может применяться и метод скользящей средней. Период скольжения принимают, естественно, другой, соответствующий периоду циклических колебаний. В нашем примере сглаживание целесообразно проводить по 33-месячной скользящей средней (см. рис. 15.3). Период можно определить по графику и с помощью спектрального анализа, представив ряд в виде непрерывной функции, которую можно разложить на сумму бесконечного числа гармонических функций с периодом от 0 до 2л с различной амплитудой.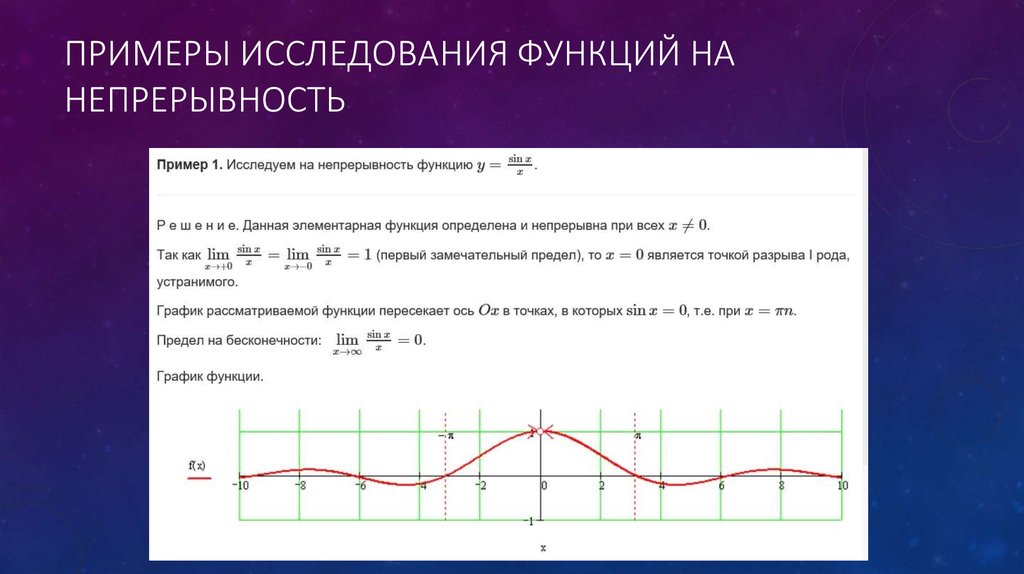

Спектральной плотностью функции называется величина амплитуды гармоники в зависимости о г ее периода. Чем больше амплитуда (спектр) данной гармоники, тем сильнее в использованной функции присутствуют колебания с этим периодом.  [c.664]

Свойства нет полного разложения не требуется установления очередности изменения факторов в модели носит достаточно искусственный характер, поскольку требует непрерывности функции / и бесконечно малого изменения признаков, чего в экономических исследованиях не может быть в принципе, так как многие показатели изменяются дискретно (по крайней мере, дело обстоит именно так в случае, когда речь идет о детерминированном факторном анализе, т.е. анализе в отношении единичного объекта, а не совокупности объектов в качестве примера можно привести показатель численности работников на заводе).  [c.103]

Совокупность исследуемых исходных данных должна быть однородной и математически описываться непрерывными функциями.  [c.114]

A5/S (см. также следующий раздел). Эту характеристику по /-му ресурсу можно задавать величиной Е] — математического ожидания недопоставки АР/Р°. В случае непрерывной функции эластичности ф/ при известной плотности распределения (k.S ISj) случайной величины A5 75j она выражается так  [c.29]

Если зависимость общей выручки от объема продукции представлена непрерывной функцией TR = f(Q), то  [c.98]

В предположении непрерывности функции /(/г) получим  [c.107]

Дифференциальное исчисление. Позволяет находить максимальные и минимальные значения для математически заданных непрерывных функций (и некоторых других).  [c.187]

Один из методов нахождения экстремума рассматриваемой непрерывной функции состоит в нахождении частных производных  [c.44]

Я/. =… = Rfi, [c.124]

Предположим, что м(-) — монотонная непрерывная функция  [c.8]

Примем сначала, что (Y) кусочно-линейная непрерывная функция  [c.12]

Колмогоров А.Н. О представлении непрерывных функций нескольких  [c. 99]

Рассмотрим непрерывные функции стимулирования следующего  [c.48]

Известно, что при монотонных непрерывных функциях затрат про-  [c.119]

Непрерывные процессы описываются непрерывными функциями. Для описания функционирования системы удобнее использовать не аналоговое, а дискретное представление. При этом функцию ЧМС дискретизируют а) по уровню, представляя процесс конечным числом разрешенных уровней б) по времени — значение основных показателей в фиксированные моменты времени в) по уровню и по времени, расчленяя процесс на предельно малые целесообразные элементы, которые можно анализировать [34].  [c.37]

Обычно относительно производственной функции (2.8) делают предположение, очень удобное с математической точки зрения,— предположение о непрерывном изменении переменных х и достаточно плавном изменении выпуска при изменении затрат ресурсов. В математической форме эти предположения имеют следующий вид функция (2.8) задана при всех неотрицательных значениях составляющих вектора х (как принято говорить, на неотрицательном ортанте) и является непрерывной (или нужное число раз дифференцируемой) функцией своих аргументов.

На практике ресурсы и продукция зачастую не могут меняться непрерывно — их количество дискретно и измеряется, например, в штуках. Описание с помощью переменных, принимающих любые вещественные значения, и непрерывных функций означает в таких-случаях, что число выпускаемых и потребляемых единиц достаточно велико, чтобы дискретностью МОЖНО было пренебречь.  [c.70]

Необходимо отметить, что в задачах планирования, в отличие от классических задач управления, не возникает необходимость определения непрерывной траектории функционирования. Приемлемая в практических ситуациях точность плановых расчетов обеспечивается кусочно-постоянной аппроксимацией непрерывных функций времени. При решении задачи календарного планирования нефтеперерабатывающих производств весь плановый период разбивается на ряд одинаковых временных отрезков, на каждом из которых решение представляет собойлибо постоянное по времени у-правление, либо среднюю или интегральную величину управляющих переменных. Точность и время решения задачи зависят от длительности этого отрезка времени.

При прочих равных условиях его уменьшение ведет к повышению точности решения и снижению потерь оптимальности за счет повышения точности аппроксимации параметров модели. Одновременно происходит увеличение затрат времени на решение задач в связи с увеличением частоты ее решения.  [c.77]

В итоге мы получим взвешенное по вероятности HPR для каждого исхода. Возможен широкий диапазон результатов, но, к сожалению, эти результаты не непрерывны. Например, время до истечения срока не задается непрерывной функцией. До истечения срока всегда остается целое число то же верно и для цены базового инструмента. Если цена акции равна, например, 35, а минимальное изменение цены равно 1/8, то между 30 и 40 находится 81 возможное значение. Зная время, через которое мы собираемся продать опцион, можно рассчитать взвешенные по вероятности HPR для всех возможных цен на этот рыночный день. В нормальном распределении вероятности 99,73% всех результатов попадают в интервал трех стандартных отклонений от среднего, которое в нашем случае является текущей ценой базового инструмента.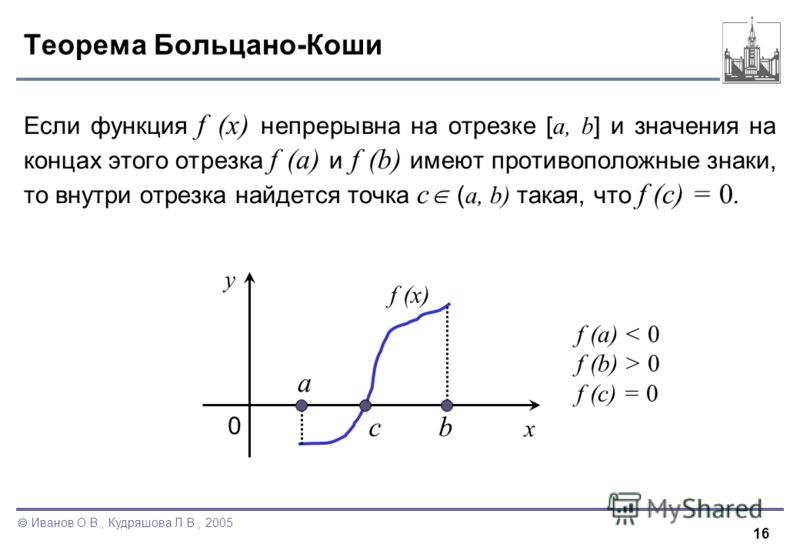

Поэтому нам необходимо рассчи-  [c.166]

Как тот. так и другой набор базисных функций обеспечивают возможность аппроксимации любой непрерывной функции с произвольной точностью. Основное различие между ними в способе кодирования информации на скрытом слое. Если персепторны используют глобальные переменные (наборы бесконечных гиперплоскостей) то сети радиального базиса опираются на компактные шары, окружающие набор опорных центров (Рисунок 15).  [c.86]

Затем были предложены STAR-, или гладкие TAR-модели. Такая модель представляет собой линейную комбинацию нескольких моделей, взятых с коэффициентами, которые являются непрерывными функциями времени. Примером может служить следующее уравнение модели, в котором 0 — гладкая функция, принимающая значения от 0 до 1  [c.56]

Для некоторых конфигураций количество весов явно превосходило число входных данных (наблюдений). Хотя недостаток степеней свободы делает оценку сомнительной, мы приводим здесь результаты работы 13-27-1 модели, чтобы проиллюстрировать доказанную Колмогоровым в 1957 г. и популяризованную Хехт-Нильсеном [137] теорему о существовании отображения. Эта теорема утверждает, что любая непрерывная функция может быть реализована трехслойной нейронной сетью, имеющей во входном слое т (в нашем случае 13) элементов, промасштабированных на [0,1], (2т-1-1) элементов-процессоров в единственном скрытом слое и п элементов в выходном слое. Таким образом, гарантируется, что иерархическая многослойная нейронная сеть может решить любую нелинейно отделимую задачу и может точно реализовать любое отображение га-мерных входных векторов в и-мерные выходные. При этом теорема ничего не говорит нам ни о возможности реализовать отображение посредством сети меньших размеров, ни о том, что для этого подойдут обычно используемые сигмоидные преобразования.  [c.100]

Непрерывные функции (Лекция №4)

СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ

Рассмотрим некоторые свойства функций непрерывных на отрезке. Эти свойства приведём без доказательства.

Функцию y = f(x) называют непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т. е. в точках a и b, непрерывна соответственно справа и слева.

Теорема 1. Функция, непрерывная на отрезке [a, b], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.

Теорема утверждает, что если функция y = f(x) непрерывна на отрезке [a, b], то найдётся хотя бы одна точка x₁ Î [a, b] такая, что значение функции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x₁) ≥ f(x). Аналогично найдётся такая точка x₂, в которой значение функции будет самым маленьким из всех значений на отрезке: f(x₁) ≤ f(x).

Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x₂ и x₂‘.

Замечание. Утверждение теоремы можно стать неверным, если рассмотреть значение функции на интервале (a, b). Действительно, если рассмотреть функцию y = x на (0, 2), то она непрерывна на этом интервале, но не достигает в нём ни наибольшего, ни наименьшего значений: она достигает этих значений на концах интервала, но концы не принадлежат нашей области.

Также теорема перестаёт быть верной для разрывных функций. Приведите пример.

Следствие. Если функция f(x) непрерывна на [a, b], то она ограничена на этом отрезке.

Теорема 2. Пусть функция y = f(x) непрерывна на отрезке [a, b] и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка [a, b] найдется, по крайней мере, одна точка x = C, в которой функция обращается в ноль: f(C) = 0, где a < C< b

Эта теорема имеет простой геометрический смысл: если точки графика непрерывной функции y = f(x), соответствующие концам отрезка [a, b] лежат по разные стороны от оси Ox, то этот график хотя бы в одной точке отрезка пересекает ось Ox. Разрывные функции этим свойством могут не обладать.

Эта теорема допускает следующее обобщение.

Теорема 3 (теорема о промежуточных значениях). Пусть функцияy = f(x) непрерывна на отрезке [a, b] и f(a) = A, f(b) = B. Тогда для любого числа C, заключённого между A и B, найдётся внутри этого отрезка такая точка CÎ [a, b], что f(c) = C.

Эта теорема геометрически очевидна. Рассмотрим график функции y = f(x). Пусть f(a) = A, f(b) = B. Тогда любая прямая y = C, где C – любое число, заключённое между A и B, пересечёт график функции, по крайней мере, в одной точке. Абсцисса точки пересечения и будет тем значением x = C, при котором f(c) = C.

Таким образом, непрерывная функция, переходя от одного своего значения к другому, обязательно проходит через все промежуточные значения.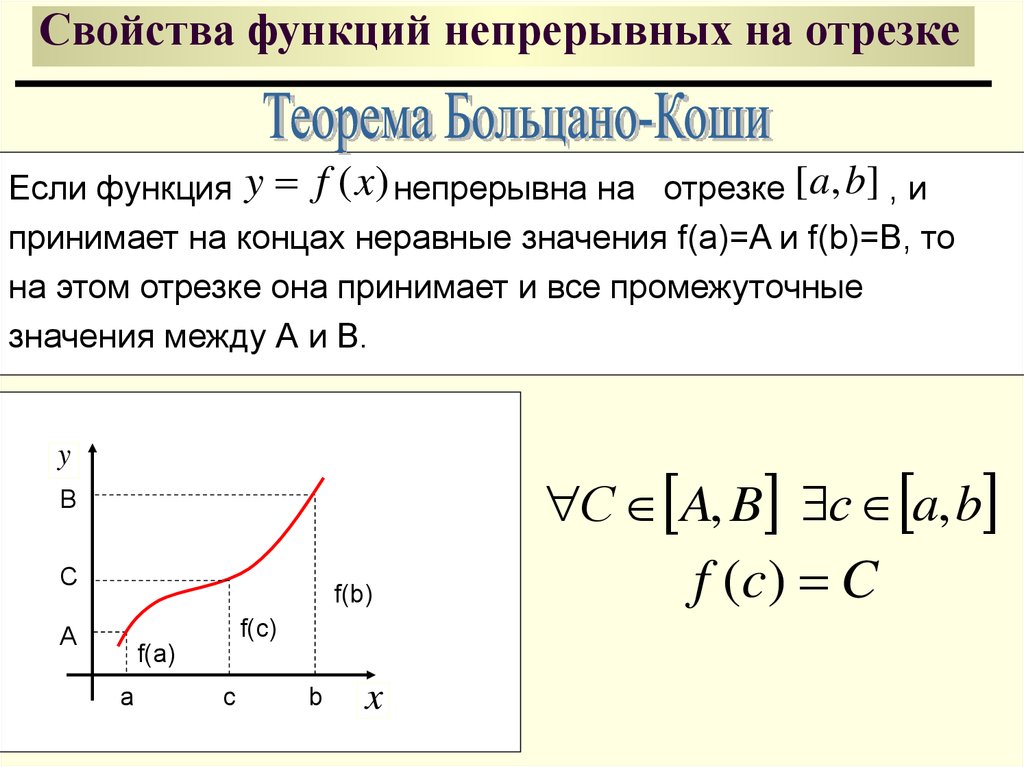 В частности:

Следствие. Если функция y = f(x) непрерывна на некотором интервале и принимает наибольшее и наименьшее значения, то на этом интервале она принимает, по крайней мере, один раз любое значение, заключённое между её наименьшим и наибольшим значениями.

ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ

Пусть имеем некоторую функцию y=f(x), определенную на некотором промежутке. Для каждого значения аргумента xиз этого промежутка функция y=f(x) имеет определенное значение.

Рассмотрим два значения аргумента: исходное x₀ и новое x.

Разность x– x₀ называется приращением аргумента x в точке x₀ и обозначается Δx. Таким образом, Δx = x – x₀ (приращение аргумента может быть как положительным, так и отрицательным). Из этого равенства следует, что x=x₀+Δx, т. е. первоначальное значение переменной получило некоторое приращение. Тогда, если в точке x₀ значение функции было f(x₀), то в новой точке x функция будет принимать значение f(x) = f(x₀ +Δx).

Разность y – y₀ = f(x) – f(x₀) называется приращением функции y = f(x) в точке x₀ и обозначается символом Δy. Таким образом,

Δy = f(x) – f(x0) = f(x0 +Δx) — f(x0).

(1)

Обычно исходное значение аргумента x₀ считается фиксированным, а новое значение x – переменным. Тогда y₀ = f(x₀) оказывается постоянной, а y = f(x) – переменной. Приращения Δy и Δxтакже будут переменными и формула (1) показывает, что Dy является функцией переменной Δx.

Составим отношение приращения функции к приращению аргумента

Найдем предел этого отношения при Δx→0. Если этот предел существует, то его называют производной данной функции f(x) в точке x₀ и обозначают f ‘(x₀). Итак,

.

Производной данной функции y = f(x) в точке x₀ называется предел отношения приращения функции Δy к приращению аргумента Δx, когда последнее произвольным образом стремится к нулю.

Заметим, что для одной и той же функции производная в различных точках xможет принимать различные значения, т.е. производную можно рассматривать как функцию аргумента x. Эта функция обозначается f ‘(x)

Производная обозначается символами f ‘(x),y ‘, . Конкретное значение производной при x = aобозначается f ‘(a) или y ‘|_x=a.

Операция нахождения производной от функции f(x) называется дифференцированием этой функции.

Для непосредственного нахождения производной по определению можно применить следующее практическое правило:

1. Придать x приращение Δx и найти наращенное значение функции f(x + Δx).
2. Найти приращение функции Δy = f(x + Δx) – f(x).
3. Составить отношение и найти предел этого отношения при Δx∞0.

Примеры.

1. Найти производную функции y = x²

   а) в произвольной точке;

   б) в точке x= 2.

   а)

   1. f(x + Δx) = (x + Δx)²;
   2. Δy = (x + Δx)² – x²=2xΔx– x²;
   3. .

      б) f ‘(2) = 4

2. Используя определение найти производную функции в произвольной точке.
1. .

МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Из физики известно, что закон равномерного движения имеет вид s = v·t, где s – путь, пройденный к моменту времени t, v– скорость равномерного движения.

Однако, т.к. большинство движений происходящих в природе, неравномерно, то в общем случае скорость, а, следовательно, и расстояние sбудет зависеть от времени t, т.е. будет функцией времени.

Итак, пусть материальная точка движется по прямой в одном направлении по закону s=s(t).

Отметим некоторый момент времени t₀. К этому моменту точка прошла путь s=s(t₀). Определим скорость vматериальной точки в момент времени t₀.

Для этого рассмотрим какой-нибудь другой момент времени t₀+Δt. Ему соответствует пройденный путь s=s(t₀+Δt). Тогда за промежуток времени Δt точка прошла путь Δs=s(t₀+Δt)–s(t).

Рассмотрим отношение . Оно называется средней скоростью в промежутке времени Δt. Средняя скорость не может точно охарактеризовать быстроту перемещения точки в момент t₀ (т. к. движение неравномерно). Для того, чтобы точнее выразить эту истинную скорость с помощью средней скорости, нужно взять меньший промежуток времени Δt.

Итак, скоростью движения в данный момент времени t₀ (мгновенной скоростью) называется предел средней скорости в промежутке от t₀ до t₀+Δt, когда Δt→0:

,

т.е. скорость неравномерного движения это производная от пройденного пути по времени.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Введем сначала определение касательной к кривой в данной точке.

Пусть имеем кривую и на ней фиксированную точку М₀ (см. рисунок).Рассмотрим другую точку М этой кривой и проведем секущую M₀M. Если точка М начинает перемещаться по кривой, а точка М₀ остается неподвижной, то секущая меняет свое положение. Если при неограниченном приближении точки М по кривой к точке М₀ с любой стороны секущая стремится занять положение определенной прямой М₀Т, то прямая М₀Т называется касательной к кривой в данной точке М₀.

Т.о., касательной к кривой в данной точке М₀ называется предельное положение секущей М₀М, когда точка М стремится вдоль кривой к точке М₀.

Рассмотрим теперь непрерывную функцию y=f(x) и соответствующую этой функции кривую. При некотором значении х₀ функция принимает значение y₀=f(x₀). Этим значениям x₀ и y₀ на кривой соответствует точка М₀(x₀; y₀). Дадим аргументу x₀ приращение Δх. Новому значению аргумента соответствует наращенное значение функции y₀+Δ y=f(x₀–Δx). Получаем точку М(x₀+Δx; y₀+Δy). Проведем секущую М₀М и обозначим через φ угол, образованный секущей с положительным направлением оси Ox. Составим отношение и заметим, что .

Если теперь Δx→0, то в силу непрерывности функции Δу→0, и поэтому точка М, перемещаясь по кривой, неограниченно приближается к точке М₀. Тогда секущая М₀М будет стремиться занять положение касательной к кривой в точке М₀, а угол φ→α при Δx→0, где через α обозначили угол между касательной и положительным направлением оси Ox. Поскольку функция tg φ непрерывно зависит от φ при φ≠π/2 то при φ→α tg φ → tg α и, следовательно, угловой коэффициент касательной будет:

т.е. f ‘(x) = tg α .

Т.о., геометрически у ‘(x₀) представляет угловой коэффициент касательной к графику этой функции в точке x₀, т. е. при данном значении аргумента x, производная равна тангенсуугла, образованного касательной к графику функции f(x) в соответствующей точке М₀ (x; y) с положительным направлением оси Ox.

Пример. Найти угловой коэффициент касательной к кривой у = х² в точке М(-1; 1).

Ранее мы уже видели, что (x²)’ = 2х. Но угловой коэффициент касательной к кривой есть tg α = y‘|_x=-1 = – 2.

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ

Функция y=f(x) называется дифференцируемой в некоторой точке x₀, если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x₀, то она в этой точке непрерывна.

Таким образом,из дифференцируемости функции следует ее непрерывность.

Доказательство. Если , то

,

где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда

Δy=f ‘(x₀) Δx+αΔx=> Δy→0 при Δx→0, т.е f(x) – f(x₀)→0 при x→x₀, а это и означает, что функция f(x) непрерывна в точке x₀. Что и требовалось доказать.

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т. е. не имеют в этих точках производной).

Рассмотрим на рисунке точки а, b, c.

В точке a при Δx→0 отношение не имеет предела (т.к. односторонние пределы различны при Δx→0–0 и Δx→0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к₁ и к₂. Такой тип точек называют угловыми точками.

В точке b при Δx→0 отношение является знакопостоянной бесконечно большой величиной . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – «точка перегиба» cвертикальной касательной.

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиесявертикальные касательные. Тип – «точка возврата» с вертикальной касательной – частный случай угловой точки.

Примеры.

1. Рассмотрим функцию y=|x|.Эта функция непрерывна в точке x = 0, т.к. .

   Покажем, что она не имеет производной в этой точке.

   f(0+Δx) = f(Δx) = |Δx|. Следовательно, Δy = f(Δx) – f(0) = |Δx|

   Но тогда при Δx< 0 (т.е. при Δx стремящемся к 0 слева)

   А при Δx > 0

   Т.о., отношение при Δx→ 0 справа и слева имеет различные пределы, а это значит, что отношение предела не имеет, т.е. производная функции y=|x| в точке x= 0 не существует. Геометрически это значит, что в точке x= 0 данная «кривая» не имеет определенной касательной (в этой точке их две).

2. Функция определена и непрерывна на всей числовой прямой. Выясним, имеет ли эта функция производную при x= 0.

   Следовательно, рассматриваемая функция не дифференцируема в точке x= 0. Касательная к кривой в этой точке образует с осью абсцисс угол p/2, т.е. совпадает с осью Oy.

Что такое непрерывная функция?

Что такое непрерывная функция?

---

Эрин Хорст

---

Давайте сначала начнем с определения непрерывной функции, затем мы рассмотрим некоторые задачи, предназначенные для помочь в развитии большего концептуального понимания понятия непрерывной функции.

Функция f непрерывна при x=a при условии, что все три из следующих правил:

Другими словами, функция f непрерывна в точке x=a , когда (i) функция f определена как a , (ii) предел f , поскольку x приближается к a от правый и левый пределы существуют и равны, и (iii) предел f , поскольку x приближается к , а равно к ф(а) .

Прежде чем двигаться дальше, давайте начнем с построения функций это , а не непрерывный. Для каждого из следующих рисунков график функции, которая является , а не непрерывной при x=2 когда:

а) (i) верно, но (ii) ложно.

б) (ii) верно, но (i) ложно.

c) (i) и (ii) верны, но (iii) ложно.

 

Теперь давайте рассмотрим график функции f ниже.

Для каких чисел x в [-3, 3] будет f не непрерывный при разрешении х ?

Теперь давайте попробуем свои силы в другой функции. Для некоторого ненулевого номер и , определите

a) Определен ли f как a ?

б) Существует ли?

c) Является ли f продолжением a ?

Теперь о более сложных задачах. Если , какое из следующих утверждений, если таковое имеется, должно быть верным?

а) ф определяется как a .

б) е(а)=L

c) f непрерывен в a .

 

Рассмотрим следующую функцию,

Теперь (1) найдите все значения a и b такие, что f является непрерывным при x=1 и (2) нарисуйте график f , когда a=1 и b=-1 .

 

По мере того, как мы начинаем лучше понимать непрерывность, определить, всегда ли следующие утверждения верны или иногда ложный. Обязательно аргументируйте свои ответы примером.

а) Если f(1)<0 и f(2)>0 , то должны — точка p в (1, 2) такая, что f(p)=0 .

б) Если f непрерывно на [1, 2], f(1)<0 и f(2)>0 , то должна быть точка p в (1, 2) такой, что f(p)=0.

в) Если f непрерывно на [1, 2] и существует точка p в (1, 2) такое, что f(p)=0 , затем f(1) и f(2) должны иметь разные знаки.

г) Если f не имеет нулей и непрерывно на [1, 2], то f(1) и f(2) имеют одинаковый знак.

 

И, для тех из вас, кто любит проблемы с путешествиями: Джон берет поездка из Портленда, штат Орегон, в Сиэтл, штат Вашингтон. Он уходит в 8:00 в понедельник и прибывает в 12:00 того же дня. Он возвращается на Вторник, вылет из Сиэтла в 8:00 и возвращение в Портленд. в 12:00 по тому же маршруту. Покажи, что там это точка на дороге, через которую он проходит одновременно оба дня.

---

Это упражнение было адаптировано из курса математики Excel, преподаваемого в Портлендский государственный университет, весенний семестр 2004 г. Джо Эдигер и Эрин Хорст.

---

Возврат

---

Непрерывная функция / Проверка непрерывности функции

Содержание (Нажмите, чтобы перейти к этому разделу):

1. Что такое непрерывная функция?
   • Порядок непрерывности: функции C0, C1, C2
2. Различные типы непрерывности
   • Абсолютно непрерывный
   • Левый непрерывный
   • Правый Непрерывный
   • Равномерно непрерывный
3. Список общих непрерывных функций.
4. Как проверить непрерывность функции.
5. Непрерывные переменные и данные

Посмотрите видео с обзором и примерами или прочитайте ниже:

Непрерывные функции

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

Эта функция непрерывна.

Говоря простым языком, непрерывная функция — это функция, которую можно нарисовать, не отрывая карандаша от бумаги. Если у вас есть отверстия, скачки или вертикальные асимптоты, вам придется поднять карандаш вверх, и поэтому у вас не будет непрерывной функции.

Если ваша функция скачет таким образом, она не непрерывна.

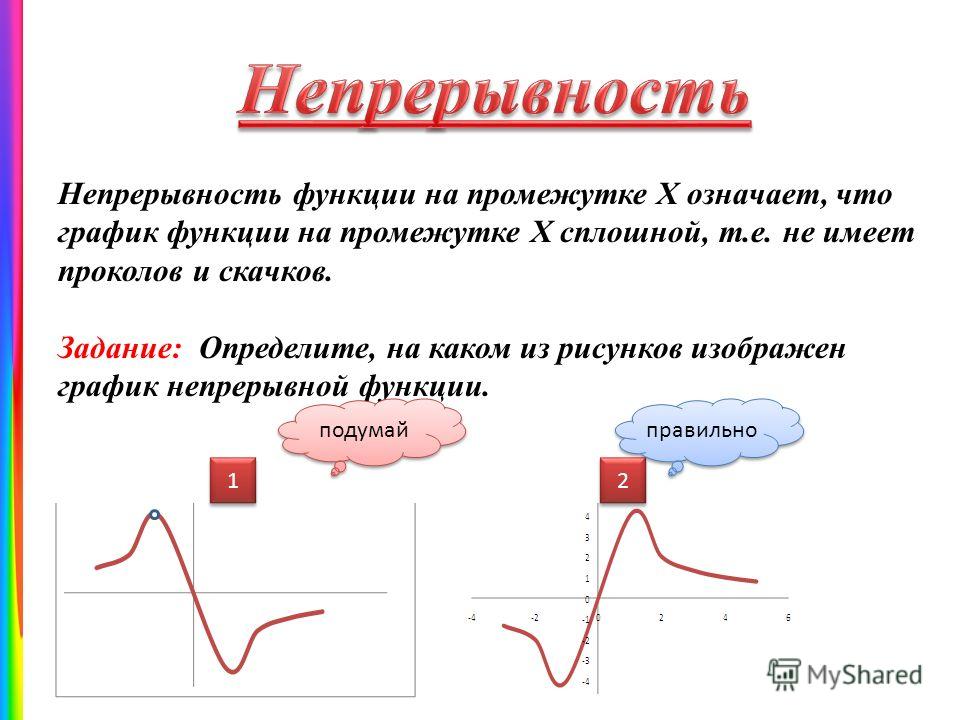
Формально функция (f) непрерывна, если для каждой точки x = a :

1. Функция определена в a . Другими словами, пункт a находится в домене f,
2. Предел функции существует в этой точке и равен x, приближающемуся к a с обеих сторон,
3. Предел функции, когда x приближается к a , совпадает с выходом функции (т. е. значением y) при a .

Порядок непрерывности, или «гладкость» функции определяется тем, как эта функция ведет себя на интервале, а также поведением производных.

Функция C0

A Функция C ⁰ является непрерывной функцией. Более конкретно, это функция с действительным знаком, которая непрерывна на определенном замкнутом интервале.

Это простое определение образует строительный блок для более высоких порядков непрерывности.

Функция C1

A C ¹ Функция непрерывна и имеет непрерывную первую производную.

Функция C2

A Функция C ² имеет как непрерывную первую производную, так и непрерывную вторую производную.

Обратите внимание, что верхний индекс равен количеству непрерывных производных , поэтому порядок непрерывности иногда описывается как « количество производных, которые должны соответствовать ». Это простой способ взглянуть на порядок непрерывности, но следует соблюдать осторожность, если вы используете это определение, поскольку производные также должны совпадать по порядку (первый, второй, третий…) без пропусков. Например, предположим, что у вас есть непрерывная первая производная и третья производная с прерывистой второй производной. Есть две «совпадающие» непрерывные производные (первая и третья), но это не будет C ² — это будет функция C ¹ из-за отсутствия непрерывности второй производной.

Моделирование с порядком непрерывности

Непрерывность в технике и физике также определяется немного более конкретно, чем просто «непрерывность». Например, этот отчет ЕС о методах геометрического моделирования на основе PDE описывает математические модели, в которых поверхности C ⁰ являются позиционными, C ¹ позиционными и тангенциальными, а C ³ — позиционное, тангенциальное и кривизнальное. Требуемая непрерывность зависит от приложения. Например, моделирование высокоскоростного транспортного средства (например, самолета) требует более высокого порядка непрерывности по сравнению с медленным транспортным средством.

Если функция просто «непрерывна» без какой-либо дополнительной информации, то вы, как правило, предполагаете, что функция непрерывна везде (т. е. множество всех действительных чисел от -∞ до + ∞). Однако иногда конкретная часть функции может быть непрерывной, а остальные — нет.

• Непрерывно на интервале: Функция f является непрерывной на интервале, если она непрерывна в каждой точке интервала. Например, вы можете определить интервал от -1 до +1. Пока функция непрерывна в этой небольшой области, вы можете сказать, что она непрерывна на этом конкретном интервале.
• Непрерывность в конечной точке: У функции есть две возможные конечные точки: полностью влево (в крайнем отрицательном направлении) и полностью вправо (в крайне положительном направлении). Предполагая, что предел существует, «непрерывность в конечной точке» означает, что функция непрерывна справа (для левого конца) или непрерывна слева (для правого конца).

Абсолютно непрерывные функции с действительными числами — это функции, для которых справедлива Основная теорема исчисления (FTC) [1]. Другими словами, абсолютная непрерывность определяет , какие функции могут быть первообразными : функция на замкнутом ограниченном интервале абсолютно непрерывна на этом интервале, если она также является первообразной на том же интервале [2].

Эти функции имеют самый «гладкий» тип непрерывности, за которым следует равномерная непрерывность, а затем обычная непрерывность. Все абсолютно непрерывные функции непрерывны, но обратное неверно.

Абсолютно непрерывные функции и случайных величин связаны друг с другом следующим образом: Действительнозначная случайная величина X абсолютно непрерывна, если ее функция распределения F _X абсолютно непрерывна [3]

Формальное определение

Формальное определение часто используется в реальном анализе, в частности, для доказательства основной теоремы исчисления для интеграла Лебега [4].

Абсолютно непрерывная функция, заданная на отрезке, обладает следующим свойством. Это свойство основано на положительном числе ε и его эквиваленте, другом положительном числе δ.

1. Возьмите интервал, для которого мы хотим определить абсолютную непрерывность, затем разбейте его на набор конечных непересекающихся интервалов. Длины этих интервалов имеют сумму меньше δ,
2. Далее рассмотрим абсолютные значения разностей значений функций на концах интервалов; Сумма по этим интервалам меньше ε [5].

В суммирующей записи мы можем сформулировать вышеизложенное как: когда конечная последовательность непересекающихся интервалов удовлетворяет:

, затем

Где (x _k , y _k ) — непересекающиеся подинтервалы.

Примеры и свойства абсолютно непрерывных функций

Каждая выпуклая функция и каждая непрерывно дифференцируемая функция абсолютно непрерывна [3].

Для вещественнозначной абсолютно непрерывной функции выполняются следующие свойства [6]:

• cf, где c ∈ ℝ
• ж + г
• фг
• 1/f, если f(x) ≠ 0 для каждого x ∈ [a, b]
• |ф|.

Несколько конкретных примеров: функция Липшица абсолютно непрерывна; Функция Кантора не является (хотя она всюду непрерывна) [7]. Функция tan(x) не является ни равномерно непрерывной, ни абсолютно непрерывной на отрезке [0, π/2].

Абсолютно непрерывный: ссылки

[1] Хейл, К. Конспект лекций по реальному анализу. 3.5. Абс. продолжение и сингулярные функции. Получено 4 мая 2021 г. с: https://people.math.gatech.edu/~heil/handouts/ac.pdf 9.0203 [2] 7.4 Абс. продолжение & Сингулярные функции. Получено 4 мая 2021 г. с: https://www.math.lsu.edu/~rich/Absolute_Continuity
[3] Hill, T. & Berger, A. (2015). Введение в закон Бенфорда. Издательство Принстонского университета.
[4] Поусо, Р. (2012). Простое доказательство основной теоремы исчисления для интеграла Лебега. Получено 5 мая 2021 г. с: https://arxiv.org/pdf/1203.1462.pdf
[5] Математический словарь McGraw-Hill, 2/E. (2002). Макгроу-Хилл.
[6] Всемирный научный. (2014). Задачи и доказательства в реальном анализе. стр. 314-352. Получено 5 мая 2021 г. с: https://www.worldscientific.com/doi/10.1142/9.789814578516_0013
[7] Реальный анализ 9 января 2016 г. Глава 6. Дифференциация и интегрирование. Получено 4 мая 2021 г. с: https://faculty.etsu.edu/gardnerr/5210/Beamer-Proofs/Proofs-6-5.pdf

Непрерывная слева функция непрерывна для всех точек только в одном направлении. (при подходе слева).

Это функция, определенная до определенной точки, c , где:

1. Функция определена на замкнутом интервале [ d, c ], лежащий слева от c ,
2. Предел в этой точке, с, равен значению функции в этой точке.

На следующем рисунке показана непрерывная влево функция до точки x = 4:

Обратите внимание, что значение функции при x = 4 равно пределу функции, когда функция приближается к точке слева.

Формальное определение непрерывной слева функции

Формально непрерывная слева функция f является непрерывной слева в точке c if

lim _{x → c —} f(x) = f(c) .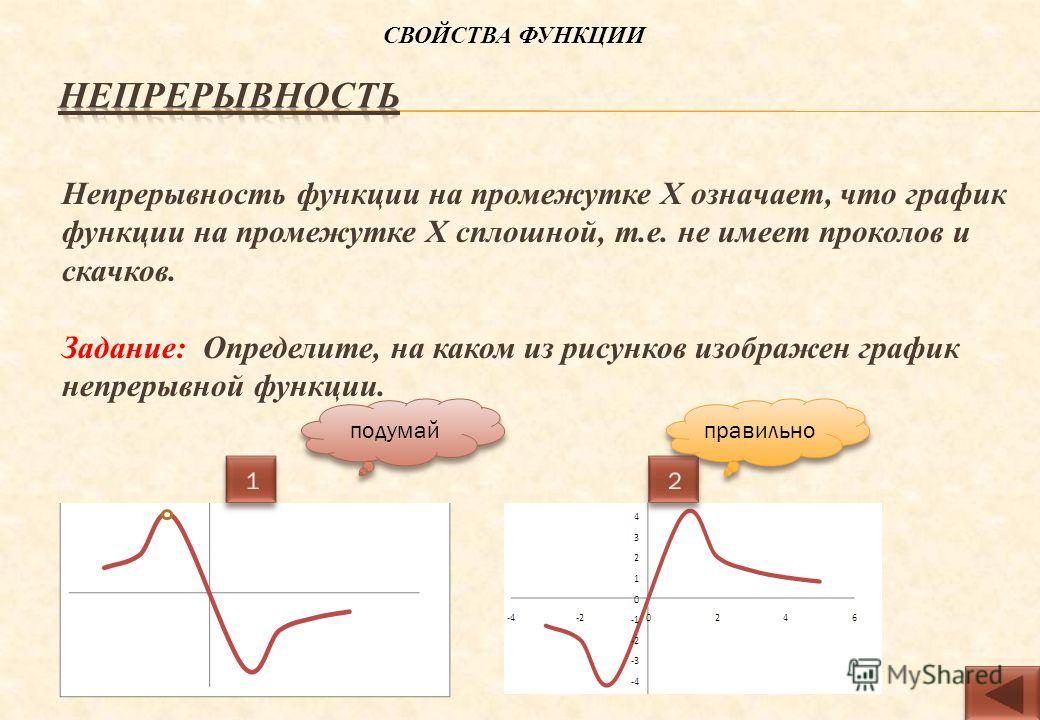

Другими словами, f(x) приближается к c снизу или слева, или для x < c (Morris, 1992). Точно так же определяется непрерывная справа функция (заменяя левый предел с- на правый предел с+ в нижнем индексе).

A правая непрерывная функция определяется до определенной точки . На следующем рисунке показана непрерывная справа функция до точки x = 4:
Эта функция непрерывна справа в точке x = 4. Предел при x = 4 равен значению функции в этой точке (y = 6). Это равно пределу функции по мере приближения к x = 4.

Обратите внимание, что точка на изображении выше заполнена. На графике это говорит о том, что точка входит в область определения функция. Если точка была представлена ​​полым кругом, то точка равна , а не , включены в домен (только каждая точка справа от него на этом графике), и функция , а не будет непрерывной справа.
Точка не существует при x = 4, поэтому функция не является непрерывной справа в этой точке.

Обратите внимание, что этот тип непрерывности определяется для точки, а не для всей функции.

Более формальное определение непрерывной справа функции

Причина, по которой функция не считается непрерывной справа, заключается в формальном определении этих функций. Должны быть истинны два условия о поведении функции, когда она ведет к точке:

1. существует: предел функций должен существовать в точке. Знак + над «а» означает, что к точке приближаются с положительного конца числовой прямой; Другими словами, он приближается справа.
2. Правый предел, ведущий к точке a, должен равняться пределу функции в этой точке.

Во втором примере выше кружок был выдолблен, указывает на то, что точка не входит в область определения функции. Поскольку точки не существует, предела в этой точке тоже не существует.

На самом деле это не непрерывные функции!

Ярлык «непрерывная правая функция» немного неверен, потому что это не непрерывные функции. Чтобы функция была непрерывной, правый предел должен быть равен f(a), а левый предел также должен быть равен f(a). В определении функции, непрерывной справа, ничего не говорится о том, что происходит слева от точки. Функция может быть там непрерывной, а может и не быть. Единственный способ узнать наверняка — рассмотреть также определение функции, непрерывной слева.

Равномерно непрерывная функция на заданном множестве A непрерывна в каждой точке на A. Это проверяется путем проверки окрестностей вокруг каждой точки, определяя небольшую область, в которой функция должна оставаться внутри.

Более формально это формулируется как:

Функция f : A → ℝ равномерно непрерывна на A, если для каждого числа ε > 0 существует δ > 0; всякий раз, когда x, y ∈ A и |x − y| < δ следует, что |f(x) − f(y)| < ε.

Это формальное определение в основном говорит о том, что нужно выбрать несколько значений ε, а затем найти δ, которое работает для всех значений x в наборе. Если работают одни и те же значения, функция соответствует определению.

График равномерно непрерывной функции

Графически найдите точки, где функция резко увеличивает или уменьшает кривизну . Определение не допускает таких больших изменений; Очень маловероятно, что вы сможете создать «коробку» одинакового размера, содержащую график. Функция может быть непрерывной, но она не является равномерно непрерывной.

Равномерно непрерывная функция g(x) = √(x) не выходит за края красного прямоугольника. Функция f(x) = 1/x проходит через верх и низ, поэтому не равномерно непрерывный. Изображение: Эскил Саймон Канне Вадшолт | Викисклад.

Игра здесь состоит в том, чтобы попытаться найти однородный ящик высотой x шириной = 2ε x 2 δ, который при перемещении сохранит граф, содержащийся внутри краев ящика. Таким образом, «однородная» часть определения относится к «коробке одинакового размера».

Свойства равномерно непрерывной функции

Эти функции имеют около общих свойств .

• Все эти функции ограничивает на отрезке [a, b] и достигает максимума на множестве (a, b).
• Всякая равномерно непрерывная функция также является непрерывной функцией. Однако 90–200 не все непрерывные функции равномерно непрерывны. Таким образом, вы можете думать об этих функциях как о «более» непрерывных.
• Они могут быть или не быть дифференцируемыми. Равномерная непрерывность не обязательно подразумевает дифференцируемость.

Все следующие функции, как правило, непрерывны:

• Функция абсолютного значения,
• Экспоненциальная функция,
• Логарифмическая функция,
• Все полиномиальные функции,
• Все силовые функции,
• Все тригонометрические функции.
• Естественная показательная функция e ^x (где e — число Эйлера)

Существует несколько общих правил , на которые можно ссылаться при попытке определить, является ли ваша функция непрерывной. Для некоторых функций вам нужно проделать небольшую детективную работу. (Более строгий подход см. в разделе «Проверка непрерывности»).

Sin(x) является примером непрерывной функции.

Шаг 1: Нарисуйте график карандашом , чтобы проверить непрерывность функции. Если ваш карандаш остается на бумаге слева направо на всем графике, не отрывая карандаша, ваша функция непрерывна. Другими словами, если ваш график имеет пробелы, дыры или является разделенным графиком, ваш график не является непрерывным.

Шаг 2: Выясните, есть ли ваша функция в списке непрерывных функций. Если да, то 902:00 дальше идти не надо; ваша функция непрерывна.

Шаг 3: Проверьте, является ли ваша функция суммой (сложением), разностью (вычитанием) или произведением (умножением) одной из непрерывных функций, перечисленных в шаге 2. Если да, то ваша функция непрерывна. Например, sin(x) * cos(x) является произведением двух непрерывных функций и поэтому является непрерывным.

Шаг 4: Проверьте свою функцию на возможность наличия нуля в знаменателе . Отношение f(x)/g(x) непрерывно во всех точках x, где знаменатель это не ноль. Другими словами, в точке x = 0 будет разрыв, что означает, что ваша функция не является непрерывной .

Вот и все!

Содержание (щелкните, чтобы перейти к этому разделу):

1. Непрерывная переменная
   • Интервальная переменная и шкала
   • Переменная соотношения и шкала
2. Дискретная переменная

Непрерывная переменная имеет бесконечное число потенциальных значений .
Это противоположность дискретной переменной, которая может принимать только конечное (фиксированное) число значений.

Посмотрите видео или прочитайте ниже:

Дискретные и непрерывные переменные

Посмотрите это видео на YouTube.

Непрерывная переменная Диапазон

Непрерывная переменная не обязательно должна включать каждых возможных чисел от отрицательной бесконечности до положительной бесконечности. В большинстве случаев он определяется в диапазоне. Например, диапазон может быть между 9и 10 или от 0 до 100. Несмотря на то, что эти диапазоны отличаются в 100 раз, они имеют бесконечное число возможных значений.

В качестве примера возьмем диапазон от 9 до 10 . Возможные непрерывные переменные включают:

• 9, 9.01, 9.001, 9.051, 9.000301, 9.000000801

.

Примеры непрерывных данных

Несколько примеров:

• Время, необходимое для бега на 100 м . Посмотрите любое спортивное мероприятие, рассчитанное на время, и вы увидите время, указанное с точностью до мельчайшей ширины волоса. На момент написания этой статьи мировой рекорд принадлежит Усэйну Болту в возрасте 9 лет.0,572 секунды.
• Ваш вес. Ваши весы в ванной, вероятно, округляют до одной десятой фунта, поэтому вы можете весить 151,1 фунта. Но вы действительно? Вы можете весить 151,14 или 151,143. Возможности для веса безграничны.
• Деньги. В далеком прошлом было время, когда деньги были конечными (это было количество банкнот и монет в обращении). С появлением банковской системы и криптовалюты «деньги» теперь неисчислимы.
• Цены на автомобили. Конечно, этот Форд может стоить вам 30 тысяч долларов прямо сейчас. Но что будет через 100 лет? 1000 лет? Цена автомобиля будет расти и расти. Вы можете возразить, что автомобили устареют в будущем, и, следовательно, есть момент, когда цены на автомобили достигнут максимума. Но у кого-то где-то будет древний автомобиль стоимостью в миллионы или миллиарды).

Рост и вес являются примерами величин, которые являются непрерывными переменными.

Дискретная переменная может принимать только значение определенное количество значений . Другими словами, у них нет бесконечного числа значений. Если вы можете сосчитать набор элементов, то переменные в этом наборе являются дискретными переменными.

Противоположностью дискретной переменной является непрерывная переменная. Непрерывные переменные могут принимать бесконечное количество возможностей.

Что такое дискретная переменная? Примеры

Некоторые примеры дискретных переменных:

• Количество монет в кошельке, банке или банке. Дискретно, потому что может быть только определенное количество монет (1, 2, 3, 4, 5…). Монеты не бывают в количестве 2,3 монеты или 10 ½ монет, поэтому невозможно бесконечное количество возможностей. Кроме того, кошелек или даже банк ограничены по размеру, поэтому монет может быть только определенное количество.
• Количество автомобилей на стоянке. Парковка может вместить только определенное количество автомобилей.
• Баллы по 10-балльной шкале. Если вы оцениваетесь по 10-балльной шкале, единственными возможными значениями являются 1, 2, 3, 4, 5, 6, 7, 8, 9и 10.
• Возраст на поздравительных открытках. Поздравительные открытки бывают только годами, а не дробями. Таким образом, существует конечное количество возможностей (предположительно, около сотни).

Дискретные случайные величины

Дискретные случайные переменные — это переменные, являющиеся результатом случайного события. Например, бросок игральной кости. Дискретные случайные величины обозначаются буквой X и имеют распределение вероятностей P(X). Если вы подбросили монету два раза и подсчитали количество решек, это дискретная случайная величина. Он представлен буквой X. X в этом случае может принимать только одну из трех возможных переменных: 0, 1 или 2 [решка].

Интервальная переменная — это просто любая переменная на шкале интервалов. Шкала интервалов имеет значимые интервалы между значениями. Интервалы между точками на шкале интервалов одинаковы. Например, разница между 10°C и 20°C такая же, как разница между 40°F и 50°F.

Интервальная переменная — это разновидность непрерывной переменной. Технически (и это действительно щепотка), шкала является интервальной переменной, а не самой переменной. Например, переменная 102°F находится на шкале интервалов; на самом деле вы бы не определили «102 градуса» как интервальную переменную. Это потому, что само по себе это довольно бессмысленно.

Проблемы с нулем

Даты являются переменными интервальной шкалы. Например, столетие длится 100 лет независимо от того, какой период времени вы измеряете: 100 лет между 29-м и 20-м веками — это то же самое, что 100 лет между 5-м и 6-м веками. Хотя это кажется интуитивно понятным, даты подчеркивают серьезную проблему с интервальными шкалами: 90–200 ноль является произвольным. Это означает, что вы должны быть очень осторожны при интерпретации интервалов. Например, в системе AD года 0 не существует (AD начинается с года 1). Однако некоторые календари включают ноль, например, буддийские и индуистские календари.

Произвольные нули означают, что нельзя сказать, что «1-е тысячелетие имеет такую ​​же длину, как и 2-е тысячелетие».

Это приводит к еще одной проблеме с нулями в шкале интервалов: ноль не означает, что чего-то не существует. Например, тот факт, что в календаре нашей эры нет нулевого года, не означает, что времени в тот момент не существовало. Наоборот, должно быть, потому что есть годы до 1 года нашей эры (до н.э.!). Точно так же нулевая температура не означает, что температуры в этой точке не существует (она должна существовать, потому что температура опускается ниже точки замерзания).

Произвольные нули также означают, что вы не можете вычислять коэффициенты. Шкалы отношений (которые имеют значащие нули) не имеют этих проблем, поэтому иногда предпочтение отдается именно этой шкале.

Вес измеряется на шкале отношений (никаких каламбуров!). Шкала отношений обладает всеми свойствами интервальной шкалы, а также фиксированным натуральным нулем.

Данные соотношения по этой шкале имеют измеримые интервалы. Например, разница между ростом в шесть футов и пять футов такая же, как интервал между двумя и тремя футами. Чем шкала отношений отличается от шкалы интервалов, так это тем, что она также имеет значащий ноль . Ноль означает, что что-то не существует или не имеет измеряемого свойства. Например, ноль на шкале температур Кельвина означает, что свойство температуры не существует при нуле.

Другие примеры шкалы соотношений:

• Возраст . Часы начинают тикать, когда вы рождаетесь, но возраст «0» технически означает, что вы не существуете.
• Вес . При 0 фунтах вы бы ничего не весили и, следовательно, не существовали бы.
• Высота . Если бы вы были 0″, у вас не было бы роста.
• Данные о продажах. Продажи, равные нулю, означают, что вы ничего не продали, поэтому продаж не было.
• Приобретенное количество . Если вы купили 0 товаров, то не было куплено ни одного количества.
• Время измеряется от «Большого взрыва».

Шкала отношений и отрицательные числа

Поскольку «0» на шкале отношений означает полное отсутствие чего-либо, на этой шкале нет отрицательных чисел.

Инвариантность при преобразовании подобия

Данные на шкале отношений инвариантны при преобразовании подобия, y=ax, a >0. Например, вы можете преобразовать фунты в килограммы с помощью преобразования подобия K = 2,2 P. Отношение остается неизменным, используете ли вы фунты или килограммы. Хотя шкала отношений описывается как имеющая «значимый» ноль, было бы точнее сказать, что она имеет значимое отсутствие свойства; Ноль на самом деле не является измерением чего-либо — это указание на то, что что-то не обладает измеряемым свойством. Например, 0 фунтов означает, что измеряемый предмет не имеет свойства «вес в фунтах».

Шкала отношений и отношения

Как следует из названия, мы можем создавать осмысленные отношения между числами на шкале отношений.
Например, количество тестов, которые вы сдали в прошлом семестре, может быть равно нулю, если вы не сдавали ни одного теста. Однако, если вы сдали два экзамена в этом семестре и четыре в прошлом семестре, вы можете сказать, что частота ваших тестов в этом семестре была вдвое меньше, чем в прошлом семестре.

Использование в математическом анализе

Шкалы измерения, такие как шкала отношений, редко упоминаются на занятиях по математическому анализу. Но в прикладном исчислении (т. е. в реальном мире) вы, вероятно, часто их используете. Например, экономические исследования с использованием векторного исчисления часто ограничены шкалой измерения; только те значения, которые образуют шкалу отношений, могут формировать поле (Nermend, 2009).).

Следующий :
Прерывистые функции

Ссылки

Изображение: Эскил Саймон Канне Вадшолт — собственная работа, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=50614728
Богачев, В. (2006). Теория меры, том 1 . Спрингер.
Карозерс, Н. Л. Реальный анализ. Нью-Йорк: Издательство Кембриджского университета, 2000.
Дартмутский университет (2005). Непрерывность. Получено 14 декабря 2018 г. с: https://math.dartmouth.edu//archive/m3f05/public_html/ionescuslides/Lecture8.pdf
Гуха, С. (2018). Компьютерная графика через OpenGL®: от теории к экспериментам. КПР Пресс.
Каплан, В. «Пределы и непрерывность». §2.4 в Advanced Calculus, 4-е изд. Чтение, Массачусетс: Addison-Wesley, стр. 82-86, 1992.
Ларсен, Р. Краткий расчет: прикладной подход.
Моррис, К. (1992). Академический пресс-словарь науки и техники. Эльзевир Наука.
Нерменд, К. (2009). Векторное исчисление в анализе регионального развития. Сравнительный региональный анализ на примере Польши.
Росс, К. (2013). Элементарный анализ: теория исчисления (тексты для студентов по математике), 2-е изд. Спрингер.
Титчмарш, Э. (1964). Теория функций, 2-е издание. Издательство Оксфордского университета.
Ценг, З. (н. д.). Непрерывность. Статья размещена на сайте PennState. Получено 14 декабря 2018 г. с: http://www.