График y log x: Логарифмическая функция

y = (log(x)/log(1/3))

Графики функций, Построение графиков Работа проверена: user814242 Время решения: 13 мин Сложность: 4.8

Дано

$$f{left (x right )} = frac{log{left (x right )}}{log{left (frac{1}{3} right )}}$$

График функции

Точки пересечения с осью координат X

График функции пересекает ось X при f = 0
значит надо решить уравнение:
$$frac{log{left (x right )}}{log{left (frac{1}{3} right )}} = 0$$
Решаем это уравнение
Точки пересечения с осью X:

Аналитическое решение
$$x_{1} = 1$$
Численное решение
$$x_{1} = 1$$

Точки пересечения с осью координат Y

График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в log(x)/log(1/3).
$$frac{log{left (0 right )}}{log{left (frac{1}{3} right )}}$$
Результат:
$$f{left (0 right )} = tilde{infty}$$

зн. {2}} f{left (x right )} = $$
Решаем это уравнение
Решения не найдены,
возможно перегибов у функции нет

Горизонтальные асимптоты

Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo
$$lim_{x to -infty}left(frac{log{left (x right )}}{log{left (frac{1}{3} right )}}right) = -infty$$
Возьмём предел
значит,
горизонтальной асимптоты справа не существует

Наклонные асимптоты

Наклонную асимптоту можно найти, подсчитав предел функции log(x)/log(1/3), делённой на x при x->+oo и x ->-oo
$$lim_{x to -infty}left(frac{log{left (x right )}}{x log{left (frac{1}{3} right )}}right) = 0$$
Возьмём предел
значит,
наклонная совпадает с горизонтальной асимптотой слева

Чётность и нечётность функции

Проверим функци чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
$$frac{log{left (x right )}}{log{left (frac{1}{3} right )}} = frac{log{left (- x right )}}{log{left (frac{1}{3} right )}}$$

– Нет
$$frac{log{left (x right )}}{log{left (frac{1}{3} right )}} = – frac{log{left (- x right )}}{log{left (frac{1}{3} right )}}$$
– Нет
значит, функция
не является
ни чётной ни нечётной

   

Графики функций | Олимпиадный Центр МатРИЦА

Перейти к содержанию

27 Фев 2018

adminEGE, Математика

Графики функций, формулы функций.

Линейная, степенная, парабола, гипербола

Название функции	Формула функции	График функции	Название графика	Примечание
Линейная	y = kx		Прямая	Линейная зависимость — прямая пропорциональность у = kx, где k ≠ 0 — коэффициент пропорциональности.
Линейная	y  = kx + b		Прямая	Линейная зависимость: коэффициенты k и b — любые действительные числа. (k = 0.5, b = 1)
Квадратичная	y = x2		Парабола	Квадратичная зависимость: симметричная парабола с вершиной в начале координат.
Квадратичная	y = xn		Парабола	Квадратичная зависимость: n — натуральное четное число > 1
Степенная	y = xn		Кубическая парабола	Нечетная степень: n — натуральное нечетное число > 1
Степенная	y = x1/2		График функции y = √x	Степенная зависимость (x1/2 = √x).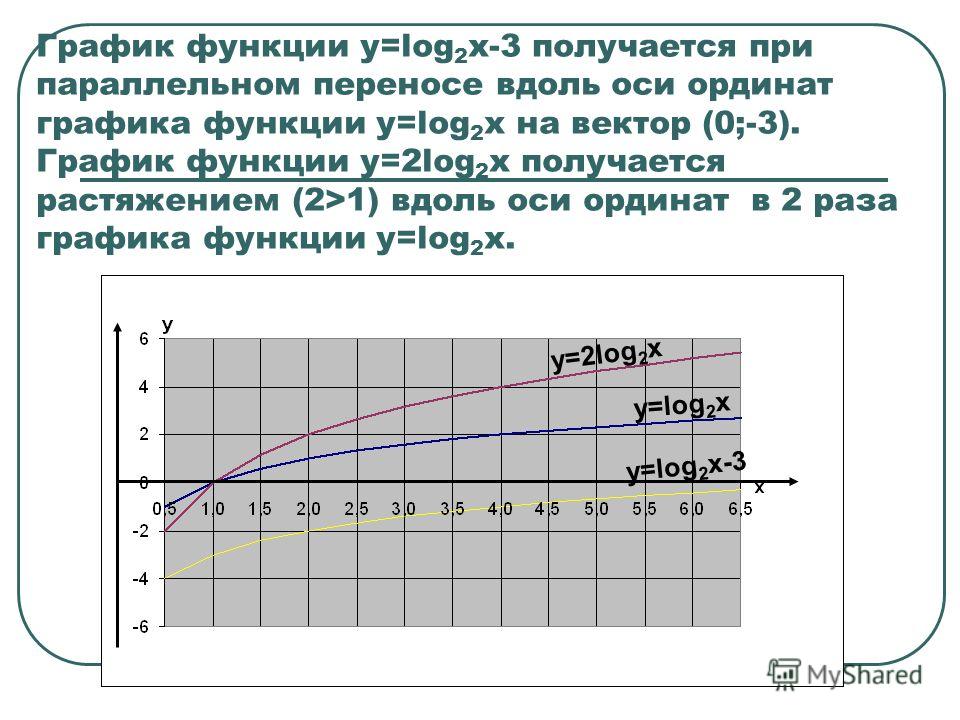
Степенная	y = k/x		Гипербола	Случай для целой отрицательной степени (1/x = x-1). Обратно-пропорциональная зависимость. (k = 1)
Показательная	y = ax		График показательной функции	Показательная функция для a > 1.
Показательная	y = ax		График показательной функции	Показательная функция для 0 < a < 1.
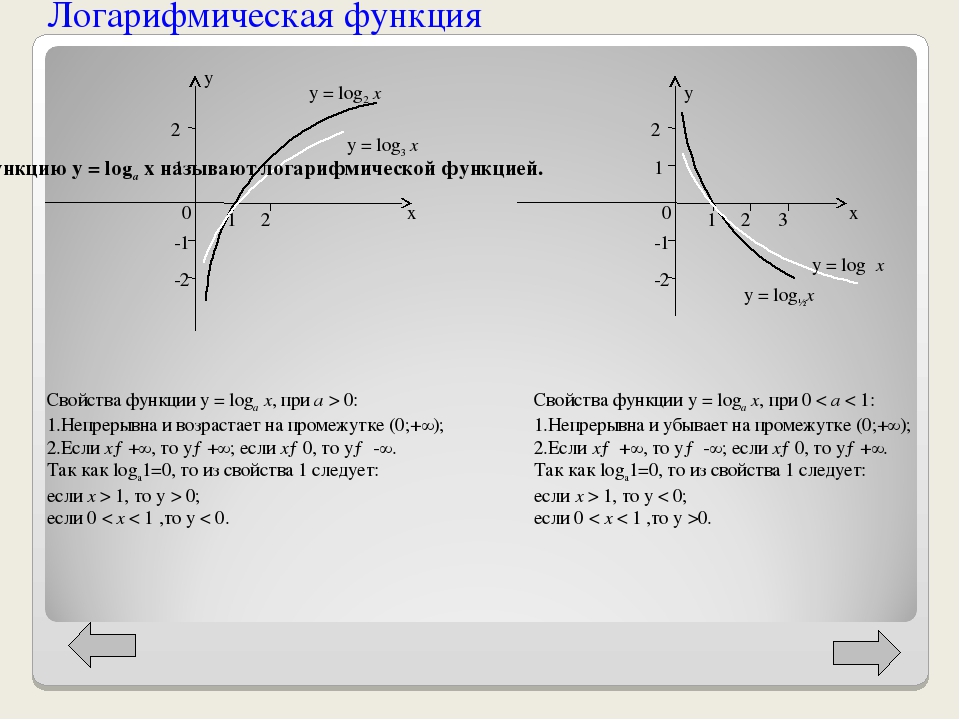
Логарифмическая	y = logax		График логарифмической функции	Логарифмическая функция: a > 1.
Логарифмическая	y = logax		График логарифмической функции	Логарифмическая функция: 0 < a < 1.
Синус	y = sinx		Синусоида	Тригонометрическая функция синус.
Косинус	y = cosx		Косинусоида	Тригонометрическая функция косинус.
Тангенс	y = tgx		Тангенсоида	Тригонометрическая функция тангенс.
Котангенс	y = сtgx		Котангенсоида	Тригонометрическая функция котангенс.

Решение задач, курсовых, выполнение дипломных работ, Вы сможете заказать здесь >>> https://student-servis.ru/

вертикальных сдвигов | Wyzant Спросите эксперта

Логарифмы Предварительное исчисление Логарифмические функции Вертикальные сдвиги Логарифмические функции Свойства журналов

Асма А.

спросил 18.03.14 График

y=logx, y=log(10x) и y=log(100x). как сравнить графики? используйте свойство журналов, чтобы показать, что графики представляют собой вертикальные сдвиги друг друга.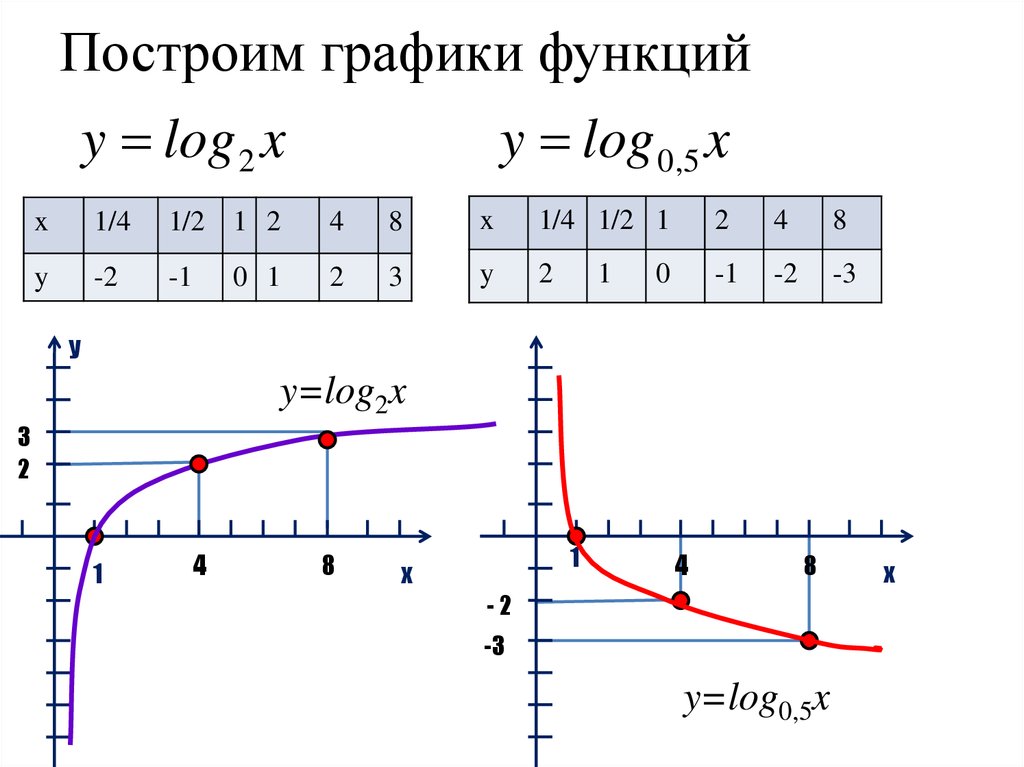

Подписаться І 2

Подробнее

Отчет

2 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Стив С. ответил 18.03.14

Репетитор

5 (3)

Обучение предварительному исчислению, тригонометрическому исчислению и дифференциальному исчислению

Смотрите подобных репетиторов 92) + log(x) = log(x) + 2 = f(x) + 2

Итак, g — это f, сдвинутое вверх на 1, а h — это f, сдвинутое вверх на 2.

Эрик также объяснил расширение («Дорогой, я уменьшился дети!»), но это не нужно для этой задачи.

Вот график GeoGebra трех функций:
http://www.wyzant.com/resources/files/265623/logs_translated

Голосовать за 0 голос против

Подробнее

Отчет

Эрик Ю.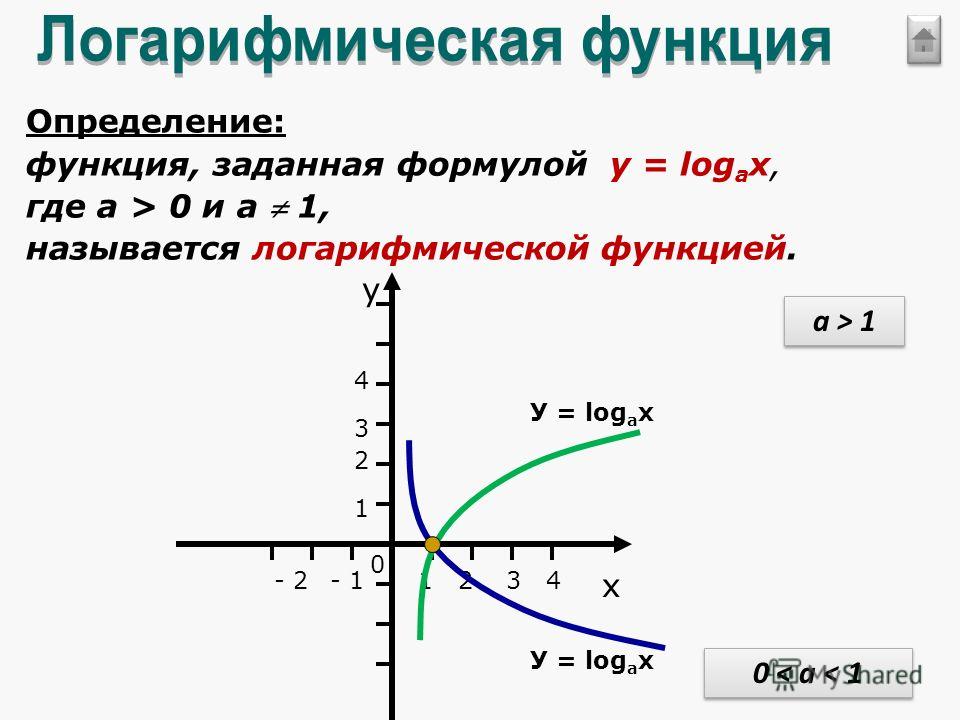 ответил 18.03.14

Репетитор

5 (5)

Подготовка к SAT

Смотрите таких репетиторов

Смотрите таких репетиторов

Есть несколько разных идей, которые вам нужно знать.

 

ПОНЯТИЯ ФУНКЦИИ ГРАФИКА

При построении графика y = f(x)…

 

Растяжение/сжатие

Замена x на (ax) означает горизонтальное растяжение/сжатие. y = f(ax)

Умножение для получения y = a*f(x) представляет собой вертикальное растяжение/сжатие.

 

Вы также должны помнить

Для вертикальных перемещений, если a>1, график растягивается по вертикали.

Для горизонтальных перемещений, если a>1, график сжимается по горизонтали.

 

Сдвиги

Замена x на (x-b) означает сдвиг по горизонтали. Перемещает весь график влево или вправо

y = f(x) + b — сдвиг по вертикали. Перемещает весь график вверх или вниз

 

 

В этом случае функция y= f(x) равна y=logx.

СОБСТВЕННОСТЬ ЛОГА

log _x (a*b) = log

x (a)+log _x (b)

 

Если основание x принято, оно не отображается, x равно 10.

 

log ₁₀ (10 ^a ) = a

—————————- ————-

Итак, зная все это, теперь мы можем приступить к проблеме… Ух ты.

 

y = logx      И     y = log10x

 

y = log(10x), мы заменяем x на 10x. x>1 Следовательно, это горизонтальное сжатие .

 

y = log10x = log10 + logx

y = 1+logx

y = logx + 1   Следовательно, это вертикальное смещение от y = logx. График движется вверх на 1.

 

Я знаю, что информации много, но если вы потратите время на то, чтобы понять все эти идеи, вы, скорее всего, опередите свой класс!

 

Голосовать за 0 голос против

Подробнее

Отчет

Все еще ищете помощи? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

Экспоненциальные и логарифмические функции Графики логарифмических функций

• Главная /
• Предварительный расчет /
• Экспоненциальные и логарифмические функции /
• Темы /
• Логарифмические функции /
• Графики логарифмических функций

• Logarithmic Functions /
• Графики Logarithmic Functions
2142142142142114141414141491421414141491414141491414141491414141411414141141411414149н.
• Введение
• Темы
• Экспоненциальные функции
• Логарифмические функции
• Основы
• Графики логарифмических функций
• Естественный логарифм
• Решение экспоненциальных и логарифмических уравнений
• В реальном мире
• Примеры
• Упражнения
• Викторины
• Условия
• Раздаточный материал
• Лучшее из Интернета
• Содержание
• НАЗАД
• СЛЕДУЮЩИЙ

Представьте, что ваш мир перевернулся с ног на голову.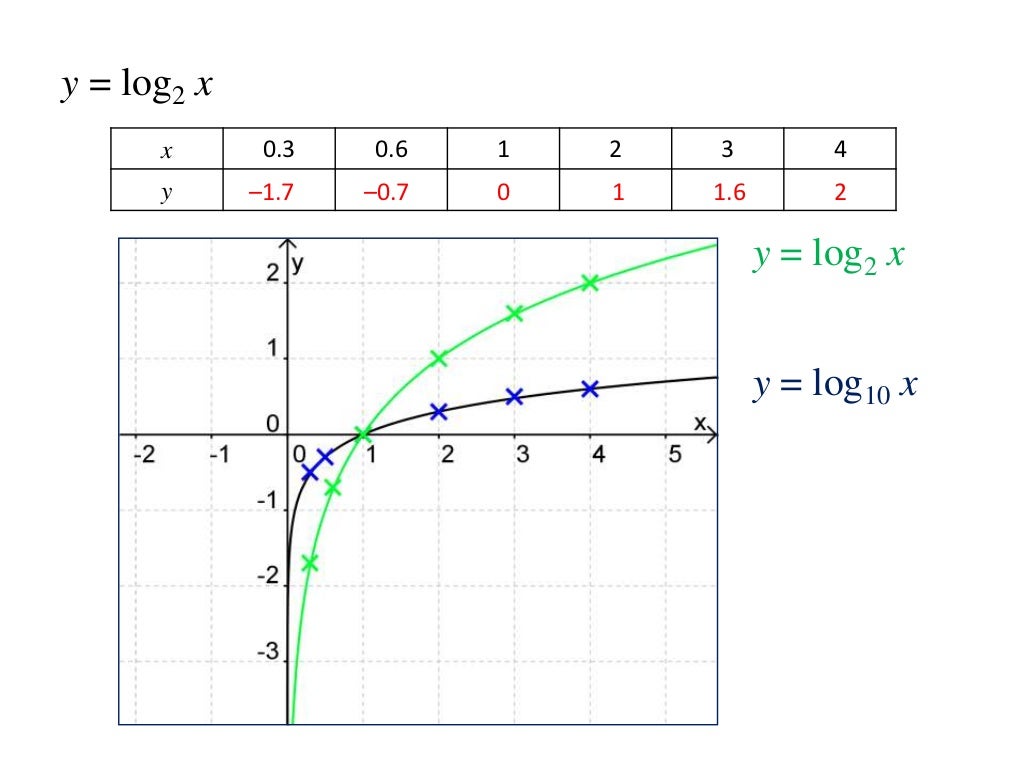 Именно это произошло с экспоненциальной функцией, и в этом разделе мы исследуем инверсия экспоненциальной функции… барабанная дробь, пожалуйста… График логарифмической функции. Мы говорим о графиках логарифмических функций и о том, что они имеют вертикальную асимптоту (по сравнению с горизонтальной у экспоненциальных функций). Мы не забудем такие хорошие вещи, как домен и диапазон. Мы также дадим вам несколько советов по нанесению этих графических изображений на технологии.

Поскольку мы уже решили, что логарифмы обратны степенной функции, мы можем видеть, что когда мы наносим их на график, они симметричны относительно диагональной линии y = x , что составляет угол 45 градусов с началом координат. Хм?

Выборка задачи

График y = 10 ^x , y = log ₁₀ x и y = x для значений

. вот игра за игрой приведенного выше графика:
• Красная линия y = 10 ^x .
   
• Синяя линия — г = логарифм ₁₀ х .
   
• Зеленая линия равна y = x .
   
• Красная и синяя линии не похожи друг на друга.

Каждая обратная функция является отражением от диагональной линии y = x . Чтобы подумать об этом в реальном мире, представьте, что вы опираетесь на прилавок под углом 45 градусов и смотрите в зеркало. Если вам повезет, вы можете смотреть прямо на свою обратную сторону. Или вы можете понять, что вам нужно почистить зеркало.

Логарифмические графики просто странные. Во-первых, они отличаются тем, что имеют вертикальную асимптоту 90 277, а не горизонтальную асимптоту 90 278.

Пример задачи

График y = log ₂ x for x > 0.

нужно преобразовать логарифм по основанию 2 в основание 10. Вот как вы это делаете:

Вместо использования:

y = log ₂ x

Используйте это:

Вы можете получить что-нибудь, чтобы преобразовать арифметику в логарифм. калькулятор, просто разделите логарифм функции x (которая, естественно, является основанием 10) на логарифм базы, в которой вы находитесь. = журнал ₄₀ x и объясните различия:

Мы изобразим и так, чтобы каждая функция находилась в одном и том же основании (десятичный десятичный логарифм).

Вот некоторые качества этого графика выше

• Красная функция y = log ₄₀ x .
    
• Синяя функция y = log ₄ x .
   
• График выглядит странно, потому что мы показываем вам минус 9Значения 0088 x также являются воображаемыми значениями (мы обычно не отображаем их на графике), но мы подумали, что будет интересно посмотреть.

  No related posts.