|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении… Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь… Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда… Интересное: Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным. Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
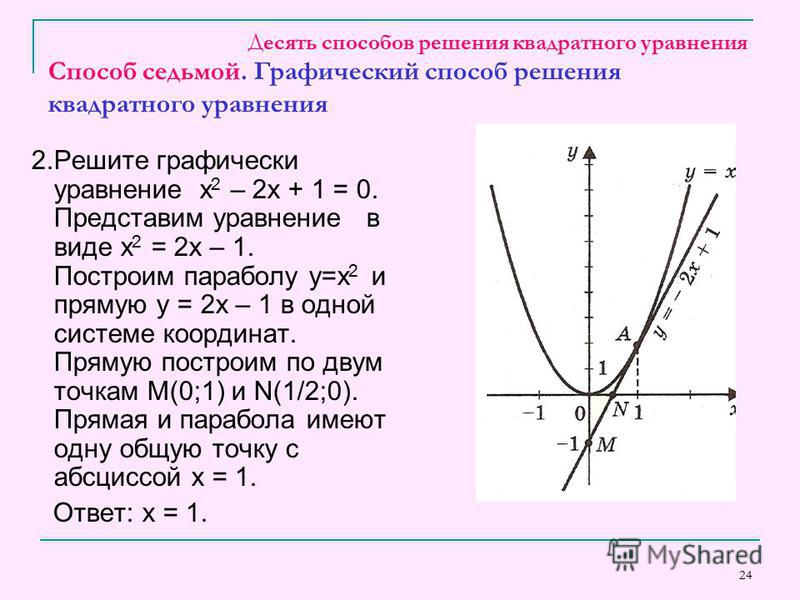
⇐ ПредыдущаяСтр 8 из 10Следующая ⇒ Цель работы: Ознакомиться с графическими методами решения уравнений и систем уравнений. Основные теоретические положения.Кроме аналитического способа решения уравнений f(x) = 0 можно пользоваться и графическим способом. Графический способ наиболее эффективен для решения трансцендентных уравнений. При графическом способе для уравнения строится график y = f(x) и решением уравнения является точка пересечения графика с осью х при у = 0. Если разбить уравнение на две произвольные части, то можно для каждой части построить график. В этом случае решением уравнения будет абсцисса точки пересечения графиков для этих частей. Такой способ может использоваться и для решения систем двух линейных уравнений с двумя неизвестными. Порядок выполнения работы Задание 1. Решить графически уравнение y = cos2(px) на интервале [0; 1]. Задание 2. Решить графически уравнение х3 – 4х2 – 3х + 6 = 0. Задание 3. Решить графически систему уравнений в диапазоне хÎ[0; 3] с шагом Dх = 0,2. |
12.1.2. Построение графика функции (см. Работу 11).
В результате получим график (рис. 31). Из графика видно, что уравнение имеет единственный корень. Что-бы получить точное решение уравнения, нужно щелкнуть левой клавишей мыши по точке пересечения графика с осью ОХ. На графике появится текст (рис. 32).
Здесь Точка “0,5” – значение х
Значение “4,633Е-05”»0 – значение у.
12.2. Выполнение задания 2
Найдем графическое решение уравнения х3-4х2-3х+6=0.
Для этого представим его в виде
х3 = 4х2 + 3х – 6 (2)
и построим на одной диаграмме графики двух функций:
у1 = х3 левая часть уравнения (2) и
у2 = 4х2 + 3х – 6 правая часть уравнения (2)
Рис. 32. График функции y=cos2(px)
32. График функции y=cos2(px)
Так как мы ищем корни кубического уравнения, число корней должно быть равно трем. Заранее значения корней неизвестны, поэтому сначала возьмем для построения графиков интервал
Очевидно, что если корней должно быть три, то точек пересечения функций у1 и у2 тоже будет три. Если точек пересечения окажется меньше, нужно увеличить рассматриваемый интервал (например, построить график на интервале хÎ[–3; 3]).
12.2.1. Открыть новый рабочий лист (Щелчок правой клавишей по имени имеющегося листа – Добавить – Лист).
12.2.2. Провести табуляцию значений аргумента х и функций у1 и у2 (см. Работу 11). В результате получим табл.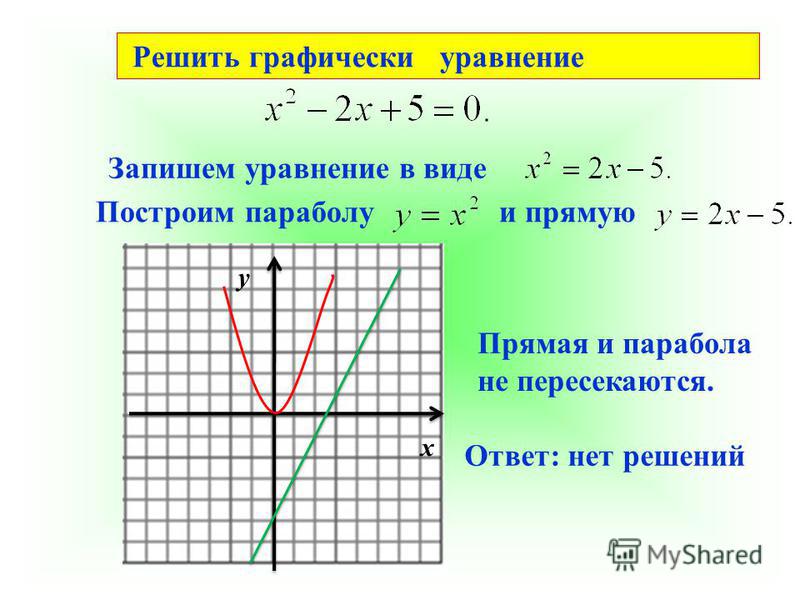 2+3*A13-6
2+3*A13-6
Рис. 33. Решение уравнения х3-4х2-3х+6=0.
12.2.3. Для нахождения третьего корня нужно увеличить диапазон решения. Из графика видно, что при х<–2 функции у1 и у2 расходятся.
Значит, решение нужно искать при х>2. Увеличим диапазон до х = 4,8, т. е. хÎ[–2; 4,8]:
а) продолжить табулирование аргумента х до ячейки А20;
б) скопировать формулу из ячейки В13 в ячейки В14:В20;
в) скопировать формулу из ячейки С13 в ячейки С14:С20;
г) построить график для этого случая. На этом графике функции у1 и у2 пересекаются трижды. Третий корень х3 = 4,4.
12.3. Выполнение задания 3
Решить графически систему уравнений значит найти координаты точек, в которых пересекаются графики функций, входящих в систему уравнений.
При выполнении задания 2 мы решили практически систему уравнений
.
Для нахождения корней уравнений системы
в диапазоне хÎ[0; 3] с шагом Dх = 0,2, следует выполнить следующие действия.
12.3.1. Добавить новый рабочий лист
12.3.2. Провести табулирование переменных х, y = sin x, y = cos x, аналогично Работе 11 и пп. 12.1, 12.2 данной работы:
— в ячейку А1 ввести заголовок Аргумент х, в ячейку А2 – значение 0, в ячейку А3 — значение 0,2 и провести табуляцию аргумента х в ячейках А2:А17;
— в ячейку В1 ввести заголовок y = sin(x);
— в ячейку В2 ввести формулу =SIN(A2) и скопировать ее в ячейки В3:В17;
— в ячейку С1 ввести заголовок y = cos(x);
— в ячейку С2 ввести формулу =COS(A2) и скопировать ее в ячейки C3:C17.
12.2.3. Построить график функций y = sin x, y = cos x на одной диаграмме:
а) выполнить команды Вставка – Диаграмма (Вставка – График);
б) в первом диалоговом окне Мастера диаграмм выберем Тип диаграммы График, Вид — Левый верхний, Далее;
в) во втором окне Мастера диаграмм на вкладке Диапазон данных ввести:
Диапазон В2:С17
Ряды в: столбцах;
Затем щелкнуть по вкладке Ряд и ввести:
Подписи оси Х А2:А17 ;
Щелкнуть по кнопке Далее;
г) в третьем окне Мастера диаграмм ввести:
Название диаграммы Система
Ось Х Аргумент
Ось У
щелкнуть по кнопке Далее;
д) на последнем шаге Мастера диаграмм выбрать опцию
На отдельном листеи щелкнуть Готово.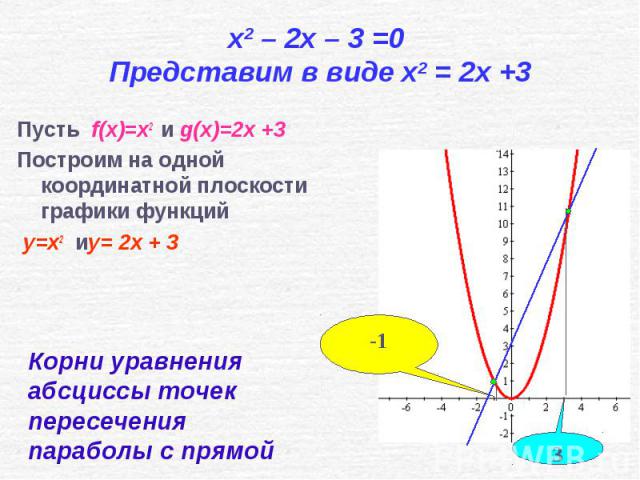
На полученном графике (рис. 34) видно, что в указанном диапазоне система имеет единственное решение (графики имеют только одну точку пересечения).
Рис. 34. Решение системы уравнений
Для нахождения решения:
— поставить указатель мыши в точку пересечения графиков;
— щелкнуть левой клавишей мыши. Появится надпись с указанием приблизительного решения системы уравнений:
Ряд “y=cos(x)” Точка “0,8”
Значение: 0,6967067
Следовательно, решением уравнения являются:
х = 0,8
у = 0,697.
12.4. Выполнение задания 4
12.4.1. Выбрать из табл. 11 индивидуальное задание
по указанию преподавателя.12.4.2. Добавить новый рабочий лист.
12.4.3. Графически решить систему уравнений в указанном диапазоне с заданным шагом по индивидуальному заданию.
Таблица 11
| № варианта | Система уравнений | Диапазон изменения аргумента | Шаг изменения Аргумента Dх |
| хÎ[0,2;3] | Dx=0,2 | ||
| хÎ[0,2;3] | Dx=0,2 | ||
| хÎ[0;2] | Dx=0,1 | ||
| хÎ[0,2;3] | Dx=0,1 | ||
| хÎ[0;2] | Dx=0,2 | ||
| | Dx=0,1 | ||
| хÎ[0;2] | Dx=0,2 | ||
| хÎ[0;2] | Dx=0,1 | ||
| хÎ[0;2] | Dx=0,1 | ||
| хÎ[0,2;3] | Dx=0,2 |
Отчет по работе: Распечатка графиков.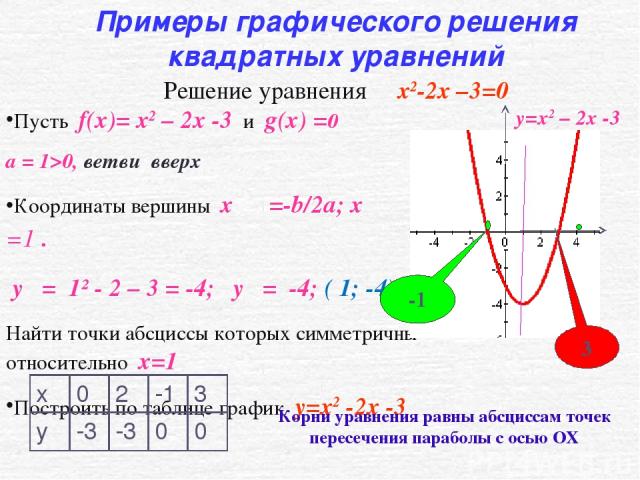
13. Приближенное решение уравнений
Цель работы: Изучение работы с процедурой Подбор параметра.
Основные теоретические положения. Нахождение корней уравнения вида f(x) = 0 даже в случае алгебраических уравнений третьей степени достаточно сложно. Поэтому широко используется приближенное решение уравнений.
Обычно применяют итерационные методы, когда сначала выбирают некоторое начальное приближение х(0), затем вычисляют последовательные приближения к истинному значению х.
В Excel для приближенного решения уравнений используются процедуры Подбор параметра и Поиск решений. В данной работе мы познакомимся с использованием процедуры Подбор параметра.
Порядок выполнения работы
Задание 1. Решить уравнение ln x=0.
Задание 2. Решить уравнение х2-3х+2=0.
Задание 3.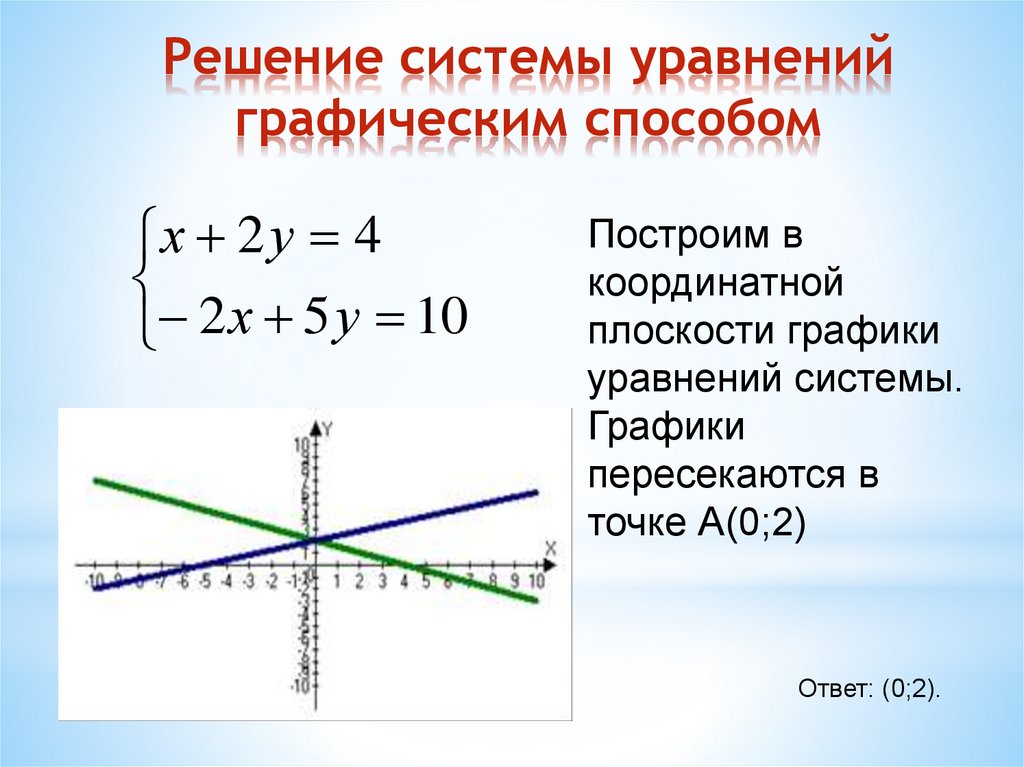 Решить уравнение согласно индивидуальному заданию.
Решить уравнение согласно индивидуальному заданию.
13.1. Выполнение задания 1
13.1.1. Создать новую рабочую книгу (команды Файл – Создатьпри работесExcel 2003или кнопкаOffice – Создатьпри работе сExcel 2007).
13.1.2. В ячейку А1 введем заголовок Приближенное значение корня.
13.1.3. В ячейку В1 вводим заголовок Левая часть уравнения.
13.1.4. В ячейку А2 вводим первое приближенное значение корня, например число 3.
13.1.5. В ячейку В2 вводим формулу для вычисления левой части уравнения в зависимости от аргумента х: =LN(A2).
Фрагмент получившейся таблицы в режиме показа вычислений приведен в табл. 12, а в режиме показа формул – в табл. 13.
|
Таблица 12
| A | B | |
| Приближенное значение корня | Левая часть уравнения | |
| 1,098612289 |
13. 1.6. Для получения приближенного решения уравнения обратимся к процедуре Подбор параметра.
1.6. Для получения приближенного решения уравнения обратимся к процедуре Подбор параметра.
а) Для вызова процедуры Подбор параметра выполнить команды Сервис – Подбор параметра(при работе сExcel 2007выполняем команды: менюДанные –вкладкаРабота с данными – Подбор параметра).
б) в появившемся диалоговом окне Подбор параметра ввести:
Установить в ячейке В2
Значение 0
Изменяя значение ячейки А2
и щелкнуть по кнопке Ок;
в) в появившемся диалоговом окне Результат подбора параметра щелкнем по Ок,чтобы сохранить полученные результаты.
В ячейке А2 получаем приближенное значение корня х=0,999872.
При этом погрешность решения показана в ячейке в ячейке В2: вместо 0 (значение правой части уравнения при его решении) там находится значение
– 0,00013.
Если округлить корень, получим х = 1, что и является известным аналитическим решением уравнения ln x = 0.
13.2. Выполнение задания 2
При решении уравнения х2 – 3х + 2 = 0 очевидно, что должны быть получены два корня. Значит, придется дважды задавать начальное приближение корня и обращаться к процедуре Подбор параметра.
13.2.1. Открыть новый рабочий лист (щелчок правой клавишей мыши по имени любого листа — Добавить — Лист).
13.2.2. В ячейку А1 ввести заголовок Приближенное значение первого корня.
13.2.3. В ячейку В1 ввести заголовок Приближенное значение второго корня.
13.2.4. В ячейку С1 внести заголовок Левая часть уравнения.
13.2.5. В ячейку А2 внести ориентировочное значение первого корня, например, число +3.
13.2.6. В ячейку С2 вводим формулу для вычисления левой части уравнения:
=А2^2-3*A2+2
13. 2-3*В2+2.
2-3*В2+2.
13.2.9. Повторить процедуру поиска приближенного решения уравнения:
а) Сервис – Подбор параметра (Данные –вкладкаРабота с данными – Подбор параметра);
б) ввести:
Установить в ячейке С2
Значение 0
Изменяя значение ячейки В2
щелкнуть по Ок;
в) щелкнуть по Ок в окне Результат подбора параметра.
В ячейке В2 получим приближенное значение второго корня: х2=0,9996.
13.3. Выполнение задания 3
13.3.1. Выбрать из табл. 14 индивидуальное задание согласно указанию преподавателя.
13.3.2. Добавить новый лист
13.3.3. Найти корни уравнения по индивидуальному заданию.
Таблица 14
| № варианта | Уравнение | № варианта | Уравнение |
| х3-3х2+х=0 | х3+х2-6х=0 | ||
| х3-7х+6=0 | х3+0,5х2-3,5х-3=0 | ||
| х3+2х2-5х-6=0 | х3+0,5х2-3х=0 | ||
| х3+3х2-4х-12=0 | х3-1,5х2-2,5х+3=0 | ||
| х3—х2-8х-12=0 | х3-3,5х2-1,5х+9=0 |
Отчет по работе: Распечатки таблиц с найденными значениями корней уравнений.
⇐ Предыдущая12345678910Следующая ⇒
Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции…
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим…
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций…
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)…
Графический метод решения уравнений: описание метода, примеры
Эта статья посвящена одному из направлений функционально-графического метода решения уравнений, а именно, графическому методу. Сначала дано описание графического метода: раскрыта его суть, сказано, на чем базируется метод, приведено его обоснование, обговорены особенности метода, связанные с точностью. Дальше идет практическая часть: записан алгоритм решения уравнений графическим методом и показаны решения характерных примеров.
Дальше идет практическая часть: записан алгоритм решения уравнений графическим методом и показаны решения характерных примеров.
В чем состоит метод и на чем он базируется
Графический метод решения уравнений состоит в использовании графиков функций, отвечающих частям уравнения, для нахождения с их помощью решения уравнения. Базируется он на следующем утверждении:
Утверждение
Решение уравнения f(x)=g(x) есть множество абсцисс точек пересечения графиков функций y=f(x) и y=g(x).
Обоснованием этого утверждения займемся в следующем пункте. А сейчас выудим из него полезные сведения.
Основное из них таково: по количеству точек пересечения графиков функций y=f(x) и y=g(x) можно судить о количестве корней уравнения f(x)=g(x), а по абсциссам точек пересечения можно судить о корнях этого уравнения. Проиллюстрируем сказанное.
Взглянем на чертеж, на котором изображены графики функций и .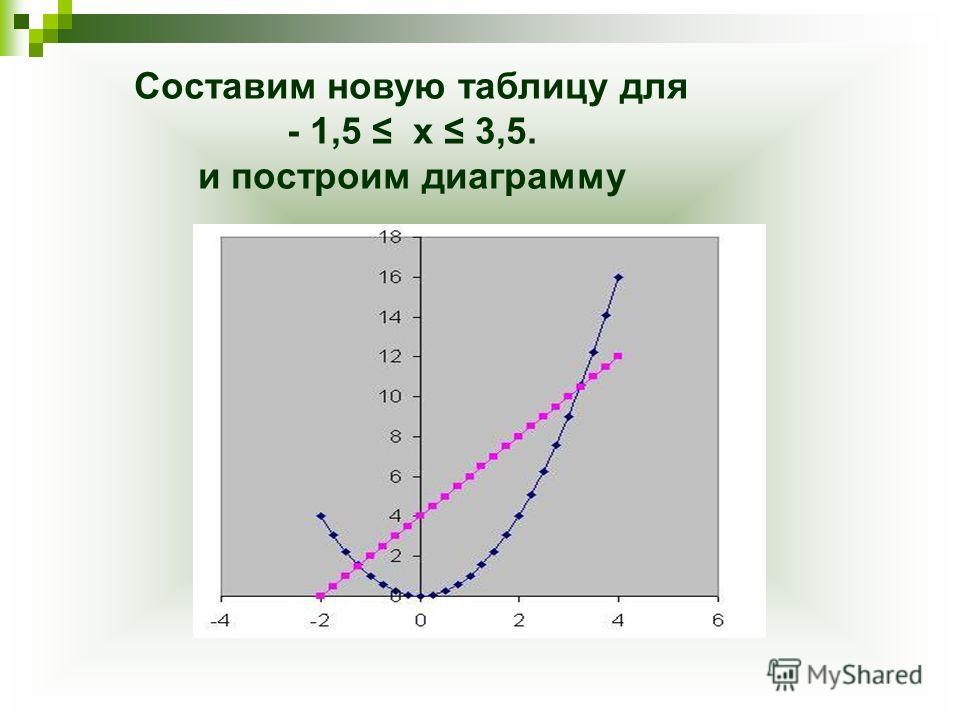
Очевидно, в видимой области графики изображенных функций не имеют точек пересечения. За пределами видимой области графики тоже не имеют точек пересечения. Это мы можем утверждать в силу известного нам поведения графиков степенных функций и линейных функций. Отсутствие точек пересечения позволяет нам сделать вывод, что уравнение не имеет решений.
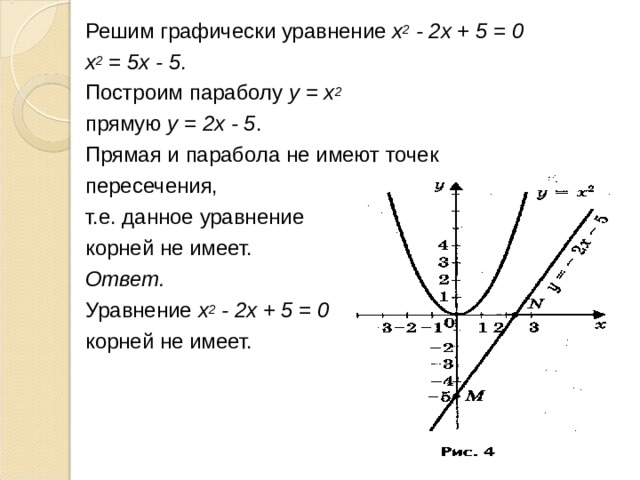
Другой пример. На следующем рисунке изображены графики функций и .
Сколько точек пересечения мы видим? Две. Известное поведение графиков показательных функций и линейных функций позволяет утверждать, что за пределами видимой области точек пересечения нет. Значит, графики функций и пересекаются в двух точках, следовательно, уравнение имеет два корня. А каковы значения этих корней? Для ответа на этот вопрос определяем абсциссы точек пересечения графиков. По рисунку находим, что абсциссы точек пересечения есть −2 и 1.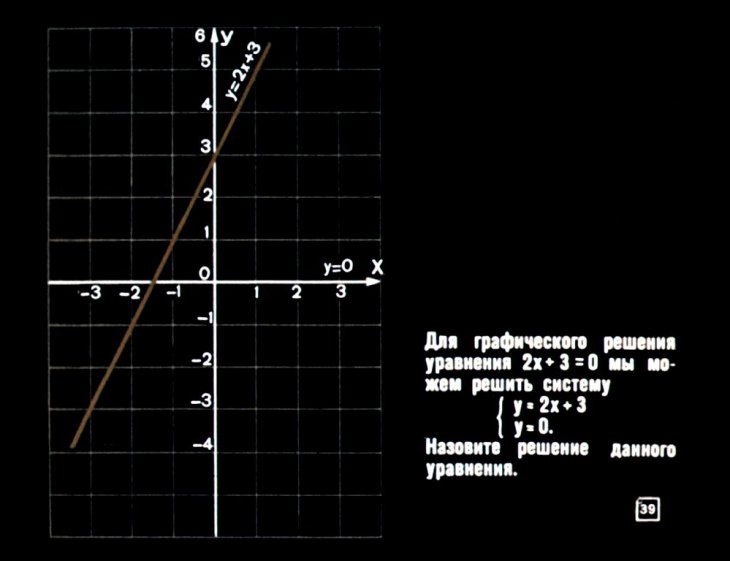 Через проверку подстановкой убеждаемся, что это действительно корни уравнения :
Через проверку подстановкой убеждаемся, что это действительно корни уравнения :
Здесь стоит заметить, что к проверке подстановкой мы обратились не случайно. Дело в том, что найденные по графикам значения корней можно считать лишь приближенными до проведения проверки. Подробнее об этом мы поговорим в одном из следующих пунктов этой статьи, раскрывающем особенности графического метода.
К началу страницы
Обоснование метода
Докажем, что множество решений уравнения f(x)=g(x) есть множество абсцисс точек пересечения графиков функций y=f(x) и y=g(x). Для этого достаточно показать, во-первых, что если x0 – корень уравнения f(x)=g(x), то x0 – это абсцисса одной из точек пересечения графиков функций y=f(x) и y=g(x), и, во-вторых, если x0 – абсцисса одной из точек пересечения графиков функций y=f(x) и y=g(x), то x0 – корень уравнения f(x)=g(x). Приступаем к доказательству.
Пусть x0 – корень уравнения f(x)=g(x). Тогда f(x0)=g(x0) – верное числовое равенство. Это равенство можно трактовать так: значения функции y=f(x) и y=g(x) в точке x0 совпадают. А из этого следует, что x0 – абсцисса одной из точек пересечения графиков функций y=f(x) и y=g(x).
Первая часть доказана. Переходим к доказательству второй части.
Пусть x0 – абсцисса одной из точек пересечения графиков функций y=f(x) и y=g(x). Это означает, что значения функций y=f(x) и y=g(x) в точке x0 равны, значит, f(x0)=g(x0). А из этого равенства следует, что x0 – корень уравнения f(x)=g(x).
Так доказана вторая часть.
К началу страницы
Особенности метода
Графический метод предполагает использование графиков функций.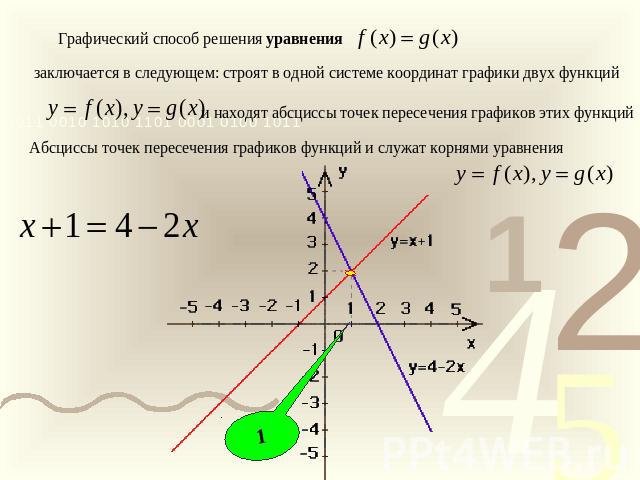 В общем случае построение графиков функций – дело непростое. Поэтому, графический метод решения уравнения обычно применяется лишь тогда, когда функции, отвечающие частям уравнения, довольно простые в плане построения графиков, и при этом не видно другого аналитического метода решения. Это одна из особенностей графического метода решения уравнений.
В общем случае построение графиков функций – дело непростое. Поэтому, графический метод решения уравнения обычно применяется лишь тогда, когда функции, отвечающие частям уравнения, довольно простые в плане построения графиков, и при этом не видно другого аналитического метода решения. Это одна из особенностей графического метода решения уравнений.
Другая особенность касается получаемых по графикам результатов. Полученные по графикам результаты можно считать лишь приближенными. Дело здесь в том, что сами по себе графики функций — вещь не совсем точная (но при этом очень наглядная и во многих отношениях удобная), особенно если говорить о графиках, построенных от руки. Это следует из принципов, которыми мы руководствуемся при построении графиков функций. Что мы делаем для построения графика функции в общем случае? Проводим исследование функции, чтобы получить ряд «опорных» точек, таких как граничные точки области определения, максимумы-минимумы, точки перегиба, и понять поведение функции на всех интервалах ее области определения. После этого определяем несколько контрольных точек. Дальше переносим все определенные в ходе исследования точки на координатную плоскость и, сейчас внимание, соединяем их плавной линией в соответствии с выясненным в ходе исследования поведением функции. Эта «плавная линия» и есть график функции. О какой точности можно здесь говорить? Понятно, что она определяется точностью нашего построения.
После этого определяем несколько контрольных точек. Дальше переносим все определенные в ходе исследования точки на координатную плоскость и, сейчас внимание, соединяем их плавной линией в соответствии с выясненным в ходе исследования поведением функции. Эта «плавная линия» и есть график функции. О какой точности можно здесь говорить? Понятно, что она определяется точностью нашего построения.
С приближенными, найденными по графикам, значениями корней уравнения можно так или иначе работать. В некоторых случаях определенные по графикам значения корней оказываются точными значениями, в чем позволяет убедиться проверка подстановкой. В других случаях есть возможность уточнить значения корней до требуемой степени точности, для этого существуют специальные методы уточнения значений корней. А вот если по графикам нет возможности определить количество корней, не говоря уже об их значении, то, почти наверняка, стоит отказываться от графического метода решения уравнения. Добавим наглядности сказанному.
Добавим наглядности сказанному.
Давайте посмотрим на изображенные в одной прямоугольной системе координат графики функций и y=−x2+6·x−5.
По этому чертежу сложно судить даже о количестве корней уравнения , не говоря уже про их значения с приемлемой степенью точности. Здесь можно лишь грубо сказать, что если корни есть, то их значения находятся на промежутке от нуля до трех. Такую прикидку мы даем по той причине, что графики функций в обозначенном промежутке очень близки, почти совпадают. Если есть возможность построить графики более точно в обозначенном промежутке, то это немного проясняет картину:
Сейчас мы видим три точки пересечения, даже можем приближенно указать их абсциссы: 1, 2 и 2,7. Но опять же, это не более чем приближенные результаты, нуждающиеся в проверке и строгом обосновании.
Учитывая оговоренные особенности графического метода решения уравнения, для себя можно принять следующее: к графическому методу стоит обращаться лишь тогда, когда функции, отвечающие частям уравнения, довольно простые в плане построения графиков, когда по построенным графикам можно с уверенностью указать точное количество точек их пересечения, и когда не просматривается альтернативный метод решения.
К началу страницы
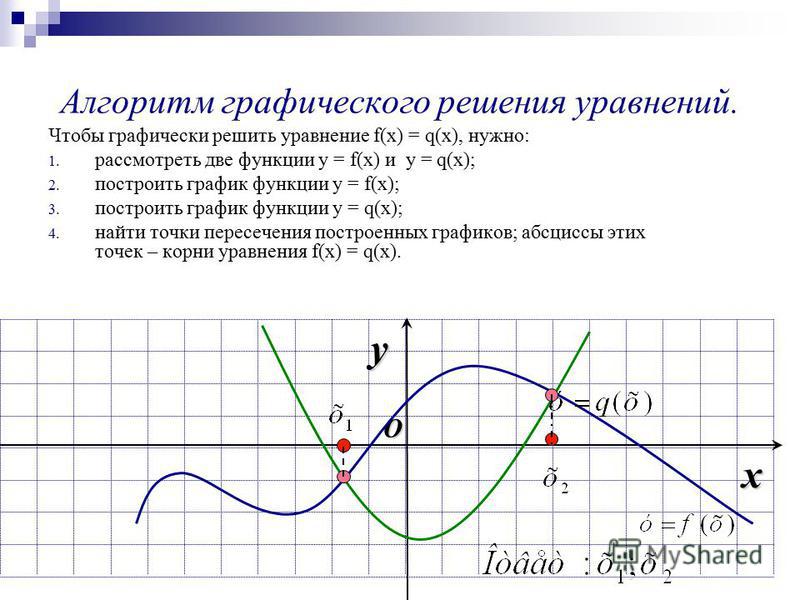
Алгоритм решения уравнений графическим методом
Анализ приведенной выше информации позволяет записать алгоритм решения уравнений графическим методом. Чтобы решить уравнение графически, надо:
- Построить в одной прямоугольной системе координат графики функций, отвечающие левой и правой частям уравнения.
-
По чертежу определить все точки пересечения графиков:
- если точек пересечения нет, то решаемое уравнение не имеет корней,
- если точки пересечения имеются, то переходим к следующему шагу алгоритма.
- По чертежу определить абсциссы всех точек пересечения графиков – это приближенные значения всех корней исходного уравнения.
-
Если есть основания полагать, что некоторые или все определенные на предыдущем шаге значения являются точными значениями корней решаемого уравнения, то осуществить их проверку, например, подстановкой.

Дадим краткий комментарий к последнему шага алгоритма. Иногда определенные по чертежу приближенные значения корней оказываются точными. Обычно это касается целых значений. Но, опять же, прежде чем утверждать, что найденные значения является точными корнями уравнения, сначала нужно осуществить проверку этих значений, например, проверку подстановкой.
К началу страницы
Решение примеров
Графический метод решения уравнений начинает входить в арсенал изучающих математику в 7 классе сразу же после знакомства с координатной плоскостью и самой первой функцией – линейной функцией y=k·x+b. Именно тогда мы сталкиваемся с заданиями, наподобие следующего: с помощью графика линейной функции y=2·x−6 определить, при каком значении x будет y=0 [1, с. 50-51]. Для ответа на поставленный вопрос мы строим график указанной линейной функции y=2·x−6.
По чертежу находим точку пересечения графика с осью Ox (ось Ox отвечает графику функции y=0), и определяем абсциссу точки пересечения: x=3. По сути, мы решаем уравнение 2·x−6=0 графическим методом.
По сути, мы решаем уравнение 2·x−6=0 графическим методом.
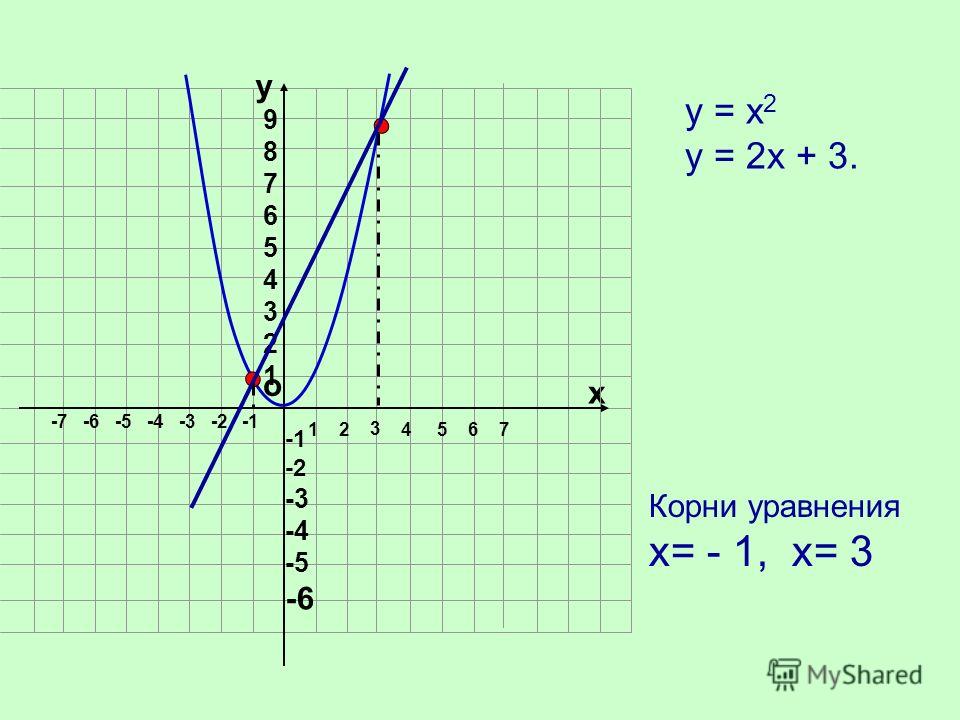
Чуть позже в 7 классе изучается функция y=x2. После этого опять заходит разговор о графическом методе решения уравнений, но уже более детальный, где метод уже называется своим именем и дается его алгоритм [1, с. 149-151; 2, с. 109]. Там с его помощью решаются уравнения, одной части которых отвечает функция y=x2, а другой – линейная функция y=k·x+b. Например, уравнение x2=x+1. Для его решения строятся в одной системе координат соответствующие графики функций y=x2 и y=x+1:
Графики, очевидно, пересекаются в двух точках. Можно определить приближенные значения их абсцисс: .
В 8 классе изучаются новые виды функций: y=k/x, квадратичная функция y=a·x2+b·x+c, . И, естественно, рассматривается графический метод решения соответствующих уравнений.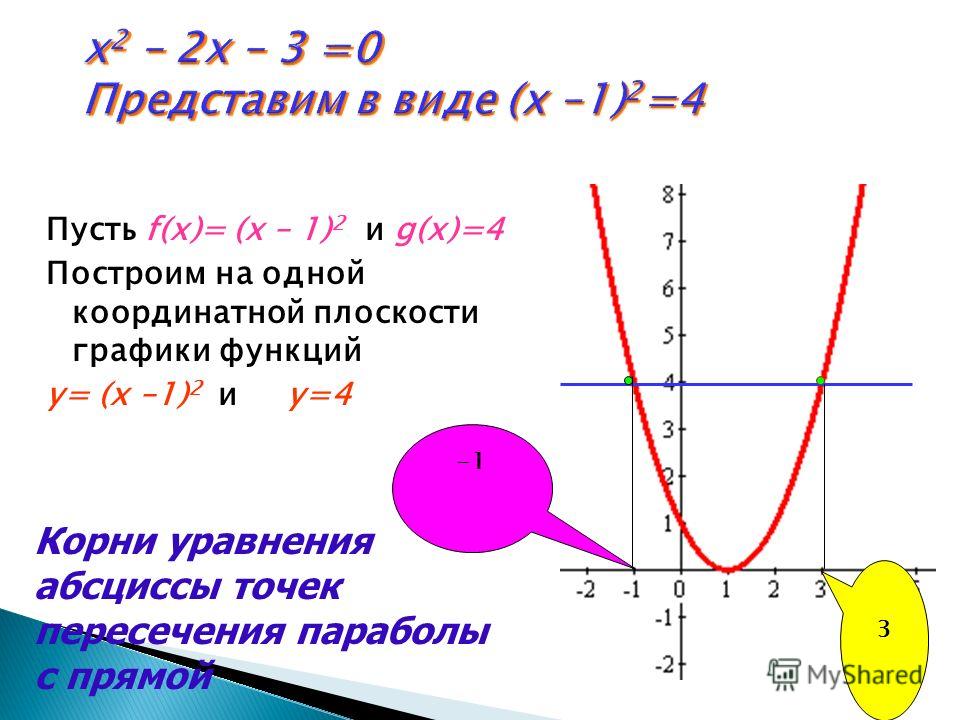 Особенно тщательно разбирается графическое решение квадратных уравнений. В учебнике Мордковича А. Г. приведены аж пять способов графического решения уравнения x2−2·x−3=0 [2, с. 127-131].
Особенно тщательно разбирается графическое решение квадратных уравнений. В учебнике Мордковича А. Г. приведены аж пять способов графического решения уравнения x2−2·x−3=0 [2, с. 127-131].
И так далее: изучаются функции , степенные функции, тригонометрические, показательные, логарифмические, …, — рассматривается решение соответствующих уравнений графическим методом. Так к концу школьного курса математики мы начинаем воспринимать графический метод решения уравнений как общий метод, позволяющий решать уравнения не только определенных видов, но и уравнения, в которых уживаются самые разнообразные функции: показательные с корнями, тригонометрические с логарифмическими и т.д. Покажем решение такого уравнения.
Пример
Решите уравнение
Смотреть решение
В заключение вспомним, что в этой статье при разговоре об особенностях графического метода решения уравнений мы обращались к иррациональному уравнению .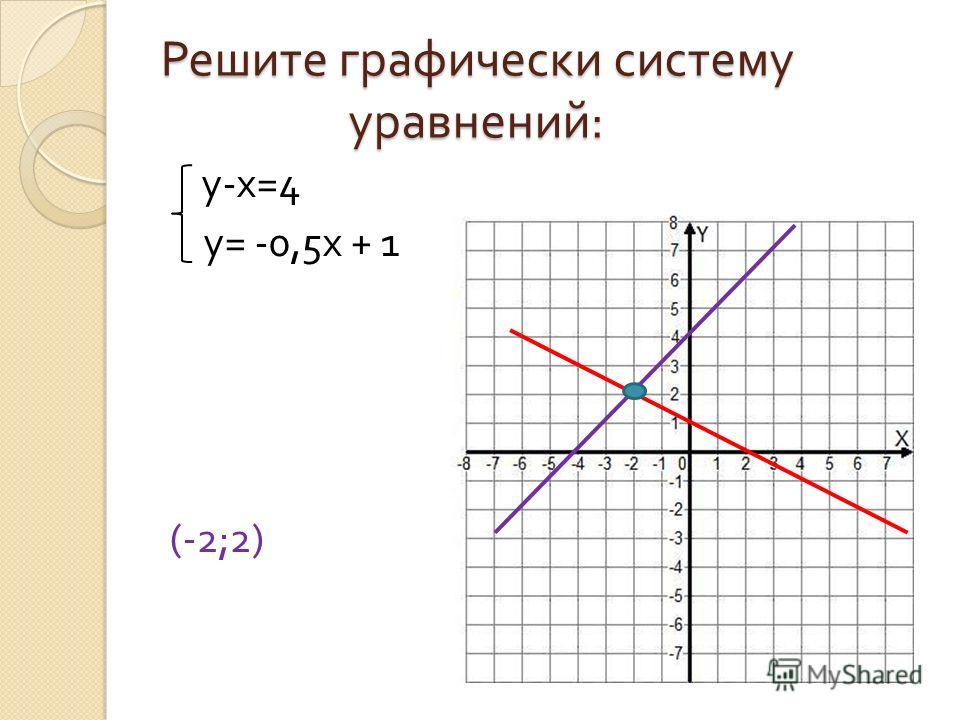 В качестве «благодарности» этому уравнению за помощь в обретении знаний приведем ссылку на его решение графическим методом.
В качестве «благодарности» этому уравнению за помощь в обретении знаний приведем ссылку на его решение графическим методом.
Графическое решений квадратных уравнений презентация, доклад
Графическое
решение
квадратных
уравнений
Алгебра 8 класс
Немного истории
Еще в древнем Вавилоне могли решить некоторые виды квадратных уравнений.
Диофант Александрийский,
Аль- Хорезми
.
Евклид Омар Хайям
Решали уравнения
геометрическими и
графическими способами
Для графического решения квадратного уравнения представьте его в одном из видов:
ax2 + bx +c = 0
ax2 = -bx – c
ax2 + c = — bx
a(x + b/2a)2 = ( 4ac — b2 )/4a
Квадратное уравнение имеет вид ax2 + bx + c = 0
Алгоритм графического решения квадратных уравнений
Ввести функцию f(x), равную левой части и g(x) , равную правой части
Построить графики функций y=f(x) и y=g(x) на одной координатной плоскости
Отметить точки пересечения графиков
Найти абсциссы точек пересечения, сформировать ответ
Способы графического решения квадратного уравнения
ах² + bх + с = 0
Способ поcтрое-
ния параболы y=ах² +bx+c
Способ поcтрое-
ния прямой
у= bx+c и параболы у = ах²
Способ поcтрое-
ния прямой
у= bx и параболы у = ах²+с
Способ выделе-ния полного квадрата
I
II
III
(a)
(b)
Способ поcтрое-
ния прямой
у= с и параболы у = ах²+ bx
(в)
«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу различными способами, чем решать три-четыре различные задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт». У. У. Сойер.
Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт». У. У. Сойер.
Графическое решение квадратного уравнения
Иллюстрация на одном примере
Алгоритм решения квадратного уравнения графическим способом
Способ 1
Построить график функции y=ax2+bx+c
Найти точки пересечения графика с осью абсцисс
Решить уравнение
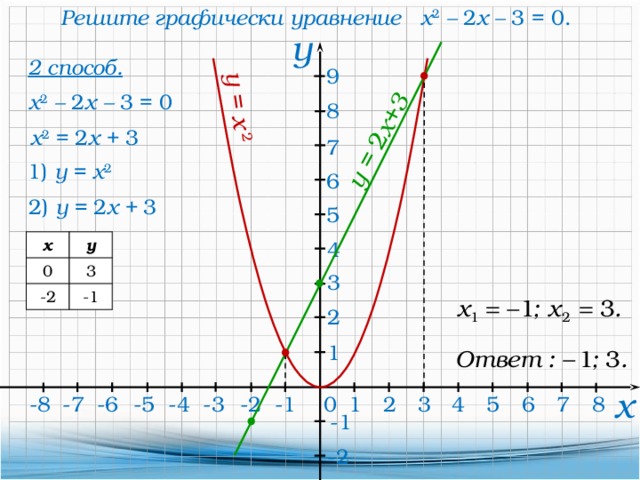
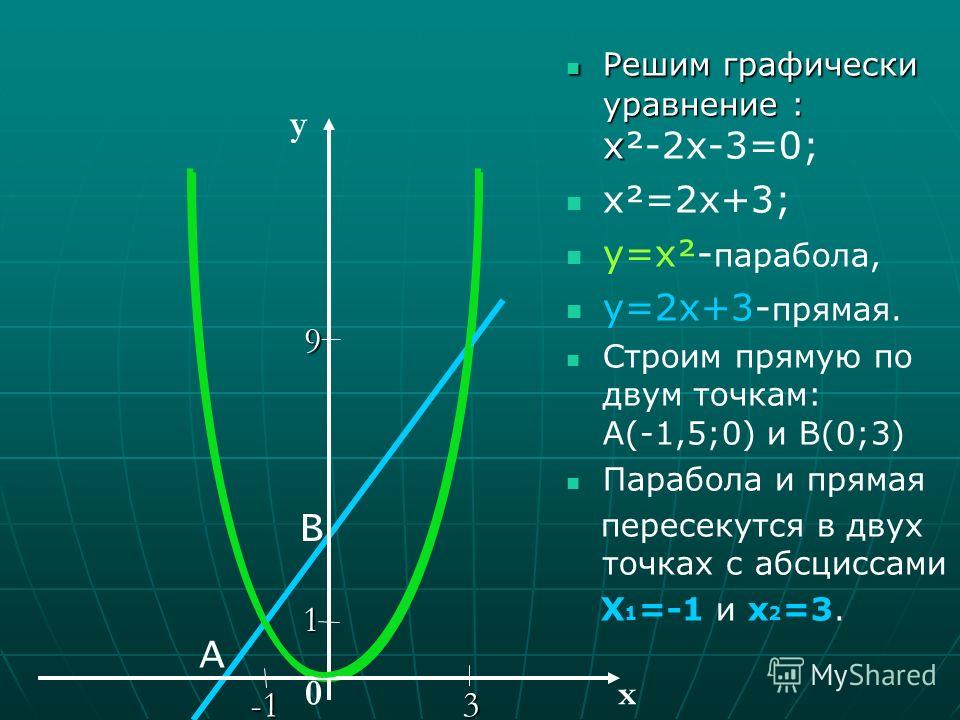
1 способ
Корнями уравнения являются
абсциссы точек пересечения графика с осью х, т.е. где у=0.
Значит, корни уравнения -1 и 3. Проверка устно. Ответ: -1; 3.
-1
1
-1
3
х
3
о
у
Алгоритм построения параболы
найти координаты вершины; провести ось параболы;
отметить на оси абсцисс две точки, симметричные относительно оси параболы; найти значения функции в этих точках;
провести параболу через полученные точки.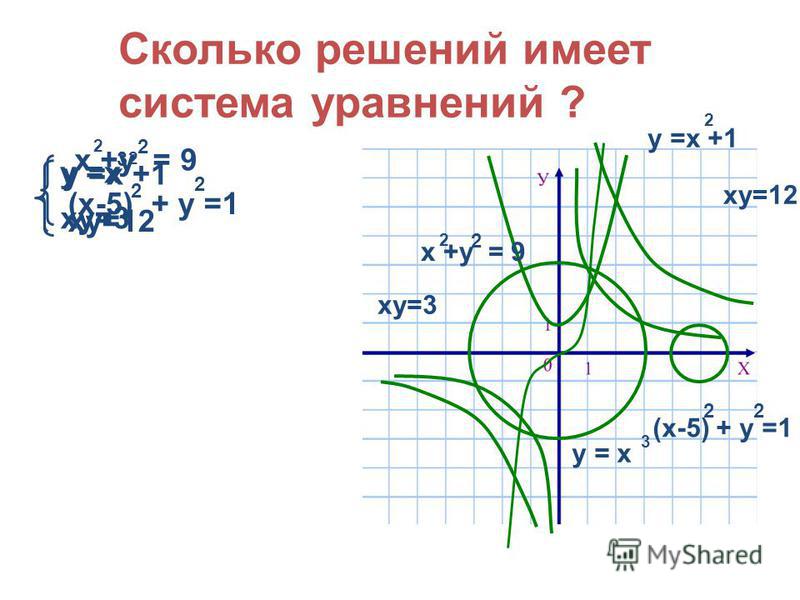
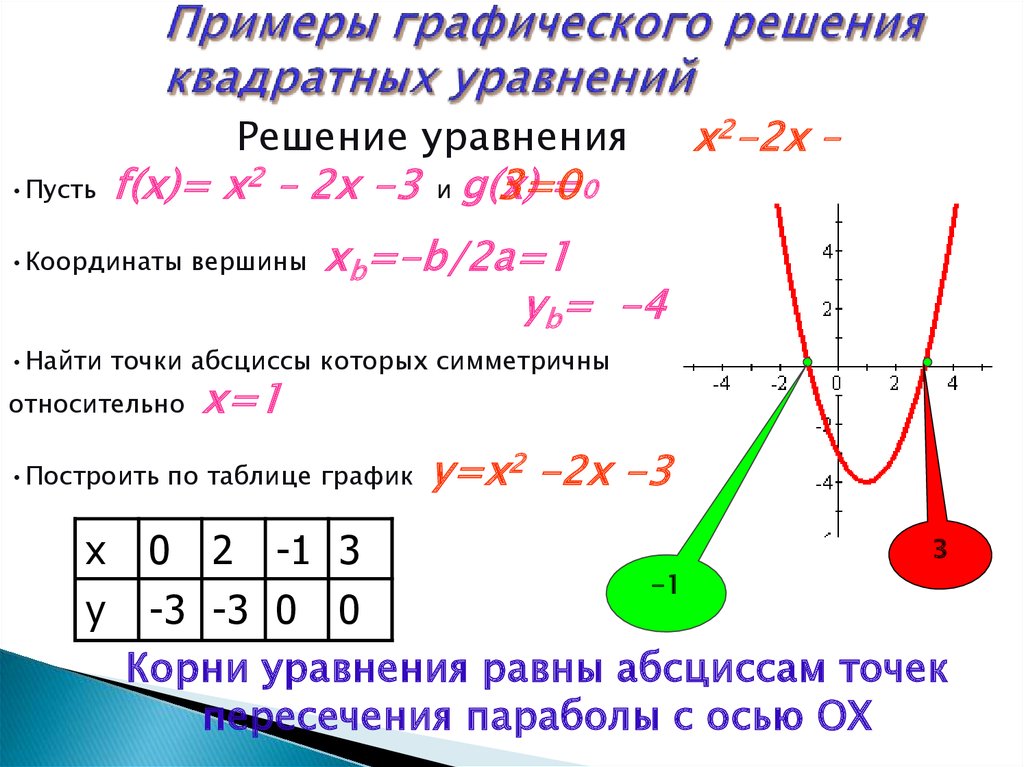
Пусть f(x)= x2 – 2x -3 и g(x) =0
а = 1>0, ветви вверх
Координаты вершины x۪۪ ο =-b/2a; x۪۪ ο =1 .
y ο = 1² — 2 – 3 = -4; y ο = -4; ( 1; -4)
Найти точки абсциссы которых симметричны относительно х=1
Построить по таблице график y=x2 -2x -3
Примеры графического решения квадратных уравнений
3
-1
Решение уравнения x2-2x –3=0
Корни уравнения равны абсциссам точек пересечения параболы с осью ОХ
у=x2 – 2x -3
Графический способ решения квадратных уравнений
Парабола и
прямая
касаются
Парабола и прямая
пересекаются
Квадратное уравнение имеет два равных корня
Квадратное уравнение не имеет корней
Квадратное уравнение имеет два различных корня
Парабола и прямая не
пересекаются и не касаются
Алгоритм решения квадратного уравнения графическим способом
Способ 2(а)
Построить графики функции y=ax2 и у = bx+ с
Найти абсциссы точек пересечения графиков.
x2 – 2x – 3 =0
Представим в виде x2 = 2x +3
Пусть f(x)=x2 и g(x)=2x +3
Построим на одной координатной плоскости графики функций
y=x2 иy= 2x + 3
3
-1
Корни уравнения абсциссы точек пересечения параболы с прямой
2 способ
Преобразуем уравнение
к виду
Построим в одной системе координат графики функций
-это парабола
-это прямая
х
у
0
1
3
5
3
-1
3
Корнями уравнения являются
абсциссы точек пересечения: -1 и 3
Корнями уравнения являются
абсциссы точек пересечения: -1 и 3
4 x2 – 4x + 1 =0
Представим в виде 4×2 = 4x -1
1). Построим графики функций:
Построим графики функций:
у = 4 x2 , у = 4x — 1
2). Строим параболу у = 4 x2
а = 4, ветви вверх
хο = — ; хο= 0; ; уο= 0.
По шаблону строим параболу
3). Строим прямую у = 4x — 1
-1
0
1
3
1
0,5
Корнем уравнения является
абсцисса точки пересечения: 0,5
-1
-1
у
х
Алгоритм решения квадратного уравнения графическим способом
Способ 2 (b)
Преобразовать уравнение к виду
ax2+с = bx
Построить:
параболу y = ax2+с и прямую y = bx
Найти абсциссы точек пересечения
графиков функции.
x2 – 2x – 3 =0
Представим в виде x2 –3 = 2x
Пусть f(x)=x2 –3 и g(x)=2x
Построим на одной координатной плоскости графики функций
y=x2 –3 и y =2x
-1
3
Корни уравнения абсциссы точек пересечения параболы с прямой
y=x2 –3
y =2x
x2 – 4x + 5 =0
Представим в виде x2 +5 = 4x
Пусть f(x)=x2 +5 и g(x)=4x
Построим на одной координатной плоскости графики функций
y=x2 +5 и y =4x
Точек пересечения параболы с прямой нет
Ответ: корней нет
y=x2 +5
y =4x
y
x
о
Алгоритм решения квадратного уравнения графическим способом
Способ 2(в)
Построить графики функции
y=ax2 + bx и у = с
Найти абсциссы точек пересечения графиков.
x2 – 2x – 3 =0
Представим в виде x2 – 2x = 3
Пусть f(x)= х² — 2х и g(x)=3
Построим на одной координатной плоскости графики функций
y= х² — 2х и y=3
-1
3
Корни уравнения абсциссы точек пересечения параболы с прямой
y=3
y= х² — 2х
y
х
о
2
-1
3
Алгоритм решения квадратного уравнения графическим способом
Способ 3
(выделение полного квадрата)
Преобразовать уравнение к виду
a(x+l)2 = m
Построить:
параболу y = a(x+l)2 и прямую y = m
Найти абсциссы точек пересечения графиков функций.
Выделение квадрата двучлена.
x2 – 2x + 1 = 3 + 1
( x –1)2=4.
x2 – 2x = 3
( x –1)2 — 4 = 0
( x –1)2 — 2² = 0
( x –1 – 2) ( x –1 + 2 ) = 0
( x –3 ) ( x + 1 ) = 0
x –3 = 0
x + 1 = 0
x = 3
x = — 1
x2 – 2x – 3 =0
Представим в виде (x –1)2=4
Пусть f(x)= (x – 1)2 и g(x)=4
Построим на одной координатной плоскости графики функций
y= (x –1)2 и y=4
-1
3
Корни уравнения абсциссы точек пересечения параболы с прямой
y=4
y= (x –1)2
Решите графически уравнение
Группа А
Бычев Андрей
Ерофеева Ксения
Каминская Света
Лобов Егор
Лукьяненко Вероника
Осипов Павел
Циорба Влад
Группа С
Григорьева Катя
Соловьев Илья
Группа В
Баличев Илья
Помигуев Павел
Фролов Саша
х² + 2х – 8= 0
4х² — 8х + 3= 0
3х² + 2х – 1= 0
Сколько нам открытий чудных готовит просвещения дух?
Решить графически уравнение
Как решить уравнение?
Построить график квадратичной функции и абсциссы точек пересечения параболы с осью x будут являться корнями уравнения.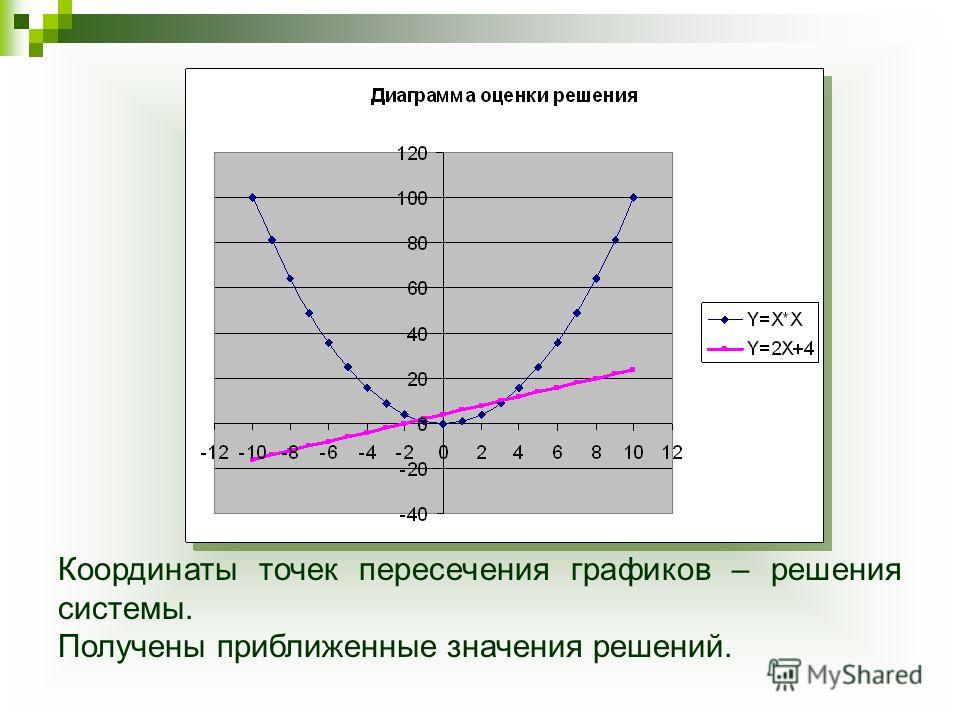
Выполнить преобразование уравнения, рассмотреть функции, построить графики этих функций, установить точки пересечения графиков функций, абсциссы которых и будут являться корнями уравнения.
Решить графически уравнение
Построить график функции
Построить график функции
Корни уравнения: абсциссы точек пересечения графиков функций
Построить график функции
Корни уравнения:
точки пересечения
параболы с осью ОХ
Решить графически уравнение
Корни уравнения:
точки пересечения
параболы и прямой
Решить графически уравнение
Корни уравнения:
точки пересечения
параболы и прямой
Итог
Познакомились:
с графическим методом решения квадратных уравнений;
с различными способами графического решения квадратных уравнений.
закрепили знания по построению графиков различных функций.
Заключительное слово учителя:
«Чем больше и глубже вам удастся усвоить азы математики и научиться пользоваться ее методами, тем дальше и быстрее вы сумеете продвинуться в использовании математических средств в той области деятельности, которой займетесь после школы»
Желаю удачи !
Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ репетитора
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
375518 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype. В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
 RU
RU
- Class
Графическое решений квадратных уравнений — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Алгебра 8 класс
2. Немного истории
Еще в древнем Вавилоне моглирешить некоторые виды
квадратных уравнений.
Диофант Александрийский,
Аль- Хорезми
Решали уравнения
геометрическими и
.
графическими способами
Евклид
Омар Хайям
Квадратное уравнение имеет вид
ax2 + bx + c = 0
Для графического решения квадратного уравнения
представьте его в одном из видов:
ax2 + bx +c = 0
2
ax = -bx – c
2
ax + c = — bx
a(x + b/2a)2 = ( 4ac — b2 )/4a
4. Алгоритм графического решения квадратных уравнений
Ввести функцию f(x), равную левой части иg(x) , равную правой части
Построить графики функций y=f(x) и y=g(x)
на одной координатной плоскости
Отметить точки пересечения графиков
Найти абсциссы точек пересечения,
сформировать ответ
Способы графического решения
квадратного уравнения
ах² + bх + с = 0
I
Способ
поcтроения
параболы
y=ах²
+bx+c
III
II
(a)
Способ
поcтроения
прямой
у= bx+c и
параболы
у = ах²
(b)
Способ
поcтроения
прямой
у= bx и
параболы
у = ах²+с
(в)
Способ
поcтроения
прямой
у= с и
параболы
у = ах²+ bx
Способ
выделения
полного
квадрата
«Человеку, изучающему алгебру,
часто полезнее решить одну и ту же
задачу различными способами, чем
решать три-четыре различные
задачи.
 Решая одну задачу
Решая одну задачуразличными способами, можно путем
сравнения выяснить, какой из них
короче и эффективнее. Так
вырабатывается опыт». У. У. Сойер.
7. Графическое решение квадратного уравнения
Иллюстрация на одном примере8. Алгоритм решения квадратного уравнения графическим способом
Способ 1• Построить график функции
y=ax2+bx+c
• Найти точки пересечения графика с
осью абсцисс
Решить уравнение
у х2 2х 3
1 способ
Построим график функции у =
1.
2.
х 2х 3 0
2
у
х2 2х 3
График-парабола, а=1>0,ветви вверх.
Вершина ( х0 ; у0)
в
х0 =- 2а
3
Хο=1
у0 12 2 3 4
о
(1; -4)-вершина
3. Ось параболы
х0 1
-1
1
3
4. Дополнительные точки:
х -1 0 1 2 3
у
0
-3 -4
-3
0
Корнями уравнения являются
абсциссы точек пересечения графика с осью х, т.е. где у=0.
Значит, корни уравнения -1 и 3. Проверка устно. Ответ: -1; 3.
х
10.
 Алгоритм построения параболынайти координаты вершины;
Алгоритм построения параболынайти координаты вершины;провести ось параболы;
отметить на оси абсцисс две точки,
симметричные относительно оси
параболы; найти значения функции в
этих точках;
провести параболу через полученные
точки.
11. Примеры графического решения квадратных уравнений
Решение уравнения•Пусть f(x)= x2 – 2x -3 и g(x) =0
x2-2x –3=0
у=x2 – 2x -3
а = 1>0, ветви вверх
•Координаты вершины x۪ ۪
ο
=-b/2a; x۪ ۪
ο
=1 .
y ο = 1² — 2 – 3 = -4; y ο = -4; ( 1; -4)
Найти точки абсциссы которых
симметричны относительно х=1
-1
2 -2x -3
•Построить
по
таблице
график
y=x
x 0 2 -1 3
y
-3 -3 0
0
3
Корни уравнения равны абсциссам точек
пересечения параболы с осью ОХ
12. Графический способ решения квадратных уравнений
Парабола и прямая неПарабола и
прямая
касаются
Квадратное
уравнение
имеет два равных
корня
Парабола и прямая
пересекаются
Квадратное
уравнение
имеет два
различных корня
пересекаются и не
касаются
Квадратное
уравнение не имеет
корней
13.
 Алгоритм решения квадратного уравнения графическим способомСпособ 2(а)
Алгоритм решения квадратного уравнения графическим способомСпособ 2(а)• Построить графики функции y=ax2 и
у = bx+ с
• Найти абсциссы точек пересечения
графиков.
14. x2 – 2x – 3 =0 Представим в виде x2 = 2x +3
Пусть f(x)=x2 и g(x)=2x +3Построим на одной
координатной плоскости
графики функций
y=x2 иy= 2x + 3
Корни уравнения
абсциссы точек
пересечения
параболы с прямой
-1
3
2 способ
Преобразуем уравнение
х2 2х 3 0
к виду
х2 2х 3
у х2 ; у 2х 3
Построим в одной системе координат графики функций
у х2
у 2х 3
-это
парабола
у
-это прямая
у 2х 3
у х2
х
0
1
у
3
5
Корнями уравнения являются
абсциссы точек пересечения: -1 и 3
3
х
-1
3
4 x2 – 4x + 1 =0
Представим в виде
4×2 = 4x -1
1). Построим графики функций:
у = 4 x2 , у = 4x — 1
2). Строим параболу у = 4 x2
а = 4, ветви вверх
хο = — в ; хο= 0; ; уο= 0.
2а
По шаблону строим параболу
у
3
1
0,5
0
-1
3). Строим прямую у = 4x — 1
x
0
1
y
-1 3
Корнем уравнения является
абсцисса точки пересечения: 0,5
1
х
17. Алгоритм решения квадратного уравнения графическим способом
Способ 2 (b)• Преобразовать уравнение к виду
ax2+с = bx
• Построить:
параболу y = ax2+с и прямую y = bx
• Найти абсциссы точек пересечения
графиков функции.
18. x2 – 2x – 3 =0 Представим в виде x2 –3 = 2x
y=x2 –3Пусть f(x)=x2 –3 и g(x)=2x
Построим на одной
координатной плоскости
графики функций
y=x2 –3 и y =2x
-1
Корни уравнения
абсциссы точек
пересечения параболы с
прямой
y =2x
3
19. x2 – 4x + 5 =0 Представим в виде x2 +5 = 4x
yПусть f(x)=x2 +5 и g(x)=4x
Построим на одной
координатной плоскости
графики функций
y=x2 +5 и y =4x
y=x2 +5
y =4x
Точек пересечения
параболы с прямой нет
Ответ: корней нет
о
x
20.
 Алгоритм решения квадратного уравнения графическим способомСпособ 2(в)
Алгоритм решения квадратного уравнения графическим способомСпособ 2(в)• Построить графики функции
• y=ax2 + bx и
у=с
• Найти абсциссы точек пересечения
графиков.
21. x2 – 2x – 3 =0 Представим в виде x2 – 2x = 3
yПусть f(x)= х² — 2х и g(x)=3
Построим на одной
координатной плоскости
графики функций
y= х² — 2х и y=3
-1
y= х² — 2х
y=3
о
Корни уравнения
абсциссы точек
пересечения параболы
с прямой
-1
2
х
3
3
22. Алгоритм решения квадратного уравнения графическим способом
Способ 3(выделение полного квадрата)
• Преобразовать уравнение к виду
a(x+l)2 = m
• Построить:
параболу y = a(x+l)2 и прямую y = m
• Найти абсциссы точек пересечения
графиков функций.
Выделение квадрата двучлена.
x2 – 2x = 3
x2 – 2x + 1 = 3 + 1
( x –1)2=4.
( x –1)2 — 4 = 0
( x –1)2 — 2² = 0
( x –1 – 2) ( x –1 + 2 ) = 0
( x –3 ) ( x + 1 ) = 0
x –3 = 0
x+1=0
x =3
x =-1
24.
 x2 – 2x – 3 =0 Представим в виде (x –1)2=4y= (x –1)2
x2 – 2x – 3 =0 Представим в виде (x –1)2=4y= (x –1)2Пусть f(x)= (x – 1)2 и g(x)=4
Построим на одной
координатной плоскости
графики функций
y= (x –1)2 и y=4
y=4
-1
Корни уравнения
абсциссы точек
пересечения параболы
с прямой
3
25. Решите графически уравнение
Группа АГруппа В
Бычев Андрей
Баличев Илья
Ерофеева Ксения
Помигуев Павел
Каминская Света
Фролов Саша
Лобов Егор
Лукьяненко Вероника
Осипов Павел
Циорба Влад
х² + 2х – 8= 0
4х² — 8х + 3= 0
Группа С
Григорьева Катя
Соловьев Илья
3х² + 2х – 1= 0
Сколько нам открытий
чудных готовит
просвещения дух?
27. Решить графически уравнение
x 2x 8 02
28. Как решить уравнение?
x 2x 8 02
Построить график квадратичной функции и
абсциссы точек пересечения параболы с осью x
будут являться корнями уравнения.
Выполнить преобразование уравнения, рассмотреть
функции, построить графики этих функций,
установить точки пересечения графиков функций,
абсциссы которых и будут являться корнями
уравнения.
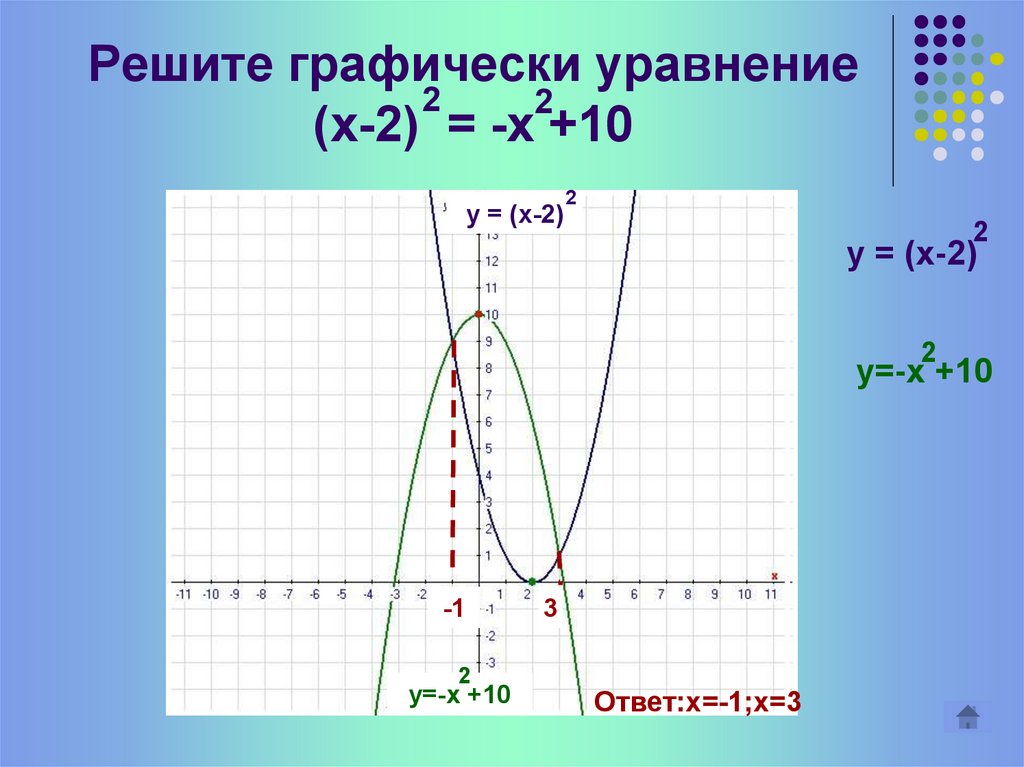
29. Решить графически уравнение
x 2 x 82
30. Построить график функции
y x2
31. Построить график функции
y 2 x 832. Корни уравнения: абсциссы точек пересечения графиков функций
x1 4x2 2
33. Построить график функции
y x 2x 82
Корни уравнения:
точки пересечения
параболы с осью ОХ
x1 4
x2 2
34. Решить графически уравнение
x 8 2 x2
Корни уравнения:
точки пересечения
параболы и прямой
x1 4
x2 2
35. Решить графически уравнение
( x 1) 92
Корни уравнения:
точки пересечения
параболы и прямой
x1 4
x2 2
Познакомились:
• с графическим методом решения
квадратных уравнений;
• с различными способами графического
решения квадратных уравнений.
• закрепили знания по построению
графиков различных функций.
37. Заключительное слово учителя:
«Чем больше и глубже вамудастся усвоить азы
математики и научиться
пользоваться ее методами, тем
дальше и быстрее вы сумеете
продвинуться в использовании
математических средств в той
области деятельности, которой
займетесь после школы»
English Русский Правила
Решение тригонометрических уравнений графически
Уравнения, с которыми приходится сталкиваться при решении практических задач, как правило, значительно отличаются от тех, которые мы рассматривали.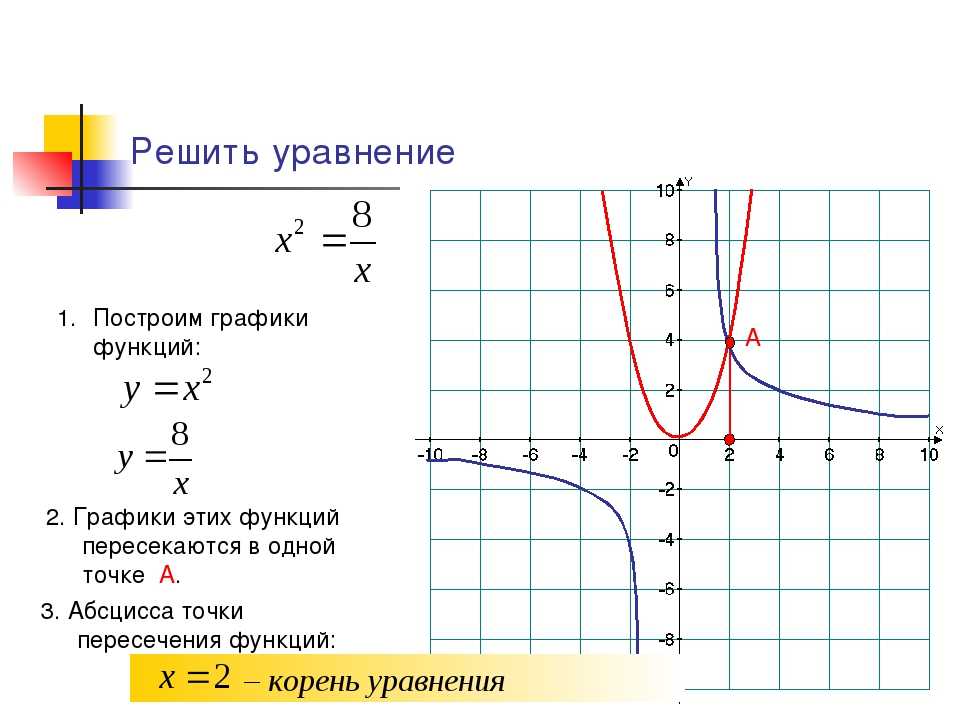 Для таких уравнений иногда вообще нельзя указать никакого способа, который позволял бы найти корни абсолютно точно. В таком случае приходится ограничиваться нахождением лишь приближенных значений корней. Современная математика располагает эффективными методами приближенного решения уравнений. Рассмотрим графический способ решения.
Для таких уравнений иногда вообще нельзя указать никакого способа, который позволял бы найти корни абсолютно точно. В таком случае приходится ограничиваться нахождением лишь приближенных значений корней. Современная математика располагает эффективными методами приближенного решения уравнений. Рассмотрим графический способ решения.
Пусть, например, нужно решить уравнение
sin х = 1 — х.
На одном и том же рисунке начертим два графика: график функции y = sin х и график функции у = 1 — х
Эти графики пересекаются в одной точке М. Абсцисса этой точки и дает нам единственный корень нашего уравнения:
х ≈ 0,5.
Для уточнения полученного результата полезно использовать тригонометрические таблицы или компьютерные программы. При х = 0,5
sin x ≈ 0,4794,
1 — х = 0,5;
следовательно, sin х < 1 — х. Но тогда, как легко понять из рисунка, корень уравнения sin х = 1 — х будет больше, чем 0,5. Проверим значение х = 0,6. Имеем (при х = 0,6):
Но тогда, как легко понять из рисунка, корень уравнения sin х = 1 — х будет больше, чем 0,5. Проверим значение х = 0,6. Имеем (при х = 0,6):
sin х ≈ 0,5446,
1 — х = 0,4;
следовательно, sin х > 1 — х. Но тогда, как легко понять из того же рисунка, искомый корень x0 должен быть меньше, чем 0,6. Теперь уже мы знаем, что x0 находится в интервале [0,5; 0,6]. Поэтому с точностью до 0,1
x0 ≈0,5 (с недостатком),
x0 ≈ 0,6 (с избытком).
С помощью таблиц можно найти приближенное значение x0 и с точностью до 0,01. Разделим интервал [0,5; 0,6] пополам. В средней точке (x = 0,55) этого интервала
sin х ≈ 0,5227,
1 — х = 0,45.
Опять получаем, что sin х > 1 — х. Следовательно, x0 < 0,55.
Проверим точку х = 0,52 (она близка к средней точке х = 0,525 интервала [0,50; 0,55], в котором заключен корень x0). При х = 0,52
sin х ≈ 0,4969,
1 — х = 0,48.
Снова sin x > 1 — х; поэтому x0 < 0,52. Итак, 0,50 < x0 < 0,52. Поэтому с точностью до 0,01
x0 ≈ 0,51.
Для примера рассмотрим уравнение
tg x/2 = 2 — x.
Графики функций у = tg x/2и у = 2 — х пересекаются в бесконечном числе точек. Значит, данное уравнение имеет бесконечное множество корней. Найдем, например, наименьший положительный корень х0. Этот корень является абсциссой точки пересечения графиков. Примерно он равен 1,2.
Чтобы найти этот корень точнее, воспользуемся таблицами тангенсов В. М. Брадиса (или рассчитаем соответствующие значения в программе «Kалькулятор» или «Excel»). Выпишем значения функций у = tg x/2 и у = 2 — х в окрестности точки х = 1,2.
М. Брадиса (или рассчитаем соответствующие значения в программе «Kалькулятор» или «Excel»). Выпишем значения функций у = tg x/2 и у = 2 — х в окрестности точки х = 1,2.
| x | 1,2 | 1,3 |
| y=tg x/2 | 0,6841 | 0,7602 |
| y=2-x | 0,8000 | 0,7000 |
| tg x/2-(2-x) | -0,1159 | 0,0602 |
Как видно из этой таблицы, при переходе от значения х = 1,2 к значению х = 1,3 разность tg x/2 — (2 — х) меняет свой знак на противоположный (с — на +). Значит, в нуль эта разность обращается где-то между значениями 1,2 и 1,3. Следовательно, с точностью до 0,1 х0 ≈ 1,2 (с недостатком) или х0 ≈ 1,3 (с избытком). Используя таблицу тангенсов, можно найти и приближенное значение этого корня
Значит, в нуль эта разность обращается где-то между значениями 1,2 и 1,3. Следовательно, с точностью до 0,1 х0 ≈ 1,2 (с недостатком) или х0 ≈ 1,3 (с избытком). Используя таблицу тангенсов, можно найти и приближенное значение этого корня
с точностью до 0,01. Для этого рассмотрим значение х = 1,25, являющееся средним значением чисел 1,2 и 1,3. При х = 1,25
tg x/2 ≈ 0,7215,
2 — х = 0,7500.
Поскольку tg x/2 < 2- х, то х0 >1,25. Итак,
1,25< х0 < 1,30.
Теперь испытаем значение х = 1,28, которое близко к среднему значению чисел 1,25 и 1,30. При х = 1,28
tg x/2 ≈ 0,7445,
2 — х = 0,7200.
Теперь уже tg x/2 >2 — х Значит , х0 < 1,28.
Аналогично, рассматривая значение х = 1,26, мы получили бы tg x/2 < 2 — х и потому х0 > 1,26. Значит,
1,26 <х0< 1,28.
Поэтому с точностью до 0,01
х0 ≈ 1,27
Если бы нужно было определить, какое это приближенное значение (с недостатком или с избытком), то пришлось бы сравнить значения tg x/2 и 2 — х в точке х = 1,27.
1.30: Графическое решение системы уравнений
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 41231
- Самар ЭльХитти, Марианна Бонаноме, Холли Карли, Томас Тредлер и Линь Чжоу
- Нью-Йоркский технологический колледж CUNY и Технологический колледж Нью-Йорка через Нью-Йоркский городской технологический колледж в CUNY Academic Works
В главе 27 мы видели, как решать систему линейных уравнений алгебраически (подстановкой и исключением). Поскольку мы знаем, что графики линейных уравнений состоят из линий , естественно изобразить линии, представляющие нашу систему, и посмотреть, где они находятся относительно друг друга в координатной плоскости. Возможных конфигураций всего три: прямые пересекаются в одной точке, прямые совпадают, прямые параллельны. Нахождение этого пересечения (если возможно) сводится к решению линейной системы.
Поскольку мы знаем, что графики линейных уравнений состоят из линий , естественно изобразить линии, представляющие нашу систему, и посмотреть, где они находятся относительно друг друга в координатной плоскости. Возможных конфигураций всего три: прямые пересекаются в одной точке, прямые совпадают, прямые параллельны. Нахождение этого пересечения (если возможно) сводится к решению линейной системы.
Пример \(\PageIndex{1}\)
Рассмотрим пример 27.1 из главы 27.
Рассмотрим пример 27.1 из главы 27.
\[\left(\begin{array}{lllll}
6 x & + & 2 y & = & 72 \\
3 x & + & 8 y & = & 78
\end{array}\right)\nonumber\]
Решение, которое мы нашли (подстановкой), было \(x=10\ ) и \(y=6\).
Чтобы решить эту систему с помощью графика, мы начнем с построения графика каждого из заданных линейных уравнений.
Сначала мы строим график \(6 x+2 y=72\). Помните, мы находим две точки:
\[x=0 \quad \Longrightarrow \quad y=36\nonumber\]
\[y=0 \quad \longrightarrow \quad x=12\nonumber\]
Аналогично , построим график \(3 x+8 y=78\), найдя две точки на этой прямой:
\[x=2 \quad \Longrightarrow \quad y=9\nonnumber\]
\[y=3 \ quad \Longrightarrow \quad x=18\nonnumber\]
Линии нарисованы в той же системе координат, как показано ниже.
Координаты точки пересечения двух графиков и есть решение системы. Обратите внимание на график, что координаты \(x\) и \(y\) точки пересечения равны \(x=10\) и \(y=6\).
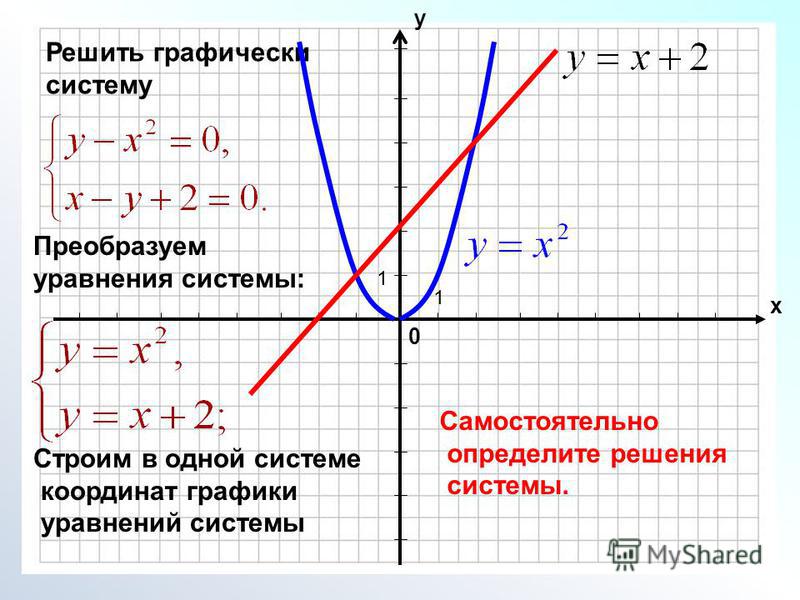
Пример \(\PageIndex{1}\)
Решить графически:
\[\left(\begin{array}{lllll}
x & + & y & = & 7 \\
5 x & + & 10 y & = & 40
\end{массив}\right)\nonumber\]
Шаг 1 Нарисуйте обе линии:
\[\begin{align*}
x+y=7: \quad & x=0, y=7 \\
& y=0, x=7
\end{align*}\nonumber\]
\[\begin{align*}
5x + 10y = 40: \quad & x = 0, y = 4 \\
& y = 0, x = 8
\end{align*}\nonumber\]
Шаг 2 Считайте координаты точка пересечения:
\[x=6, y=1\nonnumber\]
Шаг 3 Решение системы: \(x=6, y=1\).
Примечание 28.3
- Если графики двух линий делают не имеют точку пересечения, то система не имеет решения.
- Если графики прямых совпадают , то система имеет бесконечно много решений.

Решение системы двух линейных уравнений с помощью графика
- Шаг 1: Постройте график каждого линейного уравнения в одной и той же системе координат.
- Шаг 2: Отметьте точку пересечения на графике (если она есть).
- Шаг 3: Считайте координаты точки пересечения (если возможно). Если линии совпадают, то каждая точка на них считается точкой пересечения.
- Шаг 4: В зависимости от шага 3 укажите, не имеет ли система решений (прямые параллельны), бесконечно много решений (прямые совпадают) или одно решение (единственная точка пересечения).
Выход Проблема
Решить графически:
\(\begin{array}{lllll}
8 x & — & 4 y & = & 4 \\
3 x & — & 2 y & = & 3
\end{array}\)
Эта страница под названием 1.30: Графическое решение системы уравнений распространяется по лицензии CC BY-NC-ND 4.0, ее авторами, ремикшированием и/или кураторами являются Самар ЭльХитти, Марианна Бонаноме, Холли Карли, Томас Тредлер и Лин. Чжоу (Нью-Йоркский технологический колледж при CUNY Academic Works).
Чжоу (Нью-Йоркский технологический колледж при CUNY Academic Works).
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ЭльХитти, Бонаноме, Карли, Тредлер и Чжоу
- Лицензия
- СС BY-NC-ND
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги

«Решение» квадратных уравнений с помощью графика
FactoringRootsComplete the SquareFormulaExamples
Purplemath
Честно говоря, решение «по графику» — несколько фиктивная тема. Основная идея решения с помощью графика заключается в том, что, поскольку (действительные) решения любого уравнения (включая квадратные уравнения) являются точками пересечения x этого уравнения, мы можем посмотреть на точки пересечения x графика. найти решения соответствующего уравнения. Однако при таком «решении» возникают трудности.
Когда мы рисуем прямую линию, например « y = 2 x + 3″, мы можем найти точку пересечения x (с определенной степенью точности), нарисовав действительно аккуратную систему координат, отметив пару точек, взяв линейку, нарисовав красивую прямую линию и прочитав ( приблизительный) ответ на графике с достаточной степенью достоверности
Содержание продолжается ниже
MathHelp.
 com
comРешение квадратных уравнений с помощью графика
таким образом, решение состоит в том, чтобы использовать алгебру, установив уравнение прямой равным нулю и решив:
0 = 2 x + 3
−3 = 2 x
−1,5 = x
, если линейное уравнение было что -то вроде y = 47 x 33333333 годы. будет очень трудно угадать решение по графику. Мы могли бы предположить, что x -пересечение близко к x = 2, но хотя это близко, это будет не совсем правильно. Алгебра была бы единственным надежным методом решения.
Квадратичная функция более беспорядочна, чем прямая; он изображается волнистой параболой. Если мы построим несколько не- x — точки пересечения, а затем проведите через них кривую линию, как мы узнаем, получили ли мы x — пересечения, хотя бы близкие к правильным? Мы не знаем. Единственный способ, которым мы можем быть уверены в наших x -перехватах, состоит в том, чтобы установить квадратное число равным нулю и решить.
Но весь смысл «решения с помощью графика» в том, что они не хотят, чтобы мы занимались (точной) алгеброй; они хотят, чтобы мы угадывали по красивым картинкам.
Таким образом, «решение с помощью графика» не является ни «решением», ни «графическим построением». В типичном упражнении вы на самом деле ничего не рисуете и ничего не решаете. Вместо этого вам предлагается угадывать числа по распечатанному графику. Или же, если вы «используете технологию», вам говорят нажать несколько кнопок на вашем графическом калькуляторе и посмотреть на красивую картинку; а затем вам говорят нажать еще несколько кнопок, чтобы программа могла вычислить перехваты.
Я предполагаю, что преподаватели пытаются помочь вам увидеть связь между x -пересечениями графиков и решениями уравнений. Но концепция имеет тенденцию теряться во всех нажатиях кнопок.
Ладно, хватит разглагольствовать.
Чтобы решить с помощью графика, книга может дать нам очень четкий график, вероятно, по крайней мере с несколькими отмеченными точками.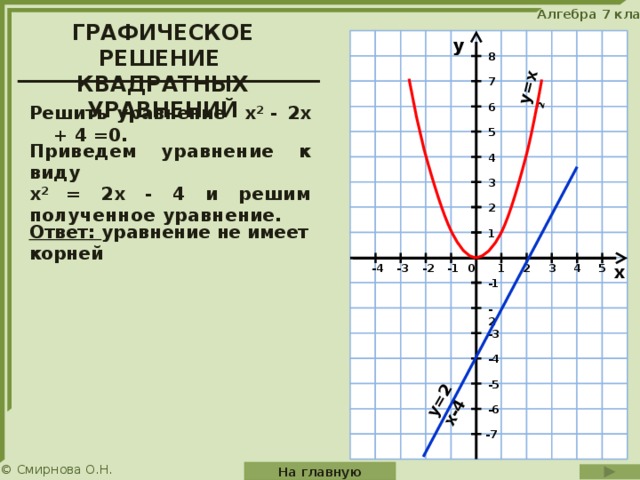 Книга попросит нас указать точки на графике, которые представляют решения. В противном случае это даст нам квадратное число, и мы будем использовать наш графический калькулятор, чтобы найти ответ. Поскольку разные модели калькуляторов имеют разные последовательности клавиш, я не могу дать инструкции о том, как «использовать технологию» для поиска ответов; вам нужно будет обратиться к руководству пользователя для любого калькулятора, который вы используете (или к файлу «Справка» для любой электронной таблицы или другого программного обеспечения, которое вы используете). Я приведу лишь пару примеров решения по картинке, которая вам дана.
Книга попросит нас указать точки на графике, которые представляют решения. В противном случае это даст нам квадратное число, и мы будем использовать наш графический калькулятор, чтобы найти ответ. Поскольку разные модели калькуляторов имеют разные последовательности клавиш, я не могу дать инструкции о том, как «использовать технологию» для поиска ответов; вам нужно будет обратиться к руководству пользователя для любого калькулятора, который вы используете (или к файлу «Справка» для любой электронной таблицы или другого программного обеспечения, которое вы используете). Я приведу лишь пару примеров решения по картинке, которая вам дана.
Уравнение, которое мне дали решить:
0 = x 2 − 8 x + 15
На картинке, которую мне дали, показан график соответствующей квадратичной функции:
y = x 2 − 8 x + 15
. картинку (надеясь, что точки действительно пересекаются в целых числах, как кажется) и прочитайте х — отсечения графика (а значит и решений уравнения) от картинки.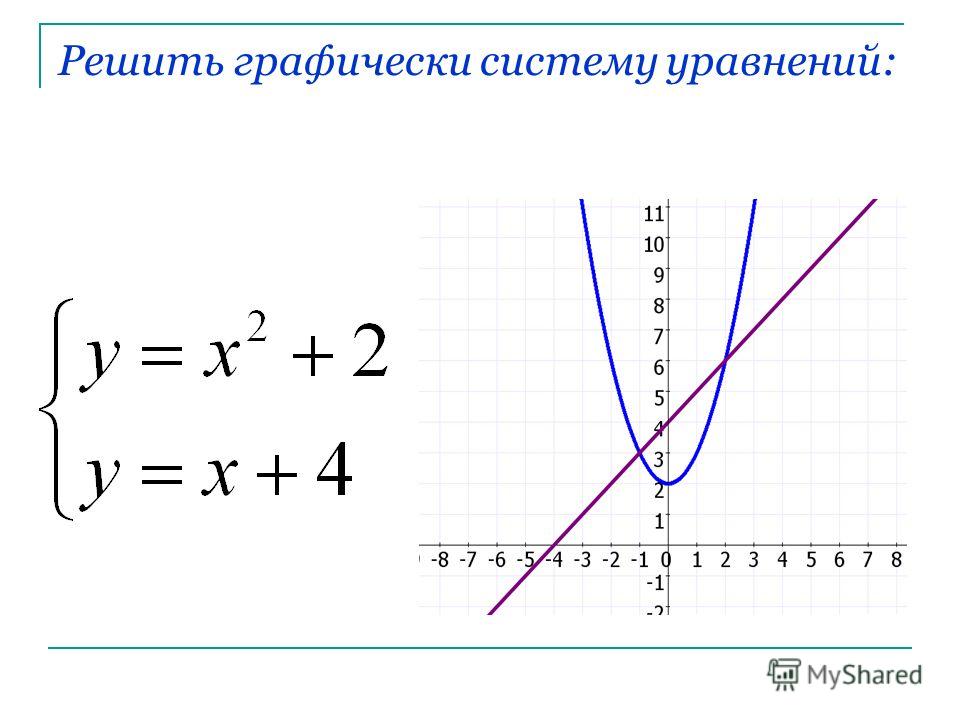
График пересекает ось x при x = 3 и при x = 5. Я должен предположить, что график точен, и то, что выглядит как целочисленное значение, на самом деле является единицей. Итак, мой ответ:
x = 3, 5
Поскольку в приведенном выше упражнении было получено квадратное уравнение, я могу проверить свое решение с помощью алгебры. Данные квадратичные множители, что дает мне:
( x — 3) ( x — 5) = 0
x — 3 = 0, x — 5 = 0
x = 3, 5
, что решения являются целыми числами. График может подсказывать решения, но только алгебра верна и точна.
A
= (−5/3, 0), B = (0, −5/3), C = (5/6, −15/8), D = (10/3, 0)
Для этой картинки они пометили кучу точек. Отчасти это должно было помочь, потому что x — перехваты беспорядочны, поэтому я не смог бы угадать их значения без меток. Но в основном это было сделано в надежде запутать меня, на случай, если я забыл, что только x -перехваты, а не вершины или y -перехваты соответствуют «решениям».
Точка B является точкой пересечения y (поскольку x = 0 для этой точки), поэтому я могу игнорировать эту точку. Точка C кажется вершиной, поэтому я также могу игнорировать эту точку. Точки A и D находятся на x -ось (поскольку y = 0 для этих точек). Таким образом, я могу предположить, что значения x этих точек на графике дают мне значения решения для соответствующего квадратного уравнения.
x = −5/3, 10/3
Поскольку они предоставили уравнение в дополнение к графику соответствующей функции, можно проверить ответ с помощью алгебры. Но целью здесь было подтвердить, что студент знает, какие точки являются x -перехваты, и знает, что эти перехваты на графике являются решениями связанного уравнения.
A = (−2,1429, 0), B = (2,8, 0), C = (0,3286, −3,0540), D = (0, −3)
Мне не дали решить квадратное уравнение , поэтому я не могу проверить свою работу алгебраически. Они дали мне только изображение параболы, созданной соответствующей квадратичной функцией, из которой я должен аппроксимировать x -отрезков, что на самом деле является другим вопросом. Но я знаю, что они означают.
Они дали мне только изображение параболы, созданной соответствующей квадратичной функцией, из которой я должен аппроксимировать x -отрезков, что на самом деле является другим вопросом. Но я знаю, что они означают.
Я могу игнорировать точку, которая, вероятно, является вершиной (точка C). Я могу игнорировать точку пересечения и (точка D). Поэтому я обращу внимание только на x -перехваты, т.е. на те точки, где y равно нулю. Итак, мой ответ таков:
x = −2,1429, 2,8
Решение квадратичных уравнений с помощью графика глупо с точки зрения «реальной жизни» и требует, чтобы решения были простыми факторинговыми решениями, такими как «». х = 3″, а не что-то вроде « x = −4 + sqrt(7)». Другими словами, они либо должны «дать» вам ответы (b, обозначающие график), либо они должны спросить вас
Практически единственное, что вы можете извлечь из этой темы, — это укрепить свое понимание связи между решениями уравнений и x — пересечениями графиков функций, т. е. что решения «(некоторый полином) равен (нулю)» соответствуют x — точки пересечения графика « y равно (тот самый многочлен)». Если вы уйдете с пониманием этой концепции, то вы будете знать, когда лучше всего использовать свой графический калькулятор или другое программное обеспечение для построения графиков, чтобы помочь вам решить общие полиномы; а именно, когда они не факторизуемы. И вы поймете, как делать первоначальные предположения и приближения к решениям, глядя на график, знания, которые могут быть очень полезны на более поздних занятиях, когда вы будете работать с программным обеспечением, чтобы найти приблизительные «числовые» решения.
е. что решения «(некоторый полином) равен (нулю)» соответствуют x — точки пересечения графика « y равно (тот самый многочлен)». Если вы уйдете с пониманием этой концепции, то вы будете знать, когда лучше всего использовать свой графический калькулятор или другое программное обеспечение для построения графиков, чтобы помочь вам решить общие полиномы; а именно, когда они не факторизуемы. И вы поймете, как делать первоначальные предположения и приближения к решениям, глядя на график, знания, которые могут быть очень полезны на более поздних занятиях, когда вы будете работать с программным обеспечением, чтобы найти приблизительные «числовые» решения.
Но на практике, если вам нужно решить квадратное уравнение на уроке алгебры, вам не следует начинать с рисования графика. В связи с этим возникает вопрос: какой метод для любого заданного квадратичного числа следует использовать для его решения?
URL: https://www.purplemath.com/modules/solvquad5.htm
Страница 1Страница 2Страница 3Страница 4Страница 6
Что означает графическое решение? Разъяснено в блоге часто задаваемых вопросов
Последнее обновление: 30 мая 2022 г.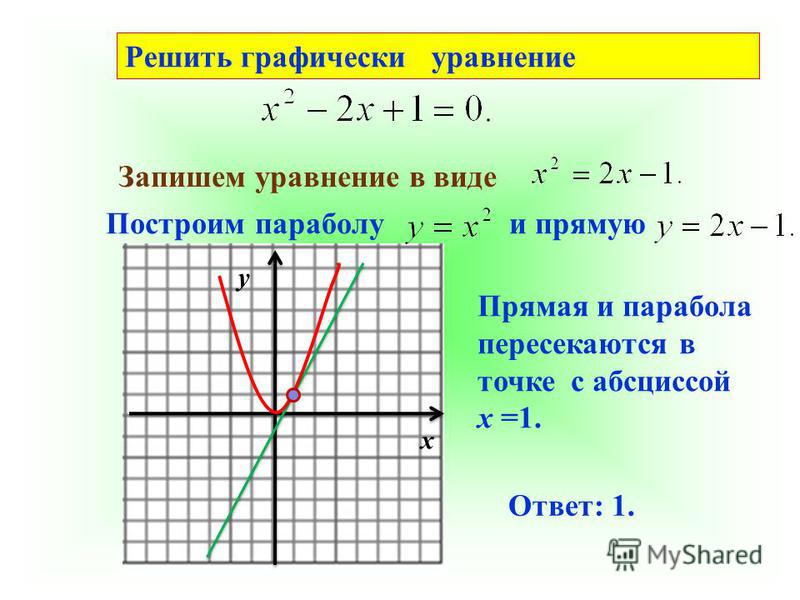
Этот вопрос время от времени задают наши эксперты. Теперь у нас есть полное подробное объяснение и ответ для всех, кто заинтересован!
Вопрос задан: Томми Просакко, доктор философии
Оценка: 4,3/5 (66 голосов)
Объяснение: Решить задачу графически означает построить графики функций в одной координатной плоскости и найти точки пересечения графиков .
Как решить графически?
Чтобы решить уравнение графически, нарисуйте график для каждой стороны, члена уравнения и посмотрите, где кривые пересекаются, равны . Значения x этих точек являются решениями уравнения.
Что такое графическая математика?
В математике граф можно определить как графическое представление или диаграмму, которая представляет данные или значения в организованном порядке. Точки на графике часто представляют отношения между двумя или более вещами. … Затем мы представляем данные с помощью гистограммы.
… Затем мы представляем данные с помощью гистограммы.
Что означает графически?
графически наречие (НА ИЗОБРАЖЕНИЯХ)
таким образом, который использует, состоит или относится к графикам, или к рисунку или печати: включите диаграмму, которая представляет эти данные графически. SMART Vocabulary: родственные слова и фразы.
Какие преимущества дает графическое решение уравнений?
Преимущество решения системы линейных уравнений с помощью графика заключается в том, что это относительно легко сделать и требует очень мало алгебры , а главный недостаток заключается в том, что ваш ответ будет приблизительным из-за необходимости читать ответ с графика .
Решение квадратных уравнений графически — Corbettmaths
24 связанных вопроса найдено
Какое решение при графическом решении уравнения?
Решением такой системы является упорядоченная пара, являющаяся решением обоих уравнений.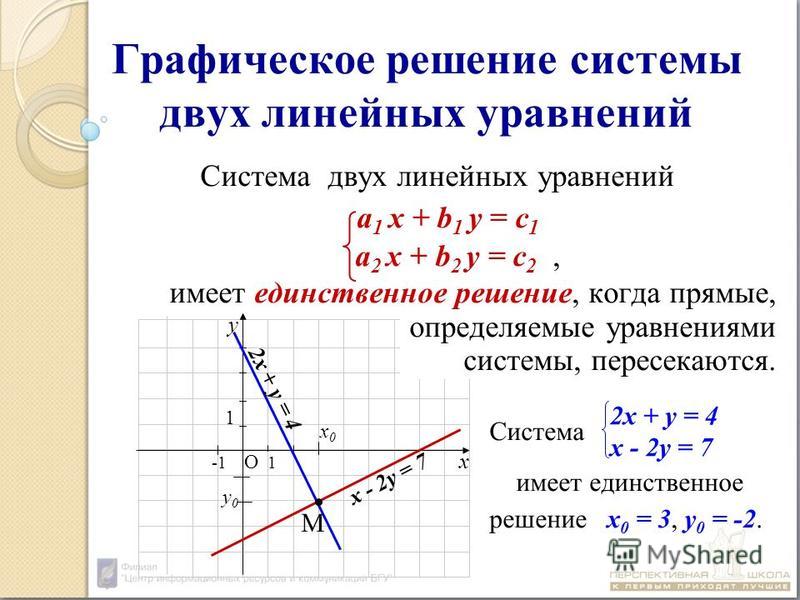 Чтобы решить систему линейных уравнений графически, мы изобразим оба уравнения в одной и той же системе координат . Решение системы будет находиться в точке пересечения двух прямых.
Чтобы решить систему линейных уравнений графически, мы изобразим оба уравнения в одной и той же системе координат . Решение системы будет находиться в точке пересечения двух прямых.
Что такое метод одного графика?
Метод одного графика — это метод, используемый в алгебре, при котором функция изображается в виде графика . Этот график показывает характер функции, вогнутость функции, а также важные точки на графике, такие как точки пересечения x и y. График функции также можно использовать для нахождения решения функции.
Что такое графическое представление линейного уравнения?
Резюме. График любого линейного уравнения с двумя переменными представляет собой прямую линию . x = 0 — уравнение оси y, а y = 0 — уравнение оси x. График x = a представляет собой прямую линию, параллельную оси y.
Зачем мы строим графики?
Графики являются распространенным методом визуальной иллюстрации отношений в данных .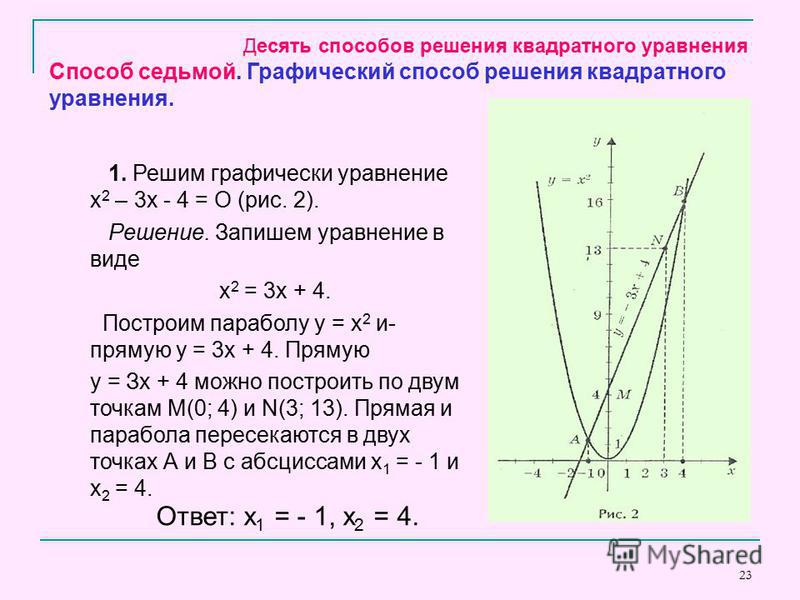 Назначение графика — представить данные, которые слишком многочисленны или сложны для адекватного описания в тексте и в меньшем объеме. … Если данные показывают ярко выраженные тенденции или выявляют отношения между переменными, следует использовать график.
Назначение графика — представить данные, которые слишком многочисленны или сложны для адекватного описания в тексте и в меньшем объеме. … Если данные показывают ярко выраженные тенденции или выявляют отношения между переменными, следует использовать график.
Что вы подразумеваете под графиком в структуре данных?
(структура данных) Определение: Набор элементов, соединенных ребрами . Каждый элемент называется вершиной или узлом. Формально граф — это множество вершин и бинарное отношение между вершинами, смежность.
При графическом решении уравнения решением является координата точки пересечения?
При пересечении линий точка пересечения является единственной общей точкой двух графиков. Таким образом, координаты этой точки являются решением для двух переменных, используемых в уравнениях.
Что является примером графика?
Определение графа — это диаграмма, показывающая отношения между двумя или более вещами. Примером графика является круговая диаграмма .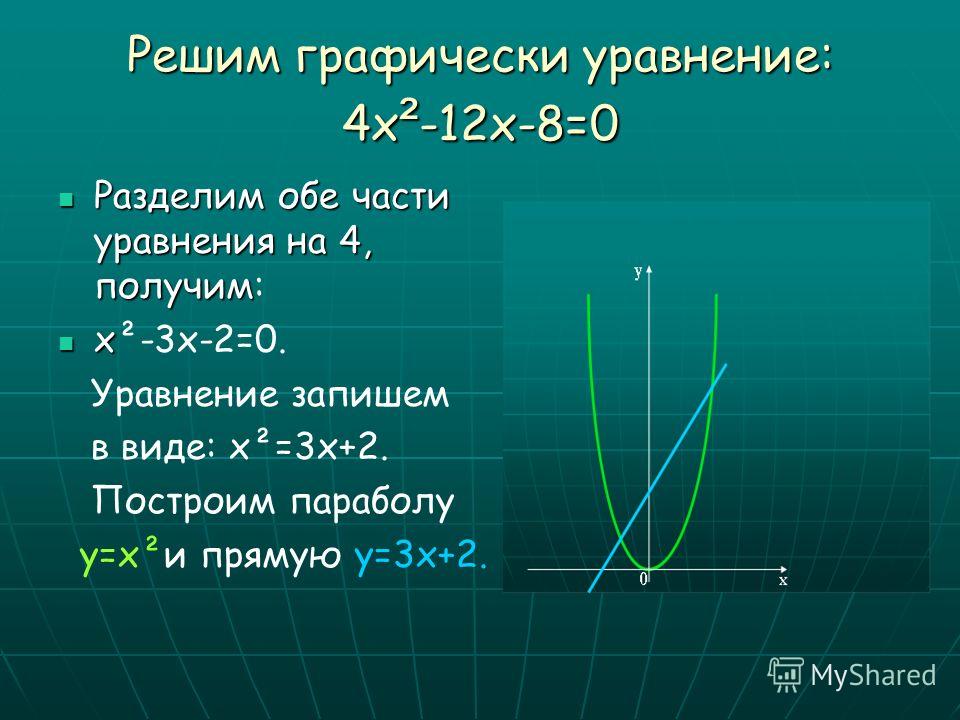 … График функции y = x 2 представляет собой параболу.
… График функции y = x 2 представляет собой параболу.
Когда вы будете использовать график в структуре данных?
Графики используются в различных отраслях и областях:
- Системы GPS и Google Maps используют графики для поиска кратчайшего пути от одного пункта назначения к другому.
- Социальные сети используют графики для представления связей между пользователями.
- Алгоритм поиска Google использует графики для определения релевантности результатов поиска.
Что такое график пояснить на примере?
Граф — это общая структура данных, состоящая из конечного набора узлов (или вершин) и набора соединяющих их ребер . … Например, один пользователь в Facebook может быть представлен как узел (вершина), а его связь с другими может быть представлена как ребро между узлами.
Как читать результаты графика?
Чтобы интерпретировать график или диаграмму, прочитайте заголовок, посмотрите на ключ, прочитайте метки.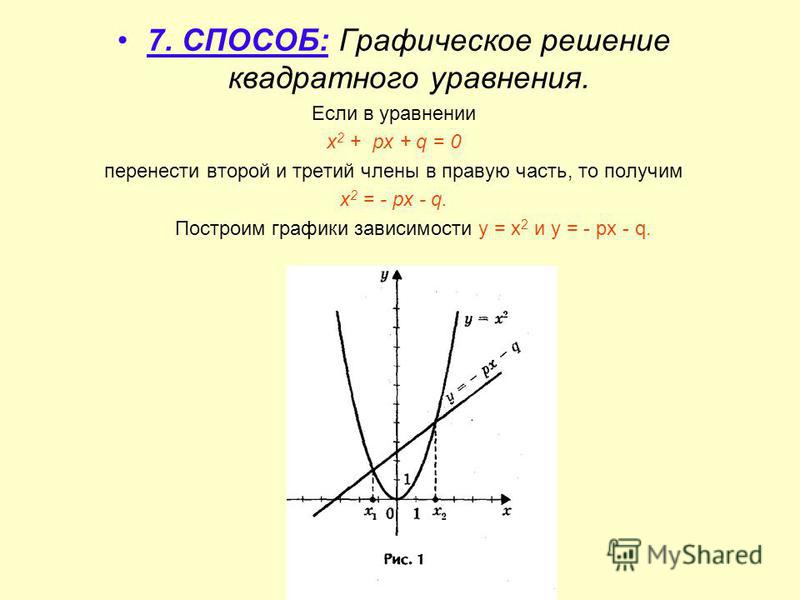 Затем изучите график, чтобы понять, что он показывает . Прочитайте название графика или диаграммы. Название сообщает, какая информация отображается.
Затем изучите график, чтобы понять, что он показывает . Прочитайте название графика или диаграммы. Название сообщает, какая информация отображается.
Что означает график при чтении?
Определение графа (Запись 3 из 4) 1 : письменное или печатное представление основной единицы речи (такой как фонема или слог), особенно: смысл графемы 1. 2 : единичное появление буквы алфавит в любой из его различных форм.
Как вы читаете графики?
Линия, идущая снизу, называется горизонтальной или осью X, а линия вверх сбоку называется вертикальной осью, или осью Y.
- Ось X может содержать категории или числа. Вы читаете это в левом нижнем углу графика.
- Ось Y обычно содержит числа, опять же начиная с нижнего левого угла графика.
Как представить уравнение графически?
Вот общий метод решения уравнений с помощью графика. Шаг 1: Пусть y равно выражениям по обе стороны от знака равенства. Шаг 2: Нарисуйте график двух созданных функций. Шаг 3: Аппроксимируйте точки, в которых пересекаются графики функций.
Шаг 2: Нарисуйте график двух созданных функций. Шаг 3: Аппроксимируйте точки, в которых пересекаются графики функций.
Что такое график временных рядов?
Графики временных рядов создаются путем нанесения агрегированного значения (количественного или статистического, такого как сумма или среднее) на временной шкале. Значения агрегируются с использованием временных интервалов, основанных на временном диапазоне отображаемых данных. На графиках временных рядов используются следующие временные интервалы: Одно десятилетие. Три года.
Что значит решить графически?
Вопрос задан: Д-р Синсер Ботсфорд
Оценка: 4,9/5 (73 голоса)
Объяснение: Решить задачу графически означает построить графики функций в одной координатной плоскости и найти точки пересечения графиков .
Как решить задачу графически?
Чтобы решить уравнение графически, нарисуйте график для каждой стороны, члена уравнения и посмотрите, где кривые пересекаются, равны . Значения x этих точек являются решениями уравнения. Есть много возможных результатов, когда кто-то решает уравнение.
Значения x этих точек являются решениями уравнения. Есть много возможных результатов, когда кто-то решает уравнение.
Что означает графически в алгебре?
В математике граф можно определить как графическое представление или диаграмму, которая представляет данные или значения в организованном порядке. Точки на графике часто представляют отношения между двумя или более вещами.
Как вы представляете графически?
Графическое представление данных
- Создайте таблицу частот, гистограмму, диаграмму Парето, пиктограмму или круговую диаграмму для представления набора данных.
- Определите особенности неэффективного представления данных.
- Создайте гистограмму, круговую диаграмму или многоугольник частот, представляющий числовые данные.
- Создайте график для сравнения двух величин.
Является ли график диаграммой?
Диаграмма может представлять табличные числовые данные, функции или некоторые виды структуры качества и предоставлять различную информацию. Термин «диаграмма» как графическое представление данных имеет несколько значений:0414 Тип диаграммы или графика , который организует и представляет набор числовых или качественных данных.
Термин «диаграмма» как графическое представление данных имеет несколько значений:0414 Тип диаграммы или графика , который организует и представляет набор числовых или качественных данных.
Решение квадратичных уравнений графически 2 — Corbettmaths
Найдено 28 связанных вопросов
Как решить два уравнения графически?
Знание построения линейных и квадратичных графиков необходимо для графического решения уравнений. Чтобы найти решения по графикам, ищите точку пересечения двух графиков. Это точка решения. Например, решением для графиков y = x + 1 и x + y = 3 является координатная точка (1, 2).
Как решить одновременные уравнения графически?
Чтобы графически решить пару одновременных уравнений, мы сначала рисуем график двух уравнений одновременно . Получаем две прямые, пересекающиеся друг с другом в общей точке. Эта общая точка пересечения двух линий дает решение пары одновременных уравнений.
Как решить линейные уравнения графически?
Решить пару линейных уравнений с двумя переменными графическим методом, сначала нарисуйте линии, представленные ими . я. Если пара прямых пересекается в точке, то говорят, что пара непротиворечива, и координаты точки дают единственное решение.
Как решить линейные уравнения с двумя переменными?
Решение систем уравнений с двумя переменными методом сложения
- Запишите оба уравнения с переменными x– и y слева от знака равенства и константами справа.
- Напишите одно уравнение над другим, выстраивая соответствующие переменные. …
- Решите полученное уравнение для оставшейся переменной.

Как решить линейные уравнения с двумя переменными графически?
Постройте линейное уравнение, используя точки пересечения.
- Найдите точку пересечения линии по осям x и y. Позволять. и решить для х. Позволять. и решить для y.
- Найдите третье решение уравнения.
- Нанесите три точки и убедитесь, что они совпадают.
- Проведите линию.
Какова формула графического метода?
Сначала решите каждое уравнение относительно «y =» Или измените каждое уравнение в y = mx + b из . После преобразования уравнений в форму y = mx + b подготовьте таблицу функций. Возьмите любые значения x, подставьте эти значения одно за другим в данное уравнение и найдите значение y. Отсюда мы получаем (x, y) координаты.
Что такое решение одновременных уравнений?
Проще говоря, решением пары одновременных уравнений является значения x и y координат точки, в которой графики пересекаются или пересекаются .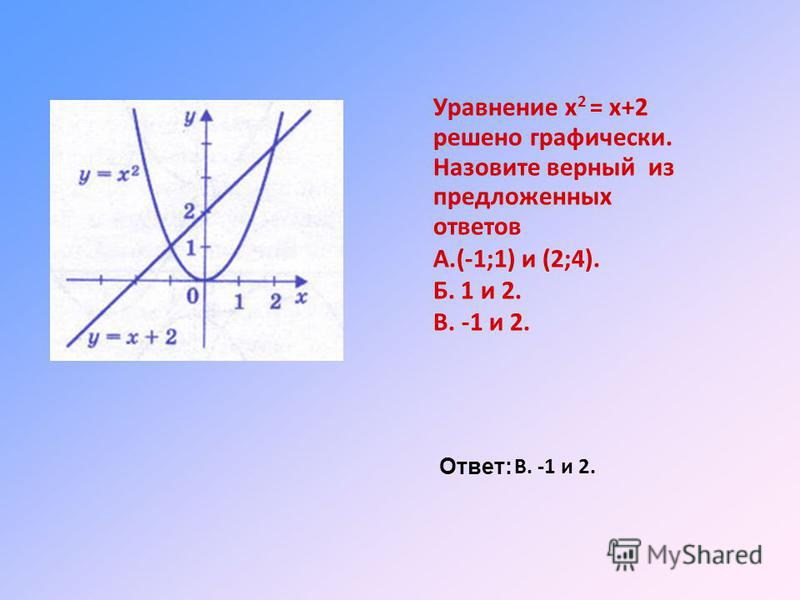
Как решать одновременные уравнения с 3 переменными?
Выберите любые две пары уравнений из системы. Удалите одну и ту же переменную из каждой пары, используя метод сложения/вычитания . Решите систему двух новых уравнений, используя метод сложения/вычитания. Подставьте решение обратно в одно из исходных уравнений и найдите третью переменную.
Каков первый шаг метода исключения?
Метод исключения
- Решение:
- Шаг 1: Умножьте одно или оба уравнения, чтобы исключить одну из переменных. …
- Шаг 2: Сложите уравнения, чтобы исключить одну из переменных.
- Шаг 3: Найдите оставшуюся переменную.
- Шаг 3: Обратно подставьте в любое уравнение или эквивалентное ему уравнение.
Какими методами можно решить систему уравнений?
Всегда есть три способа решить систему уравнений
Существует три способа решения систем линейных уравнений: замена, исключение и построение графика . Давайте рассмотрим шаги для каждого метода.
Давайте рассмотрим шаги для каждого метода.
Как вы используете графический метод в математике?
Графический метод
- Шаг 1: Сформулируйте задачу LP (линейное программирование). …
- Шаг 2: Постройте график и нанесите линии ограничения. …
- Шаг 3: Определите допустимую сторону каждой ограничительной линии. …
- Шаг 4. Определите допустимую область решения. …
- Шаг 5: Нанесите целевую функцию на график. …
- Шаг 6: Найдите оптимальную точку.
Что означает LPP?
ЛПП. Задачи линейного программирования в математике — это системный процесс нахождения максимального или минимального значения любой переменной в функции, он также известен под названием задачи оптимизации. LPP помогает в разработке и решении проблемы принятия решений с помощью математических методов.
Что такое графический метод в физике?
Резюме. Графический метод сложения векторов A и B включает в себя отрисовку векторов на графе и их сложение методом «голова к хвосту». Результирующий вектор R определяется таким образом, что A + B = R. Затем величина и направление R определяются с помощью линейки и транспортира соответственно.
Результирующий вектор R определяется таким образом, что A + B = R. Затем величина и направление R определяются с помощью линейки и транспортира соответственно.
Каковы характеристики линейных уравнений с двумя переменными?
Уравнение называется линейным уравнением с двумя переменными, если оно равно записывается в виде ax + by + c=0, где a, b и c — действительные числа, а коэффициенты при x и y, т.е. a и b соответственно, не равны нулю . Например, 10x+4y = 3 и -x+5y = 2 являются линейными уравнениями с двумя переменными.
Может ли линейное уравнение иметь 3 переменные?
(«Три переменные» — это x, y и z.) Числа a, b и c называются коэффициентами уравнения. … 3x + 4y — 7z = 2, -2x + y — z = -6, x — 17z = 4, 4y = 0 и x + y + z = 2 — все линейные уравнения с тремя переменными.
Похожие вопросы
- 25Что означает графически в математике?
- 33Графически это слово?
Реклама
Популярные вопросы
- 24Соответствует ли цена crutchfield?
- 34Кто лучше sas или sbs?
- 33 В гальванометре с подвижной катушкой?
- 22Возврат налогов осуществляется по средам?
- 45Слаборастворимый считается растворимым?
- 18Для обновления до Windows 10?
- 22Работает ли восстановление Фибоначчи в криптовалюте?
- 16Казино «Рояль» снимали на пленку?
- 28Сроки трансляций на twitch истекают?
- 22Является ли Шотландия страной?
Графический метод решения линейных уравнений с двумя переменными
Графический метод решения линейных уравнений в двух переменных Пусть система пары линейных уравнений будет
A 1 x + b 1 y = c 1 …. (1)
(1)
A 7 277777777777 27877 29877 29877 29877. x + b 2 y = c 2 ….(2)
Мы знаем, что для двух прямых на плоскости может произойти только одна из следующих трех возможностей:
(i) Две прямые пересекутся в одной точке. точка.
(ii) Две прямые не пересекутся, как бы далеко они ни были вытянуты, т. е. они параллельны.
(iii) Две линии совпадают.
Типы решений:
Существует три типа решений
- Уникальное решение.
- Бесконечное множество решений
- Нет решения.
Подробнее:
- Что такое линейное уравнение
- Линейные уравнения с двумя переменными
- Линейные уравнения с одной переменной0003 RS Aggarwal Class 9 Решения линейных уравнений с двумя переменными
- RS Aggarwal Class 8 Решения линейных уравнений
- RS Aggarwal Class 7 Решения линейных уравнений с одной переменной
- RS Aggarwal Class 6 Решения линейных уравнений с одной переменной 9001A
0 ( ) Непротиворечивость: Если система одновременных линейных уравнений имеет хотя бы одно решение, то говорят, что система непротиворечива.

(i) Совместные уравнения с единственным решением: Графики двух уравнений пересекаются в единственной точке.
Например Рассмотрим
x + 2y = 4
7x + 4y = 18
Графики (линии) этих уравнений пересекаются друг с другом в точке (2, 1), т. е. x = 2, y = 1.
Следовательно, уравнения согласуются с единственным решением.
(ii) Согласованные уравнения с бесконечным числом решений: Графики (линии) двух уравнений будут совпадать.
Например, Рассмотрим 2x + 4y = 9⇒ 3x + 6y = 27/2
Графики приведенных выше уравнений совпадают. Координаты каждой точки на прямых являются решениями уравнений. Следовательно, данные уравнения согласованы с бесконечным числом решений.
(B) Несовместимое уравнение: Если система одновременных линейных уравнений не имеет решения, то говорят, что система несовместима.
Нет Решение: График (линии) двух уравнений параллельны.
Например Рассмотрим
4x + 2y = 10
6x + 3y = 6
Графики (линии) данных уравнений параллельны. Они никогда не сойдутся в одной точке. Итак, решения нет. Следовательно, уравнения несовместимы.
7 2 2 = 0 равно
Из приведенной выше таблицы видно, что если линия a 1 x + b 1 y + c 1 = 0 и a 2 x + c 9 0Примеры графического метода
Пример 1: Путь шоссе номер 1 определяется уравнением x + y = 7, а путь номер 2 определяется уравнением 5x + 2y = 20. Представьте эти уравнения геометрически.
Соль. We have, x + y = 7
⇒ y = 7 – x ….(1)
In tabular formx 1 4 y 6 3 Очки А В and 5x + 2y = 20
⇒ y = \(\frac { 20-5x }{ 2 }\) …. (2)
(2)
In tabular formx 2 4 y 5 0 Points C D Plot the points A (1, 6), B(4, 3) and join them to form a line АБ.
Аналогичным образом нанесите точки C(2, 5). D (4, 0) и соедините их, чтобы получить линию CD. Ясно, что две прямые пересекаются в точке C. Теперь каждая точка на прямой AB дает нам решение уравнения (1). Каждая точка на CD дает нам решение уравнения (2).Пример 2: Отец говорит дочери: «Семь лет назад я был в семь раз старше тебя. Кроме того, через три года я буду в три раза старше тебя». Представьте эту ситуацию алгебраически и графически.
Соль. Пусть возраст отца в настоящее время равен x лет, а возраст дочери = y лет
Семь лет назад возраст отца = (x – 7) лет
Семь лет назад возраст дочери = (y – 7) лет
Согласно задаче
(x – 7) = 7(y – 7) или x – 7y = – 42 …. (1)
(1)
Через 3 года возраст отца = (x + 3) лет
Через 3 года возраст дочери = (y + 3) лет
Согласно условию, заданному в вопросе
x + 3 = 3(y + 3) или x – 3y = 6 ….(2)
x – 7y = –42 ⇒ \(y=\frac { x+42 }{ 7 }\)x 0 7 14 y 6 7 8 Points A B C x – 3y = 6 ⇒ \(y=\frac { x-6 }{ 3 }\)
x 6 12 18 y 0 2 4 Points D E F Plot the points A(0, 6), B(7, 7) , C(14, 8) и соединим их, чтобы получить прямую ABC. Аналогичным образом нанесите точки D(6, 0), E(12, 2) и F(18, 4) и соедините их, чтобы получить прямую линию DEF.

Пример 3: 10 учеников X класса приняли участие в викторине по математике. Если девочек на 4 больше, чем мальчиков, найдите количество мальчиков и девочек, принявших участие в викторине.
Соль. Пусть количество мальчиков равно x, а количество девочек равно y.
Тогда образуются уравнения
x + y = 10 ….(1)
и y = x + 4 ….(2)
Построим графики уравнений (1) и (2), найдя по два решения для каждого уравнений. 9Приведено 0042 решения уравнений.
x + y = 10 ⇒ y = 10 – xx 0 8 y 10 2 Points A B y = x + 4
x 0 1 3 y 4 5 7 Points C D E Нанося эти точки, мы проводим линии AB и CE, проходящие через них, чтобы представить уравнения.
 Две прямые AB и Ce пересекаются в точке E (3, 7). Итак, x = 3 и y = 7 — искомое решение пары линейных уравнений.
Две прямые AB и Ce пересекаются в точке E (3, 7). Итак, x = 3 и y = 7 — искомое решение пары линейных уравнений.
т.е. Количество мальчиков = 3
Количество девочек = 7.
Проверка:
Подставляя x = 3 и y = 7 в (1), получаем
Л.Х.С. = 3 + 7 = 10 = RHS, (1) проверено.
Полагая x = 3 и y = 7 в (2), получаем
7 = 3 + 4 = 7, (2) проверено.
Следовательно, выполняются оба уравнения.Пример 4: Половина периметра сада, длина которого в 4 раза больше ширины, равна 36 м. Найдите размеры сада.
Соль. Пусть длина сада равна x, а ширина сада равна y.
Тогда образовано уравнение:
x = y + 4 ….(1)
Полупериметр = 36
x + y = 36 ….(2)
y = x – 4x 0 4 y -4 0 Points A B y = 36 – x
x 10 20 y 26 16 Points C D Plotting these points we draw the lines AB and CD passing through them to represent the уравнения.

Две прямые AB и CD пересекаются в точке (20, 16). Таким образом, x = 20 и y = 16 — искомое решение пары линейных уравнений, т. е. длина сада 20 м, а ширина сада составляет 16 м.
Проверка:
Помещение x = 20 и y = 16 в (1). Получаем
20 = 16 + 4 = 20, (1) проверено.
Полагая x = 20 и y = 16 в (2). получаем
20 + 16 = 36
36 = 36, (2) проверено.
Следовательно, выполняются оба уравнения.Пример 5: Нарисуйте графики уравнений x – y + 1 = 0 и 3x + 2y – 12 = 0. Определите координаты вершин треугольника, образованного этими прямыми и осью x, и заштрихуйте треугольную область.
Соль. Пара линейных уравнений:x 0 4 у 1 5 Points A B 3x + 2y – 12 = 0 ⇒ y = \(\frac { 12-3x }{ 2 }\)
x 0 2 y 6 3 Points C D Plot the points A(0, 1), B(4, 5) and join them to get a линия АВ.
 Точно так же нанесите точки C(0, 6), D(2, 3) и соедините их, чтобы сформировать линию CD.
Точно так же нанесите точки C(0, 6), D(2, 3) и соедините их, чтобы сформировать линию CD.
Ясно, что две прямые пересекаются в точке D(2, 3). Следовательно, x = 2 и y = 3 являются решением
заданной пары уравнений.
Линия CD пересекает ось x в точке
E (4, 0), а линия AB пересекает ось x в точке F(–1, 0).
Следовательно, координаты вершин треугольника равны; D(2, 3), E(4, 0), F(–1, 0).
Проверка:
Оба уравнения (1) и (2) удовлетворяются при x = 2 и y = 3. Следовательно, проверено.Пример 6: Покажите графически, что система уравнений
x – 4y + 14 = 0; 3x + 2y – 14 = 0 соответствует единственному решению.
Соль. Данная система уравнений имеет вид
x – 4y + 14 = 0 ….(1)
3x + 2y – 14 = 0 …. (2)
x – 4y + 14 = 0 ⇒ y = \(\frac { x + 14 }{ 4 }\)x 6 -2 y 5 3 Points A B 3x + 2y – 14 = 0 ⇒ y = \(\frac { -3x + 14 }{ 2 }\)
x 0 4 Y 7 1 Точки C D
. Следовательно, уравнения согласуются с единственным решением.
Следовательно, уравнения согласуются с единственным решением.Пример 7: Покажите графически, что система уравнений
2x + 5y = 16; \(3x+\frac { 15 }{ 2 }=24\) имеет бесконечно много решений.
Соль. Дана система уравнений:
2x + 5y = 16 ….(1)
\(3x+\frac { 15 }{ 2 }=24\) ….(2)
2x + 5y = 16 ⇒ y = \( \frac { 16-2x }{ 5 }\)x -2 3 y 4 2 точек A B \(3x+\frac { 15 }{ 2 }=24\) ⇒ y = \(\frac { 48-6x }{ 15 }\) 9003 91
0
x
1/2 11/2 y 3 1 Points C D
The lines of two equations are coincident. Координаты каждой точки на этой прямой являются решением.
Координаты каждой точки на этой прямой являются решением.
Следовательно, данные уравнения согласованы с бесконечным числом решений.Пример 8: Покажите графически, что система уравнений
2x + 3y = 10, 4x + 6y = 12 не имеет решения.
Соль. The given equations are
2x + 3y = 10 ⇒ y = \(\frac { 10-2x }{ 3 }\)x -4 2 y 6 2 Точки A B 0034
x -3 3 y 4 0 Points C D Plot the points A (–4, 6) , B(2, 2) и соединить их, чтобы получилась линия AB. Точно так же нанесите точки C(–3, 4), D(3, 0) и соедините их, чтобы получить линию CD.

Ясно, что графики данных уравнений представляют собой параллельные прямые. Поскольку они не имеют общей точки, нет и общего решения. Следовательно, данная система уравнений не имеет решения.Пример 9: Учитывая линейное уравнение 2x + 3y – 8 = 0, напишите еще одно линейное уравнение с двумя переменными так, чтобы
геометрическое представление образованной таким образом пары было:
(i) пересекающиеся прямые
(ii) параллельные строки
(iii) совпадающие строки
Sol. Имеем, 2x + 3y – 8 = 0
(i) Другое линейное уравнение с двумя переменными, геометрическое представление образованной таким образом пары представляет собой пересекающиеся прямые:
3x – 2y – 8 = 0
(ii) Другая линия, параллельная указанной выше линии, равна
4x + 6y – 22 = 0
(iii) Другая линия, совпадающая с указанной выше линией, равна
6x + 9y – 24 = 0Пример 10: Решите следующую систему линейные уравнения графически;
3х + у – 11 = 0; x – y – 1 = 0
Закрасьте область, ограниченную этими линиями, а также ось y. Затем определите площади области, ограниченной этими линиями и осью Y.
Затем определите площади области, ограниченной этими линиями и осью Y.
Соль. Имеем
3x + y – 11 = 0 и x – y – 1 = 0
(a) График уравнения 3x + y – 11 = 0
Имеем, 3x + y – 11 = 0
⇒ y = – 3x + 11
Когда, x = 2, y = –3 × 2 + 11 = 5
При x = 3, y = – 3 × 3 + 11 = 2
Нанося точки P (2, 5) и Q(3, 2) на миллиметровую бумагу и проводя линию, соединяющую их, мы получить график уравнения 3x + y – 11 = 0, как показано на рис.
(б) График уравнения x – y – 1 = 0
Имеем,
x – y – 1 = 0
y = x – 1
Когда, x = – 1, y = –2
При x = 3, y = 2
Нанося точки R(–1, –2) и S(3, 2) на одну и ту же миллиметровую бумагу и проводя линию, соединяющую их, мы получаем график уравнения x – y – 1 = 0, как показано на рис.
Вы можете заметить, что две линии пересекаются в точке
Q(3, 2). Итак, x = 3 и y = 2. Заштрихована область, ограниченная линиями, представленными данными уравнениями, а также ось y.
Итак, закрытая площадь = Площадь заштрихованной части
= Площадь ∆QUT = 1/2 × основание × высота
= 1/2 × (TU × VQ) = 1/2 × (TO + OU) × VQ
= 1/2 (11 + 1) 3 = 1/2 × 12 × 3 = 18 кв.ед.
Отсюда необходимая площадь 18 кв.Пример 11: Нарисуйте графики следующих уравнений
2x – 3y = – 6; 2х + 3у = 18; y = 2
Найдите вершины образовавшихся треугольников, а также найдите площадь треугольника.
Соль. (a) График уравнения 2x – 3y = – 6;
Имеем, 2x – 3y = – 6 ⇒ y = \(\frac { 2x+6 }{ 3 }\)
Когда, x = 0, y = 2
Когда, x = 3, y = 4
Нанеся на миллиметровую бумагу точки P(0, 2) и Q(3, 4) и проведя линию, соединяющую их, получим график уравнения 2x – 3y = – 6, как показано на рис.
(б) График уравнения 2x + 3y = 18;
Имеем 2x + 3y = 18 ⇒ y = \(\frac { -2x+18 }{ 3 }\)
Когда x = 0, y = 6
Когда x = – 3, y = 8
Построение графика точки R(0, 6) и S(–3, 8) на той же миллиметровке и проведя линию, соединяющую их, получим график уравнения 2x + 3y = 18, как показано на рис.
(c) График уравнения y = 2
Ясно, что y = 2 для любого значения x. Мы можем взять точки T (3, 2), U(6, 2) или любые другие значения.
Нанеся точки T(3, 2) и U(6, 2) на одну и ту же миллиметровую бумагу и проведя линию, соединяющую их, получим график уравнения y = 2, как показано на рис.
Из рисунка видно, что прямые, взятые попарно, пересекаются друг с другом в точках Q(3, 4), U (6, 2) и P(0, 2). Они образуют три вершины треугольника PQU.
Найти площадь треугольника, образованного таким образом
Треугольник, образованный таким образом, равен PQU (см. рис.)
В ∆PQU
QT (высота) = 2 единицы
и PU (основание) = 6 единиц
Итак, площадь ∆ PQU = (основание × высота)
= 1/2 (PU × QT) = 1/2 × 6 × 2 кв. до
= 6 кв.Пример 12: При сравнении соотношений \(\frac{{{a}_{1}}}{{{a}_{2}}},\frac{{{b}_{1}} }{{{b}_{2}}}и\frac{{{c}_{1}}}{{{c}_{2}}}\) и, не рисуя их, выяснить, соответствуют ли линии, представляющие следующие пары линейных уравнений пересекаются в точке, параллельны или совпадают.

(i) 5x – 4y + 8 = 0, 7x + 6y – 9 = 0
(ii) 9x + 3y + 12 = 0, 18x + 6y + 24 = 0
(iii) 6x – 3y + 10 = 0, 2x – y + 9 = 0
Сол. Сравнивая данные уравнения со стандартными формами уравнений a 1 x + b 1 y + c 1 = 0 и
a 2 x + b 2 y + c 2 имеем ,
(i) а1 = 5, б 1 = – 4, в 1 = 8;
а 2 = 7, б 2 = 6, в 2 = – 9
\( \frac{{{a}_{1}}}{{{a}_{2}}}=\frac{5}{7},\frac{{{b} _{1}}}{{{b}_{2}}}=\frac{-4}{6} \)
\(\Rightarrow \frac{{{a}_{1}}}{{{ a}_{2}}}\ne \frac{{{b}_{1}}}{{{b}_{2}}} \)
Таким образом, прямые, представляющие пару линейных уравнений, пересекаются.
(ii) a1 = 9, b 1 = 3, c 1 = 12;
a 2 = 18, b 2 = 6, c 2 = 24
\( \frac{{{a}_{1}}}{{{a}_{2}}}=\ frac{9}{18}=\frac{1}{2},\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{3}{6} =\frac{1}{2}и\frac{{{c}_{1}}}{{{c}_{2}}}=\frac{12}{24}=\frac{1}{ 2}\)
\(\Rightarrow \frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{ 2}}}=\frac{{{c}_{1}}}{{{c}_{2}}} \)
Таким образом, прямые, представляющие пару линейных уравнений, совпадают.
(iii) а1 = 6, б 1 = – 3, в 1 = 10;
a 2 = 2, b 2 = – 6, c 2 = 9
\( \frac{{{a}_{1}}}{{{a}_{2}}}= \frac{6}{2}=3,\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{-3}{-1}=3and\frac {{{c}_{1}}}{{{c}_{2}}}=\frac{10}{9} \)
\(\Rightarrow \frac{{{a}_{1}} }{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}\ne \frac{{{c}_{1} }}{{{с}_{2}}} \)
Таким образом, линии, представляющие пару линейных уравнений, параллельны.Решение квадратных уравнений и построение графиков: шаги и примеры
Позвольте мне нарисовать вам картину: допустим, нам дано квадратное уравнение, и нам предлагается определить множество решений, которое имеет данное выражение. Как вы думаете, как лучше всего представить этот набор решений?
Что ж, всегда практично смотреть на математические вещи визуально. Это позволяет нам смотреть на тренды и, следовательно, исследовать вовлеченные закономерности. В этом случае будем представлять квадратные уравнения в виде графика.

Квадратные уравнения
Прежде чем мы углубимся в это, давайте сначала вспомним определение квадратного уравнения.
Стандартная форма квадратного уравнения определяется выражением y = ax 2 + bx + c, где a ≠ 0,
Квадратное уравнение может быть задано как функция y = f( х) ⇔ f(x) = ах 2 + Ьх + с.
Здесь ax 2 — квадратичный член , bx — линейный член , а c — постоянный член .
Как упоминалось ранее, графическое решение квадратных уравнений — это хитрый трюк, который позволяет нам определять их решения и замечать любое существенное поведение, присутствующее в заданном выражении. График квадратичной формулы имеет специальное имя, определенное ниже.
График любого квадратного уравнения описывается параболой .
В этом разделе мы рассмотрим методы построения графиков таких уравнений.
 Прежде чем мы начнем, давайте посмотрим на компоненты параболы.
Прежде чем мы начнем, давайте посмотрим на компоненты параболы.Компоненты параболы
График квадратного уравнения
Рассмотрим график y = ax 2 + bx + c, как показано ниже.
Компоненты параболы, Айша Амри — StudySmarter Originals
Ось симметрии параболы — это вертикальная линия, которая делит параболу на две равные половины.
Вершина — это точка, в которой ось симметрии пересекает параболу.
y-отрезок находится путем подстановки x = 0 в квадратное уравнение как y = a(0) 2 + b(0) + c = c.
Точка пересечения x находится путем приравнивания квадратного уравнения к нулю как ax 2 + bx + c = 0.
Координата x вершины равна .
Y-координата вершины .
Максимальное и минимальное значения
Y-координата вершины может быть максимальным или минимальным значением.
 Вершина известна как точка поворота параболы.
Вершина известна как точка поворота параболы.Точка поворота кривой — это точка, в которой график меняет направление, т. е. меняется с возрастания на убывание или с убывания на возрастание.
Максимальное значение — это максимально возможное значение y, которого достигает кривая.
Минимальное значение — это наименьшее возможное значение y, которого достигает кривая.
Рассматривая квадратное уравнение y = ax 2 + bx + c, параметр, который заранее сообщает нам, будет ли вершина соответствующей параболы максимальным или минимальным значением, является знаком коэффициента перед старшим членом, т. е. признак а. В таблице ниже описывается график для двух случаев, когда a может принимать a, то есть a > 0 и a < 0,9.0034
Property
y = ax 2 + bx + c, where a ≠ 0
Value of coefficient a
a is positive
a > 0
a is negative
a < 0
Opening of Parabola
Opens upward
Opens downward
Поворотная точка Y
Минимальное значение
Максимальное значение
Диапазон
Все реальные номера больше или равны, чем, чем, равно или равны, чем, равно или равны, чем, равно или равны, что равное, чем, равно или равны, что равное, чем, равно, что равное, чем, равно, что равное, чем, равно, что ранее, чем, равно или равное, чем, равно или равны, что равны, чем, равно или равны, что равны, чем, равно или равны, что равны, чем, равно или равны, что равенство
.
 максимальное
максимальноеПример графика
Минимальное значение, Айша Амри — StudySmarter Originals
Максимальное значение, Айша Амри — StudySmarter Originals
Решения квадратного уравнения
Решения квадратного уравнения, обнуленные, также являются корнями или нулями соответствующей квадратичной функции. Это точки пересечения параболы по оси x, которые решаются путем установки y равным нулю и решения для x как как узнать, сколько у него может быть решений? Вот где 9В игру вступает дискриминант 0101 ! Квадратное уравнение может иметь одно действительное решение, два действительных решения или не иметь действительных решений и определяется знаком дискриминанта.
Дискриминант
Дискриминант определяется выражением D = b 2 – 4ac.
Значение дискриминанта можно использовать для определения количества и типа корней заданного квадратного уравнения.
 Учитывая квадратное уравнение ax 2 + bx + c = 0, где a ≠ 0, есть три условия для D, которые мы должны рассмотреть. Это объясняется в таблице ниже вместе с соответствующим графическим представлением для каждого из этих случаев.
Учитывая квадратное уравнение ax 2 + bx + c = 0, где a ≠ 0, есть три условия для D, которые мы должны рассмотреть. Это объясняется в таблице ниже вместе с соответствующим графическим представлением для каждого из этих случаев.Number of Real Roots
Graph Plot
Two Real Roots
D > 0, D is a perfect square
Two real roots, Aishah Amri — StudySmarter Originals
Один из реальных корней
D = 0
Один из реальных корней, Aishah Amri — StudySmarter Originals
no ROOT0034
Нет действительных корней, Айша Амри — StudySmarter Originals
Решение квадратных уравнений с помощью графика
Для этого метода решения квадратных уравнений мы стремимся изобразить такие выражения в виде графика, составив таблицу значений. Шаги для этого метода объясняются ниже.

Установить y = ax 2 + bx + c;
Найдите точки пересечения y, подставив x = 0 в y;
Найдите ось симметрии и вершину;
Вставьте несколько значений x в y и создайте таблицу значений для этого рассчитанного набора точек;
Определите точки пересечения по оси x. Если решения не могут быть найдены явно, мы можем оценить решения, определив целые числа, между которыми расположены решения;
Постройте график.
На шаге 5 мы воспользуемся принципом расположения для оценки расположения решений данного квадратного уравнения. Ниже приводится объяснение принципа местоположения, за которым следуют три рабочих примера.
Принцип расположения
Предположим, что y = f(x) представляет собой квадратичную функцию, а a и b — два действительных числа, такие что f(a) < 0 и f(b) > 0. Тогда f имеет по крайней мере один действительный нуль. между а и б.
Как работает принцип местоположения?
Точка пересечения графика с осью x пересекает ось x в точке y = 0.
 Это, в свою очередь, меняет знак значений y, которые следуют на графике. По сути, принцип местоположения говорит нам, что мы ищем изменение знака между двумя выходами y при двух входах x.
Это, в свою очередь, меняет знак значений y, которые следуют на графике. По сути, принцип местоположения говорит нам, что мы ищем изменение знака между двумя выходами y при двух входах x.Принцип местоположения, алгебра 2 — Glencoe McGraw-Hill (2008)
Рассмотрим функцию f(x) = 2x 2 – 4x – 3.
- Решите, имеет ли функция максимальное или минимальное значение.
- Оценка максимального или минимального значения функции.
- Укажите домен и диапазон функции.
Решение
Здесь a = 2, b = –4 и c = –3.
1. Так как a > 0, то график раскрывается и функция имеет минимальное значение.
2. Минимальным значением функции является координата y вершины.
Координата x вершины .
Чтобы найти координату y вершины, вычислим функцию при x = 1.
Следовательно, минимальное значение функции равно –5.
3. Домен представляет собой множество всех действительных чисел.
 Диапазон представляет собой набор всех действительных чисел, больших или равных минимальному значению, f(x) ≥ –5. В системе обозначений [–5, +∞ [.
Диапазон представляет собой набор всех действительных чисел, больших или равных минимальному значению, f(x) ≥ –5. В системе обозначений [–5, +∞ [.График показан ниже.
Пример 1, Айша Амри — StudySmarter Originals
Рассмотрим функцию f(x) = x 2 – 6x + 3.
- Определите точку пересечения у, уравнение оси симметрии и x-координата вершины.
- Создайте таблицу значений, включающую вершину.
- Постройте график функции на основе результатов вопросов 1 и 2.
Решение
Здесь a = 1, b = –6 и c = 3.
1. Чтобы найти точку пересечения по оси y, мы оценим f при x = 0. При этом мы получим f(0) = c = 3. Таким образом, точка пересечения по оси y равна (0, 3). Уравнение оси симметрии находится по формуле
Следовательно, уравнение оси симметрии x = 3. Отсюда следует, что x-координата вершины равна 3.
2. Будем Теперь сделайте нашу таблицу значений.
 Для этого выберите значения x меньше 3 и больше 3. Это гарантирует, что точки по обе стороны от оси симметрии будут нанесены на график.
Для этого выберите значения x меньше 3 и больше 3. Это гарантирует, что точки по обе стороны от оси симметрии будут нанесены на график.x
1
2
3
4
5
6
f(x)
3
–2
–5
–6
–5
–2
3
Давайте применим принцип местоположения к этому примеру. Глядя на приведенную выше таблицу, между x = 0 и x = 1 происходит смена знака. Это указывает на то, что между этими двумя значениями x есть один действительный нуль. Точно так же мы наблюдаем изменение знака между x = 5 и x = 6, что снова говорит нам о том, что между этой парой значений x должен существовать один реальный нуль.
3. График показан ниже.

Пример 2, Айша Амри — StudySmarter Originals
Решите квадратное уравнение x 2 + 5x – 2 = 0 по графику. Если точные решения не найдены, укажите последовательные целые числа, между которыми расположены решения.
Решение
Пусть f(x) = x 2 + 5x – 2.
Теперь мы должны составить таблицу значений для домена x. Нам нужно угадать диапазон значений x, к которым мы хотим применить принцип местоположения. Мы выберем целые значения между x = –6 и x = 2.
В соответствии с принципом местоположения обратите внимание, что точки пересечения x на графике предполагают, что одно решение находится в диапазоне от –6 до –5, а другое – в диапазоне от 0 до 1.
–5
–4
–3
–2
–1
1
2
f(x)
4
–2
–6
–8
–8
–6
–2
4
12
Решение квадратных уравнений методом факторизации
Форма пересечения квадратного уравнения
корни заданного квадратного уравнения.
 Другими словами, p и q являются точками пересечения x графика, соответствующего функции.
Другими словами, p и q являются точками пересечения x графика, соответствующего функции.ВАЖНОЕ ПРИМЕЧАНИЕ
Общая форма формы точки пересечения: y = a(bx + c)(dx + e), где bx + c = 0 и dx + e = 0.
Чтобы выразить точку пересечения форму квадратного уравнения в стандартную форму квадратного уравнения, мы можем использовать метод FOIL.
Метод FOIL
Метод FOIL использует свойство распределения для умножения двучленов. По сути, мы расширяем заданную форму пересечения, чтобы получить типичное выражение для квадратного уравнения. Метод FOIL утверждает, что произведение двух биномов равно сумме произведений F первые члены, O внешние члены, I внутренние члены и L последние члены.
Бином представляет собой выражение, состоящее из двух членов.
Представьте квадратное уравнение с корнями и 4. Запишите уравнение в стандартной форме.
Решение
Форма пересечения квадратного уравнения задается формулой (x – p)(x – q) = 0, где p и q представляют собой корни выражения.
 Так как нет информации о коэффициенте х 2 в этом вопросе означает, что a = 1. Здесь нам дано
Так как нет информации о коэффициенте х 2 в этом вопросе означает, что a = 1. Здесь нам дано. Подставляя это в приведенную выше форму, мы получаем
Теперь мы хотим записать это уравнение в стандартной форме квадратного уравнения . Для этого мы должны расширить правую часть выражения, используя метод FOIL.
Умножив все уравнение на 3, мы окончательно получим
Методы факторизации для квадратных уравнений
Мы можем факторизовать квадратные уравнения, определяя определенные закономерности в заданном выражении. Факторинг — это метод, при котором мы упрощаем стандартную форму квадратного уравнения до формы пересечения. Это позволит нам найти корни выражения и построить точки пересечения по оси x для соответствующего графика. Есть четыре способа, которыми мы можем факторизовать квадратные уравнения. Это описано в таблице ниже.
Метод факторинга
General Case
Greatest Common Factor (GCF)
Difference of Two Squares
Perfect Square Trinomials
Общие трехчлены
Полезно отметить, что метод FOIL также можно использовать для разложения квадратного уравнения на произведение двух двучленов.
 Обратите внимание, что произведение коэффициента x 2 и постоянный член abcd. Точно так же умножение двух членов на коэффициент x также дает abcd. После того, как мы факторизовали данное квадратное уравнение, мы можем решить его, используя свойство нулевого продукта.
Обратите внимание, что произведение коэффициента x 2 и постоянный член abcd. Точно так же умножение двух членов на коэффициент x также дает abcd. После того, как мы факторизовали данное квадратное уравнение, мы можем решить его, используя свойство нулевого продукта.Свойство нулевого произведения
Для любых действительных чисел a и b, если ab = 0, то либо a = 0, b = 0, либо оба a и b равны нулю.
С точки зрения формы отрезка y = a(x – p)(x – q), установка y = 0 дает x – p = 0 и x – q = 0. Решая это, мы получаем x = p, x = кв. Та же концепция применима и к обобщенной форме, где y = a(bx + c)(dx + e). Здесь установка y = 0 дает bx + c = 0 и dx + e = 0. Следовательно, .
Вот несколько рабочих примеров, демонстрирующих эту концепцию.
Фактор квадратного уравнения 3x 2 = 9x и построение графика соответствующей функции.
Решение
Начнем с преобразования уравнения в стандартную форму квадратного уравнения эта функция
Поскольку коэффициент при x 2 равен a = 3 > 0, парабола открывается вверх.
 График показан ниже.
График показан ниже.Пример 3, Айша Амри — StudySmarter Originals
Фактор квадратного уравнения 6x 2 = 1 – x и построение графика соответствующей функции.
Решение
Начнем с преобразования уравнения в стандартную форму квадратного уравнения
Это общий трехчлен, который мы можем разложить на множители (ax + b)(cx + d). Обратите внимание, что коэффициент 6 можно разложить как , а константу -1 можно разложить как .
Помните, что вы должны протестировать все возможные пары и позиции для этих двух товаров. Методом проб и ошибок мы можем разложить это на множители как
. По свойству нулевого произведения корни этой функции равны
. Поскольку коэффициент при x 2 равен a = 6 > 0, парабола открывается вверх. График показан ниже.
Пример 4, Айша Амри — StudySmarter Originals
Фактор квадратного уравнения x 2 – 25 = 0 и построить график соответствующей функции.

Решение
Обратите внимание, что .
Таким образом, уравнение принимает вид разности двух квадратов. Следовательно, мы можем разложить это на множители как
. По свойству нулевого произведения корни этой функции равны
. Поскольку коэффициент при x 2 равен a = 1 > 0, парабола открывается вверх. График показан ниже.
Пример 5, Айша Амри — StudySmarter Originals
Свойство квадратного корня
Мы также можем решать квадратные уравнения, используя свойство квадратного корня. Этот метод можно использовать только для решения квадратных уравнений, где квадратное выражение представляет собой полный квадрат.
идеальный квадрат — это целое число, являющееся квадратом целого числа. В частности, это произведение некоторого целого числа на самого себя.
Мнимое число i получается как i 2 = –1. Таким образом, квадратный корень из –1 равен i.

Свойство квадратного корня
Для любого действительного числа n, если x 2 = n, то
Давайте посмотрим на некоторые рабочие примеры.
Решите квадратное уравнение x 2 – 12x + 36 = 25, используя свойство квадратного корня.
Решение
Обратите внимание, что левая часть этого выражения принимает форму совершенного квадратного трехчлена. Факторизуя это, мы получаем
Теперь, используя свойство квадратного корня, мы получаем
Таким образом, два корня равны x = 1 и x = 11. График показан ниже.
Пример 6 (1), Айша Амри — StudySmarter Originals
Увеличив масштаб этого графика, мы видим, что корни действительно x = 1 и x = 11.
Пример 6 (2), Айша Амри — StudySmarter Originals
Решите квадратное уравнение x 2 + 8x + 16 = 20, используя свойство квадратного корня.
Решение
Обратите внимание, что левая часть этого выражения принимает форму совершенного квадратного трехчлена.
 Факторизуя это, мы получаем
Факторизуя это, мы получаемТеперь, используя свойство квадратного корня, мы получаем
Таким образом, два корня равны
. Набросок этого графика показан ниже.
Пример 7 (1), Айша Амри — StudySmarter Originals
Увеличив масштаб этого графика, мы видим, что корни приблизительно равны x ≈ -8,47 и x ≈ 0,47.
Пример 7 (2), Айша Амри — StudySmarter Originals
Завершение квадрата
В большинстве случаев квадратные уравнения не являются идеальными квадратами. Однако мы можем манипулировать выражением, чтобы оно приняло форму идеального квадрата, используя метод завершения квадрата. Шаги для этой техники описаны ниже.
1. Задайте квадратное уравнение как ax 2 + bx + c = 0;
2. Разделите уравнение на
;
3. Привести константу к правой части выражения как
;
4. Половину коэффициента x и квадрат результата.
 Добавьте это значение к каждой стороне уравнения как
Добавьте это значение к каждой стороне уравнения как;
5. Заполните квадрат в левой части и вычислите константу в правой части как
;
6. Теперь мы можем использовать свойство квадратного корня для решения этого квадратного уравнения как
;
7. Таким образом, решениями данного квадратного уравнения являются
.
Решите квадратное уравнение x 2 – 10x + 24 = 0, заполнив квадрат.
Решение
Вычтите 24 из обеих частей уравнения как
Перепишем левую часть в виде полного квадрата, разложив на множители
Теперь мы можем использовать свойство квадратного корня
Таким образом, два решения равны x = 4 и x = 6. График показан ниже.
Пример 8, Айша Амри — StudySmarter Originals
Решите квадратное уравнение 3x 2 + 10x – 8 = 0, заполнив квадрат.

Решение
Разделим уравнение на коэффициент 3
Прибавим с обеих сторон
Чтобы завершить квадрат этого выражения, мы должны найти пропущенные значения
Поскольку
мы добавим к каждой стороне, чтобы сбалансировать уравнение
Перепишем левую часть в виде полного квадрата, разложив на множители
9003 4 Теперь мы можем использовать квадратный кореньТаким образом, два решения равны . График показан ниже.
Пример 9 (1), Айша Амри — StudySmarter Originals
Увеличив масштаб этого графика, мы видим, что корни соответствуют действительности.
Пример 9 (2), Айша Амри — StudySmarter Originals
Квадратная формула
Другой способ решения квадратных уравнений — использование квадратной формулы. Это очень полезный инструмент при работе с квадратными уравнениями, которые производят иррациональные корни.
 Однако мы действительно можем использовать эту формулу для решения любой формы квадратного уравнения. Это означает, что мы можем использовать эту формулу и для поиска рациональных решений!
Однако мы действительно можем использовать эту формулу для решения любой формы квадратного уравнения. Это означает, что мы можем использовать эту формулу и для поиска рациональных решений!Квадратичная формула
Корни квадратного уравнения вида ax 2 + bx + c = 0, где a ≠ 0, можно найти по формуле
.
Определите количество и тип корней квадратного уравнения 3x 2 + 5x + 1 = 0 . Определите корни этого выражения с помощью квадратичной формулы.
Решение
Здесь
Начнем с нахождения значения дискриминанта как
Поскольку D > 0, у нас должно быть два действительных корня. Также обратите внимание, что D не является идеальным квадратом, поэтому корни этого квадратного уравнения должны быть иррациональными. Теперь мы будем использовать квадратную формулу для определения этих корней.
Таким образом, два корня равны
График показан ниже.
Пример 10, Айша Амри — StudySmarter Originals
Определите количество и тип корней квадратного уравнения x 2 – 6x + 10 = 0 .
 Определите корни этого выражения с помощью квадратичной формулы.
Определите корни этого выражения с помощью квадратичной формулы.Решение
Здесь
Начнем с нахождения значения дискриминанта как
Поскольку D < 0, мы должны иметь два комплексно-сопряженных корня. Теперь мы будем использовать квадратную формулу для определения этих корней.
Таким образом, два комплексно-сопряженных корня равны
График показан ниже.
Пример 11, Айша Амри — StudySmarter Originals
Анализ графиков квадратных уравнений
В этом разделе мы познакомимся с вершинной формой квадратного уравнения. Здесь мы будем ссылаться на стандартное квадратное уравнение, т. е. y = x 2 и посмотрите, как изменение некоторых коэффициентов может изменить форму этого простого графика. Начнем со следующего определения.
Форма вершины квадратного уравнения описывается выражением y = a(x – h) 2 + k, где (h, k) – вершина параболы, а x = h – ось симметрии .

Преобразование
Вершинная форма — это умный способ выражения квадратных уравнений, чтобы мы могли соответствующим образом преобразовать график на основе стандартного квадратного уравнения. Во-первых, давайте определим, что такое перевод.
Перевод перемещает фигуру без изменения ее формы или размера.
Мы можем применить эту концепцию для построения квадратных уравнений, изменяя коэффициенты или константы в данном выражении. График основной квадратичной функции равен f(x) = x 2 . Это показано ниже.
Стандартный квадратичный граф, Айша Амри — StudySmarter Originals
Вершина здесь — начало координат, (0, 0), а ось симметрии — x = 0. Допустим, нам дано квадратное уравнение в вершинной форме, y = а(х – ч) 2 + к. Есть три способа, которыми мы можем преобразовать этот график. Это показано в таблице ниже.
Vertex Form
Change in Value
Plot of Graph
y = a (x — h) 2 + k
- If a большой, график становится более крутым (красная линия)
- Если a маленький, график становится более плоским (синяя линия)
- If a is negative, the graph becomes inverted (green line)
Varying a, Aishah Amri — StudySmarter Originals
Varying a alters the function in the y-direction , (the coefficient a affects the steepness of the graph)
y = a(x — h ) 2 + k
- If h is negative, the graph shifts h единиц слева от оси x (красная линия)
- Если H положительный, график сдвигает h единиц справа от оси X (синяя линия)
.
 изменяет функцию вдоль оси X на H единицы
изменяет функцию вдоль оси X на H единицыY = A (x — H) 2 + K
Я. график смещается вниз на k единиц по оси Y (красная линия) - IF K положительный, график перемещается вверх по k единиц в оси Y (синяя линия)
В отличие функцию вверх или вниз по оси y на k единиц
Выразите уравнение y = x 2 + 4x + 6 в вершинной форме и постройте график функции.
Решение
Обратите внимание, что y = x 2 + 4x + 6 не является идеальным квадратом. Начнем с заполнения квадрата этого выражения.
Чтобы найти пропущенные значения, мы добавляем и балансируем уравнение, вычитая 4 как находится в (–2, 2).
 Ось симметрии x = –2. Поскольку a = 1, график раскрывается и имеет ту же форму, что и график y = x 2 . Кроме того, график переместился на 2 единицы влево и на 2 единицы вверх.
Ось симметрии x = –2. Поскольку a = 1, график раскрывается и имеет ту же форму, что и график y = x 2 . Кроме того, график переместился на 2 единицы влево и на 2 единицы вверх.График показан ниже.
Пример 12, Айша Амри — StudySmarter Originals
Запишите уравнение y = –2x 2 – 12x + 17 в вершинной форме и постройте график функции.
Решение
Обратите внимание, что y = –2x 2 – 12x + 17 не является правильным квадратом. Начнем с того, что разложим первые два члена правой части как 9.0034
Далее мы завершим квадрат этого выражения.
Чтобы найти пропущенные значения, мы добавляем и уравновешиваем уравнение, вычитая –2(9) как
Теперь записав это в виде полного квадрата, мы получим
Вершина находится в (–3, 35), а ось симметрии x = –3. Поскольку a = –2, график открывается вниз и уже, чем график y = x 2 . Кроме того, график смещается на 1 единицу вправо и на 2 единицы вверх.




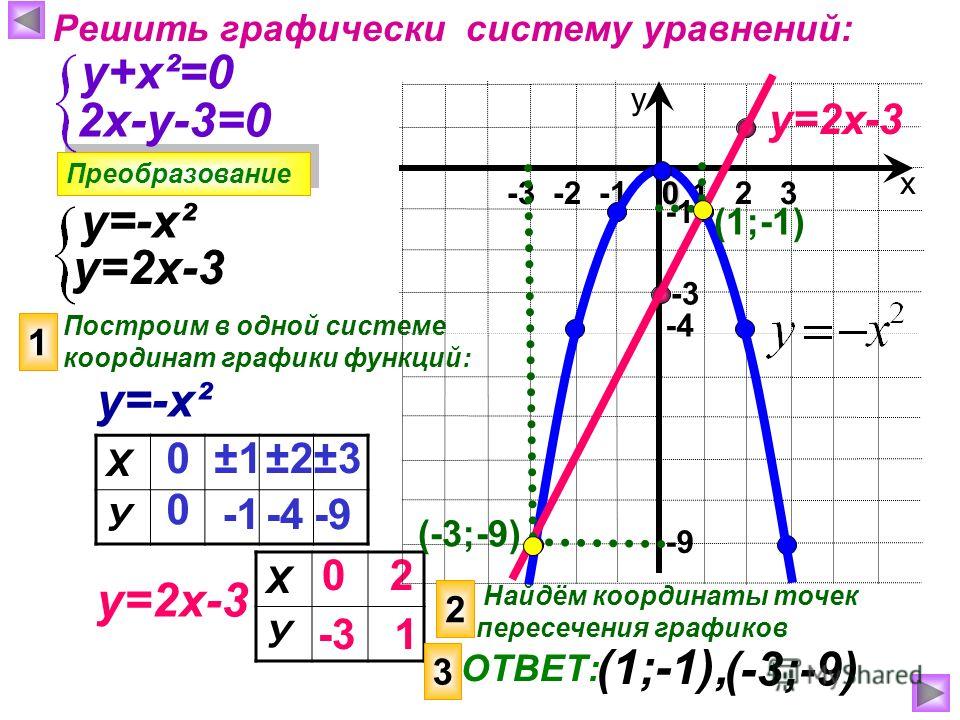 2
2

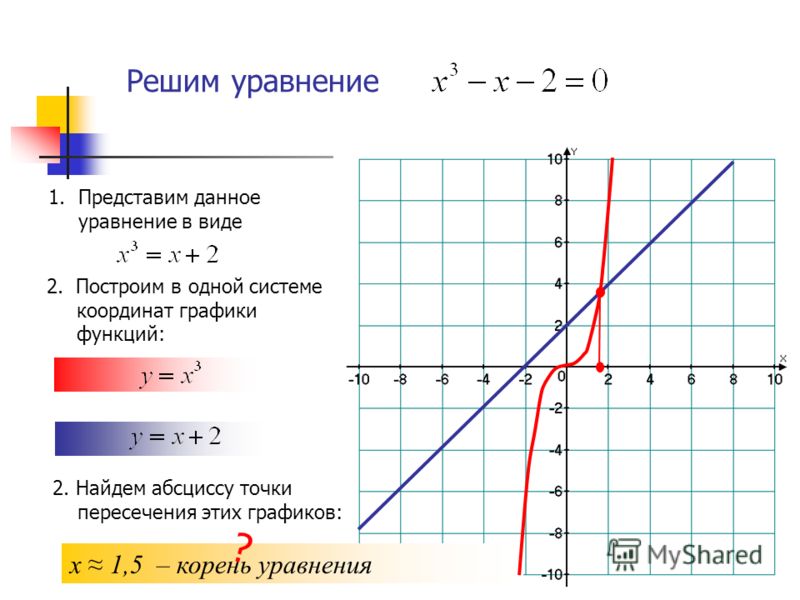 RU
RU

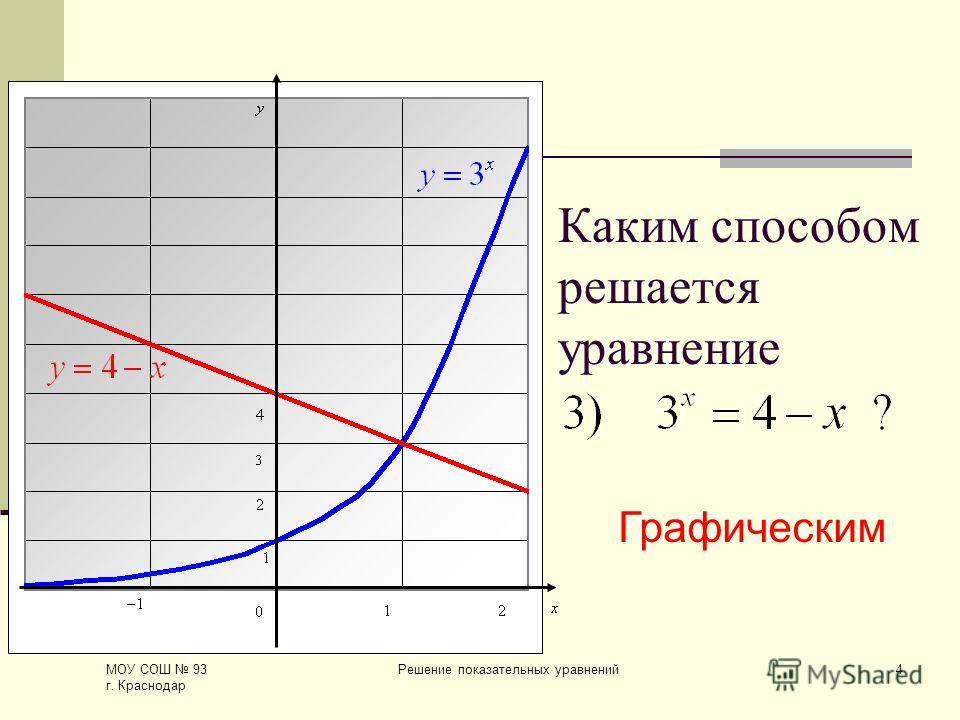
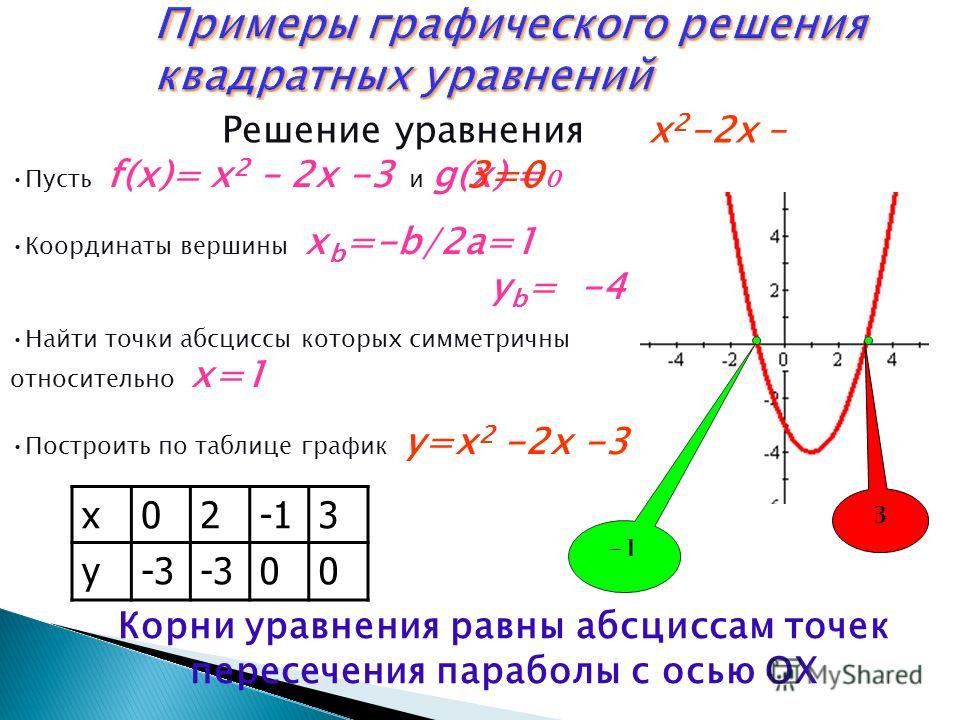
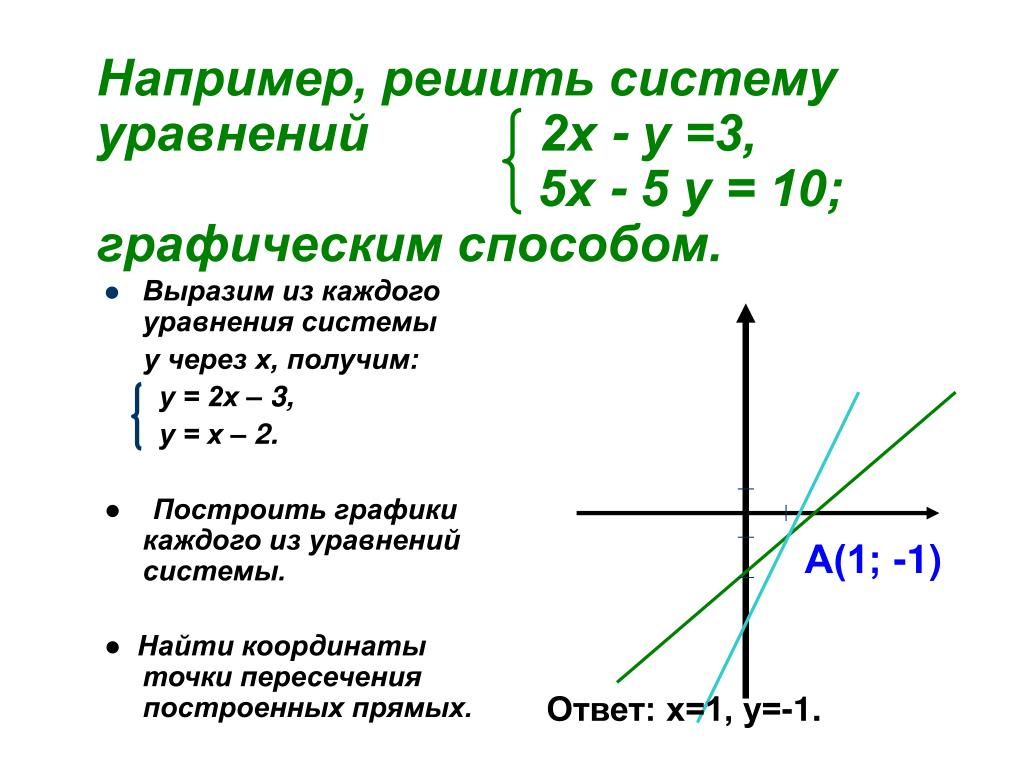

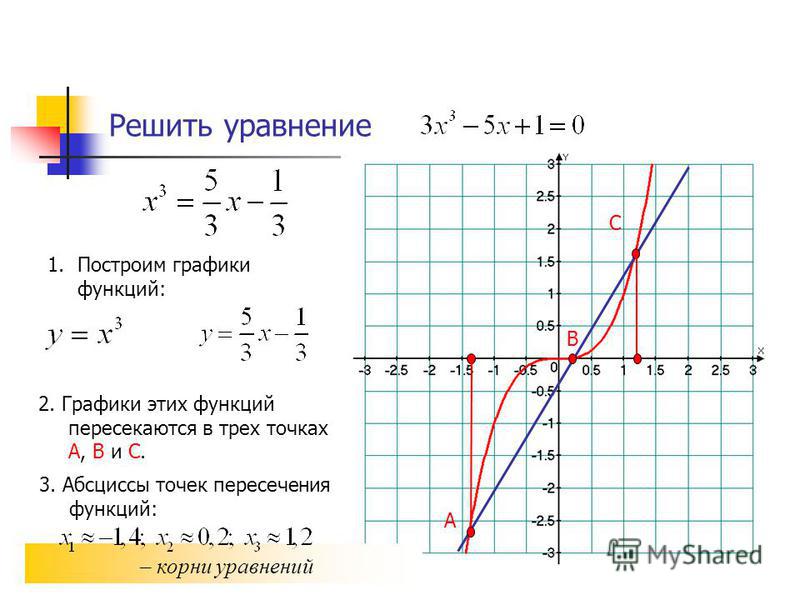 (2)
(2) 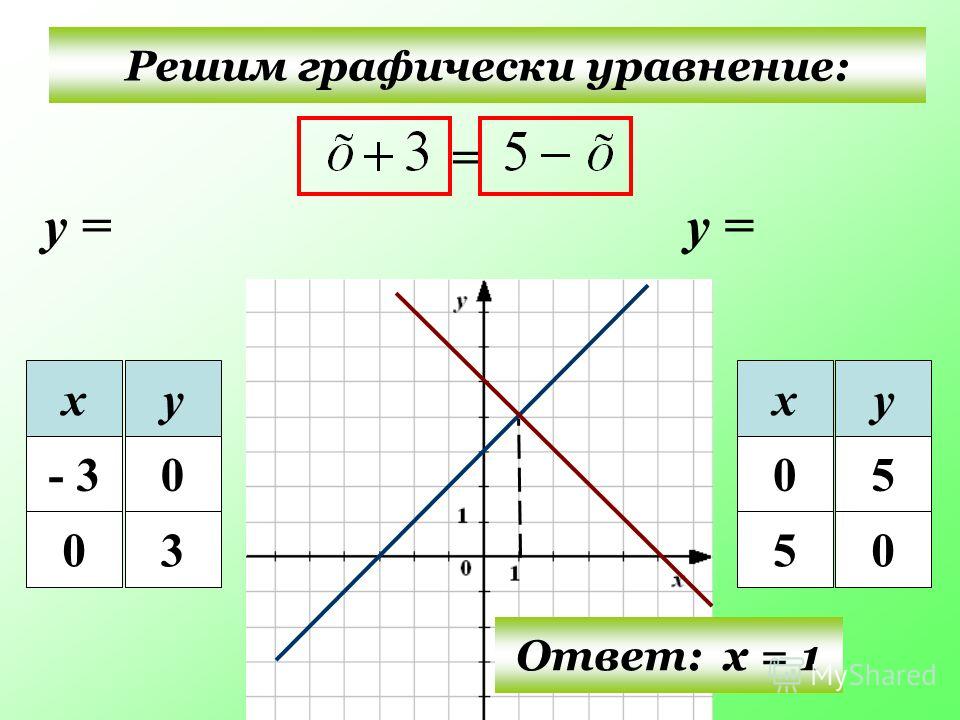 (1)
(1) 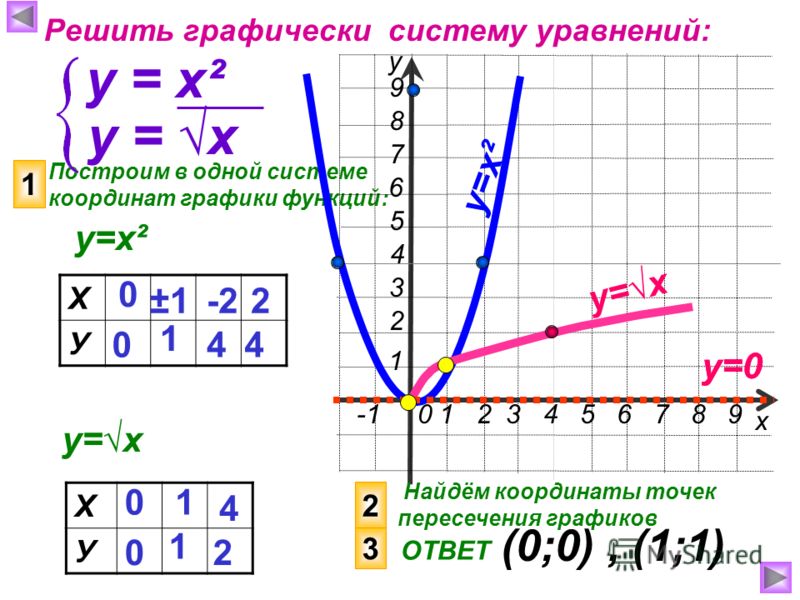
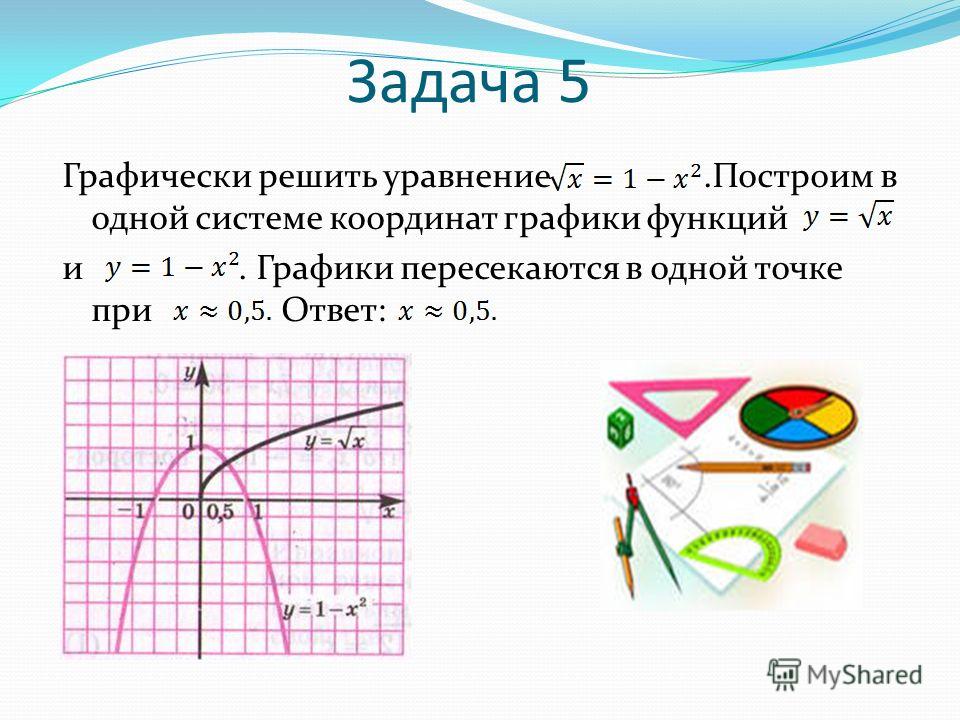 Две прямые AB и Ce пересекаются в точке E (3, 7). Итак, x = 3 и y = 7 — искомое решение пары линейных уравнений.
Две прямые AB и Ce пересекаются в точке E (3, 7). Итак, x = 3 и y = 7 — искомое решение пары линейных уравнений. 
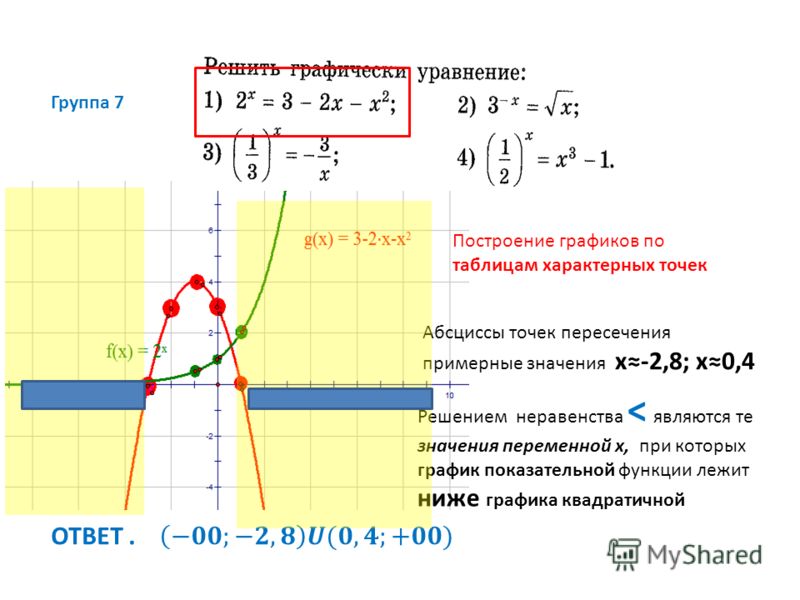 Точно так же нанесите точки C(0, 6), D(2, 3) и соедините их, чтобы сформировать линию CD.
Точно так же нанесите точки C(0, 6), D(2, 3) и соедините их, чтобы сформировать линию CD. 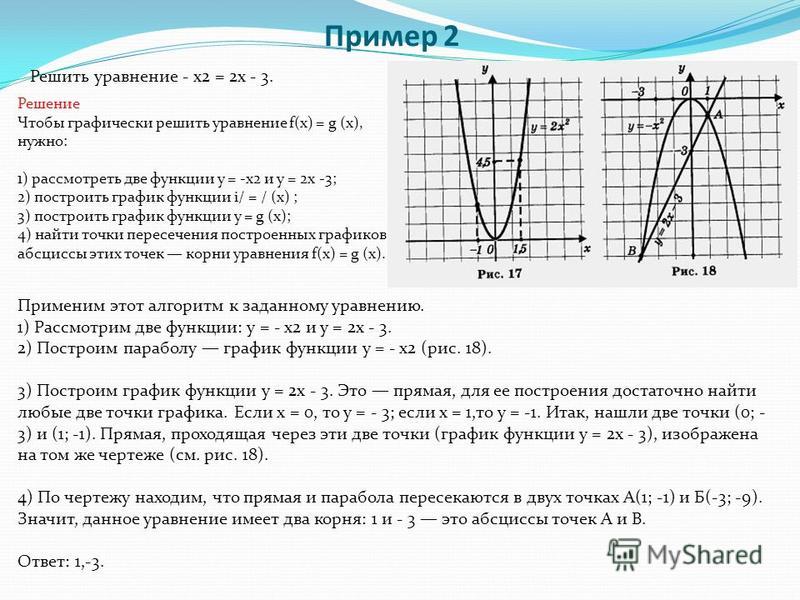 Следовательно, уравнения согласуются с единственным решением.
Следовательно, уравнения согласуются с единственным решением.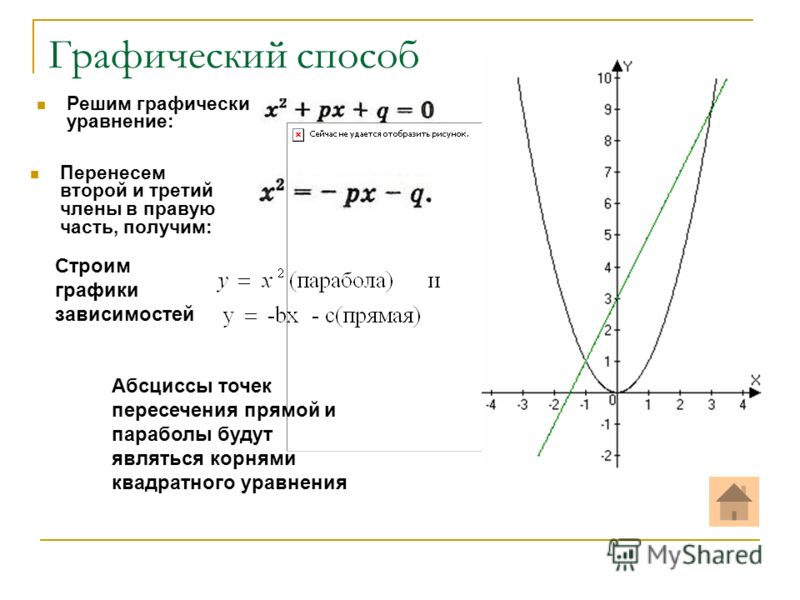 Координаты каждой точки на этой прямой являются решением.
Координаты каждой точки на этой прямой являются решением. 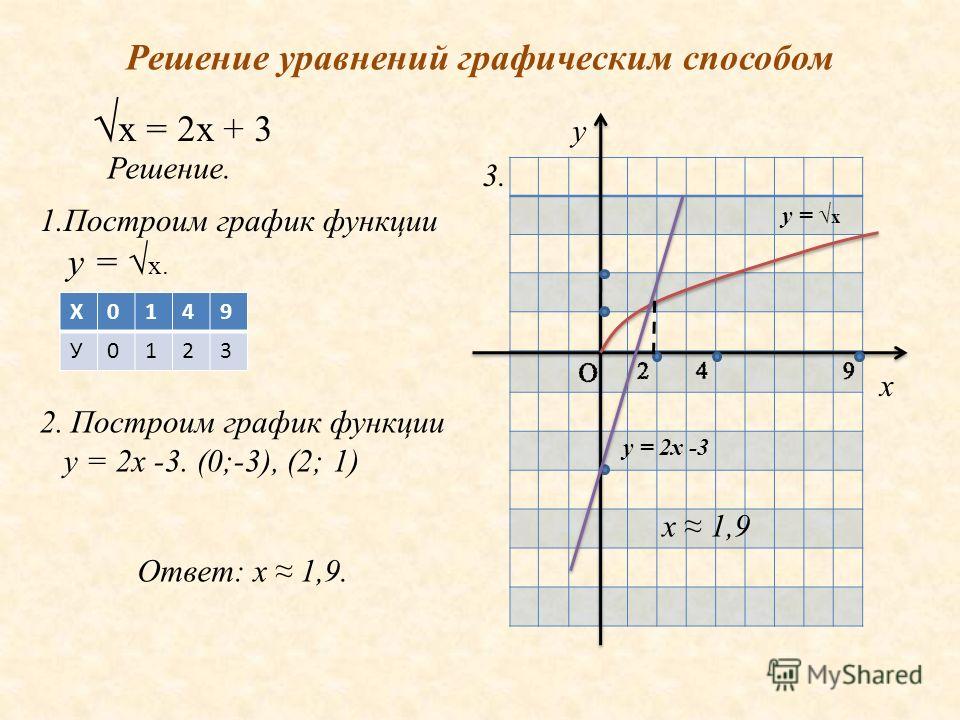
 Затем определите площади области, ограниченной этими линиями и осью Y.
Затем определите площади области, ограниченной этими линиями и осью Y. 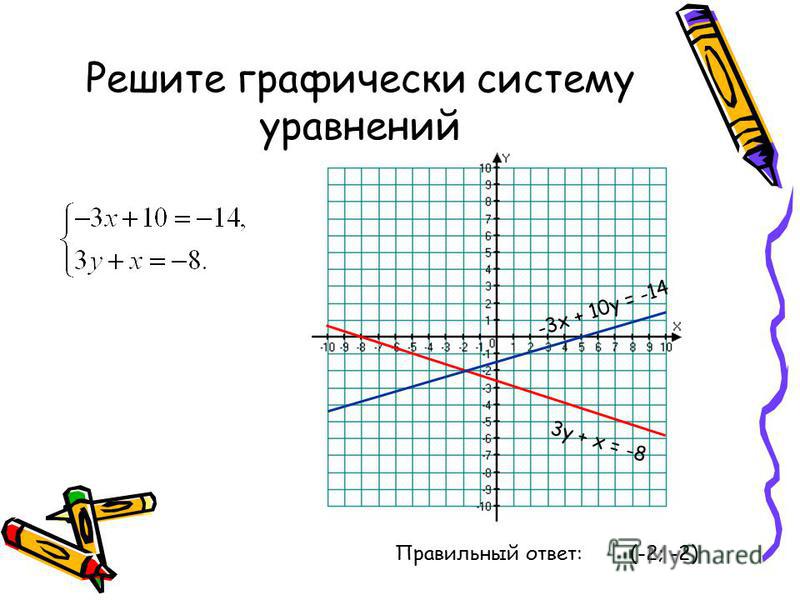

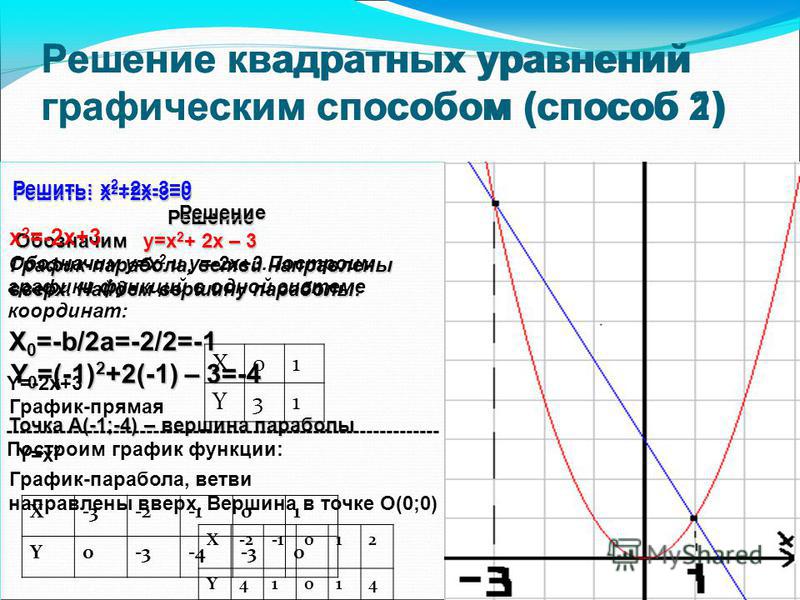
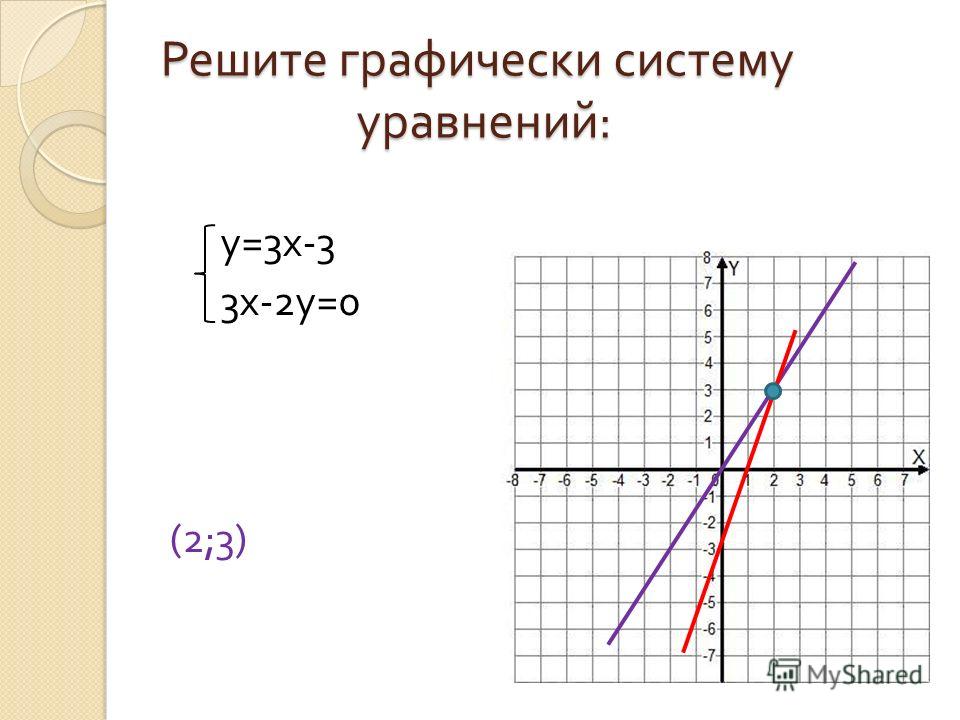

 Прежде чем мы начнем, давайте посмотрим на компоненты параболы.
Прежде чем мы начнем, давайте посмотрим на компоненты параболы. Вершина известна как точка поворота параболы.
Вершина известна как точка поворота параболы.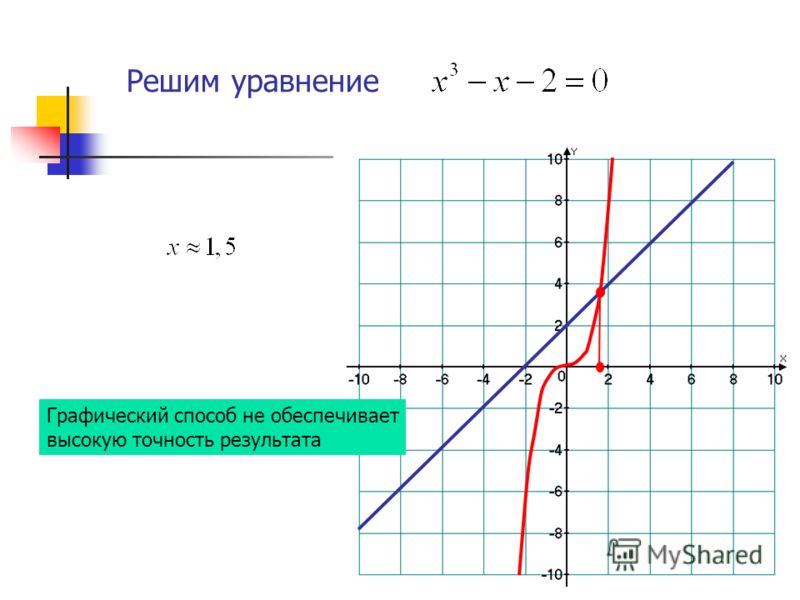 максимальное
максимальное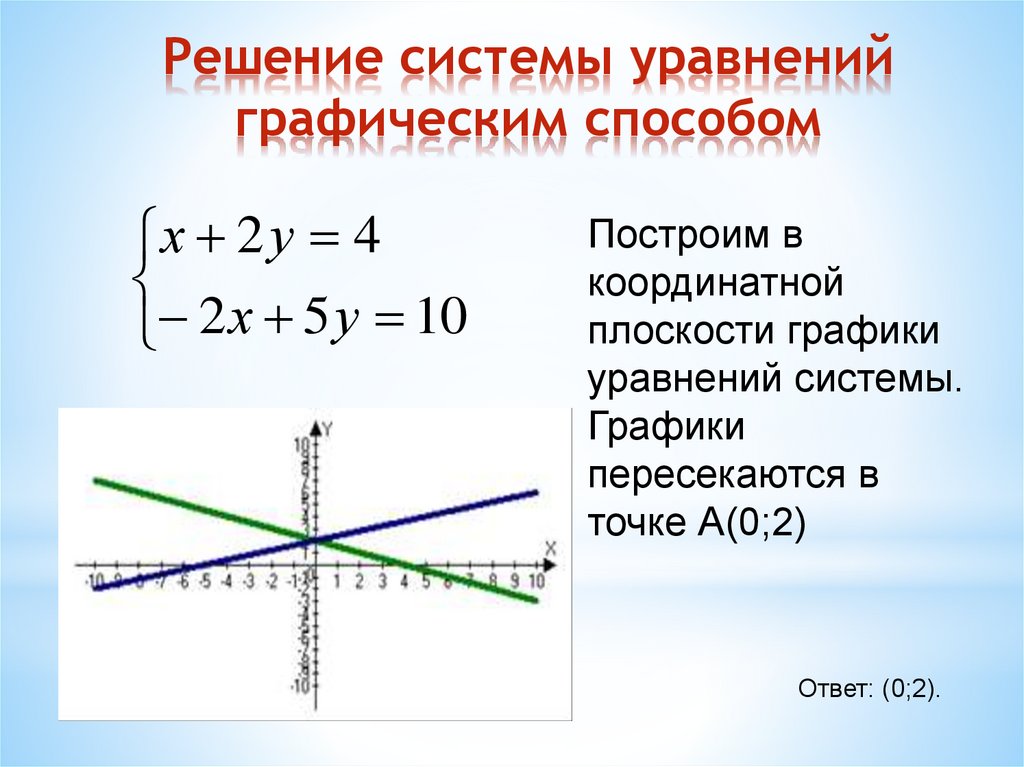 Учитывая квадратное уравнение ax 2 + bx + c = 0, где a ≠ 0, есть три условия для D, которые мы должны рассмотреть. Это объясняется в таблице ниже вместе с соответствующим графическим представлением для каждого из этих случаев.
Учитывая квадратное уравнение ax 2 + bx + c = 0, где a ≠ 0, есть три условия для D, которые мы должны рассмотреть. Это объясняется в таблице ниже вместе с соответствующим графическим представлением для каждого из этих случаев.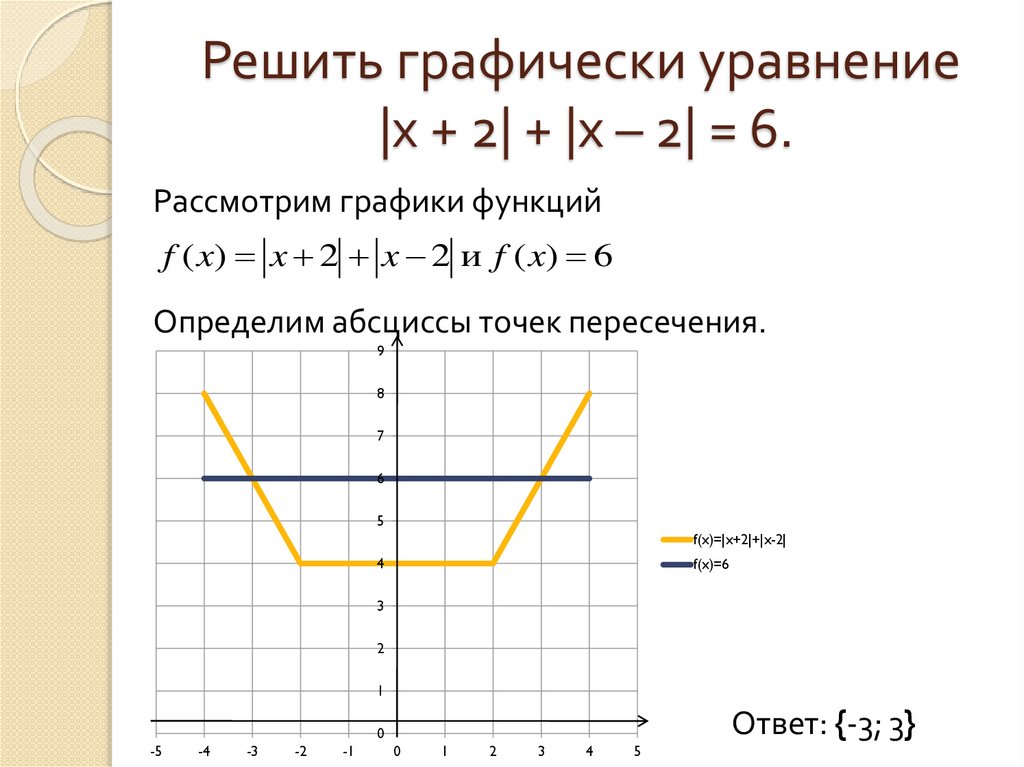
 Это, в свою очередь, меняет знак значений y, которые следуют на графике. По сути, принцип местоположения говорит нам, что мы ищем изменение знака между двумя выходами y при двух входах x.
Это, в свою очередь, меняет знак значений y, которые следуют на графике. По сути, принцип местоположения говорит нам, что мы ищем изменение знака между двумя выходами y при двух входах x. Диапазон представляет собой набор всех действительных чисел, больших или равных минимальному значению, f(x) ≥ –5. В системе обозначений [–5, +∞ [.
Диапазон представляет собой набор всех действительных чисел, больших или равных минимальному значению, f(x) ≥ –5. В системе обозначений [–5, +∞ [. Для этого выберите значения x меньше 3 и больше 3. Это гарантирует, что точки по обе стороны от оси симметрии будут нанесены на график.
Для этого выберите значения x меньше 3 и больше 3. Это гарантирует, что точки по обе стороны от оси симметрии будут нанесены на график.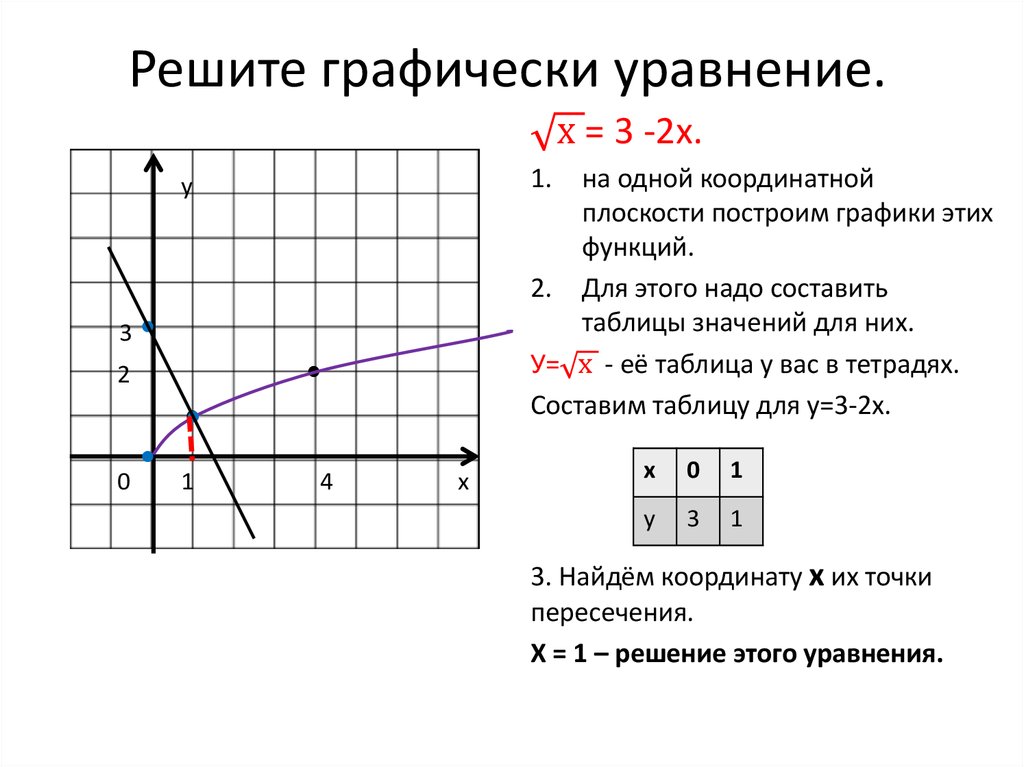
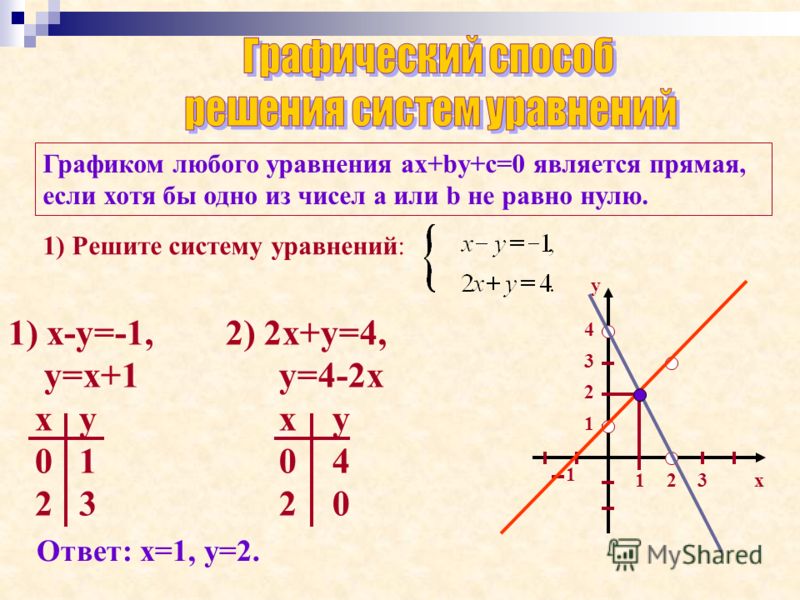 Другими словами, p и q являются точками пересечения x графика, соответствующего функции.
Другими словами, p и q являются точками пересечения x графика, соответствующего функции.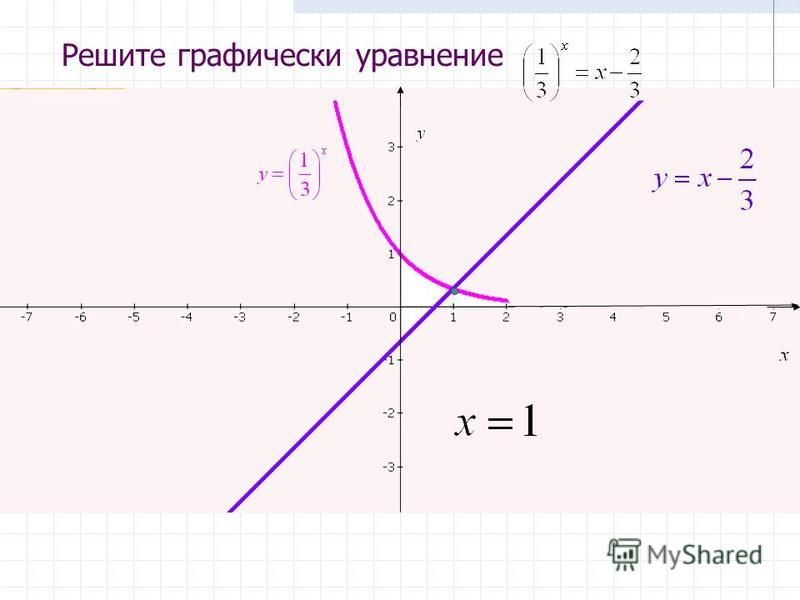 Так как нет информации о коэффициенте х 2 в этом вопросе означает, что a = 1. Здесь нам дано
Так как нет информации о коэффициенте х 2 в этом вопросе означает, что a = 1. Здесь нам дано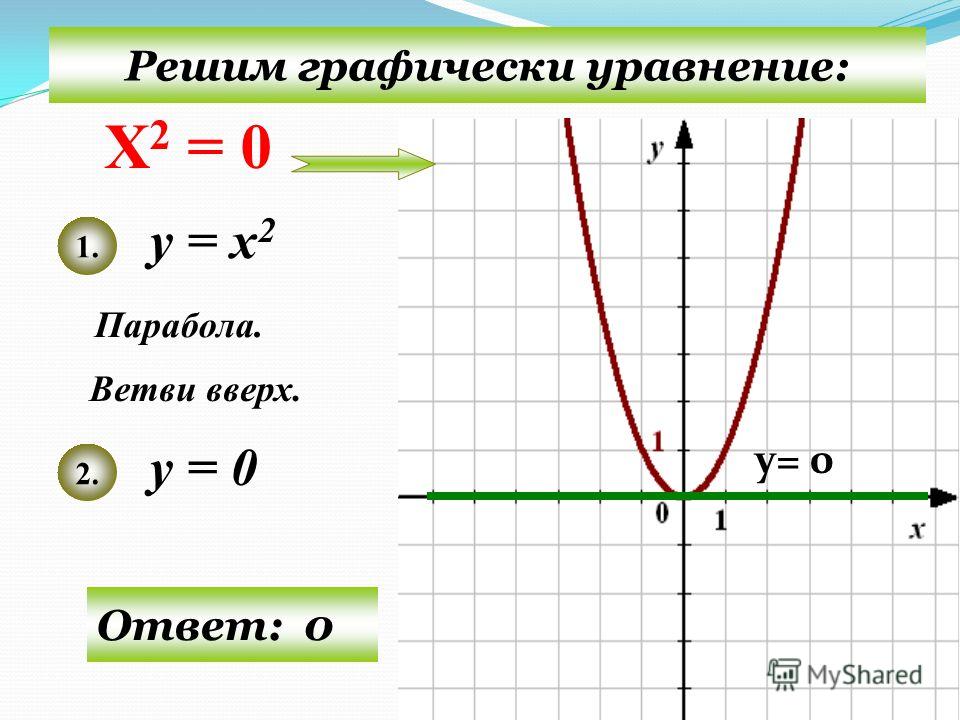 Обратите внимание, что произведение коэффициента x 2 и постоянный член abcd. Точно так же умножение двух членов на коэффициент x также дает abcd. После того, как мы факторизовали данное квадратное уравнение, мы можем решить его, используя свойство нулевого продукта.
Обратите внимание, что произведение коэффициента x 2 и постоянный член abcd. Точно так же умножение двух членов на коэффициент x также дает abcd. После того, как мы факторизовали данное квадратное уравнение, мы можем решить его, используя свойство нулевого продукта.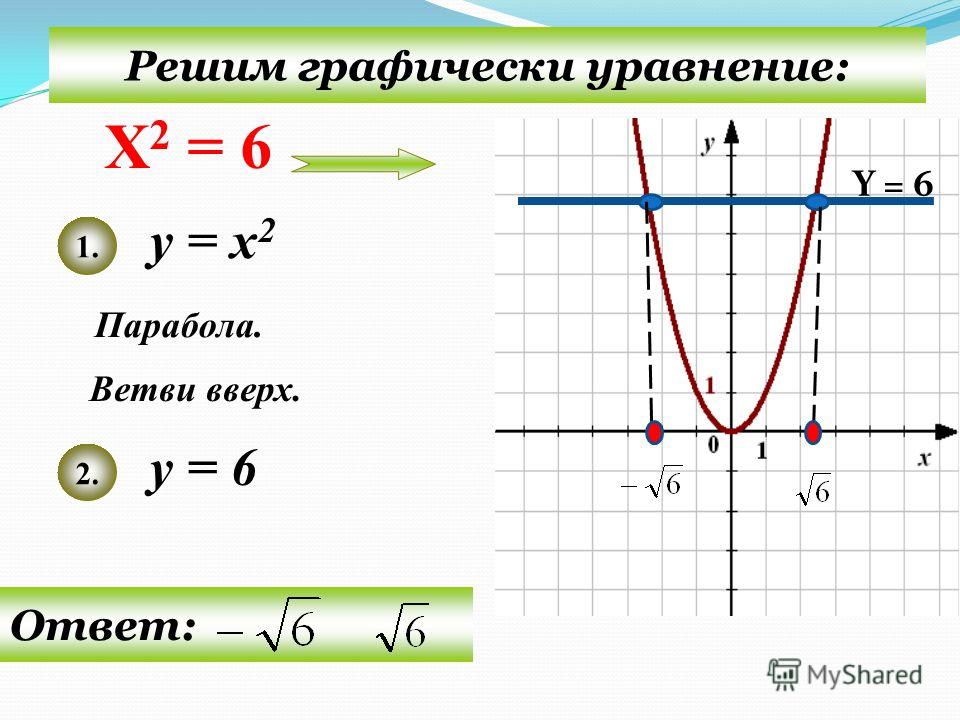 График показан ниже.
График показан ниже.
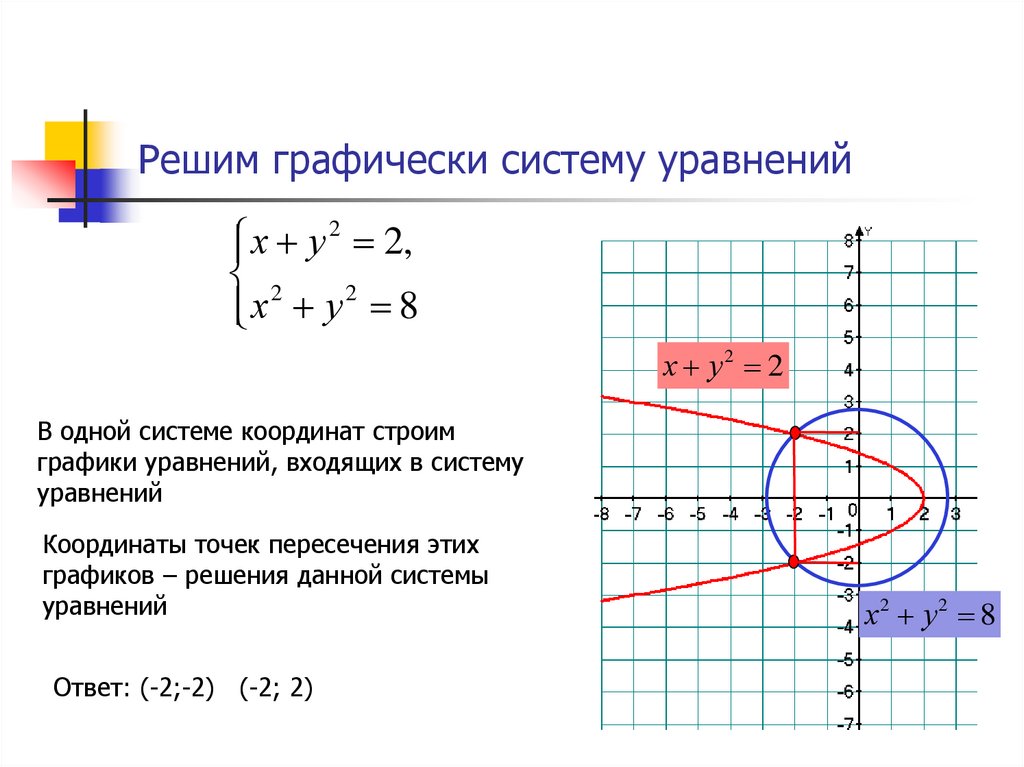
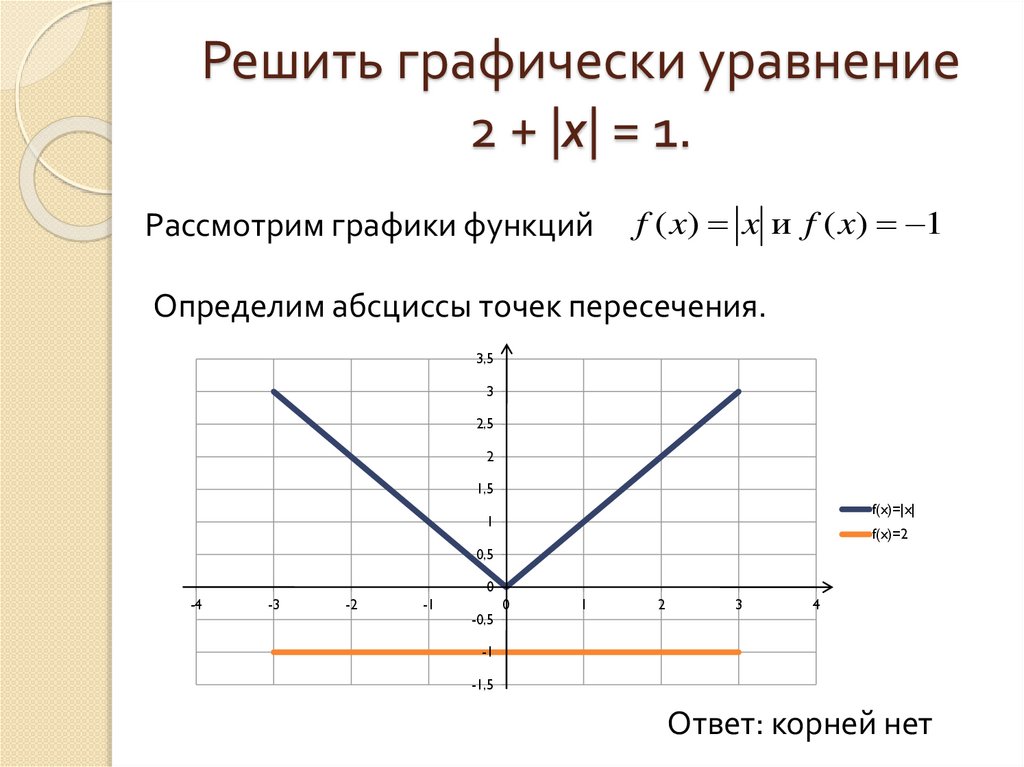 Факторизуя это, мы получаем
Факторизуя это, мы получаем Добавьте это значение к каждой стороне уравнения как
Добавьте это значение к каждой стороне уравнения как
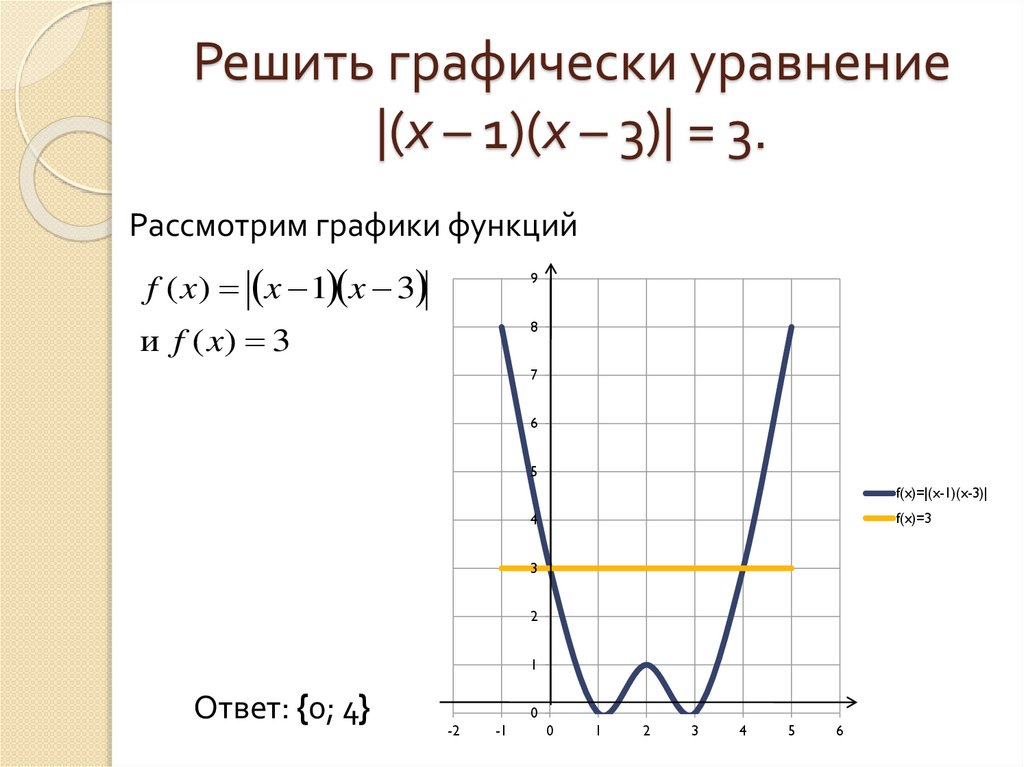 Однако мы действительно можем использовать эту формулу для решения любой формы квадратного уравнения. Это означает, что мы можем использовать эту формулу и для поиска рациональных решений!
Однако мы действительно можем использовать эту формулу для решения любой формы квадратного уравнения. Это означает, что мы можем использовать эту формулу и для поиска рациональных решений! Определите корни этого выражения с помощью квадратичной формулы.
Определите корни этого выражения с помощью квадратичной формулы.
 изменяет функцию вдоль оси X на H единицы
изменяет функцию вдоль оси X на H единицы Ось симметрии x = –2. Поскольку a = 1, график раскрывается и имеет ту же форму, что и график y = x 2 . Кроме того, график переместился на 2 единицы влево и на 2 единицы вверх.
Ось симметрии x = –2. Поскольку a = 1, график раскрывается и имеет ту же форму, что и график y = x 2 . Кроме того, график переместился на 2 единицы влево и на 2 единицы вверх.