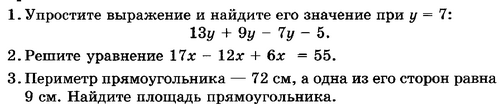Что значит упростить выражение 7 класс: Упрощение выражений

Упрощение выражений

Одно из самых распространенных заданий в алгебре звучит так: «Упростите выражение». Сделать это можно используя один из ниже перечисленных приемов, но чаще всего тебе потребуется их комбинация.

Приведение подобных слагаемых.

Это самый простой из приемов. Подобными называются те слагаемые, у которых одинаковая буквенная часть. Например, подобными будут выражения 5а и -6а; -3ху и 3ух; 2 и 10. Так вот. Складывать можно только подобные слагаемые; если буквенная часть у слагаемых различна, то такие слагаемые складывать уже нельзя. Согласись, если в жизни мы будем складывать яблоки с гвоздями, то у нас какая-то дичь получится) В математике точно так же.

Для примера упростим такое выражение:

Подобные слагаемые я выделю разными цветами и посчитаю. Кстати, знак перед слагаемым относится к этому слагаемому.

Как видишь, больше одинаковых буквенных частей нет. Выражение упрощено.

Умножение одночленов и многочленов.

Не буду спорить — числа ты умножать умеешь. А если к ним добавятся буквы, степени, скобки?

Одночлен — это выражение, состоящее из произведения чисел, букв, степеней, причем необязательно должно быть всё сразу. Удивительно, но просто число 5 тоже является одночленом, так же как и одинокая переменная х.

При умножении одночленов используют правила умножения степеней.

Перемножим три одночлена:

Разными цветами выделю то, что буду последовательно перемножать.

Многочлен — это сумма одночленов.

Чтобы умножить одночлен на многочлен выражение за скобками умножить на каждое слагаемое в скобках. Подробности в следующем примере.

Осталось вспомнить умножение многочлена на многочлен. При таком вот умножении надо каждое слагаемое в первых скобках умножить на каждое слагаемое во вторых скобках, результаты сложить или вычесть в зависимости от знаков слагаемых.

Вынесение общего множителя за скобки.

Разбираться будем на примере.

Дано такое выражение:

Что общего у этих двух слагаемых? Правильно, в них обоих присутствует множитель x. Он и будет являться общим множителем, который надо вынести за скобку.

Возьмем другой пример.

Оба числа в слагаемых делятся на 2, значит число 2 — общий множитель. Но еще в этих одночленах есть одинаковая буква а — одна в первой степени, другая — во второй. Берем ее в меньшей степени, т.е. в первой, — это и будет второй общий множитель. В общем, получится вот такая запись:

Ну и давайте третий пример, только уже без комментариев.

Проверить правильность вынесения общего множителя за скобки можно путем раскрытия скобок (умножением).

Разложение многочлена на множители способом группировки.

Если надо разложить многочлен на множители, то способ группировки тебе пригодится.

Сгруппировать выражения можно лишь путем вынесения общих множителей за скобку. Но сделать это нужно так, чтобы скобки в итоге получились одинаковые. Зачем? Да затем, чтобы потом эти скобки вынести за другие скобки. 

На примере будет яснее)

Беру пример самый простой, чисто для понимания того, что надо делать.

В первых двух слагаемых общим множителем является переменная а: выносим ее за скобку. Во вторых двух слагаемых общим множителем является число 6. Его тоже выносим за скобки.

Видишь получились две одинаковые скобки? Теперь они являются общим множителем. Выносим их за скобку и получаем милое произведение двух скобок:

Разложение квадратного трехчлена на множители.

Пусть дан квадратный трехчлен:

Чтобы разложить его на множители надо решить квадратное уравнение

Далее корни уравнения х₁ и х₂ подставить в следующую формулу:

Пробуем.

Возьмем вот такой трехчлен:

Найдем корни квадратного уравнения.

Подставим их в формулу для разложения квадратного трехчлена на множители:

Что-то слишком много минусов во второй скобке. Чуть-чуть преобразуем ее:

Теперь замечательно)

 

Еще могут тебе пригодится:

— умения работать с обыкновенными дробями;

— умение сокращать дроби;

— знание формул сокращенного умножения.

 

А вот такие задания могут тебе встретится на экзамене.

1) Упростить:

Решение тут.

2) Найти значение выражения при заданных значениях переменных:

Решение тут.

3) Найти значение выражения при заданных значениях переменных:

Решение тут.

Подобных заданий много — их все не уместишь)

 

Остались вопросы? Напиши мне!

Твой персональный преподаватель.

правила и способы упрощения, пояснение на примерах

Что значит упростить алгебраическое выражение

Определение 1

Алгебраическое выражение — одна или несколько алгебраических величин (чисел и переменных), которые объединены с помощью знаков арифметических действий в виде сложения, вычитания, умножения, деления, извлечения корня, возведения в степень (при целых значениях показателей корня и степени), знаков последовательности, определяющих порядок применения данных операций (скобки разного вида).

Обязательным условием для алгебраического выражения является конечное число величин, которые его составляют. Данный принцип пригодиться математикам для решения задач в средних классах школы.

Определение 2

Упростить выражение — это значит уменьшить число арифметических действий, необходимых для вычисления значения данного выражения с учетом определенных значений переменных.

СЛОЖНА-А-А 🙀 Ты же знаешь, что если не разобраться в теме сейчас, то потом придется исправлять оценки. Беги на бесплатное онлайн-занятие с репетитором (подробности тут + 🎁).

Правила упрощения алгебраических выражений

Существуют основные методы в алгебре для того, чтобы упростить алгебраическое выражение:

• приведение подобных;
• разложение на множители;
• сокращение дроби;
• сложение и вычитание дробей;
• умножение и деление дробей.

В процессе приведения выражения в более простую форму следует использовать полезные советы:

1. При наличии подобных их рекомендуется привести, при этом не имеет значения то, в какой момент они образовались.
2. При появлении первой возможности для сокращения дробей, рекомендуется ей сразу воспользоваться. Исключением являются дроби с одинаковыми знаменателями, которые требуется вычитать или суммировать. Такие дроби можно сократить после выполнения необходимых действий.

Приведение подобных

Правило 1

Приведение подобных слагаемых в теории заключается в сложении их коэффициентов и приписывании буквенной части.

Пример 1

2a+3c+4a+5c=6a+8c

Определение 3

Подобными являются слагаемые (одночлены), которые обладают буквенной частью.

Пример 2

В выражении 2ab+3ab+b одночлены 2ab и 3ab являются подобными слагаемыми.

Определение 4

Привести подобные — значит, выполнить сложение нескольких подобных слагаемых для получения в результате одного слагаемого.

К примеру, приведем слагаемые:

Заметим, что числа в таких слагаемых умножают на буквы. Данные числа носят названия коэффициентов.

Пример 3

Рассмотрим выражение с квадратной степенью:

Здесь число 3 является коэффициентом.

Разложение на множители

 Правило 2

Разложить выражение на множители можно, если вынести общий множитель за скобки, применить формулы сокращенного умножения и другие.

Пример 4

В распространенных случаях разложение на множители следует за приведением подобных при упрощении выражений. В итоге получаются произведения. Чтобы это понять, отдельно нужно упомянуть правила действия с дробями, а именно, при сокращении дроби числитель и знаменатель требуется записать, как произведения.

Сокращение дроби

Правило 3

В процессе сокращения дроби допустимо выполнять умножение или деление числителя и знаменателя дроби на одинаковое число, отличное от нуля, в результате чего величина дроби остается прежней.

Объяснение алгоритм действий при сокращении дробей:

• разложение на множители числителя и знаменателя;
• при наличии в числителе и знаменателе общих множителей их допустимо исключить из выражения.

Пример 5

Важно заметить, что сокращению подлежат исключительно множители.

Озвученное правило является следствием ключевого свойства дроби. Оно состоит в допустимости умножения или деления числителя и знаменателя дроби на одно и то же число, которое не равно нулю. В результате значение дроби останется без изменений.

Существует простой способ, руководствуясь которым можно определить, разложено ли выражение на множители. Арифметическое действие, выполняемое в последнюю очередь при вычислении значения выражения, считается «главным».

Данное правило состоит в том, что, когда при подстановке каких-либо чисел на замену буквам и вычислении значения выражения последнее действие представляет собой умножение, можно заключить, что перед нами произведение, то есть выражение разложено на множители. В том случае, когда на последнем шаге в процессе расчетов выполняется сложение или вычитание, разложение выражения на множители не выполнено, то есть сокращение не допускается.

Сложение и вычитание дробей

Правило 4

При сложении и вычитании обыкновенных дробей требуется найти общий знаменатель, умножить каждую из дробей на недостающий множитель и сложить или вычесть числители:

Пример 6

Разберем правило на конкретных примерах. Вычислим:

Заметим, что знаменатели являются взаимно простыми, то есть не имеют общих множителей. Таким образом, наименьший общий множитель данных чисел соответствует их произведению. В результате:

Разберем самостоятельный случай, когда знаменатели не содержат буквы. При этом алгоритм действий такой же, как и при действиях с обыкновенными дробями:

• определить общий множитель;
• умножить каждую дробь на недостающий множитель;
• сложить или вычесть числители.

Упростим выражение:

Когда знаменатели содержат буквы, схема действий существенно не меняется:

• разложение знаменателей на множители;
• определение одинаковых множителей;
• выделение всех общих множителей по одному разу;
• умножение общих множителей на оставшиеся множители, которые не являются общими.

Пример 7

Рассмотрим пример, когда требуется упростить выражение:

Умножение и деление дробей

Правило 5

Умножение и деление дробей выполняют таким образом:

Арифметические действия выполняют в следующем порядке:

• вычисление степени;
• умножение и деление;
• сложение и вычитание.

Важно заметить, что при наличии скобок, операции, которые в них заключены, необходимо выполнить в первую очередь. Далее можно приступать к раскрытию скобок. Когда имеется несколько скобок с арифметическими действиями, которые нужно умножить или разделить, в начале проводят вычисления в каждой из скобок, а затем умножение или деление полученных результатов. При наличии внутренних скобок, заключенных в скобки, действия в них выполняют в первую очередь.

Пример 8

Упростим выражение:

Во многих примерах имеются не только цифры, но и буквы. В этом случае выполняются алгебраические действия, в том числе, приведение подобных, сложение, сокращение дробей и другие операции. Отличия можно заметить при разложении многочленов на множители. Для этого следует пользоваться формулами сокращенного умножения или вынесением единого множителя за скобки.

Ключевой задачей при работе с такими выражениями является запись выражений в виде произведения или частного.

Пример 9

Попробуем упростить выражение:

Так как имеются скобки, следует начать преобразования именно с них. Упростим разность дробей, которая в них записана, чтобы получить вместо нее произведение или частное. Приведем дроби к единому знаменателю и определим сумму:

Заметим, что дальнейшие преобразования не приведут к упрощению данного выражения. Причина этого заключается в том, что каждый из множителей является элементарным. В результате:

Пояснения на примерах

Задача 1

Требуется упростить выражения:

Задача 2

Требуется упростить выражения:

Решение

Путем разложения на множители упростим данные выражения:

Задача 3

Упростить выражения:

Решение

Выполним преобразования:

Задача 4

Упростить выражения:

В первую очередь выполним разложение на множители:

Задача 5

Дано выражение, которое требуется упростить:

Решение

В данном случае требуется разложить знаменатели на множители. Первый знаменатель записан так, что можно вынести за скобки х. Второй знаменатель содержит разность квадратов. Выполним преобразования:

Рассмотрим выражение на наличие общих множителей:

Тогда получим:

Заметим, что при переносе слагаемых, заключенных в скобках, изменился знак перед дробью. Приведем выражения к единому знаменателю:

Задача 6

Упростить выражение:

Решение

Воспользуемся формулой сокращенного умножения, а именно, разностью кубов:

Заметим, что в знаменателе дроби расположено выражение, которое называют неполным квадратом суммы:

Второе по счету слагаемое в неполном квадрате суммы является произведением первого и последнего. Неполный квадрат суммы представляет собой множитель, который входит в состав разложения разности кубов:

Задача 7

Требуется упростить выражения:

Решение

Задача 8

Дано выражение, которое требуется упростить:

Решение

При наличии в знаменателях одного и того же множителя, возведенного в разные степени, то в общем знаменателе данный множитель будет обладать самой большой из имеющихся степеней. Применительно к этой задаче, общий знаменатель будет состоять из следующих выражений:

a во второй степени;

x в третьей степени;

b в третьей степени;

y в четвертой степени.

В результате получим:

Задача 9

Нужно упростить выражение:

Решение

Исключить ошибки можно, если расписать заранее порядок операций. В первую очередь целесообразно суммировать дроби, расположенные в скобках. В результате будет получена только одна дробь. Далее можно приступить к делению дробей. Полученный итог следует прибавить к последней дроби.

Выглядит этот алгоритм таким образом

Молодец! Раз ты дочитал это до конца, вероятно, ты все отлично усвоил.  Но если вдруг что-то еще непонятно — попробуй онлайн-занятие с репетитором (подробности тут + 🎁).

Математика, 7 класс, Алгебраические рассуждения, Упрощение выражений с использованием распределительных свойств

Обзор

Учащиеся используют свойство распределения для упрощения выражений. Упрощение выражений может включать умножение на отрицательное число. Учащиеся анализируют и выявляют ошибки, которые иногда допускают при упрощении выражений.

Этот урок посвящен упрощению выражений и требует понимания правил умножения отрицательных чисел. Например, учащиеся упрощают такие выражения, как 8 − 3(2 − 4 х ). Выражения такого рода часто сложны для учащихся, потому что есть несколько ошибок, которые они могут сделать из-за неправильных представлений:

• Учащиеся могут упростить 8 − 3 (2 − 4 x ) до 5 (2 − 4 x ), потому что они ошибочно отделяют 3 от умножения.
• Учащиеся могут упростить 8 − 3 (2 − 4 x ) до 8 − 3 (−2 x ) в попытке упростить выражение в скобках, даже если никакое упрощение невозможно.
• Учащиеся могут упростить 8 − 3 (2 − 4 x ) до 8 − 6 −12 x . Эта ошибка может быть основана на непонимании того, как работает распределительное свойство, или на незнании правил умножения целых чисел.

• Упрощение более сложных выражений, включающих умножение на отрицательные числа.
• Определите ошибки, которые могут быть сделаны при упрощении выражений.

Пусть учащиеся поработают над этим заданием в парах.

Дайте парам учащихся время посмотреть на рисунок и написать выражение для площади заштрихованной части рисунка. Все учащиеся должны увидеть, что выражение (10 x )(8) − 6 ( x − 3) может использоваться для представления площади.

Проем

Напишите выражение для площади заштрихованной части фигуры.

Обсудить математическую миссию. Студенты обнаружат ошибки, которые могут быть сделаны при упрощении выражений.

Открытие

Обнаружение ошибок, которые могут быть сделаны при упрощении выражений.

Предложите учащимся поработать с партнером над заданиями. Задайте несколько вопросов, чтобы убедиться, что учащиеся понимают, что значит упростить выражение:

• Должно ли упрощенное выражение содержать круглые скобки?
• Сколько членов каждой переменной должно содержать упрощенное выражение?
• Сколько чисел должно содержать упрощенное выражение?
• Как можно использовать свойство распределения для упрощения выражения?

ELL: Обеспечьте поддержку, чтобы ELL развивали словарный запас и навыки английского языка, необходимые для предоставления письменных комментариев, описывающих распространенные ошибки.

Приведите модели и примеры, которые понятны.

Студенту трудно начать.

• Все четыре ученика начали с одного и того же выражения?
• Просмотрите работу одного ученика за раз. Посмотрите на одну строку за раз. Видите ли вы ошибку?

[общая ошибка] Учащийся неправильно умножает целые числа.

• Составьте список возможных комбинаций знаков при умножении двух целых чисел.
• Как определить знак произведения при умножении двух целых чисел?

Ученик нашел решение.

• Почему вы подошли к проблеме именно так?
• Объясните свою стратегию.
• Могли ли мы использовать другой метод для решения этой проблемы?

• Решение Джека верное.
• Другие ученики допустили следующие ошибки: Карен нашла разницу 8 − 6 до завершения умножения. Люси попыталась упростить
  x — 3 до -2 x ; x − 3 нельзя упростить. Маркус упростил -6( x — 3) до -6 x — 18. Он либо неправильно понял, как работает свойство распределения, либо не знал, что умножение двух отрицательных целых чисел дает положительное произведение.

Рабочее время

Карен, Люси, Джек и Маркус упростили выражение, написанное им для этой задачи.

• Чье решение правильное?
• Какие ошибки допустили другие ученики?

Подсказка:

• Когда вы упрощаете выражение, напишите как можно более простое эквивалентное выражение. Он не должен содержать скобок. Он должен иметь только один термин с каждой переменной и только одно число без переменной. Примеры:
  2( х – 4) = 2 х – 8
  и
  х + 5 х + 4 х = (1 + 5 + 4) х 90 008 = 10 х
• Можно ли использовать свойство дистрибутива для перезаписи выражений?
• Помните: умножение двух отрицательных целых чисел дает положительное произведение.

Ищите следующие типы ответов, чтобы поделиться ими во время обсуждения «Способы мышления»:

• Учащиеся, которые могут сформулировать ошибки в задании (выберите этих учащихся в качестве докладчиков в обсуждении «Способы мышления»)
• Учащиеся, у которых есть неправильные представления об упрощении выражений (обсудите неправильные представления во время обсуждения способов мышления)
• Учащиеся, которые пытаются решить задачу, даже если их ответы неверны (обсуждение их ошибок приведет к полезному обсуждению)
• Учащиеся, которые обосновывают правильный ответ, подставив и оценив каждый шаг, чтобы доказать, что выражения для каждого шага эквивалентны

Математическое упражнение 3: Придумайте жизнеспособные аргументы и критикуйте рассуждения других.

На протяжении этого урока учащиеся обосновывают свои ответы и объясняют ошибки.

Математическая практика 6: внимание к точности.

Ищите учащихся, использующих в своих объяснениях точный математический язык.

Ответы

• 4.5 и 612 имеют смысл.
• 2 не имеет смысла, потому что длина внутреннего прямоугольника будет равна –1, что невозможно. 14 не имеет смысла, потому что высота внутреннего прямоугольника будет равна 11, что больше, чем высота внешнего прямоугольника.

Рабочее время

• Суммируйте ошибки, допущенные тремя учениками.
• Чтобы получить правильный ответ, докажите, что все шаги являются эквивалентными выражениями, используя подстановку.

Посмотрите еще раз на заштрихованный рисунок.

• Какое из этих чисел имеет смысл для значения x ?

4.5, 2, 612, 14

• Объясните свои рассуждения.

Организуйте обсуждение, чтобы помочь учащимся понять математику урока в неформальной обстановке. Предложите учащимся объяснить свои ответы. Задайте следующие вопросы:

• Как вы узнали, что нужно умножать или складывать эти числа?
• Вы думали, имеет ли смысл ваш ответ?
• Можете еще раз объяснить этот шаг?
• Как можно использовать подстановку для проверки эквивалентных выражений?
• Как выглядит выражение в простейшей форме?

SWD: Если вы знаете, что некоторым учащимся может потребоваться дополнительное время и/или побуждение к участию в этом обсуждении, предоставьте им несколько вопросов заранее (в распечатанном виде или в цифровом виде).

Performance Task

Делайте заметки о стратегиях ваших одноклассников по упрощению выражений.

Подсказка:

В присутствии одноклассников задайте такие вопросы, как:

• Откуда вы узнали, что нужно умножать/складывать эти числа?
• Проверяли ли вы эквивалентные выражения подстановкой?
• Вы думали, имеет ли смысл ваш ответ?
• Можете еще раз объяснить этот шаг?

Пусть учащиеся поработают в парах, чтобы ответить на вопросы. Пусть каждая пара представит свое объяснение ответа другой паре.

При работе над заданиями «Применить обучение» выражения учащихся не эквивалентны.

• Как вы упростили задачу (10 − 8) − 6 ( x − 3)?
• Сравните свой ответ с ответом другой пары учеников.

ELL: при формировании групп помните о своих ELL и убедитесь, что у них есть учебная среда, в которой они могут продуктивно работать. Различные типы партнерства включают:

• Объединение их с носителями английского языка, чтобы они могли овладеть языковыми навыками.
• Объединить их со студентами с таким же уровнем языковых навыков, чтобы они могли играть более активную роль и работать вместе.
• Объединить их со студентами, чей уровень владения языком ниже, чтобы они играли роль «поддерживающего».

Вы также можете объединить их в пары на основе их математических знаний.

1. Да; (8) и (10 x ) можно поменять местами, потому что умножение является коммутативным, а дополнительные скобки не нужны, но помогают прояснить организацию.
2. Да; опять же, умножение коммутативно, и +(–6) и –6 имеют одинаковое значение; (–1)3 и –3 имеют одинаковое значение.

Рабочее время

Каждое из следующих выражений эквивалентно (10 x )(8) − 6( x − 3)?

Объясните почему или почему нет.

1. (8)(10 x ) — [6( x — 3)]
2. (8)(10 x ) + (-6)[ x + (-1)3]

Проверьте свою работу, подставив значение 10 вместо переменной х .

Подсказка:

Проверьте свою работу, подставив значение 10 вместо переменной x .

Пусть каждый учащийся напишет краткое изложение математики на этом уроке, а затем напишет краткое изложение класса. Когда закончите, если вы считаете, что резюме полезно, поделитесь им с классом.

В этом уроке мы продолжили писать выражения и упрощать их. Когда вы упрощаете выражение, вы пишете максимально простое эквивалентное выражение.

Он содержит только один термин с каждой переменной и только одно число без переменной. Выражения типа 4 x , 5 a + 2, 7 − 5 y и 9 — все в простейшей форме. Когда вы упрощаете выражение, вы всегда получаете выражение, эквивалентное исходному выражению. Вы можете проверить эквивалентность выражений, подставив некоторые значения переменной и проверив, что исходное выражение и упрощенное выражение имеют одно и то же значение.

При использовании свойства распределения для упрощения выражения нужно соблюдать осторожность. Например, если вы упростите 8 − 3( x + 2), вы должны быть уверены, что умножаете как x , так и +2 на -3, а не только на 3.

Формирующее оценивание

Напишите резюме об упрощении выражений.

Подсказка:

Проверьте свое резюме:

• Объясните ли вы, как использовать свойство распределения для перезаписи выражения?
• Обсуждаете ли вы, как важно обращать внимание на знаки плюс и минус при умножении?
• Вы описываете, как проверить эквивалентность двух выражений?

Пусть каждый учащийся напишет краткое размышление перед окончанием урока. Просмотрите размышления, чтобы распознать дополнительные вопросы, которые могут возникнуть у учащихся относительно упрощения выражений, а также новых изученных понятий, понятных учащимся.

Рабочее время

Напишите размышления об идеях, обсуждавшихся сегодня в классе. Используйте начальные предложения ниже, если вы считаете их полезными.

Что-то новое, что я узнал сегодня, это …

У меня остались вопросы о …

Урок 5 | Числовые и алгебраические выражения | Математика 7 класса

Цель

---

Складывать и упрощать выражения, комбинируя одинаковые термины.

Общие базовые стандарты

---

Основные стандарты

Основные стандарты, рассмотренные в этом уроке

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

• 7.EE.A.1 — Применяйте свойства операций как стратегии для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами.

Основополагающие стандарты

Основные стандарты, рассмотренные в этом уроке

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

• 6.EE.A.3

• 6.EE.A.4

• 7.НС.А.1

Критерии успеха

Основные понятия, которые учащиеся должны продемонстрировать или понять для достижения цели урока

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

---

1. Определить и идентифицировать терминов , подобных термов , констант и коэффициентов в выражениях.
2. Поймите, почему термины, имеющие одинаковую переменную часть, можно комбинировать с помощью сложения или вычитания. Они считаются как термины.
3. Упрощайте выражения с помощью сложения и вычитания терминов, комбинируя похожие термины.
4. Сложите два выражения вместе и упростите, объединив одинаковые термины .

Fishtank Plus

Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.

Проблемы с якорем

Задачи, предназначенные для изучения ключевых моментов урока, и наводящие вопросы, помогающие ученикам понять

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

---

Проблема 1

Используйте приведенное ниже выражение, чтобы ответить на следующие вопросы.

$${\frac{1}{3}x-2y-5x+8}$$

а. Сколько членов в выражении?

б. Какие термины являются «подобными терминами»?

в. Есть константы? Если так, то кто они?

д. Какие переменные входят в выражение?

эл. Какие коэффициенты в выражении?

Наводящие вопросы

Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.

Проблема 2

Перепишите выражение $${5x+3x}$$ и выражение ${5x-3x}$$, объединив одинаковые термины.

а. Сделайте это, расширив каждый термин, используя дополнение.

б. Сделайте это, выделив общий множитель и используя распределительное свойство.

в. Можете ли вы переписать выражение $${5x+3y}$$ или выражение $${5x-3y}$$, объединив термины? Почему или почему нет? Используйте рассуждения из частей a и b, чтобы поддержать свой ответ.

Наводящие вопросы

Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.

Каталожные номера

EngageNY Mathematics Grade 7 Mathematics > Модуль 3 > Тема A > Урок 1 — Пример 1

Математика для 7 класса > Модуль 3 > Тема A > Урок 1 Общей основной учебной программы штата Нью-Йорк по математике от EngageNY и Great Minds. © 2015 Великие умы. Лицензировано EngageNY Департамента образования штата Нью-Йорк в соответствии с лицензией США CC BY-NC-SA 3. 0. По состоянию на 2 декабря 2016 г., 17:15.

Проблема 3

Найдите сумму $${\left ( 0,75x-12y \right )}$$ и $$(-5+6y-0,5x)$$. Покажите каждый шаг в своей работе и объясните, почему каждый шаг эквивалентен выражению на предыдущем шаге.

Наводящие вопросы

Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи.

Набор проблем

Набор предлагаемых ресурсов или типов задач, которые учителя могут преобразовать в набор задач а Подписка Fishtank Plus.

Целевая задача

Задача, которая представляет собой пик мышления урока — мастерство покажет, была ли достигнута цель

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

---

Учащиеся в классе мистера Джексона упрощают выражение, написанное на доске:

$${{-12p-5n+8n+20p}}$$

Амаль упростила выражение до $${8p+3n}$$, а Андре упростил выражение до $${-32p-13n }$$.

Г-н Джексон увидел несколько разных ответов в классе, поэтому он дал ученикам подсказку на доске, написав:

$${{-12p-5n+8n+20p}}$$

$${-12p+20p-5n+8n}$$

$${(-12+20)p+(-5+ 8)n}$$

а.

No related posts.