Дискриминант квадратного уравнения. Формулы дискриминанта
- Решение квадратных уравнений через дискриминант
Дискриминант квадратного уравнения — это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой D.
| Вид уравнения | Формула корней | Формула дискриминанта |
|---|---|---|
| ax2 + bx + c = 0 | b2 — 4ac | |
| ax2 + 2kx + c = 0 | k2 — ac | |
| x2 + px + q = 0 | ||
| p2 — 4q |
Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:
| Вид уравнения | Формула |
|---|---|
| ax2 + bx | , где D = b2 — 4ac |
| ax2 + 2kx + c = 0 | , где D = k2 — ac |
| x2 + px + q = 0 | , где D = |
| , где D = p2 — 4q |
Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:
- Если дискриминант больше нуля, то уравнение имеет два корня.
- Если дискриминант равен нулю, то уравнение имеет один корень.
- Если дискриминант меньше нуля, то уравнение не имеет корней.
Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:
D = b2 — 4ac,
так как она относится к формуле:
,
которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.
Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.
Пример 1. Решить уравнение:
3x2 — 4x + 2 = 0.
Определим, чему равны коэффициенты:
a = 3, b = -4, c = 2.
Найдём дискриминант:
D = b2 — 4ac = (-4)2 — 4 · 3 · 2 = 16 — 24 = -8,
D < 0.
Ответ: корней нет.
Пример 2.
x2 — 6x + 9 = 0.
Определим, чему равны коэффициенты:
a = 1, b = -6, c = 9.
Найдём дискриминант:
D = b
D = 0.
Уравнение имеет всего один корень:
Ответ: 3.
Пример 3.
x2 — 4x — 5 = 0.
Определим, чему равны коэффициенты:
a = 1, b = -4, c = -5
Найдём дискриминант:
D = b2 — 4ac = (-4)2 — 4 · 1 · (-5) = 16 + 20 = 36,
D > 0.
Уравнение имеет два корня:
x1 = (4 + 6) : 2 = 5,
x2 = (4 — 6) : 2 = -1.
Ответ: 5, -1.
Примеры решения квадратных уравнений с ответами
Простое объяснение принципов решения квадратных уравнений и 10 наглядных примеров.
В каждом примере поэтапный ход решения и ответ.
Алгоритм решения квадратных уравнений
Теорема
Квадратным уравнением называется уравнение вида:
Для решения квадратного уравнения необходимо вычислить дискриминант: .
Квадратное уравнение имеет 2 корня, если , один корень, если и не имеет корней, если .
Формулы нахождения корней квадратного уравнения.
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Примеры решений квадратных уравнений
Пример 1
Задача
Решить уравнение:
Решение
Найдём дискриминант:
Ответ
Пример 2
Задача
Решить уравнение:
Решение
Найдём дискриминант:
Ответ
Пример 3
Задача
Решить уравнение:
Решение
ОДЗ:
Ответ
Пример 4
Задача
Решить уравнение:
Решение
ОДЗ:
Ответ
Пример 5
Задача
Решить уравнение:
Решение
ОДЗ:
Обозначим:
Тогда:
Ответ
Пример 6
Задача
Решить уравнение:
Решение
ОДЗ:
Обозначим:
Тогда:
Ответ
Пример 7
Задача
Решить уравнение:
Решение
ОДЗ:
Обозначим:
Тогда:
– корней нет
Ответ
Пример 8
Задача
Решить уравнение:
Решение
ОДЗ:
Ответ
Пример 9
Задача
Решить уравнение:
Решение
ОДЗ:
Отсюда
Ответ
Пример 10
Задача
Решить уравнение:
Решение
– корней нет
Ответ
Средняя оценка 2.
1 / 5. Количество оценок: 8
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
28474
Закажите помощь с работой
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
Полезно
Формула, правила, дискриминант квадратного уравнения
Дискриминант широко используется в случае квадратных уравнений и используется для определения природы корней. Хотя найти дискриминант для любого многочлена не так просто, существуют формулы для нахождения дискриминанта квадратных и кубических уравнений, которые облегчают нашу работу.
Давайте узнаем больше о дискриминанте и его формулах, а также поймем связь между дискриминантом и природой корней.
| 1. | Что такое дискриминант в математике? |
2. | Дискриминантная формула |
| 3. | Как найти дискриминант? |
| 4. | Дискриминант и природа корней |
| 5. | Часто задаваемые вопросы о дискриминанте |
Что такое дискриминант в математике?
Дискриминант полинома в математике является функцией коэффициентов полинома. Полезно определить тип решений полиномиального уравнения, не находя их. т. е. он различает решения уравнения (как равные и неравные; действительные и недействительные), отсюда и название «дискриминант». Обычно его обозначают Δ или D. Значением дискриминанта может быть любое действительное число (т. е. положительное, отрицательное или 0).
Дискриминантная формула
Дискриминант (Δ или D) любого полинома выражается через его коэффициенты. Вот дискриминантные формулы для кубического уравнения и квадратного уравнения.
Давайте посмотрим, как использовать эти формулы для нахождения дискриминанта.
Как найти дискриминант?
Чтобы найти дискриминант кубического уравнения или квадратного уравнения, нам просто нужно сравнить данное уравнение с его стандартной формой и сначала определить коэффициенты. Затем подставляем коэффициенты в соответствующую формулу, чтобы найти дискриминант. 9{2}-4 а в}}{2 а}\). Здесь выражение, которое находится внутри квадратного корня квадратной формулы, называется дискриминантом квадратного уравнения
Пример: Найти дискриминант квадратного уравнения 2x 2 — 3x + 8 = 0.
Сравнивая уравнение с ax 2 + bx + c = 0, получаем a = 2, b = — 3 и c = 8. Таким образом, дискриминант равен 9.0093 Δ ИЛИ D = b 2 — 4ac = (-3) 2 — 4(2)(8) = 9 — 64 = -55 .
Дискриминант кубического уравнения
Дискриминант кубического уравнения ax 3 + bx 2 + cx + d = 0 выражается через a, b, c и d.
т.е. д
Пример: Найти дискриминант кубического уравнения x 3 — 3x + 2 = 0.
Сравнивая уравнение с ax 3
+ bx 2 + cx + d = 0, мы имеем a = 1, b = 0, c = -3 и d = 2. Таким образом, его дискриминантом является, Δ или D = B 2 C 2 — 4AC 3 — 4B 3 D — 27A 2 D 2 + 18ABCD
= (0) 2 (-3) 2 — 4(1)(-3) 3 — 4(0) 3 (2) — 27(1) 2 (2) 2 + 18(1)(0)(-3)(2)
= 0 + 108 — 0 — 108 + 0
= 0
Дискриминант и природа корней
Корни квадратного уравнения ax 2 + bx + c = 0 — это значения x, которые удовлетворяют уравнению. Их можно найти по квадратичной формуле: x = \(\dfrac{-b \pm \sqrt{D}}{2 a}\). Хотя мы не можем найти корни, просто используя дискриминант, мы можем определить природу корней следующим образом.
Если дискриминант положительный
Если D > 0, квадратное уравнение имеет два разных действительных корня. Это связано с тем, что при D > 0 корни задаются как x = \(\dfrac{-b \pm \sqrt{\text {Положительное число}}}{2 a}\) и квадратный корень из положительного число всегда приводит к действительному числу. Таким образом, когда дискриминант квадратного уравнения больше 0, оно имеет два корня, которые являются различными и действительными числами.
Если дискриминант отрицателен
Если D < 0, квадратное уравнение имеет два разных комплексных корня. Это связано с тем, что при D < 0 корни задаются как x = \(\dfrac{-b \pm \sqrt{\text {Отрицательное число}}}{2 a}\) и квадратный корень из отрицательного число всегда приводит к мнимому числу. Например, \(\sqrt{-4}\) = 2i. Таким образом, когда дискриминант квадратного уравнения меньше 0, оно имеет два корня, которые являются различными и комплексными числами (недействительными).
Если дискриминант равен нулю
Если D = 0, квадратное уравнение
Корень есть не что иное, как координата x точки пересечения x квадратичной функции. График квадратичной функции в каждом из этих 3 случаев может быть следующим.
Важные замечания по дискриминанту:
Связанные темы:
- Решение квадратных уравнений
- Дискриминантный калькулятор
- Факторинг Квадратика
- Квадратные выражения
- Квадратичная функция
Часто задаваемые вопросы о дискриминанте
Что такое дискриминант?
Дискриминант в математике определяется для многочленов и является функцией коэффициентов многочленов.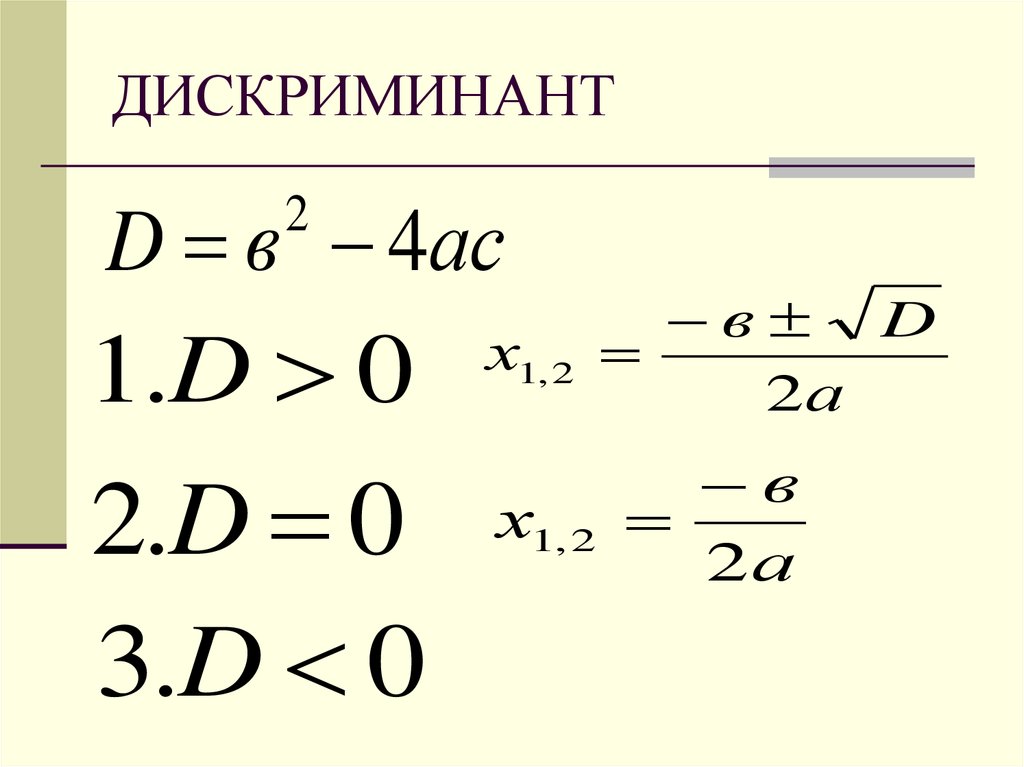
Он говорит о природе корней или, другими словами, различает корни. Например, дискриминант квадратного уравнения используется для нахождения:
- Сколько у него корней?
- Являются ли корни реальными или ненастоящими?
Что такое дискриминантная формула?
Существуют разные формулы дискриминанта для разных многочленов:
Как вычислить дискриминант квадратного уравнения?
Чтобы вычислить дискриминант квадратного уравнения:
- Определите a, b и c, сравнив данное уравнение с ax 2 + bx + c = 0,
- Подставить значения в дискриминантную формулу D = b 2 − 4ac.
Что делать, если дискриминант = 0?
Если дискриминант квадратного уравнения ax 2 + bx + c = 0 равен 0 (т.е. если b 2 — 4ac = 0), то квадратная формула принимает вид x = -b/2a и, следовательно, квадратичная уравнение имеет только один действительный корень.
Что нам говорит положительный дискриминант?
Если дискриминант квадратного уравнения ax 2 + bx + c = 0 положителен (т.
е. если b 2 — 4ac > 0), тогда квадратная формула принимает вид x = (-b ± √(положительное число)) / 2a, и, следовательно, квадратное уравнение имеет только два действительных и различных корня.
Что говорит нам отрицательный дискриминант?
Если дискриминант квадратного уравнения ax 2 + bx + c = 0 отрицателен (т. е. если b 2 — 4ac < 0), то квадратная формула принимает вид x = (-b ± √(отрицательное число) )) / 2a и, следовательно, квадратное уравнение имеет только два комплексных и различных корня.
Какая формула дискриминанта кубического уравнения?
Кубическое уравнение имеет форму ax 3 + bx 2 + cx + d = 0, а его дискриминант выражается через коэффициенты, которые задаются формулой D = b 2 c 2 − 4ac 3 − 4b 3 d − 27a 2 d 2 + 18abcd.
Полное руководство по дискриминанту квадратичных чисел – mathsathome.com
Видеоурок по дискриминанту
Что такое дискриминант квадратного уравнения?
Дискриминант — это часть квадратной формулы, находящаяся внутри квадратного корня.
Для квадратичного вида a𝑥 2 + b𝑥 + c его дискриминант равен b 2 – 4ac. Квадратное уравнение имеет 2, 1 или 0 решений в зависимости от того, является ли значение дискриминанта положительным, нулевым или отрицательным соответственно.
Дискриминант b 2 – 4ac представлен дельта-символом Δ.
Формула дискриминанта: Δ = b 2 – 4ac, где a — коэффициент при 𝑥 2 , b — коэффициент при 𝑥, а c — постоянный член квадратичного уравнения.
Например, вычислите дискриминант y = 𝑥
2 + 5𝑥 + 2.У нас есть один 𝑥 2 . Коэффициент при 𝑥 2 равен 1. Следовательно, a = 1.
Коэффициент при 𝑥 равен 5. Следовательно, b = 5.
Постоянный член равен 2. Следовательно, c = 2.
Подставляем значения a = 1, b = 5 и c = 2 в формулу для дискриминанта, b 2 – 4ач.
b 2 = 5 2 = 25
и 4ac = 4 × 1 × 2 = 8.
b 2 – 4ac становится 28 – 8 .
нет важен, потому что он говорит нам, сколько решений имеет любое квадратное уравнение.
- Если дискриминант положительный, то будет 2 решения.
- Если дискриминант равен нулю, будет 1 решение.
- Если дискриминант отрицательный, действительных решений не будет.
Количество решений квадратного уравнения говорит нам о количестве корней квадратного уравнения. Корни квадратного уравнения — это точки пересечения квадратного графика с осью 𝑥. Это точки пересечения оси 𝑥.
В следующей таблице показано количество корней для положительного, отрицательного или нулевого дискриминанта.
| Значение дискриминанта | Количество корней | |
| > 0 | Положительный | Два |
| = 0 | Ноль | Один |
| < 0 | Отрицательный | 39Как вычислить дискриминант Чтобы вычислить дискриминант квадратного уравнения, формула b 2 – 4ac. При вычислении дискриминанта важно учитывать следующие ключевые моменты:
Чтобы найти дискриминант:
Дискриминантный калькуляторЧтобы использовать дискриминантный калькулятор:
Положительный дискриминантПоложительный дискриминант означает, что значение b 2 – 4ac больше нуля. Квадратное уравнение с положительным дискриминантом имеет ровно два решения, а это означает, что оно имеет две точки пересечения оси 𝑥. Это означает, что квадратное число имеет 2 корня. Положительное значение дискриминанта означает, что график квадратного уравнения должен дважды пройти через ось 𝑥. Если квадратичный коэффициент имеет положительный коэффициент 𝑥 2 (a > 0), график вогнут вверх и точка минимума будет ниже оси 𝑥, как показано на левом изображении ниже. Если квадратичный коэффициент имеет отрицательный коэффициент 𝑥 2 (a < 0), график вогнут вниз, а точка минимума будет выше оси 𝑥, как показано на правом изображении ниже. Положительное значение дискриминанта говорит нам о том, что квадратное уравнение имеет два уникальных решения. Например, квадратное уравнение 𝑥 2 – 4𝑥 + 3 = 0 имеет два решения: 𝑥 = 3 и 𝑥 = 1. Это означает, что квадратное уравнение пересекает ось 𝑥 в точках 𝑥 = 1 и 𝑥 = 3 Значение дискриминанта равно 4, что является положительным числом. Квадратный корень из положительного числа имеет как положительный, так и отрицательный ответ. Следовательно, квадратичная формула дает 2 различных решения. Если дискриминант представляет собой полный квадрат, то решения квадратного уравнения рациональны. Это означает, что решения будут целыми числами или могут быть записаны в виде дробей. Если дискриминант не является полным квадратом, два решения будут иррациональными. Дискриминант нуляДискриминант нуля означает, что значение b 2 – 4ac равно нулю. Квадратное уравнение с нулевым дискриминантом имеет ровно одно решение. Это означает, что график квадратичного уравнения просто касается оси 𝑥 в ее минимальной или максимальной точке. Дискриминант, равный нулю, означает, что график квадратного уравнения должен коснуться оси 𝑥 один раз. Он не может проходить через ось 𝑥. Вместо этого он просто касается его одним корнем. Если квадратичный коэффициент имеет положительный коэффициент 𝑥 2 (a > 0), график вогнут вверх и точка минимума будет касаться оси 𝑥, как показано на левом изображении ниже. Если квадратичный коэффициент имеет отрицательный коэффициент 𝑥 2 (a < 0), график вогнут вниз, и точка максимума будет касаться оси 𝑥, как показано на правом изображении ниже. Для квадратного уравнения с нулевым дискриминантом будет ровно одно решение. Это означает, что мы прибавляем или вычитаем 0 при вычислении, что делает два ответа одинаковыми. Решение квадратного уравнения с нулевым дискриминантом называется повторным корнем. Это потому, что одно и то же решение появляется дважды. Например, квадратичный 𝑥 2 – 4𝑥 + 4 = 0 имеет a = 1, b = -4 и c = 4. b 2 = 16 и 4ac = 16. b 2 – 4ac = 0, а один повторяющийся корень квадратного уравнения равен 𝑥 = 2. Отрицательный дискриминантОтрицательный дискриминант означает, что значение b 2 – 4ac меньше нуля. При использовании квадратной формулы нельзя найти квадратный корень из отрицательного числа. У квадратного уравнения нет реальных решений. Два решения являются сложными и не могут быть показаны на графике. Отрицательный дискриминант означает, что график квадратного уравнения не касается оси 𝑥. Если квадратичный коэффициент имеет положительный коэффициент 𝑥 2 (a > 0), график вогнут вверх и весь график находится над осью 𝑥. Все выходы графика положительны. Если квадратичный коэффициент имеет отрицательный коэффициент 𝑥 2 (a < 0), график вогнут вниз и весь график находится ниже оси 𝑥. Все выходы графика отрицательные. Например, в квадратном уравнении 𝑥 2 – 3x + 5 = 0, a = 1, b = -3 и c = 5. дискриминант b 2 – 4ac = -11. Квадратный корень из отрицательного числа не может быть найден, поэтому невозможно найти никаких реальных решений, поскольку мы не можем завершить расчет. Квадратный корень из -11 должен быть выражен в мнимой единице, т.е. Поэтому записывается как √11 i. Это комплексное решение можно использовать. Дискриминант из графикаКоличество точек пересечения оси 𝑥 указывает значение дискриминанта:
Дискриминант кубического уравненияДискриминант кубического уравнения a𝑥 3 + b𝑥 2 + c 𝑥 + d is b 2 c 2 – 4ac 3 – 4b 3 20 0 20 д 2 + 18abcd. Если дискриминант положительный, кубический имеет 3 действительных корня. Если он отрицательный, кубический имеет один действительный корень и два комплексно-сопряженных корня. Если он равен нулю, то по крайней мере два корня равны.
|
Подставьте значения a, b и c после считывания их из квадратного уравнения вида a𝑥 2 + b𝑥 + c . Например, для 𝑥 2 – 3𝑥 + 4, a = 1, b = -3 и c = 4. b 2 = 9 и 4ac = 16. Дискриминант, b 8 2 = – 7. 
Это потому, что квадратный корень этого дискриминанта будет surd.
Это связано с тем, что квадратный корень из дискриминанта берется как часть квадратичной формулы. Квадратный корень из 0 равен 0.
