Диагностическая работа
1.1. В треугольнике ABC угол C равен 90о, AB = 10, AC = 8. Найдите sin A.
1.2. В треугольнике ABC угол C равен 90о, sin A = 0,6. Найдите cos A.
1.3. В треугольнике ABC угол C равен 90о, высота CH равна 6, AC = 10. Найдите tg A.
2.1. В треугольнике ABC AC = BC = 10, AB = 12. Найдите sin A.
2.2. В треугольнике ABC AC = BC, AB = 10, высота AH
 Найдите cos A.
Найдите cos A.
2.3. В треугольнике ABC AB = BC, высота CH равна 8, AC = . Найдите тангенс угла ACB.
3.1. В треугольнике ABC угол C равен 90о, AB = 10, BC = 6. Найдите синус внешнего угла при вершине A.
3.2. В треугольнике ABC угол C равен 90о, sin A = 0,6. Найдите косинус внешнего угла при вершине A.
3.3. В треугольнике ABC угол C равен 90о, AB = 10, AC = 8. Найдите тангенс внешнего угла при вершине A.
4.1. Найдите синус угла AOB
. В ответе укажите значение синуса, умноженное на .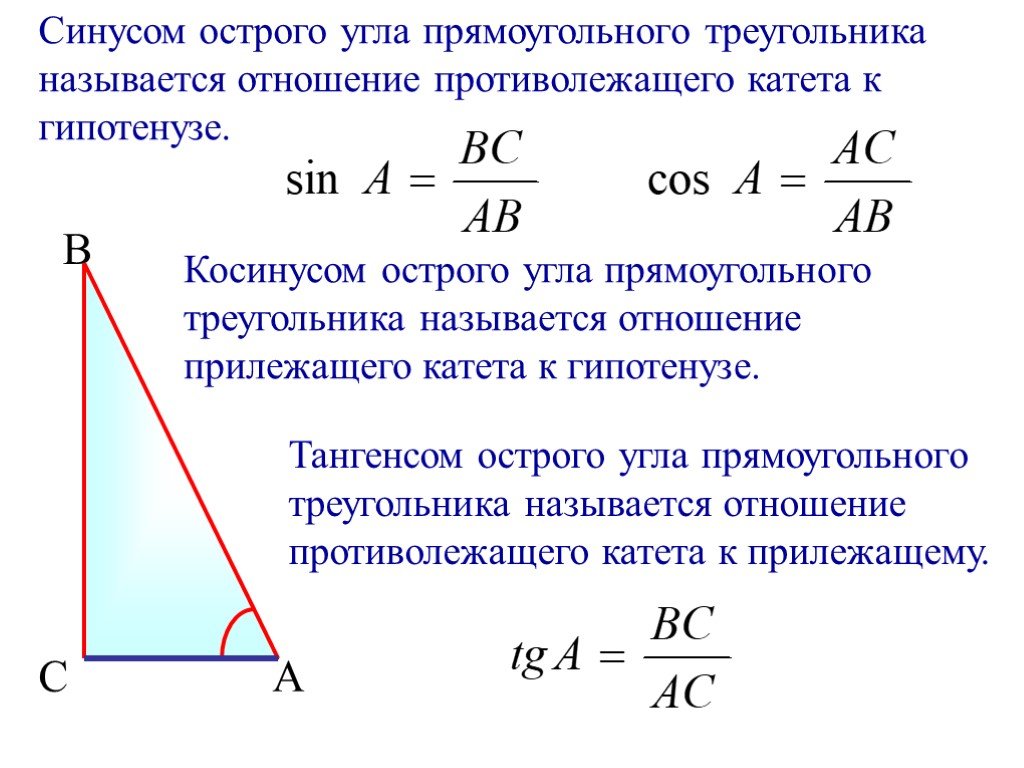
4.2. Найдите тангенс угла AOB.
4.3. Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на .
5.1. В треугольнике ABC угол C равен 90о, BC = 4, sin A = 0,8. Найдите AB.
5.2. В треугольнике ABC угол C равен 90о, tg A = 0,75, AC = 8. Найдите AB.
5.3. В треугольнике ABC угол C равен 90о
6.1. В треугольнике ABC AC = BC = 10, sin A = 0,8. Найдите AB.
Найдите AB.
6.2. В треугольнике ABC AC = BC, AB = 10, cos A = 0,6. Найдите высоту AH.
6.3. В треугольнике ABC AB = BC, высота CH равна 5, tg C = . Найдите AC.
Решения задач диагностической работы
1.1. Первое решение. В прямоугольном треугольнике ABC гипотенуза AB равна 10. Найдем катет BC. Используя теорему Пифагора, имеем BC = . Следовательно, sin A = 0,6.
Второе
решение. Так
как катет AC равен 8, а
гипотенуза AB равна 10, то
cos A = 0,8.
Воспользуемся формулой
,
выражающей косинус через синус острого
угла. Откуда sin A = 0,6.
Откуда sin A = 0,6.
Ответ. 0,6.
1.2. Первое решение. Воспользуемся формулой . Тогда cos A = = 0,8.
Второе решение. Можно считать, что гипотенуза AB и катет BC данного прямоугольного треугольника равны соответственно 10 и 6. Тогда по теореме Пифагора катет AC равен 8 и, следовательно, cos
Ответ. 0,8.
1.3. В прямоугольном треугольнике ACH катет CH равен 6, гипотенуза AC равна 10. Используя теорему Пифагора, находим AH = 8. Следовательно, tg A = 0,75.
Ответ. 0,75.
2.1.
Проведем высоту CH. В прямоугольном
треугольнике ACH гипотенуза AC равна 10, катет AH равен 6. По
теореме Пифагора находим CH = 8 и, следовательно,
sin A = 0,8.
В прямоугольном
треугольнике ACH гипотенуза AC равна 10, катет AH равен 6. По
теореме Пифагора находим CH = 8 и, следовательно,
sin A = 0,8.
Ответ. 0,8.
2.2. В прямоугольном треугольнике ABH гипотенуза AB
равна 10, катет AH равен 8. По теореме Пифагора находим BH = 6 и, следовательно, cos B = 0,6. Так как углы A и B треугольника ABC равны, то cos A = 0,6.
Ответ. 0,6.
2.3. В прямоугольном треугольнике ACH гипотенуза AC равна
,
катет CH равен 8.
По теореме Пифагора найдем AH.
Имеем AH ==
16. Откуда tg A = 0,5. Так как углы A и C треугольника ABC равны, то тангенс
угла ACB равен 0,5.
Ответ. 0,5.
3.1. Синус внешнего угла при вершине A треугольника ABC равен синусу
угла
Ответ. 0,6.
3.2. Косинус внешнего угла при вершине A равен –cos A. Воспользуемся формулой , выражающей косинус острого угла через его синус. Тогда cos A = = 0,8 и, следовательно, косинус внешнего угла при вершине A равен –0,8.
Ответ. –0,8.
3.3. Тангенс внешнего угла при вершине A равен –tg A.
По теореме Пифагора находим BC == 6 и,
следовательно, tg A = 0,75. Значит,
тангенс внешнего угла при вершине A равен –0,75.
Значит,
тангенс внешнего угла при вершине A равен –0,75.
Ответ. –0,75.
4.1. Первое решение. Рассмотрим прямоугольный треугольник OBC. Его катет BC равен 3, гипотенуза OB равна . Следовательно, sin A = .
Второе решение. Угол AOB равен 45о. Следовательно, sin A = .
Ответ. 2.
4.2. Рассмотрим прямоугольный треугольник OBC. Его катеты BC и OC равны соответственно 4 и 2. Следовательно, тангенс угла BOC равен 2. Учитывая, что тангенс смежного угла равен тангенсу данного угла, взятому с противоположным знаком, получаем, что тангенс угла AOB равен – 2.
Ответ. – 2.
4.3. Рассмотрим треугольник OBС.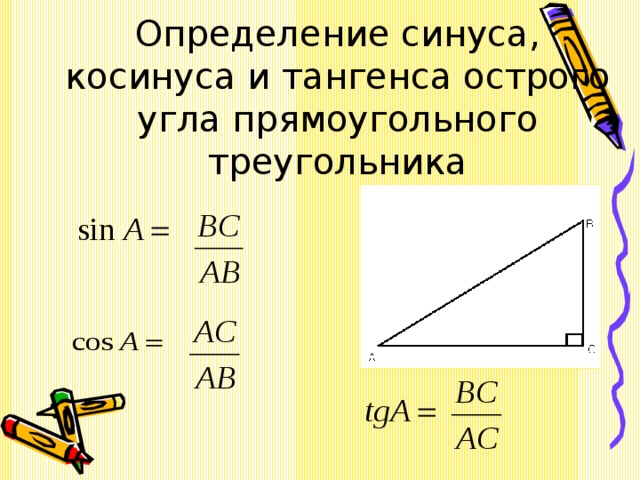
Ответ. 2.
5.1. Подставляя в формулу BC = ABsin A данные значения BC и sin A, находим AB = 5.
Ответ. 5.
5.2. Имеем BC = ACtg A = 80,75 = 6. По теореме Пифагора находим AB = = 10.
Ответ. 10.
5.3. Углы BCH и BAC равны, как острые углы с перпендикулярными сторонами, значит, cosBCH = 0,8. CH = BCcosBCH = 4,8.
Ответ. 4,8.
6.1. Первое решение. Проведем
высоту CH. Имеем CH = ACsin A = 8. По
теореме Пифагора находим AH = и, следовательно, AB = 12.
Второе решение. Проведем высоту CH. Воспользуемся формулой , выражающей косинус острого угла через его синус. Тогда cos A = = 0,6. Следовательно, AH = ACcos A = 6 и, значит, AB = 12.
Ответ. 12.
6.2. Первое решение. В равнобедренном треугольнике ABC угол A равен углу B, BH = ABcos B = 6. По теореме Пифагора находим AH = .
Второе решение. Воспользуемся формулой , выражающей синус острого угла через его косинус. Тогда sin A = = 0,8. Следовательно, поскольку в равнобедренном треугольнике A = B, получаем AH = ABsin B
Ответ. 8.
6.3. Первое решение. В равнобедренном
треугольнике ABC угол A равен углу C, значит, tg A = tg C и AH = .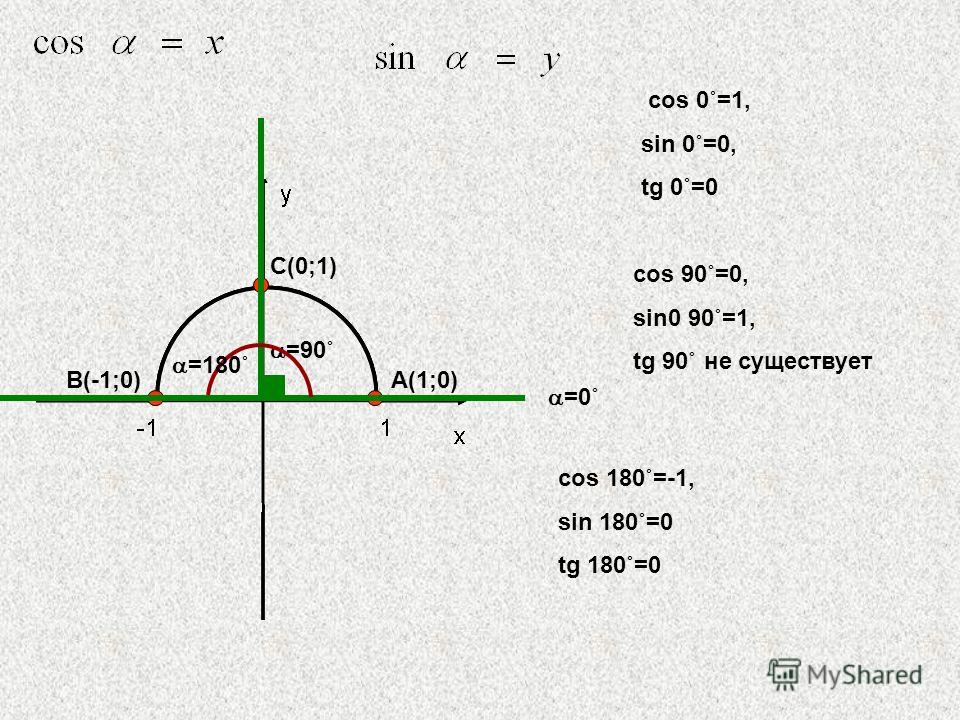 По теореме Пифагора находим AC =
= 10.
По теореме Пифагора находим AC =
= 10.
Второе решение. Так как tg C = , то угол C равен 30о. Угол A равен углу C. Так как катет прямоугольного треугольника, лежащий против угла в 30о, равен половине гипотенузы, то AC = 10.
Ответ. 10.
5.2. Соотношения между сторонами и углами произвольного треугольника
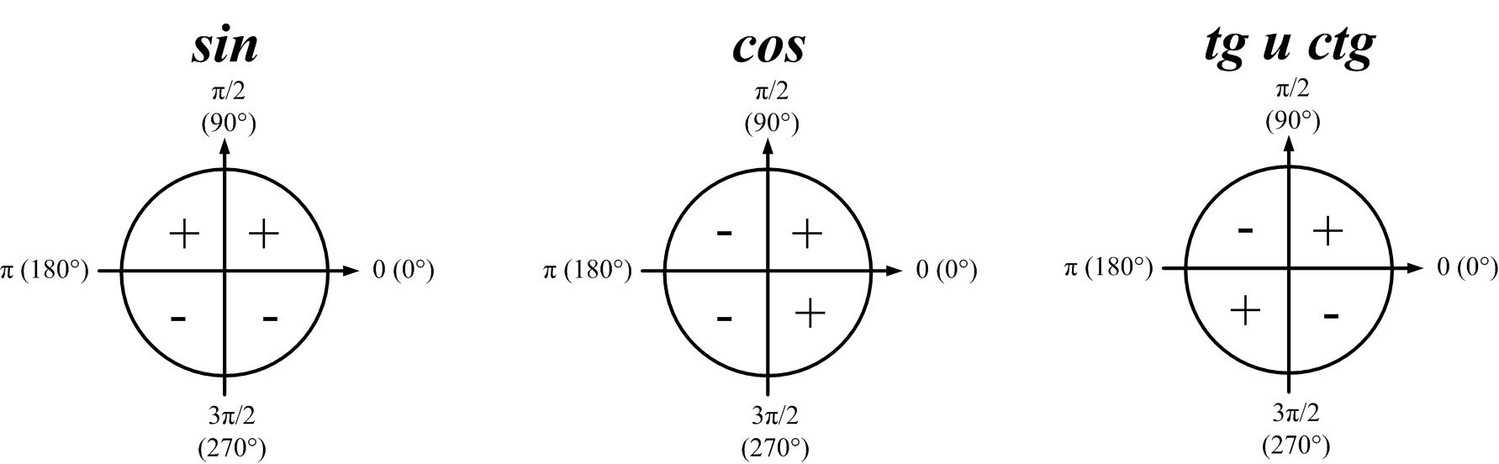
5.2. Соотношения между сторонами и углами произвольного треугольникаПод косинусом тупого угла alpha (90° < alpha < 180°) будем понимать значение косинуса смежного с ним угла, взятого со знаком минус. Косинус прямого угла будем считать равным 0.
Под синусом тупого угла будем понимать синус смежного угла. Синус прямого угла будем считать равным 1.
Из этих определений следует, что для любых углов, таких, что 0 < alpha < 180° справедливы равенства
sin alpha = sin (180° – alpha) и cos alpha = –cos (180° – alpha). |
Действительно, если alpha = 90°, то имеем верные равенства.
| sin 90° = sin (180° – 90°) и cos 90° = 0 = –cos (180° – 90°). |
Если alpha – острый угол, то 180° – alpha = beta, 90° < alpha < 180° – тупой угол. Тогда по определению
| sin beta = sin (180° – beta) или sin (180° – alpha) = sin (180° – (180° – alpha)) = sin alpha. |
| cos beta = –cos (180° – beta) или cos (180° – alpha) = –cos (180° – (180° – alpha)) = –cos alpha. |
Отсюда получаем cos alpha = cos (180° – alpha).
Наконец, если alpha (90° < alpha < 180°) – тупой угол, то равенства видны по определению.
Теорема 5. 3.
3.
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Теорема 5.4.
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов, т.е.
Следствие 5.1.
Пусть даны два треугольника ABC и A1B1C1 и углы при вершинах A, B и C одного треугольника равны углам при вершинах A1, B1, C1 соответственно, другого треугольника. Тогда отношения длин сторон этих треугольников, лежащих против равных углов равны, то есть
Лемма 5.1.
Пусть alpha и beta – угловые величины двух острых углов, причем alpha < beta. Тогда sin alpha < sin beta
Тогда sin alpha < sin beta
| Рисунок 5.2.5. К следствию 5.2. |
Следствие 5.2.
В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
Теорема 5.5. Неравенство треугольника.
Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей.
Следствие 5.3.
В любом треугольнике каждая сторона меньше суммы двух других сторон.
рабочих листов | TPT
by
SunnyDays
12,50 долл. США
9,99 долл. США
Рукописный ввод — это одна из тех областей, в которую трудно вписаться, хотя сейчас она, кажется, нужна больше, чем когда-либо.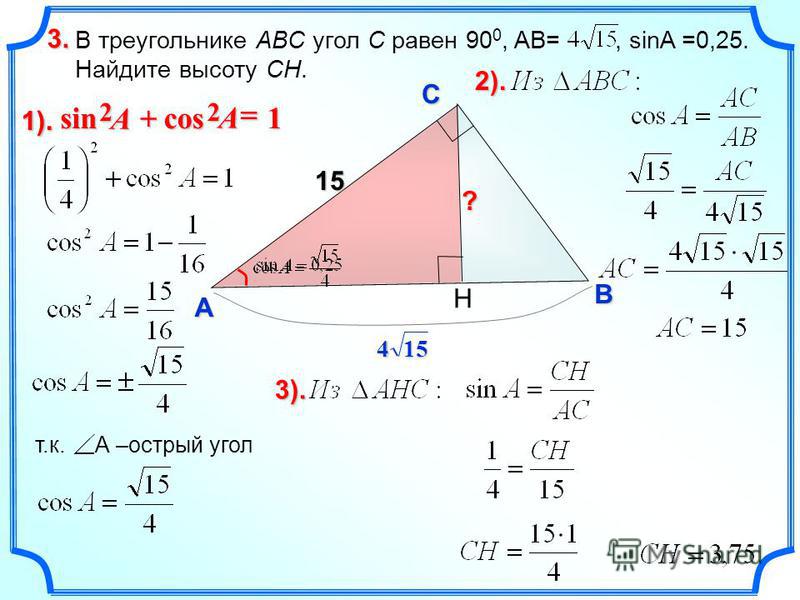 С помощью этого пакета вы можете легко проводить полноценную рукописную практику каждый день учебного года всего за несколько минут в день. Каждая страница соответствует одному и тому же формату, поэтому ваши ученики смогут заполнить ее самостоятельно после первого раза.
Отлично подходит для работы со звонком, успокоения после перемены, работы со словами, домашней работы или в любое время, когда у вас есть несколько лишних минут. Распечатать пакет на весь 9 мес.0003
С помощью этого пакета вы можете легко проводить полноценную рукописную практику каждый день учебного года всего за несколько минут в день. Каждая страница соответствует одному и тому же формату, поэтому ваши ученики смогут заполнить ее самостоятельно после первого раза.
Отлично подходит для работы со звонком, успокоения после перемены, работы со словами, домашней работы или в любое время, когда у вас есть несколько лишних минут. Распечатать пакет на весь 9 мес.0003
Тема:
Английский языковой искусство, почерк, написание
Оценки:
1 -й — 3 -е
Типы:
Дома Студенты практикуют почерк, который им нужен, в увлекательной форме. Они будут развивать выносливость при письме, повторять построение букв и цифр и практиковаться в словах, изучая новые шутки и забавные факты! и почерк, который не является «детским»? Глупые шутки и забавные факты привлекут ваших учеников, пока они
Объекты:
Сбалансированная грамотность, почерк, написание
. переходы! Эти отрывки отлично подходят для детей младшего возраста, а также подойдут для первоклассников или первоклассников, в зависимости от того, как вы их используете. В комплекте много разнообразия. Пожалуйста, проверьте изображения и предварительный просмотр, чтобы увидеть, подойдут ли эти отрывки для ваших учеников. Отрывки разбиты на три категории… Первые 20 отрывков: Основная история с 3 вопросами. Студентам дается два ответа на выбор на каждый вопрос. Вторые 20 отрывков: Базовый
переходы! Эти отрывки отлично подходят для детей младшего возраста, а также подойдут для первоклассников или первоклассников, в зависимости от того, как вы их используете. В комплекте много разнообразия. Пожалуйста, проверьте изображения и предварительный просмотр, чтобы увидеть, подойдут ли эти отрывки для ваших учеников. Отрывки разбиты на три категории… Первые 20 отрывков: Основная история с 3 вопросами. Студентам дается два ответа на выбор на каждый вопрос. Вторые 20 отрывков: Базовый
Тема:
Английский язык искусства, чтение, стратегии чтения
Оценки:
K — 1 -е
Типы:
Центры, печатные изготовления, рабочие листы
на
приводить в форму навыки самоконтроля детей! Действия сосредоточены на понимании самоконтроля, импульсивного контроля, остановке и обдумывании, чтобы принять решение, ожидании своей очереди, соблюдении правил и указаний, сохранении мотивации, выполнении нашей работы наилучшим образом, управлении эмоциями, использовании стратегий преодоления и практике самоконтроля для укрепления. навыки со временем. Также рассматриваются другие навыки, влияющие на самоконтроль, включая планирование, управление временем и настойчивость. Цифровая версия обновлена до 9.0003
навыки со временем. Также рассматриваются другие навыки, влияющие на самоконтроль, включая планирование, управление временем и настойчивость. Цифровая версия обновлена до 9.0003
Тема:
Школьное консультирование, социальное эмоциональное обучение, специальное образование
. шрифты в ZIP-файле! Большинство символов ударения включено во все шрифты. Пожалуйста, проверьте предварительный просмотр, чтобы увидеть все шрифты, включенные в этот набор! Примечания. Включено 5 шрифтов + 1 шрифт для каракулей. Все шрифты с заглавными буквами Elementary. Проверьте предварительный просмотр, чтобы увидеть все шрифты в действии! $ СЭКОНОМЬТЕ ДЕНЬГИ $ БОЛЕЕ 400 ШРИФТОВ + КАЖДЫЙ НОВЫЙ ШРИФТ БЕСПЛАТНО! ПРОВЕРЬТЕ РАСТУЩИЙ НАБОР ШРИФТОВ ЗДЕСЬУсловия использования * Шрифты
Предметы:
Для всех предметов, Товары для продавцов ТРТ, Специальность
Классы:
PreK — 12th, Высшее образование, Образование для взрослых, Персонал by
My Teaching Pal
22,00 $
15,00 $
Bundle
Этот комплект содержит ОГРОМНЫЕ 263 математических листа для первого класса! Рабочие листы охватывают сложение и вычитание, числа и разрядность, 2D и 3D фигуры, данные и графики, дроби и разбиение на части и время.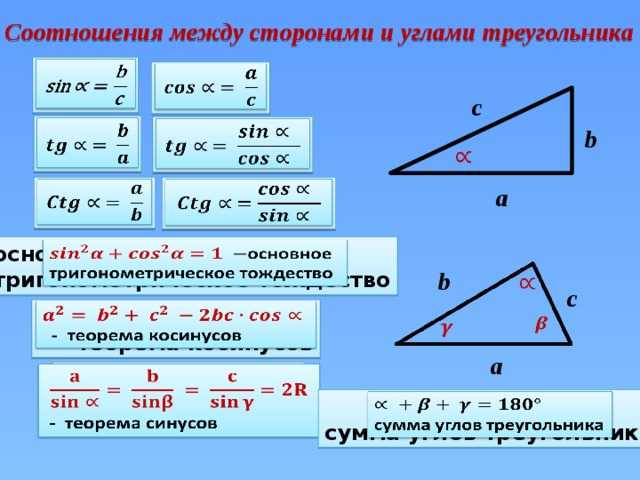 Эти веселые рабочие листы отлично подходят для использования в течение всего года, они идеально подходят для занятий в классе, математических станций, быстрых финишеров, домашних заданий и повторения. Этот комплект состоит из следующих пакетов: Рабочие листы для сложения и вычитания для первого классаРабочие листы для первого класса 2D и 3D
Эти веселые рабочие листы отлично подходят для использования в течение всего года, они идеально подходят для занятий в классе, математических станций, быстрых финишеров, домашних заданий и повторения. Этот комплект состоит из следующих пакетов: Рабочие листы для сложения и вычитания для первого классаРабочие листы для первого класса 2D и 3D
Субъекты:
Основные операции, математика, номера
. рабочие листы, которые вам когда-либо понадобятся! Этот продукт представляет собой набор из 4 моих самых продаваемых рабочих листов, включая 3 редактируемых набора рабочих листов. Каждый из этих 4 продуктов содержит 220 готовых рабочих листов со словами. Это означает, что вы получаете 880 рабочих листов в этой загрузке! Три из этих рабочих листов доступны для редактирования, так что вы можете создавать рабочие листы для любого слова! Нажмите кнопку предварительного просмотра, чтобы увидеть каждый из 4 рабочих листов крупным планом. Используйте эти страницы в качестве утренней работы, ежедневной практики в своем центре грамотности
Тема:
Английский язык искусства, орфография
Оценки:
K — 3 -й
Типы:
Центры, рабочие листы
на
Joanne Miller
Увеличение подъема и возбуждение с этими интерактивными играми, использующими. . Эти игровые доски можно использовать с любым предметом или уроком. Они идеально подходят для обзора или подготовки к тесту. Учащиеся могут работать как команды, партнеры или весь класс. Используйте свой уже распечатанный рабочий лист или рабочую тетрадь и добавьте эти игровые доски, чтобы заинтересовать и мотивировать своих учеников! Это идеальный способ оживить повторный урок или использовать его для подготовки к экзамену. ***Включены версии PowerPoint и PDF. *Эти игровые доски были дези
. Эти игровые доски можно использовать с любым предметом или уроком. Они идеально подходят для обзора или подготовки к тесту. Учащиеся могут работать как команды, партнеры или весь класс. Используйте свой уже распечатанный рабочий лист или рабочую тетрадь и добавьте эти игровые доски, чтобы заинтересовать и мотивировать своих учеников! Это идеальный способ оживить повторный урок или использовать его для подготовки к экзамену. ***Включены версии PowerPoint и PDF. *Эти игровые доски были дези
Предметы:
Английский язык, для всех предметов, математика
Классы:
2-6
Типы:
Занятия, игры, презентации PowerPoint
Также включено в: Комплект интерактивных игр | Участие учащихся
by
Хейли О’Коннор
Есть ли в вашем классе учащиеся, нуждающиеся в дополнительной поддержке поведения? Вы тратите драгоценное учебное время, постоянно перенаправляя нескольких трудных учеников, и не знаете, что делать, чтобы поддержать их? Этот пакет ПОЛЕН ресурсов, идей и инструментов, которые помогут каждому учащемуся в вашем классе добиться успеха.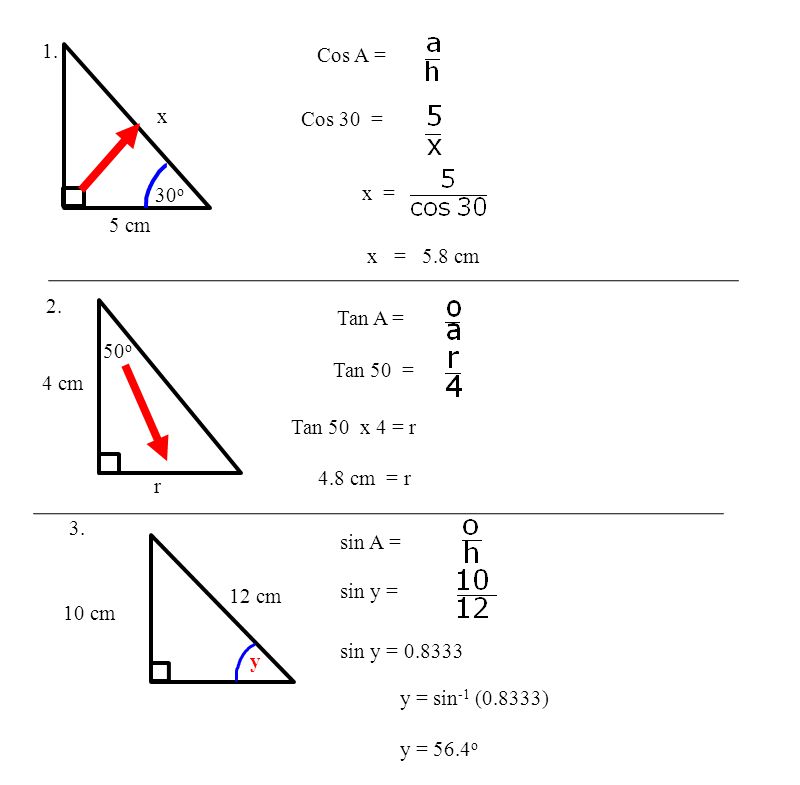 Этот ресурс идеально подходит для любого учителя начальных классов, которому нужны дополнительные ресурсы по поведению для поддержки учеников в своем классе! Работая ВМЕСТЕ со студентом, вы сможете создать сильные
Этот ресурс идеально подходит для любого учителя начальных классов, которому нужны дополнительные ресурсы по поведению для поддержки учеников в своем классе! Работая ВМЕСТЕ со студентом, вы сможете создать сильные
Объекты:
Сообщество в классе, управление классом, школьное консультирование
Оценки:
K — 2 -е
Типы:
Формы классной комнаты, печатные изделия
на
Ничего, кроме класса
$ 155
. «Отверстия» Луи Сашара содержит 124 страницы ресурсов, включая понимание и словарный запас по главам, действия по чтению ответов, оценки и многое другое. Стандарты фокусировки включают образный язык, тему, анализ персонажей, сюжет и написание мнений. Не требующее подготовки, предсказуемое и чрезвычайно удобное для пользователя, это руководство по литературе идеально подходит для всего класса, небольшой группы или самостоятельного изучения. ♥Вы можете использовать печатную или цифровую версию; ОБА входят в комплект поставки Pur 9.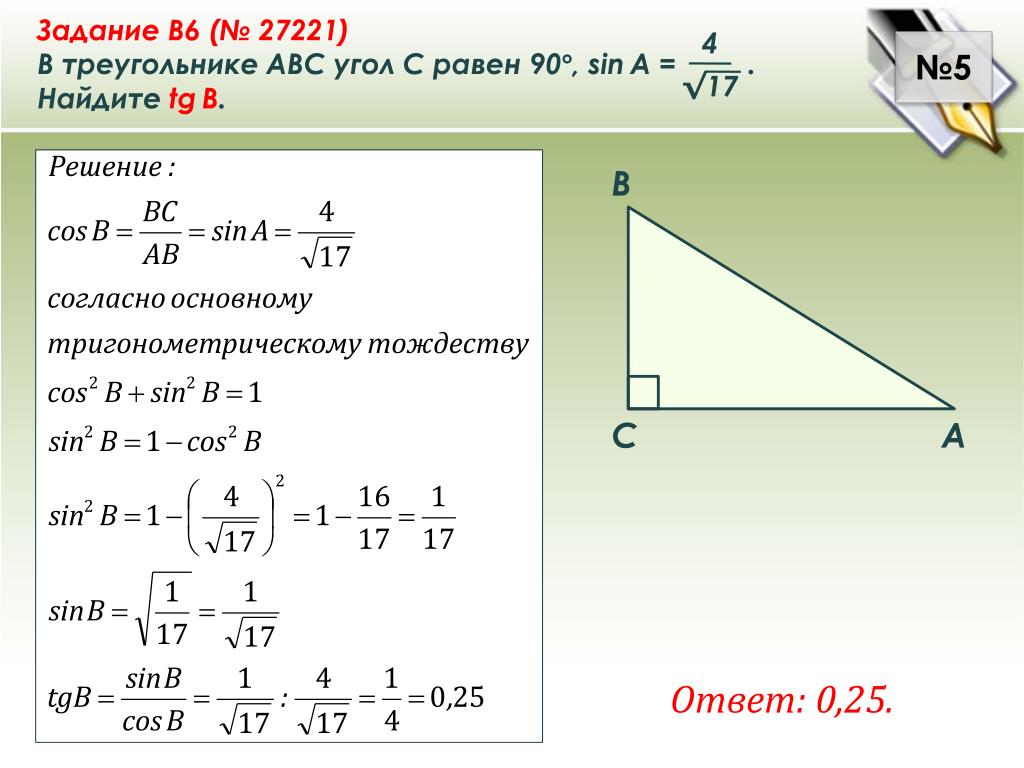 0003
0003
Субъекты:
Английский язык искусства, литература, чтение
. RL.3.6, RL.3.7…
Также включено в: Holes and The Lion, the Witch, and the Wardrobe | Novel Study Bundle
by
Deb Hanson
29,50 $
$14,75
Bundle
В этом наборе документальной текстовой структуры есть все, что вам нужно, чтобы заинтересовать учащихся старших классов начальной и средней школы при изучении ПЯТИ информационных структур текста. Он включает в себя 92 нехудожественных отрывка. Упражнения в этом наборе сделают изучение текстовых структур легким и увлекательным! Ученикам нравятся занятия, а учителям нравится удобство этих не требующих подготовки ресурсов, которые можно использовать год за годом! Эти задания по структуре научно-популярного текста можно использовать для подготовки к экзаменам, повторения,
Предметы:
Английский язык, информационный текст, чтение
Классы:
4–6
Типы:
Занятия, урок
3 CC:
3 CC: RI. 4.5, RI.5.5, RI.5.6, RI.6.5
4.5, RI.5.5, RI.5.6, RI.6.5
по
Lucky Little Curiners
$ 34,00
$ 23,00
БУМДЛЕР
ПРОМЕШНИЕ ПРОТИВЫЕ , распечатайте и используйте ресурс, который поможет учащимся превратить отдельные фонетические навыки в чтение текста! Учащиеся практикуют изолированные фонетические навыки, декодирование, беглость речи и понимание в одном ресурсе. *** НОВОЕ ОБНОВЛЕНИЕ *** Этот ресурс обновлен новой версией 2022 года! В новых ковриках для фонетики есть декодируемые отрывки, вопросы на понимание, практика написания слов и страница для разминки для каждого навыка. Обязательно загрузите превью
Предметы:
Акустика, чтение, письмо
Классы:
Типы:
Печатные формы, рабочие листы
CCSS:
RF.2.3, RF.2.3c, RF.2.3b, RF.2.2.2 .2.3d…
by
Amy Groesbeck
Сэкономьте 25% и приобретите шрифты AG в РАСТУЩЕМ НАБОРЕ! t EvenAG Понедельник BundayAG Нет, не сегодняAG Опоздание — это мое сердцеAG Извините, не извиняйтесьAG Третий — это WordВсе шрифты включают испанский, французский, норвежский и немецкий акценты, а также макронизированные гласные. **ОБНОВЛЕНО: 17.02.22** Заглавные буквы добавлено в All You Need is Sleep и Third is the Word. Ознакомьтесь с предварительным просмотром, чтобы увидеть, что именно вы получите!W
**ОБНОВЛЕНО: 17.02.22** Заглавные буквы добавлено в All You Need is Sleep и Third is the Word. Ознакомьтесь с предварительным просмотром, чтобы увидеть, что именно вы получите!W
Субъекты:
Продукты для продавцов TPT
Оценки:
Не специфические оценки
Типы:
от продавцов TPT для продавцов TPT, Fonts
также включены в: Amy Groesbeck Fonts: растущий пучок
на
. Lucky Little Learners
25,00 $
20,00 $
Bundle
Этот спиральный математический ресурс для 2-го класса С 3 УРОВНЯМИ ДИФФЕРЕНЦИАЦИИ идеально подходит для утренней математической работы, домашних заданий, ежедневного повторения математики и независимых математических центров. Это хороший спиральный обзор, который проведет вас через весь год и доступен как в печатном, так и в цифровом форматах. Обзор спиральной математики для 2-го класса на ВЕСЬ ГОД включает 40 недель листов спиральной математики с ключами для ответов. Что включено в комплект Spiral Math Review Sheets:►Краткий обзор►40 Weeks of Spiral M
Что включено в комплект Spiral Math Review Sheets:►Краткий обзор►40 Weeks of Spiral M
Предметы:
Измерение, разрядность, задачи со словами
Классы:
Типы:
Печатные формы, рабочие листы
CCSS:
2.MD.A.1, 2.2.2.A. MD.A.3, 2.MD.A.4, 2.MD.B.5…
по
Специально для образования
Если вы ищете индивидуальное расписание, визуальное расписание или сначала доску, в этом ресурсе поддержки позитивного поведения есть все! Обратите внимание: все редактируемые файлы совместимы с Microsoft PowerPoint. Некоторые страницы теперь можно редактировать с помощью Google Slides. В эту загрузку включены: — Варианты флипбука с 6 и 2 вкладками — Более 200 визуальных значков расписания (они не редактируются) — Сначала доска (отдельно от флипбука) — Сначала затем доска (отдельно от флипбука) — доски жетонов (wi
Предметы:
Снова в школу, Специальное образование, Логопедия
Классы:
PreK — 2nd
Типы:
Расписание мероприятий
реальные фотографии)
на
Плывя во второе место с Aris
Скоропись — важная часть писательского пути студента! Эти практические занятия по письму помогут вашим учащимся не только улучшить свои навыки письма, но и научатся творческому самовыражению и получат массу удовольствия. ✏️Если вы ищете страницы для практики скорописи, не ищите дальше. Этот пакет содержит более 120 страниц, полных веселых и увлекательных заданий, которые помогут вашим ученикам красиво печатать курсивом! Его используют более 12 000 учителей по всему миру, и он будет
✏️Если вы ищете страницы для практики скорописи, не ищите дальше. Этот пакет содержит более 120 страниц, полных веселых и увлекательных заданий, которые помогут вашим ученикам красиво печатать курсивом! Его используют более 12 000 учителей по всему миру, и он будет
Объекты:
Вернуться в школу, почерк, написание
Оценки:
2 -е — 5 -е
Типы:
, печатные изготовления, рабочие листы
Следующая дверь
$ 18.00
.2555444.2555444.2555444.2555449.25554 400049 Bundle
Ищете способ сделать обучение написанию абзацев намного проще? Хотите помочь своим ученикам писать хорошо продуманные абзацы? Этот полный набор для написания абзацев как в печатном, так и в цифровом виде поможет вам научить каждую часть абзаца напрямую! Он сочетает в себе четыре из моих очень популярных наборов стратегий письма: цветовое кодирование и выделение абзацев, тематические предложения, переходы в письме и заключительные предложения. Здесь есть все, что вам нужно, чтобы помочь вашим ученикам по-настоящему понять, как создавать
Здесь есть все, что вам нужно, чтобы помочь вашим ученикам по-настоящему понять, как создавать
Предметы:
Английская словесность, информационный текст, письменное разъяснение
Классы:
3-8
Типы:
Графические органайзеры, плакаты
CCSS:
4, W.3.3004, W.30003 .5.2, W.5.2a, W.5.2b…
by
Peachie Speechie
$39,00
Этот систематический, пошаговый подход к R-терапии — все, что вам нужно для обучения самым угрожающим звукам! Узнайте, почему он получил более 1300 5-звездочных отзывов! Эта тетрадь MUST HAVE у каждого логопеда! Профессиональные иллюстрации учат студентов анатомии рта, а подробные пошаговые изображения помогают врачу и студенту использовать различные методы для получения точных результатов. Вовлекающие действия включены для практики в изоляции, слоги, слова,
Предметы:
Специальное образование, логопедия
Классы:
1–6
Типы:
Занятия, рабочие тетради, рабочие листы
на
Речевые размышления
15,00 $
Целевая перспектива, получение выводов и прогнозов с использованием реальных изображений с помощью этого ресурса! Этот ресурс включает 100 карточек с реальными изображениями, которые позволяют вам обеспечить эффективное, прямое обучение тому, как делать выводы из изображений. Стратегия (вместе с начальными предложениями для студентов, чтобы обеспечить дополнительную поддержку). Рядом с фотографией есть четыре вопроса, которые требуют от ваших учеников
Стратегия (вместе с начальными предложениями для студентов, чтобы обеспечить дополнительную поддержку). Рядом с фотографией есть четыре вопроса, которые требуют от ваших учеников
Субъекты:
Школьное консультирование, Специальное образование, речевая терапия
Оценки:
K — 6th
Типы:
Действия, печатные изречения
также включены в: Real Pictures Resource Bundle для речевой терапии
Kalena Baker — Преподавание на практике
Преподавание основной идеи и вспомогательных деталей может разочаровывать учителей и быть трудным для понимания учащимися. Этот ресурс разработан, чтобы помочь всем вашим учащимся — даже учащимся, испытывающим затруднения — лучше понять основную идею и ключевые детали. В качестве дополнительного бонуса, большая часть мероприятий не требует подготовки! Эта основная идея начинается с простого (с заданий, которые отлично подходят для начинающих) и становится все труднее, чтобы помочь учащимся развить истинное понимание различий 9. 0003
0003
Предметы:
Английский язык искусства, чтение, стратегии чтения
Оценки:
2 -е — 4 -е
Типы:
, печатные изготовления, рабочие листы
CCSS:
RI.2.2, RI.3.2, RI. 4.2
Также включено в: Набор навыков чтения — практика дифференцированного понимания и обзор редактируемые параметры! Нет подготовки печати и идти и редактируемые параметры визуального расписания для студентов. В визуальном расписании используются изображения, чтобы сообщать о предстоящих мероприятиях и задачах для учащихся. Многие учащиеся могут извлечь пользу из использования визуального расписания, поскольку оно обеспечивает структуру. Эти визуальные расписания легко редактировать и модифицировать в соответствии с вашими потребностями. Полезно wi
Субъекты:
Управление в классе, для всех предметов, специальное образование
. концепция для многих видов, но этот пакет NO PREP наполнен практическими здесь, увлекательными и забавными ресурсами, чтобы помочь детям освоить эту концепцию. час⭐️ Время с шагом в десять минут⭐️ Время с шагом в пять минут⭐️ Время с шагом в 1 минутуЛУЧШЕЕ в этом пакете то, что НЕТ ПОДГОТОВКИ! БЕЗ ламинирования, БЕЗ дорогостоящих цветных чернил, БЕЗ резки… просто ПЕЧАТАЙТЕ и УЧИТЕСЬ!
час⭐️ Время с шагом в десять минут⭐️ Время с шагом в пять минут⭐️ Время с шагом в 1 минутуЛУЧШЕЕ в этом пакете то, что НЕТ ПОДГОТОВКИ! БЕЗ ламинирования, БЕЗ дорогостоящих цветных чернил, БЕЗ резки… просто ПЕЧАТАЙТЕ и УЧИТЕСЬ!
Предметы:
Классы:
1–3
Типы:
Центры, распечатки, рабочие листы
по
Патрисия Пэт Ресурсы: сложно ли составить предложение или составить предложение для учащихся
9000? Если это так, вам понравится, как эти рабочие листы для построения предложений помогут вам научить писать полные предложения. ✏️ Многочисленные изображения в рабочем листе помогут вашим ученикам ПОНЯТЬ и ЗАПОМНИТЬ правильную структуру предложения. ✏️ Это ресурс без подготовки, который понравится даже неохотным писателям, плюс вы сэкономите много времени с помощью ТРЕХ дифференциаций и строительных лесов, сделанных за вас. ✏️ Эти практические рабочие листы будут
Предметы:
EFL — ESL — ELD, английский язык, специальное образование
Классы:
K — 2nd
Типы:
Центры, Домашнее обучение, Домашнее задание
9. 1004 CCSS3: SL.1.6, L.K.1f, L.1.1c, L.1.2b
1004 CCSS3: SL.1.6, L.K.1f, L.1.1c, L.1.2b Также включено в: Центр написания предложений | Полные предложения | Структура предложения | Небольшие группы
по
Secret Stories
15,00 $
*Примечание. Этот продукт предназначен для использования вместе с Secret Stories, так как он НЕ включает постеры и рассказы Secret Stories® Phonics. Узнайте больше о Secret Stories® и загрузите БЕСПЛАТНЫЕ РЕСУРСЫ в файлах группы Secret Facebook! Песня Secret Stories® Better Alphabet™ — это САМЫЙ БЫСТРЫЙ способ выучить отдельные буквы и звуки, используя мышечную память для ускорения овладения языком всего за 2 недели для дошкольников и дошкольников. Этот продукт содержит три видеоверсии Better Alphabet™ 9.0003
Субъекты:
Фоника, стратегии чтения, орфография
Оценки:
Prek — 2nd
Типы:
Учебные программы Homeschool, песни
Krysstal: тригонометрия
Krysstal: Тригонометрия: Тригонометрия.
[Домашняя страница]
[Страница математики]
[Введение в числа]
[Введение в алгебру]
[Треугольник Паскаля]
[Тригонометрия]
[Посмотрите на логарифмы]
[Графики]
[Тригонометрические уравнения]
[Исчисление: дифференцирование]
[Сферическая тригонометрия]
[Дополнительная алгебра]
[Развлечение с формулами]
[Отзывы читателей (математика)]
[Язык]
[Путешествия]
[Затмения]
[Лондон]
[Астрономия]
[Математика]
[Физика]
[Химия]
[Биология]
[Футбол]
[Телевидение]
3 [Другое]
3 Рекламная ссылка
Чтобы разместить здесь ссылку, свяжитесь с веб-мастером.
Рассмотрим прямоугольный треугольник, изображенный на схеме.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон. Математически это записывается как a 2 + b 2 = c 2 Пример 1: Если прямоугольный треугольник имеет меньшие стороны длины 3 и 4. Какова длина гипотенузы?
Какова длина гипотенузы? Из теоремы Пифагора,
в 2 = а 2 + б 2 = 3 2 + 4 2 = (3 × 3) + (4 × 4) = 9 + 16 = 25
Если c 2 = 25, c = 5 .
Это знаменитый треугольник 3 : 4 : 5 , используемый при съемке и измерении. Таких треугольников много (например, 5 : 12 : 13 ). Вы можете проверить, что 5 : 12 : 13 является прямоугольным треугольником, выполнив приведенные выше вычисления.
Конечно, числа не обязательно должны быть целыми числами.
Пример 2. В прямоугольном треугольнике гипотенуза имеет длину 15,3, а другая его сторона равна 4,7. Найдите длину недостающей стороны. Из теоремы Пифагора,
а 2 = в 2 — б 2 = 15,3 2 — 4,7 2 = (15,3 х 15,3) — (4,7 х 4,7) = 234,09 — 22,09 = 212
Если а 2 = 212, а = 14,56 .
Площадь ( A ) прямоугольного треугольника находится по формуле A = ab/2 Пример 3: Найдите площадь прямоугольного треугольника с более короткими сторонами длиной 4,3 и 6,4 соответственно. Площадь указана по номеру
А = ab/2 = 4,3 × 6,4 / 2 = 13,76
Вернемся к схеме прямоугольного треугольника. Существуют три основные тригонометрические функции. Они называются Синус , Косинус и Тангенс .
Синус угла φ определяется как длина стороны, противоположной углу φ, деленная на гипотенузу. Это записывается как
Sin φ = а/с Косинус угла φ определяется как длина прилежащей стороны (прилежащей к углу φ), деленная на гипотенузу.
Это записывается как
Cos φ = b / c Тангенс угла φ определяется как длина противоположной стороны (противоположной углу φ), деленная на длину прилежащей стороны (прилежащей к углу φ). Это пишется как
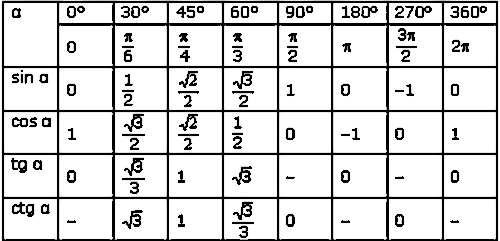
Тангенс φ = a / b В таблице ниже показаны некоторые значения этих функций для различных углов. Уголок Грех Кос Желто-коричневый 0 или 0,000 1.000 0,000 30 или 0,500 0,866 0,577 45 или 0,707 0,707 1.000 60 или 0,866 0,500 1. 732
732 90 или 1.000 0,000 Бесконечный
Sin 0 o = COS 90 O = 0 SIN 30 O = COS 60 O = 0,500 SIN 45 7 = COS SIN 45 6 = COS SIN 45 6 = COS . Sin 60 o = Cos 30 o = 0.866 = (√3) / 2 Sin 90 o = Cos 0 o = 1 Между 0 o и 90 o : Увеличение синусов от 0 до 1,
Косинусы уменьшаются от 1 до 0,
Тангенсы увеличиваются от 0 до бесконечности. Окончательно, Cos(90 — X) = Sin(X)
Sin(90 — X) = Cos(X) Значения тригонометрических функций (за исключением 0 o , 30 o , 45 o , 60 o , 90 o ) не являются целыми числами, дробями или сурдами. Они трансцендентны.
Они трансцендентны.
Три тригонометрические функции взаимосвязаны. Sin φ / Cos φ
= Тан φ Sin 2 φ + Cos 2 φ = 1 Примечание. Квадрат синуса угла, скажем, (Sin φ) 2 чаще записывается как Sin 2 φ. Эта форма применима ко всем тригонометрическим функциям.
Пример 4. Докажите, что Sin φ / Cos φ = Tan φ Используя определения тригонометрических функций
Sin φ / Cos φ
= (a/c)/(b/c) = (a/c) × (c/b) = a/b = Tan φ
Пример 5: Докажите, что Sin 2 φ + Cos 2 φ = 1 Используя определения тригонометрических функций
Sin 2 φ + Cos 2 φ
= (а / в) 2 + (б / в) 2 = (а 2 / в 2 ) + (в 2 / б 2 ) = (а 2 Ь 7 2 ) / с 2 .
Но а 2 + b 2 = c 2 (из теоремы Пифагора)
Следовательно, (а 2 + b 2 ) / с 2 = с 2 / с 2 = 1 .
Значения тригонометрических функций для определенного угла можно найти в таблицах или на калькуляторе, как и в случае с логарифмами. Мы будем использовать их сейчас в некоторых примерах.
Пример 6. Найдите длины сторон a и c в следующем прямоугольном треугольнике. Используя определение касательных и перестановку, мы имеем
a = b × Tan φ = 12,6 × Tan 51 o = 12,6 × 1,235
С помощью калькулятора или таблиц находим, что Тан 51 o = 1,235 (с точностью до трех знаков после запятой).
12,6 × 1,235 = 15,56 м .
Значение c можно найти с помощью теоремы Пифагора. Здесь мы будем использовать определение косинусов и переставлять. Это дает
Здесь мы будем использовать определение косинусов и переставлять. Это дает
c = b / Cos φ = 12,6 / Cos 51 o = 12,6 / 0,629 = 20,03м.
Пример 7. Найдите угол φ в следующем прямоугольном треугольнике. Используя определение касательных
Tan φ = a / b = 9,6 / 7,4 = 1,297.
Используя таблицы или калькулятор, φ = 52,37 o .
До сих пор мы рассматривали прямоугольные треугольники. В общем, треугольники могут иметь любые углы. Рассмотрим треугольник ниже. Сумма трех углов всегда равна 180 90 586 o 90 587 .
А + В + С = 180 o Площадь этого треугольника определяется одной из следующих трех формул Площадь = (a × b × Sin C) / 2 = (a × c × Sin B) / 2 = (b × c × Sin A) / 2 = b × ч / 2
Связь между тремя сторонами общего треугольника определяется правилом косинуса . Существует три формы этого правила. Все эквивалентны.
Существует три формы этого правила. Все эквивалентны. a 2 = b 2 + c 2 — (2 × b × c × Cos A) б 2 = а 2 + с 2 — (2 × а × с × Cos B)
с 2 = a 2 + b 2 — (2 × a × b × Cos C)
Пример 8. Покажите, что теорема Пифагора является частным случаем правила косинусов. В первой версии правила косинусов, если угол A прямой, Cos 90 o = 0 . Тогда уравнение сводится к теореме Пифагора.
a 2 = b 2 + c 2 — (2 × b × c × Cos 90 o ) = b 2 + с 2 — 0 = б 2 + с 2
Отношение между сторонами и углами общего треугольника определяется Правилом синусов .
а / Sin A = b / Sin B = c / Sin C Пример 9: Найдите недостающую длину и недостающие углы в следующем треугольнике.
По правилу косинусов,
а 2 = b 2 + c 2 — (2 × b × c × Cos A) а 2 = 6,3 2 + 4,6 2 — (2 × 6,3 × 4,6 × Cos 32 o )
а 2 = 39,69 + 21,16 — (2 × 6,3 × 4,6 × 0,848)
а 2 = 60,85 — 49,15 = 11,7
а = 3,42 м
Теперь из правила синусов
а / Sin A = c / Sin C
Это можно изменить на
Sin C = (c × Sin A) / a
Подставляя различные значения, мы получаем
. Sin C = (c × Sin A) / a = (4,6 × Sin 32 o ) / 3,42
= (4,6 × 0,530) / 3,42 = 0,713
Поэтому
С = 45,5 о
Окончательный угол можно найти из
А + В + С = 180 или
Перестановка,
В = 180 — А — С = 180 — 32 — 45,5 В = 102,5 o
Используя уравнения, описанные в этом эссе, можно узнать все о треугольнике, используя всего несколько заданных битов информации. В приведенном выше примере мы вычислили, что a = 3,42 м, B = 102,5 o ,
С = 45,5 o .
В приведенном выше примере мы вычислили, что a = 3,42 м, B = 102,5 o ,
С = 45,5 o .
Помимо трех уже определенных тригонометрических функций, есть еще три, которые являются их обратными. Секанс угла φ определяется как величина, обратная косинусу. Это записывается как
Sec φ = 1 / Cos φ Косеканс угла φ определяется как величина, обратная синусу. Это записывается как
Csc φ = 1 / Sin φ Котангенс угла φ определяется как величина, обратная тангенсу. Это пишется как
Детская кроватка φ = 1 / Тан φ Эти функции приведены здесь для полноты.
Прежде чем мы рассмотрим ряды для тригонометрических функций, я хочу поговорить об углах. Система градусов , используемая для обычных угловых измерений, восходит к вавилонским временам. Полный круг равен 360 o ; половина круга 180 o ; а прямой угол равен 90 o . Эти числа были использованы, потому что они содержат много факторов и просты в использовании. Градусы — это искусственные единицы.
Полный круг равен 360 o ; половина круга 180 o ; а прямой угол равен 90 o . Эти числа были использованы, потому что они содержат много факторов и просты в использовании. Градусы — это искусственные единицы.
При математическом рассмотрении тригонометрических функций нам требуется более фундаментальная единица измерения угла. Это Радиан .
Радиан определяется так, что полная окружность равна 2π радианам.
Полуокружность равна π радианам, а прямой угол равен π/2 радианам. 1 Радиан = 57,3 o 1 o = 0,0175 радиан
Радиан градусов Грех Кос Желтовато-коричневый 0 0 0 1 0 π/2 90 1 0 Бесконечный π 180 0 -1 0 3π/2 270 -1 0 Бесконечный 2π 360 0 1 0
Существует ряд для оценки как синуса, так и косинуса. Эти ряды работают, только если угол φ в радианах. Обе серии действительны для всех значений φ .
Эти ряды работают, только если угол φ в радианах. Обе серии действительны для всех значений φ . Преобразование угла в радианы:
45 o = π/4 радиана
поэтому
Грех 45 o = Грех π/4 =
π/4 — ((π/4) 3 )/3! +
((π/4) 5 )/5! — …. = 0,785 — 0,081 + 0,002 — … = 0,706
(до трех знаков после запятой).
Правильное значение, конечно, 0,707.
Посмотрите еще раз на две предыдущие серии. Теперь сравните их с экспоненциальной серией ниже. я .
я . Отношения:
Эти уравнения можно объединить и записать в альтернативном формате, который называется Формула Эйлера :
e iφ = Cos φ + i × Sin φ Мы начали с прямоугольных треугольников и закончили очень абстрактными уравнениями. Разве математика не забавна? Пример 11: Каково значение e iπ ? Используя формулу Эйлера и помня, что Sin π = 0 и Cos π = -1 (см. таблицу выше):
e iπ = Cos π + (i × Sin π) = -1 + (i × 0) = -1
Эти числа обсуждаются далее в эссе «Введение в числа».
© 2000, 2009 КрысТал
Знакомство с различными типами чисел: действительными, мнимыми, рациональными, иррациональными, трансцендентными.
Введение в алгебру и как решать простые, одновременные и квадратные уравнения.
 4.5, RI.5.5, RI.5.6, RI.6.5
4.5, RI.5.5, RI.5.6, RI.6.5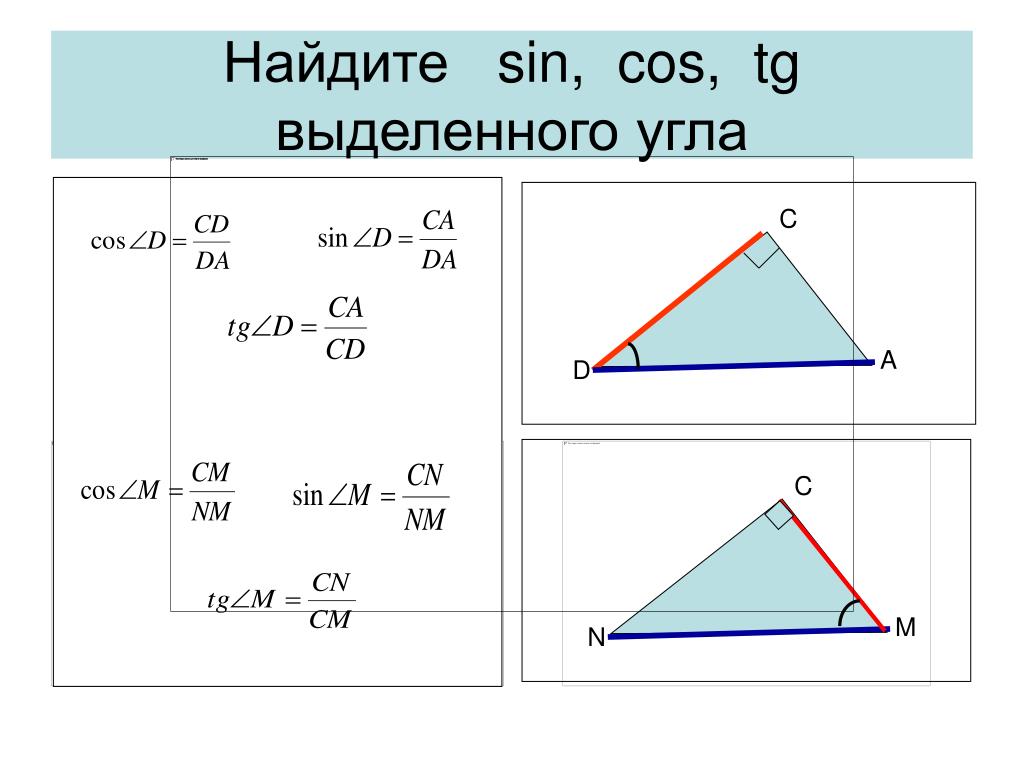 **ОБНОВЛЕНО: 17.02.22** Заглавные буквы добавлено в All You Need is Sleep и Third is the Word. Ознакомьтесь с предварительным просмотром, чтобы увидеть, что именно вы получите!W
**ОБНОВЛЕНО: 17.02.22** Заглавные буквы добавлено в All You Need is Sleep и Third is the Word. Ознакомьтесь с предварительным просмотром, чтобы увидеть, что именно вы получите!W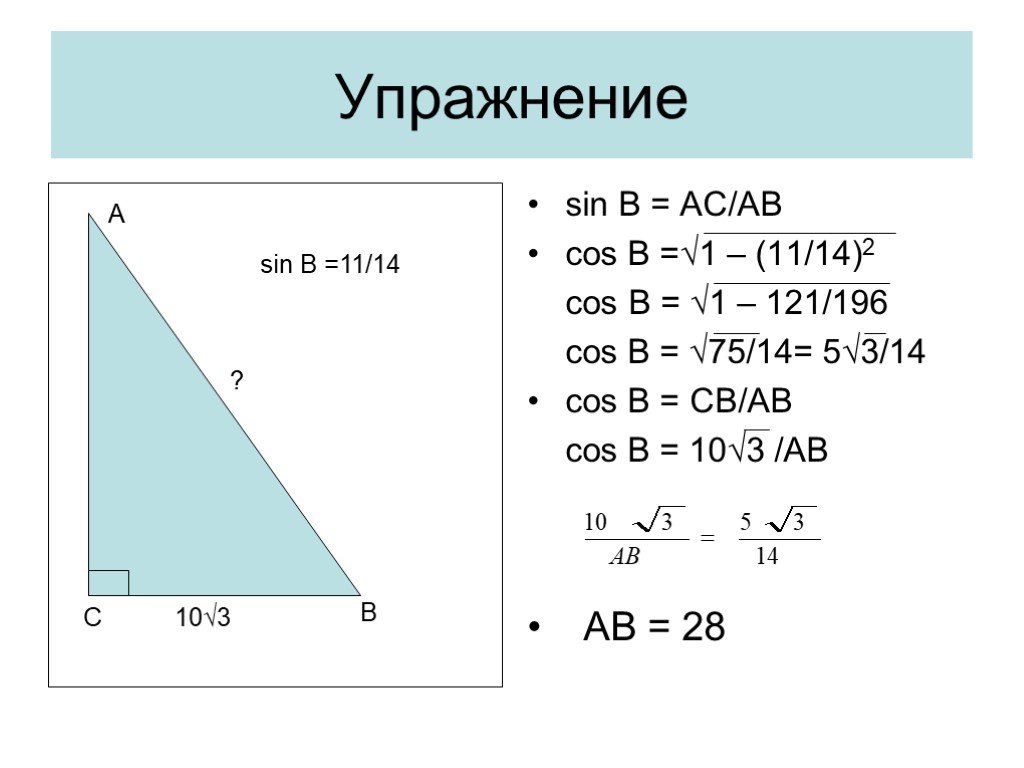 Что включено в комплект Spiral Math Review Sheets:►Краткий обзор►40 Weeks of Spiral M
Что включено в комплект Spiral Math Review Sheets:►Краткий обзор►40 Weeks of Spiral M ✏️Если вы ищете страницы для практики скорописи, не ищите дальше. Этот пакет содержит более 120 страниц, полных веселых и увлекательных заданий, которые помогут вашим ученикам красиво печатать курсивом! Его используют более 12 000 учителей по всему миру, и он будет
✏️Если вы ищете страницы для практики скорописи, не ищите дальше. Этот пакет содержит более 120 страниц, полных веселых и увлекательных заданий, которые помогут вашим ученикам красиво печатать курсивом! Его используют более 12 000 учителей по всему миру, и он будет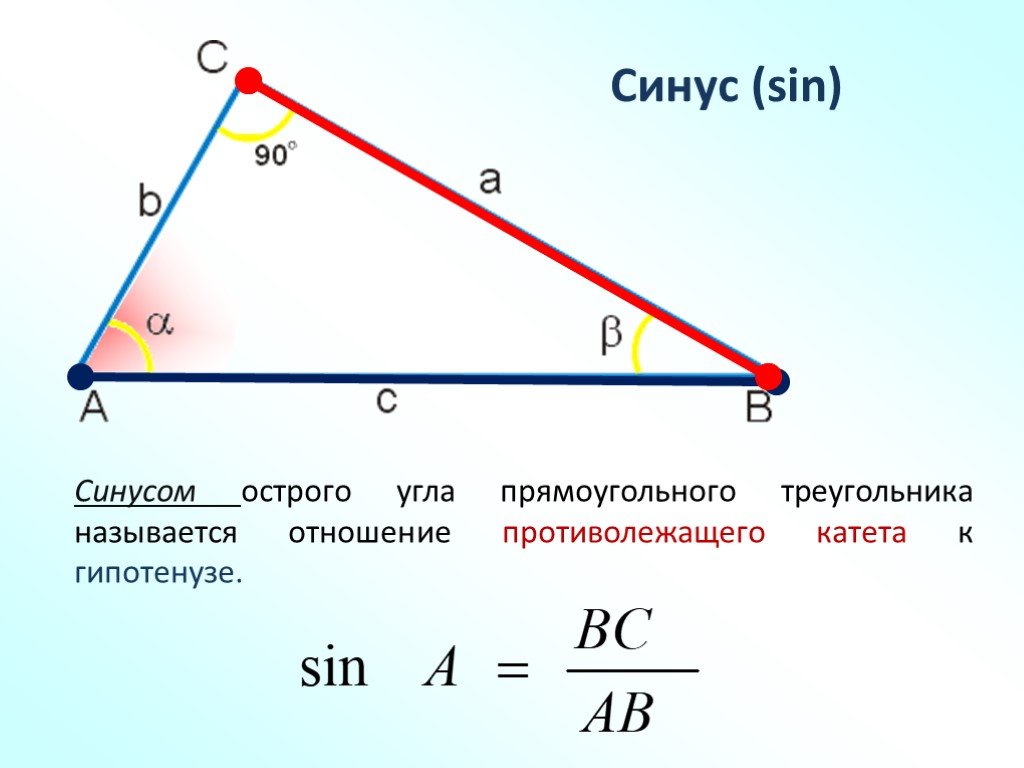 Здесь есть все, что вам нужно, чтобы помочь вашим ученикам по-настоящему понять, как создавать
Здесь есть все, что вам нужно, чтобы помочь вашим ученикам по-настоящему понять, как создавать Стратегия (вместе с начальными предложениями для студентов, чтобы обеспечить дополнительную поддержку). Рядом с фотографией есть четыре вопроса, которые требуют от ваших учеников
Стратегия (вместе с начальными предложениями для студентов, чтобы обеспечить дополнительную поддержку). Рядом с фотографией есть четыре вопроса, которые требуют от ваших учеников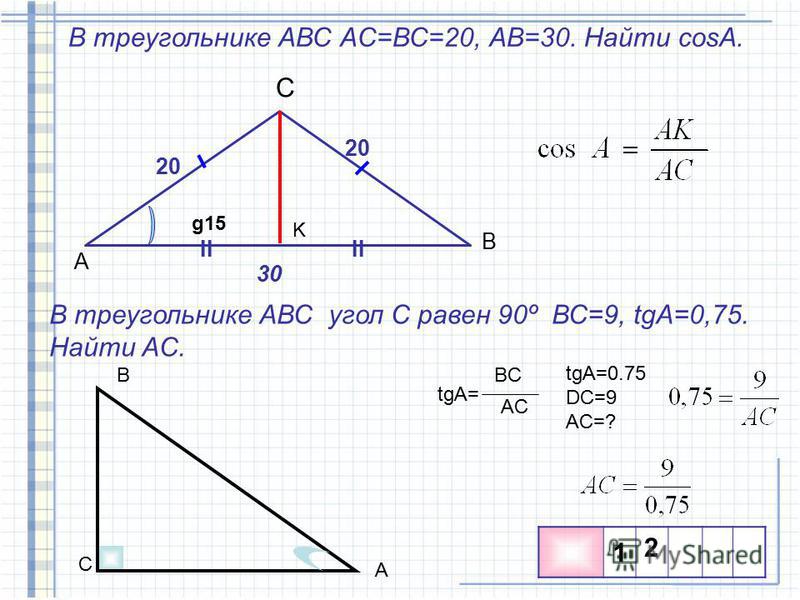 0003
0003 час⭐️ Время с шагом в десять минут⭐️ Время с шагом в пять минут⭐️ Время с шагом в 1 минутуЛУЧШЕЕ в этом пакете то, что НЕТ ПОДГОТОВКИ! БЕЗ ламинирования, БЕЗ дорогостоящих цветных чернил, БЕЗ резки… просто ПЕЧАТАЙТЕ и УЧИТЕСЬ!
час⭐️ Время с шагом в десять минут⭐️ Время с шагом в пять минут⭐️ Время с шагом в 1 минутуЛУЧШЕЕ в этом пакете то, что НЕТ ПОДГОТОВКИ! БЕЗ ламинирования, БЕЗ дорогостоящих цветных чернил, БЕЗ резки… просто ПЕЧАТАЙТЕ и УЧИТЕСЬ! [Домашняя страница] [Введение в числа] [Отзывы читателей (математика)] [Язык] |


| Уголок | Грех | Кос | Желто-коричневый |
|---|---|---|---|
| 0 или | 0,000 | 1.000 | 0,000 |
| 30 или | 0,500 | 0,866 | 0,577 |
| 45 или | 0,707 | 0,707 | 1.000 |
| 60 или | 0,866 | 0,500 | 1. 732 732 |
| 90 или | 1.000 | 0,000 | Бесконечный |
Косинусы уменьшаются от 1 до 0,
Тангенсы увеличиваются от 0 до бесконечности.
Sin(90 — X) = Cos(X)
 Здесь мы будем использовать определение косинусов и переставлять. Это дает
Здесь мы будем использовать определение косинусов и переставлять. Это дает= b × ч / 2
б 2 = а 2 + с 2 — (2 × а × с × Cos B)
с 2 = a 2 + b 2 — (2 × a × b × Cos C)
а 2 = 6,3 2 + 4,6 2 — (2 × 6,3 × 4,6 × Cos 32 o )
а 2 = 39,69 + 21,16 — (2 × 6,3 × 4,6 × 0,848)
а 2 = 60,85 — 49,15 = 11,7
а = 3,42 м
Теперь из правила синусовВ = 102,5 o
 В приведенном выше примере мы вычислили, что a = 3,42 м, B = 102,5 o ,
С = 45,5 o .
В приведенном выше примере мы вычислили, что a = 3,42 м, B = 102,5 o ,
С = 45,5 o . Полный круг равен 360 o ; половина круга 180 o ; а прямой угол равен 90 o . Эти числа были использованы, потому что они содержат много факторов и просты в использовании. Градусы — это искусственные единицы.
Полный круг равен 360 o ; половина круга 180 o ; а прямой угол равен 90 o . Эти числа были использованы, потому что они содержат много факторов и просты в использовании. Градусы — это искусственные единицы.Полуокружность равна π радианам, а прямой угол равен π/2 радианам.
1 o = 0,0175 радиан
| Радиан | градусов | Грех | Кос | Желтовато-коричневый |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| π/2 | 90 | 1 | 0 | Бесконечный |
| π | 180 | 0 | -1 | 0 |
| 3π/2 | 270 | -1 | 0 | Бесконечный |
| 2π | 360 | 0 | 1 | 0 |
= 0,785 — 0,081 + 0,002 — … = 0,706
(до трех знаков после запятой).
 1004 CCSS3: SL.1.6, L.K.1f, L.1.1c, L.1.2b
1004 CCSS3: SL.1.6, L.K.1f, L.1.1c, L.1.2b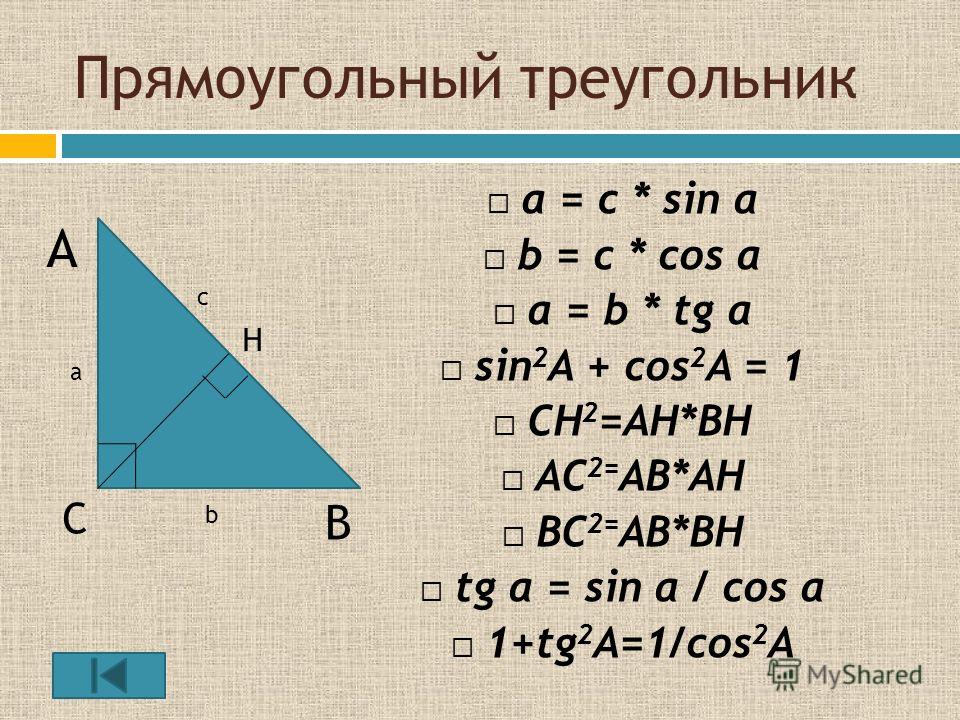
 Какова длина гипотенузы?
Какова длина гипотенузы? 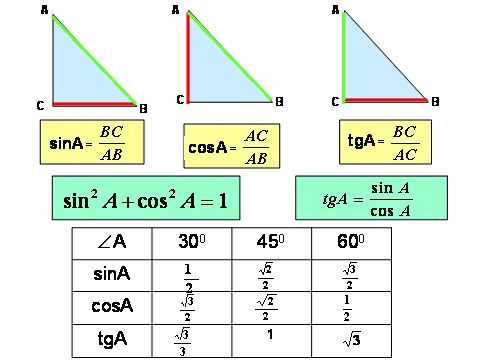 Они трансцендентны.
Они трансцендентны.