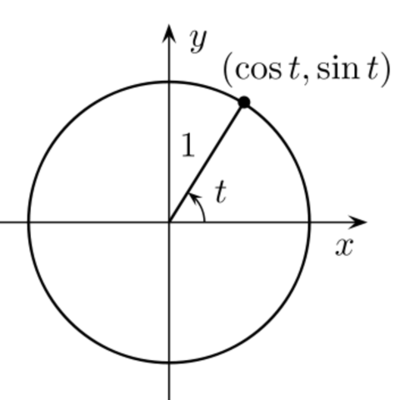
2+n-72)=1/(n+9)
2+n-72)=1/(n+9)Периодичность функций y=sin t, y=cos t 10 класс онлайн-подготовка на Ростелеком Лицей
Тема урока, введение
Периодичность функций, наличие периода – специфика тригонометрических функций. Какова причина его появления?
Причины возникновения периода
Во-первых, это определение синуса, косинуса, тангенса и котангенса.
Во-вторых, – специфика отображения аргумента на числовой оси или числовой окружности.
Рассмотрим подробнее. Пусть аргумент откладывается на координатной прямой. Вспомним, что необходимо сделать, чтобы из обычной прямой получить координатную.
1. Отметить начальную точку.
2. Задать положительное направление.
3. Определить масштаб.
На координатной прямой существует взаимно-однозначное соответствие между точкой и действительным числом. Каждому действительному числу соответствует своя точка на прямой и наоборот, каждой точке прямой соответствует одно действительное число (рис. 1).
1).
На числовой окружности числу соответствует единственная точка M. Но длина окружности радиуса 1 равна Число тоже попадет в точку M. Точка M соответствует бесчисленному множеству чисел вида .
У точки M единственная пара координат, т.е. единственные значения синуса и косинуса (рис. 2).
Еще раз посмотрим, какое существует взаимоотношение между числовой прямой и числовой окружностью. Представим себе, что бесконечная тонкая нить наматывается на тонкий обод радиуса 1. Тогда все точки попадут в одну точку окружности. В этом и причина периодичности.
Определение периодичной функции, наименьший положительный период функций y=sint, y=cost
Дадим строгое определение периодичности.
Определение: Функцию называют периодической, если существует такое отличное от нуля число T, что для любого t выполняется равенство
Число T называется периодом функции
Функции имеют много различных периодов.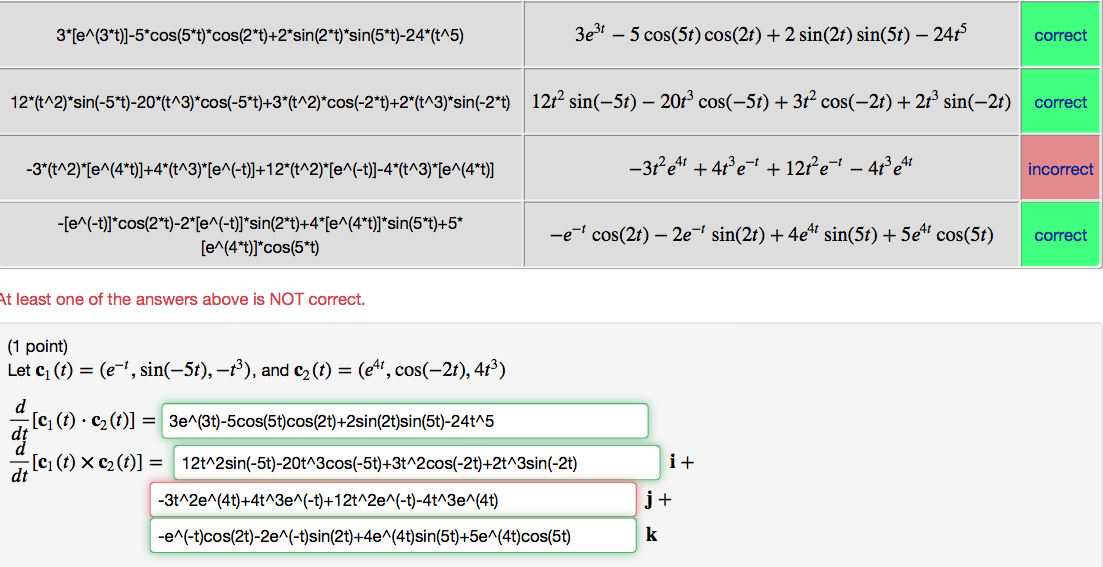 Докажем, что наименьший положительный период.
Докажем, что наименьший положительный период.
Доказательство:
Число является периодом функций
Осталось доказать, что меньшего положительного периода не существует.
Пусть T – произвольный период. Тогда для всех в частности для
(рис. 3).
Наименьшим положительным периодом вида является .
Особенности исследования периодических функций y=sint, y=cost
Заменим аргумент t на x и обсудим исследование периодических функций и
Так как наименьший положительный период, то необходимо сделать следующее:
1) Построить график и исследовать функцию на любом отрезке длиной
2) Продолжить график и сформулировать свойства на всей области определения,
При этом необходимо учесть нечетность функции и четность функции
В соответствии с изложенной схемой рассмотрим функции и
Функция – периодическая, период В силу нечетности достаточно исследовать её на участке и симметрично отобразить график относительно начала координат (рис. 4).
4).
Рассмотрим функцию Учтём, что она четная, график симметричен относительно оси y.
Мы можем построить график на участке и симметрично отобразить относительно оси y (рис. 5).
Наличие периода позволяет решать многочисленные задачи.
Решение задач
Задача 1. Вычислить
a)
b)
Решение:
a)
Ответ: 1.
b)
Ответ:
Задача 2. Доказать тождество
Доказательство:
верно для любого x.
Тождество доказано.
Задача 3. Решить уравнение
Решение:
Рис. 7.
На рисунке видно, что значению косинуса соответствуют углы
Ответ:
Вывод, заключение
Мы выяснили причины периодичности тригонометрических функций, установили, что синус и косинус имеют много периодов – все числа вида наименьший положительный период для функций
Наличие периода мы использовали для исследования функций и решения типовых задач.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
№№ 16.15, 16.18.
Дополнительные веб-ресурсы
1. Математика (Источник).
2. Интернет-портал Problems.ru (Источник).
3. Образовательный портал для подготовки к экзаменам (Источник).
Lorem Ipsum — All the facts
Հայերեն Shqip العربية Български Català 中文简体 Hrvatski Česky Dansk Nederlands English Eesti Filipino Suomi Français ქართული Deutsch Ελληνικά עברית हिन्दी Magyar Indonesia Italiano Latviski Lietuviškai македонски Melayu Norsk Polski Português Româna Pyccкий Српски Slovenčina Slovenščina Español Svenska ไทย Türkçe Українська Tiếng Việt
What is Lorem Ipsum?
Lorem Ipsum is simply dummy text of the printing and typesetting industry.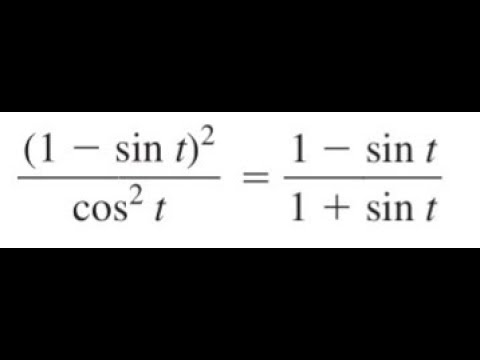 Lorem Ipsum has been the industry’s standard dummy text ever since the 1500s, when an unknown printer took a galley of type and scrambled it to make a type specimen book. It has survived not only five centuries, but also the leap into electronic typesetting, remaining essentially unchanged. It was popularised in the 1960s with the release of Letraset sheets containing Lorem Ipsum passages, and more recently with desktop publishing software like Aldus PageMaker including versions of Lorem Ipsum.
Lorem Ipsum has been the industry’s standard dummy text ever since the 1500s, when an unknown printer took a galley of type and scrambled it to make a type specimen book. It has survived not only five centuries, but also the leap into electronic typesetting, remaining essentially unchanged. It was popularised in the 1960s with the release of Letraset sheets containing Lorem Ipsum passages, and more recently with desktop publishing software like Aldus PageMaker including versions of Lorem Ipsum.
Why do we use it?
It is a long established fact that a reader will be distracted by the readable content of a page when looking at its layout. The point of using Lorem Ipsum is that it has a more-or-less normal distribution of letters, as opposed to using ‘Content here, content here’, making it look like readable English. Many desktop publishing packages and web page editors now use Lorem Ipsum as their default model text, and a search for ‘lorem ipsum’ will uncover many web sites still in their infancy. Various versions have evolved over the years, sometimes by accident, sometimes on purpose (injected humour and the like).
Various versions have evolved over the years, sometimes by accident, sometimes on purpose (injected humour and the like).
Where does it come from?
Contrary to popular belief, Lorem Ipsum is not simply random text. It has roots in a piece of classical Latin literature from 45 BC, making it over 2000 years old. Richard McClintock, a Latin professor at Hampden-Sydney College in Virginia, looked up one of the more obscure Latin words, consectetur, from a Lorem Ipsum passage, and going through the cites of the word in classical literature, discovered the undoubtable source. Lorem Ipsum comes from sections 1.10.32 and 1.10.33 of «de Finibus Bonorum et Malorum» (The Extremes of Good and Evil) by Cicero, written in 45 BC. This book is a treatise on the theory of ethics, very popular during the Renaissance. The first line of Lorem Ipsum, «Lorem ipsum dolor sit amet..», comes from a line in section 1.10.32.
The standard chunk of Lorem Ipsum used since the 1500s is reproduced below for those interested. Sections 1.10.32 and 1.10.33 from «de Finibus Bonorum et Malorum» by Cicero are also reproduced in their exact original form, accompanied by English versions from the 1914 translation by H. Rackham.
Sections 1.10.32 and 1.10.33 from «de Finibus Bonorum et Malorum» by Cicero are also reproduced in their exact original form, accompanied by English versions from the 1914 translation by H. Rackham.
Where can I get some?
There are many variations of passages of Lorem Ipsum available, but the majority have suffered alteration in some form, by injected humour, or randomised words which don’t look even slightly believable. If you are going to use a passage of Lorem Ipsum, you need to be sure there isn’t anything embarrassing hidden in the middle of text. All the Lorem Ipsum generators on the Internet tend to repeat predefined chunks as necessary, making this the first true generator on the Internet. It uses a dictionary of over 200 Latin words, combined with a handful of model sentence structures, to generate Lorem Ipsum which looks reasonable. The generated Lorem Ipsum is therefore always free from repetition, injected humour, or non-characteristic words etc.
Translations: Can you help translate this site into a foreign language ? Please email us with details if you can help.
There is a set of mock banners available here in three colours and in a range of standard banner sizes:
Donate: If you use this site regularly and would like to help keep the site on the Internet, please consider donating a small sum to help pay for the hosting and bandwidth bill. There is no minimum donation, any sum is appreciated — click here to donate using PayPal. Thank you for your support.
Donate Bitcoin: 16UQLq1HZ3CNwhvgrarV6pMoA2CDjb4tyF
NodeJS Python Interface GTK Lipsum Rails .NET Groovy
The standard Lorem Ipsum passage, used since the 1500s
«Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.»
Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.»
Section 1.10.32 of «de Finibus Bonorum et Malorum», written by Cicero in 45 BC
«Sed ut perspiciatis unde omnis iste natus error sit voluptatem accusantium doloremque laudantium, totam rem aperiam, eaque ipsa quae ab illo inventore veritatis et quasi architecto beatae vitae dicta sunt explicabo. Nemo enim ipsam voluptatem quia voluptas sit aspernatur aut odit aut fugit, sed quia consequuntur magni dolores eos qui ratione voluptatem sequi nesciunt. Neque porro quisquam est, qui dolorem ipsum quia dolor sit amet, consectetur, adipisci velit, sed quia non numquam eius modi tempora incidunt ut labore et dolore magnam aliquam quaerat voluptatem. Ut enim ad minima veniam, quis nostrum exercitationem ullam corporis suscipit laboriosam, nisi ut aliquid ex ea commodi consequatur? Quis autem vel eum iure reprehenderit qui in ea voluptate velit esse quam nihil molestiae consequatur, vel illum qui dolorem eum fugiat quo voluptas nulla pariatur?»
1914 translation by H.
 Rackham
Rackham«But I must explain to you how all this mistaken idea of denouncing pleasure and praising pain was born and I will give you a complete account of the system, and expound the actual teachings of the great explorer of the truth, the master-builder of human happiness. No one rejects, dislikes, or avoids pleasure itself, because it is pleasure, but because those who do not know how to pursue pleasure rationally encounter consequences that are extremely painful. Nor again is there anyone who loves or pursues or desires to obtain pain of itself, because it is pain, but because occasionally circumstances occur in which toil and pain can procure him some great pleasure. To take a trivial example, which of us ever undertakes laborious physical exercise, except to obtain some advantage from it? But who has any right to find fault with a man who chooses to enjoy a pleasure that has no annoying consequences, or one who avoids a pain that produces no resultant pleasure?»
Section 1.
 10.33 of «de Finibus Bonorum et Malorum», written by Cicero in 45 BC
10.33 of «de Finibus Bonorum et Malorum», written by Cicero in 45 BC«At vero eos et accusamus et iusto odio dignissimos ducimus qui blanditiis praesentium voluptatum deleniti atque corrupti quos dolores et quas molestias excepturi sint occaecati cupiditate non provident, similique sunt in culpa qui officia deserunt mollitia animi, id est laborum et dolorum fuga. Et harum quidem rerum facilis est et expedita distinctio. Nam libero tempore, cum soluta nobis est eligendi optio cumque nihil impedit quo minus id quod maxime placeat facere possimus, omnis voluptas assumenda est, omnis dolor repellendus. Temporibus autem quibusdam et aut officiis debitis aut rerum necessitatibus saepe eveniet ut et voluptates repudiandae sint et molestiae non recusandae. Itaque earum rerum hic tenetur a sapiente delectus, ut aut reiciendis voluptatibus maiores alias consequatur aut perferendis doloribus asperiores repellat.»
1914 translation by H. Rackham
«On the other hand, we denounce with righteous indignation and dislike men who are so beguiled and demoralized by the charms of pleasure of the moment, so blinded by desire, that they cannot foresee the pain and trouble that are bound to ensue; and equal blame belongs to those who fail in their duty through weakness of will, which is the same as saying through shrinking from toil and pain. These cases are perfectly simple and easy to distinguish. In a free hour, when our power of choice is untrammelled and when nothing prevents our being able to do what we like best, every pleasure is to be welcomed and every pain avoided. But in certain circumstances and owing to the claims of duty or the obligations of business it will frequently occur that pleasures have to be repudiated and annoyances accepted. The wise man therefore always holds in these matters to this principle of selection: he rejects pleasures to secure other greater pleasures, or else he endures pains to avoid worse pains.»
These cases are perfectly simple and easy to distinguish. In a free hour, when our power of choice is untrammelled and when nothing prevents our being able to do what we like best, every pleasure is to be welcomed and every pain avoided. But in certain circumstances and owing to the claims of duty or the obligations of business it will frequently occur that pleasures have to be repudiated and annoyances accepted. The wise man therefore always holds in these matters to this principle of selection: he rejects pleasures to secure other greater pleasures, or else he endures pains to avoid worse pains.»
| 1 | Найти производную — d/dx | бревно натуральное х | ||
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | ||
| 3 | Найти производную — d/dx | 92)|||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | ||
| 22 | Найти производную — d/dx | грех(2x) | ||
| 23 | Найти производную — d/dx | 9(3x) по отношению к x|||
| 41 | Оценить интеграл | |||
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | ||
| 43 | Оценка интеграла 9бесконечность | |||
| 45 | Найти производную — d/dx | х/2 | ||
| 46 | Найти производную — d/dx | -cos(x) | ||
| 47 | Найти производную — d/dx | грех(3x) | 92+1||
| 68 | Оценить интеграл | интеграл от sin(x) по x | ||
| 69 | Найти производную — d/dx | угловой синус(х) | ||
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | ||
| 85 | Найти производную — d/dx | лог х | ||
| 86 | Найти производную — d/dx | арктан(х) | ||
| 87 | Найти производную — d/dx | бревно натуральное 5х93 | ||
| 6 | Решить для ? | cos(x)=1/2 | ||
| 7 | Найти x | sin(x)=-1/2 | ||
| 8 | Преобразование градусов в радианы | 225 | ||
| 9 | Решить для ? | cos(x)=(квадратный корень из 2)/2 | ||
| 10 | Найти x | cos(x)=(квадратный корень из 3)/2 | ||
| 11 | Найти x | sin(x)=(квадратный корень из 3)/2 | 92=9 | |
| 14 | Преобразование градусов в радианы | 120 градусов | ||
| 15 | Преобразование градусов в радианы | 180 | ||
| 16 | Найти точное значение | желтовато-коричневый(195) | 92-4||
| 38 | Найти точное значение | грех(255) | ||
| 39 | Оценить | лог база 27 из 36 | ||
| 40 | Преобразовать из радианов в градусы | 2 шт. | 92-3sin(x)+1=0||
| 43 | Найти x | |||
| 44 | Найти x | sin(2x)+cos(x)=0 | ||
| 45 | Упростить | (1-cos(x))(1+cos(x)) | 92=25||
| 59 | График | f(x)=- натуральный логарифм x-1+3 | ||
| 60 | Найдите значение с помощью единичного круга | угловой синус(-1/2) | ||
| 61 | Найти домен | квадратный корень из 36-4x^2 92=0 | ||
| 66 | Найти x | cos(2x)=(квадратный корень из 2)/2 | ||
| 67 | График | у=3 | ||
| 68 | График | f(x)=- логарифмическая база 3 x-1+3 | 92 | |
| 71 | Найти x | квадратный корень из x+4+ квадратный корень из x-1=5 | ||
| 72 | Решить для ? | cos(2x)=-1/2 | ||
| 73 | Найти x | логарифмическая база x из 16=4 | 9х||
| 75 | Упростить | (cos(x))/(1-sin(x))+(1-sin(x))/(cos(x)) | ||
| 76 | Упростить | сек(х)sin(х) | ||
| 77 | Упростить | кубический корень из 24 кубический корень из 18 | 92=0||
| 96 | Найти x | 3x+2=(5x-11)/(8г) | ||
| 97 | Решить для ? | sin(2x)=-1/2 | ||
| 98 | Найти x | (2x-1)/(x+2)=4/5 | 92+n-72)=1/(n+9) |
геометрия — Как доказать, что если $\cos(t) = \cos(t’)$ и $\sin(t) = \sin(t’)$, то $t = t’ + 2k\pi $?
Спросил
Изменено 6 лет, 3 месяца назад
Просмотрено 456 раз
$\begingroup$
Как доказать, что если $\cos(t) = \cos(t’)$ и $\sin(t) = \sin(t’)$, то $t = t’ + 2k\pi$ ?
г.
Я пытался доказать приведенное выше утверждение, которое я считаю верным.
Я знаю, что $\sin(t)$ инъективен на $[-\pi/2; \pi/2]$ и $\cos(t)$ инъективен на $[0; \pi]$, но до сих пор я не мог использовать это для строгого доказательства утверждения.
- геометрия
$\endgroup$
2
$\begingroup$
также можно $$\cos{x}-\cos{y}=0\Longrightarrow 2\sin{\dfrac{xy}{2}}\sin{\dfrac{x+y}{2}}=0\tag{1 }$$ $$\sin{x}-\sin{y}=0\Longrightarrow 2\sin{\dfrac{xy}{2}}\cos{\dfrac{x+y}{2}}=0\tag{2 }$$ с $(1),(2)$ должен $$\sin{\dfrac{xy}{2}}=0$$ так как мы знаем $$\sin{(k\pi)}=0,k\in Z$$ так $$\dfrac{x-y}{2}=k\pi,\Longrightarrow x=y+2k\pi,k\in Z$$ 9\prime + 2k\pi$ они следуют из $\cos$ — четной функции, а $\sin$ — нечетной функции, и обе являются $2\pi$-периодическими. это все, что вам нужно.
$\endgroup$
$\begingroup$
Если вы хотите сделать это строго, вы можете использовать тот факт, что $\sin$ и $\cos$ ортонормированы в пространстве внутреннего произведения. См.: http://www.jimworthey.com/orthoquestions.html
См.: http://www.jimworthey.com/orthoquestions.html
$\endgroup$
$\begingroup$
Точка $P_t=(\cos t,\sin t)$ — это точка пересечения луча под углом $t$ с единичной окружностью. В ваших утверждениях говорится, что $P_t=P_{t’}$. Это означает, что два луча совпадают, поэтому их углы должны отличаться на величину, кратную полному обороту. То есть $t-t’=2k\pi$ для некоторого целого числа $k$.
$\endgroup$
$\begingroup$
я не знаю, поможет ли это, но.
имеем это для $k\in\mathbb{Z}$ $$\begin{выравнивание} \sin t=\sin t’&\iff t’=2k\pi+\pi-t\vee t’=2k\pi+t\\ \cos t=\cos t’&\iff t’=2k\pi-t\vee t’=2k\pi+t \end{выравнивание}$$ тогда, чтобы иметь $\sin t=\sin t’$ и $\cos t=\cos t’$ одновременно, вы получаете $t’=2k\pi+t$, потому что
, если $t’=2k\pi+ \pi-t$ у вас есть $\sin t’=\sin(2k\pi+\pi-t)=\sin(\pi-t)=\sin t$ но $\cos t’=\cos(2k\ pi+\pi-t)=\cos(\pi-t)=-\cos t$
если $t’=2k\pi-t$ у вас есть $\cos t’=\cos(2k\pi-t)=\cos(-t)=\cos t$ но $\sin t’=\ sin(2k\pi-t)=\sin(-t)=-\sin t$
$\endgroup$
$\begingroup$
Cos(x) и sin(x) являются периодическими функциями периода 2k(pi). Следовательно, sin(x)=sin(x’) и cos(x)=cos(x’).
Следовательно, sin(x)=sin(x’) и cos(x)=cos(x’).
$\endgroup$
2
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
г. Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
1.2: Функции косинуса и синуса
- Последнее обновление
- Сохранить как PDF г.
- Идентификатор страницы
- 7098
- Тед Сандстром и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @Grand Valley State University
- Если действительное число \(t\) представляет (со знаком) длину дуги, как мы определяем \(\cos(t)\) и \(\sin(t)\)?
- В каких квадрантах (конечной точки дуги t на единичной окружности) \(\cos(t)\) положительно (отрицательно)? В каких квадрантах (конечной точки дуги \(t\) на единичной окружности) \(\sin(t)\) положительна (отрицательна)?
- Что такое пифагорейская идентичность? Как это тождество выводится из уравнения для единичного круга? г.
- Что такое единичный круг? Что такое уравнение единичной окружности?
- Просмотрите упражнение 1.4 на стр. 9.
- Просмотрите завершенную версию рис. 1.4, которая содержится в ответах к упражнению 1.2 на стр. 6.
- Какова конечная точка дуги на единичной окружности, соответствующей интервалу \([0, \dfrac{\pi}{2}]\)?
- Какова конечная точка дуги на единичной окружности, соответствующей интервалу \([0, \pi]\)? г.
- Какова конечная точка дуги на единичной окружности, соответствующей интервалу \([0, \dfrac{3\pi}{2}]\)?
- Какова конечная точка дуги на единичной окружности, соответствующей интервалу \([0, -\dfrac{\pi}{2}]\)?

- \(\cos(\dfrac{\pi}{2})\) и \(\sin( \dfrac{\pi}{2})\).
- \(\cos(\dfrac{3\pi}{2})\) и \(\sin(\dfrac{3\pi}{2})\).
- \(\cos(0)\) и \(sin(0)\).
- \(\cos(-\dfrac{\pi}{2})\) и \(\sin(-\dfrac{\pi}{2})\).
- \(\cos(2\pi)\) и \(\sin(2\pi)\).
- \(cos(-\pi)\) и \(\sin(-\pi)\).
- Ответить
- \[\cos(\dfrac{\pi}{2}) = 0\] \[\sin(\dfrac{\pi}{2}) = 1\]
- \[\cos(\dfrac{3\pi}{2}) = 0\] \[\sin(\dfrac{3\pi}{2}) = -1\]
- \[\cos(0) = 1\] \[\sin(0) = 1\]
- \[\cos(-\dfrac{\pi}{2}) = 0\] \[\sin(-\dfrac{\pi}{2}) = -1\]
- \[\cos(2\pi) = 0\] \[\sin(2\pi) = 1\]
- \[\cos(-\pi) = -1\] \[\sin(-\pi) = 0\]
- \(\cos(1)\) и \(\sin(1)\)
- \(\cos(2)\) и \(\sin(2)\)
- \(\cos(-4)\) и \(\sin(-4)\)
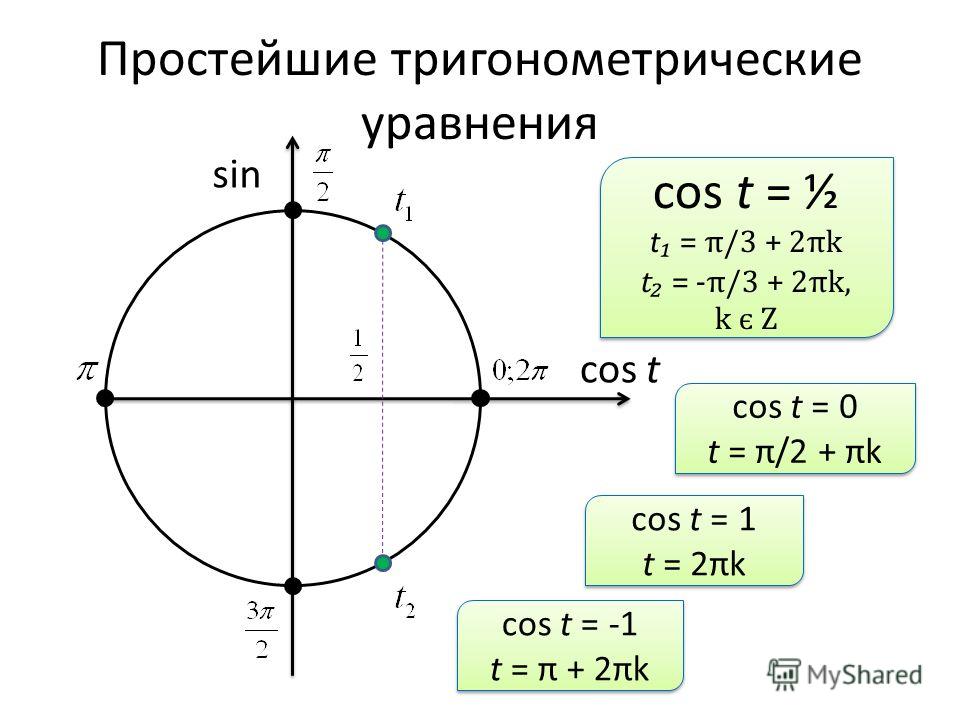
- \(\cos(5.
 5)\) и \(\sin(5.5)\)
5)\) и \(\sin(5.5)\) - \(\cos(15)\) и \(\sin(15)\)
- \(\cos(-15)\) и \(\sin(-15)\)
- Ответить
- \[\cos(1) \приблизительно 0,5403, \sin(1) \приблизительно 0,8415\]
- \[\cos(2) \приблизительно -0,4161, \sin(2) \приблизительно 0,9093\] г.
- \[\cos(-4) \приблизительно -0,6536, \sin(-4) \приблизительно 0,7568\]
- \[\cos(5.5) \приблизительно 0,7807, \sin(5.5) \приблизительно -0,7055\]
- \[\cos(15) \приблизительно -0,7597, \sin(15) \приблизительно 0,6503\]
- \[\cos(-15) \приблизительно -0,7597, \sin(-15) \приблизительно 0,6503\]
- Какова область определения функции косинуса? Почему?
- Какова область определения синуса? Почему?
- Какова наибольшая координата \(x\), которую может иметь точка на единичной окружности? Какова наименьшая координата \(x\), которую может иметь точка на единичной окружности? Что это говорит нам о диапазоне функции косинуса? Почему? г.
- Какова наибольшая координата \(y\), которую может иметь точка на единичной окружности? Какова наименьшая координата \(y\), которую может иметь точка на единичной окружности? Что это говорит нам о диапазоне функции синуса? Почему?
- Ответить
- Поскольку мы можем обернуть любое число на единичную окружность, мы всегда можем найти конечную точку дуги, соответствующую любому числу.
 Таким образом, косинус любого действительного числа определен, а область определения функции косинуса — это набор всех действительных чисел. г.
Таким образом, косинус любого действительного числа определен, а область определения функции косинуса — это набор всех действительных чисел. г. - По той же причине, что и для функции косинуса, областью определения функции синуса является множество всех действительных чисел.
- На единичном круге наибольшая координата x, которую может иметь точка, равна 1, а наименьшая координата x, которую может иметь точка, равна 1. Поскольку выход функции косинуса представляет собой координату x точки на единичном круге, диапазон функции косинуса — это закрытый интервал \([-1, 1]\). Это означает \(-1 \leq \cos(t) \leq 1\) для любого действительного числа \(t\). г.
- На единичном круге наибольшая координата y, которую может иметь точка, равна 1, а наименьшая координата y, которую может иметь точка, равна 1. Поскольку выходным сигналом функции синуса является y-координата точки на единичном круге, диапазон функции синуса — это замкнутый интервал \([-1, 1]\).
 Это означает \(-1 \leq \sin(t) \leq 1\) для любого действительного числа \(t\).
Это означает \(-1 \leq \sin(t) \leq 1\) для любого действительного числа \(t\).
- Поскольку мы можем обернуть любое число на единичную окружность, мы всегда можем найти конечную точку дуги, соответствующую любому числу.
- Если \( \dfrac{\pi}{2} < t < \pi\), то каковы знаки \(\cos(t)\) и \(\sin(t)\)?
- Если \( \pi < t < \dfrac{3\pi}{2}\), то какие знаки у \(\cos(t)\) и \(\sin(t)\)?
- Если \( \dfrac{3\pi}{2} < t < 2\pi\), то какие знаки у \(\cos(t)\) и \(\sin(t)\)?
- Если \( \dfrac{5\pi}{2} < t < 3\pi\), то какие знаки у \(\cos(t)\) и \(\sin(t)\)? г.
- Для каких значений \(t\) (между \(0\) и \(2\pi\)) является положительным значением \(\cos(t)\)? Почему?
- Для каких значений \(t\) (между \(0\) и \(2\pi\)) является положительным значением \(\sin(t)\)? Почему?
- Для каких значений \(t\) (между \(0\) и \(2\pi\)) является отрицательным значением \(\cos(t)\)? Почему?
- Для каких значений \(t\) (между \(0\) и \(2\pi\)) является отрицательным значением \(\sin(t)\)? Почему?
- Ответить
- Если \(\dfrac{\pi}{2} < t < \pi\), то конечная точка дуги \(t\) находится во втором квадранте, поэтому \(\cos(t) < 0 \) и \(\sin(t) > 0\).
 г.
г. - Если \(\pi < t < \dfrac{3\pi}{2}\), то конечная точка дуги t находится в третьем квадранте, поэтому \(\cos(t) < 0\) и \ (\sin(t) < 0\).
- Если \(\dfrac{3\pi}{2} < t < 2\pi\), то конечная точка дуги t находится в четвертом квадранте, поэтому \(\cos(t) > 0\) и \(\sin(t) < 0\).
- Если \(\dfrac{5\pi}{2} < t < 3\pi\), то конечная точка дуги t находится во втором квадранте, поэтому \(\cos(t) > 0\) и \(\sin(t) > 0\). г.
- Обратите внимание, что \(\cos(t) = 0\) при \(t = \dfrac{\pi}{2}\) и \(t = \dfrac{3\pi}{2}\). Поскольку \(\cos(t)\) является координатой x конечной точки дуги \(t\), предыдущий ответ показывает, что \(\cos(t)\) положительно, когда \(t\) находится в одном из интервалов \([0, \dfrac{\pi}{2})\) или \((\dfrac{3\pi}{2}, 2\pi]\).
- Обратите внимание, что \(\sin(t) = 0\) при \(t = 0\) и \(t = \pi\). Поскольку \(\sin(t)\) является координатой x конечной точки дуги \(t\), предыдущий ответ показывает, что \(\sin(t)\) положительно, когда \(t\) находится в одном из интервалов \((0, \pi)\).
 г.
г. - Обратите внимание, что \(\cos(t) = 0\) при \(t = \dfrac{\pi}{2}\) и \(t = \dfrac{3\pi}{2}\). Поскольку \(\cos(t)\) является координатой x конечной точки дуги \(t\), предыдущий ответ показывает, что \(\cos(t)\) положительно, когда \(t\) находится в интервале \((\dfrac{\pi}{2}, \dfrac{3\pi}{2})\).
- Обратите внимание, что \(\sin(t) = 0\) при \(t = \pi\) и \(t = 2\pi\). Поскольку \(\sin(t)\) является координатой x конечной точки дуги \(t\), предыдущий ответ показывает, что \(\sin(t)\) положительно, когда \(t\) находится в одном из интервалов \([0, \dfrac{\pi}{2})\) или \((\pi, 2\pi)\). г.
- Если \(\dfrac{\pi}{2} < t < \pi\), то конечная точка дуги \(t\) находится во втором квадранте, поэтому \(\cos(t) < 0 \) и \(\sin(t) > 0\).
- \(\cos(\dfrac{\pi}{5})\)
- \(\sin(\dfrac{\pi}{5})\)
- \(\cos(\dfrac{5\pi}{8})\)
- \(\sin(\dfrac{5\pi}{8})\)
- \(\cos(\dfrac{-9\pi}{16})\)
- \(\sin(\dfrac{-9\pi}{16})\) г.
- \(\cos(\dfrac{-25\pi}{12})\)
- \(\sin(\dfrac{-25\pi}{12})\)
- Ответить
- Поскольку \(0 < \dfrac{\pi}{5} < \dfrac{\pi}{2}\), конечная точка дуги \(\dfrac{\pi}{5}\) находится в первый квадрант. Следовательно, \(\cos(\dfrac{\pi}{5})\) положителен.
- Используя информацию о \(t\) в (1), \(\sin(\dfrac{\pi}{5})\) положительно.
- Мы можем записать \(\dfrac{\pi}{2}\) как \(\dfrac{4\pi}{8}\) и \(\pi\) как \(\dfrac{8\pi}{ 8}\), поэтому \(\dfrac{\pi}{2}\ < \dfrac{5\pi}{8} < \pi\). Это помещает конечную точку дуги \(\dfrac{5\pi}{8}\) во второй квадрант. Следовательно, \(\cos(\dfrac{5\pi}{8})\) отрицательно. г.
- Используя информацию о \(t\) в (3), \(\sin(\dfrac{5\pi}{8})\) отрицательно.
- Мы можем записать \(-\dfrac{\pi}{2}\) как \(\dfrac{-8\pi}{16}\) и \(-\pi\) как \(\dfrac{-16 \pi}{16}\), поэтому \(-\pi < \dfrac{-9\pi}{16} < -\dfrac{\pi}{2}\).
 Это помещает конечную точку дуги \(\dfrac{-9\pi}{16}\) в третий квадрант. Следовательно, (\cos(\dfrac{-9\pi}{16})\) отрицательно.
Это помещает конечную точку дуги \(\dfrac{-9\pi}{16}\) в третий квадрант. Следовательно, (\cos(\dfrac{-9\pi}{16})\) отрицательно. - Используя информацию о \(t\) в (5), (\sin(\dfrac{-9\pi}{16})\) отрицательно. г.
- Мы можем записать \(-2\pi\) как \(\dfrac{-24\pi}{12}\) и \(-\dfrac{5\pi}{2}\) как \(\dfrac{ -30\pi}{12}\), поэтому \(\dfrac{-5\pi}{2} < \dfrac{-25\pi}{12} < 2\pi\). Это помещает конечную точку дуги \(\cos(\dfrac{-25\pi}{12})\) в четвертый квадрант.
- Используя информацию о дуге \(t\) в (7), \(\sin(\dfrac{-25\pi}{12})\) отрицательно.
- Если \(\cos(t) = \dfrac{1}{2}\) и конечная точка дуги \(t \) находится в четвертом квадранте, определите значение \(\sin(t)\). 9{2}(t) = \dfrac{3}{4}\]
\[\sin(t) = \pm\dfrac{\sqrt{3}}{4}\]
Обратите внимание, что мы не можем определить знак \(\sin(t)\), используя только тождество Пифагора. Нам потребуется дополнительная информация о дуге \(t\). В этом случае нам дано, что конечная точка дуги \(t\) находится в четвертом квадранте, а значит, \(\sin(t) < 0\).
 Следовательно,
Следовательно,\[\sin(t) = -\sqrt{\dfrac{3}{4}} = -\dfrac{\sqrt{3}}{2}\]
2. Поскольку \(\sin(t) = -\dfrac{2}{3}\), мы можем использовать тождество Пифагора, чтобы получить 9{2}(t) = \dfrac{5}{9}\]
\[\sin(t) = \pm\dfrac{\sqrt{5}}{9}\]
И снова нам нужна информация о дуге \(t\), чтобы определить знак \(\cos(t)\). В этом случае нам дано, что \(\pi < t < \dfrac{3\pi}{2}\). Следовательно, конечная точка дуги t находится в третьем квадранте и, следовательно, \(\sin(t) < 0\). Таким образом,
\[\cos(t) = -\sqrt{\dfrac{5}{9}} = \dfrac{\sqrt{5}}{3}.\]
Резюме
В этом разделе мы изучили следующие важные концепции и идеи: 92 = 1\) (с положительным направлением против часовой стрелки) с начальной точкой \((1, 0)\) и конечной точкой \((x, y)\), тогда \(\cos(t) = x\) и \(\sin(t) = y\).
Основные вопросы
Следующие вопросы предназначены для того, чтобы направлять наше изучение материала в этом разделе. Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
Начало деятельности
Мы начали изучение тригонометрии с изучения единичной окружности, того, как обернуть числовую прямую вокруг единичной окружности и как построить дуги на единичной окружности. Теперь мы можем использовать эти идеи для определения двух основных круговых, или тригонометрических, функций. Эти круговые функции позволят нам моделировать периодические явления, такие как приливы, количество солнечного света в течение дней года, орбиты планет и многие другие.
Рисунок \(\PageIndex{1}\): круговые функции
Может показаться, что единичный круг — довольно простой объект и не представляет большого интереса, но математики почти всегда могут найти что-то интересное даже в таких простых объектах. . Например, мы определяем две основные круговые функции, косинус и синус в терминах единичного круга следующим образом. На рисунке \(\PageIndex{1}\) показана дуга длины \(t\) на единичной окружности. Эта дуга начинается в точке \((1, 0)\) и заканчивается в ее конечной точке \(P(t)\). Затем мы определяем косинус и синус дуги \(t\) как \(x\) и \(y\) координаты точки \(P\), так что \(P(t) = (\cos (t), sin(t))\) (косинус обозначается как \(\cos\), а синус — как \(\sin\)). Таким образом, значения косинуса и синуса определяются дугой \(t\), а косинус и синус равны функций дуги \(t\). Поскольку дуга лежит на единичной окружности, мы называем косинус и синус круговыми функциями . Важной частью тригонометрии является изучение косинуса и синуса и периодических явлений, которые эти функции могут моделировать. Это одна из причин, по которой круговые функции также называют тригонометрическими функциями
На рисунке \(\PageIndex{1}\) показана дуга длины \(t\) на единичной окружности. Эта дуга начинается в точке \((1, 0)\) и заканчивается в ее конечной точке \(P(t)\). Затем мы определяем косинус и синус дуги \(t\) как \(x\) и \(y\) координаты точки \(P\), так что \(P(t) = (\cos (t), sin(t))\) (косинус обозначается как \(\cos\), а синус — как \(\sin\)). Таким образом, значения косинуса и синуса определяются дугой \(t\), а косинус и синус равны функций дуги \(t\). Поскольку дуга лежит на единичной окружности, мы называем косинус и синус круговыми функциями . Важной частью тригонометрии является изучение косинуса и синуса и периодических явлений, которые эти функции могут моделировать. Это одна из причин, по которой круговые функции также называют тригонометрическими функциями
Примечание
Согласно веб-сайту «Раннее известное использование некоторых математических слов» jeff560.tripod.com/mathword.html, слово «синус» произошло от санскрита через арабский и латинский языки. Хотя сведения о фактическом происхождении различаются, похоже, что санскритское произведение «jya» (аккорд) было переведено на арабский язык как «jiba», но затем было переведено на латынь как «jaib» (залив), которое стало «sinus» (залив). или кривая). Затем это слово было англизировано и стало нашим «синусом». Слово косинус началось с Платона из Тиволи, который использовал выражение «chorda residui». В то время как латинское слово chorda был лучшим переводом санскритско-арабского слова для синуса, чем слово синус, это слово уже использовалось. Таким образом, «остаточная хорда» стала «косинусом».
Хотя сведения о фактическом происхождении различаются, похоже, что санскритское произведение «jya» (аккорд) было переведено на арабский язык как «jiba», но затем было переведено на латынь как «jaib» (залив), которое стало «sinus» (залив). или кривая). Затем это слово было англизировано и стало нашим «синусом». Слово косинус началось с Платона из Тиволи, который использовал выражение «chorda residui». В то время как латинское слово chorda был лучшим переводом санскритско-арабского слова для синуса, чем слово синус, это слово уже использовалось. Таким образом, «остаточная хорда» стала «косинусом».
Примечание
В математике мы всегда создаем формальные определения для объектов, которые обычно используем. Определения критически важны, потому что с согласованными определениями у всех будет общее понимание того, что означают эти термины. Без такого общего понимания было бы много путаницы, поскольку разные люди имеют разные значения для разных терминов. Поэтому необходимы тщательные и точные определения, чтобы развить математические свойства этих объектов. Чтобы изучить и понять тригонометрию, человек должен уметь объяснить, как определяются круговые функции. Так что сейчас самое время начать работать над пониманием этих определений. 92 = 1\) (с положительным направлением против часовой стрелки) с начальной точкой \((1, 0)\) и конечной точкой \((x, y)\), то косинус функции \(t\), обозначенный \(\cos(t)\), и синуса t, обозначенный \(\sin(t)\), определяются как \[\cos (t) = x\] и \[\sin ( t) = y.\]
Чтобы изучить и понять тригонометрию, человек должен уметь объяснить, как определяются круговые функции. Так что сейчас самое время начать работать над пониманием этих определений. 92 = 1\) (с положительным направлением против часовой стрелки) с начальной точкой \((1, 0)\) и конечной точкой \((x, y)\), то косинус функции \(t\), обозначенный \(\cos(t)\), и синуса t, обозначенный \(\sin(t)\), определяются как \[\cos (t) = x\] и \[\sin ( t) = y.\]
Рис. 1.6 иллюстрирует эти определения для дуги, конечная точка которой находится в первом квадранте.
В настоящее время невозможно определить точные значения функций косинуса и синуса для конкретных значений \(t\). Однако это можно сделать, если конечная точка дуги длины \(t\) лежит на оси \(х\) или оси \(у\). Например, поскольку длина окружности единичного круга равна \(2\pi\), дуга длины \(t = \pi\) будет иметь конечную точку на полпути вокруг окружности от точки \((1, 0)\). То есть конечная точка находится в \((1, 0)\). Следовательно, \[\cos (\pi) = -1\] и \[\sin (\pi) = 0.\]
Следовательно, \[\cos (\pi) = -1\] и \[\sin (\pi) = 0.\]
Упражнение \(\PageIndex{1}\)
Определите точные значения каждого из следующих параметров:
Важное примечание: поскольку косинус и синус являются функциями дуги, длина которой равна действительному числу t, ввод t определяет вывод косинуса и синуса. В результате необходимо указывать входное значение при работе с косинусом и синусом. Другими словами, мы ВСЕГДА пишем \(\cos(t)\), где \(t\) — ввод вещественного числа, и НИКОГДА просто \(\cos\). Повторим еще раз: косинус и синус — это функции, поэтому мы ДОЛЖНЫ указывать входные данные для этих функций.
Упражнение \(\PageIndex{2}\)
В этом упражнении мы будем использовать апплет Geogebra под названием «Конечные точки дуг на единичной окружности». Веб-адрес этого апплета:
http://gvsu.edu/s/JY
Для этого апплета мы контролируем значение ввода \(t\) с помощью ползунка для \(t\). Значения \(t\) варьируются от \(-20\) до \(20\) с шагом \(0,5\). Для заданного значения \(t\) рисуется дуга длины \(t\) и отображаются координаты конечной точки этой дуги. Используйте этот апплет, чтобы найти приблизительные значения для каждого из следующих параметров:
Некоторые свойства функций косинуса и синуса
Функции косинуса и синуса называются круговыми функциями , поскольку их значения определяются координатами точек на единичной окружности. Для каждого действительного числа \(t\) существует соответствующая дуга, начинающаяся в точке \((1, 0)\) (направленной) длины \(t\), которая лежит на единичной окружности. Координаты конечной точки этой дуги определяют значения \(\cos(t\) и \(\sin(t\).
Координаты конечной точки этой дуги определяют значения \(\cos(t\) и \(\sin(t\).
На предыдущих курсах математики мы узнали, что область определения функции — это набор всех входных данных, которые дают определенный результат. Мы также узнали, что диапазон функции — это набор всех возможных выходов функции.
Упражнение \(\PageIndex{3}\)
Хотя мы не можем вычислить точные значения для многих входных значений функций косинуса и синуса, мы можем использовать наши знания о системе координат и ее квадрантах, чтобы определить, являются ли определенные значения косинуса и синуса положительными или отрицательными. Идея состоит в том, что знаки координат точки \(P(x, y)\), нанесенной на координатный план, определяются квадрантом, в котором лежит точка (если только она не лежит на одной из осей). Рисунок \(\PageIndex{2}\) суммирует эти результаты для знаков значений функций косинуса и синуса. Левая колонка в таблице предназначена для положения конечной точки дуги, определяемой действительным числом \(t\).
| Квадрант | \(\cos(t)\) | \(\sin(t)\) |
|---|---|---|
| QI | положительный | положительный |
| II квартал | отрицательный | положительный |
| QIII | отрицательный | отрицательный |
| IV квартал | положительный | отрицательный |
Теперь нам нужно определить, в каком квадранте лежит конечная точка дуги, определяемой вещественным числом t.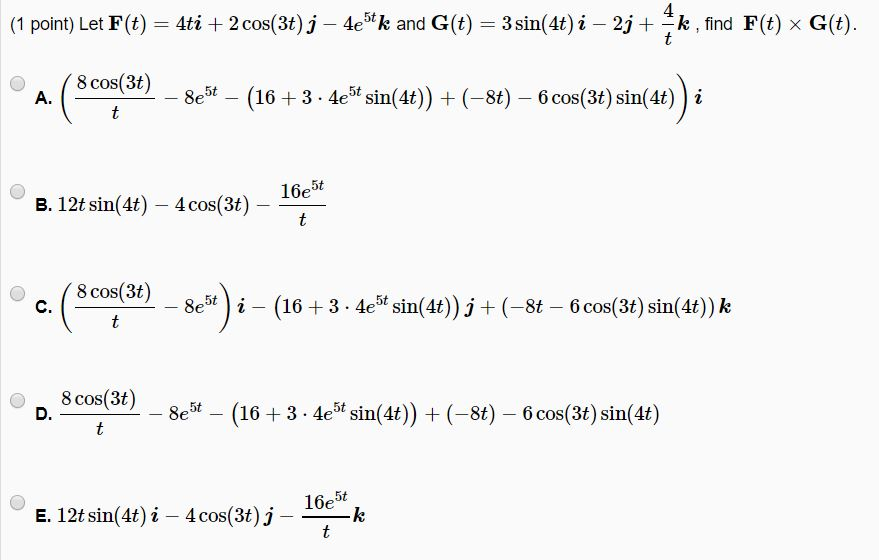 Мы можем сделать это, еще раз используя тот факт, что длина окружности единичного круга равна \(2\pi\), и когда мы движемся по единичному кругу из точки .1; 0/ в положительном (против часовой стрелки) направлении мы будем пересекать одну из осей координат каждую четверть оборота. Например, если \(0 < t < \dfrac{\pi}{2}\), конечная точка дуги, определяемой \(t\), находится в первом квадранте и \(\cos(t) > 0 \) и \(\sin(t) > 0\).
Мы можем сделать это, еще раз используя тот факт, что длина окружности единичного круга равна \(2\pi\), и когда мы движемся по единичному кругу из точки .1; 0/ в положительном (против часовой стрелки) направлении мы будем пересекать одну из осей координат каждую четверть оборота. Например, если \(0 < t < \dfrac{\pi}{2}\), конечная точка дуги, определяемой \(t\), находится в первом квадранте и \(\cos(t) > 0 \) и \(\sin(t) > 0\).
Упражнение \(\PageIndex{4}\)
Упражнение \(\PageIndex{5}\)
Используйте результаты, представленные на рисунке \(\PageIndex{2}\), чтобы определить, являются ли следующие величины положительными, отрицательными или нулевыми. (Не используйте калькулятор.)

Пифагорейское тождество
В математике тождество 92)\).
Тождество Пифагора позволяет нам определить значение \(\cos(t)\) или \(\sin(t)\), если мы знаем значение другого и квадрант, в котором конечная точка дуги \(t\) лежит. Это показано в следующем примере.
Пример \(\PageIndex{1}\)
Предположим, что \(\cos(t) = \dfrac{2}{5}\) и конечная точка дуги\((t)\) лежит в четвертый квадрант. 5 Используйте эту информацию для определения значения \(\sin(t)\).
5 Используйте эту информацию для определения значения \(\sin(t)\).
Решение 9192(t) = \dfrac{21}{25} \]
Это означает, что \(\sin(t) = \pm\sqrt{\dfrac{21}{25}}\), и поскольку конечная точка дуги \((t)\) находится в четвертом квадранте, мы знаем, что \(\sin(t) < 0\). Следовательно, \(\sin(t) = -\sqrt{\dfrac{21}{25}}\). Поскольку \(\sqrt{25} = 5\), мы можем записать
\[\sin(t) = -\sqrt{\dfrac{21}{25}} = -\dfrac{\sqrt{21}} {5}.\]
Упражнение \(\PageIndex{7}\)
- Знаки \(\cos(t)\) и \(\sin(t)\) определяются квадрантом, в котором лежит конечная точка дуги \(t\).

| Квадрант | \(\cos(t)\) | \(\sin(t)\) |
|---|---|---|
| QI | положительный | положительный |
| II квартал | отрицательный | положительный |
| QIII | отрицательный | отрицательный |
| IV квартал | положительный | отрицательный |
- Одно из наиболее важных тождеств в тригонометрии, называемое тождеством Пифагора, выводится из уравнения для единичного круга и утверждает: 92(t) = 1.
 \номер\]
\номер\]Эта страница под названием 1.2: Функции косинуса и синуса распространяется под лицензией CC BY-NC-SA 3.0, автором, ремиксом и/или куратором являются Тед Сандстром и Стивен Шликер (ScholarWorks @Grand Valley State University) через источник контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Тед Сандстром и Стивен Шликер
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 3,0
- Показать страницу TOC
- нет
- Теги
- Круговые функции
- функция косинуса
- Пифагорейское тождество
- функция синуса
- источник@https://scholarworks.
 gvsu.edu/books/12
gvsu.edu/books/12
Получите наши лучшие предложения для прямых трансляций и стриминговых сервисов (2022)
Получите дополнительную экономию на всех ваших любимых стриминговых сервисах.
Клиенты T-Mobile могут наслаждаться своими любимыми сервисами потокового телевидения и прямой трансляцией по выгодной цене.
Больше потокового видео Больше прямых трансляций Больше привилегий Телевизионный концентратор
Смотрите больше того, что вам нравится.
Следите за своими любимыми и открывайте для себя новые шоу и фильмы практически из любого места.
Смотрите свои любимые фильмы и шоу в потоковом режиме с Netflix ON US.
Подписка на Netflix включена в большинство тарифных планов Magenta и Magenta MAX без дополнительной платы.

Получить подробности
При сохранении 2+ квалификационных линий См. полные условия
Транслируйте свои любимые фильмы и шоу с Netflix ON US.
Подписка на Netflix включена в большинство тарифных планов Magenta и Magenta MAX без дополнительной платы.
Предложение может быть изменено. Получите Netflix Basic (1 экран, стоимость до $9,99 в месяц), пока вы поддерживать 1 квалификационную линию Magenta Max или 2+ квалификационных линий Magenta с хорошей репутацией. Получите Netflix Standard (2 экрана, до 15,49 долл. США)./мес. значение), пока вы поддерживаете 2+ квалификационные линии Magenta Max с хорошей репутацией. Учетная запись Netflix и совместимое устройство требуется.
г. Может применяться альтернативная скидка на другие планы потоковой передачи Netflix. Нет
обмен или возврат наличными; нельзя обменять на подарочные подписки Netflix.
Отмените Netflix в любое время. Применяются Условия использования Netflix: www.netflix.com/termsofuse. 1 предложение на
Аккаунт T-Mobile, может занять 1-2 платежных цикла. Как и все планы, функции могут измениться или быть
прекращено в любое время; подробности см. в Условиях и положениях T-Mobile на сайте T-Mobile.com.
Может применяться альтернативная скидка на другие планы потоковой передачи Netflix. Нет
обмен или возврат наличными; нельзя обменять на подарочные подписки Netflix.
Отмените Netflix в любое время. Применяются Условия использования Netflix: www.netflix.com/termsofuse. 1 предложение на
Аккаунт T-Mobile, может занять 1-2 платежных цикла. Как и все планы, функции могут измениться или быть
прекращено в любое время; подробности см. в Условиях и положениях T-Mobile на сайте T-Mobile.com.Apple TV+ теперь входит в комплект Magenta® MAX.
Просматривайте отмеченные наградами фильмы Apple Originals бесплатно, пока у вас есть Magenta MAX. Или получите Apple TV+ на 6 месяцев с планом Magenta.
Получить подробности
Требуется регистрация в приложении Apple TV.
 МАКС: Пока вы поддерживаете одну квалификационную линию Magenta Max с хорошей репутацией. Только одно предложение на аккаунт. Подробности смотрите в плане. Пурпурный: предложение ограничено по времени; подлежит изменению. Только одно предложение на аккаунт. Требуется квалификационный кредит и обслуживание. После бесплатной пробной версии план автоматически продлевается за 4,9 доллара США.9/месяц до отмены. Посмотреть полные условия
МАКС: Пока вы поддерживаете одну квалификационную линию Magenta Max с хорошей репутацией. Только одно предложение на аккаунт. Подробности смотрите в плане. Пурпурный: предложение ограничено по времени; подлежит изменению. Только одно предложение на аккаунт. Требуется квалификационный кредит и обслуживание. После бесплатной пробной версии план автоматически продлевается за 4,9 доллара США.9/месяц до отмены. Посмотреть полные условияApple TV+ теперь входит в комплект Magenta® MAX.
Просматривайте отмеченные наградами фильмы Apple Originals бесплатно, пока у вас есть Magenta MAX. Или получите Apple TV+ на 6 месяцев с планом Magenta.
MAX: получите Apple TV+ (стоимостью до 4,99 долл. США в месяц), сохранив при этом одну квалификационную линейку Magenta Max с хорошей репутацией. Действительно только для Apple TV+ в США. Завершите регистрацию в Apple в приложении Apple TV; требуется учетная запись iTunes/Apple Media Services.
 Применяются Условия и Политика конфиденциальности Apple; см. применимые условия на странице https://www.apple.com/legal/internet-services/itunes/us/terms.html. Должно быть 13+. Только одно предложение на аккаунт; может занять 1-2 платежных цикла. Apple TV+ является зарегистрированным товарным знаком Apple Inc. Apple не является спонсором данной акции. Как и все планы, функции могут измениться или быть прекращены в любое время; подробности см. в Условиях и положениях T-Mobile на сайте T-Mobile.com. Пурпурный: предложение ограничено по времени; подлежит изменению. Действительно только для Apple TV+ в США. Завершите регистрацию в Apple в приложении Apple TV; требуется учетная запись iTunes/Apple Media Services. Применяются Условия и Политика конфиденциальности Apple; см. применимые условия на странице https://www.apple.com/legal/internet-services/itunes/us/terms.html. Должно быть 13+. Только одно предложение на аккаунт. Требуется квалификационный кредит и обслуживание. После бесплатной пробной версии план автоматически продлевается за 4,9 доллара США.
Применяются Условия и Политика конфиденциальности Apple; см. применимые условия на странице https://www.apple.com/legal/internet-services/itunes/us/terms.html. Должно быть 13+. Только одно предложение на аккаунт; может занять 1-2 платежных цикла. Apple TV+ является зарегистрированным товарным знаком Apple Inc. Apple не является спонсором данной акции. Как и все планы, функции могут измениться или быть прекращены в любое время; подробности см. в Условиях и положениях T-Mobile на сайте T-Mobile.com. Пурпурный: предложение ограничено по времени; подлежит изменению. Действительно только для Apple TV+ в США. Завершите регистрацию в Apple в приложении Apple TV; требуется учетная запись iTunes/Apple Media Services. Применяются Условия и Политика конфиденциальности Apple; см. применимые условия на странице https://www.apple.com/legal/internet-services/itunes/us/terms.html. Должно быть 13+. Только одно предложение на аккаунт. Требуется квалификационный кредит и обслуживание. После бесплатной пробной версии план автоматически продлевается за 4,9 доллара США. 9/месяц до отмены. Apple TV+ является зарегистрированным товарным знаком Apple Inc. Apple не является спонсором этой акции. Может не сочетаться с некоторыми предложениями или скидками (например, с другими пробными предложениями T-Mobile Apple TV+).
9/месяц до отмены. Apple TV+ является зарегистрированным товарным знаком Apple Inc. Apple не является спонсором этой акции. Может не сочетаться с некоторыми предложениями или скидками (например, с другими пробными предложениями T-Mobile Apple TV+).Получите подписку Paramount+ на один год в США.
Смотрите популярные фильмы, эксклюзивные оригиналы, спортивные трансляции и A Mountain of Entertainment без дополнительных затрат.
Получить подробности
Подписка автоматически продлевается по цене 4,99 доллара США в месяц после первого года. Требуется кредитная карта. Посмотреть полные условия
Получите подписку Paramount+ на один год в США.

Смотрите популярные фильмы, эксклюзивные оригиналы, спортивные трансляции и A Mountain of Entertainment без дополнительных затрат.
Ограниченное по времени предложение. Доступно для активных абонентов T-Mobile и Sprint с оплатой голосовой связи, беспроводной связи и домашнего Интернета (за исключением корпоративных/государственных учетных записей), которые являются жителями 50 США и достигли возраста восемнадцати (18) лет. Получите 12-месячный ежемесячный план Paramount + Essential (стоимостью 59 долларов США)..88), когда вы регистрируетесь, чтобы получить код, а затем погасить код в течение 30 дней. Предложение требует регистрации учетной записи подписчика Paramount+ и предоставления действительного способа оплаты для продолжения обслуживания после окончания рекламного периода. ЕСЛИ ВЫ НЕ ОТМЕНИТЕ СВОЮ ПОДПИСКУ PARAMOUNT+ ДО ЗАВЕРШЕНИЯ 12-МЕСЯЧНОГО АКЦИОННОГО ПЕРИОДА, ВЫ РАЗРЕШАЕТЕ VIACOMCBS СНИЖАТЬ С ВАШЕЙ КРЕДИТНОЙ КАРТЫ 4,99 Долл. ЧТОБЫ ОТМЕНИТЬ ПОДПИСКУ И ИЗБЕЖАТЬ ОПЛАТЫ, ВЫ ДОЛЖНЫ ОТМЕНИТЬ ДО ОКОНЧАНИЯ 12-МЕСЯЧНОГО АКЦИОННОГО ПЕРИОДА.
г. Звоните (888) 274-5343 или
войдите в свою учетную запись подписчика, чтобы отменить подписку Paramount+. Если
подписка отменена, отмена вступит в силу в конце текущего
период подписки. Без возвратов. Максимум 1 код/аккаунт. ViacomCBS и T-Mobile оставляют за собой право определять ваше право на участие в рекламном периоде, а также
время от времени изменять, модифицировать или отказываться от положений и условий. Использование
Услуга Paramount+ и создание учетной записи подписчика регулируются
Условия использования VCBSI доступны по адресу www.viacomcbs.legal/us/en/cbsi/terms-of-use.
и Политику конфиденциальности на www.viacomcbsprivacy.com/en/policy. Это предложение может быть
изменены или отменены в любое время. Недействительно там, где это запрещено. Не подлежит передаче, не для
перепродажи и обмену на деньги не подлежит. Могут применяться другие ограничения и налоги.
Нельзя комбинировать с любыми другими кодами или купонами Paramount+.
Звоните (888) 274-5343 или
войдите в свою учетную запись подписчика, чтобы отменить подписку Paramount+. Если
подписка отменена, отмена вступит в силу в конце текущего
период подписки. Без возвратов. Максимум 1 код/аккаунт. ViacomCBS и T-Mobile оставляют за собой право определять ваше право на участие в рекламном периоде, а также
время от времени изменять, модифицировать или отказываться от положений и условий. Использование
Услуга Paramount+ и создание учетной записи подписчика регулируются
Условия использования VCBSI доступны по адресу www.viacomcbs.legal/us/en/cbsi/terms-of-use.
и Политику конфиденциальности на www.viacomcbsprivacy.com/en/policy. Это предложение может быть
изменены или отменены в любое время. Недействительно там, где это запрещено. Не подлежит передаче, не для
перепродажи и обмену на деньги не подлежит. Могут применяться другие ограничения и налоги.
Нельзя комбинировать с любыми другими кодами или купонами Paramount+.Больше футбола, больше оригинальных сериалов, больше с ViX+ ON US.

Эксклюзивно от T-Mobile: получите годовую подписку на ViX+ в США и испытайте страсть и драму с футбольными трансляциями, классическими и оригинальными сериалами, кинопремьерами и многим другим. Присоединяйтесь к нам сегодня для крупнейшего испаноязычного стримингового сервиса в мире.
Получите ViX+ сегодня
Ограниченное по времени предложение; подлежит изменению. Зарегистрируйтесь, чтобы получить код, а затем активируйте его в течение 30 дней. Требуется соответствующее обслуживание и новая учетная запись ViX+. Максимум 1 код/аккаунт. Применяются Условия использования и Политика конфиденциальности ViX.
Смотрите больше прямых трансляций.
Наслаждайтесь эксклюзивными скидками и специальными предложениями при потоковом вещании в прямом эфире — просто потому, что вы покупатель!
Получите YouTube TV всего за 54,9 доллара США9/мес.
 на один год.
на один год.Это экономия 10 долларов США в месяц на YouTube TV в течение 12 месяцев. Транслируйте в прямом эфире более 85 лучших развлекательных, спортивных и новостных каналов. С 6 домашних учетных записей, включенных в вашу подписку, вы можете смотреть избранное на запрос, или обязательно запишите их с неограниченным пространством DVR.
Выкупить сейчас
г.Подписка автоматически продлевается по цене 64,99 долл. США в месяц после первого года. Предложение YouTube TV доступно текущим клиентам услуг T-Mobile Wireless и Home Internet. Посмотреть полные условия
Получите YouTube TV всего за 54,99 долл. США в месяц. на один год.
Это экономия 10 долларов США в месяц на YouTube TV в течение 12 месяцев.
 Транслируйте в прямом эфире более 85 лучших развлекательных, спортивных и новостных каналов. С 6
домашних учетных записей, включенных в вашу подписку, вы можете смотреть избранное на
запрос, или обязательно запишите их с неограниченным пространством DVR.
Транслируйте в прямом эфире более 85 лучших развлекательных, спортивных и новостных каналов. С 6
домашних учетных записей, включенных в вашу подписку, вы можете смотреть избранное на
запрос, или обязательно запишите их с неограниченным пространством DVR.Ограниченное по времени предложение; подлежит изменению. Акция открыта для участников, подписавшихся на услуги T-Mobile Wireless или Home Internet. Предложение с возможностью погашения, если доступно YouTube TV. Стандартная бесплатная пробная версия доступна для новых подписчиков YouTube TV, которые никогда не участвовали в пробной версии YouTube TV. Предложение со скидкой доступно для всех клиентов T-Mobile, независимо от того, регистрировался ли пользователь в YouTube TV в прошлом. Доступность местных каналов может варьироваться. Рекламная стоимость подписки (подписок) не подлежит передаче, перепродаже и обмену на наличные. Действительная платежная форма требуется при регистрации. Пользователь получит стандартную бесплатную пробную версию, если она соответствует требованиям, а затем будет взиматься плата со скидкой в размере 54,9 доллара США.
 9 в месяц в течение 12 месяцев, прежде чем будет взиматься плата в размере 64,99 долларов США в месяц или по текущей ежемесячной цене подписки. Бесплатная отмена в любое время до окончания стандартной бесплатной пробной версии. Возврат средств за неполный расчетный период невозможен. Должен быть 18 лет или старше и в 50 Соединенных Штатах. За исключением клиентов T-Mobile для бизнеса. Требуется учетная запись Google. YouTube оставляет за собой право изменить или отменить предложение в любое время.
9 в месяц в течение 12 месяцев, прежде чем будет взиматься плата в размере 64,99 долларов США в месяц или по текущей ежемесячной цене подписки. Бесплатная отмена в любое время до окончания стандартной бесплатной пробной версии. Возврат средств за неполный расчетный период невозможен. Должен быть 18 лет или старше и в 50 Соединенных Штатах. За исключением клиентов T-Mobile для бизнеса. Требуется учетная запись Google. YouTube оставляет за собой право изменить или отменить предложение в любое время.Полные условия здесь: https://tv.youtube.com/learn/offer-terms/
Приобретите Philo TV всего за 15 долларов в месяц. на один год.
Это экономия 10 долларов в месяц на Philo TV в течение 12 месяцев. Наслаждайтесь 60+ живыми и по запросу каналов, плюс безлимитный DVR. Потоковая передача на 3 устройства одновременно. Должен оставаться Подписчики T-Mobile получают ежемесячную скидку.
Выкупить сейчас
г.
 Подписка автоматически продлевается по цене 25 долларов США в месяц после первого года. Предложение Филона
доступный текущим клиентам T-Mobile Wireless и Home Internet.
Посмотреть полные условия
Подписка автоматически продлевается по цене 25 долларов США в месяц после первого года. Предложение Филона
доступный текущим клиентам T-Mobile Wireless и Home Internet.
Посмотреть полные условияПриобретите Philo TV всего за 15 долларов в месяц. на один год.
Это экономия 10 долларов в месяц на Philo TV в течение 12 месяцев. Наслаждайтесь 60+ живыми и по запросу каналов, плюс безлимитный DVR. Потоковая передача на 3 устройства одновременно. Должен оставаться Подписчики T-Mobile получают ежемесячную скидку.
Ограниченное по времени предложение; подлежит изменению. Предлагается T-Mobile только для T-Mobile wireless или Клиенты домашнего Интернета (за исключением бизнес-клиентов), проживающие в 50 США, 18+ («Клиенты»). Соответствующие требованиям клиенты получают 7-дневную бесплатную пробную версию Philo и скидку 10 долларов США в месяц. на 12 месяцев (обычно 25 долларов США в месяц) или затем по текущей ежемесячной цене подписки.
г. Ограничение
(1) Предложение для каждого клиента, только для одноразового использования. Предложение/скидка не подлежит передаче другому лицу, не может быть
перепроданы или выкуплены за наличные и не могут сочетаться с другими предложениями, скидками или
рекламные акции (если иное прямо не разрешено Philo). Скидка заканчивается, если учетная запись T-Mobile
прекращено; Подписка Philo автоматически возвращается к текущей полной стоимости подписки.
ВАЖНОЕ ЗАМЕЧАНИЕ. Для активации требуется действительная платежная информация и подписка.
Предложение. Если вы не отмените в течение применимого пробного периода (7 дней бесплатно или 12 месяцев
со скидкой), с вас будет взиматься соответствующая месячная сумма плюс налоги на повторяющиеся
основе после завершения испытаний. Перейдите на страницу своей учетной записи Philo, чтобы отменить подписку. Отмена вступает в силу
в дату следующего ежемесячного выставления счета (без возврата за неполные расчетные периоды). Искупление этого
Предложение означает принятие настоящих Условий и всех применимых Условий и положений, см.
Ограничение
(1) Предложение для каждого клиента, только для одноразового использования. Предложение/скидка не подлежит передаче другому лицу, не может быть
перепроданы или выкуплены за наличные и не могут сочетаться с другими предложениями, скидками или
рекламные акции (если иное прямо не разрешено Philo). Скидка заканчивается, если учетная запись T-Mobile
прекращено; Подписка Philo автоматически возвращается к текущей полной стоимости подписки.
ВАЖНОЕ ЗАМЕЧАНИЕ. Для активации требуется действительная платежная информация и подписка.
Предложение. Если вы не отмените в течение применимого пробного периода (7 дней бесплатно или 12 месяцев
со скидкой), с вас будет взиматься соответствующая месячная сумма плюс налоги на повторяющиеся
основе после завершения испытаний. Перейдите на страницу своей учетной записи Philo, чтобы отменить подписку. Отмена вступает в силу
в дату следующего ежемесячного выставления счета (без возврата за неполные расчетные периоды). Искупление этого
Предложение означает принятие настоящих Условий и всех применимых Условий и положений, см. philo.com/terms/#philo-promotions для получения более подробной информации. T-Mobile оставляет за собой право изменять
настоящей Оферты в любое время. Philo оставляет за собой право изменить или отменить это Предложение в любое время.
Недействительно там, где облагаются налогом, запрещены или ограничены.
philo.com/terms/#philo-promotions для получения более подробной информации. T-Mobile оставляет за собой право изменять
настоящей Оферты в любое время. Philo оставляет за собой право изменить или отменить это Предложение в любое время.
Недействительно там, где облагаются налогом, запрещены или ограничены.Транслируйте тысячи фильмов, шоу и смотрите телепередачи бесплатно на Pluto TV.
Клиенты T-Mobile могут наслаждаться эксклюзивными впечатлениями от просмотра и ограниченными перерывами на рекламу, которые можно использовать в приложении T-Mobile Tuesdays. См. полные условия
Погасить сейчас в приложении
г.Транслируйте тысячи фильмов, шоу и смотрите телепередачи бесплатно на Pluto TV.

Клиенты T-Mobile могут наслаждаться эксклюзивными впечатлениями от просмотра и ограниченными рекламными перерывами, которые можно использовать в приложении T-Mobile вторникам.
Активируйте в приложении T-Mobile Tuesdays до 5 апреля 2023 г., 4:59 по восточноевропейскому времени, чтобы получить ограниченный по времени эксклюзивный опыт на Pluto TV на совместимых устройствах. Доступно для активных клиентов беспроводной связи T-Mobile, Sprint и Metro от T-Mobile, которые являются жителями 50 Соединенных Штатов и должны быть не моложе 18 лет или совершеннолетними в их юрисдикции, а несовершеннолетние должны быть не моложе шестнадцати лет. с согласия родителей. Доступно только на Pluto TV на совместимых устройствах, где доступен Pluto TV. Предложение требует регистрации учетной записи Pluto TV через мобильное приложение Pluto TV. Максимум 1 код/аккаунт. Pluto TV и T-Mobile оставляют за собой право определять ваше право на участие в рекламном периоде, а также время от времени вносить поправки, изменять или отменять положения и условия.
г. Использование службы Pluto TV и создание учетной записи регулируются Условиями использования Pluto Inc., доступными по адресу https://corporate.pluto.tv/terms-of-use/, и Политикой конфиденциальности по адресу https://www.viacomcbsprivacy.com/en/policy?r=pluto.tv. Это предложение и эксклюзивный опыт могут быть изменены или отменены в любое время. Недействительно там, где это запрещено. Не подлежит передаче, не для перепродажи и не подлежит обмену на наличные деньги. Могут применяться другие ограничения.
Использование службы Pluto TV и создание учетной записи регулируются Условиями использования Pluto Inc., доступными по адресу https://corporate.pluto.tv/terms-of-use/, и Политикой конфиденциальности по адресу https://www.viacomcbsprivacy.com/en/policy?r=pluto.tv. Это предложение и эксклюзивный опыт могут быть изменены или отменены в любое время. Недействительно там, где это запрещено. Не подлежит передаче, не для перепродажи и не подлежит обмену на наличные деньги. Могут применяться другие ограничения.Больше бонусов.
Получите еще больше предложений на потоковое вещание — просто за то, что являетесь покупателем.
Получите SiriusXM на 4 месяца в США.
Прослушивайте более 425 музыкальных каналов без рекламы, а также разговоры, спорт и многое другое в течение 4 месяцев в приложении SXM без дополнительной платы.
Выкупить сейчас
Автоматически продлевается после 4-месячного бесплатного периода по текущей ставке (в настоящее время 10,99 долларов США в месяц) плюс сборы и налоги.
 Отменить в любое время. Посмотреть полные условия
Отменить в любое время. Посмотреть полные условияПолучите SiriusXM на 4 месяца в США.
Слушайте более 425 музыкальных каналов без рекламы, а также разговоры, спорт и многое другое в течение 4 месяцев в приложении SXM без дополнительной платы.
Ограниченное по времени предложение; подлежит изменению. План подписки SiriusXM Streaming Platinum автоматически продлевается после 4-месячного бесплатного периода по текущей ставке (в настоящее время 10,9 долл. США).9/мес) плюс сборы и налоги. Отменить в любое время. Доступно только для новых подписчиков SiriusXM. Сервис предназначен только для личного использования; деловое / коммерческое использование не разрешено. Предложение активируется непосредственно с помощью SiriusXM. Требуется кредитная карта. Услуга регулируется Клиентским соглашением SiriusXM, доступным на сайте siriusxm.com. Необходимо зарегистрироваться, чтобы получить ссылку для погашения, и активировать ее до 31 декабря 2022 г.
г. Должен иметь соответствующую услугу T-Mobile. Максимум 1 предложение/аккаунт. Ссылки на выкуп можно использовать только один раз; не подлежат передаче, не имеют денежной стоимости и не могут быть обменены на наличные или в кредит или проданы.
Должен иметь соответствующую услугу T-Mobile. Максимум 1 предложение/аккаунт. Ссылки на выкуп можно использовать только один раз; не подлежат передаче, не имеют денежной стоимости и не могут быть обменены на наличные или в кредит или проданы.Радио по выходным без рекламы Pandora.
Кроме того, получите доступ к специальным развлечениям от SiriusXM в любой день недели.
Начать слушать
Ограниченное по времени предложение. Требуется квалификационный план. Подробности смотрите на сайте выкупа. Посмотреть полные условия
г.Получите радио по выходным Pandora без рекламы.
Кроме того, получите доступ к специальным развлечениям от SiriusXM в любой день недели.

Ограниченное предложение. Подходящие подписчики могут сохранять и использовать средства на T-Mobile до 9 января. 2023 в 23:59 ET, чтобы получить доступ к радиовыходным Pandora без рекламы и специальным Куратор SiriusXM Entertainment. Ограничьте 1 погашение/подходящий подписчик. Предложение не может быть переданы, проданы или выкуплены за наличные деньги или в кредит. Данное предложение не суммируется ни с одним другие предложения, скидки или рекламные акции. Недействительно там, где это запрещено или ограничено законом. Предложение может не быть доступными на определенных потребительских устройствах или продуктах. Могут применяться тарифы и сборы за передачу данных. Вы должны быть резидентом США, старше 18 лет и иметь активную учетную запись Pandora, чтобы воспользоваться предложением. Пользователи должно быть или потребуется установить приложение Pandora (версия, выпущенная в октябре 2020 г. или новее) на своем мобильном устройстве и должны войти в систему.
 Использование сервиса Pandora регулируется
Условия использования и политика конфиденциальности Pandora доступны на сайте www.pandora.com. Для начала каждого
Ad-Free Radio Weekend, вы увидите короткое вступительное видео на мобильном телефоне Pandora.
приложение. Пользователи Pandora с поддержкой рекламы получат доступ как к AdFree Radio Weekends, так и к
Специальное развлечение SiriusXM. Подписчики Pandora Plus и Premium получат только
Развлечение SiriusXM и не имеют права на получение наличных денег или кредита для Ad-Free Radio.
Время выходных. Ad-Free означает, что платная сторонняя реклама не будет показываться против Pandora.
Музыкальные радиостанции, за исключением того, что в начале каждого радио без рекламы может показываться реклама.
Опыт прослушивания выходного дня. Объявления станций или комментарии ведущего/исполнителя
включены в контент без рекламы. Выходные начинаются в субботу в 12:00 и заканчиваются в воскресенье.
11:59вечера.
Использование сервиса Pandora регулируется
Условия использования и политика конфиденциальности Pandora доступны на сайте www.pandora.com. Для начала каждого
Ad-Free Radio Weekend, вы увидите короткое вступительное видео на мобильном телефоне Pandora.
приложение. Пользователи Pandora с поддержкой рекламы получат доступ как к AdFree Radio Weekends, так и к
Специальное развлечение SiriusXM. Подписчики Pandora Plus и Premium получат только
Развлечение SiriusXM и не имеют права на получение наличных денег или кредита для Ad-Free Radio.
Время выходных. Ad-Free означает, что платная сторонняя реклама не будет показываться против Pandora.
Музыкальные радиостанции, за исключением того, что в начале каждого радио без рекламы может показываться реклама.
Опыт прослушивания выходного дня. Объявления станций или комментарии ведущего/исполнителя
включены в контент без рекламы. Выходные начинаются в субботу в 12:00 и заканчиваются в воскресенье.
11:59вечера.Превратите практически любой телевизор в Smart TV.

TVision HUB на базе Google TV.
Смотрите YouTube TV и Philo на своем телевизоре с помощью TVision HUB. Кроме того, он поддерживает HD, 4K и другие ваши любимые потоковые сервисы.
Получить подробности
Требуется подключение к Интернету.
Международный роуминг, звонки и тарифы на передачу данных
Все планы включают данные, звонки и текстовые сообщения в США, Канаде и Мексике без дополнительной оплаты.
- Список стран, начиная с AA
- Афганистан
- Острова Аланд
- Албания
- Alderney
- Algeria
- и Alderney
2- и Alderney
2- и Aldernene1921 Antigua & Barbuda
- Argentina
- Armenia
- Aruba
- Australia
- Austria
- Azerbaijan
- Azores
- List of countries beginning with BB
- Bahamas
- Bahrain
- Bangladesh
- Barbados
- Belarus
- Бельгия
- Белиз
- Бенин
- Бермуды
- Боливия
- Бонайре
- Босния и Герцеговина
- Brazil
- British Virgin Islands
- Brunei
- Bulgaria
- Burkina Faso
- Burundi
- List of countries beginning with CC
- Cambodia
- Cameroon
- Canada
- Canary Islands
- Cape Verde
- Каймановы острова
- Чад
- Чили
- Китай
- Остров Рождества
- Колумбия
- Конго
- Конго, Демократическая Республика
- Costa Rica
- Cote D’ivoire
- Croatia
- Curacao
- Cyprus
- Czech Republic
- List of countries beginning with DD
- Denmark
- Dominica
- Dominican Republic
- List of countries beginning с EE
- Остров Пасхи
- Эквадор
- Египет
- Сальвадор
- Эстония
- Список стран, начинающихся с FF
- Faroe Islands
- Fiji
- Finland
- France
- French Guiana
- French Polynesia
- List of countries beginning with GG
- Gabon
- Gambia
- Georgia
- Germany
- Ghana
- Gibraltar
- Греция
- Гренландия
- Гренада
- Гваделупа (включая Сен-Бартелеми и Сен-Мартен)
- Гуам
- Гватемала
- Guernsey
- Guinea
- Guinea-Bissau
- Guyana
- List of countries beginning with HH
- Haiti
- Herm
- Honduras
- Hong Kong
- Hungary
- List of countries beginning with II
- Исландия
- Индия
- Индонезия
- Ирак
- Ирландия
- Остров Мэн
- Израиль
- Италия
- List of countries beginning with JJ
- Jamaica
- Japan
- Jersey
- Jordan
- List of countries beginning with KK
- Kazakhstan
- Kenya
- Kosovo
- Kuwait
- Kyrgyzstan
- List of countries начиная с LL
- Лаос
- Латвия
- Либерия
- Лихтенштейн
- Литва
- Люксембург
- List of countries beginning with MM
- Macau
- Macedonia
- Madagascar
- Madeira
- Malawi
- Malaysia
- Maldives
- Mali
- Malta
- Marie Galante
- Martinique
- Mauritania
- Mauritius
- Майотта
- Мексика
- Молдова
- Монако
- Монголия
- Черногория
- Монтсеррат
- Марокко
- Mozambique
- Myanmar
- List of countries beginning with NN
- Nauru
- Nepal
- Netherlands
- Netherlands Antilles
- New Zealand
- Nicaragua
- Niger
- Nigeria
- Northern Ireland
- Northern Mariana Острова (Сайпан)
- Норвегия
- Список стран, начинающихся с OO
- Оман
- Список стран, начинающихся с PP
- Pakistan
- Palestine (Gaza Strip & West Bank)
- Panama
- Papua New Guinea
- Paraguay
- Peru
- Philippines
- Poland
- Portugal
- List of countries beginning with QQ
- Qatar
- Список стран, начинающихся с RR
- Реюньон
- Румыния
- Рота
- Россия
- Руанда
- List of countries beginning with SS
- Saba
- Saint Barthelemy
- Saint Eustatius
- Saint Saba
- Samoa
- San Marino
- Sark Island
- Saudi Arabia
- Scotland
- Senegal
- Serbia
- Seychelles
- Сьерра-Леоне
- Сингапур
- Синт-Мартен
- Словакия
- Словения
- Южная Африка
- Южная Корея
- Spain
- Sri Lanka
- St.



 5)\) и \(\sin(5.5)\)
5)\) и \(\sin(5.5)\) Таким образом, косинус любого действительного числа определен, а область определения функции косинуса — это набор всех действительных чисел.
Таким образом, косинус любого действительного числа определен, а область определения функции косинуса — это набор всех действительных чисел. Это означает \(-1 \leq \sin(t) \leq 1\) для любого действительного числа \(t\).
Это означает \(-1 \leq \sin(t) \leq 1\) для любого действительного числа \(t\).

 Это помещает конечную точку дуги \(\dfrac{-9\pi}{16}\) в третий квадрант. Следовательно, (\cos(\dfrac{-9\pi}{16})\) отрицательно.
Это помещает конечную точку дуги \(\dfrac{-9\pi}{16}\) в третий квадрант. Следовательно, (\cos(\dfrac{-9\pi}{16})\) отрицательно. Следовательно,
Следовательно,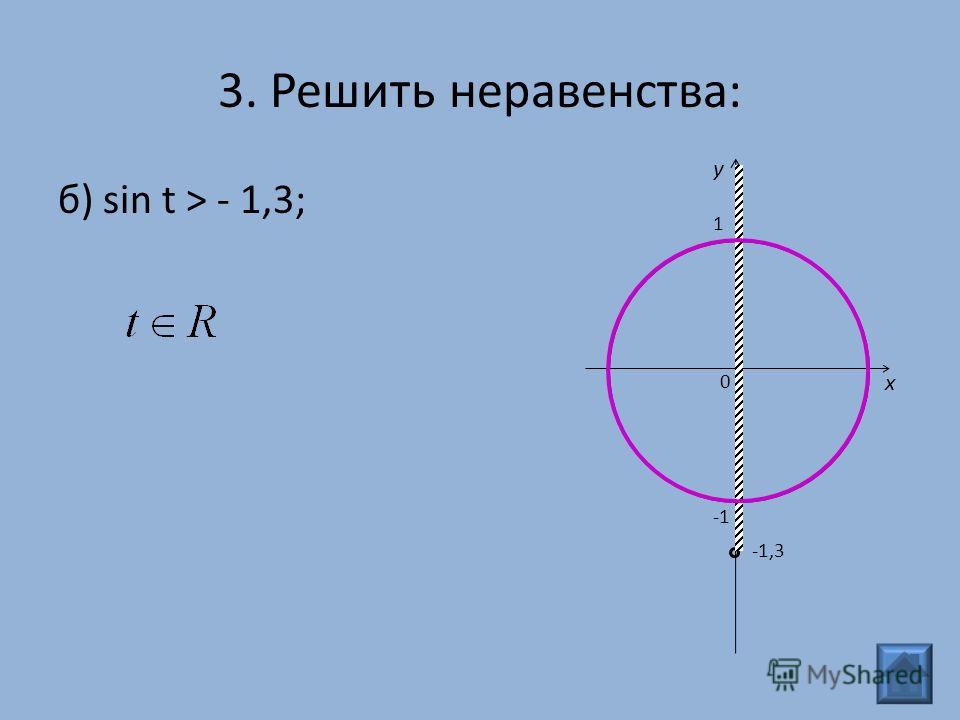
 \номер\]
\номер\] gvsu.edu/books/12
gvsu.edu/books/12
 Может применяться альтернативная скидка на другие планы потоковой передачи Netflix. Нет
обмен или возврат наличными; нельзя обменять на подарочные подписки Netflix.
Отмените Netflix в любое время. Применяются Условия использования Netflix: www.netflix.com/termsofuse. 1 предложение на
Аккаунт T-Mobile, может занять 1-2 платежных цикла. Как и все планы, функции могут измениться или быть
прекращено в любое время; подробности см. в Условиях и положениях T-Mobile на сайте T-Mobile.com.
Может применяться альтернативная скидка на другие планы потоковой передачи Netflix. Нет
обмен или возврат наличными; нельзя обменять на подарочные подписки Netflix.
Отмените Netflix в любое время. Применяются Условия использования Netflix: www.netflix.com/termsofuse. 1 предложение на
Аккаунт T-Mobile, может занять 1-2 платежных цикла. Как и все планы, функции могут измениться или быть
прекращено в любое время; подробности см. в Условиях и положениях T-Mobile на сайте T-Mobile.com. МАКС: Пока вы поддерживаете одну квалификационную линию Magenta Max с хорошей репутацией. Только одно предложение на аккаунт. Подробности смотрите в плане. Пурпурный: предложение ограничено по времени; подлежит изменению. Только одно предложение на аккаунт. Требуется квалификационный кредит и обслуживание. После бесплатной пробной версии план автоматически продлевается за 4,9 доллара США.9/месяц до отмены. Посмотреть полные условия
МАКС: Пока вы поддерживаете одну квалификационную линию Magenta Max с хорошей репутацией. Только одно предложение на аккаунт. Подробности смотрите в плане. Пурпурный: предложение ограничено по времени; подлежит изменению. Только одно предложение на аккаунт. Требуется квалификационный кредит и обслуживание. После бесплатной пробной версии план автоматически продлевается за 4,9 доллара США.9/месяц до отмены. Посмотреть полные условия Применяются Условия и Политика конфиденциальности Apple; см. применимые условия на странице https://www.apple.com/legal/internet-services/itunes/us/terms.html. Должно быть 13+. Только одно предложение на аккаунт; может занять 1-2 платежных цикла. Apple TV+ является зарегистрированным товарным знаком Apple Inc. Apple не является спонсором данной акции. Как и все планы, функции могут измениться или быть прекращены в любое время; подробности см. в Условиях и положениях T-Mobile на сайте T-Mobile.com. Пурпурный: предложение ограничено по времени; подлежит изменению. Действительно только для Apple TV+ в США. Завершите регистрацию в Apple в приложении Apple TV; требуется учетная запись iTunes/Apple Media Services. Применяются Условия и Политика конфиденциальности Apple; см. применимые условия на странице https://www.apple.com/legal/internet-services/itunes/us/terms.html. Должно быть 13+. Только одно предложение на аккаунт. Требуется квалификационный кредит и обслуживание. После бесплатной пробной версии план автоматически продлевается за 4,9 доллара США.
Применяются Условия и Политика конфиденциальности Apple; см. применимые условия на странице https://www.apple.com/legal/internet-services/itunes/us/terms.html. Должно быть 13+. Только одно предложение на аккаунт; может занять 1-2 платежных цикла. Apple TV+ является зарегистрированным товарным знаком Apple Inc. Apple не является спонсором данной акции. Как и все планы, функции могут измениться или быть прекращены в любое время; подробности см. в Условиях и положениях T-Mobile на сайте T-Mobile.com. Пурпурный: предложение ограничено по времени; подлежит изменению. Действительно только для Apple TV+ в США. Завершите регистрацию в Apple в приложении Apple TV; требуется учетная запись iTunes/Apple Media Services. Применяются Условия и Политика конфиденциальности Apple; см. применимые условия на странице https://www.apple.com/legal/internet-services/itunes/us/terms.html. Должно быть 13+. Только одно предложение на аккаунт. Требуется квалификационный кредит и обслуживание. После бесплатной пробной версии план автоматически продлевается за 4,9 доллара США.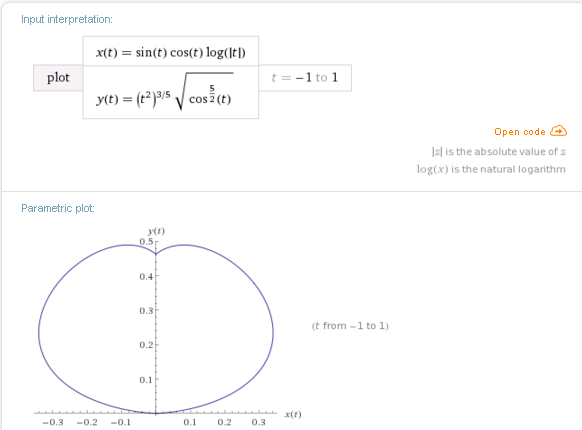 9/месяц до отмены. Apple TV+ является зарегистрированным товарным знаком Apple Inc. Apple не является спонсором этой акции. Может не сочетаться с некоторыми предложениями или скидками (например, с другими пробными предложениями T-Mobile Apple TV+).
9/месяц до отмены. Apple TV+ является зарегистрированным товарным знаком Apple Inc. Apple не является спонсором этой акции. Может не сочетаться с некоторыми предложениями или скидками (например, с другими пробными предложениями T-Mobile Apple TV+).
 Звоните (888) 274-5343 или
войдите в свою учетную запись подписчика, чтобы отменить подписку Paramount+. Если
подписка отменена, отмена вступит в силу в конце текущего
период подписки. Без возвратов. Максимум 1 код/аккаунт. ViacomCBS и T-Mobile оставляют за собой право определять ваше право на участие в рекламном периоде, а также
время от времени изменять, модифицировать или отказываться от положений и условий. Использование
Услуга Paramount+ и создание учетной записи подписчика регулируются
Условия использования VCBSI доступны по адресу www.viacomcbs.legal/us/en/cbsi/terms-of-use.
и Политику конфиденциальности на www.viacomcbsprivacy.com/en/policy. Это предложение может быть
изменены или отменены в любое время. Недействительно там, где это запрещено. Не подлежит передаче, не для
перепродажи и обмену на деньги не подлежит. Могут применяться другие ограничения и налоги.
Нельзя комбинировать с любыми другими кодами или купонами Paramount+.
Звоните (888) 274-5343 или
войдите в свою учетную запись подписчика, чтобы отменить подписку Paramount+. Если
подписка отменена, отмена вступит в силу в конце текущего
период подписки. Без возвратов. Максимум 1 код/аккаунт. ViacomCBS и T-Mobile оставляют за собой право определять ваше право на участие в рекламном периоде, а также
время от времени изменять, модифицировать или отказываться от положений и условий. Использование
Услуга Paramount+ и создание учетной записи подписчика регулируются
Условия использования VCBSI доступны по адресу www.viacomcbs.legal/us/en/cbsi/terms-of-use.
и Политику конфиденциальности на www.viacomcbsprivacy.com/en/policy. Это предложение может быть
изменены или отменены в любое время. Недействительно там, где это запрещено. Не подлежит передаче, не для
перепродажи и обмену на деньги не подлежит. Могут применяться другие ограничения и налоги.
Нельзя комбинировать с любыми другими кодами или купонами Paramount+.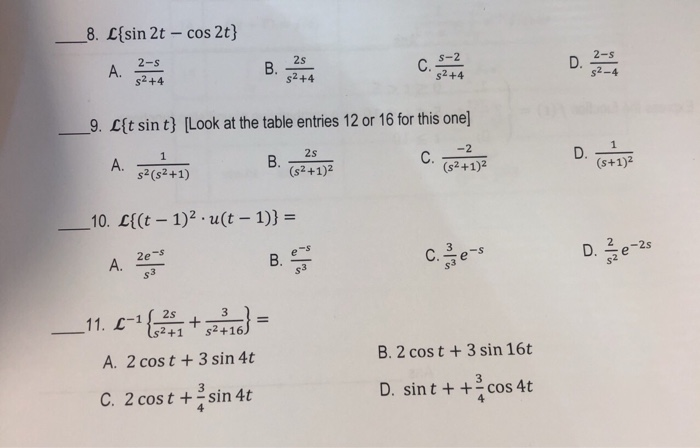
 на один год.
на один год.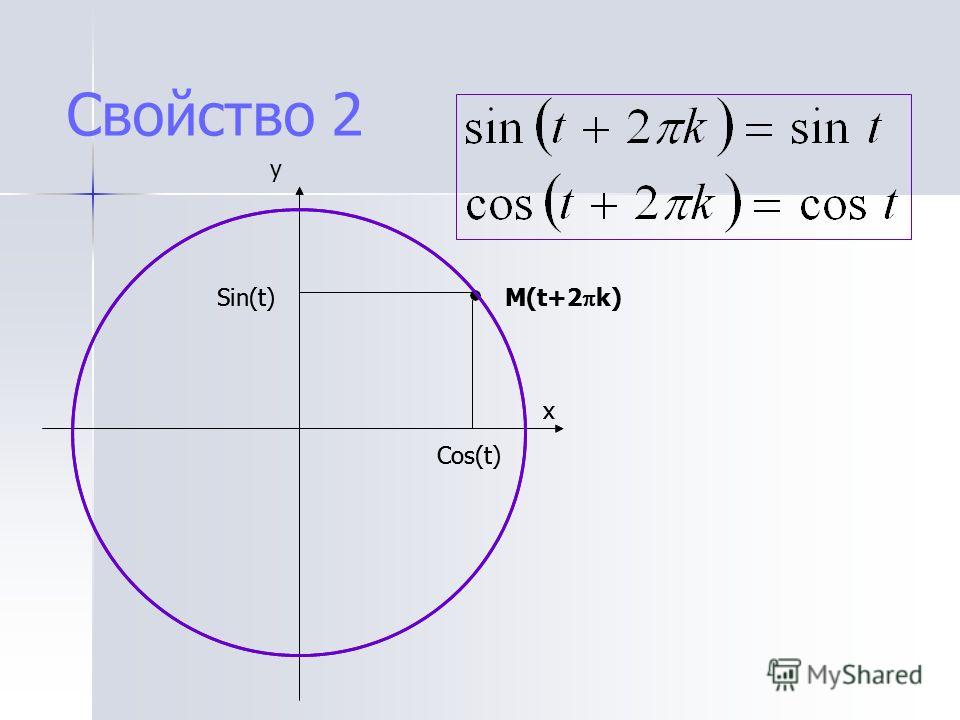 Транслируйте в прямом эфире более 85 лучших развлекательных, спортивных и новостных каналов. С 6
домашних учетных записей, включенных в вашу подписку, вы можете смотреть избранное на
запрос, или обязательно запишите их с неограниченным пространством DVR.
Транслируйте в прямом эфире более 85 лучших развлекательных, спортивных и новостных каналов. С 6
домашних учетных записей, включенных в вашу подписку, вы можете смотреть избранное на
запрос, или обязательно запишите их с неограниченным пространством DVR.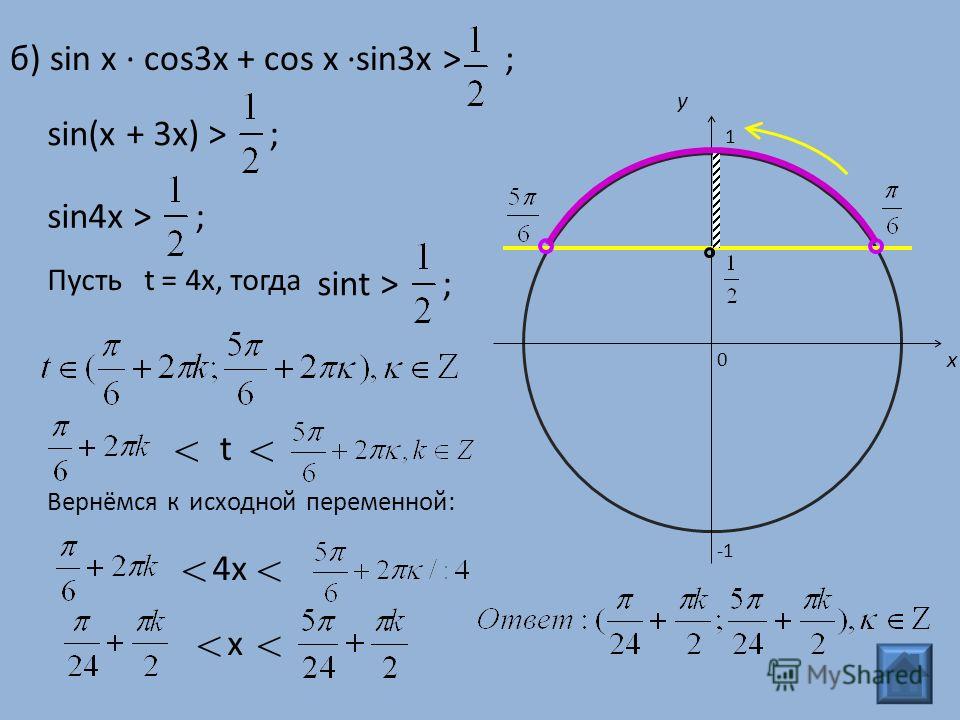 9 в месяц в течение 12 месяцев, прежде чем будет взиматься плата в размере 64,99 долларов США в месяц или по текущей ежемесячной цене подписки. Бесплатная отмена в любое время до окончания стандартной бесплатной пробной версии. Возврат средств за неполный расчетный период невозможен. Должен быть 18 лет или старше и в 50 Соединенных Штатах. За исключением клиентов T-Mobile для бизнеса. Требуется учетная запись Google. YouTube оставляет за собой право изменить или отменить предложение в любое время.
9 в месяц в течение 12 месяцев, прежде чем будет взиматься плата в размере 64,99 долларов США в месяц или по текущей ежемесячной цене подписки. Бесплатная отмена в любое время до окончания стандартной бесплатной пробной версии. Возврат средств за неполный расчетный период невозможен. Должен быть 18 лет или старше и в 50 Соединенных Штатах. За исключением клиентов T-Mobile для бизнеса. Требуется учетная запись Google. YouTube оставляет за собой право изменить или отменить предложение в любое время.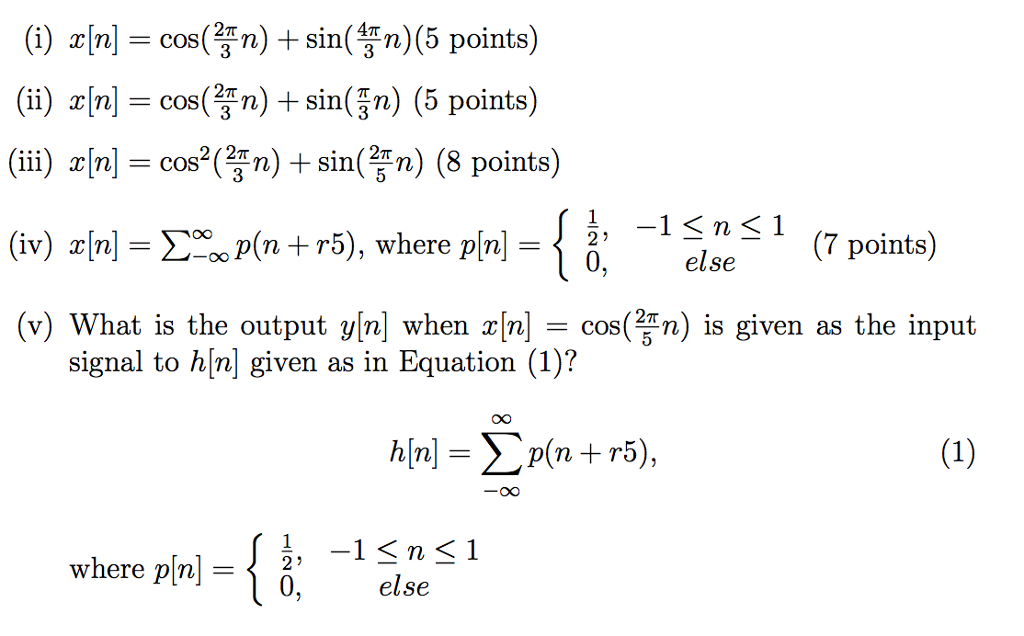 Подписка автоматически продлевается по цене 25 долларов США в месяц после первого года. Предложение Филона
доступный текущим клиентам T-Mobile Wireless и Home Internet.
Посмотреть полные условия
Подписка автоматически продлевается по цене 25 долларов США в месяц после первого года. Предложение Филона
доступный текущим клиентам T-Mobile Wireless и Home Internet.
Посмотреть полные условия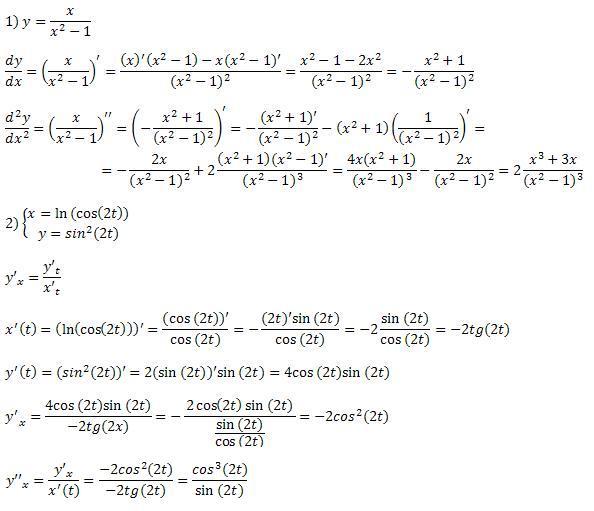 Ограничение
(1) Предложение для каждого клиента, только для одноразового использования. Предложение/скидка не подлежит передаче другому лицу, не может быть
перепроданы или выкуплены за наличные и не могут сочетаться с другими предложениями, скидками или
рекламные акции (если иное прямо не разрешено Philo). Скидка заканчивается, если учетная запись T-Mobile
прекращено; Подписка Philo автоматически возвращается к текущей полной стоимости подписки.
ВАЖНОЕ ЗАМЕЧАНИЕ. Для активации требуется действительная платежная информация и подписка.
Предложение. Если вы не отмените в течение применимого пробного периода (7 дней бесплатно или 12 месяцев
со скидкой), с вас будет взиматься соответствующая месячная сумма плюс налоги на повторяющиеся
основе после завершения испытаний. Перейдите на страницу своей учетной записи Philo, чтобы отменить подписку. Отмена вступает в силу
в дату следующего ежемесячного выставления счета (без возврата за неполные расчетные периоды). Искупление этого
Предложение означает принятие настоящих Условий и всех применимых Условий и положений, см.
Ограничение
(1) Предложение для каждого клиента, только для одноразового использования. Предложение/скидка не подлежит передаче другому лицу, не может быть
перепроданы или выкуплены за наличные и не могут сочетаться с другими предложениями, скидками или
рекламные акции (если иное прямо не разрешено Philo). Скидка заканчивается, если учетная запись T-Mobile
прекращено; Подписка Philo автоматически возвращается к текущей полной стоимости подписки.
ВАЖНОЕ ЗАМЕЧАНИЕ. Для активации требуется действительная платежная информация и подписка.
Предложение. Если вы не отмените в течение применимого пробного периода (7 дней бесплатно или 12 месяцев
со скидкой), с вас будет взиматься соответствующая месячная сумма плюс налоги на повторяющиеся
основе после завершения испытаний. Перейдите на страницу своей учетной записи Philo, чтобы отменить подписку. Отмена вступает в силу
в дату следующего ежемесячного выставления счета (без возврата за неполные расчетные периоды). Искупление этого
Предложение означает принятие настоящих Условий и всех применимых Условий и положений, см. philo.com/terms/#philo-promotions для получения более подробной информации. T-Mobile оставляет за собой право изменять
настоящей Оферты в любое время. Philo оставляет за собой право изменить или отменить это Предложение в любое время.
Недействительно там, где облагаются налогом, запрещены или ограничены.
philo.com/terms/#philo-promotions для получения более подробной информации. T-Mobile оставляет за собой право изменять
настоящей Оферты в любое время. Philo оставляет за собой право изменить или отменить это Предложение в любое время.
Недействительно там, где облагаются налогом, запрещены или ограничены.
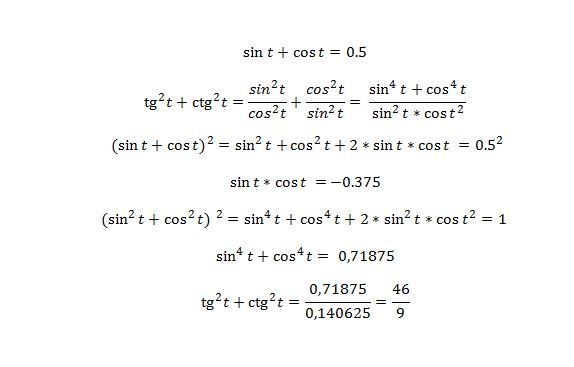 Использование службы Pluto TV и создание учетной записи регулируются Условиями использования Pluto Inc., доступными по адресу https://corporate.pluto.tv/terms-of-use/, и Политикой конфиденциальности по адресу https://www.viacomcbsprivacy.com/en/policy?r=pluto.tv. Это предложение и эксклюзивный опыт могут быть изменены или отменены в любое время. Недействительно там, где это запрещено. Не подлежит передаче, не для перепродажи и не подлежит обмену на наличные деньги. Могут применяться другие ограничения.
Использование службы Pluto TV и создание учетной записи регулируются Условиями использования Pluto Inc., доступными по адресу https://corporate.pluto.tv/terms-of-use/, и Политикой конфиденциальности по адресу https://www.viacomcbsprivacy.com/en/policy?r=pluto.tv. Это предложение и эксклюзивный опыт могут быть изменены или отменены в любое время. Недействительно там, где это запрещено. Не подлежит передаче, не для перепродажи и не подлежит обмену на наличные деньги. Могут применяться другие ограничения. Отменить в любое время. Посмотреть полные условия
Отменить в любое время. Посмотреть полные условия Должен иметь соответствующую услугу T-Mobile. Максимум 1 предложение/аккаунт. Ссылки на выкуп можно использовать только один раз; не подлежат передаче, не имеют денежной стоимости и не могут быть обменены на наличные или в кредит или проданы.
Должен иметь соответствующую услугу T-Mobile. Максимум 1 предложение/аккаунт. Ссылки на выкуп можно использовать только один раз; не подлежат передаче, не имеют денежной стоимости и не могут быть обменены на наличные или в кредит или проданы.
 Использование сервиса Pandora регулируется
Условия использования и политика конфиденциальности Pandora доступны на сайте www.pandora.com. Для начала каждого
Ad-Free Radio Weekend, вы увидите короткое вступительное видео на мобильном телефоне Pandora.
приложение. Пользователи Pandora с поддержкой рекламы получат доступ как к AdFree Radio Weekends, так и к
Специальное развлечение SiriusXM. Подписчики Pandora Plus и Premium получат только
Развлечение SiriusXM и не имеют права на получение наличных денег или кредита для Ad-Free Radio.
Время выходных. Ad-Free означает, что платная сторонняя реклама не будет показываться против Pandora.
Музыкальные радиостанции, за исключением того, что в начале каждого радио без рекламы может показываться реклама.
Опыт прослушивания выходного дня. Объявления станций или комментарии ведущего/исполнителя
включены в контент без рекламы. Выходные начинаются в субботу в 12:00 и заканчиваются в воскресенье.
11:59вечера.
Использование сервиса Pandora регулируется
Условия использования и политика конфиденциальности Pandora доступны на сайте www.pandora.com. Для начала каждого
Ad-Free Radio Weekend, вы увидите короткое вступительное видео на мобильном телефоне Pandora.
приложение. Пользователи Pandora с поддержкой рекламы получат доступ как к AdFree Radio Weekends, так и к
Специальное развлечение SiriusXM. Подписчики Pandora Plus и Premium получат только
Развлечение SiriusXM и не имеют права на получение наличных денег или кредита для Ad-Free Radio.
Время выходных. Ad-Free означает, что платная сторонняя реклама не будет показываться против Pandora.
Музыкальные радиостанции, за исключением того, что в начале каждого радио без рекламы может показываться реклама.
Опыт прослушивания выходного дня. Объявления станций или комментарии ведущего/исполнителя
включены в контент без рекламы. Выходные начинаются в субботу в 12:00 и заканчиваются в воскресенье.
11:59вечера.