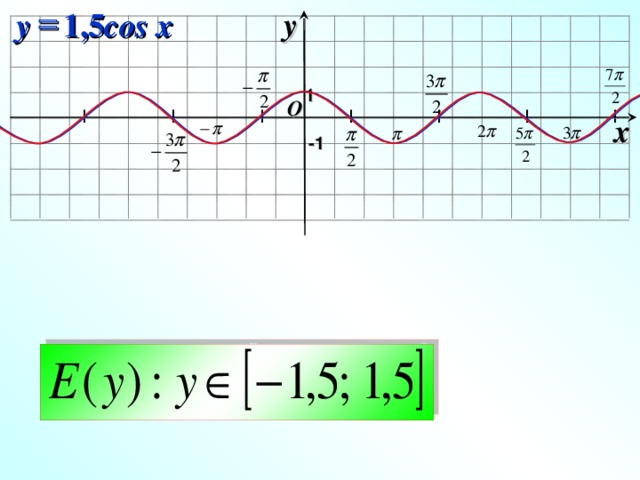
 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.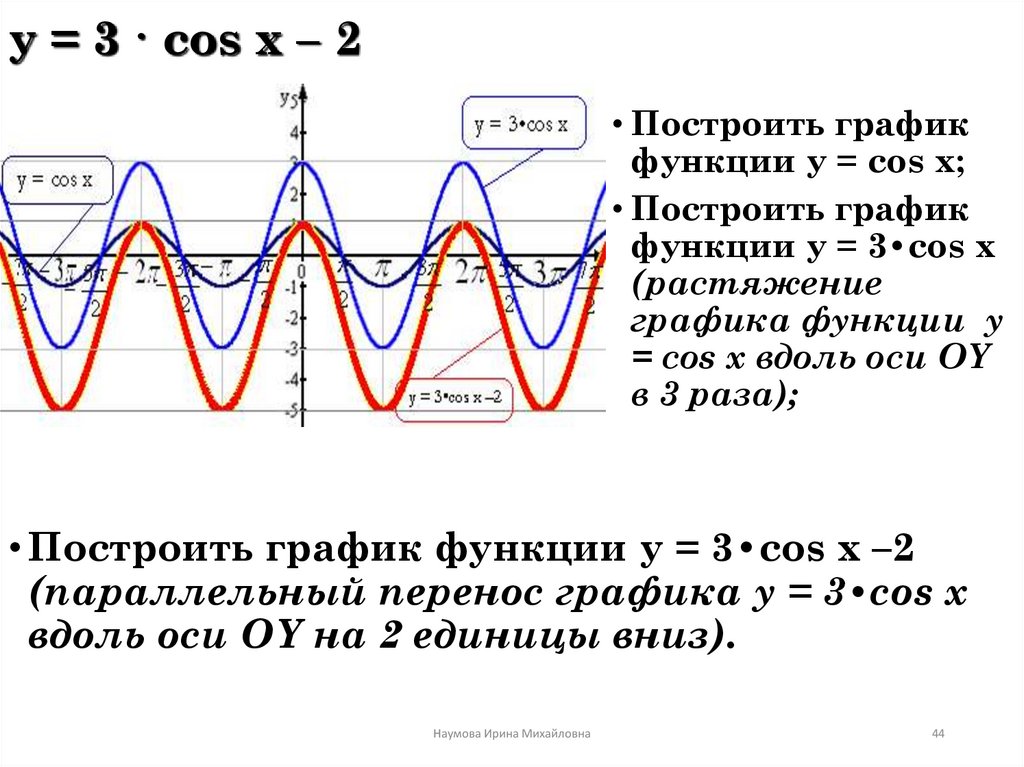 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.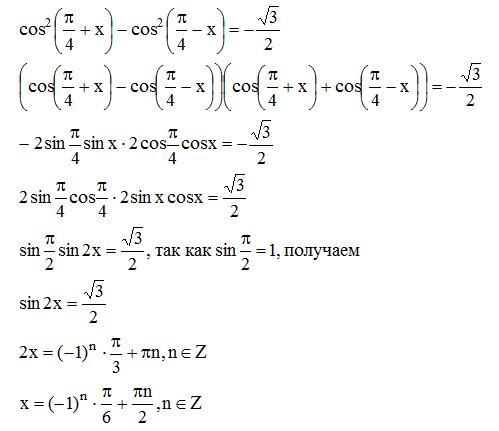 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | sin((4pi)/3) | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град.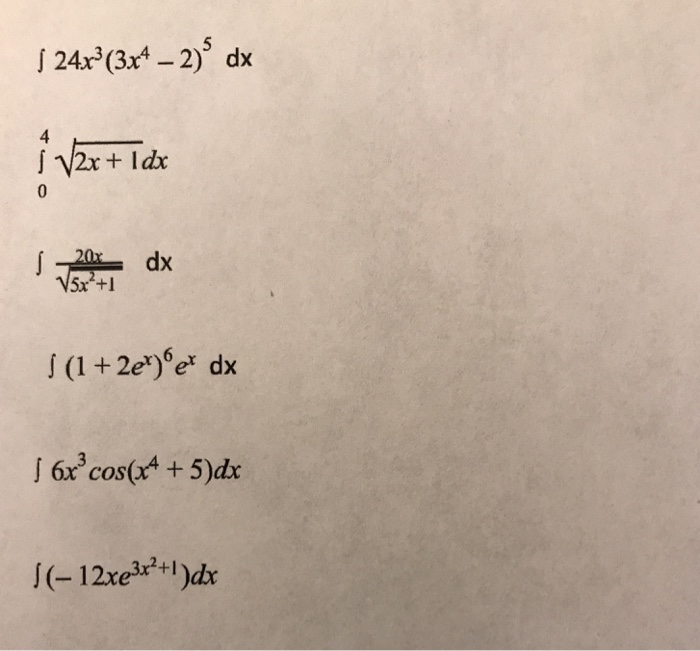 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Решение неоднородных уравнений первой степени относительно sin x и cos x
- Жукова Екатерина Александровна
При изучении темы «Решение тригонометрических уравнений» в курсе алгебры и начал анализа в 10 классе достаточное внимание уделяется рассмотрению примеров решений уравнений, сводящихся к квадратным и решению однородных уравнений первой и второй степени относительно sin x и cos x. При этом практически не рассматриваются примеры решения уравнений первой степени, являющихся неоднородными относительно функций sin x и cos x.
Изучая в школьном курсе 10 класса тему «Преобразование тригонометрических выражений», целесообразно ввести формулу a sinx + b cosx = sin(x+), где tg = . В дальнейшем она будет использоваться при решении неоднородных линейных уравнений. Формулы универсальной подстановки и формулы половинного аргумента выводятся в теме «Преобразование тригонометрических выражений» при выполнении заданий на упрощение тригонометрических выражений.
Цели:
- ввести понятие неоднородного тригонометрического уравнения I степени;
- ознакомить с алгоритмами решения неоднородных тригонометрических уравнений I степени;
- проверить прочность усвоения ранее изученных формул тригонометрии.

Тип урока: комбинированный.
Форма проведения: индивидуальная и фронтальная работа с учащимися.
I. Организационный момент
Вступительное слово учителя: Изучение темы «Решение тригонометрических уравнений» кроме рассмотренного нами ранее вопроса о способах решения однородных тригонометрических уравнений I степени предполагает также рассмотрение способов решения неоднородных тригонометрических уравнений. Но прежде, чем мы перейдем к изучению нового материала, необходимо вспомнить применение формул тригонометрии при решении уравнений и неравенств.
II. Актуализация опорных знаний, умений
Математический диктант (10-12 минут).
| I вариант | II вариант |
|
|
| Ответы варианта I | Ответы варианта II |
|
|
По окончанию самостоятельной работы учащиеся меняются тетрадями и проводят взаимопроверку. Правильные ответы заранее записаны учителем на закрытой доске.
Правильные ответы заранее записаны учителем на закрытой доске.
III. Формирование новых знаний и понятий
Слова учителя: Теперь мы переходим к новой теме нашего занятия – решению неоднородных тригонометрических уравнений I степени.
Дается определение: Уравнение вида a sin x + b cos x = c, где а, b, с не равны 0, называется неоднородным тригонометрическим уравнением I степени.
Данное уравнение может быть решено тремя способами.
Первый способ – универсальная подстановка
sin x =
cos x =
Второй способ – введение дополнительного угла
a sinx + b cosx = sin(x+), где = arctg если a + b c, то уравнение имеет корни
Третий способ – переход к функциям половинного аргумента
sin x = 2 sin cos
cos x = cos — sin
IV.
 Применение знаний, навыков, понятий
Применение знаний, навыков, понятийЗадания на отработку применения разобранных способов решения неоднородных тригонометрических уравнений. Решаются у доски учениками с помощью учителя:
1-й ученик
1) sin 2x + cos 2x = sin 3x (через введение дополнительного угла)
Решение
sin (2x + ) = sin 3x
sin (2x + ) = sin 3x
sin (2x + ) — sin 3x = 0
2 sin cos = 0sin () = 0
sin ( — ) = 0
x = + 2n, где nили cos () = 0
cos ( + ) = 0
x = + , где n
2-й ученик
2) 3 sin x – 4 cos x = 5 (применение универсальной подстановки)
Решение
3 — 4 = 5
6 tg — 4 (1 — tg) = 5 (1 + tg)
(tg — 3) = 0
x = 2 arctg3 + 2n, где n
3-й ученик
3) cos x – sin x = 1 (через переход к функциям половинного аргумента)
Решение
cos — sin — 2 sincos = sin + cos
2 sin(sin + cos) = 0sin = 0
x = 2nили sin + cos = 0 – однородное первой степени
tg = -1
x = — + 2n
Для самостоятельной работы учащихся (перед началом указываются способы решения):
1) sin x + cos x = (через введение дополнительного угла)
Решение
sin (x + ) =
sin (x + ) = 1
x = + 2n, где n
2) 3 sin x + 5 cos x= 6 (универсальная подстановка)
Решение
3 + 5 = 6
6 tg +5 — 5 tg = 6 + 6 tg
11 tg — 6 tg + 1= 0
решений нет, так как D<0
3) sin x + cos x = 1 (формулы половинного аргумента)
2 sin cos + cos — sin = cos + sin
2 sin cos — 2 sin = 0
2 sin( cos — sin) = 0sin = 0
x = 2n, где nили cos — sin = 0
tg = 1
x = + 2n, где n
V.
 Итог урока
Итог урокаПодвести итог урока. Сообщить учащимся оценки, отметить наиболее активных.
VI. Домашняя работаДомашняя контрольная работа по учебнику Колмогорова, стр. 285, № 152- 154 (задания а и б), №162 (задания а и в).
Синус и косинус равны не табличному значению. Как решить уравнение? Часть 2
Синус равен не стандартному значению
В прошлой статье мы разобрали как решать простейшие тригонометрические уравнения со стандартными значениями, т.е. вот эти:
Но бывает так, что нужно решить уравнение, в котором синус равен не табличному значению. Например, как решить уравнение \(\sinx= \frac{1}{3}\)? Давайте обо всем по порядку.
Сначала действуем, как и при решении стандартных уравнений:
1. Чертим оси и тригонометрический круг
Чертим оси и тригонометрический круг
2. На оси синусов отмечаем нужное значение
3. Проводим к оси перпендикуляр
А что дальше? Какие значения будут получаться на круге? Не \(\frac{π}{6}\), не \(\frac {π}{4}\), и даже не \(\frac{π}{7}\) — вообще никакие привычные числа не подходят. Однако при этом очевидно, что значения эти есть. Но как их записать? Вот тут-то на помощь и приходит арксинус! Значение правой точки равно \(\arcsin\frac{1}{3}\). Почему? Да потому что синус равен \(\frac{1}{3}\) .
Ок, значение правой точки найдено, как найти значение левой? Давайте подумаем. Значение дуги от нуля до правой точки равно \(\arcsin\frac{1}{3}\).
Но дуга от \(π\) до левой точки имеет такую же длину:
Значит, если мы пройдем от \(π\) против часовой стрелки на величину \(\arcsin\frac{1}{3}\) мы попадем в левую точку. Иными словами, значение в левой точке равно \(π-\arcsin\frac{1}{3}\).
Теперь мы можем записать все корни уравнения: \( \left[ \begin{gathered} x_1=\arcsin\frac{1}{3}+2πn\\ x_2=π-\arcsin\frac{1}{3}+2πn, \, n∈Z\end{gathered}\right.\). Не понимаешь откуда появилось «\(2πn\)» и «\(n∈Z\)» ? Смотри это и это видео!
Готово.
Без арксинусов решить уравнение \(\sinx=\frac{1}{3}\) не получилось бы, потому что мы не смогли бы записать итоговый ответ. Аналогично и с уравнением \(\sinx=0,125\), \(\sinx=-\frac{1}{9}\), \(\sinx=\frac{1}{\sqrt{3}}\) и многими другими. Фактически без арксинуса мы можем решать только 9 простейших, базовых, уравнений с синусом:
С арксинусом – бесконечное количество.
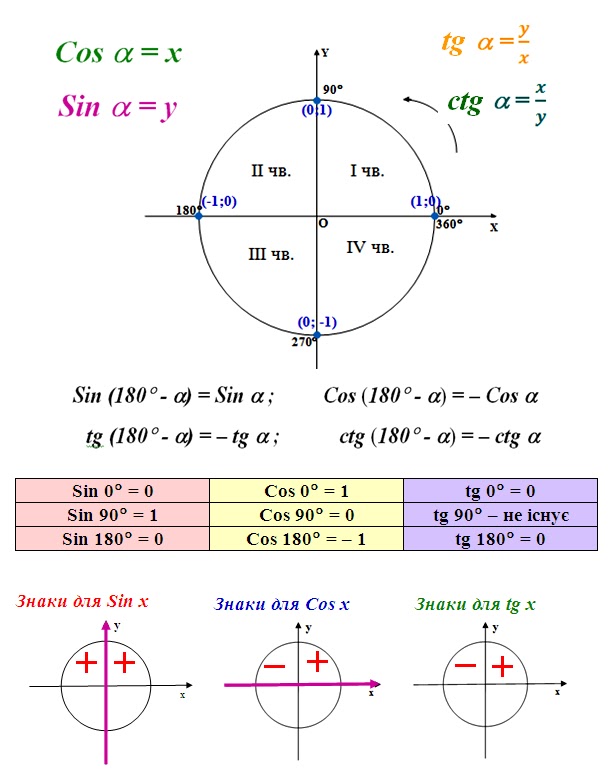
Алгоритм решения простейших уравнений с синусом
Шаг 1. Построить окружность и оси синусов и косинусов.
Шаг 2. Отметить на оси синусов значение, которому синус должен быть равен.
Шаг 3. Провести перпендикуляр и отметить точки пересечения перпендикуляра и круга. Если пересечений нет, то уравнение не имеет решений.
Провести перпендикуляр и отметить точки пересечения перпендикуляра и круга. Если пересечений нет, то уравнение не имеет решений.
Шаг 4. Найти по одному значению каждой из полученных точек на круге. Если синус равен не стандартному числу, то правую точку на круге можно отметить, как \(\arcsina\), а левую как \(π-\arcsina\).
Шаг 5. Записать все значения каждой точки используя формулу \(x=t_0+2πn\), \(n∈Z\), где \(t_0\) – как раз те значения точек, которые вы нашли в шаге 4.
Пример: \(\sinx=-\frac{\sqrt{2}}{4}\)
Или если воспользоваться свойством арксинуса \(\arcsin(-a)=-\arcsina\):
Ответ: \( \left[ \begin{gathered} x=π+\arcsin\frac{\sqrt{2}}{4}+2πn\\ x=-\arcsin\frac{\sqrt{2}}{4}+2πn, \, n∈Z\end{gathered}\right.\)
Как делать не надо:
\(\sinx=\frac{1}{2}\)
Ответ: \( \left[ \begin{gathered} x=\arcsin\frac{1}{2}+2πn\\ x=π-\arcsin\frac{1}{2}+2πn, \, n∈Z\end{gathered}\right.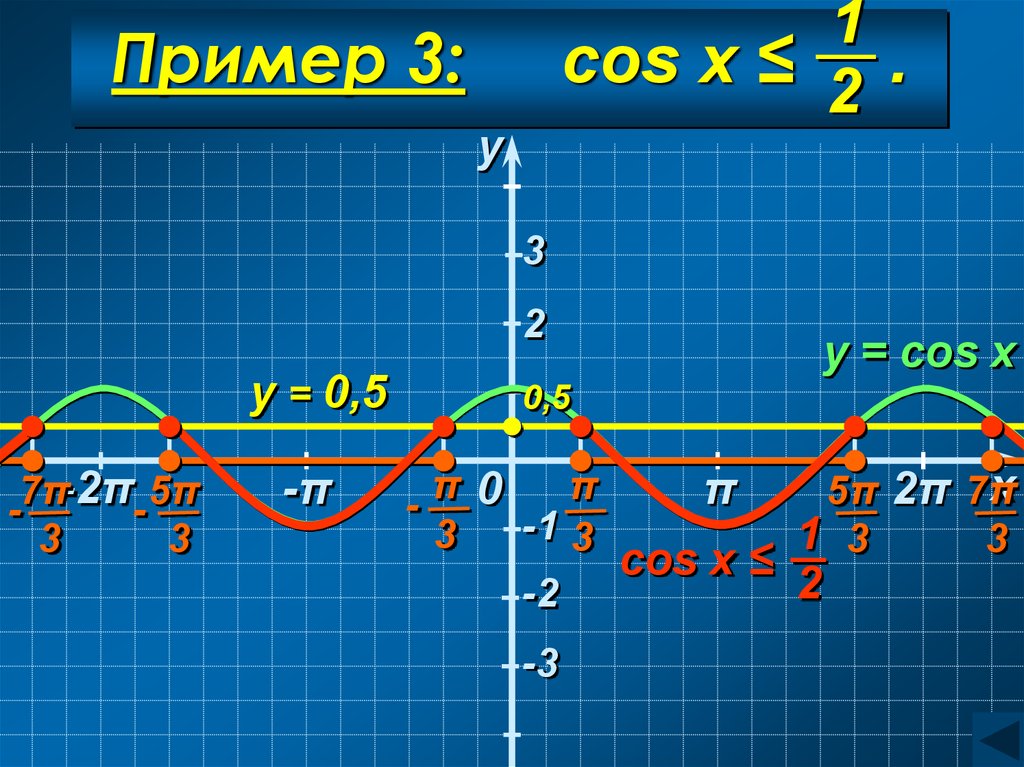 \)
\)
Это стандартное уравнение — его можно решить с помощью круга, либо просто вычислить \(\arcsin\frac{1}{2}= \frac{π}{6}\). В любом случае корректным ответом здесь будет:
\( \left[ \begin{gathered} x=\frac{π}{6}+2πn\\ x=\frac{5π}{6}+2πn, \, \end{gathered}\right.\) \(n∈Z\)
Запомните! В математике принято вычислять ответы до конца, поэтому если арксинус берется для стандартной точки и может быть посчитан – его надо вычислить. Потому что ответ с \(\arcsin\frac{1}{2}\) и тому подобным будет выглядеть столь же странно, как ответ \(x=\frac{6}{3}\) в линейном уравнении \(3x=6\).
Больше примеров использования алгоритма читай в этой статье: простейшие уравнения с синусом и косинусом.
Косинус равен не стандартному значению
Предположим, надо решить уравнение \(\cosx=\frac{1}{3}\). Как это сделать?
Тут логика такая же, как и в уравнении с синусом: косинус одной трети равняться может, следовательно, и значение должно быть таким, при котором косинус будет равен \(\frac{1}{3}\). Очевидное решение — использовать арккосинус.
Очевидное решение — использовать арккосинус.
Несложно заметить, что дуга от нуля до нижней точки имеет такую же длину, как и от нуля до верхней, но только она откладывается в отрицательном направлении (по часовой стрелке). Поэтому одно из значений второй точки: \(-\arccos\frac{1}{3}\)
И теперь можно записать общий ответ: \(x=±\arccos\frac{1}{3}+2πn\), \(n∈Z\).
Алгоритм решения простейших уравнений с косинусом
Шаг 1. Построить окружность и оси синусов и косинусов.
Шаг 2. Отметить на оси косинусов значение, которому косинус должен быть равен.
Шаг 3. Провести перпендикуляр и отметить точки пересечения перпендикуляра и круга. Если пересечений нет, то уравнение не имеет решений.
Шаг 4. Найти по одному значению каждой из полученных точек на круге. Если косинус равен не стандартному числу, то верхнюю точку на круге можно отметить, как \(\arccosa\), а нижнюю как \(-\arccosa\).
Шаг 5. Записать все значения каждой точки используя формулу \(x=t_0+2πn\), \(n∈Z\), где \(t_0\) – как раз те значения точек, которые вы нашли в шаге 4.
Пример: \(\cosx=-\frac{8}{7}\).
Решение:
Важно быть начеку, а не штампованно везде писать аркфункции. Пересечения с окружность нет, значит и решений нет.
Ответ: нет решений.
Пример: \(\cosx=-\frac{3}{4}\).
Или если применить формулу \(\arccos(-a)=π-\arccosa\)
Ответ: \(π±\arccos \frac{3}{4}+2πn\), \(n∈Z\).
3
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус (-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан( квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Калькулятор — cos(-1.
 5) — Solumaths
5) — SolumathsCos, расчет онлайн
Резюме:
Тригонометрическая функция cos вычисляет cos угла в радианах, градусов или градианов.
cos online
Описание:
Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить косинус , синус и касательная угла через одноименные функции.
Тригонометрическая функция косинус отметил косинус , позволяет вычислить косинус угла онлайн , можно использовать разные угловые единицы: градусы, грады и радианы, которые по умолчанию являются угловыми единицами.
- Расчет косинуса
- Специальные значения косинуса
- Основные свойства
Вычисление косинуса угла в радианах
Калькулятор косинуса позволяет через функцию cos вычислить г. онлайн косинус угла в радианах, вы должны сначала
выберите нужную единицу, нажав на кнопку параметров расчетного модуля.
После этого можно приступать к расчетам.
онлайн косинус угла в радианах, вы должны сначала
выберите нужную единицу, нажав на кнопку параметров расчетного модуля.
После этого можно приступать к расчетам.
Чтобы вычислить косинус онлайн от `pi/6`, введите cos(`pi/6`), после вычисления результат `sqrt(3)/2` возвращается.
Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.
г.Вычислить косинус угла в градусах
Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить косинус числа 90, введите cos(90). возвращает 0.
Вычисление косинуса угла в градианах
Чтобы вычислить косинус угла в градианах, необходимо сначала выбрать нужную единицу измерения
нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
После этого можно приступать к вычислениям.
Чтобы вычислить косинус 50, введите cos(50), после вычисления возвращается результат `sqrt(2)/2`.
Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.
Косинус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот список специальные значения косинуса :
| cos(`2*pi`) | `1` | |
| cos(`pi`) | `-1` | |
| cos(`pi/2`) 0 0 0 04 90 90 90 | ||
| cos(`pi/4`) | `sqrt(2)/2` | |
| cos(`pi/3`) | `1/2` | |
| `sqrt(3)/2` | ||
| cos(`2*pi/3`) | `-1/2` | |
| cos(`3*pi/4`) | `-sqrt(2)/2` | |
| cos(`5*pi/6`) | `-sqrt(3)/2` | |
| cos(`0`) | `1` | cos( | *s) pi`) | `1` |
| cos(`-pi`) | `-1` | |
| cos(`pi/2`) | `09` 90`90`105 90 pi/4`) | `sqrt(2)/2` |
| cos(`-pi/3`) | `1/2` | |
| cos(`-pi/6`) | `sqrt(3)/2` | |
| cos(`-2*pi/3`) | `-1/2` | |
| cos(`-3*pi/4`) | `-sqrt(2)/2` | |
| cos(`-5*pi/6`) | `-sqrt(3)/2` |
`AA x в RR, k в ZZ`,
- `cos(-x)= cos(x)`
- `cos(x+2*k*pi)=cos(x)`
- `cos(pi-x)=-cos(x) `
- `cos(pi+x)=-cos(x)`
- `cos(pi/2-x)=sin(x)`
- `cos(pi/2+x)=-sin(x) )`
Производная косинуса равна -sin(x).
Первообразная косинуса равна sin(x).
Функция косинуса является четной функцией для каждого действительного x, `cos(-x)=cos(x)`. Следствием для кривой, представляющей функцию косинуса, является то, что она допускает ось ординат как ось симметрии.
Калькулятор имеет решатель, который позволяет решать уравнение с косинусом вида cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `cos(x)=1/2` или же `2*cos(x)=sqrt(2)` с этапами расчета.
Синтаксис:
cos(x), где x — мера угла в градусах, радианах или градах.
Примеры:
cos(`0`), возвращает 1
Производная косинус :
Чтобы дифференцировать функцию косинуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции косинуса
Первообразная косинуса :
Калькулятор первообразной позволяет вычислить первообразную функции косинуса.
Первообразная cos(x) есть первопроизводная(`cos(x)`)=`sin(x)`
Предельный косинус :
Калькулятор пределов позволяет вычислять пределы функции косинуса.
предел cos(x) is limit(`cos(x)`)
Обратная функция косинуса :
обратная функция косинуса представляет собой функцию арккосинуса, отмеченную как arccos.
Графический косинус:
Графический калькулятор может строить косинусоидальную функцию в заданном интервале.
Свойство функции косинуса:
Функция косинуса является четной функцией.
Расчет онлайн с косинусом
См. также
Список связанных калькуляторов:
- г.
 Арккосинус: арккос. Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Арккосинус: арккос. Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. - Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упрощение калькулятора: упрощение. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Синус : син. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
- Касательная: рыжевато-коричневая. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
Тригонометрические функции | Реальные функции
numpy.sum — NumPy v1.23 Manual
- numpy.sum( a , axis=None , dtype=None , out=None , keepdims=<нет значения> , initial=<нет значения> , где=<нет значения> )[источник]
Сумма элементов массива по заданной оси.

- Параметры
- a array_like
Элементы для суммирования.
- ось Нет или целое или кортеж целых чисел, необязательный
Ось или оси, вдоль которых выполняется суммирование. По умолчанию, axis=None, суммирует все элементы входного массива. Если ось отрицательная, она считает от последней до первой оси.
г.Новое в версии 1.7.0.
Если ось представляет собой набор целых чисел, суммирование выполняется по всем осям указывается в кортеже вместо одной оси или всех осей как до.
- dtype dtype, необязательный
Тип возвращаемого массива и аккумулятора, в котором элементы суммируются. По умолчанию используется dtype a , если только a имеет целочисленный dtype с меньшей точностью, чем платформа по умолчанию целое число. В таком случае, если a подписывается, затем целое число платформы используется, в то время как если a без знака, то беззнаковое целое число используется та же точность, что и для целого числа платформы.

- out ndarray, необязательный
Альтернативный выходной массив, в который следует поместить результат. Он должен иметь той же формы, что и ожидаемый результат, но тип вывода значения будут преобразованы в случае необходимости.
- keepdims bool, опционально
Если установлено значение True, уменьшаемые оси остаются в результате как размеры с размером один. С этой опцией результат будет корректно транслироваться относительно входного массива.
г.Если передано значение по умолчанию, то keepdims не будет прошел через метод
суммаподклассовndarray, однако любое значение, отличное от значения по умолчанию, будет. Если метод подкласса не реализует keepdims любой исключения будут подняты.- начальный скалярный, необязательный
Начальное значение для суммы. Подробнее см.
уменьшить.
Новое в версии 1.15.0.
- где array_like of bool, необязательный
Элементы для включения в сумму. Подробнее см.
уменьшить.Новое в версии 1.17.0.
- Возвращает
- sum_along_axis ndarray
Массив той же формы, что и a , с указанным ось снята. Если a является массивом 0-d, или если ось имеет значение None, скаляр возвращается. Если указан выходной массив, ссылка на из возвращается.
См. также
-
ndarray.sum Эквивалентный метод.
-
add.reduce Эквивалентная функциональность
add.-
cumsum Накопленная сумма элементов массива.
-
trapz Интегрирование значений массива с помощью составного правила трапеций.
г.
-
среднее,среднее
Примечания
Арифметика является модульной при использовании целочисленных типов, и ошибка не возникает. поднимается при переполнении.
Сумма пустого массива является нейтральным элементом 0:
>>> np.sum([]) 0,0
Для чисел с плавающей запятой числовая точность суммы (и
np.add.reduce) обычно ограничивается прямым добавлением каждого числа индивидуально к результату, вызывая ошибки округления на каждом шаге. Однако часто numpy будет использовать численно лучший подход (частичный попарное суммирование), что приводит к повышению точности во многих случаях использования. Эта повышенная точность всегда обеспечивается, когда нетосьдана. Когдазадается ось, это будет зависеть от того, какая ось суммируется. Технически, чтобы обеспечить максимально возможную скорость, повышенная точность используется только при суммировании по быстрой оси в памяти. Обратите внимание, что точная точность может варьироваться в зависимости от других параметров.
В отличие от NumPy, функция Python
Обратите внимание, что точная точность может варьироваться в зависимости от других параметров.
В отличие от NumPy, функция Python math.fsumиспользует более медленную, но более точный подход к суммированию. Особенно при суммировании большого количества чисел с плавающей запятой более низкой точности. числа, напримерfloat32числовые ошибки могут стать значительными. В таких случаях рекомендуется использовать dtype=»float64″ для использования более высокого точность на выходе.Примеры
>>> np.sum([0.5, 1.5]) 2.0 >>> np.sum([0,5, 0,7, 0,2, 1,5], dtype=np.int32) 1 >>> np.sum([[0, 1], [0, 5]]) 6 >>> np.sum([[0, 1], [0, 5]], ось=0) массив ([0, 6]) >>> np.sum([[0, 1], [0, 5]], ось = 1) массив([1, 5]) >>> np.sum([[0, 1], [np.nan, 5]], где=[Ложь, Истина], ось=1) массив([1., 5.])
Если аккумулятор слишком мал, происходит переполнение:
>>> np.ones(128, dtype=np.int8).sum(dtype=np.int8) -128
Вы также можете начать суммирование со значения, отличного от нуля:
>>> np.
 sum([10], начальный=5)
15
sum([10], начальный=5)
15
Важные вопросы для 10 класса по математике Глава 8 Введение в тригонометрию
Введение в тригонометрию 10 класс Важные вопросы Очень короткий ответ (1 балл)
Вопрос 1.
Если tan θ + cot θ = 5, найдите значение tan2θ + раскладушка θ. (2012)
Решение:
tan θ + cot θ = 5 … [Дано
tan 2 θ + cot 2 θ + 2 tan θ cot θ = 25 … [Квадрат обеих сторон θ + 2 = 25
∴ tan 2 θ + cot 2 θ = 23
Вопрос 2.
Если sec 2A = cosec (A – 27°), где 2A — острый угол, найдите величину ∠A . (2012, 2017D)
Решение:
с 2A = cosec (A – 27°)
cosec(90° – 2A) = cosec(A – 27°) …[∵ sec θ = cosec (90° – θ)
90 ° – 2А = А – 27° 9{\circ}}{3}\) = 39°
Вопрос 3.
Если тангенс α = \(\sqrt{3}\) и тангенс β = \(\frac{1}{\sqrt{3}} \),0 < α, β < 90°, найти значение ctg (α + β). (2012)
Решение:
тангенс α = \(\sqrt{3}\) = тангенс 60° … (i)
тангенс β = \(\frac{1}{\sqrt{3}}\) = тангенс 30 ° …(ii)
Решение (i) и (ii), α = 60° и β = 30°
∴ cot (α + β) = cot (60° + 30°) = cot 90° = 0
Вопрос 4. {2} \theta+2 \cos \theta}{3 \cos \theta+2}\). (2015)
{2} \theta+2 \cos \theta}{3 \cos \theta+2}\). (2015)
Решение:
\(\sqrt{3}\) sin θ = cos θ … [Дано
Вопрос 10.
Вычислить: sin 2 19° + sin 7 71°. (2015)
Решение:
sin 2 19° + sin 2 71°
= sin 2 19° + sin 2 (90° – 19°)…[∵ sin(90° – θ) = cos θ
= sin 2 19° + cos 2 19° = 1 …[∵ sin 2 θ + cos 2 θ = 1
Вопрос 11.
Что происходит при увеличении значения cos от 0° до 9{2}/латекс] = 1 + [латекс]\)
= \(\frac{144+25}{144}=\frac{169}{144}\)
cosec B = \(\frac{13} {12}\) ∴ sin B = \(\frac{12}{13}\)
2-й метод:
tan B = \(\frac{12}{5}\)
tan B = \(\frac {AC}{BC}\)
Пусть AC = 12k, BC = 5k
In rt. ∆ACB,
AB 2 = AC 2 + BC 2 …[Pythagoras theorem
AB 2 = (12k) 2 + (5k) 2
AB 2 = 144k 2 + 25к 2 2 = 169к 2
AB = 13k
∴ sin B = \(\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{12 \mathrm{k}}{13 \mathrm{k}}= \frac{12}{13}\)
Вопрос 14.
Если ∆ABC направлена под прямым углом к B, каково значение sin (A + C). (2015)
Решение:
∠B = 90° …[Дано
∠A + ∠B + ∠C = 180° …[Свойство суммы углов a ∆
∠A + ∠C + 90° = 180°
∠ A + ∠C = 90°
∴ sin (A + C) = sin 90° = 1 …(принимая sin с обеих сторон
Введение в тригонометрию Класс 10 Важные вопросы Краткий ответ-I (2 балла)
Вопрос 15.
Оценка: tan 15° . загар 25°, загар 60°. загар 65°. тангенс 75° – тангенс 30°. (2013)
Решение:
tan 15°. загар 25°, загар 60°. загар 65°. tan 75° – tan 30°
= tan(90° – 75°) tan(90° – 65°). \(\sqrt{3}\) . загар 65°. tan 75° – \(\frac{1}{\sqrt{3}}\)
Вопрос 16.
Выразите cot 75° + cosec 75° через тригонометрические соотношения углов от 0° до 30°. (2013)
Решение:
cot 75° + cosec 75°
= cot(90° – 15°) + cosec(90° – 15°)
= tan 15° + sec 15° …[cot(90°-A) = tan A
cosec(90° – A) = sec A
Вопрос 17.
Если cos (A + B) = 0 и sin ( A – B) = 3, затем найдите значения A и B, где A и B — острые углы. (2012)
(2012)
Решение:
Подставляя значение B в (i), получаем
⇒ A = 30° + 30° = 60°
∴ A = 60°, B = 30°
Вопрос 18.
Если A, B и C — внутренние углы ∆ABC, покажите, что sin \(\left(\frac{A+B}{2}\right)\) = cos\(\left(\frac{c}{ 2}\справа)\). (2012)
Решение:
В ∆ABC, ∠A + ∠B + ∠C = 180° … (Свойство суммы углов ∆
∠A + ∠B = 180° – ∠C
Вопрос 19.
Если x = p sec (2014)
Решение: 2 – y 2
= (p сек θ + q тангенс θ) 2 – (p тангенс θ + q сек θ) 2
= p 2 сек θ 6 q θ + 2 PQ Sec 2 TAN 2 -(P 2 TAN 2 θ + Q 2 SEC 2 θ + 2PQ Sec θ Tan θ)
= P θ + 2PQ Sec θ Tan θ)
= P θ + 2PQ Sec θ θ)
= P θ + 2pq Sec θ)
= P θ + 2pq θ)
= P θ + 2pq θ)
= P θ + 2pq Sec θ)
= P θ + 2pq θ) 2 θ + 2pq θ) 2 Tan 2 θ + 2pq Sec θ tan θ — p 2 Tan 2 θ — Q 2 Sec θ — 2pq Sec θ tan θ
= P 2 (SEC 2
= P 2 (SEC 2
= P 2 (SEC 2
rail 2 θ) – q 2 (сек? 2 θ – тангенс 2 θ) =
= p 2 – q 2 …[сек 2 9{2} А}\).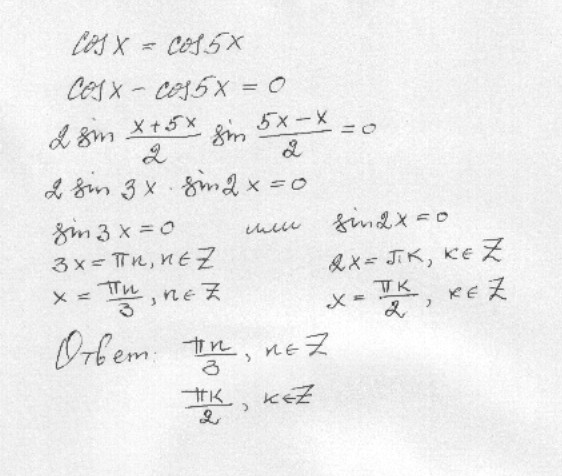 (2014)
(2014)
Решение:
Вопрос 22.
Если x = a cos θ – b sin θ и y = a sin θ + b cos θ, то докажите, что a 2 + b 2 = x 2 + у 2 . (2015)
Решение:
R.H.S. = x 2 + y 2
= (a cos θ – b sin θ) 2 + (a sin θ + b cos θ) 2
= a 2 + b 8 2 sin 2 θ – 2ab cos θ sin θ + a 2 sin 2 θ + B 2 COS 2 θ + 2AB SIN θ COS θ
= A 2 (COS 2 θ + SIN 2 θ) + B 2 (SIN 2 θ) + B 2 (SIN 2 θ) + B 2 (SIN 2 θ) + B 2 (SIN 2 . + cos 2 θ)
= a 2 + b 2 = L.H.S. …[∵ cos 2 θ + sin 2 θ = 1
Введение в тригонометрию Класс 10 Важные вопросы Краткий ответ – II (3 балла)
Вопрос 23.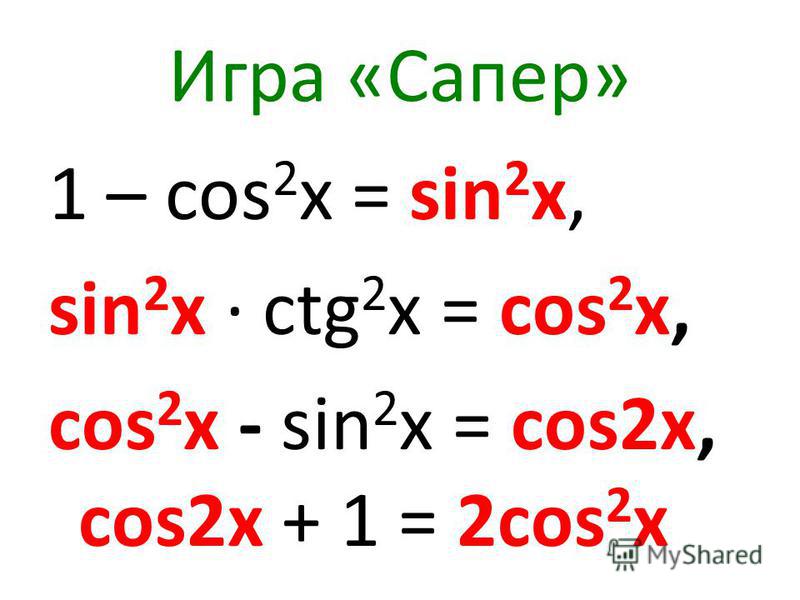
Учитывая 2 cos 3θ = \(\sqrt{3 }\), найдите значение θ. (2014)
Решение:
2 cos 3θ = \(\sqrt{3}\) …[Дано
cos 3θ = \(\frac{\sqrt{3}}{2}\) ⇒ cos 3θ = cos 30°
30 = 30° ∴ θ = 10°
Вопрос 24.
Если cos x = cos 40° . sin 50° + sin 40°. cos 50°, то найдите значение x. (2014)
Решение:
cos x = cos 40° sin 50° + sin 40° cos 50°
cos x = cos 40° sin(90° – 40°) + sin 40°.cos(90° – 40° )
cos x = cos 2 40° + sin 2 40°
cos x = 1 …[∵ cos 2 A + sin 2 A = 1
cos x = cos 0° ⇒ x = 0°
Вопрос 25.
Если sin θ = \(\frac{1}{2}\), то покажите, что 3 cos θ – 4 cos 3 θ = 0 , (2014)
Решение:
sin θ = \(\frac{1}{2}\)
sin θ = sin 30° ⇒ θ = 30°
LHS = 3 cos θ – 4 cos 3 θ
= 3 cos 30° – 4 cos 3 (30°)
Вопрос 26.
Если 5 sin θ = 4, докажите, что \(\frac{1}{\cos \theta}+\frac{1}{ \cot \theta}\) = 3 (2013
Решение:
Дано: 5 sin θ = 4
Вопрос 27.
Оценка: сек 41°. sin 49° + cos 29°.cosec 61° (2012)
Решение:
Вопрос 28.
Оценка: (2012, 2017D)
Решение:
Вопрос 29.
Q, PQ = 6 см и PR = 12 см. Определите ∠QPR и ∠PRQ. (2013)
Решение:
В рт. ∆PQR,
PQ 2 + QR 2 = PR 2 … [By Pythogoras ‘Теорема
(6) 2 + QR 2
= (12) 2 2 2 2 2 2 2 2 2 .{3} \theta-\cos \theta}\) = tan θ (2015)
Решение:
Вопрос 39.
Докажите, что: \(\frac{\sin \theta}{1+\cos \theta} +\frac{1+\cos \theta}{\sin \theta}\) = 2 cosec θ (2017OD)
Решение:
Введение в тригонометрию Класс 10 Важные вопросы Подробный ответ (4 балла)
Вопрос 40.
В остроугольном треугольнике ABC, если sin (A + B – C) = \(\frac{1}{2}\) и cos (B + C – A) = \(\frac{1}{\sqrt {2}}\), найдите ∠A, ∠B и ∠C. (2012)
Решение:
Подставляя значения A и B в (iii), получаем
67,5° + B + 75° = 180°
B = 180° – 67,5° – 75° = 37,5° 37,5 ° и ♂ = 75 °
Вопрос 41.
Оценка: (2013)
Решение:
Вопрос 42.
Оцените следующее: (2015)
Solution:
1818.103333333333333333313 гг. = 30°, проверьте следующее: (2014)
(i) cos 3θ = 4 cos 3 θ – 3 cos θ
(ii) sin 3θ = 3 sin θ – 4 sin 3 θ
Решение:
Вопрос 44.
Если тангенс (A + B) = \(\sqrt{3}\) и тангенс (A – B) = \(\frac{1}{\sqrt {3}}\) где 0 < A + B < 90°, A > B, найти A и B. Также вычислить: tan A. sin (A + B) + cos A. tan (A – B). (2015)
Решение:
Вопрос 45.
Найдите значение cos 60° геометрически. Отсюда находим cosec 60°. (2012, 2017D)
Решение:
Пусть ∆ABC — равносторонний ∆.
Пусть каждая сторона треугольника равна 2а.
Поскольку каждый угол равностороннего треугольника ∆ равен 60°
∴ ∠A = ∠B = ∠C = 60°
Draw AD ⊥ BC
В ∆ADB и A∆ADC,
AB = AC … [Каждый = 2a
AD = AD …[Общий
∠1 -∠2 … [Каждые 90°
∴ ∆ADB = ∆ADC …[правило соответствия RHS
BD = DC = \(\frac{2 a}{2}\) = a
In rt.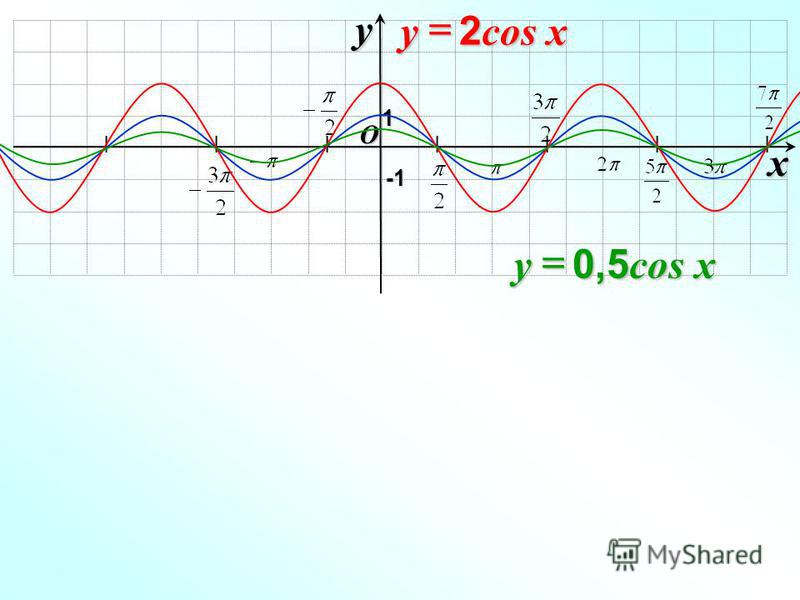 {2}}\) = 2. (2012, 2017D) 9{2}}}\) и d > 0, найти значения cos θ и tan θ. (2013)
{2}}\) = 2. (2012, 2017D) 9{2}}}\) и d > 0, найти значения cos θ и tan θ. (2013)
Решение:
Вопрос 49. Вопрос 50. Вопрос 51.
Если cot B = \(\frac{12}{5}\), докажите, что tan 2 B – sin 2 B = sin 4 B . sec 2 B. (2013)
Решение:
cot B = \(\frac{12}{5}\) :: \(\frac{A B}{B C}=\frac{12}{5}\ )
АВ = 12к, ВС = 5к
В рт. ∆ABC, …[По теореме Пифагора
AC 2 = AB 2 + BC 2
AC 2 = (12k) 2 + (5K) 2
AC 2 = 144K 2 + 25K 2
AC 2 = 169K 2 …
[
[
IVELEN.
Если \(\sqrt{3}\) кроватка 2 θ – 4 кроватка θ + \(\sqrt{3}\) = 0, то найти значение кроватки 2 θ + tan 2 θ. (2013)
Решение:
Докажите, что b 2 x 2 – a 2 y 2 = a 2 b 2 , если: (2014)
(i) x = a sec θ, y = b tan θ
(ii) x = a cosec θ, y = b cot θ
Решение:
(i) Л. Х.С. = B 2 x 2 — A 2 Y 2
Х.С. = B 2 x 2 — A 2 Y 2
= B 2 (Sec θ) 2 — A 2 (B Tan θ) 777868 2 2
= B 2 A 2 (г. 2 θ – 2 (г.2363 = b 2 a 2 (1) …[∵ sec 2 θ – tan 2 θ = 1
= a 2 b 2 = R.H.S.
(ii) L.H.S. = B 2 x 2 — A 2 Y 2
= B 2 (A COSEC θ) 2 — A 2 (B COTE θ) 68 — A 2 (B COTE θ) — A 2 (B COTE θ) — A 2 (B COTE θ) — A 2 (B Cot a 2 cosec 2 θ – a 2 b 2 cot 2 θ
= b 2 a 2 9298{2}+1}\).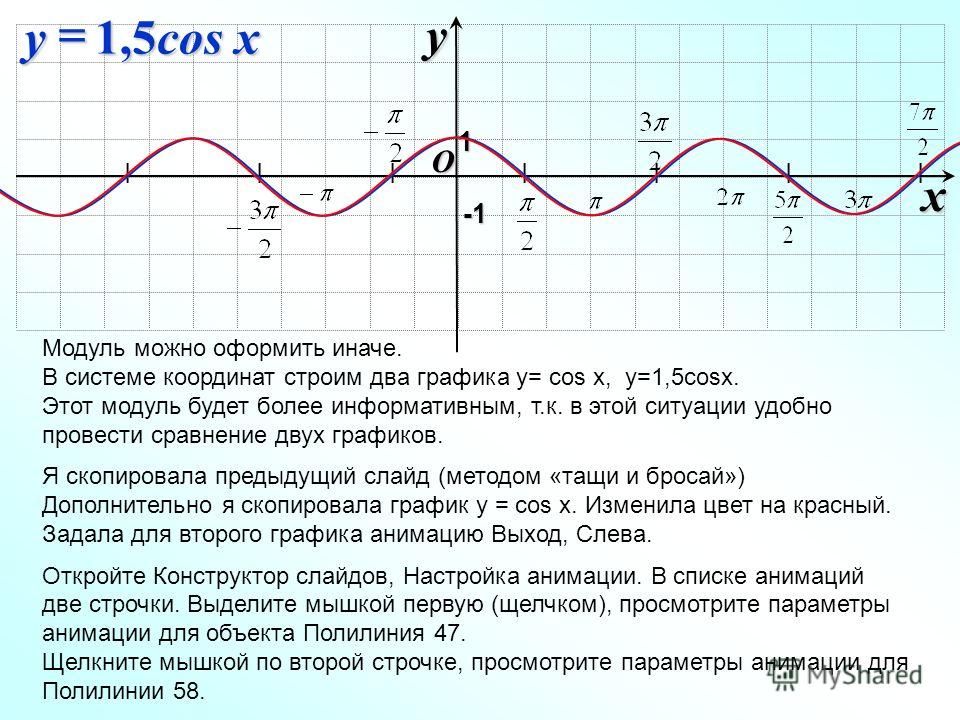 (2012)
(2012)
Решение:
cosec θ + cot θ = p
Вопрос 54.
Если tan θ + sin θ = p; тангенс θ – sin θ = q; докажите, что p 2 – q 2 = \(4 \sqrt{p q}\). (2012)
Решение:
Л.Х.С. = p 2 – q 2
= (tan θ + sin θ) 2 – (tan θ – sin θ) 2
= (tan 2 θ + 2 2,367 tanθ.sinθ) – (tan 2 θ + sin 2 θ – 2tan θ sin θ)
= 2 тангенс θ sin θ+ 2 тангенс θ sin θ
= 4 tan θ sin θ …(i)
Вопрос 55.
Если sin θ + cos θ = m и sec θ + cosec θ = n, то докажите, что n(m 2 – 1) = 2m. (2013)
Решение:
m 2 – 1 = (sin θ + cos θ) 2 – 1
= sin 2 θ + cos 2 θ + 2 sin 1 θ1 – 6 θ 3 cos 93 + 2 sin θ cos θ – 1
= 2 sin θ cos θ …[sin 2 θ + cos 2 θ = 1
L.H.S. = n(m 2 – 1)
= (sec θ + cosec θ) 2 sin θ cos θ
Вопрос 56.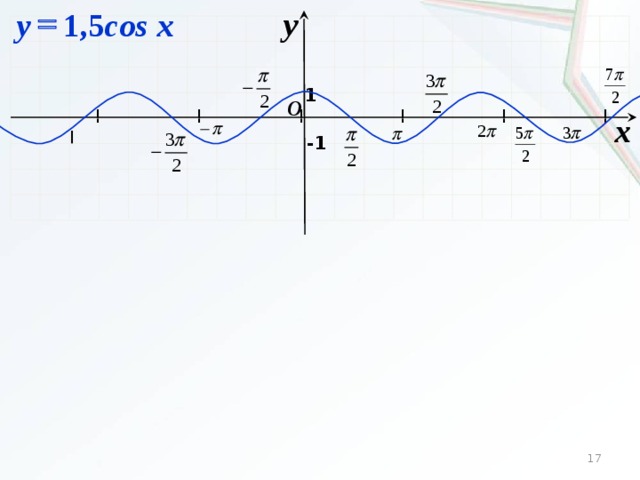
Докажите, что: = 2 cosec A (2012)
Решение:
Вопрос 57.
В ∆ABC покажите, что sin 2 \(\frac{\mathbf{A}}{2} \) + sin 2 \(\frac{\mathbf{B}+\mathbf{C}}{\mathbf{2}}\) = 1. (2013)
Решение:
In ∆ABC, ∠A + ∠B + ∠C = 180° … [Сумма углов ∆
∠B + ∠C = 180° – ∠A
Вопрос 58.
Найдите значение: (2013)
Решение:
3
Вопрос 59.Докажите, что: (sin θ + cos θ + 1). (sin θ – 1 + cos θ) . сек θ . cosec θ = 2 (2014)
Решение:
L.H.S. = (sin θ + cos θ + 1) (sin θ – 1 + cos θ) . sec θ cosec θ
= [(sin θ + cos θ) + 1] [(sin θ + cos θ) – 1] . sec θ cosec θ
= [(sin θ + cos θ) 2 – (1) 2 ] sec θ cosec θ …[∵ (a + b)(a – b) = a 2 – b 2
= (sin 2 θ + cos 2 θ + 2 sin θ cos θ – 1]. sec θ cosec θ
= (1 + 2 sin θ cos θ – 1). sin 2 θ + cos 2 θ = 1
= (2 sin θ cos θ).
 ) 9{2} A}\) (2015)
) 9{2} A}\) (2015) Решение:
Вопрос 62.
Докажите тождество: (2015)
Решение:
Вопрос 63.
Докажите следующие тригонометрические тождества: sin A (1 + tan A) + cos A (1 + cot A) = sec A + cosec A. (2015)
Решение:
L.H.S. Вопрос 64 = 2(cot A. sec B + tan B. cosec A) (2014)
Решение:
L.H.S.
= (кроватка A + сек B) 2 – (загар B – косек A) 2
= детская кроватка 2 A + сек 2 B + 2 кроватка A сек B – (tan 2 B + cosec 2 A – 2 tan B cosec A)
= cot 2 A + sec 2 B + 2 cot A sec B – tan 2 B – cosec 2 A + 2 tan B cosec A
= (sec 2 B – tan 2 B) – (cosec 2 A – cot 2 A) + 2(cot A sec B + tan B cosec A)
= 1 – 1 + 2(cot A sec B + tan B cosec A) … [∵ sec 2 B – tan 2 B = 1
cosec 2 A – cot 2 A = 1
= 2(cot A .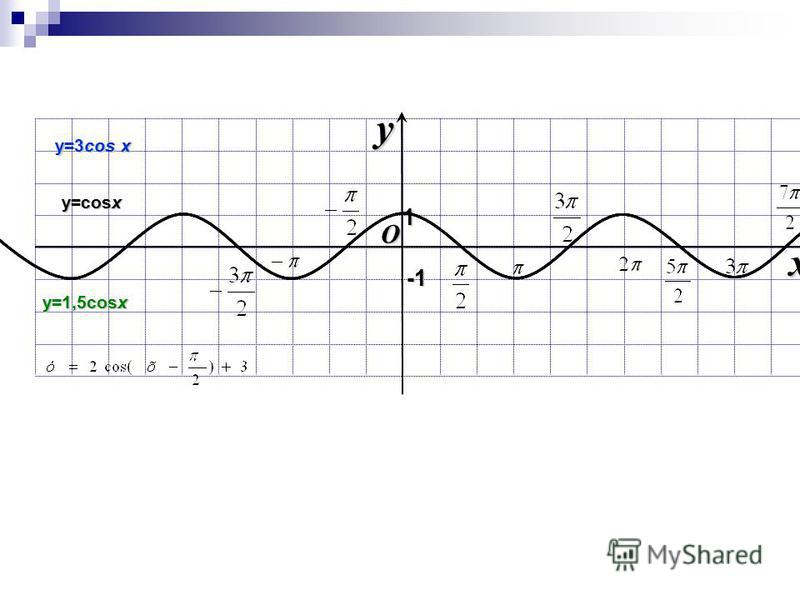 sec B + tan B . cosec A) = R.H.S.
sec B + tan B . cosec A) = R.H.S.
Вопрос 65.
Если x = r sin A cos C, y = r sin A sin C и z = r cos A, то докажите, что x 2 + y 2 + z 2 = r 2 . (2017OD)
Решение:
x = r sin A cos C; y = r sin A sin C; z = r cos A
Возведение в квадрат и сложение,
L.H.S. х 2 + y 2 + z 2 = 2 sin 2 A cos 2 C + r 2 sin 2 A sin 2 C + r 2 cos 2 A
= r 2 sin 2 A(cos 2 C + sin 2 C) + r 2 cos 2 A
= r 2 sin 2 A + r 2 cos 2 A … [cos 2 θ + sin 2 θ = 1
= r 2 (sin 2 A + cos 2 A) = r 2 = R.H.S.
Вопрос 66.
Докажите, что: (2017OD)
Решение:
Вопрос 67.
На соседнем рисунке ABCD — прямоугольник шириной BC = 7 см и ∠CAB = 30°. Найдите длину стороны АВ прямоугольника и длину диагонали АС. Если ∠CAB = 60°, то какова длина стороны AB прямоугольника. [Используйте \(\sqrt{3}\) = 1,73 и \(\sqrt{2}\) = 1,41, если необходимо) (2014OD)
Решение:
Важные вопросы по математике для 10 класса
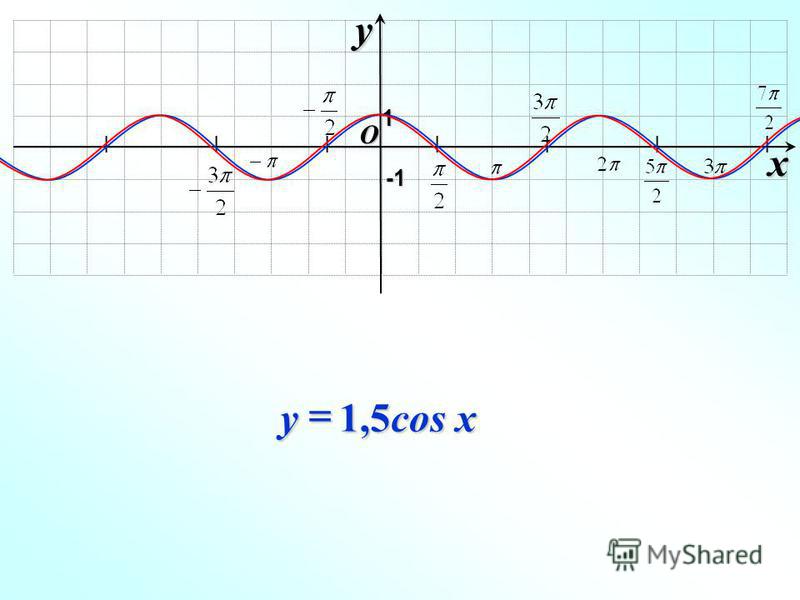
Тригонометрические функции: quais são e como calcular?
As trigonométricas funções são as funções seno, cosseno e tangente . Todas as funções trigonométricas relacionam о доблести сделать angulo em graus ou radianos com о доблести да razão trigonométrica, relação essa дие Pode сер feita пор meio сделать estudo сделать цикло trigonométrico. Com о estudo индивидуальный де cada uma das funções trigonométricas, é possível fazer a репрезентасао графика, estudar о sinal да função пункт cada um dos quadrantes, entre outras características важных.
Leia tambem: Os 4 erros mais cometidos na trigonometria básica
Tópicos deste artigo
- 1 — Quais são as funções trigonométricas?
- 2 — Função cosseno
- Domínio
- Imagem
- Gráfico da função cosseno
- Sinal
- Período da função cosseno
- Paridade
- 3 — Arcos notáveis da função cosseno
- 4 — Função seno
- Доминио
- Imagem
- Gráfico da função seno
- Sinal
- Período da função cosseno
- Paridade
- 5 — Arcos notáveis da função seno
- 6 — Função tangente
- Domínio
- Imagem
- Gráfico da função Tangente
- Sinal
- Período
- Paridade
- 7 — Arcos notáveis da função tangente
- 8 — Exercícios 91 resolves3464
В качестве тригонометрических функций, которые обычно используются в качестве тригонометрических функций, используются как обычные, так и косвенные функции и тангентные функции. O estudo delas está ligado ao ciclo trigonométrico.
O estudo delas está ligado ao ciclo trigonométrico.
Para cada valor de angulo, há um único valor para o seno e para o cosseno. As funções trigonométricas nada mais são que a relação entre o angulo e o valor da razão trigonométrica para esse angulo . Vale lembrar que o valor desse angulo pode ser dado em radianos ou em graus e que o valor do seno e do cosseno é semper um número real entre -1 e 1.
г. Доблесть сделать сено и сделать коссено пара ос principais angulos.Note na imagem que, para cada angulo, o cosseno e o seno accepte m um valor. É com base no estudo de cada uma das funções trigonométricas que observamos a relação entre o valor do angulo e o valor da razão trigonométrica.
Лея тел.: Quais são os angulos notáveis?
Não pare agora… Tem mais depois da publicidade 😉
Função cosseno A função cosseno é função f : R → R, cuja lei de formação é f (x) = cos (x). Como o cosseno de um angulo é semper um número entre 1 e -1 , então, -1 ≤ cos (x) ≤ 1.
Como o cosseno de um angulo é semper um número entre 1 e -1 , então, -1 ≤ cos (x) ≤ 1.
- Доминио
O domínio da função cosseno é o conjunto dos números reais , pois não existse nenhuma restrição para o valor de x, em que x é o angulo em radianos. Para todo número real, é possível encontrar o valor de cos(x), então, D ф = р.
- Имидж
Sabemos que o contradomínio da função cosseno é o conjunto dos números reais, entretanto, quando analisamos a imagem da função, é possível perceber que ela é semper um valor po 5 1 8 a igual ou -1 e menor o ciclo trigonométrico tem raio 1, então, o maior valor que a função cosseno pode assumir é 1, e, аналог, o menor valor que ela pode assumir é -1. Im = [-1, 1]
O gráfico da função cosseno está contido entre as retas y = — 1 e y = 1. Vale lembrar que isso acontece porque a imagem da função é semper um número entre -1 e 1 e possui parte crescente e parte decrescente, como podemos ver a seguir:
Vale lembrar que isso acontece porque a imagem da função é semper um número entre -1 e 1 e possui parte crescente e parte decrescente, como podemos ver a seguir:
Fazendo a reportência do valor do angulo com o valor da razão trigonométrica, é possível perceber que o grafico possui um comportamento cíclico ou seja, o comportamento semper se repete de forma Periodica. O grafico да função cosseno é conhecido como cossenoide.
- Синал
Sabemos que, no ciclo trigonométrico, o cosseno possui valores positivos no I e IV quadrantes. Первый квадрант между 0° и 90°, четвертый квадрант между 270° и 360°. Em radianos, função é positiva para valores de x entre 0 e π/2 e entre 3π/2 e 2π.
A função cosseno possui valores negativos no II e III quadrantes ou seja, o angulo está entre 90º e 270º.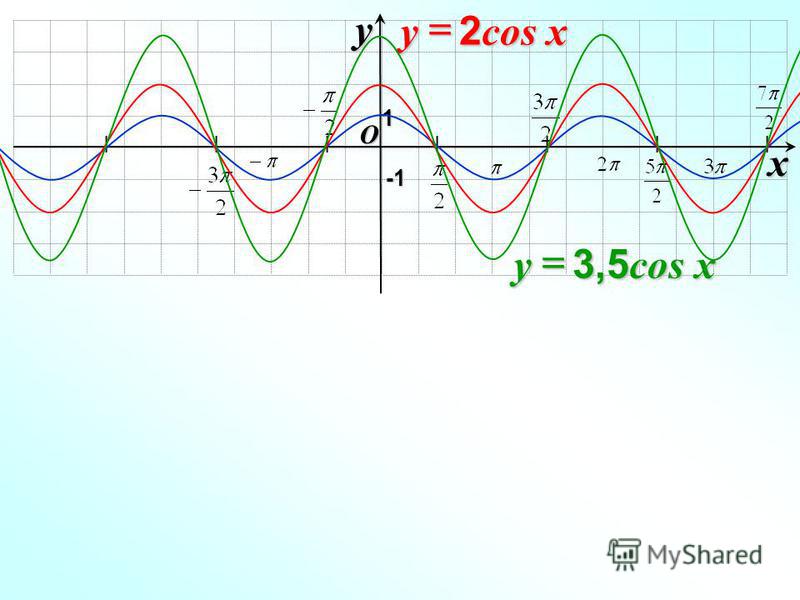 Em radianos, para que a função cosseno seja negativa, x está entre π/2 e 3π/2.
Em radianos, para que a função cosseno seja negativa, x está entre π/2 e 3π/2.
O grafico da função cosseno tem um período de 2π . Аналисандо, é possível perceber que o grafico está contido no intervalo de 0 a 2π. Para valores anteriores ou posteriores a esse intervalo, o grafico se repete.
- г. Паридад
Função cosseno é рассмотрит uma função par , pois há uma simetria no grafico em relação ao eixo y. Quando uma função é рассматривая пар, temos que f (x) = f (-x), ou seja, cos (x) = cos (-x).
Arcos notáveis da função cossenoVejamos o valor do cosseno para os principais angulos:
Arcos notáveis da função cosseno.Вежа там: Secante, cossecante e cotangente – razões trigonométricas inversas do seno, cosseno e tangente
Função seno A função cosseno é a função f : R → R, cuja lei de formação é f (x) = сен (х). Como o seno de um angulo, assim como o cosseno, é semper um número entre 1 e -1 , então, -1 ≤ sen (x) ≤ 1.
Como o seno de um angulo, assim como o cosseno, é semper um número entre 1 e -1 , então, -1 ≤ sen (x) ≤ 1.
- Доминио
O domínio da função seno г. é o conjunto dos números reais . A função f (x) = sen (x) está definida para todos os números reais, então, D f = R.
3
ИмиджA imagem da função seno possui valor máximo em f (x) = 1 e valor mínimo quando f(x) = -1 . Então, забавный образ или реальный интервал [-1, 1].
О графике функции é limitado tambem pelas retas horizontalis y = -1 e y = 1 . O comportamento é parecido com o da função seno Periodico, Tendo intervalos crescentes e intervalos decrescentes. Veja представляет график работы, который не имеет плано-картезиано, а затем:
Veja представляет график работы, который не имеет плано-картезиано, а затем:
О графике работы, который используется там же, где и периодичность, и é conhecido como senoide.
- г. Синал
Divenentemente DA Funcáo Cosseno, Funcáo Seno Vosui Valores Positivos № S Quadrante S I EI Primeiro, SEJA, SEJA, SEJA, SEJA, SEJA, SEJA, SEJA, SEJA, SEJA. Em radianos, função é positiva para valores entre 0 e π.
A função seno possui valores negativos no II I e IV quadrante s , ou seja, o angulo está entre 180º e 360º. Em radianos, para que função seno seja negativa, x está entre π e 2π.
Sinal da função seno O grafico da função seno tem um período de 2π. Isso significa que, posteriormente ou anteriormente ao intervalo de 0 a 2π, o graphico é Periodico, ou seja, repete-se.
- Паридад
Удобный номер Função IM пар , pois há uma simetria no grafico em relação à bissetriz dos quadrantes ímpares. Quando uma função é рассмотрит ímpar, temos que f (x) = — f (x), ou seja, sen (-x) = -sen (x).
Arcos notáveis da função senoVejamos o valor do seno para os principais angulos:
Arcos notáveis da função seno. Função tangenteSabemos que a tangente é a razão entre o seno e o cosseno. Diferentemente das duas funções trigonométricas anteriores, função tangente não possui valor de maximo nem valor de minimo. Além disso, existsretrições para o domínio, mas a lei de formação da função tangente é f (x) = tan(x).
- Доминио
Касательные функции, которые могут быть ограничены в отношении seu domínio, como ela é formada pela razão entre o seno e o cosseno, não existsem valores para tangente quando cos(x) = 0 .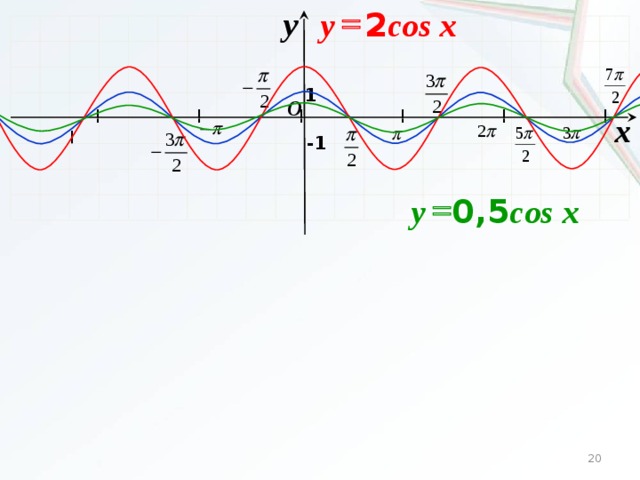 Pesando no ciclo trigonométrico de 0º a 360º, função tangente não está definida para os angulos de 90º e 270º, pois são os valores em que o cosseno é igual a 0. Quando há ângulos maiores que uma volta aqueles, to emdo volta aqueles completa valor de cosseno é 0 não fazem parte do domínio da função cosseno.
Pesando no ciclo trigonométrico de 0º a 360º, função tangente não está definida para os angulos de 90º e 270º, pois são os valores em que o cosseno é igual a 0. Quando há ângulos maiores que uma volta aqueles, to emdo volta aqueles completa valor de cosseno é 0 não fazem parte do domínio da função cosseno.
- Имидж
Различия между отдельными функциями и функциями, и образы дополнительных функций, а также числовое значение , ou seja, ela não é limitada e não possui valor de máximo nem de minimo. Im = R
Função tangente também é Periodica como as funções seno e cosseno, ou seja, ela semper se repete. Quando comparamos:
Grafico da função tangente.- Синал
A função tangente possui valor positivo para os quadrantes ímpares, ou seja, I e III quadrantes. Пара ангулос между 0º и 90º e angulos entre 180º e 270º, função possui valores positivos. Em radianos, o valor de x tem que estar entre 0 e π/2 или π e 3π/2.
Em radianos, o valor de x tem que estar entre 0 e π/2 или π e 3π/2.
- Период
O período da função tangente também é diferente das funções seno e cosseno. O período da função tangente é π .
- Паридад
Тангентная функция é uma função ímpar , pois tan(-x) = -tan(x), logo, ha uma simetria no grafico em relação à origem do plano cartesiano.
Arcos notáveis da função tangenteVejamos o valor da tangente para os principais angulos:
Arcos notáveis da função tangente.Veja tambem: Como encontrar seno e cosseno de angulos suplementares?
Exercícios resolvidos Questão 1 — (Enem 2017) Raios de luz solar estão atingindo a superfície de um lago, formando um ângulo x com a superfície in sua superfície.
Em determinadas condições, pode-se supor que a intensidade luminosa desses raios, na superfície do lago, seja dada aproximadamente por I(x) = k · sen(x), sendo kuma Constante, e supondo-se que X está между 0° и 90°.
Quando x = 30º, a intensidade luminosa se reduz a qual Percentual de seu valor maximo?
A) 33%
B) 50%
C) 57%
D) 70%
E) 86%
Resolução No intervalo de 0º a 90º, a função seno tem seu maior valor quando x = 90º, então, temos que: i = k · sen(90º) Agora, quando x = 30º, temos que: i = k · sem (30º) Note que a intensidade i foi reduzida pela metade, ou seja, 50%. Questão 2 — (Enem 2015) Segundo o Brasileiro de Geografia e Estatística (IBGE), produtos sazonais são aqueles que apresentam ciclos bem definidos de produção, consumo e preço. Resumidamente, existsem épocas do ano em que a sua disponibilidade nos mercados varejistas ora é escassa, com preços elevados, ora é riche, com preços mais baixos, o que ocorre no mês de produção maxima da safra.0 Alterniva1813
я = к · 1
i = k
я = к · 1/2
i = k/2


 Арккосинус: арккос. Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Арккосинус: арккос. Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения.



 Обратите внимание, что точная точность может варьироваться в зависимости от других параметров.
В отличие от NumPy, функция Python
Обратите внимание, что точная точность может варьироваться в зависимости от других параметров.
В отличие от NumPy, функция Python  sum([10], начальный=5)
15
sum([10], начальный=5)
15