Cosx 2 sinx 2 1: ‘(«) } ym(1313667, ‘reachGoal’, ‘adBlockDetectedWarningMessage’) } if(typeof fuckAdBlock === ‘undefined’) { adBlockDetected() } else { fuckAdBlock.onDetected(adBlockDetected) } $(document).on(‘krapi.checker.run.complete’, function() { if(typeof fuckAdBlock === ‘undefined’) { adBlockDetectedWarningMessage() } else { fuckAdBlock.check() fuckAdBlock.onDetected(adBlockDetectedWarningMessage) } }) })

alexxlab / / Разное
2

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8Найти точное значениеcos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15Найти точное значениеcsc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значение
tan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значение
sin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )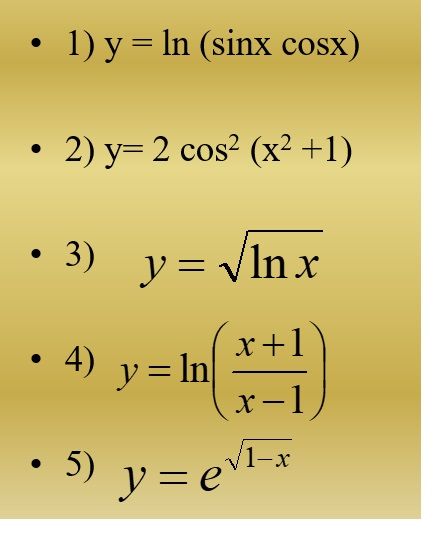
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Решутест. Продвинутый тренажёр тестов

Решутест. Продвинутый тренажёр тестов
  • Главная
  • ЕГЭ
  • Математика профильная
  • Уравнения
  • Отбор корней

Решил заданий

Не решил заданий

Осталось заданий

История решения
5487 — не приступал 1124 — не приступал 1896 — не приступал 3197 — не приступал 7716 — не приступал 2182 — не приступал 3063 — не приступал 2981 — не приступал 8068 — не приступал 3639 — не приступал 3282 — не приступал 8443 — не приступал

Формат ответа: цифра или несколько цифр, слово или несколько слов. 2+4t-3=0\\&|t|\le1\end{aligned}\right. \Leftrightarrow$

$\left\{\begin{aligned}&\left[\begin{aligned}&t_1=-1.5\\&t_2={\small\frac{1}{2}}\end{aligned}\right.\\&|t|\le1\end{aligned}\right. \Rightarrow$

t = $\displaystyle\frac{1}{2} \Leftrightarrow$

sinx = $\displaystyle\frac{1}{2} \Rightarrow$

x = (−1)k$\,\displaystyle\frac{\pi}{6}$ + πk, k ϵ $\mathbb{Z}$.

Результат решения этого уравнения разложим на два составляющих решения:

$\left[\begin{aligned}&x=\displaystyle\frac{\pi}{6}+2\pi n,\;n\in\mathbb{Z},\\[2pt]&x=\frac{5\pi}{6}+2\pi m,\;m\in\mathbb{Z}.\end{aligned}\right.$

б) Каждое из этих решений должно находиться на промежутке $\left[-\displaystyle\frac{\pi}{2};\pi\right]$.

−$\displaystyle\frac{\pi}{2}$ ≤ $\displaystyle\frac{\pi}{6}$ + 2πn ≤ π $\Leftrightarrow$

−$\displaystyle\frac{2}{3}$π ≤ 2πn ≤ $\displaystyle\frac{5}{6}$π $\Leftrightarrow$

− $\displaystyle\frac{1}{3}$ ≤ n ≤ $\displaystyle\frac{5}{12}$, n = 0.

При n = 0, получим $\displaystyle\frac{\pi}{6}$.

−$\displaystyle\frac{\pi}{2}$ ≤ $\displaystyle\frac{5\pi}{6}$ + 2πm ≤ π $\Leftrightarrow$

−$\displaystyle\frac{4}{3}$π ≤ 2πm ≤ $\displaystyle\frac{1}{6}$π $\Leftrightarrow$

−$\displaystyle\frac{4}{6}$ ≤ m ≤ $\displaystyle\frac{1}{12}$, m = 0.

При m = 0 получим x = $\displaystyle\frac{5\pi}{6}$.

№2

а) Решите уравнение 2sin2x = 4cosx – sinx + 1

б) Укажите корни уравнения, принадлежащие отрезку $\left[\displaystyle\frac{\pi}{2};\frac{3\pi}{2}\right]$.

ответ

а) Преобразуем уравнение:

4sinx·cosx – 4cosx + sinx – 1 = 0;

4cosx·(sinx – 1) + (sinx – 1) = 0;

(sinx – 1)·(4cosx + 1) = 0;

$\left[\begin{aligned}&\sin x — 1 = 0\\&4\cos x + 1 = 0\end{aligned}\right.$

Получаем: sinx = 1 или cosx = −$\displaystyle\frac{1}{4}$, откуда x = $\displaystyle\frac{\pi}{2}$ + 2πk, или x = ±arccos$\left(-\displaystyle\frac{1}{4}\right)$ + 2πk, k ϵ $\mathbb{Z}$.

б) С помощью числовой окружности отберем корни на отрезке $\left[\displaystyle\frac{\pi}{2};\frac{3\pi}{2}\right]$, в данной задаче это можно сделать визуально без каких−либо дополнительных расчётов:

Заданному интервалу принадлежат корни:

$\displaystyle\frac{\pi}{2}$, arccos$\left(-\displaystyle\frac{1}{4}\right)$, 2π − arccos$\left(-\displaystyle\frac{1}{4}\right)$.

№3

а) Решите уравнение $\;\cos\left(\displaystyle\frac{3\pi}{2}+2x\right)=\cos x$

б) Укажите корни уравнения, принадлежащие отрезку $\left[\displaystyle\frac{5\pi}{2};4\pi\right]$.

ответ

а) Используем формулу приведения:

cos$\left(\displaystyle\frac{3\pi}{2}+2x\right)$ = cosx.

Напомним, что можно обойтись без понятия формулы приведения, расписав косинус суммы двух углов и подставив в полученное выражение значения функций синус и косинус в точке $\displaystyle\frac{3\pi}{2}$.

2sinx·cosx = cosx, теперь вынесем общий множитель за скобку:

sin2x = cosx;

2sinx·cosx = cosx;

2sinx·cosx – cosx = 0;

cosx·(2sinx – 1) = 0.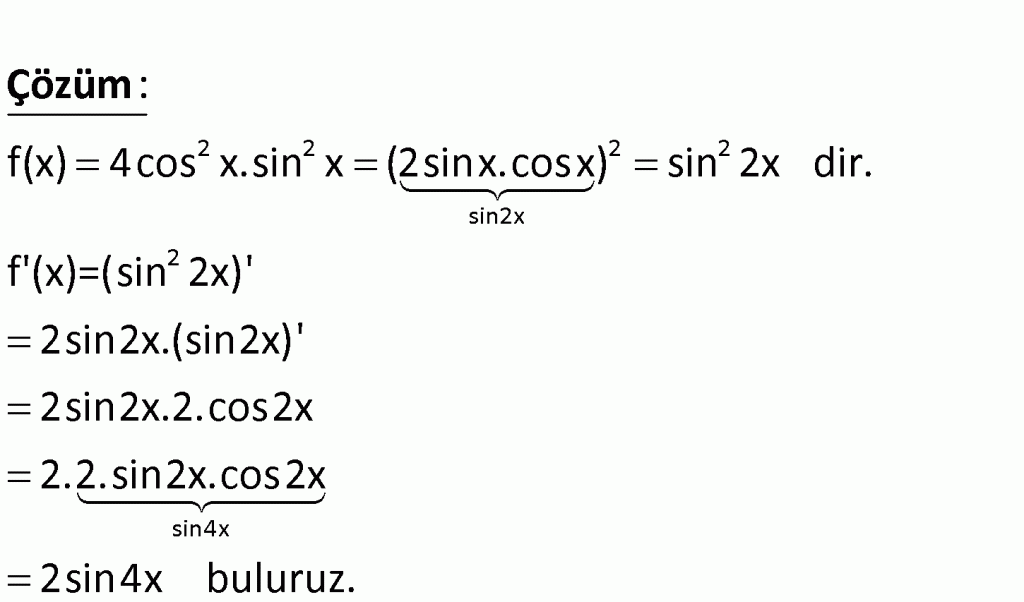

Тогда cosx = 0 или sinx = $\displaystyle\frac{1}{2}$.

Решая cosx = 0 получим: x = $\displaystyle\frac{\pi}{2}$ + πk, k ϵ $\mathbb{Z}$.

Решая sinx = $\displaystyle\frac{1}{2}$ получим: x = $\displaystyle\frac{\pi}{6}$ + 2πk, k ϵ $\mathbb{Z}$ или x = $\displaystyle\frac{5\pi}{6}$ + 2πk, k ϵ $\mathbb{Z}$.

Таким образом: x = $\displaystyle\frac{\pi}{2}$ + πk, x = $\displaystyle\frac{\pi}{6}$ + 2πk, x = $\displaystyle\frac{5\pi}{6}$ + 2πk, k ϵ $\mathbb{Z}$.

б) С помощью единичной окружности отберём корни на отрезке $\left[\displaystyle\frac{5\pi}{2};4\pi\right]$.

Находим: $\displaystyle\frac{5\pi}{2},\,\frac{17\pi}{6},\,\frac{7\pi}{2}$.

Без расчётов, визуально сходу определить корни принадлежащие отрезку может далеко не каждый, нужна серьёзная практика, поэтому покажем безошибочный способ отбора корней, которым советуем пользоваться: переведём радианы в градусы. Так как π радиан это 180º, то отрезок $\left[\displaystyle\frac{5\pi}{2};4\pi\right]$ будет выглядеть следующим образом: [450º; 720º]. Отберём корни, подставляя значения k в полученное решение уравнения:

При k = 1:

x = $\displaystyle\frac{\pi}{2}$ + π = $\displaystyle\frac{\pi}{2}$ + $\displaystyle\frac{2\pi}{2}$ = $\displaystyle\frac{3\pi}{2}$ = 270º;

x = $\displaystyle\frac{\pi}{6}$ + 2π = $\displaystyle\frac{\pi}{6}$ + $\displaystyle\frac{12\pi}{6}$ = $\displaystyle\frac{13\pi}{6}$ = 390º;

x = $\displaystyle\frac{5\pi}{6}$ + 2π = $\displaystyle\frac{5\pi}{6}$ + $\displaystyle\frac{12\pi}{6}$ = $\displaystyle\frac{17\pi}{6}$ = 510º.

При k = 2:

x = $\displaystyle\frac{\pi}{2}$ + 2π = $\displaystyle\frac{\pi}{2}$ + $\displaystyle\frac{4\pi}{2}$ = $\displaystyle\frac{5\pi}{2}$ = 450º;

x = $\displaystyle\frac{\pi}{6}$ + 4π = $\displaystyle\frac{\pi}{6}$ + $\displaystyle\frac{24\pi}{6}$ = $\displaystyle\frac{25\pi}{6}$ = 750º;

x = $\displaystyle\frac{5\pi}{2}$ + 4π = $\displaystyle\frac{5\pi}{2}$ + $\displaystyle\frac{24\pi}{6}$ = $\displaystyle\frac{29\pi}{6}$ = 870º.

При k = 3:

x = $\displaystyle\frac{\pi}{2}$ + 3π = $\displaystyle\frac{\pi}{2}$ + $\displaystyle\frac{6\pi}{2}$ = $\displaystyle\frac{7\pi}{2}$ = 630º;

x = $\displaystyle\frac{\pi}{6}$ + 6π = $\displaystyle\frac{\pi}{6}$ + $\displaystyle\frac{36\pi}{6}$ = $\displaystyle\frac{37\pi}{6}$ = 1100º;

x = $\displaystyle\frac{5\pi}{6}$ + $\displaystyle\frac{36\pi}{6}$ = $\displaystyle\frac{41\pi}{6}$ = 1230º.

При k = 4: проверять корни нет смысла, так как видно, что результат будет лежать вне пределов интервала: x = $\displaystyle\frac{\pi}{2}$ + 4π > 720º.

Отрезку [450º; 720º] принадлежат корни 390º; 450º; 510º, в радианах это $\displaystyle\frac{5\pi}{2},\,\displaystyle\frac{17\pi}{6},\,\displaystyle\frac{7\pi}{2}$. Ответ можно записывать либо в градусах, либо радианах, значения не имеет.

№4

а) Решите уравнение ctgx·sin2x + cos2x = 1

б) Укажите корни уравнения, принадлежащие интервалу (0; π).

ответ

Преобразуем уравнение:

$\displaystyle\frac{\cos x}{\sin x}$·2sinx·cosx – (1 – cos2x) = 0 $\;\Leftrightarrow\;$ 2cos2x – 2sin2x = 0 $\;\Leftrightarrow\;$ cos2x = 0 $\;\Rightarrow$

2x = $\displaystyle\frac{\pi}{2}$ + πn, n ϵ $\mathbb{Z}$;

x = $\displaystyle\frac{\pi}{4}$ + $\displaystyle\frac{\pi}{2}$n, n ϵ $\mathbb{Z}$.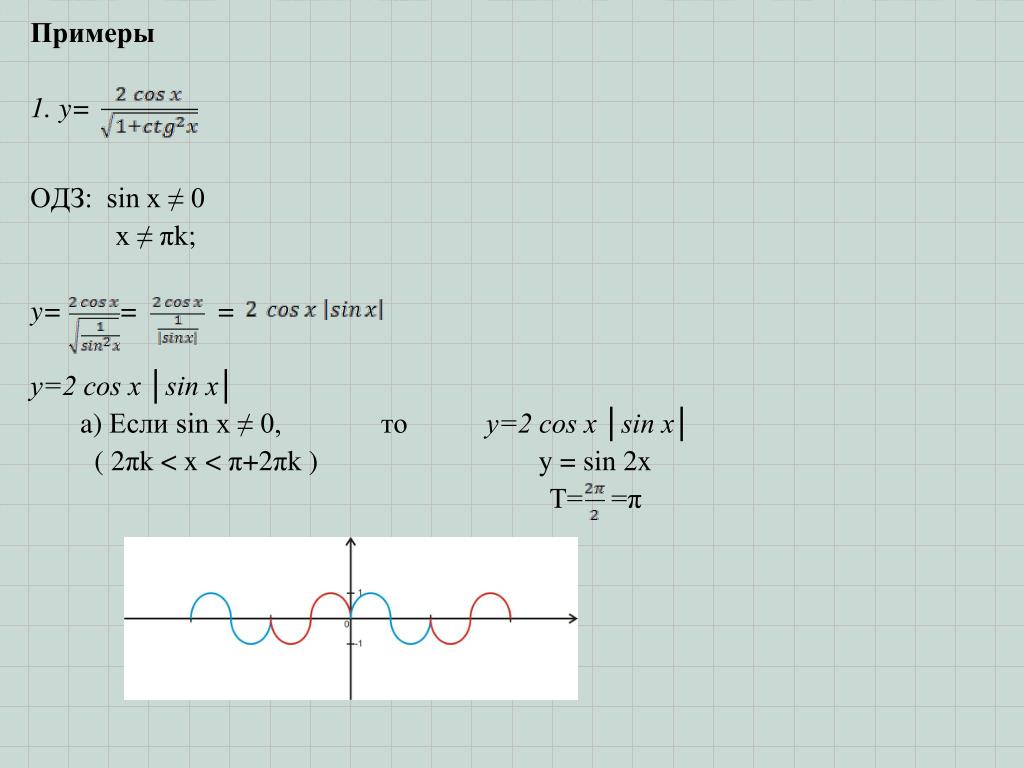 2+3t-2=0 \\[5pt] D=9+16=25 \\[3pt] t=\displaystyle\frac{-3\pm5}{4} \\ \left[\begin{aligned}&\vphantom{\Bigl{|}}t=-2\,

б) Построим график косинуса и определим корни в промежутке $\left[-\displaystyle\frac{7\pi}{2};-2\pi\right]$.

Единственный корень в промежутке – ближайший корень левее чем $-2\pi$.

$x=-2\pi-\displaystyle\frac{\pi}{3}=-\displaystyle\frac{7\pi}{3}$

 

№8

а) Решите уравнение $\,\log_{13}(\cos 2x — 9\sqrt{2}\cos x — 8)=0$

б) Укажите корни уравнения, принадлежащие отрезку $\left[-2\pi;-\displaystyle\frac{\pi}{2}\right]$.

ответ

а) Преобразуем выражение, используя свойства логарифма

$\cos x = -\displaystyle\frac{\sqrt{2}}{2} \\ x = \pm \displaystyle\frac{3\pi}{4} + 2\pi k,\,k\in\mathbb{Z}$

б) Построим график косинуса и определим корни в промежутке $\left[-2\pi;-\displaystyle\frac{\pi}{2}\right]$.

Первый корень получается движением от $-2\pi$ вправо, то есть $x=-2\pi+\displaystyle\frac{3\pi}{4}=-\displaystyle\frac{5\pi}{4}$, а второй движением от 0 влево $x=0-\displaystyle\frac{3\pi}{4}=-\displaystyle\frac{3\pi}{4}$. 2-14x-32=0$

По теореме Виета

$\left[\begin{aligned}&x=-2\\&x=16\vphantom{\bigl(}\end{aligned}\right.$

б) Так как основание логарифма больше 1, то данная функция возрастает.

Приведём к одному основанию.

$-2=\log_3\displaystyle\frac{1}{9}=\log_3\frac{10}{90} \\[1pt] \log_30.1=\log_3\displaystyle\frac{1}{10}=\log_3\frac{9}{90}$

Откуда:

$-2=\log_3\displaystyle\frac{10}{90}>\log_3\frac{9}{90}=\log_30.1$

Очевидно, что -2 меньше $5\sqrt{10}$.

Тогда корень (-2) входит в промежуток.

Заметим, что , то есть левая граница данного в условии промежутка отрицательная. Корень 16 – положительное число, значит, оно явно больше левой границы.

Сравним 16 и $5\sqrt{10}$

$\begin{aligned}16&\vee5\sqrt{10}\\256&\vee25\!\cdot\!10\\256&\vee250\\256&>250 \Rightarrow 16>5\sqrt{10},\ тогда\ корень\ 16\ не\ входит\ в\ промежуток.\end{aligned}$

№12

а) Решите уравнение $\bigl|\cos x + \sin x\bigr|=\sqrt{2}\sin 2x$

б) Укажите корни, принадлежащие отрезку $\left[3\pi;\displaystyle\frac{9\pi}{2}\right]$.

ответ

а) Отметим, что выражение √2sin2x ≥ 0, так как |cosx + sinx| имеет неотрицательное значение, поэтому sin2x ≥ 0.

Используя свойство модуля, получим два отдельных уравнения, решения каждого из них будут являться решением данного уравнения:

cosx + sinx = √2sin2x или –(cosx + sinx) = √2sin2x.

Решаем cosx + sinx = √2sin2x.

Возводим в квадрат обе части:

(cosx + sinx)2 = 2sin22x;

cos2x + 2cosx·sinx + sin2x = 2sin22x;

2sin22x − sin2x – 1 = 0.

Решая квадратное уравнение, получим: sin2x = 1 и sin2x = $-\displaystyle\frac{1}{2}$.

Так как sin2x ≥ 0 (это область допустимых значений), то второе уравнение решать нет смысла.

Решаем sin2x = 1, получим:

2x = $\displaystyle\frac{\pi}{2}$ + 2πn, n ϵ $\mathbb{Z}$ $\;\mathbf{\Biggl|}\cdot\displaystyle\frac{1}{2}$;

x = $\displaystyle\frac{\pi}{4}$ + πn, n ϵ $\mathbb{Z}$.

Решением уравнения –(cosx + sinx) = √2sin2x является тот же корень, так как при возведении в квадрат обеих частей получим то же уравнение.

б) Сделаем отбор корней на данном в условии промежутке , используя метод двойного неравенства.

Для этого подставим найденный в пункте а) корень x = $\displaystyle\frac{\pi}{4}$ + πn, n ϵ $\mathbb{Z}$ в промежуток, а затем учтем, что n может быть только целым числом.

В этот промежуток входят только два целых значения n – это n=3 и 4.

Подставим их в изначальный корень.

$x=\displaystyle\frac{\pi}{4}+\pi\!\cdot\!4=\frac{\pi+16\pi}{4}=\frac{17\pi}{4} \\[15pt] x = \displaystyle\frac{\pi}{4}+\pi\!\cdot\!3=\frac{\pi+12\pi}{4}=\frac{13\pi}{4}$

Так твой прогресс будет сохраняться.

Регистрация

Мы отправили код на:

Изменить

Получить код повторно через 00:00

Я прочитал(-а) Политику конфиденциальности и согласен(-на) с правилами использования моих персональных данных

Ништяк!

Решено верно

Браво!

Решено верно

Крутяк!

Решено верно

Зачёт!

Решено верно

Чётко!

Решено верно

Бомбезно!

Решено верно

Огонь!

Решено верно

Юхууу!

Решено верно

Отпад!

Решено верно

Шикарно!

Решено верно

Блестяще!

Решено верно

Волшебно!

Решено верно

Мэтуэй | Популярные задачи

92
1 Найти точное значение грех(30)
2 Найти точное значение грех(45)
3 Найти точное значение грех(30 градусов)
4 Найти точное значение грех(60 градусов)
5 Найти точное значение загар (30 градусов)
6 Найти точное значение угловой синус(-1)
7 Найти точное значение грех(пи/6)
8 Найти точное значение cos(pi/4)
9 Найти точное значение грех(45 градусов)
10 Найти точное значение грех(пи/3)
11 Найти точное значение арктан(-1)
12 Найти точное значение cos(45 градусов)
13 Найти точное значение cos(30 градусов)
14 Найти точное значение желтовато-коричневый(60)
15 Найти точное значение csc(45 градусов)
16 Найти точное значение загар (60 градусов)
17 Найти точное значение сек(30 градусов)
18 Найти точное значение cos(60 градусов)
19 Найти точное значение cos(150)
20 Найти точное значение грех(60)
21 Найти точное значение cos(pi/2)
22 Найти точное значение загар (45 градусов)
23 Найти точное значение arctan(- квадратный корень из 3)
24 Найти точное значение csc(60 градусов)
25 Найти точное значение сек(45 градусов)
26 Найти точное значение csc(30 градусов)
27 Найти точное значение грех(0)
28 Найти точное значение грех(120)
29 Найти точное значение соз(90)
30 Преобразовать из радианов в градусы пи/3
31 Найти точное значение желтовато-коричневый(30)
32
35 Преобразовать из радианов в градусы пи/6
36 Найти точное значение детская кроватка(30 градусов)
37 Найти точное значение арккос(-1)
38 Найти точное значение арктан(0)
39 Найти точное значение детская кроватка(60 градусов)
40 Преобразование градусов в радианы 30
41 Преобразовать из радианов в градусы (2 шт. )/3
42 Найти точное значение sin((5pi)/3)
43 Найти точное значение sin((3pi)/4)
44 Найти точное значение тан(пи/2)
45 Найти точное значение грех(300)
46 Найти точное значение соз(30)
47 Найти точное значение соз(60)
48 Найти точное значение соз(0)
49 Найти точное значение соз(135)
50 Найти точное значение cos((5pi)/3)
51 Найти точное значение cos(210)
52 Найти точное значение сек(60 градусов)
53 Найти точное значение грех(300 градусов)
54 Преобразование градусов в радианы 135
55 Преобразование градусов в радианы 150
56 Преобразовать из радианов в градусы (5 дюймов)/6
57 Преобразовать из радианов в градусы (5 дюймов)/3
58 Преобразование градусов в радианы 89 градусов
59 Преобразование градусов в радианы 60
60 Найти точное значение грех(135 градусов)
61 Найти точное значение грех(150)
62 Найти точное значение грех(240 градусов)
63 Найти точное значение детская кроватка(45 градусов)
64 Преобразовать из радианов в градусы (5 дюймов)/4
65 Найти точное значение грех(225)
66 Найти точное значение грех(240)
67 Найти точное значение cos(150 градусов)
68 Найти точное значение желтовато-коричневый(45)
69 Оценить грех(30 градусов)
70 Найти точное значение сек(0)
71 Найти точное значение cos((5pi)/6)
72 Найти точное значение КСК(30)
73 Найти точное значение arcsin(( квадратный корень из 2)/2)
74 Найти точное значение загар((5pi)/3)
75 Найти точное значение желтовато-коричневый(0)
76 Оценить грех(60 градусов)
77 Найти точное значение arctan(-( квадратный корень из 3)/3)
78 Преобразовать из радианов в градусы (3 пи)/4 
79 Найти точное значение sin((7pi)/4)
80 Найти точное значение угловой синус(-1/2)
81 Найти точное значение sin((4pi)/3)
82 Найти точное значение КСК(45)
83 Упростить арктан(квадратный корень из 3)
84 Найти точное значение грех(135)
85 Найти точное значение грех(105)
86 Найти точное значение грех(150 градусов)
87 Найти точное значение sin((2pi)/3)
88 Найти точное значение загар((2pi)/3)
89 Преобразовать из радианов в градусы пи/4
90 Найти точное значение грех(пи/2)
91 Найти точное значение сек(45)
92 Найти точное значение cos((5pi)/4)
93 Найти точное значение cos((7pi)/6)
94 Найти точное значение угловой синус(0)
95 Найти точное значение грех(120 градусов)
96 Найти точное значение желтовато-коричневый ((7pi)/6)
97 Найти точное значение соз(270)
98 Найти точное значение sin((7pi)/6)
99 Найти точное значение arcsin(-( квадратный корень из 2)/2)
100 Преобразование градусов в радианы 88 градусов

Мэтуэй | Популярные задачи

1 Найти точное значение грех(30)
2 Найти точное значение грех(45)
3 Найти точное значение грех(30 градусов)
4 Найти точное значение грех(60 градусов)
5 Найти точное значение загар (30 градусов)
6 Найти точное значение угловой синус(-1)
7 Найти точное значение грех(пи/6)
8 Найти точное значение cos(pi/4)
9 Найти точное значение грех(45 градусов)
10 Найти точное значение грех(пи/3)
11 Найти точное значение арктан(-1)
12 Найти точное значение cos(45 градусов)
13 Найти точное значение cos(30 градусов)
14 Найти точное значение желтовато-коричневый(60)
15 Найти точное значение csc(45 градусов)
16 Найти точное значение загар (60 градусов)
17 Найти точное значение сек(30 градусов)
18 Найти точное значение cos(60 градусов)
19 Найти точное значение соз(150)
20 Найти точное значение грех(60)
21 Найти точное значение cos(pi/2)
22 Найти точное значение загар (45 градусов)
23 Найти точное значение arctan(- квадратный корень из 3)
24 Найти точное значение csc(60 градусов)
25 Найти точное значение сек(45 градусов)
26 Найти точное значение csc(30 градусов)
27 Найти точное значение грех(0)
28 Найти точное значение грех(120)
29 Найти точное значение соз(90)
30 Преобразовать из радианов в градусы пи/3
31 Найти точное значение желтовато-коричневый(30)
32 Преобразование градусов в радианы 92
35 Преобразовать из радианов в градусы пи/6
36 Найти точное значение детская кроватка(30 градусов)
37 Найти точное значение арккос(-1)
38 Найти точное значение арктан(0)
39 Найти точное значение детская кроватка(60 градусов)
40 Преобразование градусов в радианы 30
41 Преобразовать из радианов в градусы (2 шт. )/3
42 Найти точное значение sin((5pi)/3)
43 Найти точное значение sin((3pi)/4)
44 Найти точное значение тан(пи/2)
45 Найти точное значение грех(300)
46 Найти точное значение соз(30)
47 Найти точное значение соз(60)
48 Найти точное значение соз(0)
49 Найти точное значение соз(135)
50 Найти точное значение cos((5pi)/3)
51 Найти точное значение cos(210)
52 Найти точное значение сек(60 градусов)
53 Найти точное значение грех(300 градусов)
54 Преобразование градусов в радианы 135
55 Преобразование градусов в радианы 150
56 Преобразовать из радианов в градусы (5 дюймов)/6
57 Преобразовать из радианов в градусы (5 дюймов)/3
58 Преобразование градусов в радианы 89 градусов
59 Преобразование градусов в радианы 60
60 Найти точное значение грех(135 градусов)
61 Найти точное значение грех(150)
62 Найти точное значение грех(240 градусов)
63 Найти точное значение детская кроватка(45 градусов)
64 Преобразовать из радианов в градусы (5 дюймов)/4
65 Найти точное значение грех(225)
66 Найти точное значение грех(240)
67 Найти точное значение cos(150 градусов)
68 Найти точное значение желтовато-коричневый(45)
69 Оценить грех(30 градусов)
70 Найти точное значение сек(0)
71 Найти точное значение cos((5pi)/6)
72 Найти точное значение КСК(30)
73 Найти точное значение arcsin(( квадратный корень из 2)/2)
74 Найти точное значение загар((5pi)/3)
75 Найти точное значение желтовато-коричневый(0)
76 Оценить грех(60 градусов)
77 Найти точное значение arctan(-( квадратный корень из 3)/3)
78 Преобразовать из радианов в градусы (3 пи)/4 
79 Найти точное значение sin((7pi)/4)
80 Найти точное значение угловой синус(-1/2)
81 Найти точное значение sin((4pi)/3)
82 Найти точное значение КСК(45)
83 Упростить арктан(квадратный корень из 3)
84 Найти точное значение грех(135)
85 Найти точное значение грех(105)
86 Найти точное значение грех(150 градусов)
87 Найти точное значение sin((2pi)/3)
88 Найти точное значение загар((2pi)/3)
89 Преобразовать из радианов в градусы пи/4
90 Найти точное значение грех(пи/2)
91 Найти точное значение сек(45)
92 Найти точное значение cos((5pi)/4)
93 Найти точное значение cos((7pi)/6)
94 Найти точное значение угловой синус(0)
95 Найти точное значение грех(120 градусов)
96 Найти точное значение желтовато-коричневый ((7pi)/6)
97 Найти точное значение соз(270)
98 Найти точное значение sin((7pi)/6)
99 Найти точное значение arcsin(-( квадратный корень из 2)/2)
100 Преобразование градусов в радианы 88 градусов

Интеграция по частям

Интеграция по частям — это специальный метод интеграции, который часто бывает полезен при перемножении двух функций, но также полезен и в других случаях.

Скоро вы увидите множество примеров, но сначала давайте посмотрим на правило:

∫u v dx = u∫v dx −∫u’ (∫v dx) dx

  • u есть функция u(x)
  • v есть функция v(x)
  • u’ — производная функции u(x)
    • г.

Правило в виде диаграммы:

Давайте сразу перейдем к примеру:

Пример: Что такое ∫x cos(x) dx ?

Хорошо, у нас есть x , умноженное на cos(x) , поэтому интегрирование по частям — хороший выбор.

Сначала выберите функции для u и v :

  • u = x
  • v = cos(x)

Так что теперь в формате ∫ u v dx мы можем продолжить:

Дифференцировать u : u’ = x’ = 1

Интегрировать v : ∫v dx = 9x ∫sin(x) Правила интегрирования)

Теперь мы можем сложить это вместе:

Упростить и решить:

x sin(x) − ∫sin(x) dx

x sin(x) + cos(x) + C

Готово!

 

Итак, мы выполнили следующие шаги:

  • Выберите u и v
  • Дифференцировать и: и’
  • Интегрировать v: ∫v dx
  • Поместите u, u’ и ∫v dx в: u∫v dx −∫u’ (∫v dx) dx
  • Упрости и реши

По-английски мы можем сказать, что ∫u v dx становится:

(u интеграл v) минус интеграл от (производная u, интеграл v)

 

Давайте попробуем еще несколько примеров:

Пример: чему равно ∫ln(x)/x

2 dx ?

Сначала выберите u и v:

  • u = ln(x)
  • v = 1/х 2

Differentiate u: ln(x)’ = 1 x

Integrate v: ∫1/x 2 dx = ∫x -2 dx = −x -1 = −1 x   (по степенному правилу)

Теперь сложим вместе:

Упростим:

−ln(x)/x − ∫−1/x 2 ∫−1/x 2 −lx 1 dx / х — 1 / х + С

− ln(x) + 1 x + С

 


Пример.

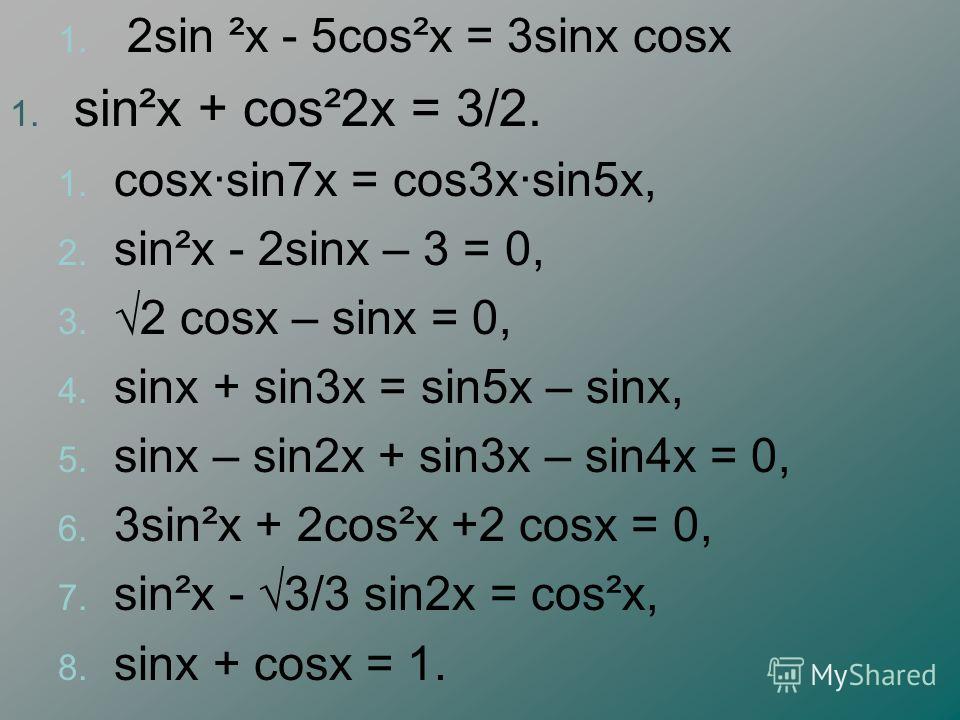Что такое ∫ln(x) dx ?

Но есть только одна функция! Как мы выбираем u и v ?

Эй! Мы можем просто выбрать v как «1»:

  • u = ln(x)
  • v = 1

Продифференцировать u: ln(x)’ = 1/x

Проинтегрировать v: ∫1 dx = x

Теперь сложить вместе:

Упростить:

x ln(x) − x1

х пер(х) — х + С

 

Пример: Что такое ∫e

x x dx ?

Выберите u и v:

  • u = e x
  • v = х

Дифференцировать u: (e x )’ = e x

Интегрировать v: ∫x dx = x 2 /2

Теперь сложим вместе:

0

Стало только хуже!

Что ж, это была захватывающая катастрофа.

: Может быть, мы могли бы выбрать другие u и v?

Пример: ∫e

x x dx (продолжение)

Выберите u и v по-разному:

  • u = x
  • v = е х

Дифференциал u: (x) ‘= 1

Integrate V: ∫e x DX = E x

Теперь. Сделайте вместе:

Упрощение:

x

:

x

. + С

e x (х-1) + С

г.

Мораль этой истории: тщательно выбирайте и и против !

Выберите и , которые упрощаются при дифференциации, и и , которые не усложняются при интеграции.

Полезное эмпирическое правило: Я ПОЗДНЕЕ. Выберите u в зависимости от того, какой из них будет первым:

  • I : обратные тригонометрические функции, такие как sin -1 (x), cos -1 (х), желто-коричневый -1 (х)
  • L : Логарифмические функции, такие как ln(x), log(x)
  • A : Алгебраические функции, такие как x 2 , x 3
  • T : тригонометрические функции, такие как sin(x), cos(x), tan (x)
  • E : Экспоненциальные функции, такие как e x , 3 x

И последний (и хитрый) пример:

Пример: ∫e

x sin(x) dx

Выберите u и v:

  • u = sin(x)
  • v = е х

Дифференцировать u: sin(x)’ = cos(x)

Интегрировать v: ∫e x dx = e x

Теперь сложите вместе:

∫dxe sin = sin(x) e x −∫cos(x) e x dx

 

Выглядит хуже, но будем настаивать! Чтобы найти ∫cos(x) e x dx, мы можем использовать интегрирование по частям снова :

Выберите u и v:

  • u = cos(x)
  • v = е х

Дифференцировать u: cos(x)’ = -sin(x)

Интегрировать v: ∫e x dx = e x

Теперь сложите вместе:

∫e x sin(x) dx = sin(x) e x — (cos(x) e x -∫-sin(x) e x dx)

Упрощение:

∫e x sin(x) dx = e x sin(x) — e x cos(x) −∫ e x sin(x)dx

Теперь у нас есть одинаковых интегралов с обеих сторон (кроме одного вычтенного) . ..

… так что мы можем вывести правый интеграл влево, и мы получаем:

2∫e x sin(x) dx = e x sin(x) − e x cos(x)

Упрощение:

∫e x sin(x) dx = ½ e x (sin(x) − cos(x)) + C

 

Определенные интегралы

Когда интеграл имеет интервал, подобный [a, b], мы можем использовать любой из них:

и v дх = [ и

в дх −

u'(

v dx) dx ]

и v дх = [ и

в дх ]

−

u'(

v dx) dx

Где u и v — функции от x, а a и b — пределы x.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *