Cosx больше или равно -1/корень 2, помогите решить тригонометрическое неравенство и желательно с окружностью — Школьные Знания.net
Все предметы
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Информатика
Українська література
Қазақ тiлi
Экономика
Музыка
Беларуская мова
Французский язык
Немецкий язык
Психология
Оʻzbek tili
Кыргыз тили
Астрономия
Физкультура и спорт
Ответ дан
daibabahubum
Пошаговое объяcнение:Задание Решить неравенство
[ sin xle frac{sqrt{3}}{2} ]
Решение Поскольку
[ left| frac{sqrt{3}}{2} right|<1 ]
, то это неравенство имеет решение и его можно решить двумя способами.
Первый способ. Решим это неравенство графически. Для этого построим в одной системе координат график синуса y=sin x и прямой y=frac{sqrt{3}}{2} (рис. 2).
Рис. 2
Выделим промежутки, на которых синусоида расположена ниже графика прямой y=frac{sqrt{3}}{2}. Найдем абсциссы {{x}_{1}} и {{x}_{2}} точек пересечения этих графиков:
[{{x}_{1}}=pi -arcsin frac{sqrt{3}}{2}=pi -frac{pi }{3}=frac{2pi }{3} ]
[{{x}_{2}}=arcsin frac{sqrt{3}}{2}+2pi =frac{pi }{3}+2pi =frac{7pi }{3}]
Получили интервал left[ -frac{4pi }{3}; frac{pi }{3} right], но так как функцию y=sin x периодическая и имеет период 2pi, то ответом будет объединение интервалов: left[ frac{2pi }{3}+2pi k; frac{7pi }{3}+2pi k right],quad kin Z.
Второй способ. Построим единичную окружность и прямую y=frac{sqrt{3}}{2}, точки их пересечения обозначим {{P}_{{{x}_{1}}}} и {{P}_{{{x}_{2}}}} (рис.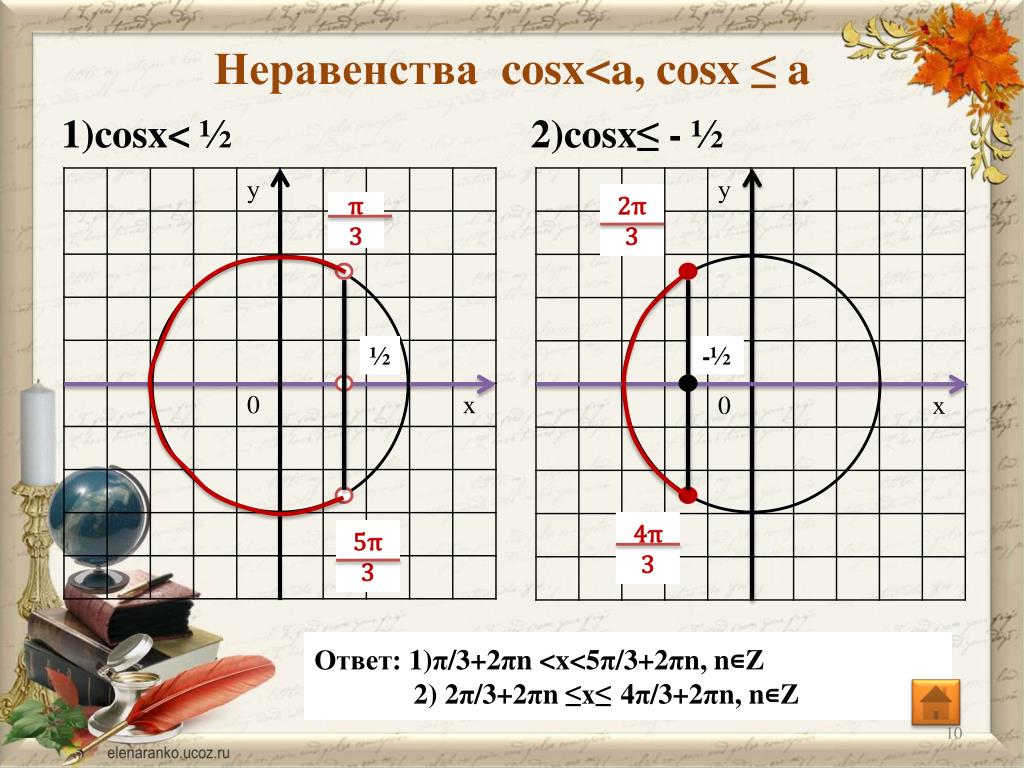
3). Решением исходного неравенства будет множество точек ординаты, которых меньше frac{sqrt{3}}{2}. Найдем значение {{x}_{1}} и {{x}_{2}}, совершая обход против часовой стрелки, {{x}_{1}}<{{x}_{2}}:
Рис. 3
[{{x}_{1}}=pi -arcsin frac{sqrt{3}}{2}=pi -frac{pi }{3}=frac{2pi }{3} ]
[{{x}_{2}}=arcsin frac{sqrt{3}}{2}+2pi =frac{pi }{3}+2pi =frac{7pi }{3}]
Учитывая периодичность функции синус, окончательно получим интервалы left[ frac{2pi }{3}+2pi k; frac{7pi }{3}+2pi right],quad kin Z.
Ответ xin left[ frac{2pi }{3}+2pi k; frac{7pi }{3}+2pi right],quad kin Z
ПРИМЕР 2
Задание Решить неравенство sin x>2
Решение Синус – функция ограниченная: left| sin x right|le 1, а правая часть данного неравенства больше единицы, поэтому решений нет.
Ответ решений нет.
Ответов пока нет | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
.. — Учеба и наука
Мы знаем, что $\frac{\text{df}(x)}{\text{dx}}=x-\sin (x)$ при $x>0$. Согласно МВТ, если $x>0$, то $f(x)-f(0)=(x+0) f'(c)$ для некоторого $c>0$.
Тут я запутался:
Итак, $f(x)>f(0)=1$, но почему? Это проявляется в моем отсутствии неравенства или чего я упускаю? $f'(x)\cdot x=1$ или что происходит?
- реальный анализ
- неравенство
$\endgroup$
92/2+1=1$ Из вашего уравнения: $$f(x)-f(0)=(x)f'(c)=x(c-\sin c)$$
Пусть $g(x)=x-\sin x$ Опять же, вы можете показать, что $g'(x)=1-\cos x$, что всегда больше, чем $0$ из-за ограниченного характера $\cos x$. Так как $g(0)=0$ и это возрастающая функция $\{g'(x)>0\;\forall x>0$}, поэтому $g(x)>0 \;\forall x>0$.
Итак, $f(x)-f(0)>0\;\forall x>0$ при $x>0$ и $c-\sin c >0\;\forall c>0${as $0< с<х$}.
Итак, $f(x)>f(0)=1$
$\endgroup$
$\begingroup$
Вы хорошо начали.