Ctg 3 2: Вычислите tg^2 t + ctg^2 t, если tg t + ctg t= 3

Mathway | Популярные задачи

1	Найти число возможных исходов	7 выбор 3
2	Найти число возможных исходов	8 выбор 3
3	Найти число возможных исходов	5 выбор 2
4	Найти число возможных исходов	4 выбор 2
5	Найти число возможных исходов	8 выбор 4
6	Найти число возможных исходов	10 выбор 3
7	Найти число возможных исходов	7 выбор 4
8	Найти число возможных исходов	6 выбор 3
9	Найти число возможных исходов	9 выбор 3
10	Найти число возможных исходов	3 выбор 2
11	Найти число возможных исходов	6 выбор 4
12	Найти число возможных исходов	5 выбор 4
13	Найти число возможных исходов	7 перестановка 3
14	Найти число возможных исходов	7 выбор 2
15	Найти число возможных исходов	10 выбор 5
16	Найти число возможных исходов	10 выбор 6
17	Найти число возможных исходов	13 выбор 5
18	Найти число возможных исходов	3 выбор 3
19	Найти число возможных исходов	4 выбор 1
20	Найти число возможных исходов	4 выбор 4
21	Найти число возможных исходов	5 выбор 1
22	Найти число возможных исходов	6 перестановка 3
23	Найти число возможных исходов	8 выбор 5
24	Найти число возможных исходов	9 перестановка 4
25	Найти число возможных исходов	13 выбор 3
26	Найти число возможных исходов	12 выбор 2
27	Найти число возможных исходов	12 выбор 4
28	Найти число возможных исходов	12 выбор 3
29	Найти число возможных исходов	9 выбор 5
30	Найти число возможных исходов	9 выбор 2
31	Найти число возможных исходов	7 выбор 5
32	Найти число возможных исходов	6 перестановка 6
33	Найти число возможных исходов	8 перестановка 5
34	Найти число возможных исходов	8 перестановка 3
35	Найти число возможных исходов	7 перестановка 5
36	Найти число возможных исходов	52 выбор 5
37	Найти число возможных исходов	5 перестановка 3
38	Найти число возможных исходов	12 выбор 5
39	Найти число возможных исходов	3 выбор 1
40	Найти число возможных исходов	11 выбор 5
41	Найти число возможных исходов	10 выбор 2
42	Найти число возможных исходов	15 выбор 3
43	Найти число возможных исходов	52 выбор 4
44	Найти число возможных исходов	9 выбор 4
45	Найти число возможных исходов	9 перестановка 3
46	Найти число возможных исходов	7 перестановка 4
47	Найти число возможных исходов	7 перестановка 2
48	Найти число возможных исходов	11 выбор 4
49	Найти число возможных исходов	11 выбор 2
50	Найти число возможных исходов	11 выбор 3
51	Найти число возможных исходов	10 перестановка 5
52	Найти число возможных исходов	5 выбор 5
53	Найти число возможных исходов	6 выбор 1
54	Найти число возможных исходов	8 перестановка 4
55	Найти число возможных исходов	8 выбор 6
56	Найти число возможных исходов	13 выбор 4
57	Вычислить	e
58	Найти уравнение, перпендикулярное прямой	-7x-5y=7
59	Найти число возможных исходов	13 выбор 2
60	Найти число возможных исходов	10 перестановка 2
61	Найти число возможных исходов	10 перестановка 3
62	Найти число возможных исходов	10 выбор 7
63	Найти число возможных исходов	20 выбор 4
64	Найти число возможных исходов	6 перестановка 4
65	Найти число возможных исходов	5 перестановка 4
66	Найти число возможных исходов	6 выбор 5
67	Найти число возможных исходов	52 выбор 3
68	Найти число возможных исходов	4 выбор 0
69	Найти число возможных исходов	9 перестановка 7
70	Найти число возможных исходов	6 выбор 2
71	Найти число возможных исходов	5 перестановка 5
72	Найти число возможных исходов	5 перестановка 2
73	Найти число возможных исходов	6 выбор 6
74	Найти число возможных исходов	7 выбор 6
75	Найти число возможных исходов	8 перестановка 6
76	Найти число возможных исходов	7 перестановка 7
77	Найти число возможных исходов	9 перестановка 5
78	Найти число возможных исходов	2 перестановка 2
79	Найти число возможных исходов	10 выбор 8
80	Найти число возможных исходов	12 выбор 7
81	Найти число возможных исходов	15 выбор 5
82	Найти обратный элемент	[[1,0,1],[2,-2,-1],[3,0,0]]
83	Определить область значений	1/4x-7
84	Найти число возможных исходов	10 перестановка 7
85	Найти число возможных исходов	12 выбор 6
86	Найти число возможных исходов	2 выбор 1
87	Найти число возможных исходов	30 выбор 3
88	Найти число возможных исходов	9 выбор 6
89	Найти число возможных исходов	8 перестановка 2
90	Найти число возможных исходов	7 выбор 1
91	Найти число возможных исходов	6 перестановка 2
92	Найти число возможных исходов	4 перестановка 2
93	Найти число возможных исходов	4 перестановка 3
94	Найти число возможных исходов	3 перестановка 3
95	Найти число возможных исходов	46 выбор 6
96	Найти число возможных исходов	5 перестановка 1
97	Найти число возможных исходов	52 выбор 7
98	Найти число возможных исходов	52 перестановка 5
99	Найти число возможных исходов	9 выбор 1
100	Найти число возможных исходов	9 перестановка 6

Преобразование тригонометрических выражений.

Вывод тригонометрических формул

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Университетский лицей №1523
Предуниверситария НИЯУ МИФИ
Лекции по алгебре и началам анализа
10 класс
© Хомутова
Лариса Юрьевна
Преобразование
тригонометрических
выражений
(вывод тригонометрических
формул)
I-a. Формулы приведения
Выведем вспомогательные формулы, позволяющие
находить
sin
cos и
2
2
по тригонометрическим функциям угла .
(0; / 2 )
AOB = A1OC по гипотенузе и
острому углу: AO = 1 = A1O.
A1OC = / 2 — COA = AOB;
( / 2; )
AOB = A1OC по гипотенузе и острому
углу: AO = 1 = A1O.
A1OC = + / 2 — = — / 2 = AOB;
( ; 3 / 2)
Покажем, что AOB = A1OC по
гипотенузе и острому углу: AO = 1 = A1O.
Кроме того, на
A1OC = + / 2 — 3 / 2 = — = AOB;
(3 / 2; 2 )
Покажем, что AOB = A1OC по
гипотенузе и острому углу: AO = 1 = A1O.
A1OC = + / 2 — 2 = — 3 / 2 = AOB.
I-a. Формулы приведения
,
.
cos sin
2
sin cos
2
I-b. Формулы приведения
Выведенные формулы сложения позволяют получить
формулы приведения, упрощающие тригонометрические
функции углов вида k 2
cos 3 2 cos3 2 cos sin 3 2 sin sin
1
0
:
/2– /2+
–
+
3 / 2 –
3 / 2 +
2 –
2 +
sin
cos
cos
sin
–sin
–cos
–cos
–sin
sin
cos
sin
–sin
–cos
–cos
–sin
sin
cos
cos
tg
ctg
–ctg
–tg
tg
ctg
–ctg
–tg
tg
ctg
tg
–tg
–ctg
ctg
tg
–tg
–ctg
ctg
II. Формулы сложения
M ( )
j
M ( )
M ( )
2) Введем единичные вектора
i и j
0
1) Отметим на единичной
окружности точки M ( ) и
3) M ( ) cos ; sin
i
M ( ) cos ; sin
4) OM ( ) (cos ; sin )
OM ( ) (cos ; sin )
5) Угол между векторами OM ( ) и OM ( ) равен
6) По свойству скалярного произведения найдем
OM ( ) OM 1 1 cos cos cos cos sin sin
7) Учитывая четность тригонометрических функций получаем
cos cos cos cos( ) sin sin
cos cos sin sin
8)
sin cos cos ( )
2
2
cos cos sin sin
2
2
sin cos cos sin
9)
sin cos cos ( )
2
2
cos cos sin sin
2
2
sin cos cos sin
II. Формулы сложения
sin sin cos cos sin ,
cos cos cos sin sin
sin
sin cos cos sin
tg
cos cos cos sin sin
Поделим числитель и знаменатель полученной дроби на
cos cos
cos 0 и cos 0 , т.е. в случае, когда
tg
и
tg определены:
tg tg
tg
1 tg tg
cos
cos cos sin sin ctg ctg 1
ctg
sin sin cos cos sin
ctg ctg
II. Формулы сложения
tg tg
tg
,
1 tg tg
ctg ctg 1
ctg
ctg ctg
III. Формулы двойных углов
Чтобы вывести формулы для вычисления
тригонометрических функций двойного аргумента,
подставим = в формулы сложения:
sin sin cos cos sin ,
sin 2 sin cos cos sin 2sin cos ,
cos cos cos sin sin ,
tg tg
,
1 tg tg
ctg ctg 1
ctg
ctg ctg
tg
cos 2 cos cos sin sin cos 2 sin 2 ,
tg tg
2tg
tg 2
,
2
1 tg tg 1 tg
ctg ctg 1 ctg 2 1
ctg 2
.
ctg ctg
2ctg
III. Формулы двойных углов
sin 2 2sin cos
cos 2 cos sin
2
2
cos 2 cos 2 sin 2 1 sin 2 sin 2 1 2sin 2
cos 2 cos sin cos 1 cos 2 cos 1
2
2
2
2
2
III. Формулы двойных углов
2tg
tg 2
2
1 tg
ctg 1
ctg 2
2ctg
2
\ : cos2
2sin cos
sin 2 2sin cos
sin 2 cos2
2tg
cos 0 tg 2 1
\ : sin 2
2sin cos
sin 2 2sin cos
sin 2 cos2
\ : cos2
cos sin
2
2
cos 2 cos sin
sin 2 cos2
2
2
2
1 tg 2
cos 0 tg 2 1
\ : sin 2
cos sin
2
2
cos 2 cos sin
2
2
sin cos
2
2ctg
sin 0 ctg 2 1
ctg 2 1
sin 0 1 ctg 2
III.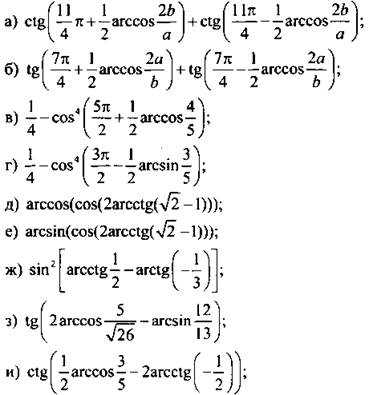 Формулы двойных углов
2tg
sin 2 2
tg 1
2ctg
sin 2
ctg 2 1
1 tg
cos 2
1 tg 2
2
ctg 2 1
cos 2
ctg 2 1
IV. Формулы тройных углов
sin 3 sin 2 sin 2 cos cos 2 sin 2sin cos 2 1 2sin 2 sin
2sin 1 sin 2 sin 2sin 3 2sin 2sin 3 sin 2sin 3 3sin 4sin 3
cos 3 cos 2 cos 2 cos sin 2 sin 2 cos 2 1 cos 2sin 2 cos
.
2 cos3 cos 2 1 cos 2 cos 2 cos 3 cos 2 cos 2 cos 3 4 cos 3 3cos
tg 3
3sin sin 2 cos 2 4sin 3
sin 3 3sin 4sin
3
3
2
2
cos 3 4 cos 3cos 4 cos 3cos sin cos
3
\ : cos3
3sin cos sin
cos3 3cos sin 2
2
.
3
3tg tg 3
cos 0 1 3tg 2
\ : sin 3
cos 3cos sin
ctg 3
3sin cos 2 sin 3
3
2
ctg 3 3ctg 3ctg ctg 3
2
3ctg 1
1 3ctg 2
sin 0
IV. Формулы тройных углов
sin3 3sin 4sin
3
cos3 4cos3 3cos
3tg tg 3
tg 3
1 3tg 2
3ctg ctg 3
ctg 3
1 3ctg 2
V. Формулы половинных углов
cos 1 2sin
2
1 cos
sin
2
2
cos 2cos
1
2
1 cos
cos
2
2
2
.
2
2
2
\ 2 cos
sin 2
tg
2
cos 2
2
2sin 2 cos 2
sin
2
1 cos
2 cos 2
2
sin
2 1 cos
2
tg
2
2 cos 2 1 cos
;
\ 2sin
cos 2
ctg
2
sin 2
2
2sin 2 cos 2
sin
2
1 cos
2sin 2
2
cos
2 1 cos
2
ctg
2
2 sin 2 1 cos
V. Формулы половинных углов
1 cos
sin
2
2
2
1 cos
cos
2
2
1 cos
sin
2
tg
tg
2 1 cos
2 1 cos
2
,
,
.
.
sin
ctg
2 1 cos
1 cos
ctg
2 1 cos
2
VI. Формулы преобразования произведения
тригонометрических функций в сумму
sin sin cos cos sin ,
sin sin cos cos sin ,
cos cos cos sin sin ,
cos cos cos sin sin .
.
1
2
3
4
Сложив почленно равенства (1) и (2), получим:
.
sin cos
1
sin sin
2
Сложив почленно равенства (3) и (4), получим:
1
cos cos cos cos
2
Вычтя из равенства (4) равенство (3), получим:
sin sin
1
cos cos
2
VI. Формулы преобразования произведения
тригонометрических функций в сумму
1
sin cos sin sin
2
1
cos cos cos cos
2
1
sin sin cos cos
2
VII. Формулы преобразования суммы
тригонометрических функций в
произведение
sin sin sin
cos
cos
sin
sin
cos
sin
sin
2
2
2
2
2
2
2
2
2
2
cos
sin
2sin
cos
2
2
2
2
sin sin sin
sin
sin
cos
cos
sin
sin
cos
2
2
2
2
2
2
2
2
2
2
.
cos
sin
2cos
sin
2
2
2
2
cos cos cos
cos
sin
sin
cos
cos
cos
cos
2
2
2
2
2
2
2
2
2
2
sin
sin
2cos
cos
2
2
2
2
.
cos cos cos
cos
sin
sin
cos
cos
cos
cos
2
2
2
2
2
2
2
2
2
2
sin
.
sin
2sin
sin
2sin
sin
2
2
2
2
2
2
VII. Формулы преобразования суммы
тригонометрических функций в
произведение
sin sin 2sin 2 cos 2 ,
sin sin 2 cos sin ,
2
2
cos cos 2 cos cos ,
2
2
cos cos 2sin
sin
.
2
2

English     Русский Правила

CTG 3-дюймовый реверсивный отрезной инструмент с гибкой головкой

Сейчас: 97,99 долларов США

(пока отзывов нет) Написать рецензию

КТГ

CTG 3-дюймовый реверсивный отрезной инструмент с гибкой головкой

Рейтинг Обязательно Выберите рейтинг1 звезда (худший)2 звезды3 звезды (средний)4 звезды5 звезд (лучший)

Имя Обязательно

Электронная почта Обязательно

Тема обзора Обязательно

Комментарии Обязательно

Артикул:

CT-LDB2521

Наличие:

В наличии

• Описание
• Информация о гарантии

Этот новый и очень популярный пневматический инструмент  CTG станет настоящим дополнением к вашему ящику для инструментов.

3-дюймовый Flex Head Reversible  Инструмент для отсечки воздуха имеет:

• уникальную гибкую головку, регулируемую для 3 различных положения.0067 лучше доступ в узких местах .
• реверсивная функция , позволяющая изменить направление резки на помощь в управлении направлением искр.

Характеристики:

• Отрезной диск:          3 дюйма
• Длина:                  9,8″
• Свободная скорость: 16 000 об/мин
• Воздухозаборник:             1/4 дюйма
• Ср. Минусы воздуха 3,6 кубических футов в минуту
• Размер мини-шланга: 3/8 дюйма
• Мощность:              0,75 л.с.

Наш бренд CTG — это наша верхняя линия пневматических инструментов. Отлично подходит для профессионального механика или любителя-любителя , который хочет иметь в своем магазине пневматический инструмент очень высокого качества .

На все наши пневмоинструменты распространяется ограниченная гарантия сроком на 1 год .

На все наши пневматические инструменты распространяется ограниченная гарантия сроком на 1 год.

• сопутствующие товары
• Клиенты также просмотрели

триплетных повторов ДНК CTG, участвующих в динамических мутациях неврологически родственных генных последовательностей, образуют стабильные дуплексы | Исследование нуклеиновых кислот

Фильтр поиска панели навигации Исследование нуклеиновых кислотЭтот выпускЖурналы NARНаука и математикаКнигиЖурналыOxford Academic Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Исследование нуклеиновых кислотЭтот выпускЖурналы NARНаука и математикаКнигиЖурналыOxford Academic Термин поиска на микросайте

Расширенный поиск

Журнальная статья

Кеннет Г. Смит,

Кеннет Г. Смит

Ищите другие работы этого автора на:

Оксфордский академический

пабмед

Google ученый

Цзи Цзе,

Джи Джи

Ищите другие работы этого автора на:

Оксфордский академический

пабмед

Google ученый

Джордж Э. Фокс,

Джордж Э. Фокс

Ищите другие работы этого автора на:

Оксфордский академический

пабмед

Google ученый

Сяолянь Гао

Сяолиан Гао ^*

Ищите другие работы этого автора на:

Оксфордский академический

пабмед

Google ученый

Nucleic Acids Research , том 23, выпуск 21, 11 ноября 1995 г. , страницы 4303–4311, https://doi.org/10.1093/nar/23.21.4303

Опубликовано2:

9519 январь 1991 История статьи

Опубликовано:

01 января 1995 г.

Получено:

16 августа 1995

Принято:

22 сентября 1995 г.

Фильтр поиска панели навигации Исследование нуклеиновых кислотЭтот выпускЖурналы NARНаука и математикаКнигиЖурналыOxford Academic Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Исследование нуклеиновых кислотЭтот выпускЖурналы NARНаука и математикаКнигиЖурналыOxford Academic Термин поиска на микросайте

Advanced Search

Триплетные повторы ДНК, 5’d(CTG) _n и 5′-d(CAG) _n присутствуют в генах, которые вовлечены в несколько нейродегенеративных заболеваний. Чтобы исследовать возможные стабильные структуры, образованные этими повторяющимися последовательностями, мы исследовали d(CTG) _n , d(CAG) _n и d(CTG)*d(CAG) _n (n = 2 и 3) с использованием ЯМР и УФ-оптическая спектроскопия. Эти исследования показывают, что одноцепочечные (CTG) _n (n > 2) образуют стабильные антипараллельные спиральные дуплексы, в то время как одноцепочечные (CAG) _n требует не менее трех повторяющихся блоков для формирования дуплекса. ЯМР- и УФ-эксперименты по плавлению показывают, что T ^m увеличивается в следующем порядке: ₃ . Дуплекс (CTG) ₃ стабилен и имеет аналогичные спектры ЯМР в растворах, содержащих 0,1–4 М NaCl, и в диапазоне рН от 4,6 до 8,8. Дуплекс (CTG) ₃ a, который содержит множественные несовпадения Т.Т, демонстрирует многие спектральные характеристики ЯМР, сходные с характеристиками ДНК В-формы. Однако уникальный NOE и ¹ H- ³¹ P паттерны сцепления, связанные с повторяющимися несовпадениями T.