Итак, я запишу здесь: для $%y≥-2$%. Также в скобках мы можем записать, что ($%x≤1$%).Мы еще полностью не выяснили, какие значения $%x$% и $%y$% нам нужны, так что, пусть эти два условия побудут здесь. Что у нас здесь получается?
Чтобы найти $%x$%, нам нужно извлечь корень квадратный из обеих частей равенства. Посмотрим на правую часть: здесь у нас получится: ($%x-1$%), именно для этого мы и извлекали корень квадратный. Мы так и хотели, чтобы здесь у нас было простое выражение ($%x-1$%).
А теперь вопрос: ($%x-1$%) – это положительное или отрицательное число?
Обратите внимание, здесь у нас ограничение значений $%x$%: $%x$% должен быть меньше или равен единице. Следовательно, в данном случае мы имеем дело только с теми значениями $%x$%, которые меньше или равны единице. А значит, вот это выражение будет отрицательным. Таким образом, мы должны взять отрицательный корень.

До скорой встречи!
Мне не понятен вот этот процесс, почему мы получили отрицательный квадратный корень? $%-\sqrt{(y+2)}$% ведь при $%x≤1$% $%1-1 = 0$%, а $%0$% это не отрицательное число?
Помогите, пожалуйста.
Функции (обратная, кубическая)
Контрольная работа
Функции
Вариант 1
Задание 1
Обратной пропорциональностью является функции
Задание 2
Графиком функции является:
а) прямая; б) парабола; в) гипербола; г) ветвь параболы.
Задание 3
Укажите неверное утверждение:
А) функция неотрицательная на промежутке ;
Б) функция имеет единственный нуль;
В) функция не имеет промежутков возрастания;
Г) график функции у=х3 не пересекает ось абсцисс;
Д) область значений функции – все действительные числа, кроме нуля.
Задание 4
Найдите нули функции, заданной таблицей:
х | -11 | -1 | 0 | 6 | |||
у | 3 | 0 | -2 | 5 | 7 | 0 | 0 |
Задание 5
Постройте график функции, заданной формулой .
Задание 6
С помощью графика функции, изображенного на рисунке, найдите:
а) нули функции;
б) промежутки возрастания и убывания функции;
в) промежутки знакопостоянства;
г) наибольшее и наименьшее значения функции на отрезке ;
Задание 7
Дана функция у= — х3 , D(y) =[-3; 2]. Найдите множество значений данной функции.
Найдите множество значений данной функции.
Задание 8
Известно, что график функции проходит через точкуN (-2;1). Найдите значение к.
Задание 9
Найдите область определения функции, заданной формулой .
Задание 10
Постройте график функции, заданной формулой .
Контрольная работа
Функции
Вариант 2
Задание 1
Прямой пропорциональностью является функция:
Задание 2
Графиком функции является:
а) прямая; б) парабола; в) гипербола; г) ветвь параболы.
Задание 3
Укажите верное утверждение:
А) областью определения функция является промежуток ;
Б) графиком функция является прямая;
В) множеством значений функции является множество всех отрицательных чисел;
Г) число 4,75 является нулем функции ;
Д) функция у=х3 убывает на области определения.
Задание 4
Найдите нули функции, заданной таблицей:
х | -17 | -2 | 0 | 7 | |||
у | 2 | 0 | -3 | 4 | 6 | 0 | 0 |
Задание 5
Постройте график функции, заданной формулой
Задание 6
С помощью графика функции, изображенного на рисунке, найдите:
а) нули функции;
б) промежутки возрастания и убывания функции;
в) промежутки знакопостоянства;
г) наибольшее и наименьшее значения функции на отрезке .
Задание 7
Дана функция у= — х3 , D(y) =[-1; 4]. Найдите множество значений данной функции.
Задание 8
Известно, что график функции проходит через точкуN (-3;2). Найдите значение к.
Задание 9
Найдите область определения функции, заданной формулой .
Задание 10
Постройте график функции, заданной формулой .
Обратная квадратичная функция
Общая форма квадратичной функции:
f(x) = ax 2 + bx + c
Тогда обратная квадратичная функция выше:
f -1 (x)
Например, рассмотрим квадратичную функцию
g(x) = x 2
Тогда обратная квадратичная функция g(x) = x 2 равна
g (x) -1 = √x
Нахождение обратной квадратичной функции:
Пусть f(x) — квадратичная функция.
Шаг 1:
Замените f(x) на y и поменяйте местами переменные x и y.
Шаг 2:
Найдите y и замените y на f -1 (x).
Пример 1:
Найдите обратную квадратичную функцию и постройте ее график.
f(x) = x 2
Решение:
Замените f(x) на y.
y = x 2
Поменять местами x и y.
x = y 2
y 2 = x
Найдите y.
Извлеките квадратный корень с обеих сторон.
y = ±√x
Замените y на f -1 (x).
f -1 (x) = ±√x
График обратной функции f(x) :
Мы можем построить график исходной функции, построив вершину (0, 0). Парабола раскрывается, потому что положительно.
И мы получаем f(1) = 1 и f(2) = 4, которые также являются одинаковыми значениями f(-1) и f(-2) соответственно.
Чтобы построить график f -1 (x) , , мы должны взять координаты каждой точки на исходном графике и поменять местами координаты x и y.
Например, (2, 4) становится (4, 2).
Мы должны сделать это, потому что входное значение становится выходным значением в обратном порядке, и наоборот.
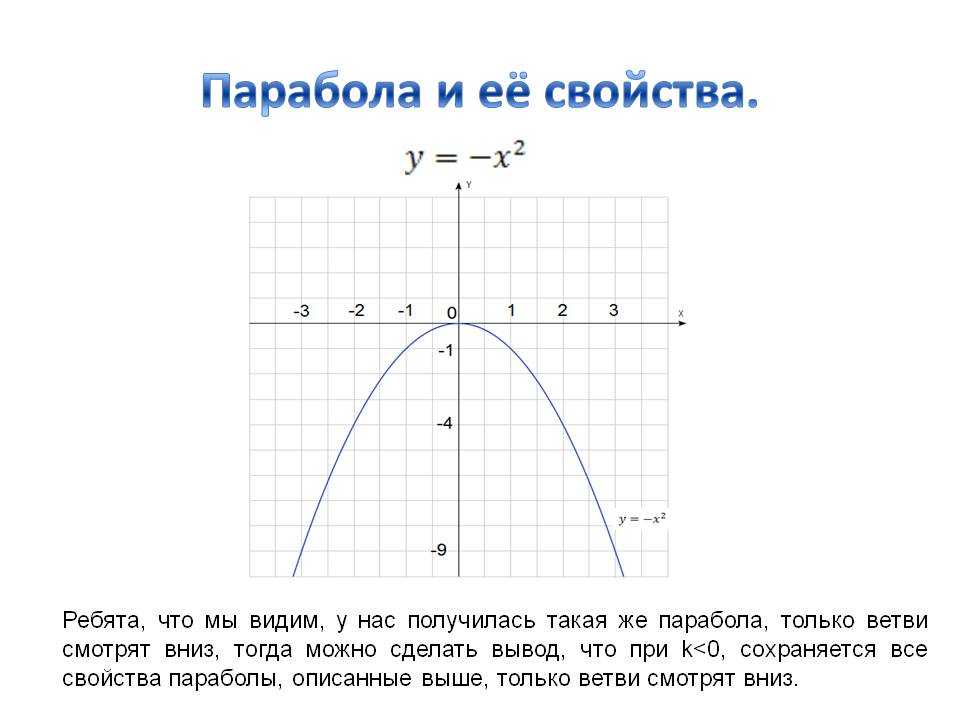
График обратной функции является отражением исходной функции относительно прямой y = x.
Пример 2 :
Найдите обратную квадратичную функцию и постройте ее график.
f(x) = 2(x + 3) 2 — 4
Решение:
Заменить f(x) на y.
y = 2(x + 3) 2 — 4
Поменять местами x и y.
x = 2(y + 3) 2 — 4
Найдите y.
x + 4 = 2(y + 3) 2
(x + 4)/2 = (y + 3) 2
Извлеките квадратный корень из обеих сторон.
±√[(x + 4)/2] = y + 3
±√[(x + 4)/2] — 3 = y
y = -3 ± √[(x + 4)/2 ]
Заменить y на f -1 (x).
f -1 (x) = -3 ± √[(x + 4)/2]
График обратной функции f(x) :
Мы можем построить график исходной функции, построив вершину (- 3, -4). Парабола раскрывается, потому что положительно.
Парабола раскрывается, потому что положительно.
И мы получаем f(-2) = -2 и f(-1) = 4, которые также являются теми же значениями f(-4) и f(-5) соответственно.
Чтобы построить график f -1 (x) , , мы должны взять координаты каждой точки на исходном графике и поменять местами координаты x и y.
Например, (-1, 4) становится (4, -1).
Мы должны сделать это, потому что входное значение становится выходным значением в обратном порядке, и наоборот.
Если вам нужны какие-либо другие материалы по математике, помимо материалов, указанных выше, воспользуйтесь нашим пользовательским поиском Google здесь.
Пожалуйста, отправьте ваш отзыв на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
3.8: Обратные и радикальные функции
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 18291
- OpenStax
- OpenStax
Развитие навыков
В этом разделе вы: 93 \конец{выравнивание*}\]
Мы записали объем \(V\) через радиус \(r\).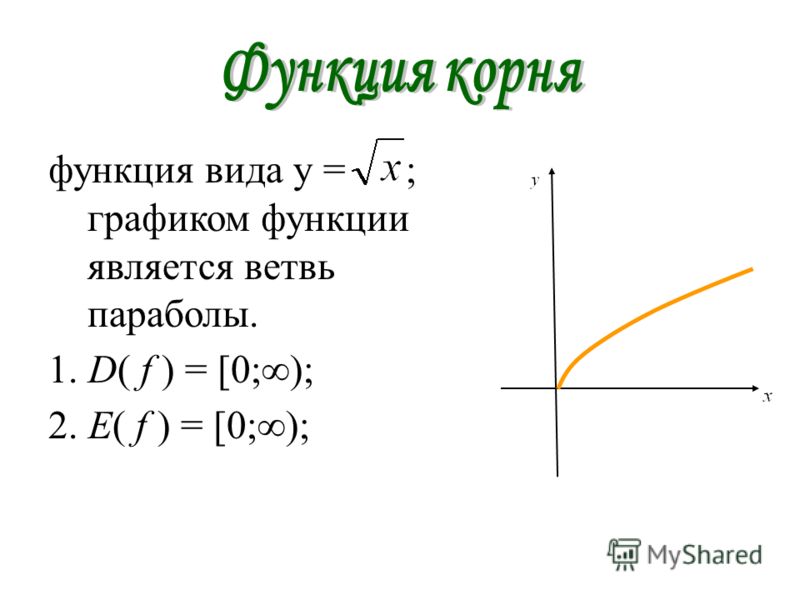
\[r=\sqrt[3]{\dfrac{3V}{2\pi}} \nonnumber\]
Эта функция является обратной формуле для \(V\) через \(r\).
В этом разделе мы исследуем обратные полиномиальные и рациональные функции, а также радикальные функции, с которыми мы сталкиваемся в процессе.
Две функции \(f\) и \(g\) являются обратными функциями, если для каждой пары координат \((a,b)\) в \(f\) существует соответствующая пара координат \((b, a )\) в обратной функции \(g\). Другими словами, у пар координат обратных функций вход и выход поменялись местами. Только взаимно однозначные функции имеют обратные. Напомним, что функция «один к одному» имеет уникальное выходное значение для каждого входного значения и проходит тест горизонтальной линии.
Например, предположим, что водосборник построен в форме параболического желоба, как показано на рисунке \(\PageIndex{2}\). Мы можем использовать информацию на рисунке, чтобы найти площадь поверхности воды в желобе в зависимости от глубины воды.
Рисунок \(\PageIndex{2}\)
Поскольку будет полезно иметь уравнение для параболической формы поперечного сечения, мы наложим систему координат на поперечное сечение, где \ (x\) измеряется по горизонтали и \(y\) измеряется по вертикали, с началом в вершине параболы (рисунок \(\PageIndex{3}\)). 92\)
Нас интересует площадь поверхности воды, поэтому мы должны определить ширину наверху воды как функцию глубины воды. Для любой глубины \(y\) ширина будет равна \(2x\), поэтому нам нужно решить приведенное выше уравнение для \(x\) и найти обратную функцию. Однако обратите внимание, что исходная функция не является взаимно однозначной, и действительно, при любом выходе есть два входа, которые дают один и тот же результат, один положительный и один отрицательный.
Чтобы найти обратную, мы можем ограничить нашу исходную функцию ограниченной областью, в которой она 92}{2}\), \(x>0\)
Поскольку \(x\) — это расстояние от центра параболы до любой стороны, вся ширина воды наверху будет равна \(2x \). Желоб имеет длину 3 фута (36 дюймов), поэтому площадь поверхности будет:
\({Площадь}=l⋅w\)
\(=36⋅2x\)
\(=72x\)
\(=72\sqrt{2y}\)
Этот пример иллюстрирует два важных момента: один. 9{−1}\)
Обратите внимание, что обратная функция переключает домен и диапазон исходной функции.
ПРОВЕРКА ОБРАЩЕНИЯ ДВУХ ФУНКЦИЙ ДРУГОЙ ДРУГОЙ \(g\),
\(g(f(x))=f(g(x))=x\)
Для заданной полиномиальной функции найдите обратную функцию, ограничив область определения таким образом, чтобы новая функция была взаимно однозначной
- Замените \(f(x)\) на \(y\). 93−4\)
До сих пор нам удавалось найти обратные функции кубических функций без ограничения их области определения.
 Однако, как известно, не все кубические полиномы взаимно однозначны. Домен некоторых функций, которые не являются однозначными, может быть ограничен таким образом, чтобы они были однозначными, но только в пределах этого домена. Тогда функция над ограниченным доменом будет иметь обратную функцию . Поскольку квадратичные функции не являются взаимно однозначными, мы должны ограничить их область определения, чтобы найти их обратные.
Однако, как известно, не все кубические полиномы взаимно однозначны. Домен некоторых функций, которые не являются однозначными, может быть ограничен таким образом, чтобы они были однозначными, но только в пределах этого домена. Тогда функция над ограниченным доменом будет иметь обратную функцию . Поскольку квадратичные функции не являются взаимно однозначными, мы должны ограничить их область определения, чтобы найти их обратные.ОГРАНИЧЕНИЕ ОБЛАСТИ
Если функция не является взаимно однозначной, она не может иметь обратной. Если мы ограничим область определения функции так, чтобы она стала взаимно однозначной, тем самым создав новую функцию, эта новая функция будет иметь обратную.Для заданной полиномиальной функции ограничьте область определения функции, которая не является взаимно однозначной, а затем найдите обратную
- Ограничьте область определения, определив меньшую область, в которой исходная функция является взаимно однозначной.
 {−1}\) всегда будут лежать на прямой \(y=x\). 92−3\).
{−1}\) всегда будут лежать на прямой \(y=x\). 92−3\).Решение:
Мы видим, что это парабола с вершиной в \((2,–3)\), которая открывается вверх. Поскольку граф будет убывать с одной стороны вершины и возрастать с другой стороны, мы можем ограничить эту функцию областью, в которой она будет взаимно однозначной, ограничив область до \(x≥2\).
Чтобы найти обратную, мы будем использовать вершинную форму квадратного. Начнем с замены \(f(x)\) на переменную \(y\), затем найдем \(x\).
9{−1}(x)=\sqrt{x−1}\)Нахождение инверсий радикальных функций
Обратите внимание, что все функции из предыдущих примеров были многочленами, а их инверсии были радикальными функциями. Если мы хотим найти обратную радикальную функцию, нам нужно будет ограничить область ответа, потому что диапазон исходной функции ограничен.
Для заданной радикальной функции найти обратную
- Определить диапазон исходной функции.

- Замените \(f(x)\) на \(y\), затем найдите \(x\).
- При необходимости ограничьте область определения обратной функции диапазоном исходной функции.
Пример \(\PageIndex{5}\): поиск обратной радикальной функции
Найдите обратную функцию \(f(x)=\sqrt{x−4}\) и затем ограничьте ее область определения до диапазон исходной функции.
Решение
Обратите внимание, что исходная функция имеет диапазон \(f(x)≥0\). Замените \(f(x)\) на \(y\): 92+4\), \(х≥0\)
Анализ
Обратите внимание на рисунок \(\PageIndex{8}\), что обратная функция является отражением исходной функции по линии \(y=x\). Поскольку исходная функция имеет только неотрицательные выходные параметры, обратная функция имеет только неотрицательные входные параметры.
Рисунок \(\PageIndex{8}\)
\(\PageIndex{5}\): Ограничьте домен, а затем найдите обратную функцию \(f(x)=\sqrt{2x+3}\).
−3}{2}\), \(х≥0\)
Решение приложений радикальных функций
Радикальные функции широко распространены в физических моделях, как мы видели в начале раздела. Теперь у нас достаточно инструментов, чтобы решить задачу, поставленную в начале раздела.
Пример \(\PageIndex{6}\): Решение приложения с кубической функцией
Насыпь из гравия имеет форму конуса с высотой, равной удвоенному радиусу. Объем конуса по радиусу равен 93\), определяющая объем \(V\) конуса и являющаяся функцией радиуса \(r\). Затем используйте обратную функцию, чтобы вычислить радиус такой насыпи из гравия размером 100,00 кубических футов. Используйте \(\pi=3.1416\).
Решение:
Начните с данной функции для \(V\). Обратите внимание, что значимая область для функции — \(r>0\), так как отрицательные радиусы не имеют смысла в этом контексте, равно как и радиус \(0\). Также обратите внимание, что диапазон функции (следовательно, область определения обратной функции) равен \(V>0\).
 Решите для \(r\) через \(V\), используя метод, описанный ранее. Обратите внимание, что в реальных приложениях мы не меняем местами переменные при поиске инверсий. Вместо этого мы изменяем, какая переменная считается независимой переменной. 93 =\dfrac{3V}{2\pi} \nonumber\]
Решите для \(r\) через \(V\), используя метод, описанный ранее. Обратите внимание, что в реальных приложениях мы не меняем местами переменные при поиске инверсий. Вместо этого мы изменяем, какая переменная считается независимой переменной. 93 =\dfrac{3V}{2\pi} \nonumber\]Найдите \(r\):
\[ r=\sqrt[3]{\dfrac{3V}{2\pi}} \ nonumber \]
Это результат, указанный в начале раздела. Теперь оцените это для \(V=100,00\) и \(\pi=3,1416\).
\[ \begin{align*} r&=\sqrt[3]{\dfrac{3V}{2\pi}} \\[5pt] &=\sqrt[3]{\dfrac{3⋅100.00}{ 2⋅3.1416}} \\[5pt] &≈\sqrt[3]{47.7707} \\[5pt] &≈3.63 \end{align*}\]
Следовательно, радиус составляет около 3,63 фута (любой, кто специалист по естественным наукам знает, сколько значащих цифр мы должны использовать в ответе.Ваш профессор угадывает 3. Если вы можете записать правила для значащих цифр в расчетных количествах, передайте их своему профессору и заставьте ее поставить вам дополнительный балл.)
Определение домена радикальной функции, составленной из других функций
Когда радикальные функции составлены из других функций, определение домена может стать более сложным.

Пример \(\PageIndex{7}\): Нахождение области определения радикальной функции, составленной из рациональной функции
Нахождение области определения функции:
\[f(x)=\sqrt{\frac{( х+2)(х-3)}{(х-1)}}. \nonumber\]
Решение
Поскольку квадратный корень определяется только тогда, когда величина под радикалом неотрицательна, нам нужно определить, где
\[\frac{(x+2)(x−3)}{(x−1)}≥0. \nonumber\]
Выход рациональной функции может менять знак (с положительного на отрицательный или наоборот) на точках пересечения x и на вертикальных асимптотах. Для этого уравнения график мог менять знаки при \(x=–2\), \(1\) и \(3\).
Чтобы определить интервалы, на которых рациональное выражение положительно, мы могли бы проверить некоторые значения в выражении или начертить график. Хотя оба подхода работают одинаково хорошо, в этом примере мы будем использовать график, показанный на рисунке \(\PageIndex{9).}\).
Рисунок \(\PageIndex{9}\)
Эта функция имеет две точки пересечения x , обе из которых демонстрируют линейное поведение вблизи точек пересечения x .
 Имеется одна вертикальная асимптота, соответствующая линейному множителю; это поведение похоже на базовую функцию обратного инструментария, и здесь нет горизонтальной асимптоты, поскольку степень числителя больше степени знаменателя. Существует y -перехват в точке \((0,\sqrt{6})\).
Имеется одна вертикальная асимптота, соответствующая линейному множителю; это поведение похоже на базовую функцию обратного инструментария, и здесь нет горизонтальной асимптоты, поскольку степень числителя больше степени знаменателя. Существует y -перехват в точке \((0,\sqrt{6})\).Из точки пересечения y и точки пересечения x в точке \(x=−2\) мы можем нарисовать левую часть графика. По поведению на асимптоте мы можем набросать правую часть графика.
Теперь по графику мы можем сказать, на каких интервалах выходные значения будут неотрицательными, так что мы можем быть уверены, что исходная функция \(f(x)\) будет определена. \(f(x)\) имеет область определения \(−2≤x<1\) или \(x≥3\), или в интервальной записи, \([−2,1)∪[3,\infty)\ ).
Нахождение инверсий рациональных функций
Как и при нахождении обратных квадратичных функций, иногда желательно найти обратную рациональную функцию , особенно рациональных функций, которые являются отношением линейных функций, например, в приложениях концентрации.

Пример \(\PageIndex{8}\): нахождение обратной рациональной функции концентрация \(С\) раствора кислоты после добавления \(n\) мл 40%-ного раствора к 100 мл 20%-ного раствора. Сначала найдите обратную функцию; то есть найдите выражение для \(n\) через \(C\). Затем используйте полученный результат, чтобы определить, сколько 40%-ного раствора нужно добавить, чтобы конечная смесь была 35%-ным раствором.
Решение
Сначала нам нужна обратная функция, чтобы определить, сколько мл нам нужно для данной концентрации. Мы будем решать для \(n\) в терминах \(C\).
\[ \begin{align*} C&=\dfrac{20+0.4n}{100+n} \\[5pt] C(100+n)&=20+0.4n\\[5pt] 100C+Cn& =20+0,4n\\[5pt] 100C−20&=0,4n−Cn\\[5pt] 100C−20&=(0,4−C)n\\[5pt] n&=\dfrac{100C−20}{0,4− C}\end{align*}\]
Теперь оцените эту функцию как 35%, что равно \(C=0,35\).
9{−1}(x)=\frac{2x+3}{x−1}\)Медиа
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с обратными и радикальными функциями.

- График базовой функции извлечения квадратного корня
- Найдите обратную функцию квадратного корня
- Найдите обратную рациональную функцию
- Найдите обратную рациональную функцию и значение обратной функции
- Обратные функции
- Определить диапазон исходной функции.
- Хотя невозможно найти обратную форму большинства полиномиальных функций, некоторые базовые полиномы обратимы.
- Чтобы найти обратную функцию, мы должны ограничить функцию областью, в которой она будет взаимно однозначной.
- При нахождении обратной радикальной функции необходимо ограничение на область определения ответа.
- Обратные и радикальные функции могут использоваться для решения прикладных задач.
Эта страница под названием 3.8: Inverses and Radical Functions распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

- Ограничьте область определения, определив меньшую область, в которой исходная функция является взаимно однозначной.

 Однако, как известно, не все кубические полиномы взаимно однозначны. Домен некоторых функций, которые не являются однозначными, может быть ограничен таким образом, чтобы они были однозначными, но только в пределах этого домена. Тогда функция над ограниченным доменом будет иметь обратную функцию . Поскольку квадратичные функции не являются взаимно однозначными, мы должны ограничить их область определения, чтобы найти их обратные.
Однако, как известно, не все кубические полиномы взаимно однозначны. Домен некоторых функций, которые не являются однозначными, может быть ограничен таким образом, чтобы они были однозначными, но только в пределах этого домена. Тогда функция над ограниченным доменом будет иметь обратную функцию . Поскольку квадратичные функции не являются взаимно однозначными, мы должны ограничить их область определения, чтобы найти их обратные.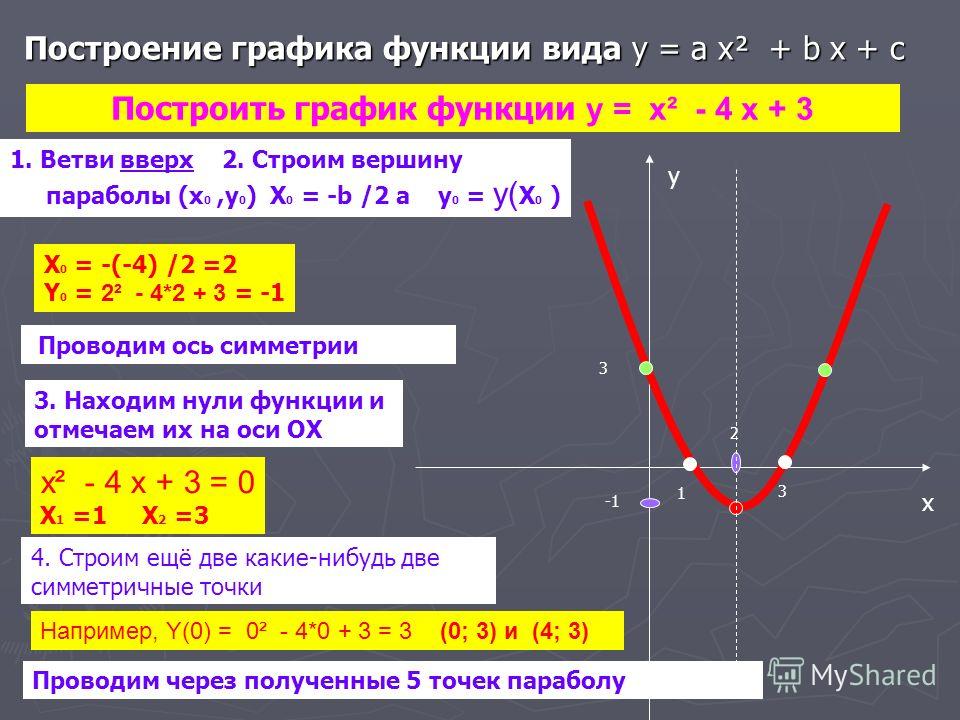 {−1}\) всегда будут лежать на прямой \(y=x\). 92−3\).
{−1}\) всегда будут лежать на прямой \(y=x\). 92−3\).
 Решите для \(r\) через \(V\), используя метод, описанный ранее. Обратите внимание, что в реальных приложениях мы не меняем местами переменные при поиске инверсий. Вместо этого мы изменяем, какая переменная считается независимой переменной. 93 =\dfrac{3V}{2\pi} \nonumber\]
Решите для \(r\) через \(V\), используя метод, описанный ранее. Обратите внимание, что в реальных приложениях мы не меняем местами переменные при поиске инверсий. Вместо этого мы изменяем, какая переменная считается независимой переменной. 93 =\dfrac{3V}{2\pi} \nonumber\]
 Имеется одна вертикальная асимптота, соответствующая линейному множителю; это поведение похоже на базовую функцию обратного инструментария, и здесь нет горизонтальной асимптоты, поскольку степень числителя больше степени знаменателя. Существует y -перехват в точке \((0,\sqrt{6})\).
Имеется одна вертикальная асимптота, соответствующая линейному множителю; это поведение похоже на базовую функцию обратного инструментария, и здесь нет горизонтальной асимптоты, поскольку степень числителя больше степени знаменателя. Существует y -перехват в точке \((0,\sqrt{6})\).