Начальные и центральные моменты случайной величины. Теория вероятностей
- Краткая теория
- Примеры решения задач
Краткая теория
Начальные моменты
Начальным моментом порядка случайной величины называют математическое ожидание величины :
В частности:
Пользуясь этими моментами, формулу для вычисления дисперсии можно записать так:
Центральные моменты
Кроме моментов случайной величины целесообразно рассматривать моменты отклонения .
Центральным моментом порядка случайной величины называют математическое ожидание величины :
В частности,
Взаимосвязь центральных и начальных моментов
Легко выводятся соотношения, связывающие начальные и центральные моменты:
Моменты
более высоких порядков применяются редко.
Формулы для вычисления моментов дискретных и непрерывных случайных величин
| Момент | Случайная величина | |
| Дискретная | Непрерывная | |
| Начальный | ||
| Центральный | ||
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Нетрудно
заметить, что при
первый
начальный момент случайной величины
есть ее
математическое ожидание, то есть
, при
второй
центральный момент – дисперсия, то есть
.
Асимметрия и эксцесс случайной величины
Третий центральный момент служит для характеристики асимметрии (скошенности) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на , где – среднее квадратическое отклонение случайной величины . Полученная величина называется коэффициентом асимметрии случайной величины:
Если распределение симметрично относительно математического ожидания, то коэффициент асимметрии .
Четвертый центральный момент служит для характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом (или коэффициентом эксцесса) случайной величины называется число
Число 3 вычитается из отношения
потому, что для
наиболее часто встречающегося нормального распределения отношение
. Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные – отрицательным
эксцессом.
Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные – отрицательным
эксцессом.
Смежные темы решебника:
- Асимметрия и эксцесс распределения
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
Дискретная случайная величина X задана законом распределения:
| 1 | 3 | 4 | 5 | |
| 0,2 | 0,3 | 0,1 | 0,4 |
Найти начальные моменты первого, второго и третьего
порядков.
Решение
Найдем начальный момент 1-го порядка:
Начальный момент 2-го порядка:
Начальный момент 3-го порядка:
Ответ: .
Пример 2
Дискретная случайная величина X задана законом распределения:
| 0 | 3 | 5 | 6 | |
| 0,3 | 0,2 | 0,3 | 0,2 |
Найти центральные моменты первого, второго, третьего и четвертого порядков.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Центральный момент первого порядка равен нулю:
Для вычисления центральных моментов удобно воспользоваться формулами, выражающими центральные моменты через начальные, поэтому предварительно найдем начальные моменты:
Начальный момент 2-го порядка:
Начальный момент 3-го порядка:
Начальный момент 4-го порядка:
Найдем центральные моменты:
Ответ: .
Пример 3
Непрерывная случайная величина X задана плотностью распределения:
Найти математическое ожидание, дисперсию, асимметрию и эксцесс.
Решение
Математическое ожидание (начальный момент первого порядка):
Начальный момент второго порядка:
Дисперсия (центральный момент второго порядка):
Среднее квадратическое отклонение:
Начальный момент третьего порядка:
Начальный момент четвертого порядка:
Вычисляем центральные моменты третьего и четвертого порядков:
Коэффициент асимметрии:
Эксцесс:
Ответ:
.
- Краткая теория
- Примеры решения задач
Центральный момент — Central moment
В теории вероятностей и статистике, центральный момент является моментом из распределения вероятностей в виде случайной величины около случайной переменного среднего ; то есть это ожидаемое значение указанной целочисленной степени отклонения случайной величины от среднего. Различные моменты образуют один набор значений, с помощью которых можно эффективно охарактеризовать свойства распределения вероятностей. Центральные моменты используются вместо обычных моментов, вычисляемых в терминах отклонений от среднего, а не от нуля, потому что центральные моменты более высокого порядка относятся только к разбросу и форме распределения, а не также к его местоположению .
Наборы центральных моментов могут быть определены как для одномерного, так и для многомерного распределения.
СОДЕРЖАНИЕ
- 1 Одномерные моменты
- 1.1 Свойства
- 1.
 {n} f (x) \, \ mathrm {d} x.}
{n} f (x) \, \ mathrm {d} x.}Для случайных величин, не имеющих среднего значения, таких как распределение Коши, центральные моменты не определены.
Первые несколько центральных моментов имеют интуитивное толкование:
- «Нулевой» центральный момент μ 0 равен 1.
- Первый центральный момент μ 1 равен 0 (не путать с первым необработанным моментом или ожидаемым значением μ ).
- Второй центральный момент μ 2 называется дисперсией и обычно обозначается σ 2, где σ представляет собой стандартное отклонение .
- Третий и четвертый центральные моменты используются для определения стандартизованных моментов, которые используются для определения асимметрии и эксцесса соответственно.
Характеристики
П — й центральный момент является перевод-инвариантным, то есть для любой случайной величины X и любой константы с, мы имеем
- μп(Икс+c)знак равноμп(Икс).
 {n} \ mu _ {n} (X). \,}
{n} \ mu _ {n} (X). \,}
Только для п таких, что п равно 1, 2 или 3 мы имеем свойство аддитивности для случайных величин X и Y, которые являются независимыми :
- μп(Икс+Y)знак равноμп(Икс)+μп(Y){\ Displaystyle \ му _ {п} (Х + Y) = \ му _ {п} (Х) + \ му _ {п} (Y) \,}если n ∈ {1, 2, 3 }.
Связанный функционал, который разделяет свойства трансляционной инвариантности и однородности с n- м центральным моментом, но продолжает иметь это свойство аддитивности, даже когда n ≥ 4 является n- м кумулянтом κ n ( X ). Для n = 1 n- й кумулянт — это просто ожидаемое значение ; для n = либо 2, либо 3, n- й кумулянт — это просто n- й центральный момент; для п ≥ 4, п — й кумулянт является п — й степени унитарный многочлен в первых п моментов (около нуля), а также (проще) п — й степени многочлен в первых п центральных моментов.

Центральный момент второго порядка β 2 называется дисперсией из X, тогда как центральный момент второго порядка α 2 является псевдо-дисперсией из X .
Смотрите также
- Стандартизированный момент
- Момент изображения
- Нормальное распределение § Моменты
- Комплексная случайная величина
использованная литература
<img src=»https://en.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»»>
Моменты случайной величины с примерами решения
Содержание:
- Примеры с решением
Моменты случайной величины Определение и основные свойства
Мы уже видели в предыдущей главе, какое большое значение имеют такие числовые характеристики распределения, как математическое ожидание и дисперсия.
 Обобщением этих понятий являются начальные и центральные моменты.
Обобщением этих понятий являются начальные и центральные моменты.Определение. Начальным моментом порядка случайной величины называют математическое ожидание степени
Из определения ясно, что начальный момент первого порядка совпадает с математическим ожиданием.
Для дискретных случайных величин с законом распределения формула для начального момента порядка выглядит следующим образом:
для абсолютно непрерывных случайных величин с плотностью
если ряд (6.3) и интеграл (6.4) сходятся абсолютно.
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Предмет теория вероятности Определение. Центральным моментом порядка случайной величины называют математическое ожидание степени отклонения где математическое ожидание Мы уже видели, что первый центральный момент равен нулю, а второй центральный момент совпадает с дисперсией случайной величины
Для дискретных случайных величин формула для центрального момента порядка выглядит следующим образом:
для непрерывных случайных величин
Возможно вам будут полезны данные страницы:
Законы распределения случайных величин
Числовые характеристики непрерывной случайной величины
Моменты высших порядков
Случайный вектор распределения
Разлагая бином и пользуясь свойствами математического ожидания, нетрудно получить формулы, выражающие центральные моменты через начальные.
 Например,
Например,откуда
так что
Полученная формула полностью идентична с уже известной формулой для дисперсии. Аналогично получаются следующие формулы, вывод которых предоставляется читателю:
Отметим следующие свойства третьего и четвертого центральных моментов. Свойство. Если величины независимы, то
Доказательство. Используя формулу куба суммы и свойство математического ожидания, имеем
По теореме умножения математического ожидания для независимых величин получим
Поскольку центральные моменты первого порядка равны нулю, то формула (6.12) отсюда следует непосредственно.
Доказанная формула непосредственно обобщается на произвольное число независимых слагаемых:
Для моментов четвертого порядка аналогичное свойство выглядит более сложным образом.
Свойство. Для независимых случайных величин выполняется формула
Доказательство полностью аналогично предыдущему и оставляется читателю.
 Для произвольного числа независимых слагаемых формула (6.14) приобретает следующий вид:
Для произвольного числа независимых слагаемых формула (6.14) приобретает следующий вид:Рассмотрим ряд примеров нахождения моментов высших порядков для типичных законов распределения.
Примеры с решением
Пример 1:
Найти все центральные моменты до четвертого порядка включительно для случайной величины распределенной по биномиальному закону с параметрами
Решение:
Что касается нахождения центральных моментов первого и второго порядка, то ответ нам известен:
Чтобы найти воспользуемся формулой (6.13) и представлением случайной величины виде суммы индикаторов появления события испытании:
Для каждого слагаемого третий центральный момент находится непосредственно
Поэтому
Для нахождения центрального момента четвертого порядка воспользуемся формулой (6.15). Вначале найдем моменты для каждого слагаемого:
Отсюда
откуда окончательно получаем
Для нахождения всех начальных моментов непрерывной случайной величины проще использовать производящую функцию моментов.

Определение. Производящей функцией моментов случайной величины называют математическое ожидание случайной величины где действительный параметр:
Производящая функция моментов позволяет находить все начальные моменты случайной величины X. Справедлива следующая теорема.
Теорема 6.1. Если случайная величина имеет начальный момент порядка то производящая функция раз дифференцируема по и для всех выполняется соотношение
Если оставить в стороне вопрос о дифференцируемости данной функции, то соотношение (6.20) получается формально дифференцированием соотношения (6.19) раз по
Подставляя в последнее соотношение получим
откуда непосредственно вытекает равенство (6.19).
Сравнивая разложение производящей функции моментов в ряд Маклорена с равенствами (6.19), получим ее разложение в ряд с использованием начальных моментов:
Пример 2:
Найти производящую функцию моментов для случайной величины распределенной по нормальному закону
Решение:
Имеем по определению
Для вычисления этого интеграла рассмотрим отдельно показатель экспоненты, стоящей под знаком интеграла.
 Имеем
ИмеемВыделим в числителе последней дроби полный квадрат по После небольшого числа тождественных преобразований получим:
Таким образом, выражение для характеристической функции приобретет вид:
Поскольку первый множитель равен 1 как интеграл от плотности нормальной случайной величины то окончательное выражение для характеристической функции нормального закона имеет вид:
Особенно простой вид имеет характеристическая функция стандартного нормального закона
Теперь нам будет нетрудно найти все начальные моменты стандартной нормальной случайной величины. Вместо того чтобы дифференцировать функцию (6.22), можно разложить ее в ряд и сравнить с рядом (6.20):
откуда имеем выражения для начальных моментов:
Центральный момент — расчеты и формулы
ALL#ABCDEFGHIJKLMNOPQRSTUVWXYZ
Центральный момент (22171 просмотров — Расчеты (Mech&Elec))
В теории вероятностей и статистике центральный момент — это момент распределения вероятностей случайной величины относительно среднего значения случайной величины; то есть это ожидаемое значение заданной целочисленной степени отклонения случайной величины от среднего.
 Различные моменты образуют один набор значений, с помощью которых можно с пользой охарактеризовать свойства распределения вероятностей. Центральные моменты используются вместо обычных моментов, вычисляемых в терминах отклонений от среднего, а не от нуля, потому что центральные моменты более высокого порядка относятся только к разбросу и форме распределения, а не к его местоположению.
Наборы центральных моментов могут быть определены как для одномерного, так и для многомерного распределения.
Различные моменты образуют один набор значений, с помощью которых можно с пользой охарактеризовать свойства распределения вероятностей. Центральные моменты используются вместо обычных моментов, вычисляемых в терминах отклонений от среднего, а не от нуля, потому что центральные моменты более высокого порядка относятся только к разбросу и форме распределения, а не к его местоположению.
Наборы центральных моментов могут быть определены как для одномерного, так и для многомерного распределения.
Перейти к артикулуЦентральный момент
Центральный момент
Эта статья требует дополнительных ссылок для проверки . Пожалуйста, помогите улучшить эту статью, добавив ссылки на надежные источники. Неисходный материал может быть оспорен и удален. (сентябрь 2014 г.) (узнайте, как и когда удалить это шаблонное сообщение)
В теории вероятностей и статистике центральный момент — момент распределения вероятностей случайной величины относительно среднего значения случайной величины; то есть это ожидаемое значение заданной целочисленной степени отклонения случайной величины от среднего.
 Различные моменты образуют один набор значений, с помощью которых можно с пользой охарактеризовать свойства распределения вероятностей. Центральные моменты используются вместо обычных моментов, вычисляемых в терминах отклонений от среднего, а не от нуля, потому что центральные моменты более высокого порядка относятся только к разбросу и форме распределения, а не к его местоположению.
Различные моменты образуют один набор значений, с помощью которых можно с пользой охарактеризовать свойства распределения вероятностей. Центральные моменты используются вместо обычных моментов, вычисляемых в терминах отклонений от среднего, а не от нуля, потому что центральные моменты более высокого порядка относятся только к разбросу и форме распределения, а не к его местоположению.Наборы центральных моментов могут быть определены как для одномерного, так и для многомерного распределения.
Содержание
- 1 Одномерные моменты
- 1.1 Свойства
- 1.2 Отношение к моментам о происхождении
- 1.3 Симметричные распределения
- 2 Многомерные моменты
- 3 См. также
Одномерные моменты
n -й момент относительно среднего (или n th central moment ) of a real-valued random variable X is the quantity μ n := E[( X − E[ X ]) n ] , где E — оператор ожидания.
 {n}f( х)\,\mathrm {d} х.} [1]
{n}f( х)\,\mathrm {d} х.} [1] Для случайных величин, не имеющих среднего значения, таких как распределение Коши, центральные моменты не определяются.
Первые несколько центральных моментов имеют интуитивную интерпретацию:
- «Нулевой» центральный момент μ 0 равен 1.
- Первый центральный момент μ 1 равен 0 (не путать с самим первым (необработанным) моментом, ожидаемым значением или средним значением).
- Второй центральный момент μ 2 называется дисперсией и обычно обозначается σ 2 , где σ представляет собой стандартное отклонение.
- Третий и четвертый центральные моменты используются для определения стандартизированных моментов, которые используются для определения асимметрии и эксцесса соответственно.
Свойства
n -й центральный момент трансляционно-инвариантен, т.е. для любой случайной величины X и любой константы c имеем
- μn (X + c) = μn (X).
 {\ displaystyle \ mu _ {n} (X + c) = \ mu _ {n} (X). \,} 9009{n}\mu _{n}(X).\,}
{\ displaystyle \ mu _ {n} (X + c) = \ mu _ {n} (X). \,} 9009{n}\mu _{n}(X).\,}
Только для n таких, что n равно 1, 2 или 3, у нас есть свойство аддитивности для случайных величин X и Y , которые являются независимыми:
- μn (X + Y) = μn (X) + μn (Y) {\ displaystyle \ mu _ {n} (X + Y) = \ mu _ {n} (X) + \ mu _ {n} (Y)\,} при n ∈ {1, 2, 3}.
Родственный функционал, который разделяет свойства трансляционной инвариантности и однородности с n -м центральным моментом, но продолжает обладать этим свойством аддитивности даже при n ≥ 4 является n -м кумулянтом κ n ( X ). Для n = 1 n -й кумулянт является просто ожидаемым значением; для n = либо 2, либо 3, n -й кумулянт — это просто n -й центральный момент; для n ≥ 4, n -й кумулянт является n -й степенью монического полинома в первые n моментов (около нуля), а также является (более простым) n -й степени полиномом в первые 9{n}]} определяется как ноль для j = 0 {\ displaystyle j = 0}.

Симметричные распределения
В симметричном распределении (на которое не влияет отражение относительно его среднего значения) все нечетные центральные моменты равны нулю, потому что в формуле для n -го момента каждый член включает значение X меньше, чем среднее значение на определенную величину, точно нейтрализует член, включающий значение X больше, чем среднее значение на ту же величину.
Многомерные моменты 9{k}f(x,y)\,dx\,dy.}
См. также
- Нормированный момент
- Момент изображения
- Нормальное распределение#Моменты
Критерий Чебычева–Грюблера–Куцбаха
В этой статье используется материал из статьи в Википедии. «Центральный момент», который выпускается под Лицензия Creative Commons Attribution-Share-Alike 3.0. есть список всех авторы в Википедии
Расчеты (Механика и электроэнергетика)
Flächenträgheitsmoment
решающих моментов
определяющий моментj-й момент случайной величины x i которое происходит с вероятностью p i , может быть определено как ожидаемое или среднее значение x в j-й степени, т.
 е.:
е.:.
Таким образом, среднее значение x является первым моментом его распределения, а тот факт, что распределение вероятностей нормировано, означает что нулевой момент всегда равен 1.
j-й центральный момент о x o , в свою очередь, может быть определен как математическое ожидание величины x минус x o , этой величины в j-й степени, т.е.
.
Таким образом, дисперсия x является вторым центральным моментом распределение вероятностей, когда x o является средним значением или первый момент. Первый центральный момент равен нулю, если он определен по отношению к среднему, так что центральные моменты могут фактически использоваться для «корректировки» ненулевого среднего значения.
Поскольку стандартное отклонение «среднеквадратичное» σ равно квадрату корень дисперсии, это также считается величиной «второго момента». Третий и четвертый центральные моменты относительно среднего равны называются «асимметрией» и «эксцессом» соответственно.
 Примечание: Центральные моменты иногда определяются с произвольным центром,
вместо только среднего распределения.
Примечание: Центральные моменты иногда определяются с произвольным центром,
вместо только среднего распределения.Игра с приведенными выше уравнениями позволяет выразить центральные моменты как многочлены от нецентрированных моментов. Например, можете ли вы показать, что дисперсия есть среднее х в квадрате минус среднее х в квадрате?
Примечание: Вам может понадобиться использовать тот факт, что индивидуальные вероятности гарантированно дают в сумме единицу.
В более общем смысле, я думаю, можно сказать так:
.
В более общем смысле теперь используется биномиальный символ вместо факторное отношение, дающее способы «из n выбрать j», можно показать, что центральные моменты относительно x 1 и относительно х o связаны:
.
Примеры для изучения в этом отношении могут включать непрерывные распределения типа гауссова (сумма вероятностей для конкретные значения x заменяются интегралом по всем x), а также в виде дискретных распределений типа Пуассона.

Например, на рисунке ниже показана вероятность k серьезных травмы в драке в баре В ЭТУ ПЯТНИЦУ НОЧЬЮ, для k от 0 до 20, если в сопоставимые вечера пятницы в среднем происходит 2,5 травмы. Как видите, есть 8% шанс, что никто не пострадает, и 20% шанс, что только один человек получит травму. На рисунке также указаны с нулевого по 5-й нецентрированные моменты и соответствующие центральные моменты (относительно среднего).
Аналогичный график для непрерывного нормального распределения с то же среднее значение и стандартное отклонение приведены ниже для сравнения. Обратите внимание, что в дополнение к непрерывности (функция, которая усложняет обсуждение юнитов с некоторой неожиданностью информационные меры), она же (в отличие от пуассоновской) гарантирует ненулевая вероятность для отрицательных значений.
Среднее значение и дисперсия также являются членами другого класса, связанного с моментом. параметры распределения вероятностей, называемые кумулянты.
Если все моменты известны, то в принципе можно определить и само распределение вероятностей. Один из путей к этому результату включает характеристическую функцию распределения , которая может быть выражена экспонентой в ряд Тейлора, что дает бесконечную сумму моментов:
.
В свою очередь, j-й момент можно восстановить из характеристической функции, взяв ее j-ю производную по t с последующим ограничением при стремлении t к нулю, а затем умножив на (- и ) и . Внимание: Только в уравнениях этого раздела i — это квадратный корень из минус единицы.
На приведенном выше рисунке в качестве примера перечислены первые несколько моментов, а также характеристическая функция для дискретного распределения Пуассона. Таким образом, моменты дают нам характеристическую функцию распределения вероятностей. Можем ли мы использовать эту характеристическую функцию для определения самих вероятностей?
Одна из возможностей состоит в том, чтобы отметить, что, используя соглашение «классической физики» для определения преобразований Фурье, характеристическая функция является комплексно-сопряженным P[t], непрерывным преобразованием Фурье p[x].
 Обратное преобразование и обозначение комплексного сопряжения или обращения фазы Фурье чертой сверху, поэтому мы могли бы сказать, что:
Обратное преобразование и обозначение комплексного сопряжения или обращения фазы Фурье чертой сверху, поэтому мы могли бы сказать, что:.
Таким образом, характеристическая функция немного больше, чем преобразование Фурье распределения вероятностей.
В качестве примера рассмотрим характеристическую функцию одномерного нормального распределения, приведенную на рисунке нормального распределения выше. Преобразование Фурье его комплексно-сопряженного есть не что иное, как само одномерное нормальное распределение, т.е.
.
Если допускаются только дискретные значения x, то в соответствии с вышеприведенной записью суммирования результатом должна быть сумма дельта-функций Дирака, которые отличны от нуля только при этих значениях. Можете ли вы показать, что это верно для распределения Пуассона? Объединив первые два выражения в этом разделе, можем ли мы получить более прямое выражение для p[x] через моменты? Есть ли у результата проблемы со сходимостью? Имеет ли это также отношение к приведенному ниже выражению?
Интересное, но, возможно, более абстрактное разложение вероятностей с точки зрения центральных моментов обсуждается в статье Дэниела Гиллеспи, опубликованной в American Journal of Physics в 1981 году ( AJP 49 , 552-555):
,
, где дельта-символ с (n) в верхнем индексе относится к n-й производной дельта-функции Дирака по ее аргументу (в квадратных скобках).

Хотя приведенное выше выражение кажется довольно явным, преобразование его в явную формулу для p как функции от x может быть нетривиальным, поскольку производные дельта-функции обычно определяются тем, что происходит, когда их интегрируют по x. Следовательно, некоторые примеры этого в действии могут очень помочь.
Гиллеспи продолжает это обсуждение, отмечая, что можно аппроксимировать производные дельта-функции через распределение Гаусса в качестве предела. Это приводит его к странному утверждению:
.,
, откуда может быть получена явная формула для вероятности в любой точке x через центральные моменты относительно xo.
KL-дивергенция включает сравнение двух вероятностных распределений, один (p), который мы назовем действительным, а другой (p или ), что мы здесь вызов окружения или ссылки. Тем не менее расхождение KL также может быть записывается как бесконечная сумма моментов (или усредненных мощностей), в этом случае безразмерного отклонения от окружающего σ i = (p i /p oi -1) для этих двух дистрибутивы.
 Другими словами:
Другими словами:.
Здесь нижний индекс p в угловых скобках обозначает среднее значение по факт (стр i ), а не окружающая среда (p oi ) вероятности. Обратите также внимание на то, что использование натурального логарифма, а не логарифма по основанию 2 дает информационные единицы NAT, а не биты. Моменты низкого порядка имеют тенденцию доминировать над бесконечной суммой справа, пока σ i =p i /p oi -1<1 для всех значений i. Дивергенция KL сходится еще быстрее в моменты σ, усредненные по вероятности окружения p o :
.
Это последнее равенство использует тот факт, что окружающее среднее значение σ равна нулю и показывает, что для значений σ, намного меньших 1, KL-дивергенция составляет примерно половину оценки дисперсии окружающей среды о 2 .
На рисунке ниже показано одно двумерное (двухслойное) распределение. Вместо того, чтобы сравнивать это распределение со специальным эталоном, мы сравниваем его к собственному «продукту маргиналов».
 Таким образом, мы также можем сравнить
взаимная информация как мера корреляции, со вторым моментом
коэффициент корреляции rho, определяющий распределение.
Таким образом, мы также можем сравнить
взаимная информация как мера корреляции, со вторым моментом
коэффициент корреляции rho, определяющий распределение.Наряду с изображением коррелированного распределения по отдельные «слои» и возникающая в результате взаимная информационная среда, рисунок также иллюстрирует изменение «безразмерного отклонения от эмбиент», о котором говорилось выше, и как различные основанные на удивлении меры распределения зависят от коэффициента корреляции ρ.
Двумерное нормальное распределение, от из которого следует вышеизложенное, можно записать в виде:
.
Обратите внимание, что сигма с индексом ценности в этом уравнения представляют собой стандартные отклонения по x и y только для некоррелированный случай.
Распределение сокращается до произведение двух одномерных нормальных распределений, когда коэффициент корреляции ρ стремится к нулю, а к двумерному линейному дельта-функция вдоль линии корреляции как ρ 2 идет к 1.
 Как видите, взаимная информация
связанный с этим совместным распределением (т.е. дивергенция KL
по отношению к продукту предельной вероятности) представляет собой
мера корреляции, равная половине второго момента
безразмерного отклонения от окружающего при малом ρ.
Как видите, взаимная информация
связанный с этим совместным распределением (т.е. дивергенция KL
по отношению к продукту предельной вероятности) представляет собой
мера корреляции, равная половине второго момента
безразмерного отклонения от окружающего при малом ρ.В двумерном нормальном случае для небольшой коэффициент корреляции, график выше показывает, что взаимная информация в нац также идет как ρ 2 больше 2. Есть ли аналогичная взаимосвязь между взаимной информацией и коэффициент корреляции существуют для других распределений также? Несмотря на это, взаимная информация и расхождение KL таким образом, являются расширенными версиями знакомого r-квадрата коэффициент корреляции, предназначенный для учета данных о все моменты распределения вероятностей в работе.
Дополнительные примеры этого типа анализа см. страница на многослойных изображениях.
Central Moments
Блог, Риск, Статистика и ЭконометрикаОпубликовано
Иногда я читаю научную литературу, и часто в этих статьях есть доказательства. Я обычно приукрашиваю некоторые невинные на вид предположения о существовании моментов, неизменно всплывающие перед выводами теорем или лемм. Вот один из бесчисленных примеров, фактически взятых из «Составления и оценки точечных прогнозов»: «Если второй момент конечен…», термин «момент» вкрался в статистическую литературу из физики, а раньше из механики. Как именно я не мог понять. Термин «момент» относится к среднему (или ожидаемому) расстоянию от некоторой точки. Если эта точка является ожиданием (а не нулем), то мы говорим, что момент равен 9.0341 центральный момент . Расстояние также может быть возведено в квадрат, или оно может быть в степени 3, или в степени общего числа k. Таким образом, момент первого порядка относительно среднего значения всегда равен нулю (необработанный первый момент, равный нулю, является средним значением). Момент второго порядка относительно среднего дает нам дисперсию.
 Момент третьего порядка относительно среднего дает нам асимметрию и так далее.
Момент третьего порядка относительно среднего дает нам асимметрию и так далее.Понятие о существовании моментов трудно понять, возможно, не так сложно понять, как то, как бесконечный ряд, членами которого являются натуральные числа, в сумме дает -1/12, но все же это ошеломляет. Причина трудности ясна, мы занимаемся повседневностью, а не метафизической. В реальной жизни у нас есть выборки, и держу пари, вы еще не сталкивались с выборкой, которая имеет бесконечное стандартное отклонение.
Формальное определение центральных моментов
Формально центральный момент совокупности случайной величины X определяется как:
(1)
Уравнение (1) является теоретическим. В реальной жизни большинство данных даже не подчиняются четко определенному распределению, как, например, один из хорошо функционирующих экспоненциальных семейных наборов вероятностных распределений.
Мы всегда и только вычисляем центральные моменты выборки
(2)
Эти члены в уравнении (2) являются оценками этих членов в уравнении (1).
 За исключением сложных мультимодальных распределений, если мы хорошо оценим первые четыре момента (необработанный первый момент: среднее значение, центральные моменты порядка 2, 3 и 4: асимметрия дисперсии и эксцесс), эти четыре дают хорошее описание того, как выглядит распределение. Таким образом, запись их в виде таблицы может заменить плотность или гистограмму без большой потери информации.
За исключением сложных мультимодальных распределений, если мы хорошо оценим первые четыре момента (необработанный первый момент: среднее значение, центральные моменты порядка 2, 3 и 4: асимметрия дисперсии и эксцесс), эти четыре дают хорошее описание того, как выглядит распределение. Таким образом, запись их в виде таблицы может заменить плотность или гистограмму без большой потери информации.Симуляция
Мы можем призвать на помощь симуляцию, чтобы понять сложную концепцию существования центральных моментов. Эта концепция во многом связана с теорией экстремальных значений и поведением тяжелого хвоста. Мы можем смоделировать распределение, для которого мы знаем, что некоторые моменты не определены должным образом, и посмотреть на него.
Одним из хрестоматийных примеров такого распределения является распределение Коши. Мы видели распределение Коши раньше, когда обсуждали тяжелые хвосты в прошлом. Тяжелые хвосты означают экстремальные значения с непренебрежимо малой вероятностью, именно поэтому центральные моменты не определены, потому что они никогда не стабилизируются из-за непренебрежимо малой вероятности большого отклонения.
 Чтобы ясно это увидеть, представьте, что у вас есть процесс, который следует распределению Коши. Вас интересует определение второго момента, теоретического стандартного отклонения процесса (k=2 в уравнении (1) выше). Вы пытаетесь оценить эту величину, используя ее эмпирический аналог. Таким образом, с каждым новым наблюдением вы вычисляете стандартное отклонение на основе всех наблюдений, которые у вас есть до сих пор, ожидая, пока ваша оценка установится. Не задерживайте дыхание. Это не.
Чтобы ясно это увидеть, представьте, что у вас есть процесс, который следует распределению Коши. Вас интересует определение второго момента, теоретического стандартного отклонения процесса (k=2 в уравнении (1) выше). Вы пытаетесь оценить эту величину, используя ее эмпирический аналог. Таким образом, с каждым новым наблюдением вы вычисляете стандартное отклонение на основе всех наблюдений, которые у вас есть до сих пор, ожидая, пока ваша оценка установится. Не задерживайте дыхание. Это не.Взгляните:
Вы можете видеть, как оценка стандартного отклонения вот-вот сойдется к некоторому значению примерно после 5000 розыгрышей, но поступают очень большие наблюдения, которые искажают сходимость.Мы можем выполнить то же упражнение для другого распределения, для которого, как мы знаем, второй момент хорошо определен:
На втором рисунке мы видим то же самое вычисление, хотя теперь процесс следует стандартному нормальному распределению. Вы можете видеть, как вычисление стандартного отклонения стабилизируется по мере продолжения процесса.
Помните, что поддержка нормального распределения такая же, как поддержка распределения Коши, но для нормального распределения вероятность экстремальных значений незначительна. Вероятность больших отклонений от среднего слишком мала, чтобы мешать сходимости.
Другим побочным эффектом, который вы получаете из этого упражнения, является то, что вы можете видеть, что они имеют в виду, когда люди используют разговорный термин «период выгорания», который часто можно услышать, имея дело с вычислением цепи Маркова Монте-Карло (MCMC). Если мы начнем вычисление стандартного отклонения слишком рано, потребуется гораздо больше времени, чтобы сходиться к реальному стандартному отклонению, равному единице. Так что мы можем (должны ли?) избавиться от первой части, которая довольно волнительна и мешает. Мы увидим гораздо более быструю сходимость к фактическому значению стандартного отклонения (которое равно 1), если мы сожжем эту волнистую часть.
Без помощи компьютеров статистические гиганты прошлого были вынуждены воображать те или иные цифры, используя только мысленные эксперименты.
 Интересно, какие мысленные эксперименты нужны в наши дни, когда мы можем сделать так много даже с помощью одного ноутбука.
Интересно, какие мысленные эксперименты нужны в наши дни, когда мы можем сделать так много даже с помощью одного ноутбука.Данные об акциях
Наконец, давайте теперь рассмотрим результат того же упражнения с использованием данных об акциях. Я извлекаю данные за 2006 год для тикера SPY и вычисляю оценку стандартного отклонения, используя расширяющееся окно:
Обратите внимание на сходство этой цифры с той, что получена из распределения Коши. Во время мирового финансового кризиса мы наблюдали довольно необычные отклонения от среднего, они были достаточно сильными, чтобы нарушить ряды и прервать конвергенцию. Это та же история с тяжелым хвостом, рассказанная под другим углом. Угол несуществующего стандартного отклонения.Расширение расчета SD
библиотека (квантмод) ; цитата(«квантмод») symetf = c(‘ШПИОН’) конец <- формат(Sys.Date(),"%Y-%m-%d") начало<-"2006-01-01" l = длина (symetf) dat0 <- lapply(symetf, getSymbols,src="yahoo", from=start, to=end, auto.
 assign = F,предупреждения = FALSE,symbol.lookup = F)
xd <- dat0[[1]]
время <- индекс (xd)
retd <- as.numeric(xd[2:NROW(xd),4])/as.numeric(xd[1:(NROW(xd)-1),4]) -1
ветер <- 30
sd_ret <- NULL
TT <- длина (ретд)
для (я на ветру: ТТ) {
sd_ret[i] <- 100*sd(retd[1:i])
}
сюжет (sd_ret)
assign = F,предупреждения = FALSE,symbol.lookup = F)
xd <- dat0[[1]]
время <- индекс (xd)
retd <- as.numeric(xd[2:NROW(xd),4])/as.numeric(xd[1:(NROW(xd)-1),4]) -1
ветер <- 30
sd_ret <- NULL
TT <- длина (ретд)
для (я на ветру: ТТ) {
sd_ret[i] <- 100*sd(retd[1:i])
}
сюжет (sd_ret)1
2
3
4
5
6
7
8
10
110003
12
13
14
19999111100019000 2
14
9000 3 9000 3 9000 3 9000 2 9000 214 9000 3
9000 3 9000 29000 3 9000 3 9000 3
18
19
библиотека (квантмод) ; citation(«quantmod»)
symetf = c(‘SPY’)
end<- format(Sys.Date(),"%Y-%m-%d")
start<-"2006-01- 01"
l = length(symetf)
dat0 <- lapply(symetf, getSymbols,src="yahoo", from=start, to=end,
auto.assign = F,warnings = FALSE,symbol.


 {n} f (x) \, \ mathrm {d} x.}
{n} f (x) \, \ mathrm {d} x.} {n} \ mu _ {n} (X). \,}
{n} \ mu _ {n} (X). \,}
 Обобщением этих понятий являются начальные и центральные моменты.
Обобщением этих понятий являются начальные и центральные моменты. Например,
Например,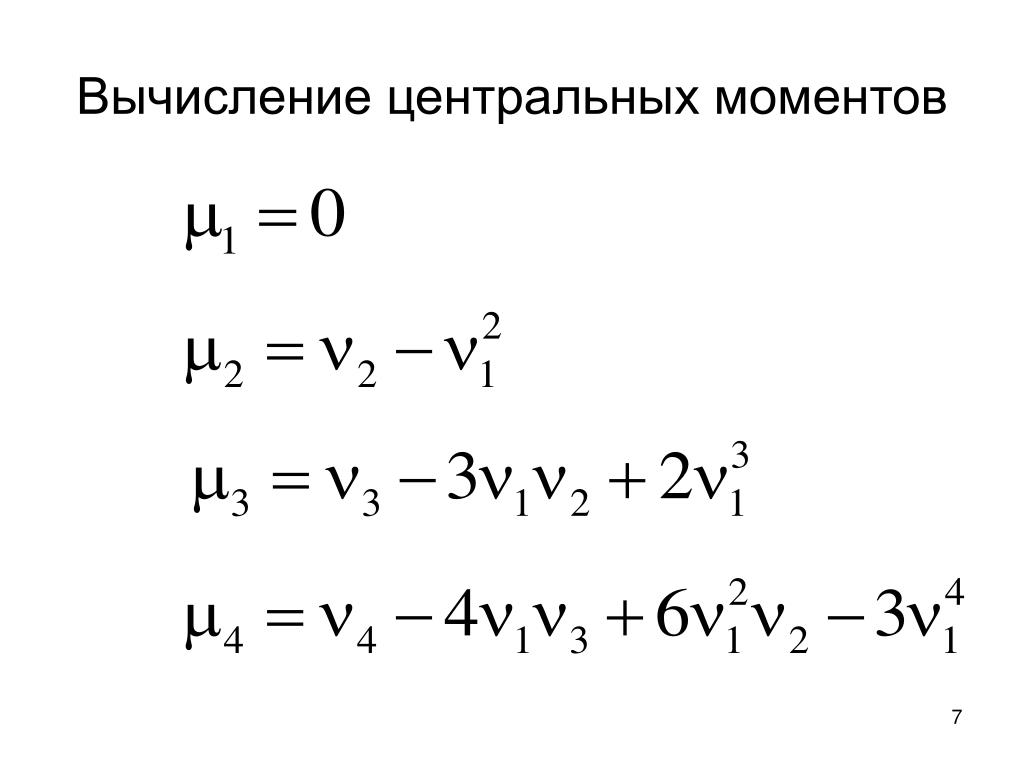 Для произвольного числа независимых слагаемых формула (6.14) приобретает следующий вид:
Для произвольного числа независимых слагаемых формула (6.14) приобретает следующий вид:
 Имеем
Имеем Различные моменты образуют один набор значений, с помощью которых можно с пользой охарактеризовать свойства распределения вероятностей. Центральные моменты используются вместо обычных моментов, вычисляемых в терминах отклонений от среднего, а не от нуля, потому что центральные моменты более высокого порядка относятся только к разбросу и форме распределения, а не к его местоположению.
Наборы центральных моментов могут быть определены как для одномерного, так и для многомерного распределения.
Различные моменты образуют один набор значений, с помощью которых можно с пользой охарактеризовать свойства распределения вероятностей. Центральные моменты используются вместо обычных моментов, вычисляемых в терминах отклонений от среднего, а не от нуля, потому что центральные моменты более высокого порядка относятся только к разбросу и форме распределения, а не к его местоположению.
Наборы центральных моментов могут быть определены как для одномерного, так и для многомерного распределения.  Различные моменты образуют один набор значений, с помощью которых можно с пользой охарактеризовать свойства распределения вероятностей. Центральные моменты используются вместо обычных моментов, вычисляемых в терминах отклонений от среднего, а не от нуля, потому что центральные моменты более высокого порядка относятся только к разбросу и форме распределения, а не к его местоположению.
Различные моменты образуют один набор значений, с помощью которых можно с пользой охарактеризовать свойства распределения вероятностей. Центральные моменты используются вместо обычных моментов, вычисляемых в терминах отклонений от среднего, а не от нуля, потому что центральные моменты более высокого порядка относятся только к разбросу и форме распределения, а не к его местоположению. {n}f( х)\,\mathrm {d} х.} [1]
{n}f( х)\,\mathrm {d} х.} [1]  {\ displaystyle \ mu _ {n} (X + c) = \ mu _ {n} (X). \,}
{\ displaystyle \ mu _ {n} (X + c) = \ mu _ {n} (X). \,}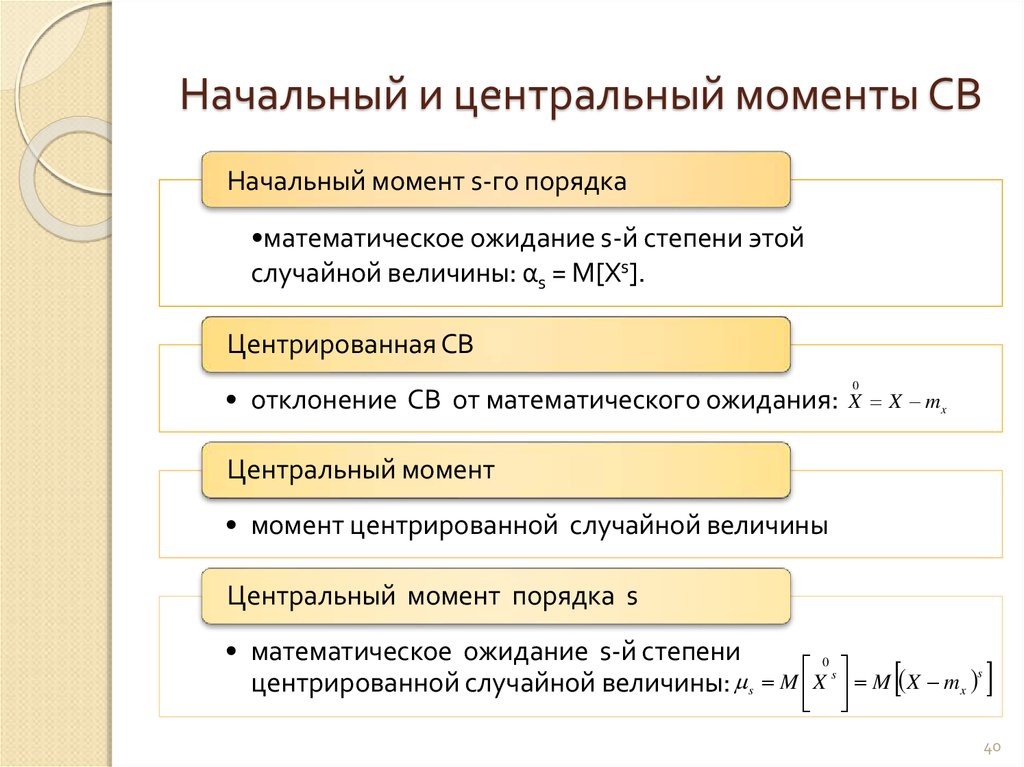
 е.:
е.: Примечание: Центральные моменты иногда определяются с произвольным центром,
вместо только среднего распределения.
Примечание: Центральные моменты иногда определяются с произвольным центром,
вместо только среднего распределения.

 Обратное преобразование и обозначение комплексного сопряжения или обращения фазы Фурье чертой сверху, поэтому мы могли бы сказать, что:
Обратное преобразование и обозначение комплексного сопряжения или обращения фазы Фурье чертой сверху, поэтому мы могли бы сказать, что:
 Другими словами:
Другими словами: Таким образом, мы также можем сравнить
взаимная информация как мера корреляции, со вторым моментом
коэффициент корреляции rho, определяющий распределение.
Таким образом, мы также можем сравнить
взаимная информация как мера корреляции, со вторым моментом
коэффициент корреляции rho, определяющий распределение. Как видите, взаимная информация
связанный с этим совместным распределением (т.е. дивергенция KL
по отношению к продукту предельной вероятности) представляет собой
мера корреляции, равная половине второго момента
безразмерного отклонения от окружающего при малом ρ.
Как видите, взаимная информация
связанный с этим совместным распределением (т.е. дивергенция KL
по отношению к продукту предельной вероятности) представляет собой
мера корреляции, равная половине второго момента
безразмерного отклонения от окружающего при малом ρ. Момент третьего порядка относительно среднего дает нам асимметрию и так далее.
Момент третьего порядка относительно среднего дает нам асимметрию и так далее. За исключением сложных мультимодальных распределений, если мы хорошо оценим первые четыре момента (необработанный первый момент: среднее значение, центральные моменты порядка 2, 3 и 4: асимметрия дисперсии и эксцесс), эти четыре дают хорошее описание того, как выглядит распределение. Таким образом, запись их в виде таблицы может заменить плотность или гистограмму без большой потери информации.
За исключением сложных мультимодальных распределений, если мы хорошо оценим первые четыре момента (необработанный первый момент: среднее значение, центральные моменты порядка 2, 3 и 4: асимметрия дисперсии и эксцесс), эти четыре дают хорошее описание того, как выглядит распределение. Таким образом, запись их в виде таблицы может заменить плотность или гистограмму без большой потери информации. Чтобы ясно это увидеть, представьте, что у вас есть процесс, который следует распределению Коши. Вас интересует определение второго момента, теоретического стандартного отклонения процесса (k=2 в уравнении (1) выше). Вы пытаетесь оценить эту величину, используя ее эмпирический аналог. Таким образом, с каждым новым наблюдением вы вычисляете стандартное отклонение на основе всех наблюдений, которые у вас есть до сих пор, ожидая, пока ваша оценка установится. Не задерживайте дыхание. Это не.
Чтобы ясно это увидеть, представьте, что у вас есть процесс, который следует распределению Коши. Вас интересует определение второго момента, теоретического стандартного отклонения процесса (k=2 в уравнении (1) выше). Вы пытаетесь оценить эту величину, используя ее эмпирический аналог. Таким образом, с каждым новым наблюдением вы вычисляете стандартное отклонение на основе всех наблюдений, которые у вас есть до сих пор, ожидая, пока ваша оценка установится. Не задерживайте дыхание. Это не.
 Интересно, какие мысленные эксперименты нужны в наши дни, когда мы можем сделать так много даже с помощью одного ноутбука.
Интересно, какие мысленные эксперименты нужны в наши дни, когда мы можем сделать так много даже с помощью одного ноутбука. assign = F,предупреждения = FALSE,symbol.lookup = F)
xd <- dat0[[1]]
время <- индекс (xd)
retd <- as.numeric(xd[2:NROW(xd),4])/as.numeric(xd[1:(NROW(xd)-1),4]) -1
ветер <- 30
sd_ret <- NULL
TT <- длина (ретд)
для (я на ветру: ТТ) {
sd_ret[i] <- 100*sd(retd[1:i])
}
сюжет (sd_ret)
assign = F,предупреждения = FALSE,symbol.lookup = F)
xd <- dat0[[1]]
время <- индекс (xd)
retd <- as.numeric(xd[2:NROW(xd),4])/as.numeric(xd[1:(NROW(xd)-1),4]) -1
ветер <- 30
sd_ret <- NULL
TT <- длина (ретд)
для (я на ветру: ТТ) {
sd_ret[i] <- 100*sd(retd[1:i])
}
сюжет (sd_ret)