ГДЗ: Алгебра 7 класс Звавич, Кузнецова
Вариант I. С-1.Вычисление значения числового выражения
1 2 3 4 5 6Вариант I. С-2.Вычисление значения числового выражения
1 2 3 4Вариант I. С-3. Решение задач на проценты
1 2 3 4 5 6 7 8 9Вариант I. С-4. Нахождение значений буквенных выражений
1 2 3 4 5 6 7 8Вариант I. С-5. Сравнение значений выражений
1 2 3 4 5 6 7 8Вариант I. С-6. Применение свойств действий над числами к вычислениям
1 2 3 4 5Вариант I. С-7. Приведение подобных слагаемых и раскрытие скобок
1 2 3 4 5 6 7Вариант I. С-8. Решение линейных уравнений
1 2 3 4 5Вариант I. С-9. Решение уравнений, сводящихся к линейным
1 2 3 4 5Вариант I. С-10. Решение задач с помощью уравнений
1 2 3 4 5 6 7 8Вариант I. С-11. Построение точек в координатной плоскости
1 2 3 4 5 6Вариант I. С-12. Нахождение значений функции по формуле. Статистические характеристики
1 2 3 4 5 6 7Вариант I.
С-13. Построение графика функции вида у = кх + y1 2 3 4 5 6 7Вариант I. С-14. Построение графика функции вида у = кх
1 2 3 4 5 6 7Вариант I. С-15. Чтение графика линейной функции
1 2 3 4Вариант I. С-16. Взаимное расположение графиков на координатной плоскости
1 2 3 4 5 6 7Вариант I. С-17. Построение и чтение графиков линейных функций (практические задания)
1 2Вариант I. С-18. Вычисление значения числового выражения, содержащего степень
1 2 3 4 5 6 7 8 9Вариант I. С-19. Вычисление значения буквенного выражения, содержащего степень
1 2 3 4 5Вариант I. С-20. Умножение и деление степеней с одинаковыми основаниями
1 2 3 4 5 6 7 8 9 10Вариант I. С-21. Возведение в степень произведения и степени
1 2 3 4 5 6 7 8 9Вариант I. С-22. Различные преобразования выражений, содержащих степени
1 2 3 4 5Вариант I. С-23. Вычисление значения одночлена
1 2 3 4Вариант I. С-24. Умножение многочленов и возведение одночлена в степень
1 2 3 4 5 6 7 8Вариант I.
С-25. Приведение многочленов к стандартному виду1 2 3 4 5 6 7 8Вариант I. С-26. Сложение и вычитание многочленов
1 2 3 4 5 6Вариант I. С-27. Заключение многочленов в скобки
1 2 3 4Вариант I. С-28. Умножение одночлена на многочлен
1 2 3 4 5Вариант I. С-29. Решение уравнений
1 2 3 4Вариант I. С-30. Решение уравнений
1 2Вариант I. С-31. Решение задач
1 2Вариант I. С-32. Вынесение общего множителя за скобки
1 2 3 4 5Вариант I. С-33. Умножение многочленов
1 2 3 4Вариант I. С-34. Умножение многочленов
1 2 3 4 5Вариант I. С-35. Разложение многочленов на множители способом группировки
1 2 3 4Вариант I. С-36. Чтение и запись алгебраических выражений
1 2 3 4Вариант I. С-37. Возведение в квадрат по формулам
1 2 3 4Вариант I. С-38. Преобразование выражений с применением формул квадрата суммы и квадрата разности
1 2 3 4Вариант I. С-39. Разложение на множители с помощью формул квадрата суммы и квадрата разности
1 2 3Вариант I.
С-40. Умножение многочленов с использованием формулы (a-fe)(a + 6) = a2-fe21 2 3Вариант I. С-41. Применение формул к преобразованию выражений
1 2 3 4 5Вариант I. С-42. Разложение на множители по формуле
1 2 3Вариант I. С-43. Преобразование целых выражений
1 2 3 4 5Вариант I. С-44. Разложение многочленов на множители с использованием нескольких способов
1 2 3 4 5Вариант I. С-45. Графическое решение систем линейных уравнений
1 2 3 4 5Вариант I. С-46. Решение систем линейных уравнений способом подстановки
1 2 3 4Вариант I. С-47. Решение систем линейных уравнений способом сложения
1 2 3 4Вариант I. С-48. Решение систем линейных уравнений
1 2 3 4Вариант I. С-49. Составление системы уравнений по условию задачи
1 2 3Вариант I. С-50. Решение задач с помощью составления системы уравнений
1 2 3 4 5 6 7Вариант I. С-51. Нахождение значения алгебраической дроби. Нахождение допустимых значений букв, входящих в дробь
1 2 3 4Вариант I.
С-52. Сокращение алгебраических дробей1 2 3Вариант I. С-53. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями
1 2 3Вариант I. С-54. Сложение и вычитание алгебраических дробей с разными знаменателями
1 2 3 4Вариант I. С-55. Умножение и деление алгебраических дробей
1 2 3Вариант I. С-56. Умножение и деление алгебраических дробей
1 2 3Вариант II. С-1. Вычисление значения числового выражения
1 2 3 4 5 6 7Вариант II. С-2. Вычисление значения числового выражения
1 2 3 4Вариант II. С-3. Решение задач на проценты
1 2 3 4 5 6 7 8 9Вариант II. С-4. Нахождение значений буквенных выражений
1 2 3 4 5 6 7 8Вариант II. С-5. Сравнение значений выражений
1 2 3 4 5 6 7 8Вариант II. С-6. Применение свойств действий над числами к вычислениям
1 2 3 4 5Вариант II. С-6. Применение свойств действий над числами к вычислениям
1 2 3 4 5 6 7Вариант II. С-9. Решение уравнений, сводящихся к линейным
1 2 3 4 5Вариант II.
С-9. Решение уравнений, сводящихся к линейным1 2 3 4 5Вариант II. С-10. Решение задач с помощью уравнений
1 2 3 4 5 6 7 8Вариант II. С-11. Построение точек в координатной плоскости:
1 2 3 4 5 6Вариант II. С-12. Нахождение значений функции по формуле. Статистические характеристики
1 2 3 4 5 6 7Вариант II. С-13. Построение графика функции вида у = кх + y
1 2 3 4 5 6 7Вариант II. С-14. Построение графика функции вида у = кх
1 2 3 4 5 6 7Вариант II. С-15. Чтение графика линейной функции
1 2 3 4Вариант II. С-16. Взаимное расположение графиков на координатной плоскости
1 2 3 4 5 6 7Вариант II. С-17. Построение и чтение графиков линейных функций (практические задания)
1 2Вариант II. С-18. Вычисление значения числового выражения, содержащего степень:
1 2 3 4 5 6 7 8 9Вариант II. С-19. Вычисление значения буквенного выражения, содержащего степень
1 2 3 4 5Вариант II. С-20. Умножение и деление степеней с одинаковыми основаниями
1 2 3 4 5 6 7 8 9 10Вариант II.
С-21. Возведение в степень произведения и степени1 2 3 4 5 6 7 8 9Вариант II. С-22. Различные преобразования выражении, содержащих степени
1 2 3 4 5Вариант II. С-23. Вычисление значения одночлена
1 2 3 4Вариант II. С-24. Умножение многочленов и возведение одночлена в степень
1 2 3 4 5 6 7 8Вариант II. С-25. Приведение многочленов к стандартному виду
1 2 3 4 5 6 7 8Вариант II. С-26. Сложение и вычитание многочленов
1 2 3 4 5 6Вариант II. С-27. Заключение многочленов в скобки
1 2 3 4Вариант II. С-28. Умножение одночлена на многочлен
1 2 3 4 5Вариант II. С-29. Решение уравнений
1 2 3 4Вариант II. С-30. Решение уравнений
1 2Вариант II. С-31. Решение задач
1 2Вариант II. С-32. Вынесение общего множителя за скобки
1 2 3 4 5Вариант II. С-33. Умножение многочленов
1 2 3 4Вариант II. С-34. Умножение многочленов
1 2 3 4 5Вариант II. С-35. Разложение многочленов на множители способом группировки
1 2 3 4Вариант II.
С-36. Чтение и запись алгебраических выражений1 2 3 4Вариант II. С-37. Возведение в квадрат по формулам
1 2 3 4Вариант II. С-38. Преобразование выражений с применением формул квадрата суммы и квадрата разности
1 2 3 4Вариант II. С-39. Разложение на множители с помощью формул квадрата суммы и квадрата разности
1 2 3Вариант II. С-40. Умножение многочленов с использованием формулы
1 2 3Вариант II. С-41. Применение формул к преобразованию выражений
1 2 3 4 5Вариант II. С-42. Разложение на множители по формуле
1 2 3Вариант II. С-43. Преобразование целых выражений
1 2 3 4Вариант II. С-44. Разложение многочленов на множители с использованием нескольких способов
1 2 3 4 5Вариант II. С-45. Графическое решение систем линейных уравнений
1 2 3 4 5Вариант II. С-46. Решение систем линейных уравнений способом подстановки
1 2 3 4Вариант II. С-47. Решение систем линейных уравнений способом сложения
1 2 3 4Вариант II.
С-48. Решение систем линейных уравнений1 2 3 4Вариант II. С-49. Составление системы уравнений по условию задачи
1 2 3Вариант II. С-50. Решение задач с помощью составления системы уравнений
1 2 3 4 5 6 7Вариант II. С-51. Нахождение значения алгебраической дроби. Нахождение допустимых значений букв, входящих в дробь
1 2 3 4Вариант II. С-52. Сокращение алгебраических дробей
1 2 3Вариант II. С-53. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями
1 2 3Вариант II. С-54. Сложение и вычитание алгебраических дробей с разными знаменателями
1 2 3 4Вариант II. С-55. Умножение и деление алгебраических дробей
1 2 3Вариант II. С-56. Умножение и деление алгебраических дробей
1 2 3Контрольная работа 1
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 1A
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 2
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 2a
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 3
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 3a
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 4
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 4a
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 5
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 5a
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 6
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 6a
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 7
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 7a
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 8
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 8a
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 9
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 9a
Вариант 1 Вариант 2 Вариант 3 Вариант 4Итоговая контрольная работа 1
Вариант 1 Вариант 2 Вариант 3 Вариант 4Итоговая контрольная работа 2
Вариант 1 Вариант 2 Вариант 3 Вариант 4Итоговая контрольная работа 3
Вариант 1 Вариант 2 Вариант 3 Вариант 4Задания для школьных олимпиад.
Осенняя олимпиадаВариант 1 Вариант 2Задания для школьных олимпиад. Новогодняя олимпиада
Вариант 1 Вариант 2Задания для школьных олимпиад. Весенняя олимпиада
Вариант 1 Вариант 2Наибольший общий делитель / Обыкновенные дроби / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Обыкновенные дроби
- Наибольший общий делитель
Число 36 имеет такие делители: 1, 2, 4, 6, 9, 12, 18, 36.
Число 126 имеет такие делители: 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126.
Синим цветом мы выделили числа 1, 2, 6, 9, 18, которые являются общими делителями чисел 36 и 126. Наибольшим из данных множителей является 18.
| Наибольшее натуральное число, на которое делятся нацело каждое из двух данных натуральных чисел, называют наибольшим общим делителем этих чисел. |
Наибольший общий делитель чисел и обозначают так: НОД(; ), то есть мы можем записать НОД(36; 126) = 18.
Предварительно разложив числа на простые множители, мы упростим нахождение
Найдем НОД(240; 165).
240 = 222235 165 = 3511.
Синим мы выделили все общие простые делители рассматриваемых чисел, это 3 и 5. Значит, оба данных числа делятся и на произведение данных чисел, то есть на 35 = 15, оно и будет являться наибольшим общим делителем чисел 240 и 165, то есть НОД(240; 165) = 35 = 15.
Найдем НОД(2520; 4620).
2 520 = 2223357 4 620 = 2235711.
Рассмотрев разложения данных чисел, мы можем заметить, что некоторые простые множители повторяются, например, число 2 в разложении числа 2520 повторяется трижды, а в разложении числа 4620 — дважды. Заметим, что число 4 = 22 является делителем и числа 2520, и числа 4620, а число 8 = 222, является делителем только числа 2520.
Мы получили, что числа 2520 и 4620 делятся без остатка на каждое из чисел 4, 3, 5, 7, на их произведение 4357 рассматриваемые числа тоже делятся без остатка, то есть мы получили, что НОД(2520; 4620) = 4357 = 420.
Таким образом, можно найти НОД, разложив числа на простые множители и выписав те, что входят в разложение обоих чисел (или можно просто зачеркнуть те множители, которые есть только в разложении одного числа, например, в разложении числа 2520 нам надо вычеркнуть одну 2 и одну 3, а в разложении числа 4620 число 11).
Таким же образом можно найти НОД трех и более чисел.
Чтобы найти НОД нескольких натуральных чисел, надо:
|
Заметим, что если все данные числа делятся на одно из них, то это число и является НОД данных чисел.
| Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1. |
Нам известно, что разложение на простые множители, мы можем записать в виде произведения степеней, то есть в последнем примере мы можем записать, что:
2 520 = 23325171
4 620 = 22315171111.
Тогда НОД мы можем найти по следующему правилу:
|
Полученное произведение является искомым наибольшим общим делителем.Найдем НОД(2520; 4620):
- Выписываем общие основания: 2, 3, 5, 7.
- Выбираем наименьшие показатели данных степеней: 22, 31, 51, 71.
- Находим произведение данных степеней, то есть искомый наибольший общий делитель: НОД(2520; 4620) = 22315171 = 420.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Сравнение дробей
Делители и кратные
Признаки делимости на 10, на 5 и на 2
Четные и нечетные числа
Признаки делимости на 9 и на 3
Простые и составные числа
Разложение на простые множители
Наименьшее общее кратное
Деление и дроби
Сложение и вычитание дробей с одинаковыми знаменателями
Смешанное число
Сложение и вычитание смешанных чисел
Основное свойство дроби
Решето Эратосфена
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Умножение обыкновенных дробей
Деление обыкновенных дробей
Обыкновенные дроби
Правило встречается в следующих упражнениях:
6 класс
Номер 141, Мерзляк, Полонский, Якир, Учебник
Номер 144, Мерзляк, Полонский, Якир, Учебник
Номер 149, Мерзляк, Полонский, Якир, Учебник
Номер 223, Мерзляк, Полонский, Якир, Учебник
Задание 147, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 152, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 187, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 231, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 485, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 190, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 351, Мерзляк, Полонский, Якир, Учебник
Умножение одинаковых чисел с разными степенями.
Правила умножения степеней с разным основанием. Основные свойства степеней с целыми показателямиГлавная > Коэффициенты > Умножение одинаковых чисел с разными степенями. Правила умножения степеней с разным основанием. Основные свойства степеней с целыми показателями
Если не обращать внимание на восьмую степень, что мы здесь видим? Вспоминаем программу 7 класса. Итак, вспомнили? Это формула сокращенного умножения, а именно — разность квадратов! Получаем:
Внимательно смотрим на знаменатель. Он очень похож на один из множителей числителя, но что не так? Не тот порядок слагаемых. Если бы их поменять местами, можно было бы применить правило.
Но как это сделать? Оказывается, очень легко: здесь нам помогает четная степень знаменателя.
Магическим образом слагаемые поменялись местами. Это «явление» применимо для любого выражения в четной степени: мы можем беспрепятственно менять знаки в скобках.
Но важно запомнить: меняются все знаки одновременно !
Вернемся к примеру:
И снова формула:
Целыми мы называем натуральные числа, противоположные им (то есть взятые со знаком « ») и число.
целое положительное число , а оно ничем не отличается от натурального, то все выглядит в точности как в предыдущем разделе.
А теперь давайте рассмотрим новые случаи. Начнем с показателя, равного.
Любое число в нулевой степени равно единице :
Как всегда, зададимся вопросом: почему это так?
Рассмотрим какую-нибудь степень с основанием. Возьмем, например, и домножим на:
Итак, мы умножили число на, и получили то же, что и было — . А на какое число надо умножить, чтобы ничего не изменилось? Правильно, на. Значит.
Можем проделать то же самое уже с произвольным числом:
Повторим правило:
Любое число в нулевой степени равно единице.
Но из многих правил есть исключения. И здесь оно тоже есть — это число (в качестве основания).
С одной стороны, в любой степени должен равняться — сколько ноль сам на себя ни умножай, все-равно получишь ноль, это ясно. Но с другой стороны, как и любое число в нулевой степени, должен равняться.
Так что из этого правда? Математики решили не связываться и отказались возводить ноль в нулевую степень. То есть теперь нам нельзя не только делить на ноль, но и возводить его в нулевую степень.
Поехали дальше. Кроме натуральных чисел и числа к целым относятся отрицательные числа. Чтобы понять, что такое отрицательная степень, поступим как в прошлый раз: домножим какое-нибудь нормальное число на такое же в отрицательной степени:
Отсюда уже несложно выразить искомое:
Теперь распространим полученное правило на произвольную степень:
Итак, сформулируем правило:
Число в отрицательной степени обратно такому же числу в положительной степени. Но при этом основание не может быть нулевым: (т.к. на делить нельзя).
Подведем итоги:
I. Выражение не определено в случае. Если, то.
II. Любое число в нулевой степени равно единице: .
III. Число, не равное нулю, в отрицательной степени обратно такому же числу в положительной степени: .
Задачи для самостоятельного решения:Ну и, как обычно, примеры для самостоятельного решения:
Разбор задач для самостоятельного решения:Знаю-знаю, числа страшные, но на ЕГЭ надо быть готовым ко всему! Реши эти примеры или разбери их решение, если не смог решить и ты научишься легко справляться с ними на экзамене!
Продолжим расширять круг чисел, «пригодных» в качестве показателя степени.
Теперь рассмотрим рациональные числа. Какие числа называются рациональными?
Ответ: все, которые можно представить в виде дроби, где и — целые числа, причем.
Чтобы понять, что такое «дробная степень» , рассмотрим дробь:
Возведем обе части уравнения в степень:
Теперь вспомним правило про «степень в степени» :
Какое число надо возвести в степень, чтобы получить?
Эта формулировка — определение корня -ой степени.
Напомню: корнем -ой степени числа () называется число, которое при возведении в степень равно.
То есть, корень -ой степени — это операция, обратная возведению в степень: .
Получается, что. Очевидно, этот частный случай можно расширить: .
Теперь добавляем числитель: что такое? Ответ легко получить с помощью правила «степень в степени»:
Но может ли основание быть любым числом? Ведь корень можно извлекать не из всех чисел.
Никакое!
Вспоминаем правило: любое число, возведенное в четную степень — число положительное.
То есть, извлекать корни четной степени из отрицательных чисел нельзя!
А это значит, что нельзя такие числа возводить в дробную степень с четным знаменателем, то есть выражение не имеет смысла.
А что насчет выражения?
Но тут возникает проблема.
Число можно представить в виде дргих, сократимых дробей, например, или.
И получается, что существует, но не существует, а ведь это просто две разные записи одного и того же числа.
Или другой пример: раз, то можно записать. Но стоит нам по-другому записать показатель, и снова получим неприятность: (то есть, получили совсем другой результат!).
Чтобы избежать подобных парадоксов, рассматриваем только положительное основание степени с дробным показателем .
Итак, если:
- — натуральное число;
- — целое число;
Примеры:
Степени с рациональным показателем очень полезны для преобразования выражений с корнями, например:
5 примеров для тренировкиРазбор 5 примеров для тренировки
1.
Не забываем об обычных свойствах степеней:
2. . Здесь вспоминаем, что забыли выучить таблицу степеней:
ведь — это или. Решение находится автоматически: .
Ну а теперь — самое сложное. Сейчас мы разберем степень с иррациональным показателем .
Все правила и свойства степеней здесь точно такие же, как и для степени с рациональным показателем, за исключением
Ведь по определению иррациональные числа — это числа, которые невозможно представить в виде дроби, где и — целые числа (то есть, иррациональные числа — это все действительные числа кроме рациональных).
При изучении степеней с натуральным, целым и рациональным показателем, мы каждый раз составляли некий «образ», «аналогию», или описание в более привычных терминах.
Например, степень с натуральным показателем — это число, несколько раз умноженное само на себя;
…число в нулевой степени — это как-бы число, умноженное само на себя раз, то есть его еще не начали умножать, значит, само число еще даже не появилось — поэтому результатом является только некая «заготовка числа», а именно число;
.
..степень с целым отрицательным показателем — это как будто произошел некий «обратный процесс», то есть число не умножали само на себя, а делили.
Между прочим, в науке часто используется степень с комплексным показателем, то есть показатель — это даже не действительное число.
Но в школе мы о таких сложностях не думаем, постичь эти новые понятия тебе представится возможность в институте.
КУДА МЫ УВЕРЕНЫ ТЫ ПОСТУПИШЬ! (если научишься решать такие примеры:))
Например:
Реши самостоятельно: Разбор решений:1. Начнем с уже обычного для нас правила возведения степени в степень:
Теперь посмотри на показатель. Ничего он тебе не напоминает? Вспоминаем формулу сокращенного умножения разность квадратов:
В данном случае,
Получается, что:
Ответ: .
2. Приводим дроби в показателях степеней к одинаковому виду: либо обе десятичные, либо обе обычные. Получим, например:
Ответ: 16
3. Ничего особенного, применяем обычные свойства степеней:
ПРОДВИНУТЫЙ УРОВЕНЬ
Определение степени
Степенью называется выражение вида: , где:
- — основание степени;
- — показатель степени.
Степень с натуральным показателем {n = 1, 2, 3,…}
Возвести число в натуральную степень n — значит умножить число само на себя раз:
Степень с целым показателем {0, ±1, ±2,…}
Если показателем степени является целое положительное число:
Возведение в нулевую степень :
Выражение неопределенное, т.к., с одной стороны, в любой степени — это, а с другой — любое число в -ой степени — это.
Если показателем степени является целое отрицательное число:
(т.к. на делить нельзя).
Еще раз о нулях: выражение не определено в случае. Если, то.
Примеры:
Степень с рациональным показателем
- — натуральное число;
- — целое число;
Примеры:
Свойства степеней
Чтобы проще было решать задачи, попробуем понять: откуда эти свойства взялись? Докажем их.
Посмотрим: что такое и?
По определению:
Итак, в правой части этого выражения получается такое произведение:
Но по определению это степень числа с показателем, то есть:
Что и требовалось доказать.
Пример : Упростите выражение.
Решение : .
Пример : Упростите выражение.
Решение : Важно заметить, что в нашем правиле обязательно должны быть одинаковые основания. Поэтому степени с основанием мы объединяем, а остается отдельным множителем:
Еще одно важное замечание: это правило — только для произведения степеней !
Ни в коем случае нелья написать, что.
Так же, как и с предыдущим свойством, обратимся к определению степени:
Перегруппируем это произведение так:
Получается, что выражение умножается само на себя раз, то есть, согласно определению, это и есть -я степень числа:
По сути это можно назвать «вынесением показателя за скобки». Но никогда нельзя этого делать в сумме: !
Вспомним формулы сокращенного умножения: сколько раз нам хотелось написать? Но это неверно, ведь.
Степень с отрицательным основанием.До этого момента мы обсуждали только то, каким должен быть показатель степени.
Но каким должно быть основание? В степенях с натуральным показателем основание может быть любым числом .
И правда, мы ведь можем умножать друг на друга любые числа, будь они положительные, отрицательные, или даже. Давайте подумаем, какие знаки (« » или « ») будут иметь степени положительных и отрицательных чисел?
Например, положительным или отрицательным будет число? А? ?
С первым все понятно: сколько бы положительных чисел мы друг на друга не умножали, результат будет положительным.
Но с отрицательными немного интереснее. Мы ведь помним простое правило из 6 класса: «минус на минус дает плюс». То есть, или. Но если мы умножим на (), получится — .
И так до бесконечности: при каждом следующем умножении знак будет меняться. Можно сформулировать такие простые правила:
- четную степень, — число положительное .
- Отрицательное число, возведенное в нечетную степень, — число отрицательное .
- Положительное число в любой степени — число положительное.
- Ноль в любой степени равен нулю.
Определи самостоятельно, какой знак будут иметь следующие выражения:
| 1. | 2. | 3. |
| 4. | 5. | 6. |
Справился? Вот ответы:
1) ; 2) ; 3) ; 4) ; 5) ; 6) .
В первых четырех примерах, надеюсь, все понятно? Просто смотрим на основание и показатель степени, и применяем соответствующее правило.
В примере 5) все тоже не так страшно, как кажется: ведь неважно, чему равно основание — степень четная, а значит, результат всегда будет положительным. Ну, за исключением случая, когда основание равно нулю. Основание ведь не равно? Очевидно нет, так как (потому что).
Пример 6) уже не так прост. Тут нужно узнать, что меньше: или? Если вспомнить, что, становится ясно, что, а значит, основание меньше нуля.
То есть, применяем правило 2: результат будет отрицательным.
И снова используем определение степени:
Все как обычно — записываем определение степеней и, делим их друг на друга, разбиваем на пары и получаем:
Прежде чем разобрать последнее правило, решим несколько примеров.
Вычисли значения выражений:
Решения :
Если не обращать внимание на восьмую степень, что мы здесь видим? Вспоминаем программу 7 класса. Итак, вспомнили? Это формула сокращенного умножения, а именно — разность квадратов!
Получаем:
Внимательно смотрим на знаменатель. Он очень похож на один из множителей числителя, но что не так? Не тот порядок слагаемых. Если бы их поменять местами, можно было бы применить правило 3. Но как это сделать? Оказывается, очень легко: здесь нам помогает четная степень знаменателя.
Если домножить его на, ничего не поменяется, верно? Но теперь получается следующее:
Магическим образом слагаемые поменялись местами. Это «явление» применимо для любого выражения в четной степени: мы можем беспрепятственно менять знаки в скобках.
Но важно запомнить: меняются все знаки одновременно! Нельзя заменить на, изменив только один неугодный нам минус!
Вернемся к примеру:
И снова формула:
Итак, теперь последнее правило:
Как будем доказывать? Конечно, как обычно: раскроем понятие степени и упростим:
Ну а теперь раскроем скобки. Сколько всего получится букв? раз по множителей — что это напоминает? Это не что иное, как определение операции умножения : всего там оказалось множителей. То есть, это, по определению, степень числа с показателем:
Пример:
Степень с иррациональным показателем
В дополнение к информации о степенях для среднего уровня, разберем степень с иррациональным показателем. Все правила и свойства степеней здесь точно такие же, как и для степени с рациональным показателем, за исключением — ведь по определению иррациональные числа — это числа, которые невозможно представить в виде дроби, где и — целые числа (то есть, иррациональные числа — это все действительные числа, кроме рациональных).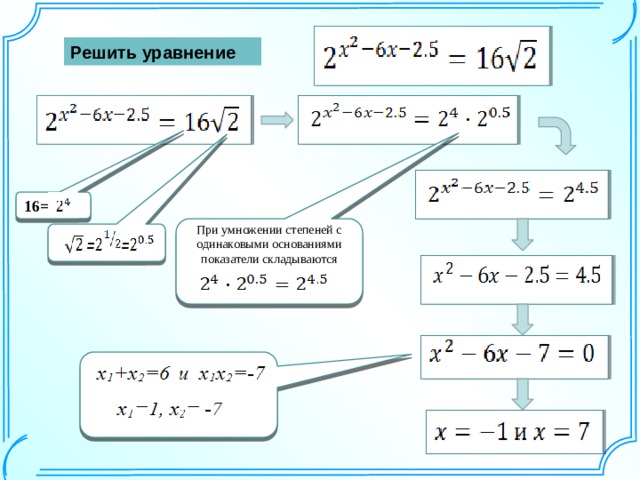
При изучении степеней с натуральным, целым и рациональным показателем, мы каждый раз составляли некий «образ», «аналогию», или описание в более привычных терминах. Например, степень с натуральным показателем — это число, несколько раз умноженное само на себя; число в нулевой степени — это как-бы число, умноженное само на себя раз, то есть его еще не начали умножать, значит, само число еще даже не появилось — поэтому результатом является только некая «заготовка числа», а именно число; степень с целым отрицательным показателем — это как будто произошел некий «обратный процесс», то есть число не умножали само на себя, а делили.
Вообразить степень с иррациональным показателем крайне сложно (так же, как сложно представить 4-мерное пространство). Это, скорее, чисто математический объект, который математики создали, чтобы расширить понятие степени на все пространство чисел.
Между прочим, в науке часто используется степень с комплексным показателем, то есть показатель — это даже не действительное число.
Но в школе мы о таких сложностях не думаем, постичь эти новые понятия тебе представится возможность в институте.
Итак, что мы делаем, если видим иррациональный показатель степени? Всеми силами пытаемся от него избавиться!:)
Например:
Реши самостоятельно:
| 1) | 2) | 3) |
Ответы:
- Вспоминаем формулу разность квадратов. Ответ: .
- Приводим дроби к одинаковому виду: либо обе десятичные, либо обе обычные. Получим, например: .
- Ничего особенного, применяем обычные свойства степеней:
КРАТКОЕ ИЗЛОЖЕНИЕ РАЗДЕЛА И ОСНОВНЫЕ ФОРМУЛЫ
Степенью называется выражение вида: , где:
Степень с целым показателем
степень, показатель которой — натуральное число (т.е. целое и положительное).
Степень с рациональным показателем
степень, показатель которой — отрицательные и дробные числа.
Степень с иррациональным показателем
степень, показатель которой — бесконечная десятичная дробь или корень.
Свойства степеней
Особенности степеней.
- Отрицательное число, возведенное в четную степень, — число положительное .
- Отрицательное число, возведенное в нечетную степень, — число отрицательное .
- Положительное число в любой степени — число положительное.
- Ноль в любой степени равен.
- Любое число в нулевой степени равно.
ТЕПЕРЬ ТЕБЕ СЛОВО…
Как тебе статья? Напиши внизу в комментариях понравилась или нет.
Расскажи о своем опыте использования свойств степеней.
Возможно у тебя есть вопросы. Или предложения.
Напиши в комментариях.
И удачи на экзаменах!
Одной из главных характеристик в алгебре, да и во всей математике является степень. Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.
В данной статье рассмотрим самые важные вопросы, касающиеся этого определения.
А именно, поймем что это вообще такое и каковы основные его функции, какие имеются свойства в математике.
Рассмотрим на примерах то, как выглядит расчет, каковы основные формулы. Разберем основные виды величины и то, чем они отличаются от других функций.
Поймем, как решать с помощью этой величины различные задачи. Покажем на примерах, как возводить в нулевую степень, иррациональную, отрицательную и др.
Онлайн-калькулятор возведения в степень
Что такое степень числа
Что же подразумевают под выражением «возвести число в степень»?
Степенью n числа а является произведение множителей величиной а n-раз подряд.
Математически это выглядит следующим образом:
a n = a * a * a * …a n .
Например:
- 2 3 = 2 в третьей степ. = 2 * 2 * 2 = 8;
- 4 2 = 4 в степ. два = 4 * 4 = 16;
- 5 4 = 5 в степ. четыре = 5 * 5 * 5 * 5 = 625;
- 10 5 = 10 в 5 степ. = 10 * 10 * 10 * 10 * 10 = 100000;
- 10 4 = 10 в 4 степ. = 10 * 10 * 10 * 10 = 10000.
= 10 * 10 * 10 * 10 = 10000.Ниже будет представлена таблица квадратов и кубов от 1 до 10.
Таблица степеней от 1 до 10
Ниже будут приведены результаты возведения натуральных чисел в положительные степени – «от 1 до 100».
| Ч-ло | 2-ая ст-нь | 3-я ст-нь |
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 279 |
| 10 | 100 | 1000 |
Свойства степеней
Что же характерно для такой математической функции? Рассмотрим базовые свойства.
Учеными установлено следующие признаки, характерные для всех степеней:
- a n * a m = (a) (n+m) ;
- a n: a m = (a) (n-m) ;
- (a b) m =(a) (b*m) .
Проверим на примерах:
2 3 * 2 2 = 8 * 4 = 32. С другой стороны 2 5 = 2 * 2 * 2 * 2 * 2 =32.
Аналогично: 2 3: 2 2 = 8 / 4 =2. Иначе 2 3-2 = 2 1 =2.
(2 3) 2 = 8 2 = 64. А если по-другому? 2 6 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.
Как видим, правила работают.
А как же быть со сложением и вычитанием ? Всё просто. Выполняется сначала возведение в степень, а уж потом сложение и вычитание.
Посмотрим на примерах:
- 3 3 + 2 4 = 27 + 16 = 43;
- 5 2 – 3 2 = 25 – 9 = 16. Обратите внимание: правило не будет выполняться, если сначала произвести вычитание: (5 — 3) 2 = 2 2 = 4.
А вот в этом случае надо вычислять сначала сложение, поскольку присутствуют действия в скобках: (5 + 3) 3 = 8 3 = 512.
Как производить вычисления в более сложных случаях ? Порядок тот же:
- при наличии скобок – начинать нужно с них;
- затем возведение в степень;
- потом выполнять действия умножения, деления;
- после сложение, вычитание.
Есть специфические свойства, характерные не для всех степеней:
- Корень n-ой степени из числа a в степени m запишется в виде: a m / n .
- При возведении дроби в степень: этой процедуре подвержены как числитель, так и ее знаменатель.
- При возведении произведения разных чисел в степень, выражение будет соответствовать произведению этих чисел в заданной степени. То есть: (a * b) n = a n * b n .
- При возведении числа в отрицательную степ., нужно разделить 1 на число в той же ст-ни, но со знаком «+».
- Если знаменатель дроби находится в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени.
- Любое число в степени 0 = 1, а в степ. 1 = самому себе.
Эти правила важны в отдельных случаях, их рассмотрим подробней ниже.
Степень с отрицательным показателем
Что делать при минусовой степени, т. е. когда показатель отрицательный?
Исходя из свойств 4 и 5 (смотри пункт выше), получается :
A (- n) = 1 / A n , 5 (-2) = 1 / 5 2 = 1 / 25.
И наоборот:
1 / A (- n) = A n , 1 / 2 (-3) = 2 3 = 8.
А если дробь?
(A / B) (- n) = (B / A) n , (3 / 5) (-2) = (5 / 3) 2 = 25 / 9.
Степень с натуральным показателем
Под ней понимают степень с показателями, равными целым числам.
Что нужно запомнить:
A 0 = 1, 1 0 = 1; 2 0 = 1; 3.15 0 = 1; (-4) 0 = 1…и т. д.
A 1 = A, 1 1 = 1; 2 1 = 2; 3 1 = 3…и т. д.
Кроме того, если (-a) 2 n +2 , n=0, 1, 2…то результат будет со знаком «+». Если отрицательное число возводится в нечетную степень, то наоборот.
Общие свойства, да и все специфические признаки, описанные выше, также характерны для них.
Дробная степень
Этот вид можно записать схемой: A m / n . Читается как: корень n-ой степени из числа A в степени m.
С дробным показателем можно делать, что угодно: сокращать, раскладывать на части, возводить в другую степень и т. д.
Степень с иррациональным показателем
Пусть α – иррациональное число, а А ˃ 0.
Чтобы понять суть степени с таким показателем, рассмотрим разные возможные случаи:
- А = 1. Результат будет равен 1. Поскольку существует аксиома – 1 во всех степенях равна единице;
А r 1 ˂ А α ˂ А r 2 , r 1 ˂ r 2 – рациональные числа;
- 0˂А˂1.
В этом случае наоборот: А r 2 ˂ А α ˂ А r 1 при тех же условиях, что и во втором пункте.
Например, показатель степени число π. Оно рациональное.
r 1 – в этом случае равно 3;
r 2 – будет равно 4.
Тогда, при А = 1, 1 π = 1.
А = 2, то 2 3 ˂ 2 π ˂ 2 4 , 8 ˂ 2 π ˂ 16.
А = 1/2, то (½) 4 ˂ (½) π ˂ (½) 3 , 1/16 ˂ (½) π ˂ 1/8.
Для таких степеней характерны все математические операции и специфические свойства, описанные выше.
Заключение
Подведём итоги — для чего же нужны эти величины, в чем преимущество таких функций? Конечно, в первую очередь они упрощают жизнь математиков и программистов при решении примеров, поскольку позволяют минимизировать расчеты, сократить алгоритмы, систематизировать данные и многое другое.
Где еще могут пригодиться эти знания? В любой рабочей специальности: медицине, фармакологии, стоматологии, строительстве, технике, инженерии, конструировании и т. д.
Если вам нужно возвести какое-то конкретное число в степень, можете воспользоваться . А сейчас мы более подробно остановимся на свойствах степеней .
Экспоненциальные числа открывают большие возможности, они позволяют нам преобразовать умножение в сложение, а складывать гораздо легче, чем умножать.
Например, нам надо умножить 16 на 64. Произведение от умножения этих двух чисел равно 1024. Но 16 – это 4×4, а 64 – это 4х4х4. То есть 16 на 64=4x4x4x4x4, что также равно 1024.
Число 16 можно представить также в виде 2х2х2х2, а 64 как 2х2х2х2х2х2, и если произвести умножение, мы опять получим 1024.
А теперь используем правило . 16=4 2 , или 2 4 , 64=4 3 , или 2 6 , в то же время 1024=6 4 =4 5 , или 2 10 .
Следовательно, нашу задачу можно записать по-другому: 4 2 х4 3 =4 5 или 2 4 х2 6 =2 10 , и каждый раз мы получаем 1024.
Мы можем решить ряд аналогичных примеров и увидим, что умножение чисел со степенями сводится к сложению показателей степени , или экспонент, разумеется, при том условии, что основания сомножителей равны.
Таким образом, мы можем, не производя умножения, сразу сказать, что 2 4 х2 2 х2 14 =2 20 .
Это правило справедливо также и при делении чисел со степенями, но в этом случае экспонента делителя вычитается из экспоненты делимого . Таким образом, 2 5:2 3 =2 2 , что в обычных числах равно 32:8=4, то есть 2 2 . Подведем итоги:
a m х a n =a m+n , a m: a n =a m-n , где m и n — целые числа.
С первого взгляда может показаться, что такое умножение и деление чисел со степенями не очень удобно, ведь сначала надо представить число в экспоненциальной форме. Нетрудно представить в такой форме числа 8 и 16, то есть 2 3 и 2 4 , но как это сделать с числами 7 и 17? Или как поступать в тех случаях, когда число можно представить в экспоненциальной форме, но основания экспоненциальных выражений чисел сильно различаются.
Например, 8×9 – это 2 3 х3 2 , и в этом случае мы не можем суммировать экспоненты. Ни 2 5 и ни 3 5 не являются ответом, ответ также не лежит в интервале между этими двумя числами.
Тогда стоит ли вообще возиться с этим методом? Безусловно стоит. Он дает огромные преимущества, особенно при сложных и трудоемких вычислениях.
Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.
Число c является n -ной степенью числа a когда:
Операции со степенями.
1. Умножая степени с одинаковым основанием их показатели складываются:
a m ·a n = a m + n .
2. В делении степеней с одинаковым основанием их показатели вычитаются:
3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:
(abc…) n = a n · b n · c n …
4. Степень дроби равняется отношению степеней делимого и делителя:
(a/b) n = a n /b n .
5. Возводя степень в степень, показатели степеней перемножают:
(a m) n = a m n .
Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.
Например . (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4 .
Операции с корнями.
1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:
2. Корень из отношения равен отношению делимого и делителя корней:
3. При возведении корня в степень довольно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и в тоже время возвести в n -ую степень подкоренное число, то значение корня не поменяется:
5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:
Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:
Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m n
.
Например . a 4:a 7 = a 4 — 7 = a -3 .
Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.
Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.
Например . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.
Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n -ой степени из m -ой степени этого числа а .
Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
Запомните!
При умножении степеней с одинаковыми основаниями основание остаётся без изменений,
а показатели степеней складываются.
a m · a n = a m + n , где «a » — любое число, а «m », «n » — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
- Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15 - Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17 - Представить в виде степени.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15
Важно!
Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями . Оно не относится к их сложению.
Нельзя
заменять сумму
(3 3 + 3 2)
на 3 5
. Это понятно, если
посчитать
(3 3 + 3 2) = (27 + 9) = 36
, а
3 5 = 243
Свойство № 2
Частное степеней
Запомните!
При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
= 11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
Решить уравнение. Используем свойство частного степеней. 3 8: t = 3 4
T = 3 8 − 4
Ответ: t = 3 4 = 81Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
- Пример. Упростить выражение.
4 5m + 6 · 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5 - Пример. Найти значение выражения, используя свойства степени.
= = =
=2 9 + 2 2 5
= 2 11 − 5 = 2 6 = 642 11 2 5 Важно!
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.
Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4
Будьте внимательны!
Свойство № 3
Возведение степени в степеньЗапомните!
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(a n) m = a n · m , где «a » — любое число, а «m », «n » — любые натуральные числа.
Свойства 4
Степень произведенияЗапомните!
При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.
(a · b) n = a n · b n , где «a », «b » — любые рациональные числа; «n » — любое натуральное число.
- Пример 1.
(6 · a 2 · b 3 · c) 2 = 6 2 · a 2 · 2 · b 3 · 2 · с 1 · 2 = 36 a 4 · b 6 · с 2 - Пример 2.
(−x 2 · y) 6 = ((−1) 6 · x 2 · 6 · y 1 · 6) = x 12 · y 6
Важно!
Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
(a n · b n)= (a · b) nТо есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.
- Пример. Вычислить.
2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000 - Пример. Вычислить.
0,5 16 · 2 16 = (0,5 · 2) 16 = 1
В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.
Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216
Пример возведения в степень десятичной дроби.
4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4Свойства 5
Степень частного (дроби)Запомните!
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a: b) n = a n: b n , где «a », «b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.
- Пример. Представить выражение в виде частного степеней.
(5: 3) 12 = 5 12: 3 12
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.
- Пример 1.
Как вычитать степени — ACT Math
Все ресурсы ACT Math
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept
ACT Math Help » Алгебра » Экспоненты » Экспоненциальные операции » Как вычитать степени
Привести к простейшей форме.
Возможные ответы:
Правильный ответ:
Объяснение:
При делении терминов с одинаковыми основаниями, но разными показателями степени вам нужно будет вычесть все соответствующие показатели степени.
становится,
становится,
и остается прежним, потому что нет другого z-члена, который можно комбинировать с ним.
Таким образом, получается:
Сообщить об ошибке
Упростить: 3 2 * (4 23 — 4 21 21*5
Объяснение:
Прежде всего обратите внимание, что группа (4 23 — 4 21 ) имеет общий делитель, а именно 4 21 .
Вы можете рассматривать это как любую другую константу или переменную и учитывать ее. Это даст вам: 4 21 (4 2 — 1). Поэтому мы знаем, что:
3 2 * (4 23 — 4 21 ) = 3 2 * 4 21 (4 2 — 1)
Теперь 4 2 0042 — 1 = 16 — 1 = 15 = 5 * 3. Замените это в оригинале:
3 2 * 4 21 (4 2 — 1) = 3 2 2 90 4 0 0 4 4 3 * 5)
Объединив множители с одинаковым основанием, вы получите:
3 3 * 4 21 * 5
Сообщить об ошибке
Упрощение. Не оставляйте отрицательных показателей в окончательном ответе.
Возможные ответы:
Ни один из этих ответов не является правильным.
Правильный ответ:
Объяснение:
Первым шагом в задаче является объединение одинаковых членов в числителе, помня, что :
Затем мы разрешаем числитель, используя и :
Наконец, упрощаем отрицательный показатель, используя
Таким образом,
Сообщить об ошибке
Упростить, чтобы удалить дроби:
Возможные ответы:
Ни один из них не является правильным.
Правильный ответ:
Объяснение:
Первый шаг — упростить каждую дробь, разделив одинаковые члены, помня об этом, чтобы получить:
Затем объедините, используя умножение и правило:
Поскольку в задаче указано, что мы должны избегать дробей, мы не будем исключать отрицательные показатели.
Итак,
Сообщить об ошибке
Упростите следующее:
Возможные ответы:
Правильный ответ:
5 Объяснение:
При делении экспоненциальных выражений с одинаковым основанием вычтите показатели степени. В этой задаче показатели равны и . При вычитании получается . Таким образом, правильный ответ .
Сообщить об ошибке
может быть записано как что из следующего?
A.
B.
C.
Возможные ответы:
B и C
A, B и C
A и C
C только
B только
Правильный ответ: Ответ: Ответ: Ответ: Ответ: Ответ: Ответ: Ответ: Ответ: Ответ: Ответ: Ответ: Правильный ответ:.
Б и С
Объяснение:
A не эквивалентно, потому что показатели степени в знаменателях означают вычитание показателей степени, а не их деление. Кроме того, при вычислении A получается вместо .
B эквивалентно вышеупомянутому экспоненциальному свойству, в то время как C просто вычисляет выражение.
Сообщить об ошибке
Упрощение:
Возможные ответы:
Правильный ответ:
Объяснение:
При делении двух показателей степени с одинаковым основанием вычтите показатель степени знаменателя из показателя степени числителя, чтобы получить новый показатель степени.
Приложите этот показатель к основанию, и это будет вашим ответом.
В этом случае вычтите из . Это дает как новый показатель степени и как ответ.
Сообщить об ошибке
Уведомление об авторских правах
Все математические ресурсы ACT
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept
Добавление показателей — Как обсудить
Добавление показателей
Вы добавляете степени или умножаете их? Правило 1. Чтобы умножить одни и те же основания, сложите показатели степени. Правило 2: Чтобы разделить равные основания, вычтите степени. Правило 3: Если имеется два или более показателей степени и только одно основание, умножьте показатели степени.
Когда добавлять или вычитать показатели степени?
Когда вы умножаете два числа на степени, они складываются только в том случае, если они имеют общее основание.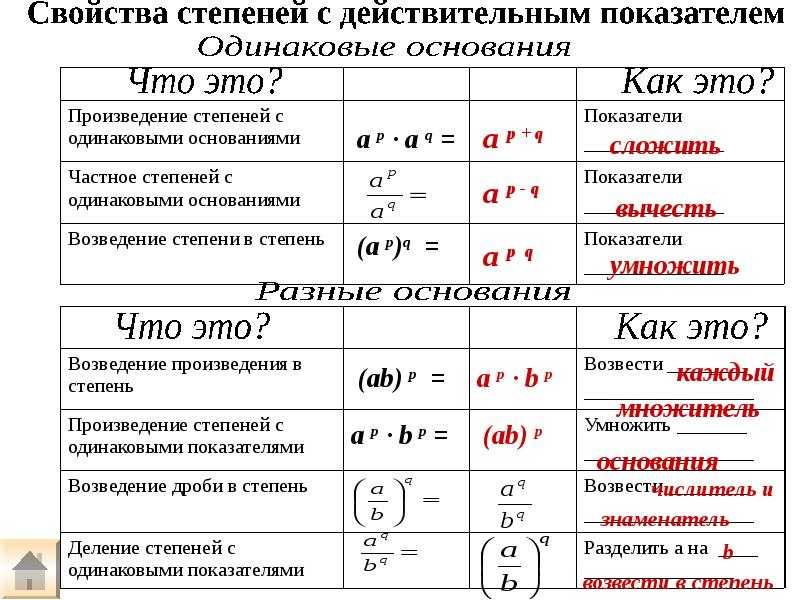
Точно так же при делении двух чисел на показатели степени вы должны вычесть показатель степени в знаменателе из показателя степени в числителе, если они имеют общий корень.
Как складывать числа с показателями степени?
Добавьте числа к показателям степени. Чтобы добавить показатель степени, сначала найдите каждый показатель степени, а затем добавьте: an + b m. Пример: 4 2 + 2 5 = 4⋅4 + 2⋅2⋅2⋅2⋅2 = 16 + 32 = 48. Сложите те же основания. по показателям п: бн + бн = 2бн.
Каковы правила сложения и вычитания показателей степени?
Сложение и вычитание баллов не требует правил. Когда одно число возводится в степень другого, оно добавляется к другому числу, возведенному в степень (с использованием другого основания или показателя степени), вычисляя результат члена показателя степени, а затем добавляя его непосредственно к, чтобы сложить другие.
Как складывать числа с разными показателями степени?
Добавление чисел к показателям степени вручную Решите первое экспоненциальное выражение.
Показательное выражение имеет основание (большое число) и показатель степени (маленькое число). Решите второе показательное выражение. Для этого умножьте само основание столько раз, сколько указано в показателе степени. Добавьте два значения.
Как добавить переменные с показателями степени?
Сумма экспоненциальных переменных Находит термины с одинаковым основанием и показателем. Добавьте термины с одинаковым основанием и показателем степени. Сложите вероятности при одинаковых обстоятельствах. Напишите последнее предложение упрощенной суммы.
Как разделить показатели с разными основаниями?
Разделить показатели по нескольким причинам. Если основания различны, а показатели а и b равны, можно сначала разделить а и b: an / bn = (a / b) n. Пример: 6 3/2 3 = (6/2) 3 = 3 3 = 3⋅3⋅3 = 27. Если основания и размеры разные, нужно вычислить каждый размер и затем разделить: ан/б м.
Как вы знаете, чтобы добавить экспоненты?
Баллы суммируются, сначала подсчитывая каждый балл, а затем добавляя: an + bm 4 2 + 2 5 = 4⋅4 + 2⋅2⋅2⋅2⋅2 = 16 + 32 = 48 миллиардов + bn = 2b n 4 2 + 4 2 = 2⋅4 2 = 2⋅4⋅4 = 32 ан + бм = 1 / ан + 1 / бм 4 2 + 2 5 = 1/4 2 + 1/2 5 = 1 / (4 4) + 1/(2⋅2⋅2⋅2⋅2) = 1/16 + 1/32 = ан/м + бк/дж.
Когда вы добавляете показатели степени или умножаете их
Сложение и вычитание баллов не требует правил. Когда число возводится в степень одного числа, оно добавляется к другому числу, возведенному в степень (с использованием другого основания или показателя степени), путем вычисления результата члена показателя степени, а затем прибавления его непосредственно к другому для подсчета.
Почему вы вычитаете, когда вы делите степени?
Чтобы разделить степени (или степени) по одному и тому же основанию, вычтите степени. Деление противоположно умножению, поэтому имеет смысл вычитать показатели степени при делении чисел с одинаковым основанием, так как вы добавляете показатели степени при умножении чисел с одинаковым основанием.
При объединении одинаковых терминов вы складываете показатели вместе?
Вы не можете комбинировать x2 и 2x, потому что первый член имеет показатель степени (2), а второй не имеет показателя степени, поэтому вы не можете их сложить! При объединении похожих терминов убедитесь, что все переменные и меры одинаковы, прежде чем добавлять их.
Когда при умножении числа вы добавляете показатели степени?
Когда два числа умножаются на показатель степени, это называется показателем степени умножения. Чтобы умножить эти числа, они добавляют показатели степени, то есть находят общее количество раз, когда переменная или число умножались сами на себя. Давайте двигаться дальше и узнать больше об этом.
Каковы правила работы с экспонентами?
Первым правилом при сложении показателей степени является порядок операций: скобки, возведения в степень, умножение, деление, сложение, вычитание. Эта последовательность операций помещает показатели на вторую позицию схемы решения. Поэтому, если вы знаете и основание, и показатель степени, решите их, прежде чем двигаться дальше.
Можно ли добавлять разные степени?
При умножении выражений с одинаковым старшим основанием на разные показатели степени можно складывать показатели степени.
Сложение или вычитание дробей
Вы можете складывать или вычитать дроби, только если они имеют одинаковый знаменатель. Следовательно, им нужно найти наименьший общий делитель, прежде чем складывать или вычитать эти дроби. Если дроби имеют одинаковый знаменатель, вы можете складывать или вычитать их как обычно.
Что такое сложение и вычитание дробей?
Сложите и вычтите дроби с разными знаменателями (включая смешанные числа) и замените эти дроби эквивалентными дробями, чтобы получить эквивалентную сумму или разность дробей с одинаковыми знаменателями. Например, 2/3 + 5/4 = 8/12 + 15/12 = 23/12.
Как сложить дроби?
Чтобы сложить дроби, выполните три простых шага:
Шаг 1 : Сопоставьте меньшие числа (знаменатели).
Шаг 2 : Добавьте первые цифры (числители), поместите этот ответ над знаменателем.
Шаг 3 : Упростите дробь (при необходимости).Как вычитать дроби в простейшей форме?
Вы можете составить эквивалентные дроби, умножив или разделив верхнее и нижнее число на одно и то же число. Чтобы складывать или вычитать дроби, вы должны использовать эквивалентные дроби, чтобы числа ниже были равны. Простейшей формой дроби является дробь с наименьшим возможным числом сверху и снизу.
Как сложить дробь?
Есть три простых шага, чтобы сложить дроби:
Шаг 1 : Сопоставьте меньшие числа (знаменатели).
Шаг 2 : Сложите первые числа (числители), поместите этот ответ над знаменателем.
Шаг 3 : Упростите дробь (при необходимости).Когда прибавлять или вычитать показатели степени в делении
Экспоненциальное правило для деления экспоненциальных членов называется правилом отношения. Факторное правило для показателей степени состоит в том, что при делении экспоненциальных членов на одно и то же основание сохраняется одно и то же основание, а затем вычитаются показатели степени.
Как вы делите показатели степени с переменными?
Разделите коэффициенты и разделите переменные. Используйте экспоненциальный закон, чтобы разделить переменные путем вычитания показателей степени. Некоторые люди предпочитают писать ответ с x в знаменателе и положительным показателем степени, чем в числителе с отрицательным показателем степени, но вы все равно можете это сделать.
Как вы делите дроби с показателями?
Чтобы разделить показатели степени одного основания, вычтите показатель степени второго основания (знаменатель дроби) из показателя степени первого основания (числитель дроби). Общее правило: x a ÷ x b = x (a — b) Это правило можно применять только в том случае, если основание одинаковое.
При делении переменных с показателями степени вычитать показатели степени?
Вы вычитаете показатели степени путем деления двух экспоненциальных чисел или переменных с одинаковым основанием. Если вы разделите показатель степени на себя, показатель степени будет равен 0.
n, вы можете просто вычесть два показателя степени (mn) и сохранить то же самое основание.
2 дважды. Найдите каждый член по отдельности, если основания, показатели степени или и то, и другое различны.Можете ли вы добавить экспоненты?
Правило произведения степени говорит им, что, умножая две степени одного и того же основания, вы можете сложить степени. Этот пример показывает, как это работает. Добавление участников — это просто ярлык!
Что такое частное свойство показателей?
Частное свойство (свойство степенных отношений, степенной закон) гласит, что вы можете разделить две степени с одним и тем же основанием, просто вычитая их показатели степени и сохраняя их общее основание.
Как добавить экспоненты с разными основаниями в математике
Добавление экспонентов с разными экспонентами и базами. Чтобы добавить индикаторы, каждый индикатор сначала рассчитывается, а затем добавляется: Обзор этих индикаторов: a + b m. Пример 1. 4 2 + 2 5 = 4⋅4 + 2⋅2⋅2⋅2⋅ 2 = 16 + 32 = 48 8 3 + 9 2 = (8) (8) (8) + (9) (9) = 512 + 81 = 593 3 2 + 5 3 = (3) (3) + (5) (5) (5) = 9 + 125 = 134 6 2 + 6 3 = 252,3 4 + 3 6 = 81 + 729 = 810.
Как умножать степени с одинаковым основанием?
Умножение участников с одинаковой базой Убедитесь, что у участников одинаковая база. Корень — это большое экспоненциальное число. Добавьте числа. Перепишите выражение с тем же корнем, но используйте сумму исходных показателей в качестве нового показателя. Найдите выражение.
В чем разница между показателем степени и основанием?
Экспонент | Основы | заключается в том, что показатель степени (математика) представляет собой величину, на которую необходимо увеличить число, символ или выражение, например. 3 на х 3, а база (математика) является альтернативой базе.
Как добавить экспоненты с разными основаниями в химии
Добавление экспонентов с разными экспонентами и базами. Для суммирования показателей каждый показатель сначала рассчитывается, а затем суммируется: Общий обзор этих показателей: a + b m. Пример 1. 4 2 + 2 5 = 4⋅4 + 2⋅2⋅2⋅2⋅ 2 = 16 + 32 = 48 8 3 + 9 2 = (8) (8) (8) + (9) (9) = 512 + 81 = 593 3 2 + 5 3 = (3) (3) + (5) (5) (5) = 9 + 125 = 134 6 2 + 6 3 = 252,3 4 + 3 6 = 81 + 729 = 810.
Добавьте индикаторы с одинаковыми базами и индикаторами.Как добавить экспоненты с разными основаниями в геометрии
Добавление экспонентов с разными экспонентами и базами. Показатели складываются, сначала рассчитывается каждый показатель, а затем складывается: Общий обзор этих показателей: an + b m. Пример 1. 4 2 + 2 5 = 4⋅4 + 2⋅2⋅2⋅2⋅2 = 16 + 32 = 48,8 3 + 9 2 = (8) (8) (8) + (9) (9) = 512 + 81 = 593.
Как складывать экспоненты с разными основаниями диаграмма
Чтобы сложить индикаторы, каждый индикатор сначала рассчитывается, а затем суммируется: 4 2 + 2 5 = 4⋅4 + 2⋅2⋅2⋅2⋅2 = 16 + 32 = 48 Добавьте те же базы по указателям севера. : Один миллиард + один миллиард = 2 миллиарда.
Что такое показательные правила?
- Нулевое правило. Нулевой показатель переменной равен единице.
- Линейка
- Отрицательное правило. Отрицательный показатель степени переменной можно записать следующим образом.
- Правила продукта. (i) Произведение показателей степени по одному и тому же основанию дает сумму показателей степени по этому основанию.
- Факторные правила.
- Создать правила.
(i) Произведение показателей степени по одному и тому же основанию дает сумму показателей степени по этому основанию.Что такое экспоненциальные правила?
Экспоненциальное правило является частным случаем цепного правила. Это полезно для нахождения степенной производной e. Экспоненциальное правило говорит, что эта производная равна нулю в степени функции, умноженной на производную функции.
Вычитание показателей степени
Чтобы вычесть положительную степень m и отрицательную степень n, просто объедините два члена, изменив знак вычитания на положительный и записав результат как m + n. Следовательно, вычтите положительный и отрицательный неравные показатели степени m и n = m + n. Пример 2 4 2 — 3 2 = 16 — 9 = 7.
Вы умеете вычитать показатели?
При вычитании показателей степени применим тот же вывод: просто посчитайте результат, если можете, а затем вычтите как обычно.
Если показатели степени и основание равны, вы можете складывать и вычитать их, как любой другой соответствующий символ в алгебре. Например, xy + xy = 2_x y y 3_xy — 2_x y = _xy.
Каковы правила сложения и вычитания показателей степени с одинаковым основанием
Помните, что для сложения или вычитания чисел с показателями степени вы должны сначала убедиться, что основание и показатель степени двух членов, которые вы хотите сложить или вычесть, одинаковы. Если они одинаковы, вам просто нужно добавить их коэффициенты и сохранить ту же основу и показатель степени.
Есть ли более простой способ умножения показателей степени?
Способ 2 из 3. Умножение экспоненциальных чисел по разным основаниям Найдите первое экспоненциальное выражение. Так как индикаторы имеют разную базу, нет простого способа их умножить. Найдите второе экспоненциальное выражение. Для этого умножьте основание само на себя столько раз, сколько указано в показателе степени. Перепишите задачу с новыми вычислениями.
Умножьте два числа.Каковы правила для показателей с одинаковым основанием?
При делении показателей степени общее эмпирическое правило для показателей степени одного основания состоит в том, чтобы вычесть показатель степени из знаменателя числителя. Есть еще чему поучиться, но это общее правило.
Каковы семь правил экспонентов?
- Умножение степеней с одинаковым основанием. При умножении показателей степени, если основания равны, необходимо складывать показатели степени.
- Распределение власти на равных условиях. Если основание деления одинаковое, то показатели степени необходимо вычесть.
- Сила силы.
- Умножить показатели на один и тот же показатель.
- Отрицательные показатели.
- Нулевой градус.
Сколько будет 5 во второй степени?
(Сколько пять к двум?) Вы решаете математическую задачу? Математически 5 — это основание, а 2 — это показатель степени, например: предыдущая задача (5, увеличенная до 2) означает, что вы умножаете 5 на себя.
Другими словами, 5*5,
Что такое экспоненциальные законы?
Законы об экспонентах. Законы экспоненты, также называемые индексными законами (Higgens, 1998) или степенными правилами (Derbyshire, 2004, стр. 65), представляют собой правила для комбинации степеней (степеней). в этом случае предполагается, что значения знаменателя отличны от нуля.
Как можно использовать показатель степени?
- Ученые против. Бизнес-калькулятор. Научные калькуляторы легко отличить от бизнес-калькуляторов благодаря множеству дополнительных функциональных клавиш.
- Использование ключа экспонента. Предположим, вам нужно значение y x.
- Читать экспонентов. Некоторые числа, такие как B.265 миллиардов, содержат слишком много цифр, чтобы их можно было отобразить на калькуляторе.
Добавляете ли вы показатели степени, если у них одинаковая база?
Если основания одинаковы, добавьте числа оснований. Если базы разные, то показатели делятся.
Если показатель степени отрицательный, не забудьте включить отрицательный показатель степени при добавлении.
Сложение и вычитание степеней на GMAT 9m\) не будет равняться а-степени чего-либо в частности.
Нет удобного способа объединить сумму или разность степеней в одно выражение мощности.
Распределение и факторинг
Но не все потеряно! Мы можем воспользоваться одним из свойств фундаментальных чисел, Законом Распределения, и его обратным процессом, «разложением на множители».
Это довольно примечательное уравнение, которое часто недооценивают.
Прежде всего, это утверждение Распределительного Закона. Помните \(a\times(b + c) = a\times b + a\times c\)?
Если мы начнем слева и пойдем направо, мы раздадим «а». Обратный процесс называется разложением на множители : если мы начнем с правой стороны и пойдем налево, мы разложим на множители «а».
Умножение распределяется между сложением и вычитанием: мы могли бы заменить оба знака «плюс» на «минус» в этом уравнении, и оно все равно было бы верным.