Презентация и конспект урока по теме Подобие (9 класс) доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экономика
Презентация на тему Презентация и конспект урока по теме Подобие (9 класс), предмет презентации: Геометрия. Этот материал в формате pptx (PowerPoint) содержит 13 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Этот материал в формате pptx (PowerPoint) содержит 13 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
«Любопытный отыскивает радости только затем, чтобы им удивляться,
любознательный же затем, чтобы узнать их и перестать удивляться». Р.Декарт
Устная работа
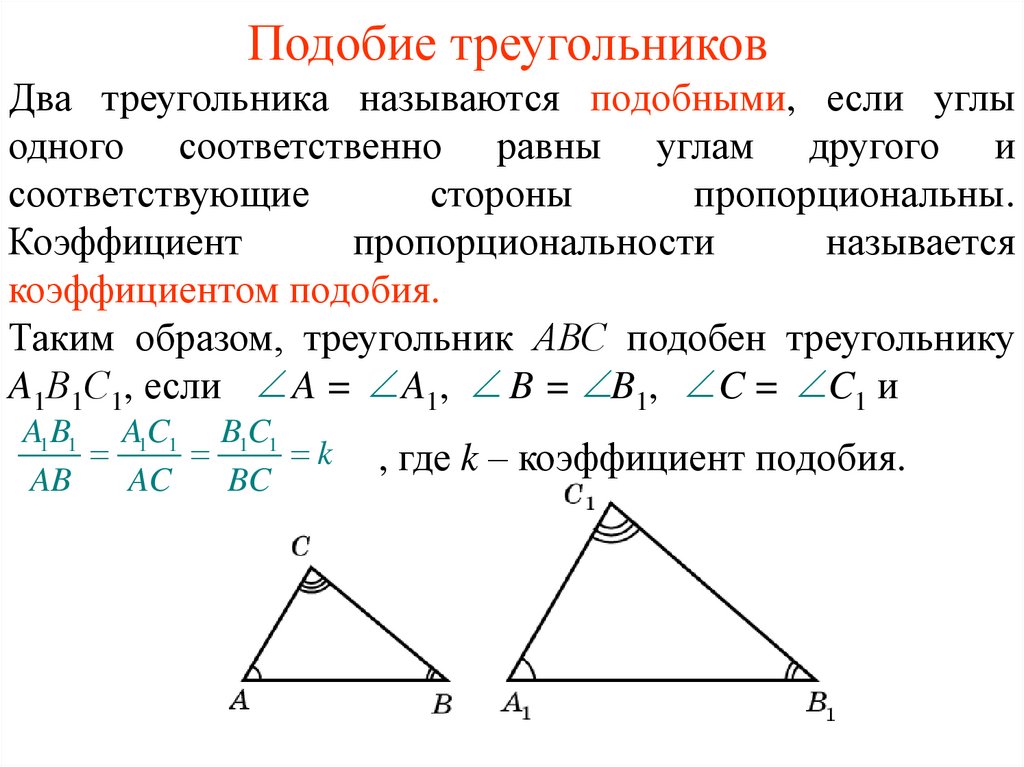
Назовите соответственные углы треугольников.
Назовите сходственные стороны треугольников.
Устная работа
Сформулируйте признаки подобия треугольников.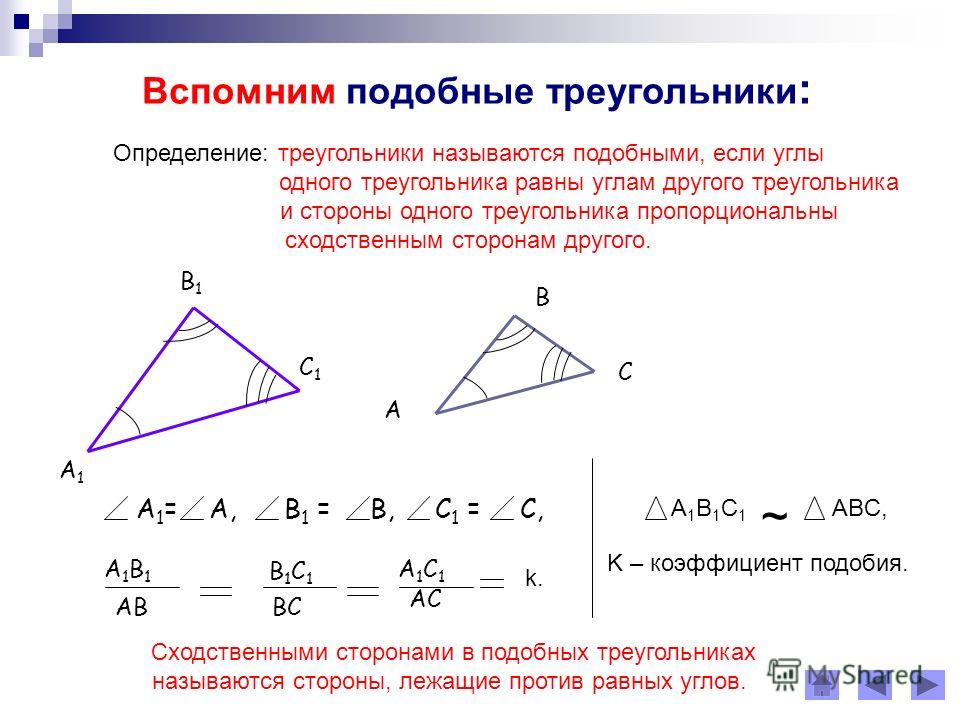
Устная работа. Какие из следующих утверждений верны?
1. Любые два равносторонних треугольника подобны.
2. Если два угла одного треугольника соответственно пропорциональны двум углам
другого треугольника, то такие треугольники
подобны.
3. Если два треугольника подобны, то их сходственные стороны пропорциональны.
Устная работа. Какие из следующих утверждений НЕ верны?
1. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники подобны.
2. Любые два прямоугольных треугольника подобны.
3. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Устная работа
Докажите, что треугольники подобны.
Устная работа
В квадрате ABCD через середины соседних сторон ВС и CD проведена прямая KL. Диагональ квадрата равна 18 см. Найти длину отрезка KL.
Устная работа
В треугольнике АВС проведена прямая FD параллельно ВС. Определите, какую часть площади ΔАВС составляет площадь ΔAFD, если AF : АВ = 1 : 4.
Устная работа
Гипотенуза FD ΔFCD равна 13 см, а гипотенуза BF ΔFAB равна 39 см. Найти периметр Δ FAB, если периметр ΔFCD равен 30 см.
Повторительно-обобщающий урок по теме
Подобие
треугольников
Возникнет ли необходимость применять признаки подобия треугольников в жизни?
Работа в тетрадях
Задача №1.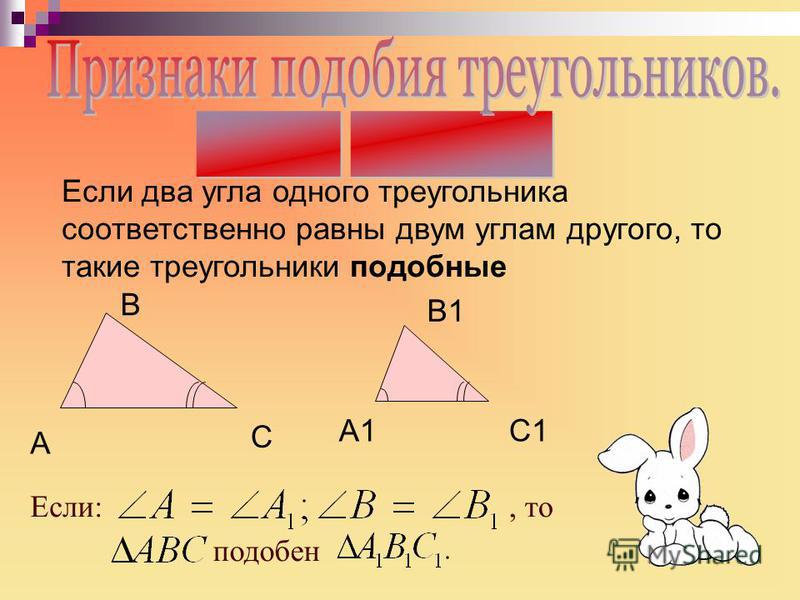 Длина тени дерева 21м. В это же время суток тень человека ростом 1,8 м составляет 2,7 м. Какова высота дерева?
Длина тени дерева 21м. В это же время суток тень человека ростом 1,8 м составляет 2,7 м. Какова высота дерева?
Спасибо за урок!
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
Подобие треугольников. Применение подобия к решению задач | План-конспект урока по геометрии (8 класс):
Геометрия 8 класс.
План — конспект урока по теме:
«Подобие треугольников и применение подобия к решению задач»
Цели урока:
Образовательная – совершенствование навыков решения прикладных задач на применение признаков подобия треугольников.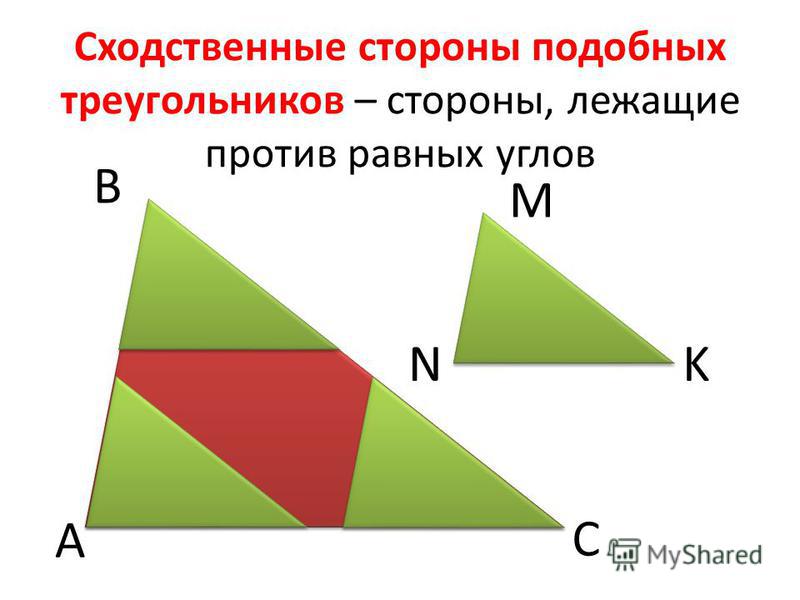
Развивающая – обобщение и систематизация знаний по теме «Подобные треугольники и признаки подобия»; овладение общеучебными приемами решения прикладных задач.
Воспитательная – приобщение детей к выбору профессии, к ценностям постижения геометрических знаний.
Ход урока.
I. Организационный момент
Сообщить тему урока, сформулировать цели урока.
II Актуализация знаний учащихся
а) Фронтальный опрос
— Дайте определение подобных треугольников,
— Сформулируйте признаки подобных треугольников
б) Решаем задачи по готовым чертежам № 1 AB || CD AO = 1,5 см OB = 1 см СО = 3 см СD = 4,5 см 1) Подобны ли треугольники AOB и DOC? 2) Укажите сходственные стороны, К 3) АВ — ? OD — ? | в) Найти А1В1-? |
— Давайте вспомним, какие существую признаки подобия треугольников?
— Назовите: первый признак подобия; второй признай и третий.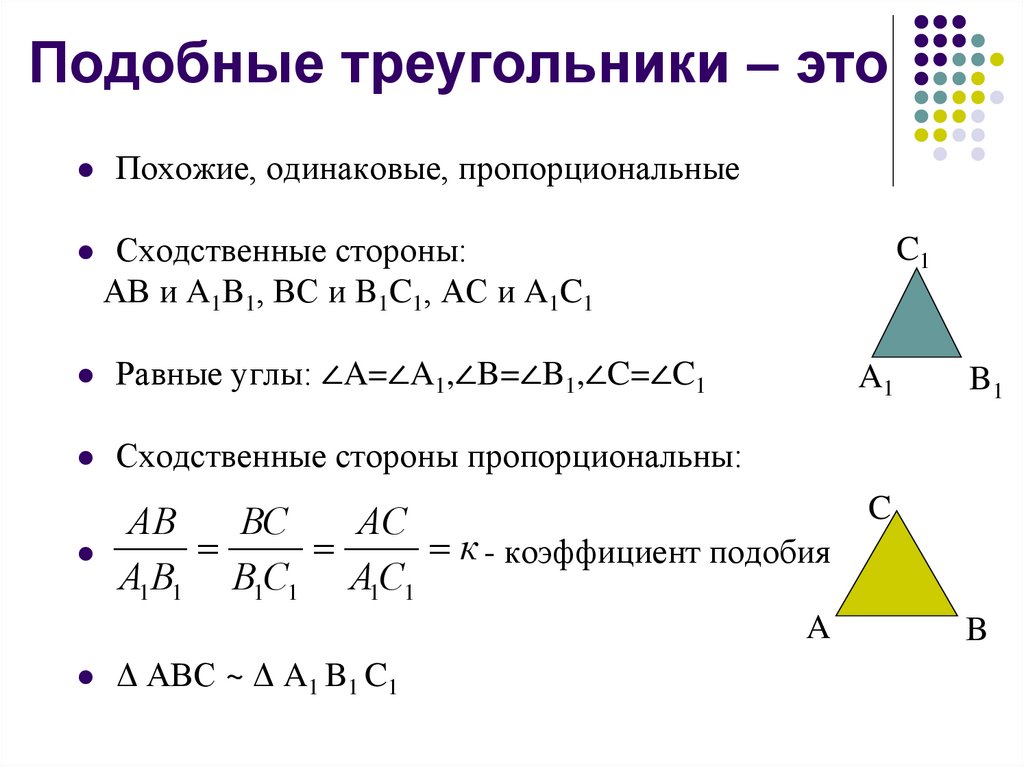
Сейчас мы будем решать задачи и обязательно указывать, какие признаки подобия треугольников мы применяем.
Решим задачи:
1. Стороны треугольника 3 см, 6 см, 7 см. Большая сторона подобного ему треугольника равна 28 см. Чему равна меньшая сторона этого треугольника? 12 см
Как решали? Что использовали для решения?
2. Два угла одного треугольника 1240 и 360, а два угла другого треугольника 200 и 360. Подобны ли треугольники? нет
3. Решает ученик у доски.
треугольник ABC подобен треугольнику MNK
Решение:
, значит ,
тогда . значит =?
Аналогично , значит =?
4. Решают самостоятельно по плану.
Стороны треугольника 15 см , 35 см, 30 см. Большая сторона подобного ему треугольника 7 см. Чему равна меньшая сторона этого треугольника?
- Построй два треугольника MNP и M1N1P1. M = M1, N = N1, P = P1
- Составь отношения сходственных сторон (сходственные стороны лежат против равных углов)
- Найди коэффициент подобия k
- Ответь на вопрос задачи
Тест на установление истинности или ложности высказываний (отвечать “да” или “нет”).
- Два треугольника подобны, если их углы соответственно равны и сходственные стороны пропорциональны.
- Два равносторонних треугольника всегда подобны.
- Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
- Стороны одного треугольника имеют длины 3, 4, 6 см, стороны другого треугольника равны 9, 14, 18 см. Подобны ли эти треугольники?
- Периметры подобных треугольников относятся как квадраты сходственных сторон.
- Если два угла одного треугольника равны 60 и 50 градусов, а два угла другого треугольника равны 50 и 80 градусов, то такие треугольники подобны.
- Два прямоугольных треугольника подобны, если имеют по равному острому углу.
- Два равнобедренных треугольника подобны, если их боковые стороны пропорциональны.
- Если отрезки гипотенузы, на которые она делится высотой, проведенной из вершины прямого угла, равны 2 и 8 см, то эта высота равна 4 см.

- Если медиана треугольника равна 9 см, то расстояние от вершины треугольника до точки пересечения медиан равно 6 см.
Ключ к тесту: 1. да; 2. да; 3. да; 4. нет; 5. нет; 6. нет; 7. да; 8. нет; 9. да; 10. да.
Форма проверки теста – самопроверка).
Продолжим решение задач.
- Треугольники ABC и MNK подобны. Их сходственные стороны относятся как 8:5. Площадь треугольника ABC больше площади треугольника MNK на 25 кв.см. Найдите площади треугольников. (Ответ: 16 1/39 и 41 1/39 см 2).
В прямоугольном треугольнике ABC к гипотенузе AC проведена высота BD, BC=2см, AD=3см. Найдите DC, BD, AB. (Ответ: DC = 1см, BD = √3 см, AB = 2√3 см).
Основания трапеции равны 8 и 12 см. Боковые стороны, равные 4,5 см и 5,2 см, продолжены до пересечения в точке M. Найдите расстояния от точки M до концов меньшего основания. (Ответ: 9 и 10,4 см).
В прямоугольном треугольнике с углом 30° и меньшим катетом 6 см проведены средние линии. Найдите периметр треугольника, образованного средними линиями. (Ответ: 9 + 3√3 (см)).
Найдите периметр треугольника, образованного средними линиями. (Ответ: 9 + 3√3 (см)).
Итог урока:
Итак, давайте подведем итог нашего урока. Мы вспомнили определение и признаки подобия треугольников, а также порешали задачи различного типа на применение подобия треугольников.
Как вы думаете, достигли ли мы с вами целей нашего урока?
Представляют ли теперь для вас трудность задачи на подобие треугольников?
Домашнее задание:
Повторительно-обобщающий урок математики по теме «Подобие треугольников». 8-й класс
- Образовательные:
- обобщить и систематизировать знания учащихся по теме «Подобные треугольники. Признаки подобия треугольников»;
- устранить пробелы в знаниях учащихся по теме;
- совершенствовать навыки решения задач на применение признаков подобия треугольников;
- способствовать формированию навыков
применения теоретических знаний в повседневной
жизни, решение практических задач.

- Воспитательные:
- воспитание общечеловеческих ценностей таких, как трудолюбие, уважительное отношение к старшим и друг к другу, взаимопомощи;
- расширение кругозора.
- Развивающие:
- развитие памяти, внимания, логики и математического мышления, умения правильно и последовательно рассуждать.
Оборудование: компьютер, мультимедиапроектор, презентация.
ХОД УРОКА
1. Организационный момент. (Слайд 1)
— Добрый день, ребята! Сегодня на уроке мы
повторим теоретический материал по теме
«Подобие треугольников». Если у кого-то остались
вопросы по этой теме, поможем устранить пробелы в
знаниях. Выясним, возникнет ли необходимость
применять признаки подобия треугольников в
жизни? Откройте, пожалуйста, тетради и запишите
число.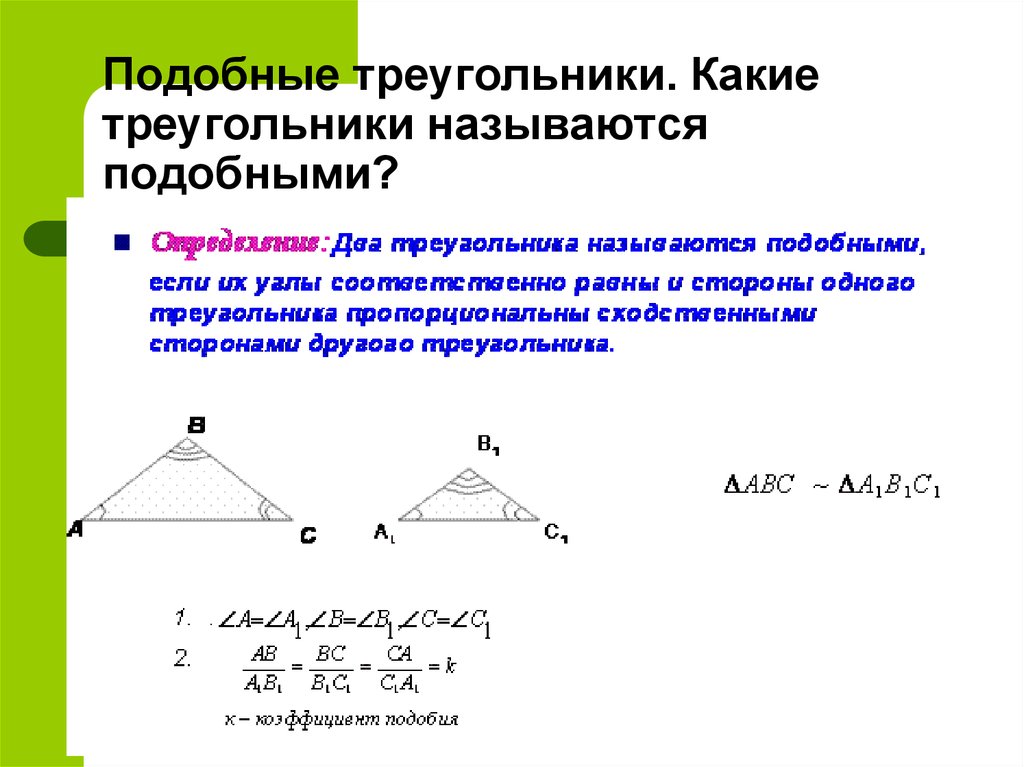 Итак, начинаем урок!
Итак, начинаем урок!
2. Актуализация знаний учащихся
а) Фронтальный опрос
Слайд 2.
- Назовите соответственные углы треугольников.
- Назовите сходственные стороны треугольников.
- Дайте определение подобных треугольников.
Слайд 3.
Сформулируйте признаки подобия треугольников.
Слайд 4.
Какие из следующих утверждений верны?
1. Любые два равносторонних треугольника
подобны.
2. Если два угла одного треугольника
соответственно пропорциональны двум углам
другого треугольника, то такие треугольники
подобны.
3. Если два треугольника подобны, то их
сходственные стороны пропорциональны.
Ответ: 1 и 3.
Слайд 5.
Какие из следующих утверждений НЕ верны?
1. Если сторона и два прилежащих к ней угла
одного треугольника соответственно равны
стороне и двум прилежащим к ней углам другого
треугольника, то такие треугольники подобны.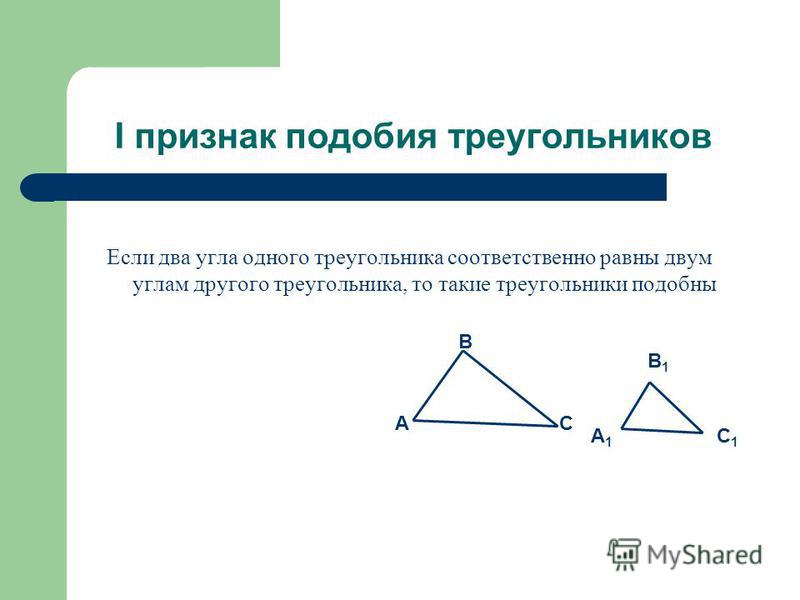
2. Любые два прямоугольных треугольника подобны.
3. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Ответ: 1 и 2.
Слайд 6.
Какие из следующих утверждений НЕ верны?
1. Если две стороны одного треугольника
пропорциональны сходственным сторонам другого
треугольника, и углы, заключенные между этими
сторонами равны, то такие треугольники подобны.
2. Любые два равнобедренных треугольника подобны.
3. Если угол одного треугольника равен углу
другого треугольника, то такие треугольники
подобны.
Ответ: 2 и 3.
Слайд 7.
Сформулируйте свойство биссектрисы треугольника.
m : a = n : b
б) Устная работа. Решение задач по готовым чертежам.
Слайд 8.
Докажите, что треугольники подобны.
Слайд 9.
В квадрате ABCD через середины соседних сторон ВС
и CD проведена прямая KL.
Ответ: 9 см.
Слайд 10.
В треугольнике АВС проведена прямая FD параллельно ВС. Определите, какую часть площади ΔАВС составляет площадь ΔAFD, если AF : АВ = 1 : 4.
Ответ: .
Слайд 11.
Гипотенуза FD ΔFCD равна 13 см, а гипотенуза BF ΔFAB равна 39 см. Найти периметр ΔFAB, если периметр ΔFCD равен 30 см.
Ответ: 90 см.
Слайд 12.
В ΔАВС проведена биссектриса угла BD. Точка D делит сторону АС на отрезки AD и DC, соответственно равные 6 см и 10 см. Найти сторону ВС, если сторона АВ равна 9 см.
Ответ: 15см.
Слайд 13.
Найти AD.
Ответ: 11.
Слайд 14.
Найти KL.
Ответ: 5.
3. Работа в тетрадях (Слайд 15)
Задача №1. Биссектриса прямого угла
прямоугольного треугольника делит гипотенузу на
отрезки длиной 20 см и 15 см.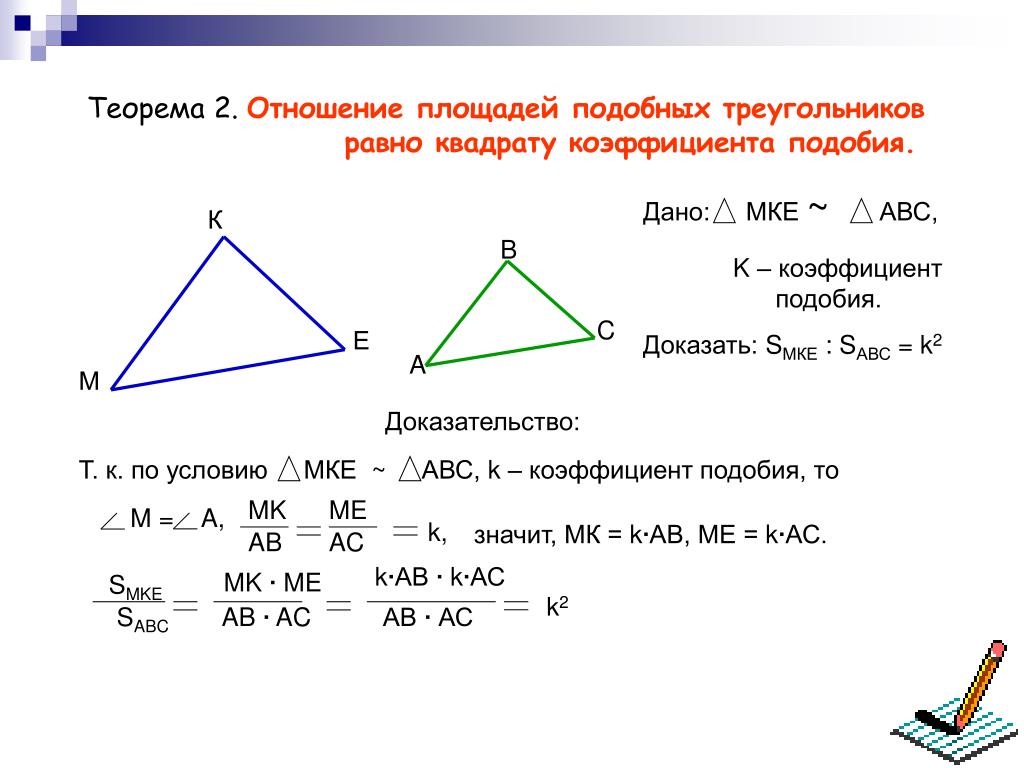 Найти площадь
треугольника, образованного биссектрисой и
высотой, выходящими из вершины прямого угла
данного треугольника.
Найти площадь
треугольника, образованного биссектрисой и
высотой, выходящими из вершины прямого угла
данного треугольника.
Решение.
1) Используя свойство биссектрисы треугольника,
найдем отношение катетов данного прямоугольного
треугольника: ВС = АС. С помощью теоремы Пифагора вычисляем
длины катетов: АС = 28 см, ВС = 21 см.
2) Используем свойство высоты прямоугольного
треугольника: ΔСНВ ~ΔАСВ. Запишем отношение
сходственных сторон: . подставим известные величины: . Откуда, СН =16,8 см, НВ = 12,6
см. Следовательно, в ΔСНМ нам известны два катета:
СН = 16,8 см и НМ = 2,4см.
3) Найдем площадь ΔСНМ: S = СН·НМ = 20,16 см
Ответ: 20,16 см2.
4. Творческое домашнее задание
Просмотр работ учащихся «Подобие вокруг нас».
(Слайды 16-18). В повседневной жизни нас окружают
предметы, подобные друг другу: часы, картины и т.д.
В живой природе также можно встретиться с
подобием.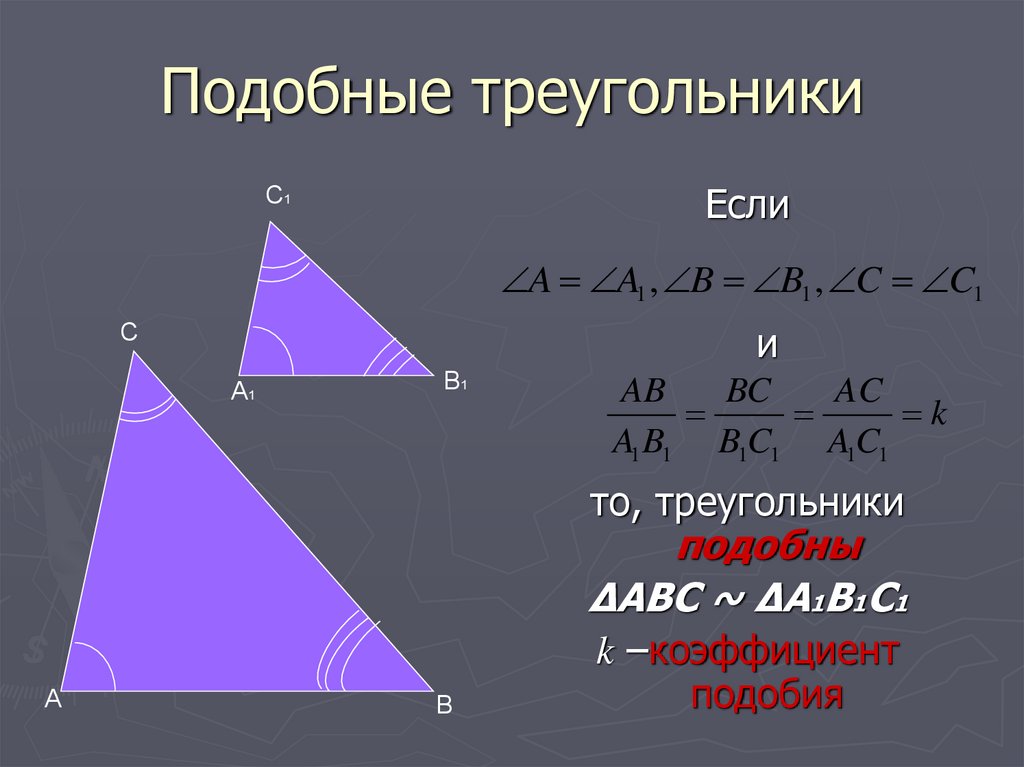 Давайте попробуем ответить на вопрос
(Слайд 19) «Возникнет ли необходимость применять
признаки подобия треугольников в жизни?».
Продолжаем работать в тетрадях. Решим следующие
задачи.
Давайте попробуем ответить на вопрос
(Слайд 19) «Возникнет ли необходимость применять
признаки подобия треугольников в жизни?».
Продолжаем работать в тетрадях. Решим следующие
задачи.
Слайд 20.
Задача №2. Длина тени дерева 21м. В это же время суток тень человека ростом 1,8 м составляет 2,7 м. Какова высота дерева? Ответ: 14 м.
Слайд 21.
Задача №3. Человек ростом 1,6 м стоит на расстоянии 6 шагов от столба, на котором висит фонарь на высоте 3,2 м. Найдите длину тени человека.
Ответ: 6 шагов.
Слайд 22.
Решение задач из учебника. № 579, № 581, № 582.
5. Домашнее задание. (Слайд 23)
1 вариант. Доказать, что периметр
треугольника, образованного средними линиями
данного треугольника, вдвое меньше периметра
данного треугольника.
2 вариант. Доказать, что площадь
треугольника, образованного средними линиями
данного треугольника, вчетверо меньше площади
данного треугольника.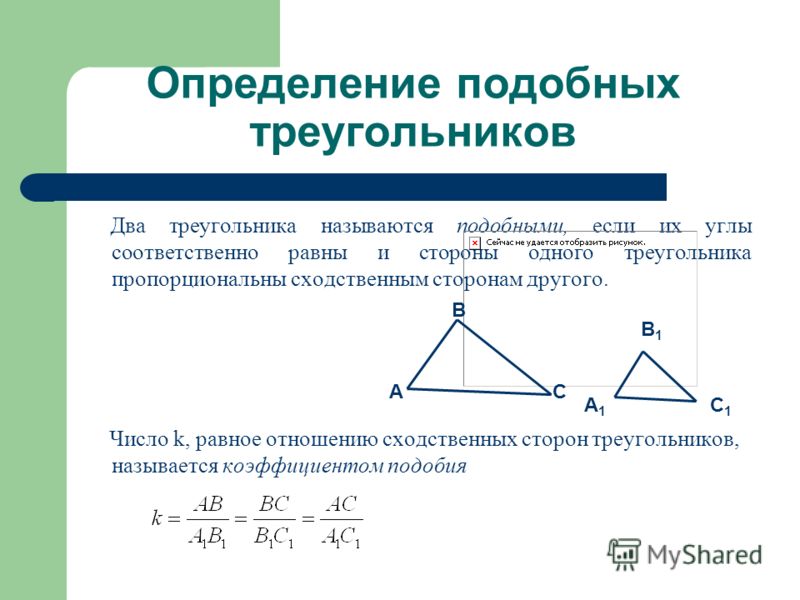
6. Рефлексия
Наш урок подошел к концу. Ребята, сегодня мы с вами повторили все, что изучали по теме «Подобие треугольников». Оцените, пожалуйста, свои знания по этой теме. Заполните, пожалуйста, следующую табличку.
| Усвоил материал, умею применять при решении задач | Усвоил материал, но не умею применять при решении задач | Усвоил материал частично, есть вопросы по данной теме | Не усвоил материал | |
| Определение подобных треугольников. Нахождение соответственных углов, сходственных сторон. Нахождение коэффициента подобия треугольников. | ||||
Формулы периметра и площади подобных
треугольников. |
||||
| Свойство биссектрисы треугольника. | ||||
| Признаки подобия треугольников. | ||||
| Применение признаков подобия при решение практических задач. |
Слайд 24. Спасибо за урок!
Теоремы для доказательства подобия треугольников — Криста Кинг Математика
Подобные фигуры имеют одинаковую форму, но могут быть разных размеров
В этом уроке мы рассмотрим, как доказать, что треугольники подобны друг другу.
В математике слово «подобие» имеет очень конкретное значение.
Вне математики, когда мы говорим, что две вещи похожи, мы просто имеем в виду, что они в целом похожи друг на друга.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Но в математике сказать, что две фигуры похожи, означает, что они имеют одинаковую форму, но разные размеры. Вот примеры подобных квадратов, подобных пятиугольников и подобных треугольников:
Подобные треугольники
Подобные треугольники имеют одинаковую форму, но разные размеры. Помните, что если два треугольника имеют одинаковую форму и одинаковый размер, то они идентичны, и мы говорим, что они «конгруэнтны».
В паре из подобных треугольников все три соответствующие пары углов конгруэнтны, а соответствующие пары сторон пропорциональны. \circ???.
\circ???.
Сторона Сторона Сторона (SSS)
Если пара треугольников имеет три пропорциональные соответствующие стороны, то мы можем доказать, что треугольники подобны. Причина в том, что если все соответствующие длины сторон пропорциональны, то это заставит соответствующие меры внутренних углов быть конгруэнтными, что означает, что треугольники будут подобны.
???\frac{a}{d}=\frac{b}{e}=\frac{c}{f}???
Side Angle Side (SAS)
Если пара треугольников имеет одну пару соответствующих конгруэнтных углов, зажатую между двумя парами пропорциональных сторон, то мы можем доказать, что треугольники подобны.
???\frac{a}{d}=\frac{b}{e}???
Теоремы для доказательства подобия двух треугольников
Пройти курс
Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого.
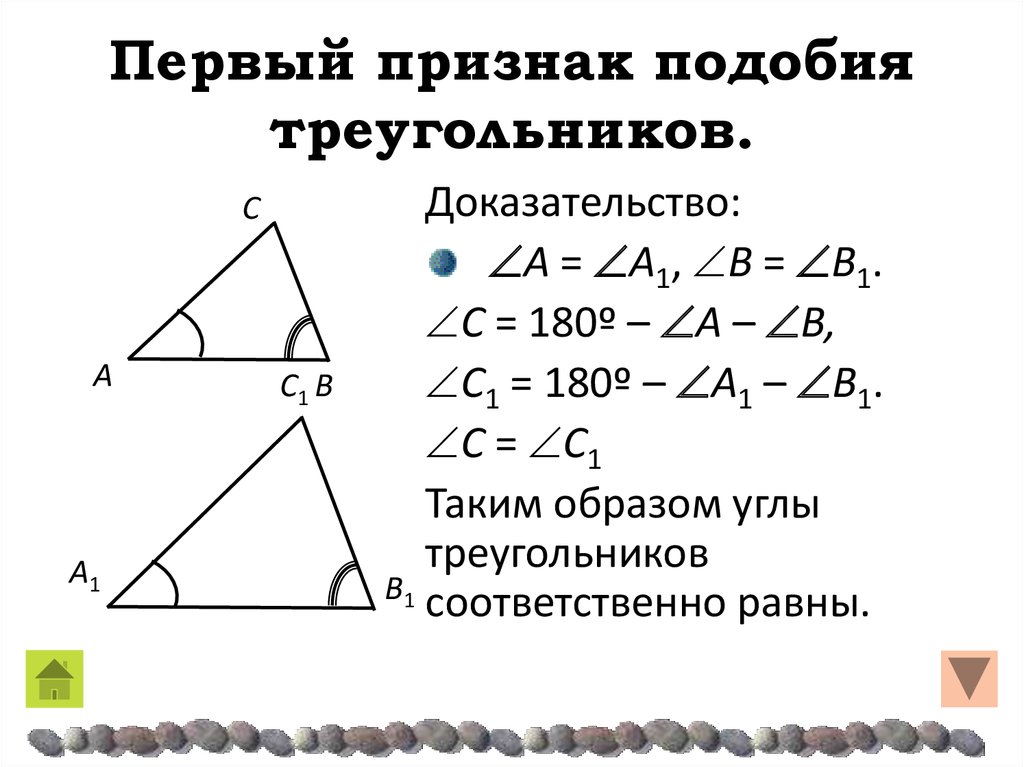 \circ???. Итак, у нас есть пара конгруэнтных углов, и нам нужно посмотреть, есть ли у нас пропорциональные длины сторон.
\circ???. Итак, у нас есть пара конгруэнтных углов, и нам нужно посмотреть, есть ли у нас пропорциональные длины сторон.???\frac{\overline{ZY}}{\overline{AC}}=\frac{18}{3}=6???
???\frac{\overline{ZX}}{\overline{AB}}=\frac{54}{9}=6???
У нас такое же соотношение между соответствующими длинами сторон.
Собрав все это вместе, мы можем сказать, что треугольники подобны по стороне, углу, стороне (SAS). Когда мы сопоставляем соответствующие части, выражение подобия будет ???\треугольник ABC\sim \треугольник ZXY???.
В паре подобных треугольников 9\ круг???. У нас также есть пара вертикальных углов ???Y???, и помните, что вертикальные углы конгруэнтны друг другу.
Сложив все это вместе, мы можем сказать, что треугольники подобны по углу угла (АА). Когда мы сопоставляем соответствующие части, выражение подобия будет ???\треугольник WXY\sim \треугольник VZY???.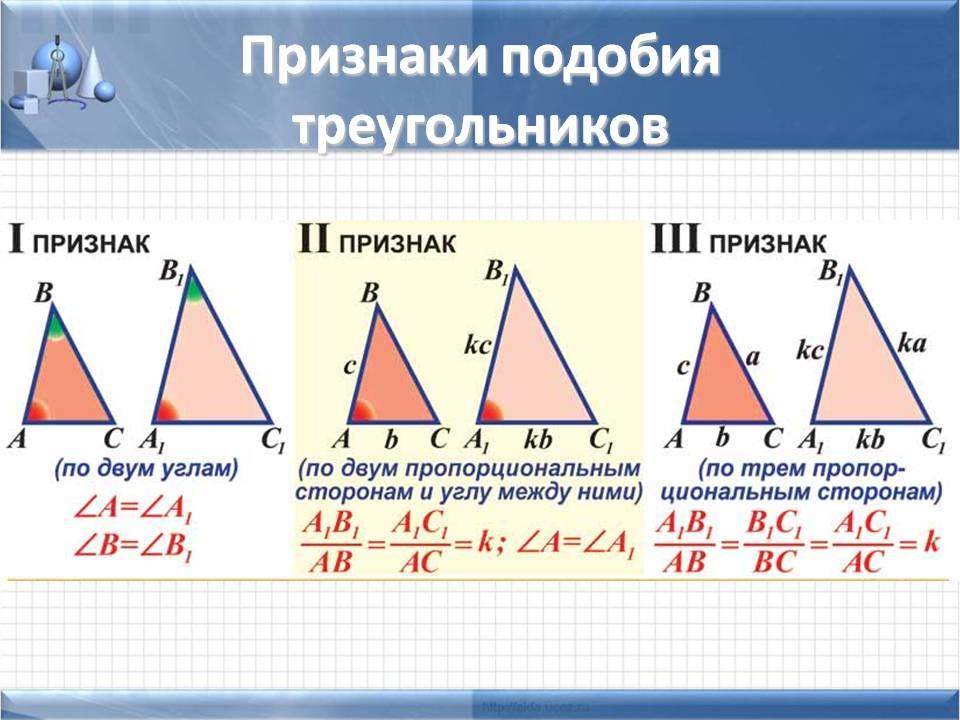
Получить доступ к полному курсу геометрии
Начать
Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, геометрия, сходство, подобные треугольники, теоремы подобия, утверждения о сходстве треугольников, теоремы о сходстве треугольников, AA, SAS, SSS, SSA, пропорциональные стороны, пропорциональные длины сторон, конгруэнтные углы, теорема AA, теорема SSS, теорема SAS
0 лайков7.8: Сходство SSS — K12 LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5303
Треугольники подобны, если их соответствующие стороны пропорциональны.
SSS Теорема подобия
По определению, два треугольника подобны, если все их соответствующие углы конгруэнтны и их соответствующие стороны пропорциональны. Нет необходимости проверять все углы и стороны, чтобы определить, подобны ли два треугольника. На самом деле, если вы знаете только то, что все стороны пропорциональны, этой информации достаточно, чтобы понять, что треугольники подобны. Это называется Теорема подобия SSS .
SSS Теорема подобия: Если все три пары соответствующих сторон двух треугольников пропорциональны, то эти два треугольника подобны.
Рисунок \(\PageIndex{1}\)Если \(\dfrac{AB}{YZ}=\dfrac{BC}{ZX}=\frac{AC}{XY}\), то \(\Delta ABC \сим \Дельта YZX\).
Что, если бы вам дали пару треугольников и длины всех трех сторон? Как вы могли бы использовать эту информацию, чтобы определить, подобны ли два треугольника?
Для примеров 1 и 2 используйте следующую схему:
Рисунок \(\PageIndex{2}\)Пример \(\PageIndex{1}\)
Is \(\Delta DEF\sim \Delta GHI \)?
\(\dfrac{15}{30}=\dfrac{16}{33}=\dfrac{18}{36}\)?
Решение
\(\dfrac{15}{30}=\dfrac{1}{2}\), \(\dfrac{16}{33}=\dfrac{16}{33}\) и \(\dfrac{18}{36}=\dfrac{1}{2}\).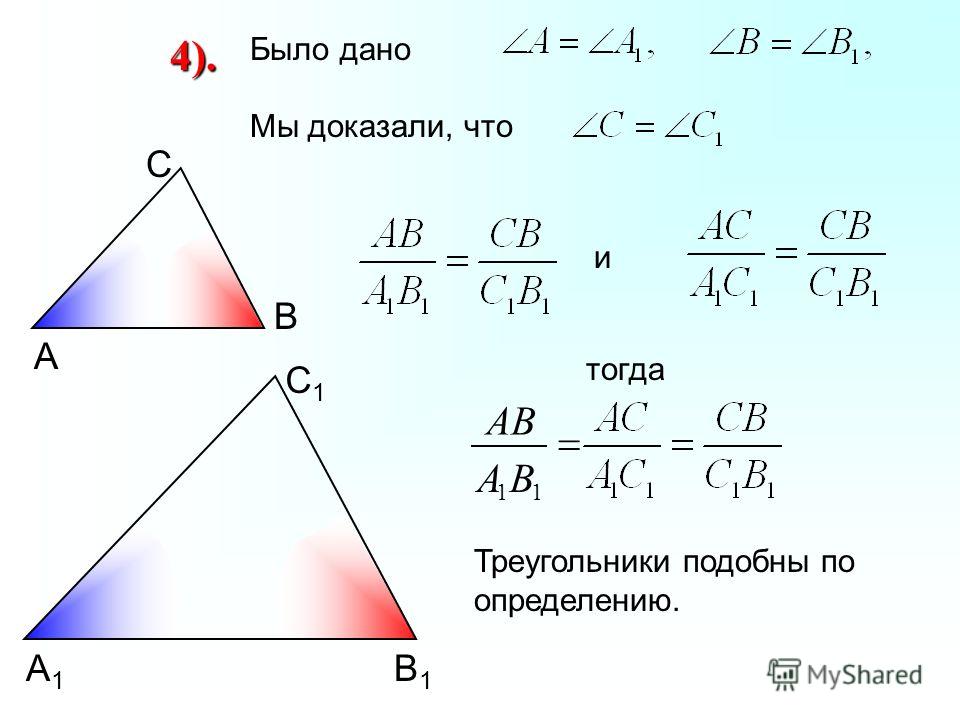 \(\dfrac{1}{2}\neq \dfrac{16}{33}\), \(\Delta DEF\) равно , а не , как \(\Delta GHI\).
\(\dfrac{1}{2}\neq \dfrac{16}{33}\), \(\Delta DEF\) равно , а не , как \(\Delta GHI\).
Пример \(\PageIndex{2}\)
Является ли \(\Delta ABC\sim \Delta GHI\)?
\(\dfrac{20}{30}=\dfrac{22}{33}=\dfrac{24}{36}\)?
Решение
\(\dfrac{20}{30}=dfrac{2}{3}\), \(\dfrac{22}{33}=\dfrac{2}{3}\), и \(\dfrac{24}{36}=\dfrac{2}{3}\). Все три коэффициента сводятся к \(\dfrac{2}{3}\), \(\Delta ABC\sim \Delta GHI\).
Пример \(\PageIndex{3}\)
Определите, подобны ли следующие треугольники. Если да, объясните почему и напишите утверждение о сходстве.
Рисунок \(\PageIndex{3}\)Решение
Нам нужно найти отношения соответствующих сторон треугольников и посмотреть, все ли они одинаковы. Начните с самых длинных сторон и двигайтесь вниз к самым коротким сторонам.
\(\begin{align} \dfrac{BC}{FD}&=\dfrac{28}{20}=\dfrac{7}{5} \\ \dfrac{BA}{FE}&=\dfrac {21}{15}=\dfrac{7}{5} \\ \dfrac{AC}{ED}&=\dfrac{14}{10}=\dfrac{7}{5}\end{aligned}\ )
Поскольку все отношения одинаковы, \(\Delta ABC\sim \Delta EFD\) по теореме подобия SSS.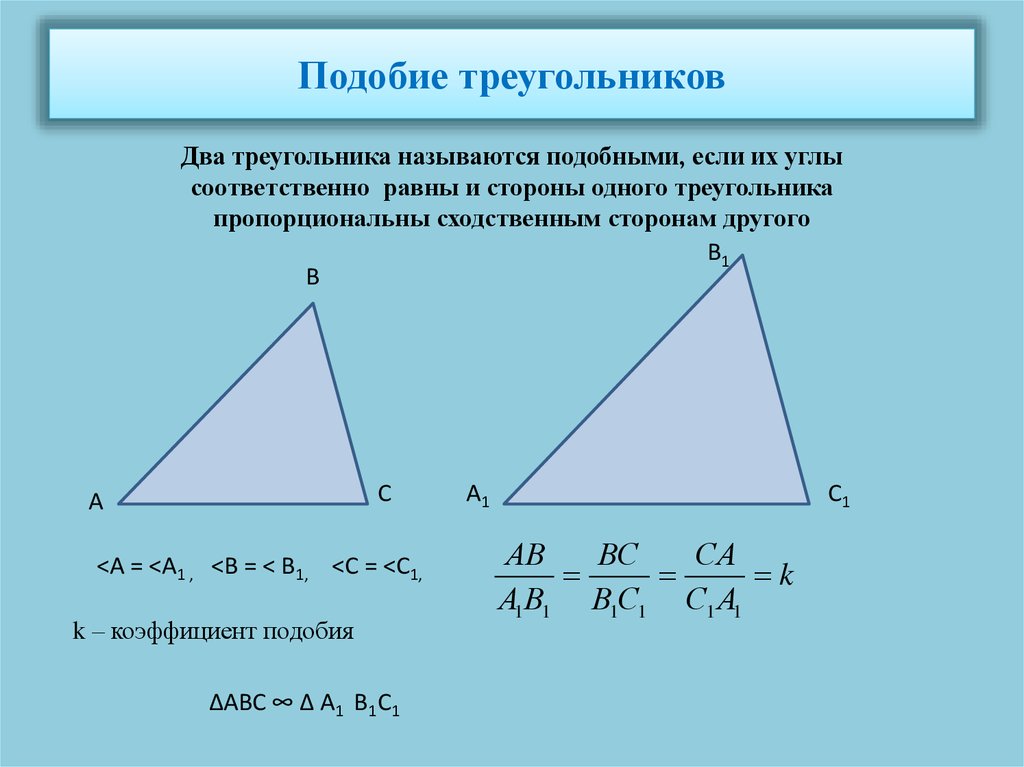
Пример \(\PageIndex{4}\)
Найти \(x и \(y, такие, что \(\Delta ABC\sim \Delta DEF\).
Рисунок \(\PageIndex{4}\)Решение
Согласно утверждению о подобии соответствующие стороны равны: \(\dfrac{AB}{DE}=\dfrac{BC}{EF}=\dfrac{AC}{DF}\). мы знаем, у нас есть \(\dfrac{9}{6}=\dfrac{4x−1}{10}=\dfrac{18}{y}\).
\(\begin{aligned}
\frac {9}{6} &=\frac{4 x-1}{10} & \frac{9}{6} &=\frac{18}{y} \\
9(10) &=6(4 x-1) & & 9 y=18(6) \\
90 &=24 x-6 & & 9 y=108 \\
96 &=24 x & & y =12 \\
x &=4 &
\end{aligned}\)
Пример \(\PageIndex{5}\)
Определите, подобны ли следующие треугольники. Если да, объясните почему и напишите утверждение о сходстве.
Рисунок \(\PageIndex{5}\)Решение
Нам нужно найти отношения соответствующих сторон треугольников и посмотреть, все ли они одинаковы. Начните с самых длинных сторон и двигайтесь вниз к самым коротким сторонам.
\(\begin{align} \dfrac{AC}{ED}&=\dfrac{21}{35}=\dfrac{3}{5} \\ \dfrac{BC}{FD}&=\dfrac {15}{25}=\dfrac{3}{5} \\ \dfrac{AB}{EF}&=\dfrac{10}{20}=\dfrac{1}{2} \end{aligned}\ )
Поскольку отношения не все одинаковы, треугольники не подобны.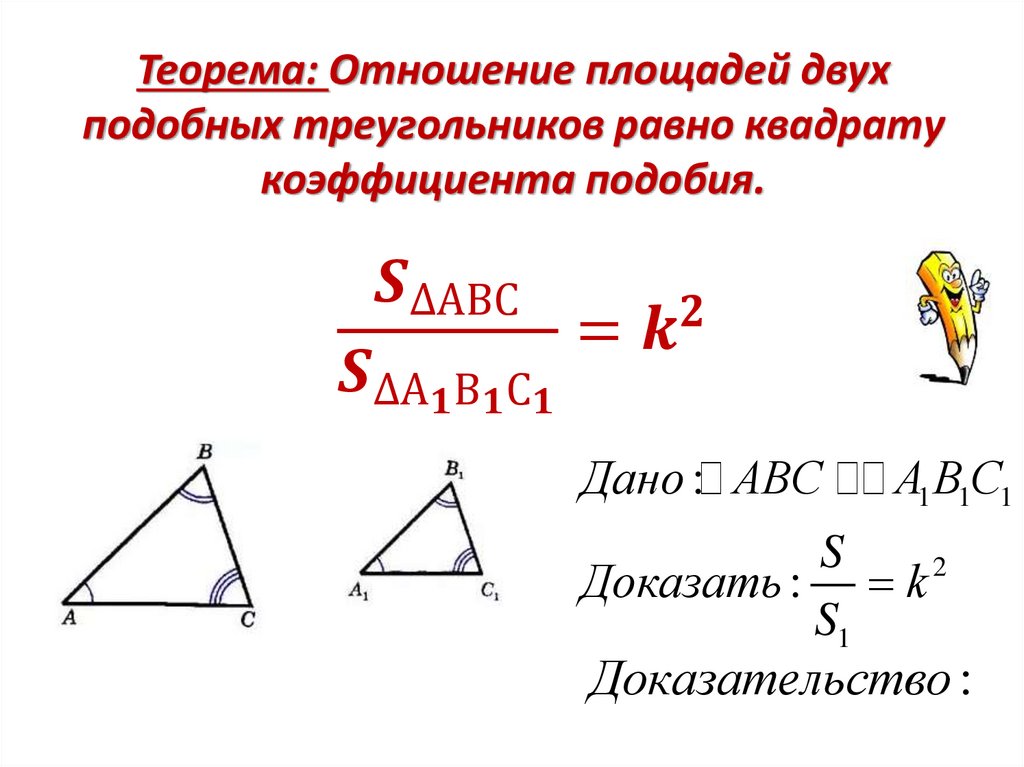
Обзор
Заполните пропуски.
- Если все три стороны одного треугольника __________________ трем сторонам другого, то эти треугольники подобны.
- Два треугольника подобны, если соответствующие стороны _____________.
Используйте следующую диаграмму для ответов на вопросы 3–5. Схема выполнена в масштабе.
Рисунок \(\PageIndex{6}\)- Два треугольника похожи? Поясните свой ответ.
- Два треугольника равны? Поясните свой ответ.
- Каков масштабный коэффициент для двух треугольников?
Заполните пропуски в утверждениях ниже. Используйте схему слева.
Рисунок \(\PageIndex{7}\)- \(\Delta ABC\sim \Delta _____\)
- \(\dfrac{AB}{?}=\dfrac{BC}{?}=\dfrac{AC}{?}\)
- Если бы \(\Delta ABC\) имела высоту, \(AG=10\), какой длины была бы высота \(\overline{DH}\)?
- Найдите периметр \(\Delta ABC\) и \(\Delta DEF\).
 Найдите отношение периметров.
Найдите отношение периметров.
Используйте диаграмму справа для вопросов 10-15.
Рисунок \(\PageIndex{8}\)- \(\Delta ABC\sim \Delta _____\)
- Почему два треугольника подобны?
- Найти \(ЭД\).
- \(\dfrac{BD}{?}=\dfrac{?}{BC}=\dfrac{DE}{?}\)
- Верно ли \(\dfrac{AD}{DB}=\dfrac{CE}{EB}\)?
- Верно ли \(\dfrac{AD}{DB}=\dfrac{AC}{DE}\)?
Найдите значение отсутствующей переменной (переменных), которое делает два треугольника похожими.
- Рисунок \(\PageIndex{9}\)
Обзор (ответы)
Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 7.6.
Ресурсы
Словарь
| Срок | Определение |
|---|---|
| Теорема подобия ААА | Теорема подобия AAA утверждает, что если все три пары соответствующих сторон двух треугольников пропорциональны, то эти два треугольника подобны.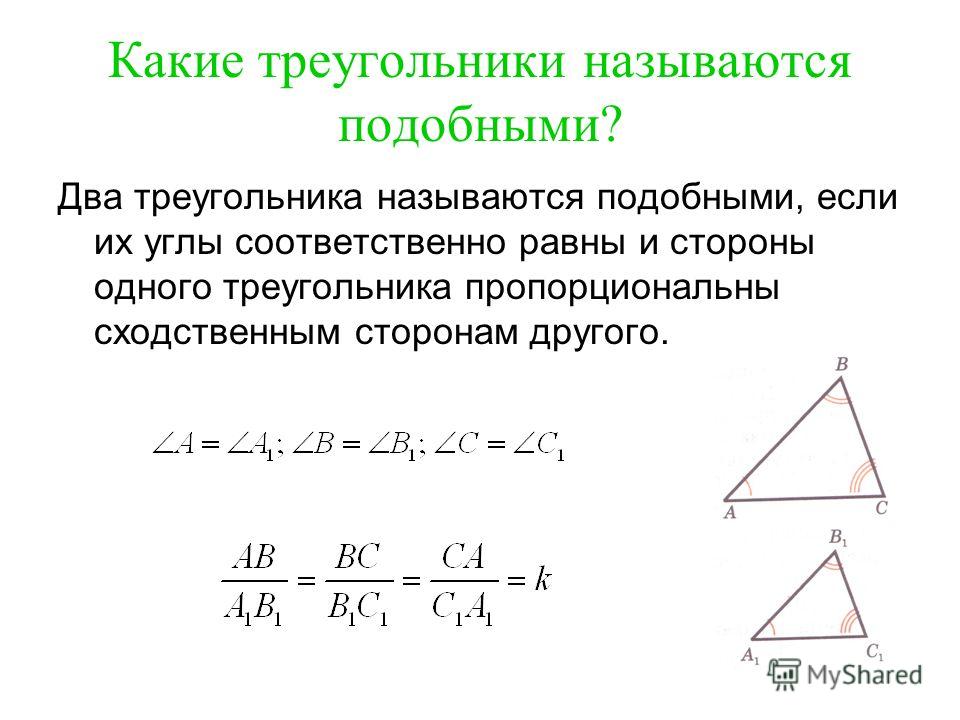 |
| Конгруэнтность | Конгруэнтные фигуры одинаковы по размеру, форме и размеру. |
| Расширение | Уменьшение или увеличение фигуры в соответствии с коэффициентом масштабирования является расширением. |
| Соотношение | Отношение — это сравнение двух величин, которое может быть записано в виде дроби, с двоеточием или со словом «к». |
| ССС | SSS означает сторона, сторона, сторона и относится к тому факту, что в задаче известны все три стороны треугольника. |
| Жесткая трансформация | Жесткое преобразование — это преобразование, сохраняющее расстояние и углы, оно не изменяет размер или форму фигуры.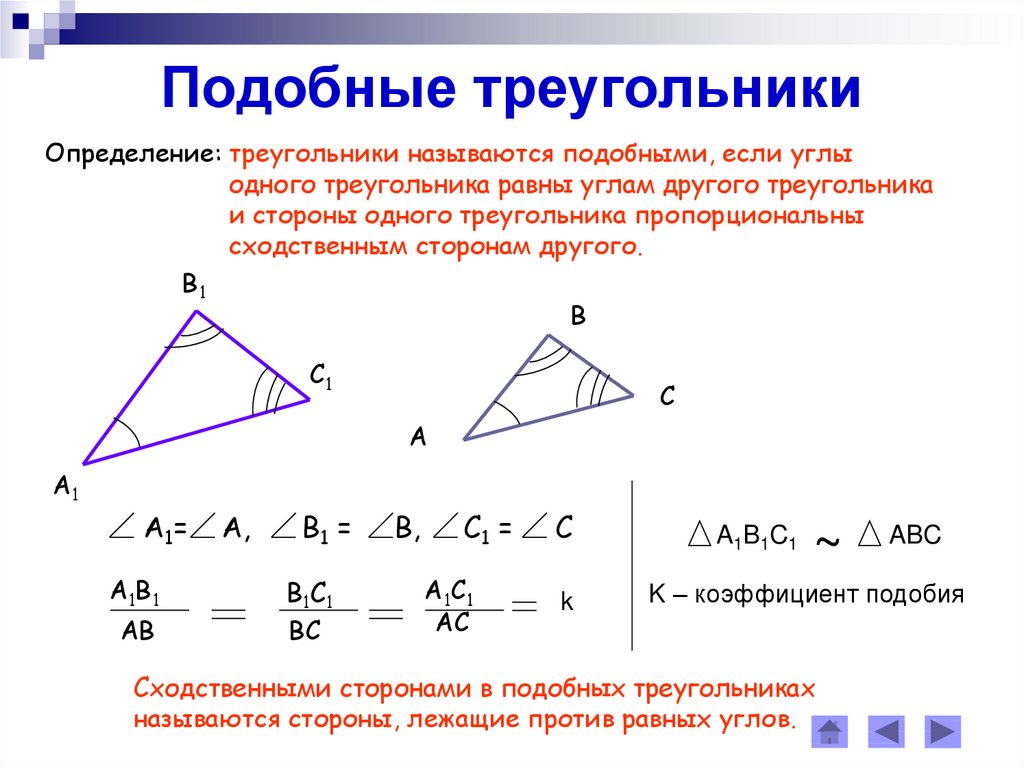 |
Дополнительные ресурсы
Интерактивный элемент
Видео: Конгруэнтные и подобные треугольники
Упражнения: SSS Вопросы для обсуждения подобия
Учебные пособия: Учебное пособие по сходству полигонов
Практика: Сходство SSS
Реальный мир: Crazy Quilt
Эта страница под названием 7.8: Сходство SSS распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
ПОД ЛИЦЕНЗИЕЙ
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- СК12
- Лицензия
- СК-12
- Программа ООР или издатель
- СК-12
- Показать оглавление
- нет
- Теги
- источник@https://www.
 ck12.org/c/geometry
ck12.org/c/geometry
- источник@https://www.
Похожие фигурки
| ||||||||||||
| Домашняя страница | Заказать программное обеспечение по математике | О сериале | Учебники по математическому программному обеспечению |
| Программное обеспечение по математике для 7 класса | Программное обеспечение по математике для 8 класса | Программное обеспечение по математике для 9 классов | Программное обеспечение по математике для 10 класса |
| Программное обеспечение для домашних заданий | Программное обеспечение для репетиторов | Математическая программная платформа | Пробное математическое программное обеспечение |
| Обратная связь | О mathsteacher.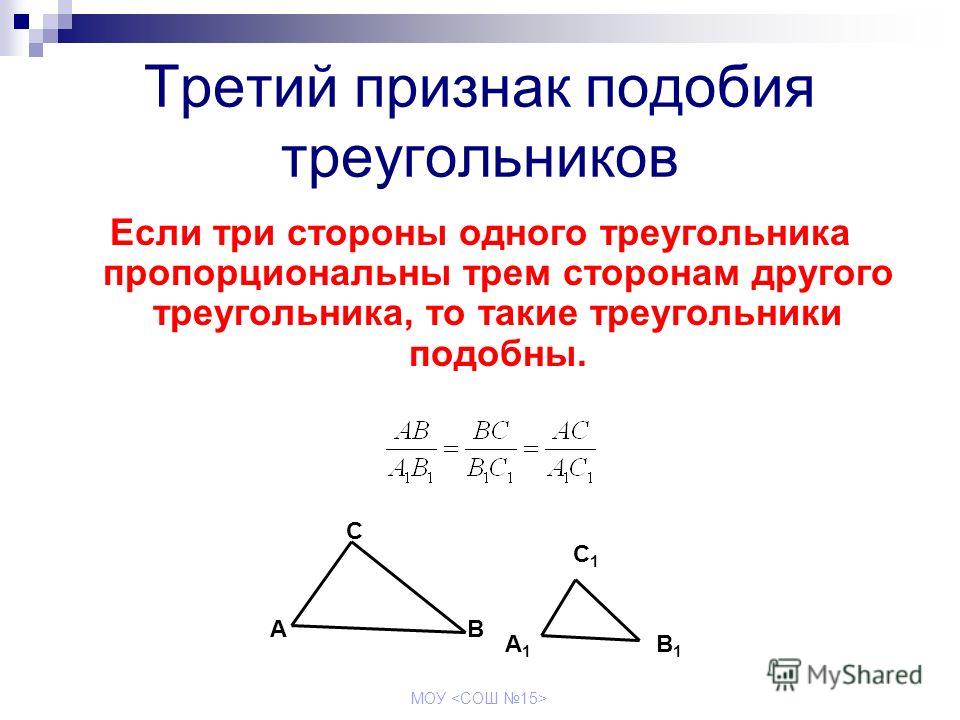

 Найдите периметр треугольника, образованного средними линиями. (Ответ: 9 + 3√3 (см)).
Найдите периметр треугольника, образованного средними линиями. (Ответ: 9 + 3√3 (см)).
 Найдите отношение периметров.
Найдите отношение периметров. ck12.org/c/geometry
ck12.org/c/geometry пропорциональны и соответствующие им углы равны.
пропорциональны и соответствующие им углы равны.