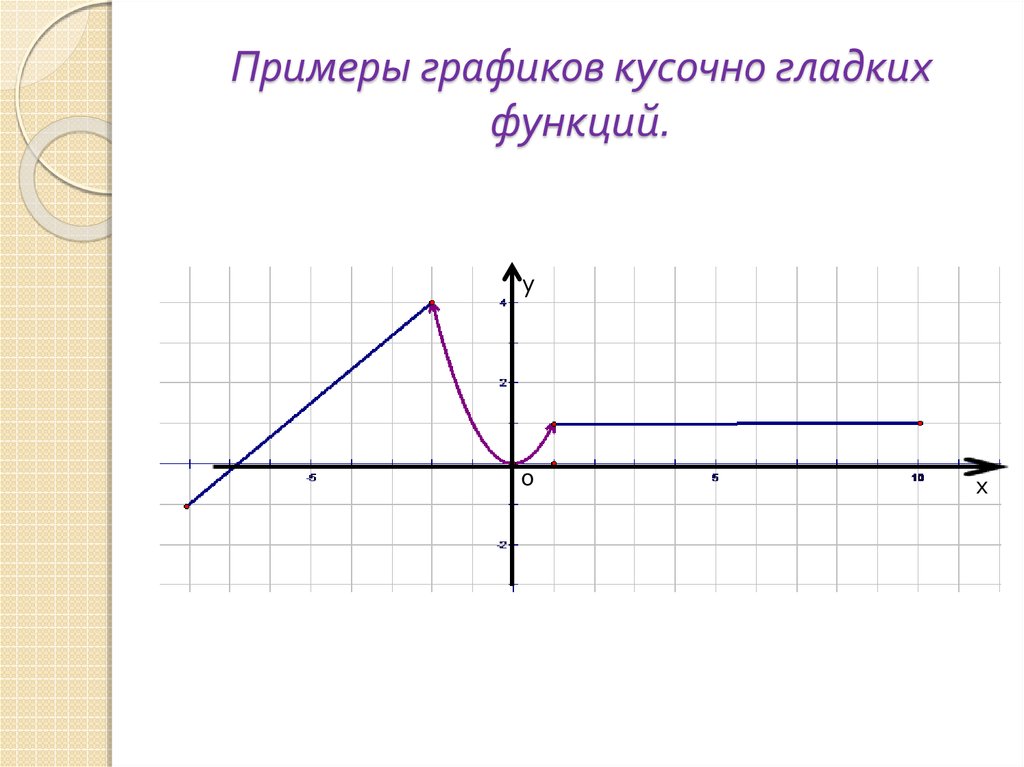
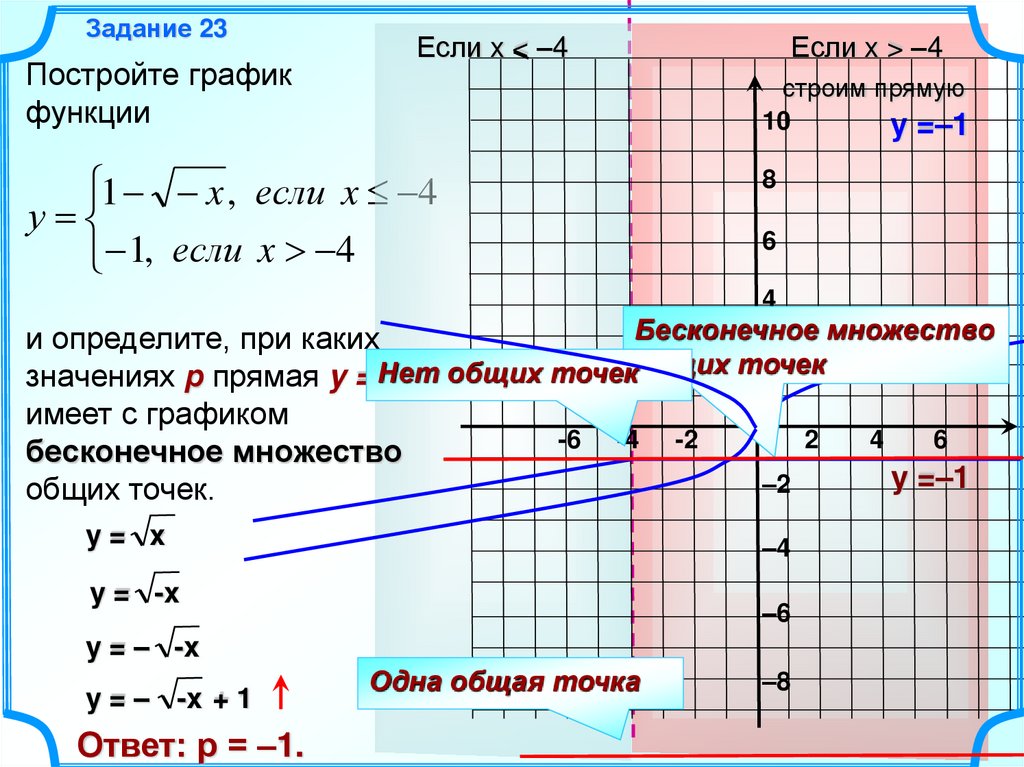
Кусочно-заданная функция · Калькулятор Онлайн
Кусочно-заданная функция
при
при
при
при
при
при
при
при
при
при
при
при
при
при
при
при
при
при
при
при
На данной странице вы можете выполнить различные действия с кусочно-заданной функцией, а также для большинства сервисов — получить подробное решение.
- Производная кусочно-заданной функции
- Построить график
- Исследовать график
- Определённый интеграл
- Неопределённый интеграл от таких функций
- Предел кусочно-заданной
- Ряд Фурье (в примерах для нахождения ряда в основном используются кусочно-заданные функции)
- Ряд Тейлора
Сначала задайте соответствующую функцию.
Как задавать условия?
Приведём примеры, как задавать условия:
- x≠0
- x не равен нулю
- x > pi
- x больше, чем число Пи
- -pi/2
- x меньше или равно, чем Пи пополам, но нестрого больше, чем Пи пополам
- true
- означает «в любых других случаях»
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- ctg(x)
- Функция — Котангенс от x
- arcctg(x)
- Функция — Арккотангенс от x
- arcctgh(x)
- Функция — Гиперболический арккотангенс от x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- gamma(x)
- Гамма-функция
- LambertW(x)
- Функция Ламберта
- x! или factorial(x)
- Факториал от x
- DiracDelta(x)
- Дельта-функция Дирака
- Heaviside(x)
- Функция Хевисайда
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Примеры
Для ряда Фурье
1 - x если -pix если -2С параболой и модулем
8 - (x + 6)^2 если x = 5
Непрерывная функция
-5/x если x -1
Функция с разрывом
x + 1 если x = 0
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
Интегральные функции:
В выражениях можно применять следующие операции:
Другие функции:
Постоянные:
построение графика, формула, знак модуля и примеры
- Графики и формулы кусочно-линейных функций
- Знак модуля в линейных функциях
- Примеры
Графики и формулы кусочно-линейных функций
Ситуация, когда движение или другое явление можно описать одной линейной функцией, определенной на интервале $-\infty \lt t \lt +\infty$, в действительности невозможна. Хотя бы потому, что возраст Вселенной велик, но не бесконечен.
На практике в течение некоторого времени тело может двигаться, потом – покоиться, потом – опять прийти в движение, но уже с другой скоростью и в другом направлении и т. п. Как задать подобную зависимость?
п. Как задать подобную зависимость?
Допустим, турист идет из начальной точки по прямой тропинке в течение 2 ч со скоростью 5 км/ч, затем останавливается отдохнуть на 1ч и возвращается обратно по той же тропинке со скоростью 4 км/ч. Нам нужно найти формулу для расстояния s(t) от начальной точки на протяжении всего похода.
Изобразим зависимость s(t) графически:
Первый отрезок AB легко записать: $ s_1 (t) = 5t,0 \le t \lt 2$
С отрезком BC тоже всё ясно: $s_2 (t) = 10,2 \le t \lt 3$
Осталось найти формулу для отрезка CD. Для него известен угловой коэффициент, равный скорости k = -4; знак «минус» оттого, что турист возвращается обратно. Формула имеет вид $s_3 (t) = -4t+b$. Также, нам известны координаты C(3;10).
Подставляем: $10 = -4 \cdot 3+b \Rightarrow b =22$. Осталось рассчитать момент возвращения:
$$0 = -4t_{back}+22 \Rightarrow t_{back} = 22:4 = 5,5$$ (ч)
Значит, формула движения на отрезке $CD:s_3 (t) = -4t+22,3 \le t \le 5,5.$
Получаем:
$$s(t) = {\left\{ \begin{array}{c} 5t,0 \le t \lt 2 \\ 10,2 \le t \lt 3 \\ -4t+22,3 \le t \le 5,5 \end{array} \right. } $$
} $$
Важным свойством заданной функции является выполнение условий согласования:
$$ s_1 (2) = s_2 (2) = 10,s_2 (3) = s_3 (3) = 10$$
Наша функция «сшита» на концах промежуточных интервалов.
В общем случае:
Знак модуля в линейных функциях
По правилу раскрытия скобок модуля (см. §4 данного справочника)
$$ |x| = \left[ \begin{array}{cc} x, x\ge0 \\ -x, x \lt 0\end{array} \right.$$
Например:
$$ y = 2|x|+5 = {\left\{ \begin{array}{c} -2x+5, x\ge0 \\ 2x+5, x \lt 0\end{array} \right.} $$
Мы заменили квадратную скобку со значением «или» на фигурную скобку со значением «и», поскольку именно смысл объединения — «и того, и другого» — вкладывается в определение кусочно-линейной функции .
Примеры
Пример 1. Представьте функцию с модулем в виде кусочно-линейной и постройте её график:
а) $ y = |x| = {\left\{ \begin{array}{c} -x, x \lt0 \\ x, x \ge 0 \end{array} \right.}$
б) $ y = 2|x|-1 = {\left\{ \begin{array}{c} -2x-1, x \lt0 \\ 2x-1, x \ge 0 \end{array} \right.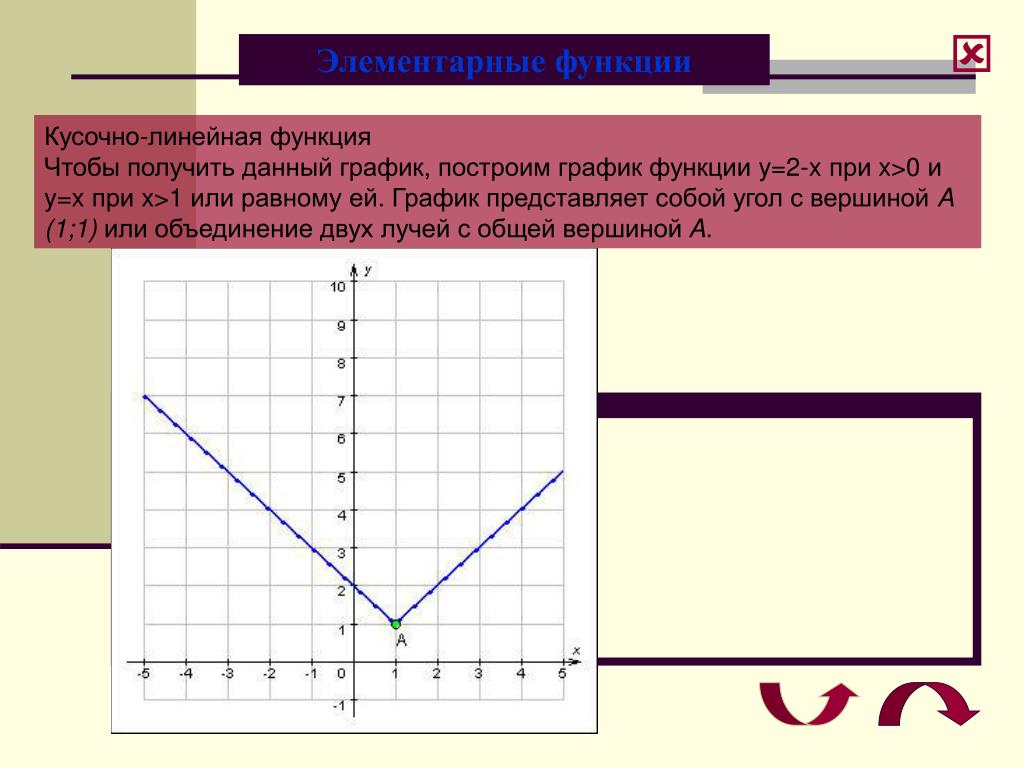 }$
}$
в) $ y = |x+1| = {\left\{ \begin{array}{c} -x-1, x \lt0 \\ x+1, x \ge 0 \end{array} \right.}$
г) $ y = |x-2| = {\left\{ \begin{array}{c} -x+2, x \lt0 \\ x-2, x \ge 0 \end{array} \right.}$
Пример 2*. Представьте функцию с модулем в виде кусочно-линейной и постройте её график:
$$ y = |2|x|-1| = {\left\{ \begin{array}{c} |-2x-1|, x\lt0 \\ |2x-1|,x \ge 0 \end{array} \right.} = {\left\{ \begin{array}{c} 2x+1, {\left\{ \begin{array}{c} -2x-1 \lt 0 \\ x \lt 0 \end{array} \right.} \\ -2x-1, {\left\{ \begin{array}{c} -2x-1 \ge 0 \\ x \lt 0\end{array} \right.} \\ -2x+1, {\left\{ \begin{array}{c}2x-1 \lt 0 \\ x \ge 0\end{array} \right.} \\ 2x-1, {\left\{ \begin{array}{c}2x-1 \ge 0 \\ x \ge 0\end{array} \right.} \end{array} \right.}= $$
$$ = {\left\{ \begin{array}{c} 2x+1, {\left\{ \begin{array}{c} -2x \lt 1 \\ x \lt 0 \end{array} \right.} \\ -2x-1, {\left\{ \begin{array}{c} -2x \ge 1 \\ x \lt 0\end{array} \right.} \\ -2x+1, {\left\{ \begin{array}{c}2x \lt 1 \\ x \ge 0\end{array} \right. } \\ 2x-1, {\left\{ \begin{array}{c}2x \ge 1 \\ x \ge 0\end{array} \right.} \end{array} \right.}= {\left\{ \begin{array}{c} 2x+1, {\left\{ \begin{array}{c} x \gt — \frac{1}{2} \\ x \lt 0 \end{array} \right.} \\ -2x-1, {\left\{ \begin{array}{c} x \le — \frac{1}{2} \\ x \lt 0\end{array} \right.} \\ -2x+1, {\left\{ \begin{array}{c}x \lt \frac{1}{2} \\ x \ge 0\end{array} \right.} \\ 2x-1, {\left\{ \begin{array}{c}x \ge \frac{1}{2} \\ x \ge 0\end{array} \right.} \end{array} \right.}= {\left\{ \begin{array}{c} -2x-1, x \le — \frac{1}{2} \\ 2x+1, — \frac{1}{2} \lt x \lt 0 \\ -2x+1, 0 \le x \lt \frac{1}{2} \\ 2x-1, x \ge \frac{1}{2} \end{array} \right.} $$
} \\ 2x-1, {\left\{ \begin{array}{c}2x \ge 1 \\ x \ge 0\end{array} \right.} \end{array} \right.}= {\left\{ \begin{array}{c} 2x+1, {\left\{ \begin{array}{c} x \gt — \frac{1}{2} \\ x \lt 0 \end{array} \right.} \\ -2x-1, {\left\{ \begin{array}{c} x \le — \frac{1}{2} \\ x \lt 0\end{array} \right.} \\ -2x+1, {\left\{ \begin{array}{c}x \lt \frac{1}{2} \\ x \ge 0\end{array} \right.} \\ 2x-1, {\left\{ \begin{array}{c}x \ge \frac{1}{2} \\ x \ge 0\end{array} \right.} \end{array} \right.}= {\left\{ \begin{array}{c} -2x-1, x \le — \frac{1}{2} \\ 2x+1, — \frac{1}{2} \lt x \lt 0 \\ -2x+1, 0 \le x \lt \frac{1}{2} \\ 2x-1, x \ge \frac{1}{2} \end{array} \right.} $$
Как видно из этого примера, аналитически выводить формулу для двух модулей очень нелегко.
Гораздо легче сразу построить график, если следовать следующим простым правилам преобразования.
Шаг 1. Строим y = 2x-1
Шаг 2. Строим y = 2|x|-1 по правилу: |x| отражает часть графика для положительных $x \ge 0$ влево, зеркально относительно оси Y
Шаг 3. 2
2
Кусочная функция | Как построить график кусочных функций?
- Введение
- Примеры: как построить график кусочно-определяемой функции?
- Как с помощью калькулятора кусочных функций нарисовать ее график?
- Узнайте, как использовать Desmos Graphing Calculator для наброска кусочной функции
- Использование/применение кусочных функций
- Заключение
Некоторые функции определяются по-разному в разных частях своей области и, таким образом, более естественно выражаются в терминах более чем одной формулы. Назовем такую функцию кусочно-функция или кусочно-определенная функция . Кусочные функции будут нам полезны при изучении пределов, непрерывности и производной как примеры и контрпримеры функций, обладающих определенными свойствами.
Назовем такую функцию кусочно-функция или кусочно-определенная функция . Кусочные функции будут нам полезны при изучении пределов, непрерывности и производной как примеры и контрпримеры функций, обладающих определенными свойствами.
Если у вас недостаточно времени, чтобы закончить эту статью за одно чтение, не забудьте добавить эту страницу в закладки для дальнейшего насыщения, если вы не хотите пропустить этот полезный контент.
Примеры: как построить график кусочно-определяемой функции?Пример №1
Пусть f — функция, определяемая выражением;
\[ f(x) = \begin{case} х-1, \текст{ если } х <3 \\ 5, \text{ если } x =3 \\ 2x+1 , \text{ если } 3 < x \end{случаи} \]
Определить область определения и область значений f и начертить ее график .
Решение:-
Область определения f равна (-∞, +∞), на следующем рисунке показан график f;
состоит из части прямой y=x-1, для которой x<3, точки (3,5) и части прямой y = 2x+1, для которой 3 Определите область определения и область значений g и нарисуйте его кусочный график. Решение:- Область определения g равна (-∞, +∞), ниже приведен график функции;
График содержит участок прямой y= 3x-2, для которого x<1, и участок параболы y = x 2 , для которого 1 ≤ x. Диапазон составляет (-∞, +∞).
Пример №3
H — функция, определяемая формулой;
\[ H(x) = \begin{case} х+3, \текст{ если } х ≠ 3 \\ 2 , \текст{ если } х = 3 \end{случаи} \]
Определите домен и область значений H и нарисуйте его график.
Решение: —
Поскольку H определено для всех x, его область определения равна (-∞, +∞), график показан ниже;
Диапазон — это набор всех действительных чисел, кроме 6, поэтому с точки зрения набора мы можем выразить диапазон как ℝ-{6}. 92, \text{ если } х ≠ 2 \\ 7 , \text{ если } х = 2 \end{случаи} \]
Определить область определения и область значений f и начертить ее график.
Решение: —
Поскольку f определено для всех x, домен равен (-∞, +∞). График ниже;
состоит из точки (2, 7) и всех точек параболы y = x 2 кроме (2, 4). Диапазон равен [0, +∞).
Пример №5
Определите область определения и диапазон функции абсолютного значения ‘f’, для которой f(x) = |x| и нарисуйте его график.
Решение: —
Из определения функции абсолютного значения |x|, f(x) определяется кусочно, как показано ниже,
\[ f(x) = \begin{s } х, \текст{ если } х ≥ 0 \\ -x , \text{ если } x < 0 \end{случаи} \]
Домен (-∞, +∞).
один имеет наклон 1, а другой имеет наклон -1. Диапазон равен [0, +∞).
Example#6
Кусочная функция f определяется как;
\[ f(x) = \begin{case} -2, \text{ если } x ≤ 3 \\ 2 , \текст{ если } 3 < х \end{случаи} \]
Определить домен и диапазон f и начертить его график.
Решение:-
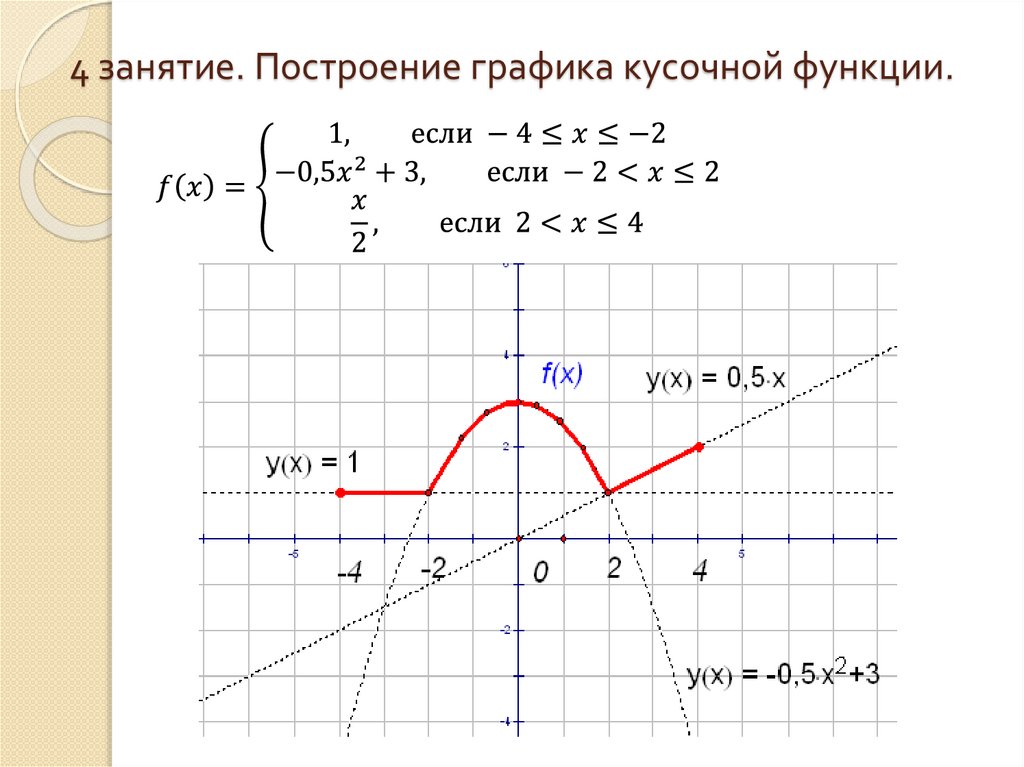
Область определения g равна (-∞, +∞), ниже приведен график функции; 92 , \text{ если } x < 0 \\ 3x + 1 , \text{ если } 0 ≤ x \end{случаи} \]
Определить домен и диапазон f и начертить его график.
Решение:-
Область определения g равна (-∞, +∞), ниже приведен график функции;
Это непрерывный график с диапазоном (-∞, +∞).
Пример# 8
Кусочная функция f определяется как;
\[ f(x) = \begin{case} 6x + 7 , \text{ если } x ≤ -2 \\ 4 – х , \текст{ если } -2 < х \end{случаи} \]
Определить домен и диапазон f и начертить его график.
Решение:-
Область определения g равна (-∞, +∞), ниже приведен график функции;
Диапазон: (-∞, 6).
Пример № 9
Нарисуйте график знаковая функция (или знаковая функция), обозначаемая как «знак» и определяемая кусочно, как показано ниже;
\[ sign(x) = \begin{case} -1 , \text{ если } x < 0 \\ 0 , \текст{ если } х = 0 \\ 1 , \текст{ если } 0 < х \end{случаи} \]
знак х читается как «знак ‘х’».
Решение: —
Область определения знака x равна (-∞, +∞). Ниже приведен график знаковой (сигнум) функции;
Диапазон содержит всего три целых числа, как указано в вопросе, то есть {-1, 0, 1}. 92} , \text{ если } -5 ≤ x≤ 5 \\
3-x , \text{ если } 5 Решение:- Область (-∞, +∞), вот как мы набросали график; И диапазон равен (-∞, -2) ∪ [0, 5]. Существуют различные доступные онлайн и загружаемые графические калькуляторы, которые облегчают пользователям набросок кусочных функций, некоторые из них, как показано ниже; Здесь я собираюсь подробно рассказать о том, как набросать график кусочных функций, используя Графический калькулятор Desmos ? В приведенном выше видео я выбрал несколько примеров, которые были решены и нарисованы вручную в этой статье, и ввел их кусочные определения с соответствующими областями, чтобы получить их график, I have picked Example#1 here and tried to substitute commands on Desmos interface , let’s try to understand step by step . ШАГ №1 ШАГ № 2 Поскольку «3» не входит в первую кусочную область «x < 3», это означает, что субъективный граф не содержит (3, 2), поэтому мы должны разработайте там «дырку» для этой цели; Первая кусочная обработка завершена. ШАГ №3 STEP#5 For more examples, you can watch my aforementioned video . Кусочные функции в дополнение к исчислению великодушно способствуют математическому моделированию различных повседневных задач реальной жизни, которые впоследствии оцениваются для получения оптимальных и точных решений. Я попытался собрать несколько примеров из области счетов, физики, биологии и т. \[ f(x) = \begin{case}
0, \text{ если } x < $10 000 \\
10\text{%} , \text{ если } 10 000 долларов США ≤ x≤ 20 000 долларов США \\
15\text{%} , \text{ если } x> 20 000 долларов
\end{случаи}
\] \[ C(x) = \begin{case}
7x, \text{ если } 0 Где C(x) — общая стоимость крышек, а «x» — количество заказанных крышек.
Learn how to use Desmos Graphing Calculator to sketch a кусочная функция 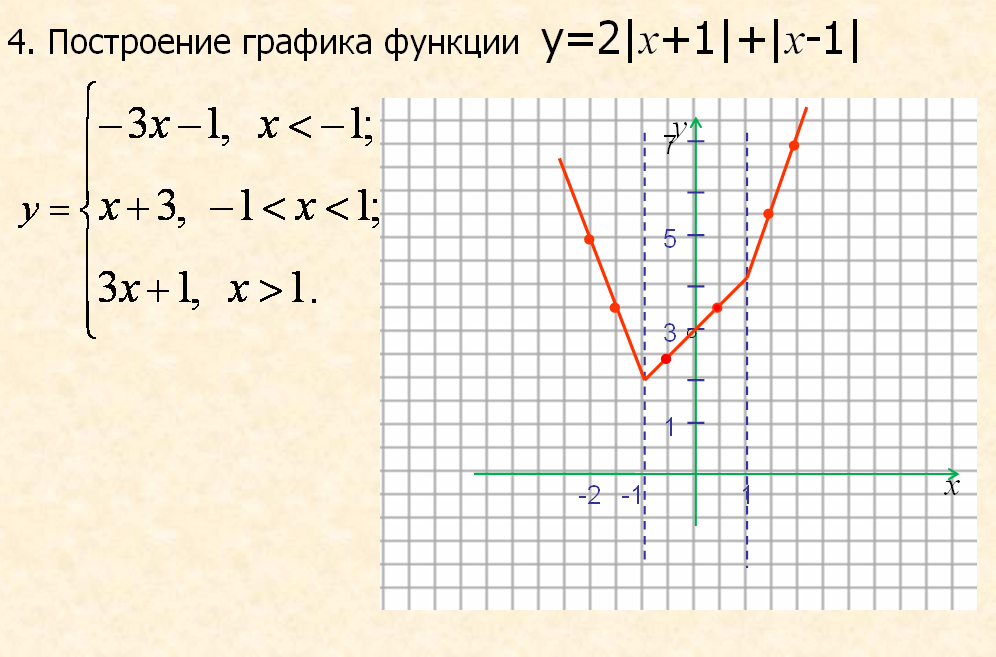

 д., которые помогут вам получить представление о приложениях и значении кусочных функций.
д., которые помогут вам получить представление о приложениях и значении кусочных функций. 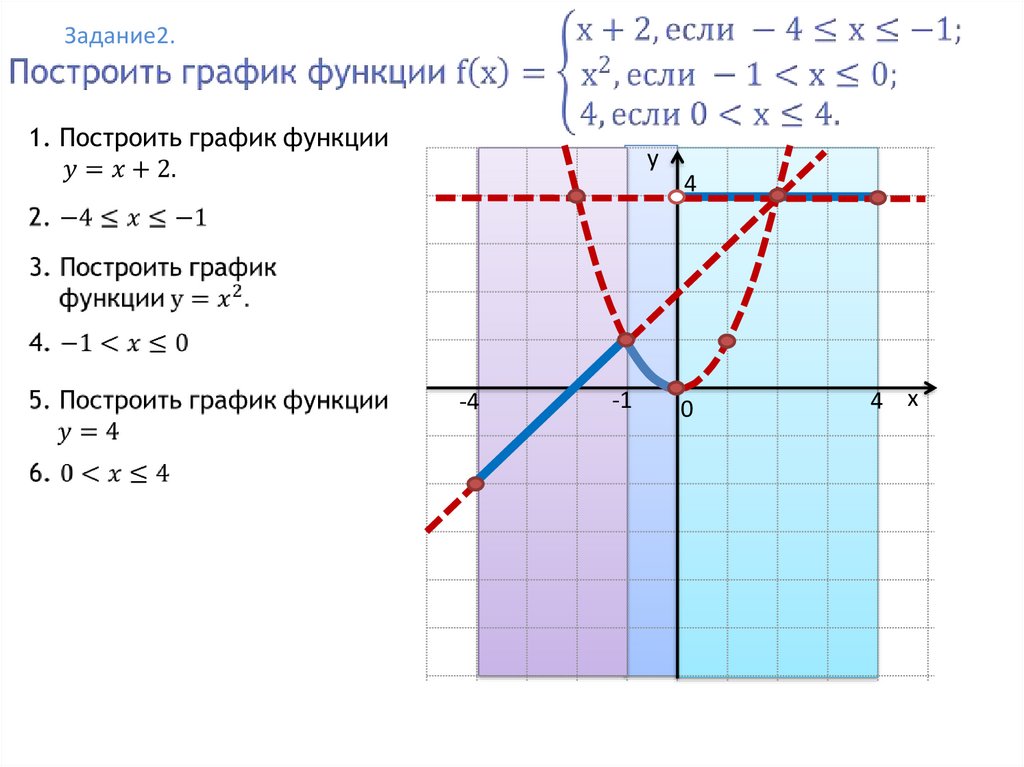
- Большегрузный автомобиль движется по шоссе с переменной скоростью, определенной кусочно ниже;
\[ v(t) = \begin{case} 5t, \text{ если } 0 \le t < 15 \\ 70 , \text{ если } 15 ≤ x< 50 \\ 250-3t , \text{ если } т \geq 50 \end{случаи} \]
ЗаключениеКусочная функция действительно является отличительной чертой в области исчисления и глубоко вовлечена в концепции пределов, непрерывности, дифференциального и интегрального исчисления. Вне всякого сомнения, кусочные функции упростили многие сложные цели из
- Virtual strain fields
- Artificial intelligence
- Random field modelling
- Optical Science
- Pharmaceutical sciences (Pharmacokinetics)
- Laser scanning for environmental sciences
- Scientific расчет в электротехнике
- Решение вопросов по геологии и минералогии
- Бизнес, социальные науки и науки о жизни
Все, что мы изучаем в математике, имеет свое глубокое значение и существенный вклад в различные области реальной жизни, кусочная функция является ярким примером этого.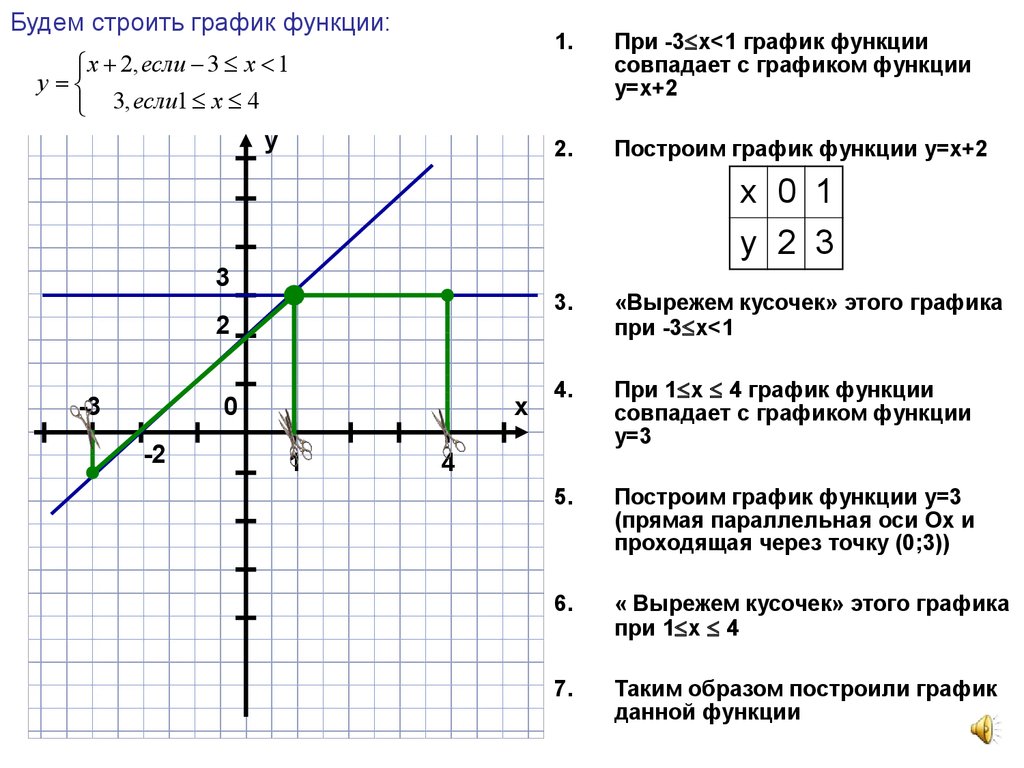
Статьи по теме:
Эпсилон и Дельта Определение предела
Непрерывные и разрывные функции
Теорема о сжатии и непрерывность тригонометрических функций
Хотите улучшить свои академические оценки?
Не стесняйтесь обращаться к нам за качественным и стандартизированным онлайн-сервисом обучения математике
НАЖМИТЕ НА ССЫЛКИ НИЖЕ Примеры, вычисление Кусочная функция — это функция, график которой состоит из нескольких частей кривых. Это означает, что он имеет разные определения в зависимости от значения ввода. т. е. кусочная функция ведет себя по-разному для разных входных данных. Давайте узнаем больше о кусочной функции, а также о том, как построить ее график, как ее оценить и как найти ее область определения и диапазон. 1. Что такое кусочная функция? 2. 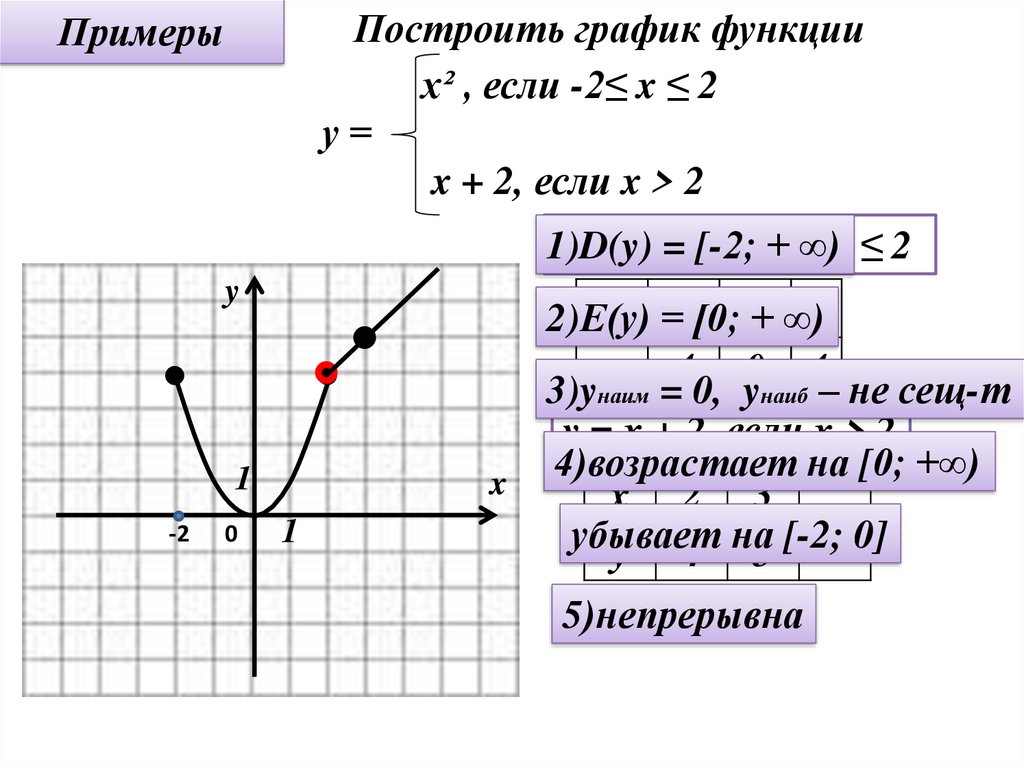
Кусочно-функциональный график 3. Домен и диапазон кусочной функции 4. Оценка кусочной функции 5. Кусочно-непрерывная функция 6. Часто задаваемые вопросы о кусочной функции Что такое кусочная функция?
Кусочная функция — это функция f(x), которая имеет разные определения в разных интервалах x. График кусочной функции имеет разные части, соответствующие каждому из ее определений. Функция абсолютного значения — очень хороший пример кусочной функции. Давайте разберемся, почему он так называется. Мы знаем, что функция абсолютного значения есть f(x) = |x| и определяется как: \(f(x)=\left\{\begin{array}{ll}
х, & \текст { если } х \geq 0 \\
-x, & \text { если } x < 0
\end{массив}\right.\). Мы должны читать эту кусочную функцию как
- f(x) равно x, когда x больше или равно 0 и
- f(x) равно -x, когда x меньше 0
Тогда график функции абсолютного значения f(x) состоит из двух частей: одна соответствует x (когда x находится в интервале [0, ∞) ), а другая часть соответствует -x (когда x находится в интервале ( -∞, 0)). Его график выглядит следующим образом:
Его график выглядит следующим образом:
Кусочно-функциональный график
Мы уже знаем, что график кусочной функции состоит из нескольких частей, каждая из которых соответствует своему определению на интервале. Вот шаги для построения графика кусочной функции.
- Во-первых, поймите, что представляет собой каждое определение функции. Например, f(x) = ax + b представляет собой линейную функцию (которая дает прямую), f(x) = ax 2 + bx + c представляет квадратичную функцию (которая дает параболу) и т. д., так что мы будем иметь представление о том, к какой форме приведет часть функции.
- Запишите интервалы, показанные в определении функции, вместе с их определениями.
- Создайте таблицу с двумя столбцами, помеченными x и y, соответствующими каждому интервалу. Обязательно включать конечные точки интервала. Если конечная точка исключена из интервала, обратите внимание, что мы получаем открытую точку, соответствующую этой точке на графике.

- В каждой таблице возьмите больше чисел (случайных чисел) в столбце x, которые лежат в соответствующем интервале, чтобы получить идеальную форму графика. Если кусок представляет собой прямую линию, то достаточно двух значений x. Возьмите 3 или более чисел для x, если кусок НЕ является прямой линией. 9{2} и х>0
\end{массив}\right.\).Решение:
f(x) имеет 3 определения:
- -2 x , когда x меньше -2, и это экспоненциальная функция.
- -|х| когда -2 меньше или равно x меньше или равно 0, и это функция абсолютного значения.
- 2-x 2 , когда x больше 0 и это квадратичная функция.
Запишем интервалы и соответствующие им определения. Кроме того, давайте создадим таблицы, которые включают конечные точки интервалов, а также несколько других случайных чисел из каждого интервала. Мы будем вычислять значение y в каждом случае, используя соответствующее определение.
Теперь давайте нанесем все эти точки на график, имея в виду общие формы соответствующих функций.
 Обратите внимание, что мы должны поставить открытые точки в (-2, -0,25) (первая таблица) и (0, 2) (последняя таблица), поскольку их соответствующие координаты x исключены из интервала. Кроме того, расширьте график в соответствующих интервалах за пределы точек, показанных в таблицах, где это необходимо.
Обратите внимание, что мы должны поставить открытые точки в (-2, -0,25) (первая таблица) и (0, 2) (последняя таблица), поскольку их соответствующие координаты x исключены из интервала. Кроме того, расширьте график в соответствующих интервалах за пределы точек, показанных в таблицах, где это необходимо.Обратите внимание, что самая левая (светло-оранжевая) кривая расширена влево, поскольку она соответствует интервалу x < -2. Кроме того, крайняя правая (синяя) кривая расширена в интервале x > 0. Средняя (темно-оранжевая) кривая НЕ расширена ни в одну из сторон, так как принадлежит интервалу -2 ≤ x ≤ 0,9.0937
Домен и диапазон кусочной функции
Чтобы найти область определения кусочной функции, мы можем просто посмотреть на определение данной функции. Возьмите объединение всех интервалов с x, и это даст нам домен. В приведенном выше примере область определения f(x) равна {x | х < -2} U {х | -2 ≤ х ≤ 0} U {х | х > 0}. Объединение всех этих множеств есть просто множество всех действительных чисел.
 Таким образом, область определения f(x) (в приведенном выше примере) равна R.
Таким образом, область определения f(x) (в приведенном выше примере) равна R.Чтобы найти диапазон кусочной функции, проще всего построить ее график и посмотреть на ось y. Посмотрите, какие значения y охватываются графиком. В приведенном выше примере все значения y меньше 2 (исключая 2, так как в точках (0, 2) есть открытая точка) покрываются графиком. Таким образом, его диапазон равен {y | y < 2} (или) (-∞, 2).
Точно так же мы можем найти область определения и область значений любой кусочной функции, просто построив ее график.
Оценка кусочной функции
Чтобы вычислить кусочную функцию на любом заданном входе,
- сначала посмотрите, какому из заданных интервалов (или неравенств) принадлежит данный вход.
- Затем просто подставьте данный ввод в определение функции, соответствующее этому конкретному интервалу.
Вот пример для понимания шагов. 92, \text { если } x<0 \\-2 \sqrt{x}, \text { если } x>0 \\ 5, \text { если } x=0\end{массив}\right.
 \) .
\) .Решение:
Нам нужно найти f(4). Здесь x = 4, и оно удовлетворяет условию x > 0. Таким образом, соответствующая функция равна f(x) = -2√x.
Замените x = 4 в этом определении:
f(4) = -2 √4 = -2 (2) = -4.
Следовательно, f(4) = -4.
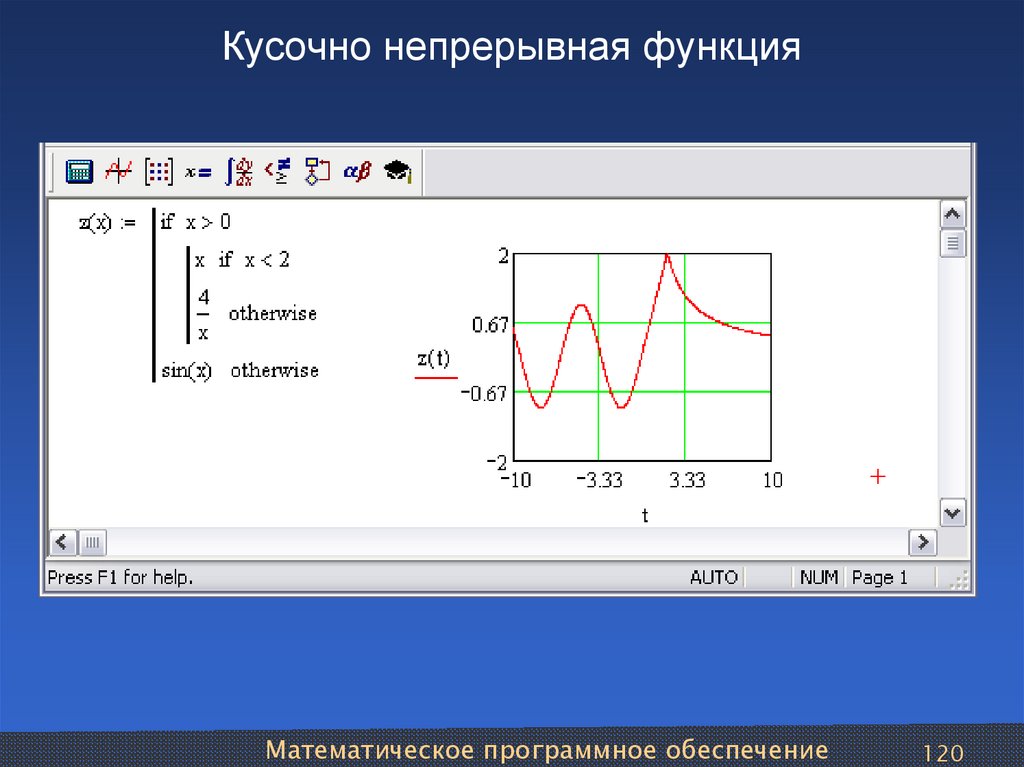
Кусочно-непрерывная функция
Кусочно-непрерывная функция, как следует из ее названия, является кусочно-непрерывной функцией. Это означает, что ее график состоит из разных частей, но тем не менее мы сможем нарисовать график, не отрывая карандаша. Вот пример кусочно-непрерывной функции.
\(f(x)=\left\{\begin{array}{l} x-1, \text {if } x<-2 \\-3, \text {if } x\geq -2\ конец {массив}\справа.\).
Его график показан ниже.
Важные замечания по кусочным функциям
- Чтобы оценить кусочную функцию на входе, посмотрите, какому интервалу она принадлежит, и подставьте его в соответствующее определение функции.
- При построении графика кусочной функции используйте открытые точки в точках, координаты x которых не принадлежат соответствующим интервалам.
 Открытая точка в точке означает, что конкретная точка НЕ является частью функции.
Открытая точка в точке означает, что конкретная точка НЕ является частью функции. - Чтобы найти область определения кусочной функции, просто возьмите объединение всех интервалов, заданных в определении функции.
- Чтобы найти диапазон кусочной функции, просто постройте ее график и найдите значения y, которые охватываются графиком.
☛ Похожие темы:
- Калькулятор графических функций
- Калькулятор квадратичных функций
- Графический калькулятор
- Калькулятор линейной функции 92-2 & \text { если } x \geq 3
\end{массив}\right.\).Как строить графики кусочных функций?
Чтобы нарисовать кусочно-функциональный график:
- Составьте таблицу (с двумя столбцами x и y) для каждого определения функции в соответствующих интервалах.
- Включить конечные точки (в столбце x) каждого интервала в соответствующую таблицу вместе с несколькими другими случайными числами из интервала.

- Подставьте каждое значение x в соответствующее выражение f(x), которое дает значение в столбце y.
- Нанесите на график все точки (поставьте открытые точки для исключенных значений x) и соедините их кривыми.
- Если левая/правая конечная точка равна ∞ или -∞, то соответствующим образом удлините кривую с этой стороны.
Как решать кусочные функции?
Чтобы решить значение кусочной функции на определенном входе:
- Просто посмотрите, в каком из заданных интервалов находится этот вход.
- Возьмите соответствующую функцию.
- Заменить данный ввод в функции из последнего шага.
Приведите пример кусочно-линейной функции.
Кусочно-линейная функция — это кусочно-линейная функция, в которой все части соответствуют прямым линиям. Например, функция абсолютного значения, ступенчатая функция (функция минимального значения или функция наибольшего целого числа), функция потолка и т. д. являются примерами кусочно-линейных функций.


 3
3 14159..
14159..
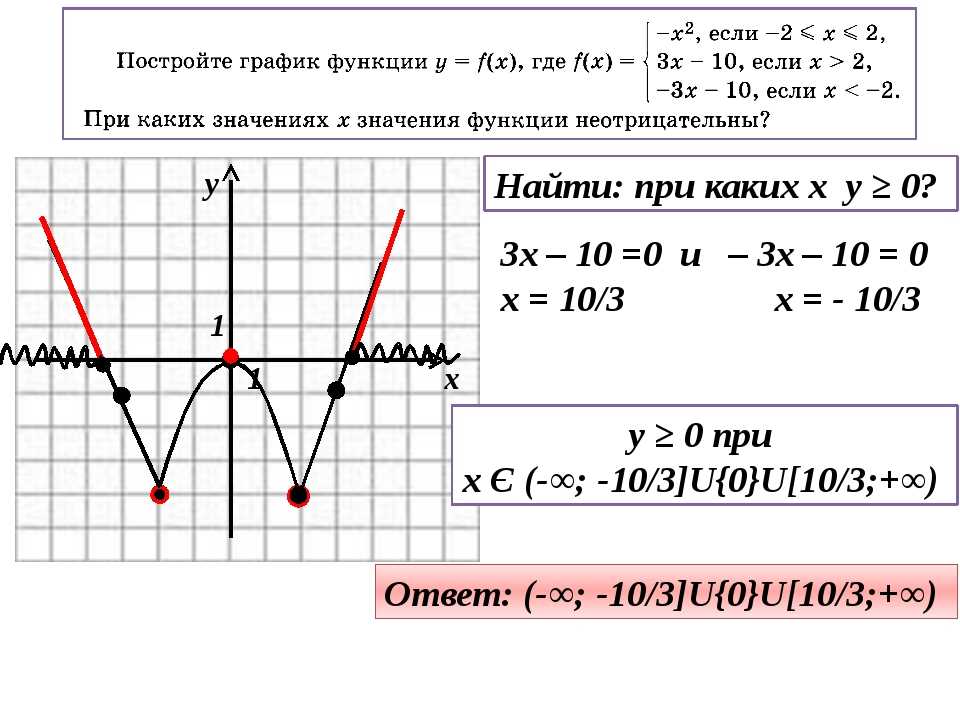 Обратите внимание, что мы должны поставить открытые точки в (-2, -0,25) (первая таблица) и (0, 2) (последняя таблица), поскольку их соответствующие координаты x исключены из интервала. Кроме того, расширьте график в соответствующих интервалах за пределы точек, показанных в таблицах, где это необходимо.
Обратите внимание, что мы должны поставить открытые точки в (-2, -0,25) (первая таблица) и (0, 2) (последняя таблица), поскольку их соответствующие координаты x исключены из интервала. Кроме того, расширьте график в соответствующих интервалах за пределы точек, показанных в таблицах, где это необходимо. Таким образом, область определения f(x) (в приведенном выше примере) равна R.
Таким образом, область определения f(x) (в приведенном выше примере) равна R. \) .
\) . Открытая точка в точке означает, что конкретная точка НЕ является частью функции.
Открытая точка в точке означает, что конкретная точка НЕ является частью функции.