Данные в матрице 6 букв: Данные в матрице, 6 (шесть) букв

Сортировка данных в таблице — Служба поддержки Майкрософт

Таблицы

• Создание и форматирование таблиц
  Статья
• Сортировка данных в таблице
  Статья
• Фильтрация данных в диапазоне или таблице
  Статья
• Данные итогов в таблице Excel
  Статья
• Использование срезов для фильтрации данных
  Статья

Далее: Диаграммы

Таблицы

Таблицы

Таблицы

Сортировка данных в таблице

• Создание и форматирование таблиц
  Статья
• Сортировка данных в таблице
  Статья
• Фильтрация данных в диапазоне или таблице
  Статья
• Данные итогов в таблице Excel
  Статья
• Использование срезов для фильтрации данных
  Статья

Далее: Диаграммы

Сортировка — это один из основных инструментов управления данными. В Excel можно отсортировать таблицу по одному или нескольким столбцам в порядке возрастания или убывания либо выполнить настраиваемую сортировку.

Сортировка таблицы

1. Выберите ячейку данных.

2. На вкладке Главная нажмите кнопку Сортировка и фильтр.

   или выберите «> сортировку».
   

3. Выберите один из следующих вариантов:

   • Сортировка по возрастанию — сортирует выбранный столбец в порядке возрастания.

   • Сортировать по убыванию — сортирует выбранный столбец в порядке убывания.

   • Настраиваемая сортировка — сортирует данные в нескольких столбцах на основе различных условий сортировки.

     Ниже описано, как выполнить пользовательскую сортировку.

     1. Выберите пункт Настраиваемая сортировка.

     2. org/ListItem»>

        Нажмите кнопку Добавить уровень.
        

     3. В столбце Столбец выберите столбец, по которому вы хотите выполнить сортировку, в раскрывающемся списке Сортировать по, а затем выберите такой второй столбец в раскрывающемся списке

        Затем по. Например, в списке Сортировать по можно выбрать столбец «Отдел», а в списке Затем по — «Состояние».

     4. В столбце Сортировка выберите вариант Значения.

     5. В столбце Порядок выберите нужный вариант, например От А до Я,По возрастанию или По убыванию.

     6. Повторите действия 2–5 для каждого дополнительного столбца, по которому вы хотите выполнить сортировку.

        Примечание: Чтобы удалить уровень, нажмите кнопку Удалить уровень.

     7. Если данные содержат строку заголовков, установите флажок Мои данные содержат заголовки.

     8. Нажмите кнопку ОК.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Небольшой обзор на Шифр Хилла (Краткое пособие) / Хабр

1.   Введение

В современном мире, полном информационных технологий, мы доверяем свои данные интернет – сервисам. Разумно предположить, что доступ к этим данным должен иметь только определенный круг лиц. Как раз для этого и существует шифрование. Шифрование – это кодирование информации, процесс использующийся для обеспечения конфиденциальности и безопасности данных, таких как тестовые сообщения, банковские реквизиты и т.д. Исходное сообщение (данные) называется открытым текстом, зашифрованное сообщение (данные) называется шифротекстом. Процедура шифрования обычно включает в себя использование определенного алгоритма и ключа. Алгоритм — это определенный способ засекречивания сообщения (список инструкций). Ключ же конкретизирует процедуру засекречивания.

В этой статье мы затронем такой вариант шифрования, как шифр Хилла, а именно алгоритм шифрования, расшифрования, криптостойкость и варианты различных модификаций.

Шифр Хилла – полиграммный шифр подстановки (элементы исходного открытого текста заменяются зашифрованным текстом в соответствии с некоторым правилом), в котором буквы открытого текста заменяются группами с помощью линейной алгебры. Для латинского алфавита каждой букве сопоставляется число, например, A – 0, B – 1, C – 2, …, Z – 25. В общем случае соответствия “буква – число” можно выбрать произвольно.

2.   Шифрование

Открытый текст представляет собой n-мерный вектор. Ключ – квадратная матрица размера n x n. Для получения шифротекста ключ умножается на открытый текст по модулю выбранной числовой схемы, в случае латинского алфавита — 26.

Пусть «p1p2p3» – открытый текст, ключ – матрица размера 3 x 3 и шифротекст – вектор размерности – 3, «c1c2c3» соответственно. В матричном виде эта система описывается так:

Или в качестве системы уравнений:

Из уравнений видно, что каждый символ открытого текста участвует в шифровании шифротекста. Именно поэтому шифр Хилла принадлежит к категории блочных шифров.

Рассмотрим пример: Алиса хочет передать Бобу сообщение “hello”, используя следующую числовую схему:

A	0	N	13
B	1	O	14
C	2	P	15
D	3	Q	16
E	4	R	17
F	5	S	18
G	6	T	19
H	7	U	20
I	8	V	21
J	9	W	22
K	10	X	23
L	11	Y	24
M	12	Z	25

Открытый текст, обозначим как P, будет выглядеть следующим образом:

Чтобы зашифровать данное сообщение нужно выбрать ключ – матрицу размером 5 x 5 (mod 26). Возьмем следующую матрицу:

что соответствует ключевому слову “GYBCHNQKNBURPVOSCXPHJELQV”.

Тогда шифротекст C может быть получен, как K x P.

 C — зашифрованное сообщение (“JGUAU”).

3.   Расшифрование

Чтобы Боб смог расшифровать сообщение, переданное Алисой, ключ – матрица должна иметь обратную матрицу. Такое возможно, если детерминант матрицы не равен нулю и не имеет общих делителей с основанием модуля. Именно это условие позволяет упростить задачу, можно выбрать в качестве основания модуля простое число, путем добавления в числовую схему новых элементов, например, знаков препинания. Таким образом детерминант любой матрицы не будет иметь общих делителей с основанием такого модуля.

Детерминант ключ – матрицы K, приведенной выше:

det(K) = -413965 – не равен 0.

Делители детерминанта = 413965: 5, 82, 793, 413965.

Делители основания модуля = 26: 2, 13, 26.

Следовательно, данная ключ – матрица имеет обратную матрицу K-1 (mod 26).

Берем зашифрованный раннее текст C = “ JGUAU” и расшифруем его:

Таким образом Боб успешно расшифровал сообщение, переданное Алисой, которое содержало слово “hello”.

4.   Криптостойкость шифра Хилла

1)     Атаковать грубой силой шифр Хилла сложно. Если размерность матрицы – ключа n x n, то всего существует 26n² таких матриц. Но не каждая матрица обратима, поэтому область несколько сужается. Количество обратимых матриц можно рассчитать с помощью китайской теоремы об остатках. Например, количество обратимых матриц по модулю 26 равно:

               |K| = 26n²(1 – 1/2)(1 – 1/22)…(1 – 1/2n) (1 – 1/13)(1 – 1/132)…(1 – 1/13n)

В результате эффективное пространство ключей составляет около 4.64n² – 1.7. Для ключа размера 5×5 этот параметр будет равен 114 битам, что делает вариант полного перебора неприменимым.

2)     Так же шифр Хилла не поддается частотному анализу, так как каждый символ открытого текста принимает участие в шифровании.  Однако, можно провести анализ частоты слов размера n, в связи с этим не стоит применять шифр Хилла на данных имеющих такое строение.

3)     Шифр Хилла очень уязвим для атаки по открытому тексту, так как в нем используются линейные операции. Если Ева знает m пар “открытое сообщение”/ “зашифрованное сообщение”, то она может вычислить ключ. Предположим, что Ева перехватила 3 пары “открытое сообщение”/ “зашифрованное сообщение”:

Если составить матрицы P и C из этих пар, то можно найти ключ K. Если матрица P не будет являться обратимой, то необходимо задействовать другие m наборов пар “открытое сообщение”/ “зашифрованное сообщение”. В данном случае матрица P обратима.

Теперь Ева может расшифровать любое перехваченное сообщение.

5.   Вариации и модификации шифра Хилла

Оригинальный шифр Хилла не нашел практического применения в криптографии из-за слабой устойчивости ко взлому и отсутствия описания алгоритмов генерации прямых и обратных матриц большого размера. Большинство модифицированных криптосистем предполагают при шифровании/дешифровании использовать не одну пару ключей, а несколько, что многократно повышает стойкость системы. При шифровании каждый блок открытого текста обрабатывается отдельным ключом. Использование данного принципа позволяет в значительной степени скрыть статистические свойства открытого и шифрованного текста, а также взаимосвязь между ними. Несколько примеров ниже:

1)     Халаф и др. предложили трехэтапный модифицированный алгоритм шифрования Хилла, где каждый этап рассматривается как блочный шифр с длиной блока 128 бит и длиной ключа 256 бит. Процесс шифрования состоит из трех этапов, и ключи генерируются случайным образом с помощью генератора случайных чисел. Следовательно, он более надежен и обеспечивает высокий уровень безопасности данных, правда сильно проигрывает по скорости.

2)     Мани и Вишвамбари предложили детерминированный метод генерации ключевой матрицы на основе магического прямоугольника. Матрица ключей более высокого порядка генерируется на основе m. Чтобы сгенерировать матрицу ключей, сначала магический прямоугольник порядка m × n преобразуется в магический квадрат порядка m × m, из которого формируется требуемая матрица ключей.

3)     Криптостойкость шифра Хилла можно повысить, если использовать меняющуюся длину ключа. Длина открытого текста меняется случайным образом: m = 2k (k = 3, 4, 5, …), вследствие чего меняются шифрующие и дешифрующие матрицы.

4)     Так же был предложен вариант генерации ключа с помощью LU разложения без фракций. Если взять случайно сгенерированную матрицу, получить LU разложение этой матрицы, то так как матрица L всегда обратима, она может быть использована в качестве ключа. Рассмотрим по подробнее этот процесс:

Генерация ключа с помощью LU разложения

Самой большой проблемой в шифре Хилла является поиск матрицы, соответствующей ключу, которая имеет обратную матрицу. Одним из способов разрешения является генерация ключ – матриц с помощью LU разложения (матрица L обратима всегда). Но матрицы L и U могут содержать дроби, следовательно, они не будут подходить для ключа. Однако это решается LU разложением без фракций. Мы можем получить LU разложение матрицы A без дробей в виде P x A = L x D^-1 x U, где P – матрица перестановок, а D – диагональная матрица. Это очень сложная задача — вручную определить разложение LU без фракций с помощью ручки и бумаги. Но с помощью компьютера это можно легко вычислить. Так как матрицы L и U свободны от фракций, числа в матрице становятся довольно большими, а также имеют смешанные значения, такие как положительное целое число, отрицательное целое число и нули, что усложняет ключ.

Рассмотрим на примере:

В качестве разлагаемой матрицы можно взять симметричные, так и асимметричные. Рассмотрим случайную симметричную матрицу:

6.   Выводы

Достоинства шифра Хилла:

1)     Устойчивость к частотному анализу

2)     Устойчивость к полному перебору, даже при относительно небольших размерах ключа

3)     Простота и скорость применения

Недостатки:

1)     Уязвимость к атаке по открытому тексту

2)     Высокая сложность генерации ключ – матриц, особенно больших размерностей

2.5: Применение матриц в криптографии

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

37850

• Рупиндер Секон и Роберта Блум
• Колледж Де Анза

Цели обучения

В этом разделе мы научимся находить обратную матрицу, если она существует.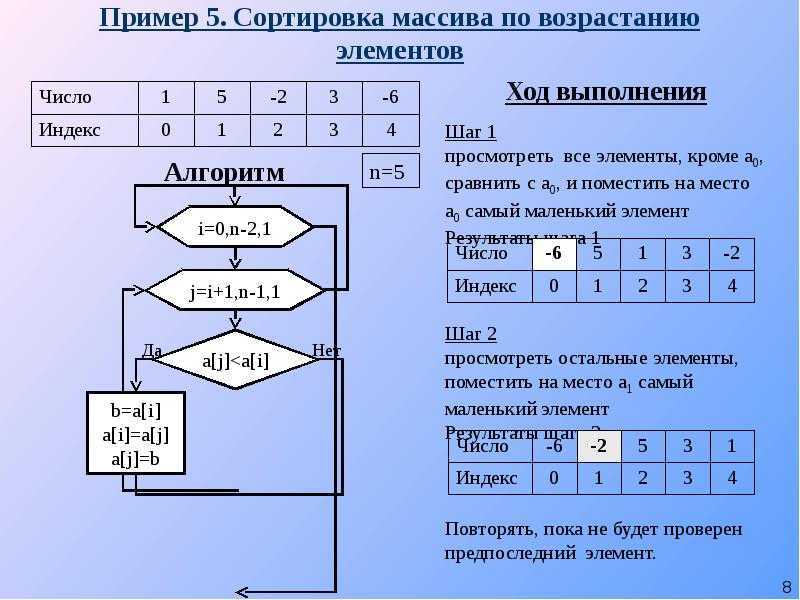 Позже мы будем использовать обратные матрицы для решения линейных систем. В этом разделе вы научитесь

1. кодировать сообщение, используя матричное умножение.
2. декодировать закодированное сообщение, используя обратную матрицу и матричное умножение

Шифрование насчитывает примерно 4000 лет. Исторические отчеты показывают, что китайцы, египтяне, индийцы и греки каким-то образом зашифровывали сообщения для различных целей. Одна известная схема шифрования, называемая шифром Цезаря, также называемая шифром подстановки, использовалась Юлием Цезарем и включала сдвиг букв в алфавите, например замену A на C, B на D, C на E и т. д., для кодирования сообщения. Подстановочные шифры слишком просты по своей конструкции, чтобы сегодня их можно было считать безопасными.

В средние века европейские народы начали использовать шифрование. Различные методы шифрования использовались в США со времен Войны за независимость, Гражданской войны и до наших дней.

Применение математической теории и методов к шифрованию получило широкое распространение в военных целях в 20 ^-м -м веке. Военные кодировали сообщения перед отправкой, а получатель расшифровывал сообщение, чтобы отправлять информацию о военных операциях таким образом, чтобы обеспечить безопасность информации в случае перехвата сообщения. Во время Второй мировой войны шифрование играло важную роль, поскольку и союзники, и державы Оси отправляли зашифрованные сообщения и выделяли значительные ресурсы на укрепление собственного шифрования, одновременно пытаясь взломать шифрование оппозиции.

В этом разделе мы рассмотрим метод шифрования, использующий умножение матриц и обращение матриц. Этот метод, известный как алгоритм Хилла, был создан Лестером Хиллом, профессором математики, который преподавал в нескольких колледжах США, а также занимался военным шифрованием. Алгоритм Хилла знаменует собой введение современной математической теории и методов в область криптографии.

В настоящее время алгоритм Хилла не считается безопасным методом шифрования; относительно легко сломать с помощью современных технологий. Однако в 1929, когда он был разработан, современных вычислительных технологий не существовало. Этот метод, с которым мы можем легко справиться с помощью современных технологий, был слишком громоздким для ручных вычислений. Хилл разработал механическую шифровальную машину, чтобы помочь с математикой; его машина опиралась на шестерни и рычаги, но так и не получила широкого распространения. Метод Хилла считался сложным и мощным в свое время и является одним из многих методов, влияющих на методы, используемые сегодня. Другие методы шифрования в то время также использовали специальные шифровальные машины. Алан Тьюринг, ученый-компьютерщик, пионер в области искусственного интеллекта, изобрел машину, способную расшифровывать сообщения, зашифрованные немецкой машиной Enigma, что помогло переломить ход Второй мировой войны.

С приходом компьютерной эры и интернет-коммуникаций использование шифрования стало широко использоваться в общении и для обеспечения безопасности личных данных; он больше не ограничивается военным использованием.

Современные методы шифрования более сложны, часто объединяя несколько шагов или методов для шифрования данных, чтобы сделать их более безопасными и трудными для взлома. Некоторые современные методы используют матрицы как часть процесса шифрования и дешифрования; другие области математики, такие как теория чисел, играют большую роль в современной криптографии.

Чтобы использовать матрицы при кодировании и декодировании секретных сообщений, наша процедура выглядит следующим образом.

Сначала мы преобразуем секретное сообщение в строку чисел, произвольно назначая номер каждой букве сообщения. Затем мы преобразуем эту строку чисел в новый набор чисел, умножая строку на квадратную матрицу по нашему выбору, которая имеет обратную. Этот новый набор чисел представляет закодированное сообщение.

Чтобы расшифровать сообщение, мы берем строку закодированных чисел и умножаем ее на обратную матрицу, чтобы получить исходную строку чисел. Наконец, связывая числа с соответствующими им буквами, мы получаем исходное сообщение.

В этом разделе мы будем использовать соответствие, показанное ниже, где буквы от A до Z соответствуют числам от 1 до 26, пробел представлен числом 27, а знаки препинания игнорируются.

\[\begin{array}{cccccccccccccc}
\mathrm{A} & \mathrm{B} & \mathrm{C} & \mathrm{D} & \mathrm{E} & \mathrm{F} & \mathrm {G} & \mathrm{H} & \mathrm{I} & \mathrm{J} & \mathrm{K} & \mathrm{L} & \mathrm{M} \\
1 & 2 & 3 & 4 & 5 и 6 и 7 и 8 и 9& 10 & 11 & 12 & 13 \\
\hline \mathrm{N} & \mathrm{O} & \mathrm{P} & \mathrm{Q} & \mathrm{R} & \mathrm{S} & \ mathrm{T} & \mathrm{U} & \mathrm{V} & \mathrm{W} & \mathrm{X} & \mathrm{Y} & \mathrm{Z} \\
14 & 15 & 16 & 17 & 18 & 19 & 20 & 21 & 22 & 23 & 24 & 25 & 26
\end{массив} \nonumber \]

Пример \(\PageIndex{1}\)

Использовать матрицу \(A=\left[\begin{array}{ll}
1 & 2 \\
1 & 3
\end{массив}\right]\) для кодирования сообщения: АТАКУЙТЕ СЕЙЧАС!

Решение

Мы делим буквы сообщения на группы по два.

\[\begin{array}{lllll}\text {AT} & \text {TA} & \text {CK} & \text {-N} & \text {OW}\end{array} \nonumber \ ]

Мы присвоим этим буквам числа из приведенной выше таблицы и преобразуем каждую пару чисел в матрицы \(2 \times 1\). В случае, когда в конце остается одна буква, добавляется пробел, чтобы сделать ее парой.

\[\left[\begin{array}{c}
\mathrm{A} \\
\mathrm{T}
\end{массив}\right]=\left[\begin{массив}{c}
1 \\
20
\end{массив}\right] \quad\left[\begin{array}{l}
\mathrm{T} \\
\mathrm{A}
\end{массив}\right ]=\left[\begin{array}{c}
20 \\
1
\end{array}\right] \quad\left[\begin{array}{l}
\mathrm{C} \\
\mathrm{K}
\end{массив}\right]=\left[\begin{array}{l}
3 \\
11
\end{массив}\right] \nonumber \]

\[\left[\begin{array}{c}
— \\
\mathrm{N}
\end{array}\right]=\left[\begin{array}{l}
27 \\
14
\end{массив}\right] \quad\left[\begin{array}{l}
\mathrm{O} \\
\mathrm{W}
\end{массив}\right]=\left[ \begin{array}{l}
15 \\
23
\end{array}\right] \nonumber \]

Таким образом, на данном этапе наше сообщение, выраженное в виде матриц \(2 \times 1\), выглядит следующим образом .

\[\left[\begin{array}{c}
1 \\
20
\end{массив}\right]\left[\begin{array}{c}
20 \\
1
\end{массив}\right]\left[\begin{array}{c}
3 \\
11
\end{массив}\right]\left[\begin{массив}{ c}
27 \\
14
\end{массив}\right]\left[\begin{массив}{c}
15 \\
23
\end{массив}\right] \quad \bf{(I )} \nonumber \]

Теперь, чтобы закодировать, мы умножаем слева каждую матрицу нашего сообщения на матрицу \(A\). Например, произведение \(A\) на нашу первую матрицу равно: \(\left[\begin{array}{ll}
1 & 2 \\
1 & 3
\end{array}\right]\ слева[\begin{массив}{c}
1 \\
20
\end{массив}\right]=\left[\begin{array}{l}
41 \\
61
\end{массив}\right]\)

И произведение \(A\) с нашей второй матрицей: }{l}
20 \\
1
\end{массив}\right]=\left[\begin{массив}{l}
22 \\
23
\end{массив}\right]\)

Умножение каждой матрицы в \(\bf{(I)}\) на матрицу \(A\), в свою очередь, дает желаемое закодированное сообщение:

\[\left[\begin{array}{l}
41 \\
61
\end{массив}\right]\left[\begin{array}{l}
22 \\
23
\end {массив}\right]\left[\begin{array}{l}
25 \\
36
\end{массив}\right]\left[\begin{массив}{l}
55 \\
69
\end{массив}\right]\left[\begin{array}{l}
61 \\
84
\end{массив}\right] \nonumber \]

Пример \(\PageIndex{2}\)

Декодируйте следующее сообщение, закодированное с помощью матрицы \(A=\left[\begin{array}{ll}
1 & 2 \\
1 & 3
\end{массив}\right]\).

\[\left[\begin{array}{l}
21 \\
26
\end{array}\right]\left[\begin{array}{l}
37 \\
53
\end {массив}\right]\left[\begin{array}{l}
45 \\
54
\end{массив}\right]\left[\begin{массив}{c}
74 \\
101
\end{array}\right]\left[\begin{array}{l}
53 \\
69
\end{array}\right] \quad(\bf {II}) \nonumber \]

Решение

Поскольку это сообщение было закодировано путем умножения на матрицу \(A\) в примере \(\PageIndex{1}\), мы декодируем это сообщение, сначала умножая каждую матрицу слева на обратную матрицу \(A\) приведен ниже. 9{-1}\), получаем следующее.

\[\left[\begin{array}{c}
11 \\
5
\end{массив}\right]\left[\begin{array}{c}
5 \\
16
\end {массив}\right]\left[\begin{массив}{c}
27 \\
9
\end{массив}\right]\left[\begin{массив}{c}
20 \\
27
\end{array}\right]\left[\begin{array}{c}
21 \\
16
\end{array}\right] \nonumber \]

Наконец, связав числа с соответствующими им буквами , получаем:

\[\left[\begin{array}{l}
\mathrm{K} \\
\mathrm{E}
\end{массив}\right]\left[\begin{array}{l}
\mathrm{E} \\
\mathrm{P}
\ конец {массив}\право]\лево[\начало{массив}{л}
— \\
\mathrm{I}
\конец{массив}\право]\лево[\начало{массив}{л}
\ mathrm{T} \\
—
\end{массив}\right]\left[\begin{array}{l}
\mathrm{U} \\
\mathrm{P}
\end{массив}\right ] \nonumber \]

И сообщение гласит: KEEP IT UP.

Теперь предположим, что мы хотим использовать матрицу \(3 \times 3\) для кодирования сообщения, тогда вместо разделения букв на группы по два мы разделим их на группы по три.

Пример \(\PageIndex{3}\)

Использование матрицы \(B=\left[\begin{array}{ccc}
1 & 1 & -1 \\
1 & 0 & 1 \\
2 & 1 & 1
\end{массив}\right] \nonnumber\), закодируйте сообщение: АТАКУЙТЕ СЕЙЧАС!

Решение

Мы делим буквы сообщения на группы по три.

ATT ACK -NO W- —

Обратите внимание, что поскольку в конце осталась одна буква «W», мы добавили два пробела, чтобы сделать ее тройной.

Теперь мы присвоим числам соответствующие им буквы из таблицы и преобразуем каждую тройку чисел в \(3 \times 1\) матрицы. Получаем

\[\left[\begin{array}{l}
\mathrm{A} \\
\mathrm{T} \\
\mathrm{T}
\end{array}\right]=\ left[\begin{array}{c}
1 \\
20 \\
20
\end{array}\right]\left[\begin{array}{l}
\mathrm{A} \\
\ mathrm{C} \\
\mathrm{K}
\end{массив}\right]=\left[\begin{массив}{l}
1 \\
3 \\
11
\end{массив}\right]\left[\begin{array}{l}
— \\
\mathrm{N} \\
\mathrm{O}
\end{массив}\right]= \left[\begin{array}{l}
27 \\
14 \\
15
\end{массив}\right]\left[\begin{array}{l}
\mathrm{W} \\
— \\
—
\end{массив}\right]=\left[\begin{array}{l}
23 \\
27 \\
27
\end{массив}\right] \nonumber \]

Пока у нас есть

\[\left[\begin{array}{c}
1 \\
20 \\
20
\end{array}\right]\left[\begin{array}{c }
1 \\
3 \\
11
\end{array}\right]\left[\begin{array}{c}
27 \\
14 \\
15
\end{array}\right]\ left[\begin{array}{c}
23 \\
27 \\
27
\end{array}\right] \quad \bf{(III)} \nonumber \]

Умножаем слева , каждую матрицу нашего сообщения матрицей \(B\).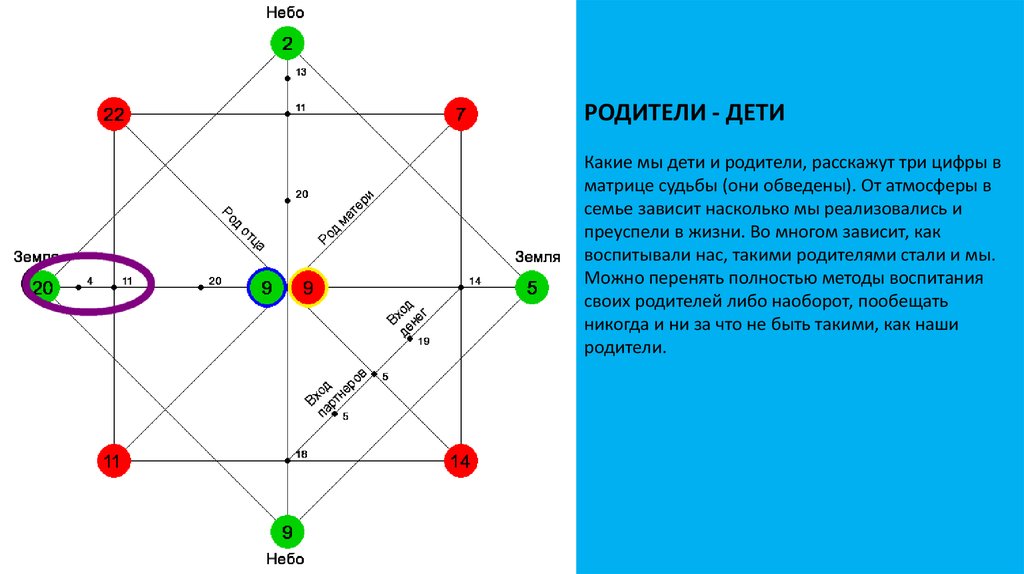 Например,

\[\left[\begin{array}{ccc}
1 & 1 & -1 \\
1 & 0 & 1 \\
2 & 1 & 1
\end{массив}\right] \left[\begin{массив}{c}
1 \\
20 \\
20
\end{array}\right]=\left[\begin{array}{c}
1 \\
21 \\
42
\end{array}\right] \nonumber \]

Умножая каждую из матриц в \(\bf{(III)}\) на матрицу \(B\), мы получаем искомое закодированное сообщение следующим образом:

\[\left [\begin{array}{c}
1 \\
21 \\
42
\end{array}\right]\left[\begin{array}{c}
-7 \\
12 \\
16
\end{массив}\right]\left[\begin{массив}{c}
26 \\ 9{-1}\) для декодирования зашифрованного сообщения.

Пример \(\PageIndex{4}\)

Декодируйте следующее сообщение, закодированное с помощью матрицы \(B=\left[\begin{array}{lll}
1 & 1 & -1 \\
1 & 0 & 1 \\
2 & 1 & 1
\end{массив}\right] \).

\[\left[\begin{array}{l}
11 \\
20 \\
43
\end{array}\right]\left[\begin{array}{l}
25 \\
10 \\
41
\end{array}\right]\left[\begin{array}{l}
22 \\
14 \\ 9{-1}\) дает следующее.

\[\left[\begin{array}{c}
8 \\
15 \\
12
\end{array}\right]\left[\begin{array}{c}
4 \\
27 \\
6
\end{массив}\right]\left[\begin{array}{c}
9 \\
18 \\
5
\end{массив}\right] \nonumber \]

Наконец, связывая числа с соответствующими им буквами, мы получаем

\[\left[\begin{array}{l}
\mathrm{H} \\
\mathrm{O} \\
\mathrm{L}
\конец{массив}\правый]\левый[\начало{массив}{л}
\mathrm{D} \\
— \\
\mathrm{F}
\end{массив}\right]\left[\begin{array}{l}
\mathrm{I} \\
\mathrm{ R} \\
\mathrm{E}
\end{массив}\right] \quad \text { Сообщение гласит: } \mathrm{HOLD} \text { FIRE } \nonumber \]

Сообщение гласит: HOLD ОГОНЬ.

Подводим итоги:

ДЛЯ КОДИРОВАНИЯ СООБЩЕНИЯ

1. Разделите буквы сообщения на группы по две или три.

2. Преобразуйте каждую группу в строку чисел, назначив номер каждой букве сообщения. Не забудьте назначить буквы на пустые места.

3. Преобразуйте каждую группу чисел в матрицы-столбцы.

3. Преобразуйте эти матрицы-столбцы в новый набор матриц-столбцов, умножив их на совместимую квадратную матрицу по вашему выбору, имеющую обратную. Этот новый набор чисел или матриц представляет закодированное сообщение.

ДЛЯ РАСШИФРОВКИ СООБЩЕНИЯ

1. Возьмите строку закодированных чисел и умножьте ее на обратную матрицу, которая использовалась для кодирования сообщения.

2. Свяжите числа с соответствующими им буквами.

---

Эта страница под названием 2.5: Применение матриц в криптографии распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Рупиндером Секоном и Робертой Блум с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Рупиндер Сехон и Роберта Блум

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Показать страницу TOC

   нет

2. Теги

   1. source@https://www. deanza.edu/faculty/bloomroberta/math21/afm3files.html.html

Что такое матричная диаграмма или диаграмма? Анализ взаимосвязи данных

• Дом /
• Качественные ресурсы /
• Матричная диаграмма

Глоссарий качества Определение: матрица

Также называется: матрица, матричная диаграмма

Матричная диаграмма определяется как новый инструмент планирования управления, используемый для анализа и отображения взаимосвязи между наборами данных. Матричная диаграмма показывает взаимосвязь между двумя, тремя или четырьмя группами информации. Он также может дать информацию о взаимосвязи, такой как ее сила, роли, которую играют различные люди или измерения.

Возможны шесть матриц различной формы: L, T, Y, X, C и в форме крыши, в зависимости от того, сколько групп необходимо сравнить.

Когда использовать ту или иную форму матричной диаграммы

В таблице 1 приведены сводные данные о том, когда следует использовать каждый тип матрицы. Нажмите на ссылки ниже, чтобы увидеть пример каждого типа. В примерах оси матриц заштрихованы, чтобы подчеркнуть букву, которая дает каждой матрице ее имя.

• Г-образная матрица связывает две группы элементов друг с другом (или одну группу с самой собой).
• Т-образная матрица связывает три группы элементов: каждая из групп B и C связана с A; группы B и C не связаны друг с другом.
• Y-образная матрица связывает три группы элементов: каждая группа связана с двумя другими по кругу.
• С-образная матрица одновременно связывает три группы элементов в трехмерном пространстве.
• X-образная матрица связывает четыре группы элементов: каждая группа связана с двумя другими по кругу.
• Матрица в форме крыши связывает одну группу элементов с самой собой; обычно используется вместе с Г- или Т-образной матрицей.

Таблица 1: Когда использовать матрицы различной формы

L-образный	2 группы	А Б (или А А)
Т-образный	3 группы	B A C, но не B C
Y-образный	3 группы	А Б В А
С-образный	3 группы	Все три одновременно (3D)
X-образный	4 группы	A B C D A, но не A C или B D
Крышевидный	1 группа	A A, если также A B в L или T

Эта L-образная матрица суммирует требования клиентов.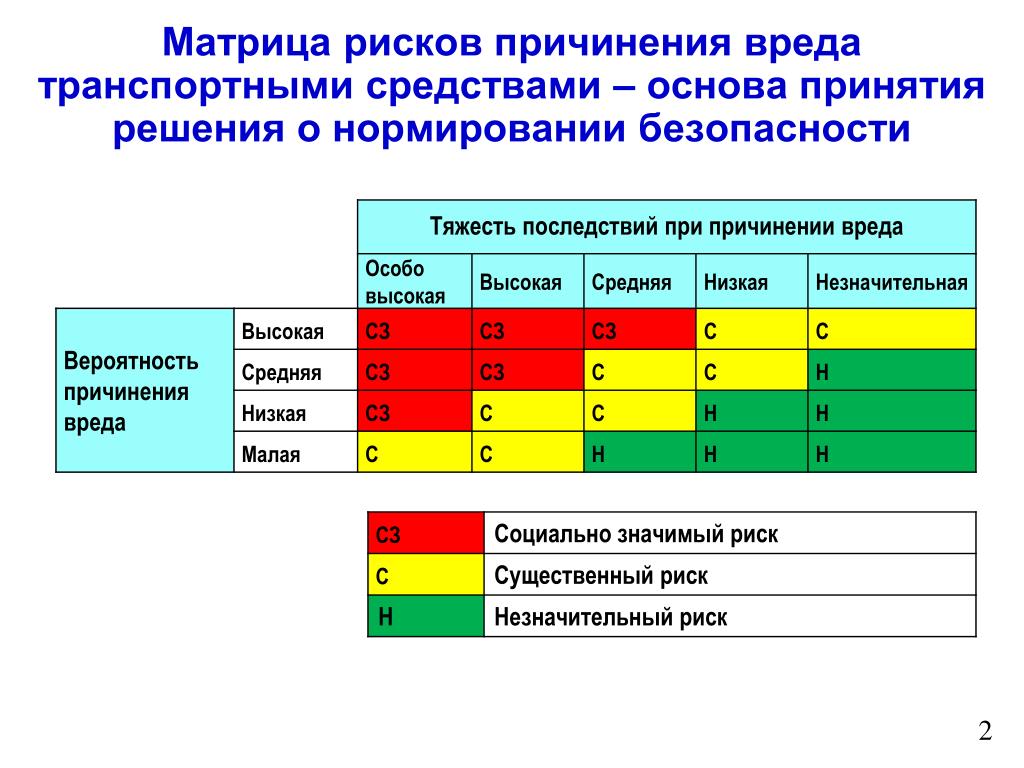 Команда разместила числа в коробках, чтобы показать числовые характеристики, и использовала галочки, чтобы показать выбор упаковки. L-образная матрица на самом деле образует перевернутую букву L. Это самый простой и наиболее распространенный формат матрицы.

  Г-образная матричная диаграмма: требования клиентов

907:00

Клиент
Т

907:00

< 10

907:00

	Клиент D	Клиент М	Клиент Р
Чистота %	> 99,2	> 99,2	> 99,4	> 99,0
Металлы в следовых количествах (частей на миллион)	< 5	—	< 10	< 25
Вода (частей на миллион)	< 5	< 10	—
Вязкость (сП)	20-35	20-30	10-50	15-35
Цвет	< 10	< 10	< 15	< 10
Барабан
Грузовик
Вагон

Вернуться к началу

Эта Т-образная матрица связывает модели продуктов (группа A) с их производственными площадками (группа B) и их клиентами (группа C).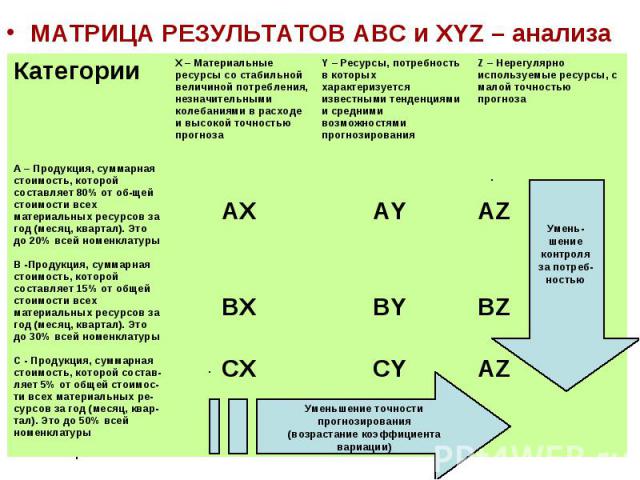

Изучение матрицы (ниже) по-разному дает разную информацию. Например, сосредоточение внимания на модели А показывает, что она производится в больших объемах на заводе в Техасе и в малых объемах на заводе в Алабаме. Time Inc. является основным покупателем модели A, в то время как Arlo Co. покупает небольшое количество. Сосредоточение внимания на рядах клиентов показывает, что только один клиент, Arlo Co., покупает все четыре модели. Zig Corp. покупает только один. Time Inc. совершает крупные закупки A и D, в то время как Lyle Co. является относительно мелким покупателем.

Т-образная матричная диаграмма: продукты — места производства — клиенты

Вернуться к началу

Эта Y-образная матрица показывает взаимосвязь между требованиями клиентов, внутренними показателями процессов и вовлеченными отделами. Символы показывают силу взаимосвязей: первичные взаимосвязи, такие как ответственность производственного отдела за производственные мощности; вторичные отношения, такие как связь между доступностью продукта и уровнем запасов; второстепенные отношения, такие как ответственность отдела дистрибуции за время выполнения заказа; и никакой взаимосвязи, например, между отделом закупок и своевременной доставкой.

Y-образная матричная диаграмма: обязанности по выполнению требований заказчика

Вернуться к началу

Поскольку эта матрица является трехмерной, ее трудно нарисовать и она используется нечасто. Если важно сравнить три группы одновременно, рассмотрите возможность использования трехмерной модели или компьютерного программного обеспечения, которое может обеспечить четкое визуальное изображение.

С-образная матричная диаграмма

Вернуться к началу

На этом рисунке пример с Т-образной матрицей расширяется до Х-образной матрицы за счет включения отношений грузовых линий с производственными площадками, которые они обслуживают, и клиентами, которые используют их. Каждая ось матрицы связана с двумя соседними, но не с той, что находится поперек. Таким образом, модели продуктов связаны с заводскими площадками и клиентами, но не с грузовыми линиями.

X-образная матричная диаграмма: Производственные площадки — Продукция — Клиенты — Грузовые линии

Вернуться к началу

Матрица в форме крыши используется с L- или T-образной матрицей для отображения одной группы элементов относящийся к себе.