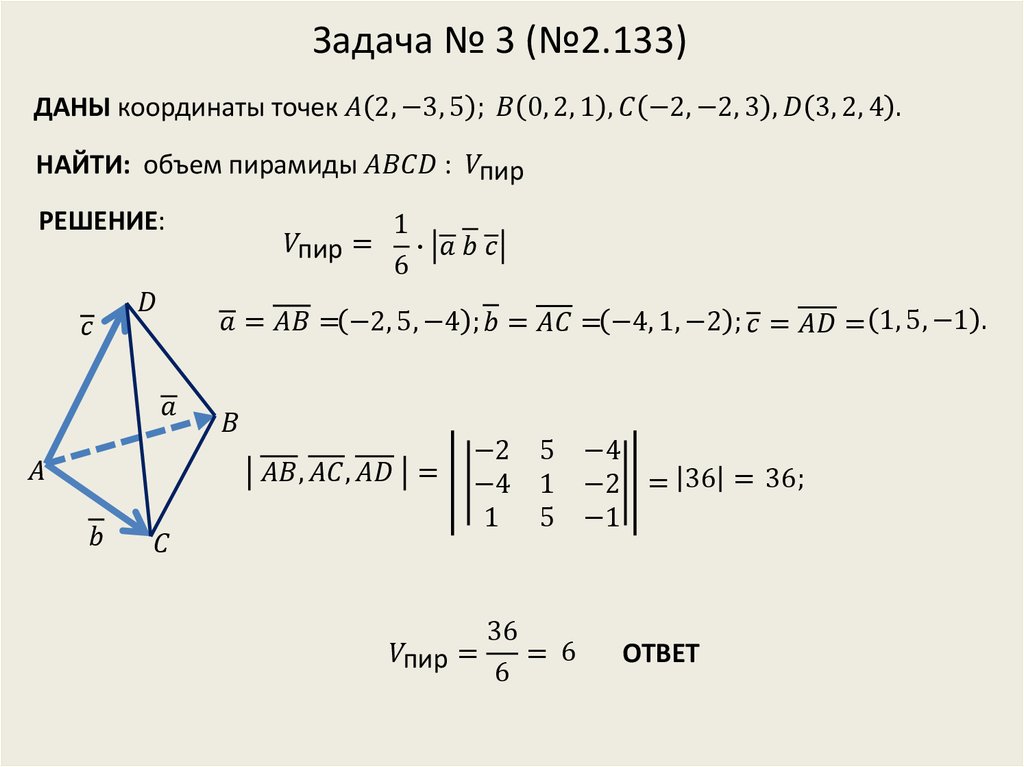
Даны координаты вершин пирамиды (тетраэдра)… Решение задач и контрольных работ по высшей математике онлайн
Краткая теория
Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат. Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное — разобраться и уделить задаче достаточно времени.
Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.
Пример решения задачи
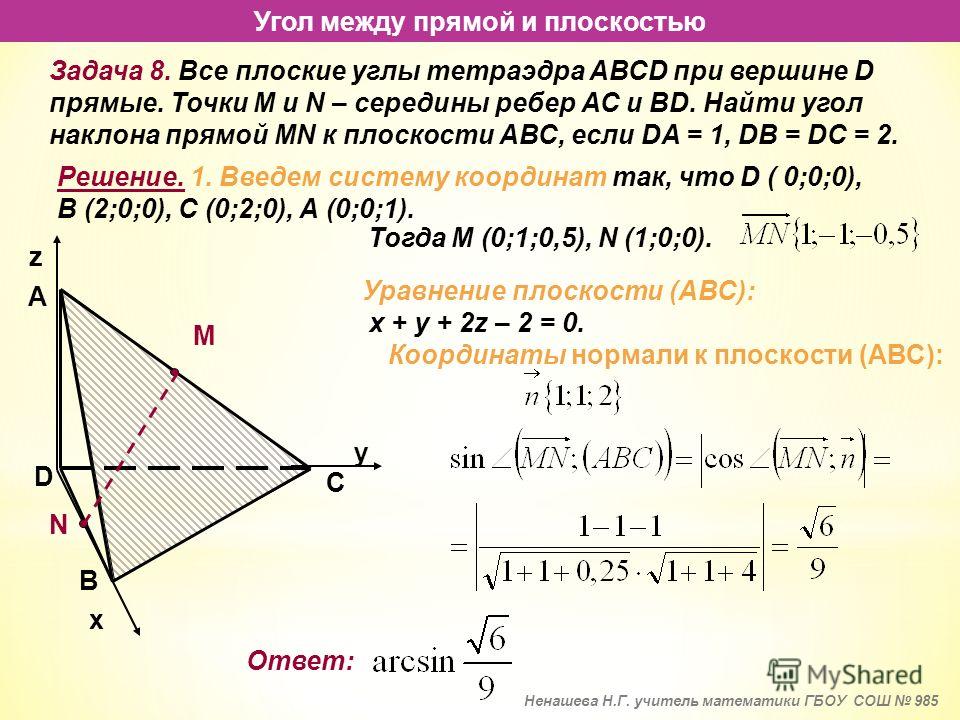
Даны координаты вершин пирамиды . Найти:
- длину ребра ;
- угол между ребрами и ;
- угол между ребром и гранью ;
- площадь грани ;
- объем пирамиды;
- уравнения прямой ;
- уравнение плоскости ;
- уравнения высоты,
опущенной из вершины
на грань
.
Сделать чертеж.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Длина ребра
Длину ребра найдем по формуле расстояния между 2-мя точками:
Угол между ребрами
Угол между ребрами и найдем как угол между направляющими векторами и :
Косинус угла между векторами:
Угол между ребром и гранью. Векторное произведение
Вычислим угол между
ребром
и гранью
.
Для этого вычислим координаты нормального вектора плоскости –им будет векторное произведение векторов и .
Найдем векторное произведение. Для этого вычислим определитель:
Нормальный вектор плоскости:
Синус угла:
Площадь грани
Вычислим площадь грани . Она будет численно равна половине модуля векторного произведения векторов и :
Искомая площадь:
Объем пирамиды. Смешанное произведение векторов
Вычислим объем пирамиды. Он будет равен шестой части модуля смешанного произведения векторов и :
Для того чтобы вычислить смешанное произведение, необходимо найти определитель квадратной матрицы, составленной из координат векторов:
Искомый объем пирамиды:
Уравнение прямой в пространстве
Вычислим уравнение
прямой
.
Направляющим
вектором искомой прямой является вектор
. Кроме того, прямая проходит через точку
Уравнение искомой прямой:
Уравнение плоскости
Вычислим уравнение плоскости . Нормальный вектор плоскости . кроме того, плоскость проходит через точку
-уравнение грани
Уравнение высоты, опущенной на грань
Составим уравнение высоты, опущенной на грань из вершины :
Нормальный вектор является направляющим вектором высоты, кроме того, высота проходит через точку
Искомое уравнение высоты:
Сделаем схематический чертеж:
Резников е.А.
ТИПОВОЙ РАСЧЕТ № 1
Матрицы
и системы линейных уравнений.
Векторная алгебра и аналитическая геометрия
Челябинск
2011
ВАРИАНТ 1
1) Вычислить определитель .
2) Найти матрицу , где .
3) Решить систему линейных уравнений тремя способами: а)по формулам Крамера; б)с помощью обратной матрицы; в)методом Гаусса.
4) Найти площадь параллелограмма и острый угол между диагоналями параллелограмма, построенного на векторах: , если .
5) Найти единичный вектор , перпендикулярный векторам и такой, что векторы образуют левую тройку.
6)Даны вершины треугольника А(-1; 7; 1), B(3; -1; -2), C(-5; 3; 1). Вычислить его высоту, проведенную из вершины В и косинус внутреннего угла В.
7) Даны вершины треугольника А(7; 14), В(10; -5), С(1; 12). Найти точку пересечения высоты, опущенной из вершины В, и медианы, проведенной из вершины С. Найти острый угол между ними и расстояние от этой медианы до вершины А.
8) Найти точку В,
симметричную точке А( 1; 4; 15) относительно
плоскости .
9) Даны вершины треугольника А(3; -1; -5), В(-9;-37; -29), С(-3; -31; -13) . Найти канонические уравнения высоты и медианы, проведенных из вершины С, а также острый угол между ними.
10) Составить уравнение плоскости, проходящей через точку А(2; -4; 1) параллельно прямой и вектору .
11) Даны вершины тетраэдра A( 3; -1 ; 0 ), B( -6 ; 0; 1), C( 0; 8; 0), D( 4; 5 ; -5). Найти длину высоты тетраэдра, опущенную из вершины D, угол между гранью ABD и основанием ABC и угол между ребром AD и плоскостью основания АВС.
12) Установить, что уравнение определяет гиперболу, и найти координаты ее центра, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. Изобразить эту линию на чертеже.
1) Вычислить определитель .
2) Найти матрицу , где .
3) Решить систему линейных уравнений тремя способами: а)по формулам Крамера; б)с помощью обратной матрицы; в)методом Гаусса.
4) Найти площадь
параллелограмма и острый угол между
диагоналями параллелограмма, построенного
на векторах: ,
если .
5) Найти единичный вектор , перпендикулярный векторам и такой, что векторы образуют левую тройку.
6) Даны вершины треугольника А(2; -1; 0), B(-2; 1; 1), C(2; 2; -1). Вычислить его высоту, проведенную из вершины В и косинус внутреннего угла В.
7) Даны вершины треугольника А(5; -13), В(22; 4), С(1; 3). Найти точку пересечения высоты, опущенной из вершины В, и медианы, проведенной из вершины С. Найти острый угол между ними и расстояние от этой медианы до вершины А.
8) Найти точку В, симметричную точке А( -8; -1; -25) относительно плоскости .
9) Даны вершины треугольника А(3; -1; 5), В(-9; -13;-19), С(-3; -15; -9) . Найти канонические уравнения высоты и медианы, проведенных из вершины С, а также острый угол между ними.
10) Составить уравнение плоскости, проходящей через две точки А(4; -3; 4) и В(3; 1; 3) параллельно прямой .
11)Даны вершины тетраэдра
A( 3 ; -6; 6), B(
9; 7; 3), C( 6; 1; -7), D(
-6 ; 5; 8). Найти длину высоты тетраэдра,
опущенную из вершины D,
угол между гранью ABD и
основанием ABC и угол между
ребром AD и плоскостью
основания АВС.
12) Установить, что уравнение определяет гиперболу, и найти координаты ее центра, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис. Изобразить эту линию на чертеже.
Геометрия. Как найти длину от вершины тетраэдра до его грани с помощью векторных методов?
спросил
Изменено 5 лет, 6 месяцев назад
Просмотрено 4к раз
$\begingroup$
Предположим, что длина каждого ребра правильного тетраэдра равна $x$ и
Я думал, что должен использовать концепцию скалярных произведений и т.
д., чтобы ответить на этот вопрос, но мое решение не включает никаких векторов и в значительной степени геометрическое. Ответ не совпадает.
Мой мыслительный процесс:
Поскольку это правильный тетраэдр, все его стороны являются равносторонними треугольниками.
Я разделил основание тетраэдра (один треугольник) на 3 области, используя центр тяжести грани, чтобы получить 3 равнобедренных треугольника.
Пусть расстояние от вершины до центроида треугольной грани тетраэдра равно $k$. Поскольку я знаю, что длина наибольшей стороны равнобедренного треугольника равна $x$, я использую правило синусов $\frac{\sin(30)}{k} = \frac{\sin(120)}{x}$ чтобы получить мое значение $k$ с точки зрения $x$.
Теперь у меня есть новый треугольник с гипотенузой $x$ и основанием $k$. Я использую теорему Пифагора, чтобы получить ответ.
Может ли кто-нибудь показать мне, где мой мыслительный процесс пошел не так, или указать направление, в котором я должен подойти к этому вопросу?
- геометрия
- векторы
$\endgroup$
4
$\begingroup$
Используем ортогональную систему отсчета с $O$ в начале координат, $\mathbf a$ вдоль первой оси (единичный вектор $\hat i$), $\mathbf b$ в $\hat i\hat j$ плоскости и $\mathbf c$ с компонентами по всем трем осям.
$\endgroup$
2
$\begingroup$
Поскольку вы должны использовать «векторные методы», вот способ приблизиться к этому. Вектор $\mathbf n=\mathbf a\times\mathbf b$ ортогонален грани $\triangle{OAB}$. Тогда расстояние $C$ от этой грани равно длине проекции $\mathbf c$ на $\mathbf n$, а именно, $${|\mathbf n\cdot\mathbf c|\over\|\mathbf n\|}={|\mathbf a \times\mathbf b\cdot\mathbf c| \over \|\mathbf a\times\mathbf b\|}.$$
$\endgroup$
$\begingroup$
Поместите тетраэдр в четырехмерное пространство с вершинами в точках $ (1,0,0,0),(0,1,0,0),(0,0,1,0)$ и $( 0,0,0,1)$. Ребра равны $\sqrt{2}$. Центр одной стороны равен $(1/3,1/3,1/3,0)$, а его расстояние от $(0,0,0,1)$ равно $\sqrt{4/3}$.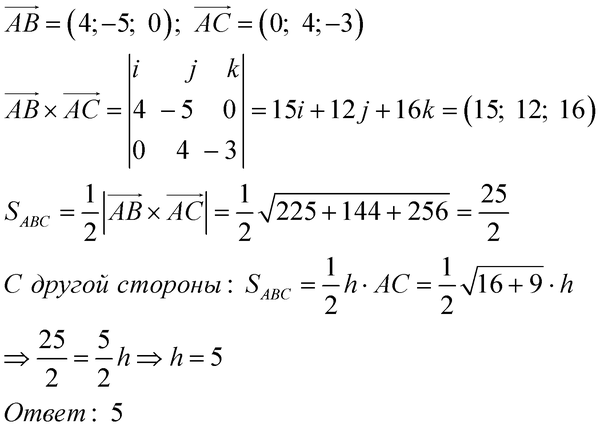
Таким образом, ваш ответ $\sqrt{2/3}$
$\endgroup$
5
Как найти объем тетраэдра
Все математические ресурсы верхнего уровня ISEE
6 Диагностические тесты 244 практических теста Вопрос дня Карточки Learn by Concept
Справка по математике верхнего уровня ISEE » Геометрия » Твердая геометрия » Тетраэдры » Как найти объем тетраэдра
В трехмерном пространстве четыре вершины тетраэдра — тела с четырьмя гранями — имеют декартовы координаты.
Назовите его объем.
Возможные ответы:
Правильный ответ:
Пояснение:
Тетраэдр — это треугольная пирамида, и его можно рассматривать как таковую.
Три вершины — — находятся на -плоскости и могут рассматриваться как вершины треугольного основания. Этот треугольник, как показано ниже, равнобедренный:
Его основание и высота равны 18, поэтому его площадь равна
Четвертая вершина находится вне -плоскости; его перпендикулярное расстояние к вышеупомянутой грани равно его -координате, 9, так что это высота пирамиды. Объем пирамиды
Сообщить об ошибке
В трехмерном пространстве четыре вершины тетраэдра — тела с четырьмя гранями — имеют декартовы координаты, где .
Укажите его объем в единицах .
Возможные ответы:
Правильный ответ:
Пояснение:
Тетраэдр — это треугольная пирамида, и его можно рассматривать как таковую.
Три вершины — — находятся на горизонтальной плоскости и могут рассматриваться как вершины треугольного основания.
Этот треугольник, как показано ниже, равнобедренный:
Его основание равно 12, а высота – 15, поэтому его площадь равна
. Четвертая вершина находится вне этой плоскости; его перпендикулярное (вертикальное) расстояние до вышеупомянутой грани — это разница между -координатами, , так что это высота пирамиды. Объем пирамиды
Сообщить об ошибке
В трехмерном пространстве четыре вершины тетраэдра — тела с четырьмя гранями — имеют декартовы координаты.
Укажите его объем в единицах .
Возможные ответы:
Правильного ответа нет среди других вариантов.
Правильный ответ:
Объяснение:
Тетраэдр — это треугольная пирамида, и его можно рассматривать как таковую.
Три вершины — — находятся на горизонтальной плоскости и могут рассматриваться как вершины треугольного основания.
Этот треугольник, как показано ниже, является равнобедренным (рисунок не в масштабе):
Его основание равно 20, а высота 9, поэтому его площадь равна
. Четвертая вершина находится вне этой плоскости; его перпендикулярное (вертикальное) расстояние до вышеупомянутой грани — это разница между -координатами, , это высота пирамиды. Объем пирамиды
Сообщить об ошибке
В трехмерном пространстве четыре вершины тетраэдра — тела с четырьмя гранями — имеют декартовы координаты.
Каков объем этого тетраэдра?
Возможные ответы:
Правильный ответ:
Объяснение:
Тетраэдр выглядит так:
это начало координат и другие три точки, которые находятся на расстоянии двенадцати единиц от начала координат, каждая на одной из трех (взаимно перпендикулярных) осей.