Что такое действительное число?
Что такое действительное число?
Действительными или вещественными числами называются все положительные числа, отрицательные числа и нуль. Множество действительных чисел объединяет в себе множество рациональных и иррациональных чисел. Обозначается множество действительных чисел R . Например.
Что такое любое действительное число?
Действительные числа – это числа, которые могут быть записаны в виде конечной или бесконечной (периодической или непериодической) десятичной дроби. Итак, по определению действительным числом является любое рациональное, а также любое иррациональное число. Это позволяет нам привести примеры действительных чисел.
Что не входит в действительные числа?
Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно. Еще одно название для действительных чисел — вещественные числа.
Еще одно название для действительных чисел — вещественные числа.
Как обозначаются все числа?
Множество всех натуральных чисел обозначают так: N. Целые числа – натуральные числа, числа обратные натуральным и нуль. Множество всех целых чисел обозначают так: Z. Рациональные числа – числа, которые можно представить в виде дроби , где m – целое число, а n – натуральное число.
Как записываются натуральные числа?
Любое натуральное число можно записать в виде разрядных слагаемых. Числа 1, 10, 100, 1000… называются разрядными единицами. С их помощью натуральное число записывается в виде разрядных слагаемых.
Как найти наименьшее натуральное число?
Нахождение путём последовательного нахождения НОК
- Сначала находят НОК каких-нибудь двух из данных чисел.
- Потом, НОК найденного наименьшего общего кратного и третьего данного числа.

- Затем, НОК полученного наименьшего общего кратного и четвёртого числа и т. …
- Таким образом поиск НОК продолжается до тех пор, пока есть числа.
Для чего человеку нужны натуральные числа?
Натуральные числа — это числа, используемые для счета предметов или для указания порядкового номера того или иного предмета среди однородных предметов. Например: 3, 132, 68, 126, 548, 10050. … Наибольшего натурального числа нет, так как ряд натуральных чисел бесконечен.
Какое число 0?
Ноль (0, нуль от лат. nullus — никакой) — целое число, которое при сложении с любым числом или вычитании из него не меняет последнее, то есть даёт результат, равный этому последнему; умножение любого числа на ноль даёт ноль.
Сколькими нулями оканчивается произведение всех натуральных чисел от 12 до 40?
Среди простых множителей от 12 до 40 — 6 чисел делятся на 5 без остатка (30,35,40) — это 6 пятерок, кроме того, среди этих чисел есть число 25, которое делится на 5 дважды, тогда 6+1=7 пятерок, так как четных чисел гораздо больше, то произведение всех натуральных чисел от 12 до 40 заканчивается 7 нулями.
Сколькими нулями оканчивается произведение всех натуральных чисел от 18 до 45?
Ответ: 7 нулей.
Сколькими нулями заканчивается произведение всех натуральных чисел от 1 до 15?
Произведение всех натуральных чисел от 1 до 15 заканчивается тремя 0.
Сколькими нулями заканчивается произведение всех натуральных чисел от 10 до 50?
Среди простых множителей от 10 до 50 — 9 чисел делятся на 5 без остатка (10,45,50) — это 9 пятерок, кроме того, среди этих чисел есть два числа (25 и 50), которые делятся на 5 дважды, тогда 9+2=11 пятерок, так как четных чисел гораздо больше, то произведение всех натуральных чисел от 10 до 50 …
Действительные (вещественные) числа — rajak.rs
Арифметика и алгебра
Действительные (вещественные) числа
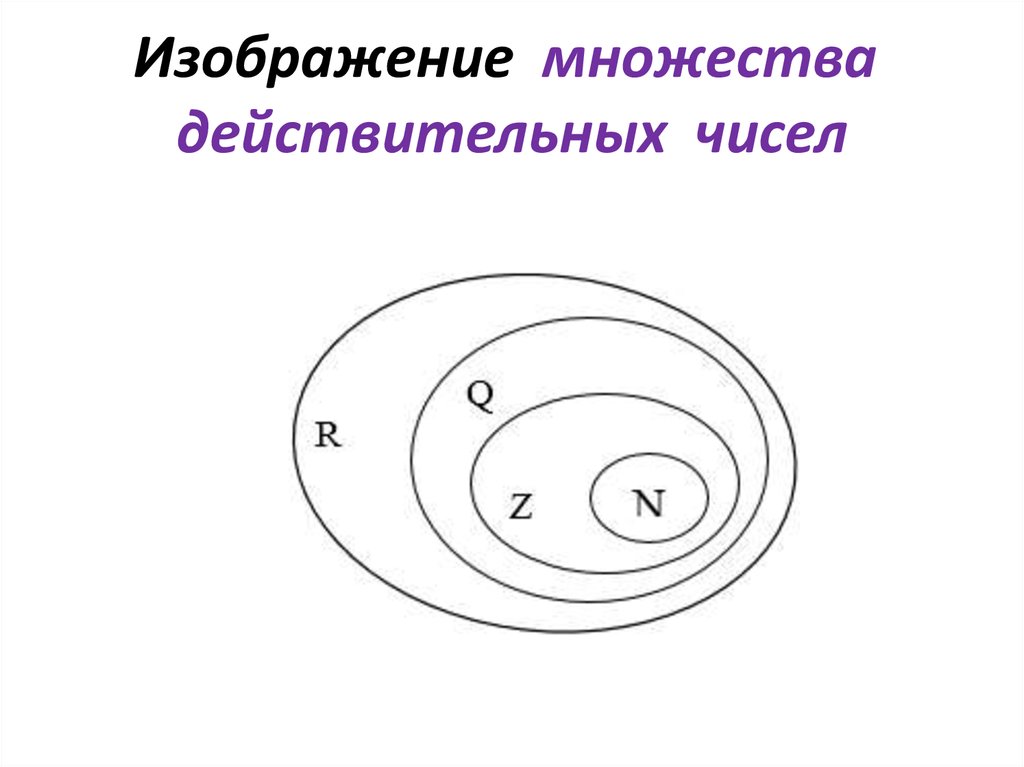
Действительные (вещественные) числа — это рациональные и иррациональные числа. Множество действительных чисел обозначается $\mathbb{R}$.
Свойства действительных чисел
Для любых действительных чисел $a$, $b$ и $c$ справедливо:
упорядоченность: для двух чисел $a$ и $b$ всегда или $a = b$ или $a \ne b$, (т.е. $a > b$ или $a< b$)
рефлексивность: $a = a$,
симметричность: из $a = b$ следует $b = a$,
транзитивность: из $a = b$ и $b = c$ следует $a = c$.
Свойства сложения и умножения:
Замкнутость: если $a,b \in \mathbb{R}$, тогда $a + b \in \mathbb{R}$ и $ab \in \mathbb{R}$.
Если $a = {a_1}$ и $b = {b_1}$, тогда $$a + b = {a_1} + {b_1},$$ $$ab = {a_1}{b_1}$$
Коммутативность: $$a + b = b + a,$$ $$ab = ba$$
Ассоциативность: $$a + \left( {b + c} \right) = \left( {a + b} \right) + c = a + b + c,$$ $$a\left( {bc} \right) = \left( {ab} \right)c = abc$$
Нейтральный элимент для операции сложения (нуль) и операции умножеия (единица): $$a + \left( { — a} \right) = a — a = 0$$ $$a\left( {{a^{ — 1}}} \right) = a{a^{ — 1}} = 1, \left( {a \ne 0} \right)$$
дистрибутивность: $$a\left( {b + c} \right) = ab + ac. $$
$$
Также можно доказать следующие свойства:
- $a \cdot 0 = 0$,
- для $a,b \in \mathbb{R}$, существует $x \in \mathbb{R}$ таой, что $a + x = b$,
- из $a + x = b + x$, следует, что $a = b$,
- для $a \in \mathbb{R}$, $a \ne 0$, существует $x \in \mathbb{R}$ такой, что $ax = 1$,
- из $ax = bx,x \ne 0$, следует, что $a = b$,
- из $ab = 0$, следует, что $a = 0$ или $b = 0$,
- из $ab \ne 0$, следует, что $a\ne 0$ и $b \ne 0$.
Неравенства
Действительное число $a$ может быть положительно ($a > 0$), отрицательно ($a < 0$) или равно нулю ($a = 0$)
Действительное число $a$ больше действительного числа $b\left( {a > b,b < a} \right)$, если $a = b + x$, где $x$ положительное действительное число.
Свойства неравенств:
- из $a > b$ следует, что $a + c > b + c$, $ac > bc$, если $c > 0$ и $ac > bc$, если $c < 0$.

- из $a > b$ следует, что $\frac{1}{a} < \frac{1}{b},$ если $ab > 0$ и $\frac{1}{a} > \frac{1}{b},$ если $ab < 0$,
- из $a \ge b$ и $b \ge c$ следует, что $a \ge c$,
- из $a \le A$ и $b \le B$ следует, что $a + b \le A + B,$ где ${\rm{ }}A,B \in \mathbb{R}$
Абсолютная величина (модуль) действительного числа
Абсолютная величина (модуль) $\left| a \right|$ действительного числа $a$ — это само число $a$, если $a \ge 0$, и $- a$, если $a < 0$ , т.е. $$\left|a \right| = \left\{ {\begin{array}{*{20}{c}} {{a, a \ge 0,}\\ { — a, a < 0.}} \end{array}} \right.$$
Свойства абсолютной величины:
- $\left| a \right| \ge 0$
- $\left| a \right| = 0$ тогда и только тогда, когда $a=0$,
- $\left| {\left| a \right| — \left| b \right|} \right| \le \left| {a \pm b} \right| \le \left| a \right| + \left| b \right|$,
- $\left| {ab} \right| = \left| a \right|\left| b \right|$,
- $\left| {\frac{a}{b}} \right| = \left| {\frac{a}{b}} \right|$ ако је $b \ne 0$,
- из $\left| a \right| \le A$ и $\left| b \right| \le B$ следует, что $\left| {a + b} \right| \le A + B$ и $\left| {ab} \right| \le AB,$ где ${\rm{ A}}{\rm{,B}} \in \mathbb{R}$,
- из $\left| a \right| \le \left| b \right|$ следует, что ${a^2} \le {b^2}$ и обратно.

Другие определения
Что такое реальное число? | Определение и свойства реальных чисел
В этом посте мы собираемся обсудить; что такое действительное число, его определение, классификация и свойства, связанные с действительными числами.
Что такое реальное число?
Вещественное число — это значение, которое может быть представлено вдоль числовой прямой как
Классификация действительных чисел
Вещественные числа подразделяются на следующие:
- Рациональные числа
- Дроби
- Integers
- Целые номера
- Натуральные номера
- ZERO
- Отрицательные целые числа
- Целые номера
- IRRATION NUMPLE
Теперь мы обсудим все.
1 – Рациональные числа
Рациональные числа можно записать как отношение двух целых чисел в форме p/q, где p и q оба являются целыми числами, а q не равно нулю. Оно обозначается буквой Q. Несколько примеров рациональных чисел:
Несколько примеров рациональных чисел:
Существует два вида десятичного представления рациональных чисел.
- Конечные десятичные дроби – фиксированное количество цифры в его десятичной части. Например,
- Бесконечный или повторяющиеся десятичные дроби – нет фиксированного количества цифр в ее десятичной части или некоторые цифры повторяясь снова и снова. Например,
1.1 – Дроби
Дробь может быть записывается как
Например,
Типы дробей;
- Правильные дроби – В правильных дробях числитель всегда меньше знаменателя, т.е.
- Неправильные дроби – В неправильных дробях числитель всегда равен или больше знаменателя, например.
- Смешанные дроби – В смешанных дробях есть и правильная дробь, и целое число, например.
1.
 2 – Целые числа
2 – Целые числаЭто может быть целое число или отрицательное целое число, не имеющее дробной части после запятой. Обозначается буквой Z, т. е.
1.2.1 — Целые числа
Целые числа — это целые числа без отрицательных целых чисел, которые начинаются с нуля и далее в числовой строке.
Целые числа обозначаются буквой W. т. е.
Здесь уместно упомянуть, что положительные целые числа похожи на целые числа, но они начинаются с 1 и далее без 0, т. е.
1.2.1 (a) Натуральные числа
Натуральные числа — это все целые числа, начинающиеся с 1 и далее, то есть 1, 2, 3, 4, 5,……………. Натуральные числа обозначаются буквой N. Например,
1.2.1 (b) Ноль
Ноль считается целым числом, но не имеет положительного или отрицательного значения.
1.2.2 – Отрицательные целые числа
Отрицательные целые числа начинаются с минус единицы и далее, т. е.
е.
2 – Иррациональные числа
Иррациональные числа – это действительные числа, которые нельзя записать в виде отношения двух целых чисел. Обозначается Q’. Несколько примеров иррациональных чисел:
Свойства действительных чисел
Свойства действительных чисел относительно сложения, вычитания, умножения и:
, b
— два действительных числа и a + b = c, тогда c равно также целое число.5 + 3 = 8. Где 8 тоже целое число.
2.2 – Переместительное свойство
Если a, b два вещественных числа, тогда
a + b = b + a.
Например,
a = 5, b = 3
⇒ 5 + 3 = 8 = 3 + 5
а + (б + с) = (а + б) + с = (а + с) + б.
Например,
a = 3, b = 5, c = 4
3 + (5 + 4) = (3 + 5) + 4 = (3 + 4) + 5 = 12
2.4 – Идентификатор добавки
В дополнение идентичность, существует отличное действительное число, т. е. 0, следовательно,
a + 0 = a = 0 + a
Например,
3 + 0 = 3 = 0 + 3
2,5 – Аддитивное обратное
Аддитивное обратное из a обозначается – a, тогда
a + (–a) = 0 = (–a) + a
Значит, аддитивное обратное 1 равно – 1. Например,
Например,
5 + (–5) = 0 = (–5) + 5
2 – Свойства вычитания
2.1 – Свойство замыкания
Если a, b два действительных числа и a – b = c, то c не является всегда целое число. Например,
Пусть a = 5 и b = 3, тогда
5 – 3 = 2 (целое число), тогда как
3 – 5 = -2, что равно не целое число.
2.2 – Переместительное свойство
Если a, b два вещественных числа, тогда
Например,
a = 5, b = 3
2.3 – Ассоциативное свойство
Пусть a, b, c — 3 целых числа, тогда
Например,
a = 3, b = 5, c = 4
3 — Свойства умножения
3.1 — Закрытие Свойство
Если a, b — два целых числа, а
, то c — тоже целое число. Например,
Пусть a = 5 и b = 3, тогда
(целое число) и
, что тоже является целым числом.
3.2 – Коммутативное свойство
Если a, b два действительных числа, тогда,
Например,
a = 5, b = 3
3.3 – Ассоциативное свойство
Пусть, a, b, c три целых числа, тогда, например,
,
a = 3, b = 5, c = 4
3.4 – Мультипликативное свойство нуля
Мультипликативное свойство нуля,
Например,
3.5 – Мультипликативная идентичность
Мультипликативная тождество задается как,
Например,
4 – Свойства Раздела
4.1 – Свойство Закрытия
Это свойство говорит о том, что результат деления двух числа не всегда являются целыми числами. Например,
(целое число), тогда как
4.2 – Переместительное свойство
Если a, b два действительных цифры, то
Например,
a = 20, b = 10
4.
 3 – Ассоциативное свойство
3 – Ассоциативное свойствоПусть, a, b, c три целых числа, тогда,
30 Например,
3 = 3, b = 5, c = 4
1.1: Вещественные и рациональные числа
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7916
- Юджин Боман и Роберт Роджерс
- Государственный университет Пенсильвании и SUNY Fredonia через OpenSUNY 9002
Цели обучения
- Объяснение действительных и рациональных чисел
Набор действительных чисел (обозначаемый \(\Re\)) назван неправильно. Действительные числа не более и не менее реальны — в нематематическом смысле, в котором они существуют, — чем любой другой набор чисел, точно так же, как набор рациональных чисел (\(\mathbb{Q}\)), набор целых чисел (\(\mathbb{Z}\)), или множество натуральных чисел (\(\mathbb{N}\)).
 Название «действительные числа» является (почти) исторической аномалией, мало чем отличающейся от названия «Теорема Пифагора», которое на самом деле было известно и понято задолго до жизни Пифагора. 9{го}\) века числа были хорошо изучены, или так считалось. В конце концов, это были просто цифры. Объедините их. Мы называем это добавлением. Если вы добавляете их повторно, мы называем это умножением. Точно так же понимались вычитание и деление.
Название «действительные числа» является (почти) исторической аномалией, мало чем отличающейся от названия «Теорема Пифагора», которое на самом деле было известно и понято задолго до жизни Пифагора. 9{го}\) века числа были хорошо изучены, или так считалось. В конце концов, это были просто цифры. Объедините их. Мы называем это добавлением. Если вы добавляете их повторно, мы называем это умножением. Точно так же понимались вычитание и деление.Было (и остается) полезно визуализировать эти вещи более конкретным образом. Если мы возьмем палку длиной \(2\) и другую длиной \(3\) и сложим их встык, мы получим длину \(5\). Это дополнение. Если мы положим их встык, но под прямым углом, то наши две палочки будут иметь длину и ширину прямоугольника, площадь которого равна \(6\). Это умножение.
Конечно, измерение длины целыми числами имеет ограничения, но их несложно исправить. Если у нас есть длина (палка) длины \(1\) и другая длина \(2\), то мы можем найти другую, длина которой по сравнению с \(1\) такая же (имеет ту же пропорцию, что и) как \(1\) к \(2\).
Это число, конечно же, \(1/2\).
Рисунок \(\PageIndex{1}\): Длина стержня.
Обратите внимание, как представление дробей отражает операцию сравнения \(1\) с \(2\). Это сравнение обычно называют отношением \(1\) к \(2\), поэтому числа такого рода называются рациональными числами. Множество рациональных чисел обозначается \(\mathbb{Q}\) для частных. В начальной школе они были представлены вам как дроби. Как только дроби понятны, эта визуализация с использованием отрезков (палочек) вполне естественно приводит к их представлению с помощью линии рациональных чисел.
Рисунок \(\PageIndex{2}\): Строка рациональных чисел.
Кажется, это работает как визуализация, потому что точки на линии и рациональные числа имеют общие свойства. Главный из них состоит в том, что между любыми двумя точками на рациональной прямой есть другая точка, точно так же, как между любыми двумя рациональными числами есть другое рациональное число.

Упражнение \(\PageIndex{1}\)
Пусть \(a,b,c,d ∈ N\) и найдем рациональное число между \(a/b\) и \(c/d\).
Это все очень чисто и удовлетворительно, пока мы не рассмотрим это поближе. Тогда это становится совсем загадочным. Рассмотрим снова рациональные числа \(a/b\) и \(c/d\). Если мы представим их как длины, мы можем спросить: « Существует ли третья длина, скажем, \(α\), такая, что мы можем разделить \(a/b\) на \(M\) частей, каждая из которых имеет длину \ (α\), а также разделить \(c/d\) на \(N\) кусков длины \(α\) каждый? » Несколько минут размышлений должны убедить вас, что это то же самое, что и задача нахождения общего знаменателя, так что \(α = \frac{1}{bd}\) будет работать хорошо. (Подтвердите это сами.)
Вам может быть интересно, из-за чего мы поднимаем всю эту суету. Очевидно, это всегда верно. На самом деле предыдущий абзац дает набросок очень хорошего небольшого доказательства этого. Здесь теорема и ее доказательство представлены формально.

Теорема \(\PageIndex{1}\)
Пусть \(a\), \(b\), \(c\) и \(d\) — целые числа. Существует число \(α ∈ Q\) такое, что \(Mα = a/b\) и \(Nα = c/d\), где \(M\) и \(N\) также целые числа.
Доказательство:
Чтобы доказать эту теорему, мы будем отображать \(α\), \(M\) и \(N\). Вы несете ответственность за подтверждение того, что они действительно работают. Вот они: \(α = 1/bd\), \(M = ad\) и \(N = cb\).
Упражнение \(\PageIndex{2}\)
Подтвердите, что \(α\), \(M\) и \(N\), указанные в доказательстве теоремы \(\PageIndex{1}\), удовлетворяют требования теоремы.
Должно быть ясно, что необходимо, чтобы \(a\), \(b\), \(c\) и \(d\) были целыми числами, чтобы все работало. В противном случае \(M\) и \(N\) также не будут целыми числами, как это требуется.
Это наводит на следующий очень глубокий и важный вопрос: существуют ли длины, которые нельзя выразить как отношение двух целых длин? Ответ, конечно же, да. Иначе мы бы не задавали этот вопрос.
 Обратите внимание, что для таких чисел наше доказательство теоремы \(\PageIndex{1}\) неверно (почему бы и нет?).
Обратите внимание, что для таких чисел наше доказательство теоремы \(\PageIndex{1}\) неверно (почему бы и нет?).Одним из самых известных примеров такого числа является длина окружности круга диаметром \(1\). Это число обычно обозначается \(π\). Но круги — чрезвычайно сложные объекты — они кажутся простыми только потому, что они такие знакомые. Возникнув из круга, можно было бы ожидать, что число \(π\) также будет очень сложным, и это правда. На самом деле \(π\) — исключительно странное число по целому ряду причин. Давайте начнем с чего-то более легкого для размышления.
Квадраты просты. Два набора параллельных прямых под прямым углом одинаковой длины. Что может быть проще? Если мы построим квадрат со стороной, имеющей длину \(1\), то его диагональ будет иметь длину \(\sqrt{2}\).
Рисунок \(\PageIndex{3}\): Квадрат.
Это число не может быть выражено как отношение двух целых чисел. То есть нерационально. Это было известно с древних времен, но до сих пор сбивает с толку при первом знакомстве.
 Это кажется настолько нелогичным, что интеллект бунтует. Этого не может быть, », — говорится в нем. « Это просто безумие! »
Это кажется настолько нелогичным, что интеллект бунтует. Этого не может быть, », — говорится в нем. « Это просто безумие! »Тем не менее, это верно, и мы можем доказать это следующим образом.
Что произойдет, если мы предположим, что квадратный корень из двух можно выразить как отношение целых чисел? Мы покажем, что это необратимо ведет к выводу, который явно неверен.
Предположим, \(\sqrt{2} = a/b\), где \(a\) и \(b\) — целые числа. Предположим далее, что дробь \(a/b\) является наименьшим членом. Это допущение имеет решающее значение, потому что если \(a/b\) находится в наименьших терминах, мы знаем, что не более чем одно из них четно. 92\) тоже четно, а значит, \(b\) тоже должно быть четным. Но это невозможно. Мы только что пришли к выводу, что \(a\) и \(b\) оба четны, и этот вывод непосредственно следует из нашего исходного предположения, что не более одного из них может быть четным.
Это ерунда. Где наша ошибка? Его нет ни в одном отдельном шаге наших рассуждений.
 Это все было солидно. Проверьте еще раз, чтобы убедиться.
Это все было солидно. Проверьте еще раз, чтобы убедиться.Следовательно, наша ошибка должна заключаться в исходном предположении, что \(\sqrt{2}\) может быть выражено в виде дроби. Следовательно, это предположение должно быть ложным. Другими словами, \(\sqrt{2}\) не может быть выражено таким образом.
Упражнение \(\PageIndex{3}\)
Покажите, что каждое из следующих чисел иррационально:
- \(\sqrt{3}\)
- \(\sqrt{5}\)
- \(\sqrt[3]{2}\)
- \(i(= \sqrt{-1}) \)
- Квадратный корень каждого положительного целого числа, не являющегося квадратом целого числа.
Тот факт, что \(\sqrt{2}\) не является рациональным, мил и интересен, но если вы, подобно пифагорейцам в Древней Греции, не придерживаетесь сильного религиозного убеждения в том, что все числа рациональны, это не кажется ужасно важным . С другой стороны, само существование \(\sqrt{2}\) вызывает некоторые интересные вопросы.
 {\sqrt{2}}\)? Имеет ли это вообще какое-то значение.
{\sqrt{2}}\)? Имеет ли это вообще какое-то значение.Чем больше вы думаете об этом, тем более загадочным становится существование иррациональных чисел. Предположим, например, что мы пересматриваем построение отрезка длины \(\sqrt{2}\). Понятно, что конструкция работает и что такой отрезок действительно можно построить. Это существует.
Повторите построение, но на этот раз поместите сторону основания на рациональную линию.
Рисунок \(\PageIndex{4}\): Построение отрезка длины \(\sqrt{2}\) с основанием на рациональной прямой.
Мы знаем, что диагональ этого квадрата равна \(\sqrt{2}\), как указано. И мы знаем, что \(\sqrt{2}\) не является рациональным числом.
Теперь оставьте диагональ закрепленной в точке \((0,0)\), но позвольте ей повернуться вниз так, чтобы она совпала с осью \(x\)−.
Рисунок \(\PageIndex{5}\): Диагональ повернута вниз, чтобы совпасть с осью x.

Конец нашей диагонали будет очерчивать дугу окружности с радиусом \(\sqrt{2}\). Когда диагональ совпадает с осью \(x\)−, ее конечной точкой, очевидно, будет точка \((\sqrt{2} ,0)\), как показано.
Но подождите! Мы используем линию рациональных чисел для нашей оси \(x\)−. Это означает, что единственные точки на оси \(x\) — это те, которые соответствуют рациональным числам (дробям). Но мы знаем, что \(\sqrt{2}\) не рационально! Вывод: нет точки \((\sqrt{2} ,0)\). Его просто не существует.
Иными словами, в строке рациональных чисел есть дыра именно там, где должно быть \(\sqrt{2}\). Это странно!
Напомним, что между любыми двумя рациональными числами всегда есть другое. Именно этот факт привел нас к представлению рациональных чисел линией.
Рисунок \(\PageIndex{6}\): Строка рациональных чисел.
Но это еще хуже. Несложно показать, что \(\sqrt{3}\), \(\sqrt{5}\) и т. д. тоже иррациональны. Так же как \(π\) и \(e\), хотя их не так просто показать.
 Кажется, что в рациональной линии есть куча дыр. Бесконечно много. И тем не менее верна следующая теорема.
Кажется, что в рациональной линии есть куча дыр. Бесконечно много. И тем не менее верна следующая теорема.Теорема \(\PageIndex{2}\)
- Между любыми двумя различными действительными числами существует рациональное число.
- Между любыми двумя различными действительными числами находится иррациональное число.
Обе части этой теоремы основаны на разумном использовании того, что сейчас называется архимедовым свойством системы действительных чисел, которое можно формально сформулировать следующим образом.
Свойство Архимеда
Для любых двух положительных действительных чисел, \(a\) и \(b\), существует натуральное число \(n\), такое что \(na > b\).
Физически это означает, что мы можем опустошить океан \(b\) чайной ложкой a, при условии, что мы готовы использовать чайную ложку большое количество раз \(n\).
Это настолько интуитивно понятная концепция, что ее легко принять без доказательства. До изобретения исчисления и даже какое-то время после этого это просто предполагалось.
 Однако по мере того, как основные проблемы, связанные с концепциями исчисления, были поняты и решены, мы в конечном итоге пришли к более глубокому пониманию сложностей системы действительных чисел. Архимедово свойство больше не воспринимается как недоказанная аксиома, а скорее понимается как следствие других аксиом. Мы покажем это позже, а пока примем это так же очевидно, как и Архимед.
Однако по мере того, как основные проблемы, связанные с концепциями исчисления, были поняты и решены, мы в конечном итоге пришли к более глубокому пониманию сложностей системы действительных чисел. Архимедово свойство больше не воспринимается как недоказанная аксиома, а скорее понимается как следствие других аксиом. Мы покажем это позже, а пока примем это так же очевидно, как и Архимед.С изобретением исчисления математики семнадцатого века начали использовать объекты, которые не удовлетворяли архимедову свойству (фактически, то же самое делал и Архимед). Как мы увидим в следующей главе, когда Лейбниц написал первую статью о своей версии исчисления, он следовал этой практике, явно излагая правила манипулирования бесконечно малыми величинами (бесконечно малыми). Они считались действительными числами, которые не равны нулю и все же меньше любого действительного числа. Он использовал следующие обозначения: \(dx\) (бесконечно малое смещение в направлении \(x\)) и \(dy\) (бесконечно малое смещение в направлении \(y\)).
 {th}\) веке существование бесконечно малых чисел было, мягко говоря, шатким. Однако это не помешало математикам успешно использовать эти бесконечно малые величины.
{th}\) веке существование бесконечно малых чисел было, мягко говоря, шатким. Однако это не помешало математикам успешно использовать эти бесконечно малые величины.Мы вернемся к этой саге в последующих главах, а пока вернемся к теореме \(\PageIndex{2}\).
Набросок доказательства теоремы \(\PageIndex{2}\)
Мы наметим доказательство части (a) теоремы \(\PageIndex{2}\) и укажем, как его можно использовать для доказательства части (b ).
Пусть \(α\) и \(β\) — действительные числа с \(α > β\). Есть два случая.
- Случай 1: \(α — β > 1\). В этом случае между \(α\) и \(β\) лежит хотя бы одно целое число. Поскольку целые числа рациональны, мы закончили.
- Случай 2: \(α — β ≤ 1\). В этом случае по архимедову свойству существует натуральное число, скажем \(n\), такое, что \(n(α — β) = nα — nβ > 1\). Теперь между \(nα\) и \(nβ\) будет целое число. Теперь вы должны быть в состоянии найти рациональное число между \(α\) и \(β\).

Для части (b) разделите \(α\) и \(β\) на любое положительное иррациональное число и примените часть (a). Есть пара деталей, о которых следует помнить. Они рассматриваются в следующей задаче.
Упражнение \(\PageIndex{4}\)
- Докажите, что произведение ненулевого рационального числа на иррациональное число иррационально.
- Превратите приведенные выше идеи в доказательство теоремы \(\PageIndex{2}\).
С практической точки зрения существование иррациональных чисел не так уж важно. В свете теоремы \(\PageIndex{2}\) любое иррациональное число может быть сколь угодно точно аппроксимировано рациональным числом. Поэтому, если мы проектируем мост и требуется \(\sqrt{2}\), мы просто используем вместо него \(1.414\). Внесенная ошибка меньше \(0,001 = 1/1000\), так что, вероятно, это не имеет значения.
Но с теоретической точки зрения это разрушительно. Когда было изобретено исчисление, рациональные числа внезапно перестали соответствовать задаче обоснования понятий и операций, с которыми нам нужно было работать.

Ньютон явно основал свою версию исчисления на предположении, что мы можем думать о переменных величинах как о порожденных непрерывным движением. Если в нашей системе счисления есть дыры, такое непрерывное движение невозможно, потому что у нас нет возможности перепрыгнуть через дыры. Итак, Ньютон просто постулировал, что дырок нет. Он заполнил дыру там, где должно быть \(\sqrt{2}\). Он просто сказал, да, там есть число, называемое \(\sqrt{2}\), и он сделал то же самое со всеми другими отверстиями. 9{го}\) века свойства действительной системы счисления (\(\mathbb{R}\)) как расширения рациональной системы счисления (\(\mathbb{Q}\)) были хорошо изучены. Вот обе системы, визуализированные в виде линий:
Рисунок \(\PageIndex{7}\): Реальные и рациональные системы счисления.
Впечатляет, не так ли? Причина, по которой они выглядят одинаково, за исключением меток \(\mathbb{R}\) и \(\mathbb{R}\), конечно, заключается в том, что наша способность рисовать эскизы объектов, которые мы изучаем, полностью терпит неудачу, когда мы попробуйте сделать набросок \(\mathbb{R}\), а не \(\mathbb{Q}\).
 Все дыры в \(\mathbb{R}\) действительно есть, но не-дырки упакованы вместе так плотно, что мы не можем разделить их на рисунке. Эта неспособность зарисовать объекты, которые мы изучаем, будет частым источником разочарования.
Все дыры в \(\mathbb{R}\) действительно есть, но не-дырки упакованы вместе так плотно, что мы не можем разделить их на рисунке. Эта неспособность зарисовать объекты, которые мы изучаем, будет частым источником разочарования.Конечно, это не помешает нам рисовать эскизы. Когда мы это сделаем, наше воображение спасет нас, потому что можно представить \(\mathbb{Q}\) в отличие от \(\mathbb{R}\). Но отбросьте мысль, что набросок — это точное изображение чего-либо. В лучшем случае наши наброски будут лишь вспомогательными средствами для воображения.
Итак, на данный момент мы просто предположим существование действительных чисел. Предположим также, что они обладают всеми свойствами, к которым мы привыкли. Это вполне приемлемо, пока мы делаем наши предположения явными. Однако мы должны знать, что до сих пор существование и свойства действительных чисел были предположением, которое не было логически выведено. Всякий раз, когда мы делаем предположение, мы должны быть готовы либо полностью отказаться от него, если мы обнаружим, что оно приводит к бессмысленным результатам, либо пересмотреть предположение в свете этих результатов, чтобы посмотреть, сможем ли мы найти другое предположение, которое включало бы его в себя.





 Название «действительные числа» является (почти) исторической аномалией, мало чем отличающейся от названия «Теорема Пифагора», которое на самом деле было известно и понято задолго до жизни Пифагора. 9{го}\) века числа были хорошо изучены, или так считалось. В конце концов, это были просто цифры. Объедините их. Мы называем это добавлением. Если вы добавляете их повторно, мы называем это умножением. Точно так же понимались вычитание и деление.
Название «действительные числа» является (почти) исторической аномалией, мало чем отличающейся от названия «Теорема Пифагора», которое на самом деле было известно и понято задолго до жизни Пифагора. 9{го}\) века числа были хорошо изучены, или так считалось. В конце концов, это были просто цифры. Объедините их. Мы называем это добавлением. Если вы добавляете их повторно, мы называем это умножением. Точно так же понимались вычитание и деление.


 Обратите внимание, что для таких чисел наше доказательство теоремы \(\PageIndex{1}\) неверно (почему бы и нет?).
Обратите внимание, что для таких чисел наше доказательство теоремы \(\PageIndex{1}\) неверно (почему бы и нет?). Это кажется настолько нелогичным, что интеллект бунтует. Этого не может быть, », — говорится в нем. « Это просто безумие! »
Это кажется настолько нелогичным, что интеллект бунтует. Этого не может быть, », — говорится в нем. « Это просто безумие! » Это все было солидно. Проверьте еще раз, чтобы убедиться.
Это все было солидно. Проверьте еще раз, чтобы убедиться. {\sqrt{2}}\)? Имеет ли это вообще какое-то значение.
{\sqrt{2}}\)? Имеет ли это вообще какое-то значение.
 Кажется, что в рациональной линии есть куча дыр. Бесконечно много. И тем не менее верна следующая теорема.
Кажется, что в рациональной линии есть куча дыр. Бесконечно много. И тем не менее верна следующая теорема.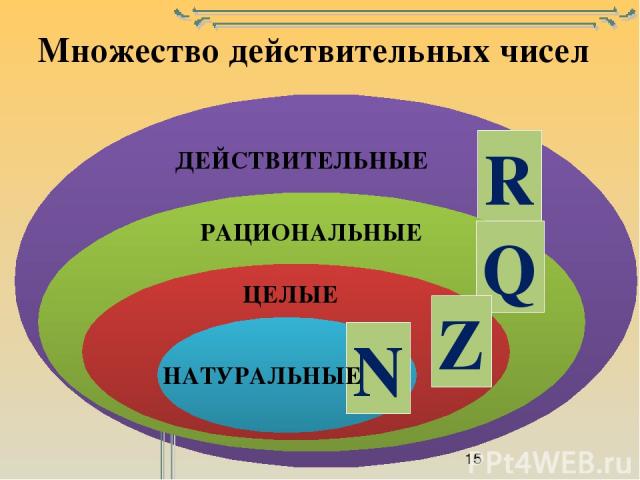 Однако по мере того, как основные проблемы, связанные с концепциями исчисления, были поняты и решены, мы в конечном итоге пришли к более глубокому пониманию сложностей системы действительных чисел. Архимедово свойство больше не воспринимается как недоказанная аксиома, а скорее понимается как следствие других аксиом. Мы покажем это позже, а пока примем это так же очевидно, как и Архимед.
Однако по мере того, как основные проблемы, связанные с концепциями исчисления, были поняты и решены, мы в конечном итоге пришли к более глубокому пониманию сложностей системы действительных чисел. Архимедово свойство больше не воспринимается как недоказанная аксиома, а скорее понимается как следствие других аксиом. Мы покажем это позже, а пока примем это так же очевидно, как и Архимед. {th}\) веке существование бесконечно малых чисел было, мягко говоря, шатким. Однако это не помешало математикам успешно использовать эти бесконечно малые величины.
{th}\) веке существование бесконечно малых чисел было, мягко говоря, шатким. Однако это не помешало математикам успешно использовать эти бесконечно малые величины.

 Все дыры в \(\mathbb{R}\) действительно есть, но не-дырки упакованы вместе так плотно, что мы не можем разделить их на рисунке. Эта неспособность зарисовать объекты, которые мы изучаем, будет частым источником разочарования.
Все дыры в \(\mathbb{R}\) действительно есть, но не-дырки упакованы вместе так плотно, что мы не можем разделить их на рисунке. Эта неспособность зарисовать объекты, которые мы изучаем, будет частым источником разочарования.