Конспект урока «Действия над матрицами»
Конспект урока по теме «Действия над матрицами»
Учитель математики: Григорьева Е. Д.
Цели:
Образовательные:
— рассмотреть операции сложения, вычитания, умножения матрицы на число и матрицы на матрицу, возведение в степень, нахождение обратной матрицы;
Развивающие:
— содействовать развитию у учащихся мыслительных операций: умение анализировать, синтезировать, сравнивать;
— отрабатывать навыки самооценивания знаний и умений, выбора заданий, соответствующего уровню мыслительной деятельности;
— формировать и развивать умения и навыки: обобщение, поиск способов решения.
Воспитательные:
— воспитание личных качеств, обеспечивающих успешность творческой деятельности;
—
воспитание требовательности, принципиальности, самокритичности, благородства,
чувства товарищества.
Тип урока: комбинированный.
Структура урока.
1) Организационный этап.
2) Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
3) Актуализация знаний.
4) Изучение нового материала.
5) Закрепление изученного материала.
6) Домашнее задание.
1. Организационный этап.
Приветствия учащихся; проверка их явки и готовности аудитории к уроку.
2. Постановка цели и задач урока.
Сообщает тему и цели практического занятия. Слушают, записывают в тетрадь.
3. Актуализация знаний.
Организует фронтальный опрос по теоретическим вопросам с использованием записей на диске.
Продумывают ответы, работают с лекционным материалом, анализируют, сравнивают, обобщают, отвечают на вопросы преподавателя, аргументируют ответы.
Беседа.
4. Изучение нового материала.
Операции над матрицами, свойства операций.
В этой статье мы
разберемся как проводится операция сложения над матицами одного порядка,
операция умножения матрицы на число и операция умножения матриц подходящего
порядка, аксиоматически зададим свойства операций, а также обсудим приоритет
операций над матрицами.
Сразу заметим, что все нижесказанное относится к матрицам, элементами которых являются действительные (или комплексные) числа.
Операция сложения двух матриц.
Определение операции сложения двух матриц.
Операция сложения определена ТОЛЬКО ДЛЯ МАТРИЦ ОДНОГО ПОРЯДКА. Другими словами, нельзя найти сумму матриц разной размерности и вообще нельзя говорить о сложении матриц разной размерности. Также нельзя говорить о сумме матрицы и числа или о сумме матрицы и какого-нибудь другого элемента.
Определение.
Сумма двух матриц и — это матрица, элементы которой равны сумме соответствующих элементов матриц А и В, то есть, .
Таким образом, результатом операции сложения двух матриц является матрица того же порядка.
Свойства операции сложения матриц.
Какими же
свойствами обладает операция сложения матриц? На этот вопрос достаточно легко
ответить, отталкиваясь от определения суммы двух матриц данного порядка и
вспомнив свойства операции сложения действительных (или комплексных) чисел.
1. Для матриц А, В и С одного порядка характерно свойство ассоциативности сложенияА+(В+С)=(А+В)+С.
2. Для матриц данного порядка существует нейтральный элемент по сложению, которым является нулевая матрица. То есть, справедливо свойство А+О=А.
3. Для ненулевой матрицы А данного порядка существует матрица (–А), их суммой является нулевая матрица: А+(-А)=О.
4. Для матриц А и В данного порядка справедливо свойство коммутативности сложения А+В=В+А.
Операция умножения матрицы на число.
Определение операции умножения матрицы на число.
Операция умножения матрицы на число определена ДЛЯ МАТРИЦ ЛЮБОГО ПОРЯДКА.
Определение.
Произведение
матрицы и
действительного (или комплексного) числа —
это матрица, элементы которой получаются умножением соответствующих элементов
исходной матрицы на число , то есть, .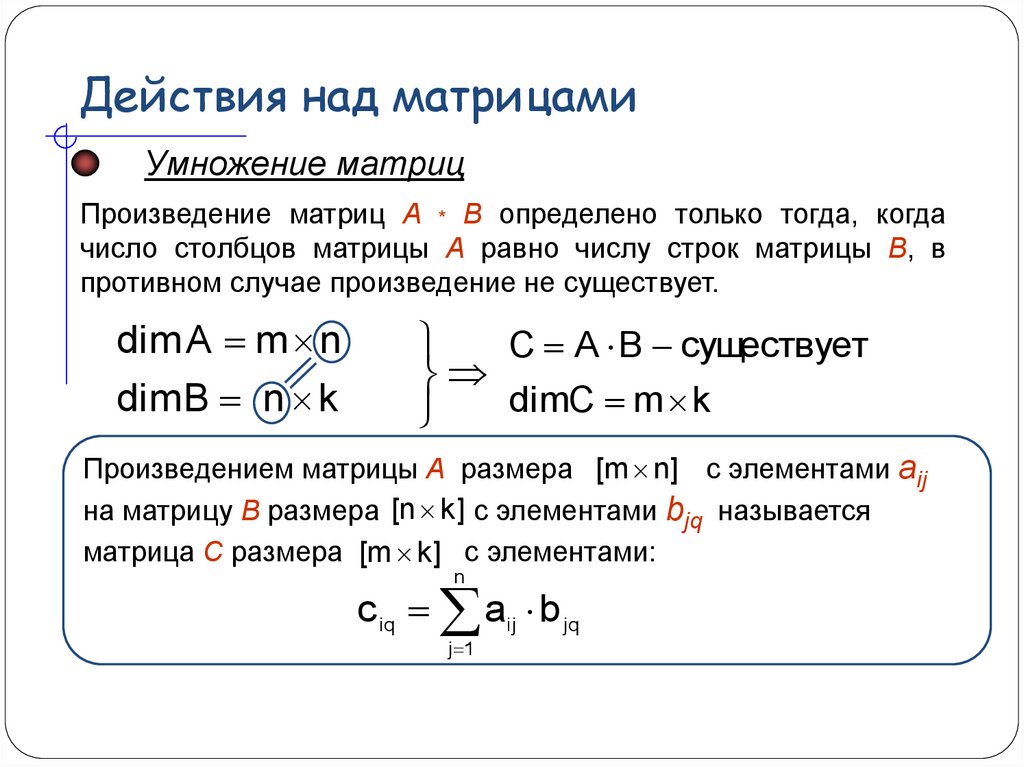
Таким образом, результатом умножения матрицы на число является матрица того же порядка.
Свойства операции умножения матрицы на число.
1. Для матриц одного порядка А и В, а также произвольного действительного (или комплексного) числа справедливо свойство дистрибутивности умножения относительно сложения .
2. Для произвольной матрицы А и любых действительных (или комплексных) чисел и выполняется свойство дистрибутивности .
3. Для произвольной матрицы А и любых действительных (или комплексных) чисел и справедливо свойство ассоциативности умножения .
4. Нейтральным числом по умножению на произвольную матрицу А является единица, то есть, .
Из свойств
операции умножения матрицы на число следует, что умножение нулевой матрицы на
число ноль даст нулевую матрицу, а произведение произвольного числа и нулевой
матрицы есть нулевая матрица.
Операция умножения двух матриц.
Определение операции умножения двух матриц.
Операция умножения двух матриц А и В определяется только для случая, когда ЧИСЛО СТОЛБЦОВ МАТРИЦЫ А РАВНО ЧИСЛУ СТРОК МАТРИЦЫ В.
Определение.
Произведение
матрицы А порядка и
матрицы В порядка —
это такая матрица С порядка , каждый элемент
которой равен сумме произведений элементов i-ой строки
матрицы А на соответствующие элементы j-ого столбца
матрицы В, то есть,
Таким образом, результатом операции умножения матрицы порядка на матрицу порядка является матрица порядка .
Свойства операции умножения матриц.
Если матрицы А, В и С подходящих порядков, то справедливы следующие свойства операции умножения матриц.
1.
Свойство ассоциативности умножения
матриц .
2. Два свойства дистрибутивности и .
3. В общем случае операция умножения матриц некоммутативна .
4. Единичная матрица Е порядка n на n является нейтральным элементом по умножению, то есть, для произвольной матрицы А порядка p на n справедливо равенство , а для произвольной матрицы А порядка n на p — равенство .
Следует отметить, что при подходящих порядках произведение нулевой матрицы О на матрицуА дает нулевую матрицу. Произведение А на О также дает нулевую матрицу, если порядки позволяют проводить операцию умножения матриц.
Среди квадратных матриц существуют так называемые перестановочные матрицы, операция умножения для них коммутативна, то есть . Примером перестановочных матриц является пара единичной матрицы и любой другой матрицы того же порядка, так как справедливо .
5. Закрепление
изученного материала.
Сложение матриц — решения примеров.
Рассмотрим несколько примеров сложения матриц.
Пример.
Найдите сумму матриц и .
Решение.
Порядки
матриц А и В совпадают и равны 4 на 2,
поэтому мы можем проводить операцию сложения матриц и в результате должны
получить матрицу порядка 4 на 2. Согласно
определению операции сложения двух матриц, сложение производим поэлементно:
Пример.
Найдите сумму двух матриц и элементами которых являются комплексные числа.
Решение.
Так как порядки
матриц равны, то мы можем выполнить сложение.
Пример.
Выполните сложение трех матриц .
Решение.
Сначала сложим
матрицу А с В, затем к полученной матрице
прибавим С:
Получили нулевую матрицу.
Умножение матрицы на число — примеры и их решение.
Разберемся с проведением
операция умножения матрицы на число на примерах.
Пример.
Найдите произведение числа 2 и матрицы .
Решение.
Чтобы умножить
матрицу на число, нужно каждый ее элемент умножить на это число:
Пример.
Выполните умножение матрицы на число .
Решение.
Умножаем каждый
элемент заданной матрицы на данное число:
Умножение матрицы на матрицу — решения примеров.
Разберемся с умножением матриц на примерах, после этого перейдем к перечислению свойств операции умножения матриц.
Пример.
Найдите все элементы матрицы С, которая получается при умножении матриц и .
Решение.
Порядок
матрицы А равен p=3 на n=2,
порядок матрицы В равен n=2 на q=4,
следовательно, порядок порядок произведения этих матриц будет p=3 на q=4.
Воспользуемся формулой
Последовательно
принимаем значения i от 1 до 3 (так
как p=3) для каждого j от 1 до 4(так
как q=4), а n=2 в нашем случае, тогда
Так вычислены все
элементы матрицы С, и матрица, полученная при умножении двух
заданных матриц, имеет вид .
Пример.
Выполните умножение матриц и .
Решение.
Порядки исходных
матриц позволяют провести операцию умножения. В результате мы должны получить
матрицу порядка 2 на 3.
Пример.
Даны матрицы и . Найдите произведение матриц А и В, а также матриц В и А.
Решение.
Так как порядок
матрицы А равен 3 на 1, а
матрицы В равен 1 на 3, то А⋅В будет
иметь порядок 3 на 3, а произведение матриц В и A будет
иметь порядок 1 на 1.
Как видите, . Это одно из свойств операции умножения матриц.
Пример.
Даны матрицы . Выполните с заданными матрицами указанные действия .
Решение.
Начинаем с умножения
матрицы А на матрицу В:
Теперь умножаем
единичную матрицу второго порядка Е на два:
Складываем две
полученные матрицы:
Осталось выполнить
операцию умножения полученной матрицы на матрицу А:
Следует заметить,
что операции вычитания матриц одного порядка А и В как
таковой не существует.
Разность двух матриц по сути есть сумма матрицы А и
матрицы В, предварительно умноженной на минус единицу: .
Операция возведения квадратной матрицы в натуральную степень так же не самостоятельна, так как является последовательным умножением матриц.
Подведем итог.
На множестве матриц определены три операции: сложение матриц одного порядка, умножение матрицы на число и умножение матриц подходящих порядков.
6. Домашнее задание.
Линейные операции над матрицами: сложение и умножение матриц
О чем статья
Сложение матриц
Сумма двух матриц и размером x называется матрица того же размера, каждый элемент которой равняется сумме соответствующих элементов матриц-слагаемых, то есть и обозначается .
Если же , тогда – разница матриц.
Любые действия: вычитание, сложение или умножение матриц называются линейными действиями над матрицами.
У матриц есть такие свойства:
- .
- .
- .
- .
- x = – в случае, если число , то есть коэффициент 1 можно отпустить, как в алгебре.
- .
- .
- .
Здесь обозначено – – нулевая матрица, а – противоположная матрице .
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Умножение матриц
Иногда в работе с таблицами (матрицами) приходится совершать определённые действия. Сложение мы рассмотрели, а теперь рассмотрим умножение матриц..
Произведением числа на матрицу размера x называется новая матрица того же размера, каждый элемент которой равняется соответствующему элементу матрицы умноженному на число , то есть:
Матрица (-1) – противоположна матрице , и обозначается . Действие сложения применяется только для тех матриц, которые одного и того же размера.
Умножение матриц имеет такие свойства:
- – произведение матриц ассоциативно;
- , где – число;
- x = – произведение матриц дистрибутивно;
- .
Произведение матрицы размером x на матрицу размером x называется матрица размером x, элементы которой равняются сумме произведений элементов -той строки матрицы на соответствующие элементы -того столбца матрицы , то есть:
.
Из структуры элементов понятна необходимость согласованности матриц и : каждому элементу в -той строке матрицы (первого сомножителя) и в -том столбце матрицы (второго сомножителя). Число строк и матрицы равняется числу строк первого сомножителя, а число столбцов – числу второго сомножителя.
Примеры на сложение и умножение матриц
Как уже описывалось ранее, сложение матриц производится тогда, когда матрицы одинаковые по размерам. Рассмотрим несколько примеров.
Примеры на сложение матриц
Пример 1
Даны матрицы:
Найти: 1); 2) – x
Решение:
Теперь находим – x и получим результат:
Рассмотрим ещё один пример, но более большой.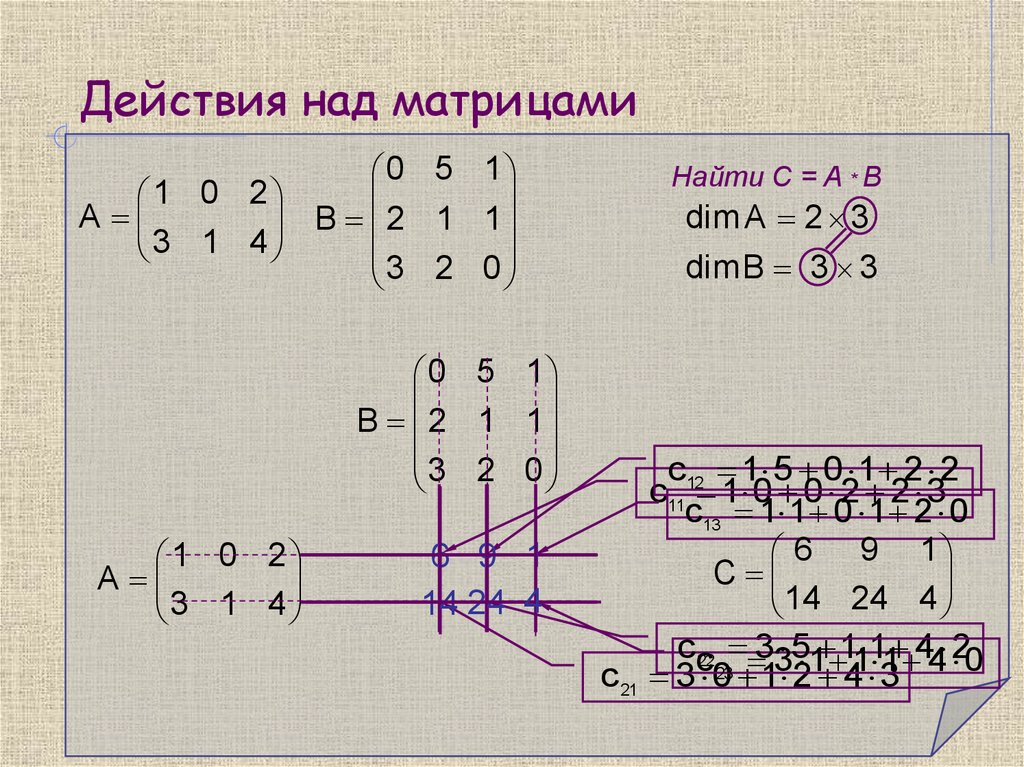
Будьте внимательны и не спешите, так как очень часто можно ошибиться в знаках:
Пример 2
Даны матрицы:
Примеры на умножение матриц
Приведём первый пример, на котором рассмотрим умножение матриц, где становится понятно, как составлять матрицы и какие операции с ними проводятся:
Пример 1
Шахтёры выполняют два вида работ: выемка пород и крепление. Эти работы при постоянной площади поперечного сечения могут измеряться в погонных метрах. Допустим, что в течение суток каждая из трёх смен добились таких результатов:
| Смены | Выемка (в м.) | Крепление (в м.) |
| первая смена | ||
| вторая смена | ||
| третья смена |
Эти результаты можно записать в виде матрицы размером :
Возьмём этот пример при подсчёте денежных затрат на выполнение робот в шахте.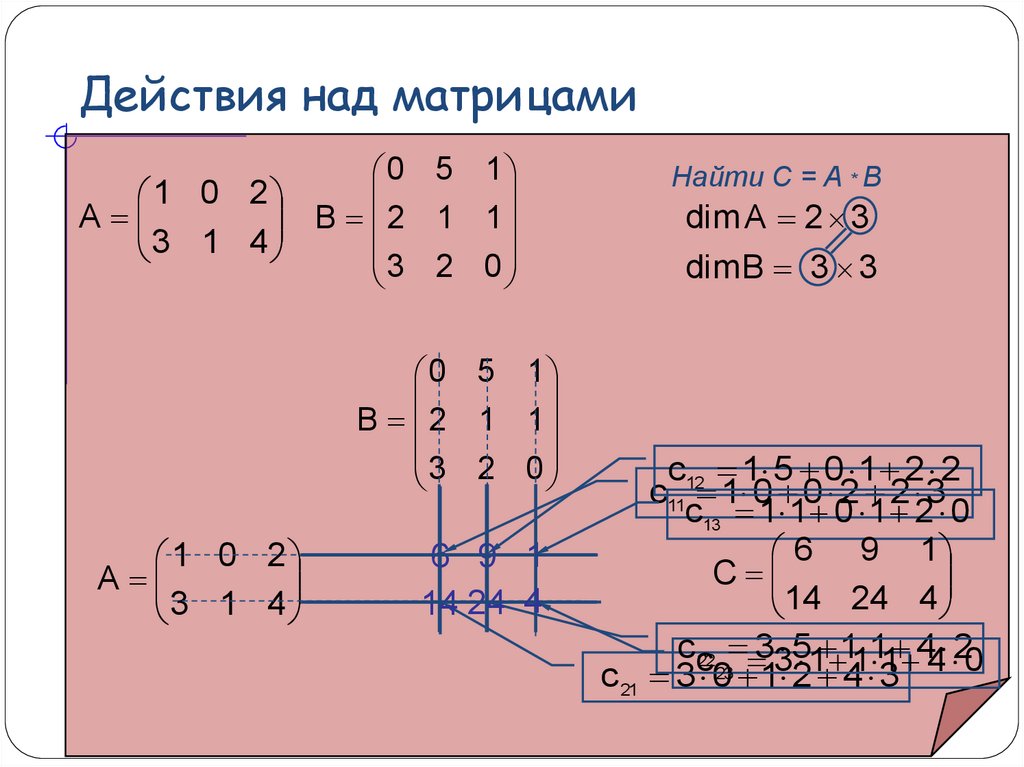
В матрице, которая у нас уже есть, записаны результаты работы за сутки каждой смены. Как уже упоминалось выше, результат работ измеряется в погонных метрах.
Заказчику необходимо знать, какую сумму придётся выделить на зарплату работникам, а какую на капитальные затраты. Это представим с виде матрицы расценок:
где первый столбец , – нормы зарплаты трудящихся: за 1 погонный метр по выемке породы, и, соответственно, за 1 погонный метр по креплению.
Второй столбец: , – капитальные затраты за 1 погонный метр выемки и за 1 погонный метр крепления.
Общие затраты на зарплату для каждой смены равняются произведению пройденного количества метров для каждого вида работ на определённые нормы расценок. Обозначим через сумму средств, которую заработала смена (). Аналогично подсчитываются капитальные затраты для смены по выемке и креплению.
Получим таблицу затрат:
| Смены | Затраты на зарплату по выемке и креплению | Капитальные затраты по выемке и креплению |
| первая смена | ||
| вторая смена | ||
| третья смена |
Эти данные запишем в виде новой матрицы затрат x, что получена из матриц и при помощи действий, которые называются умножение матриц, и обозначают:
Для умножения матрицы размером x на матрицу размером x необходима её согласованность, то есть, чтобы число столбцов матрицы (первого сомножителя) совпадало с числом строк матрицы (второго сомножителя).
В приведенном примере матрица согласована с матрицей (для каждого вида работ – нормы расценок). Однако, в примере, который представлен выше, матрица не согласована с матрицей .
Пример 2
Найти произведение матриц и , если:
Решение:
У матрицы размер x, а размер матрицы – x. У матрицы 2 столбца, а у матрицы 2 строки, а это значит, что матрицы согласованы, так как можно умножать матрицу на матрицу . В результате получим матрицу размером x, то есть:
Пример 3
Убедитесь, что для данных матриц:
,
.
Обратите внимание, что в данном случае
Пример 4
Посмотрите, что получается, когда даны матрицы:
Видите, какие иногда получаются матрицы после решения? В нашем случае произведение двух ненулевых матриц дал нулевую матрицу, и, кроме этого,
Средняя оценка 2.3 / 5. Количество оценок: 3
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
5233
Закажите помощь с работой
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
Шаблон матрицы ударных усилий| Miro
О шаблоне матрицы воздействия
Вам сложно расставить приоритеты задач? Или вы хотите определить действия, которые дадут вашим клиентам лучший опыт? Матрица воздействия может быть именно тем, что вам нужно.
Используйте шаблон матрицы воздействия усилий, чтобы расставить приоритеты в своей работе на основе требуемых усилий и влияния, которое она окажет на ваших клиентов. Выровняйте свои приоритеты и выполняйте проекты, сокращая потери времени и энергии.
Что такое шаблон матрицы воздействия?
Матрица усилий воздействия (также известная как матрица приоритетов действий) — это инструмент для принятия решений. Заполнение этого шаблона матрицы результативности усилий помогает руководителям команд расставлять приоритеты в отношении следующего:
Задачи и проекты, которые приносят наилучшие результаты за наименьшее время
Проекты, которые требуют больше времени, но все же стоят того, чтобы их выполнить
Задачи и проекты, которые мало повлияют на ваших клиентов
Матрица разделена на четыре квадранта:
Минимальные усилия и малое влияние: Эти действия, также известные как заполнения, требуют небольшой работы и мало влияют на ваших клиентов.
Максимальные усилия и минимальное влияние: Задачи, которые требуют много времени и усилий с вашей стороны, но мало влияют на ваших клиентов. Их также называют пожирателями времени или неблагодарными задачами.
Высокая отдача и минимальные усилия: Эти задачи — ваши быстрые победы. Это действия, которые значительно влияют на ваших клиентов и не требуют от вас много работы.
Высокоэффективный и требующий максимальных усилий: Крупные проекты, требующие большого внимания, но оказывающие большое влияние на ваших клиентов.
Используя эти квадранты, вы можете легко визуализировать, какие задачи принесут наибольшую пользу вашим клиентам.
Как создать матрицу воздействия усилий?Создать матрицу воздействия легко и просто с помощью шаблона Миро:
Шаг 1: Соберите всю команду вместе. Крайне важно, чтобы матрица заполнялась реальными заинтересованными сторонами, заинтересованными в игре.
Почему? Потому что у них есть непосредственный взгляд на то, как выполняются задачи и сколько усилий требуется.
Шаг 2: Определите задачи и цели команды. Проведите мозговой штурм, чтобы определить основные задачи и цели команды. Это объединяет команду в общей миссии.
Шаг 3: Создайте четырехквадрантную диаграмму. Матрица усилий по воздействию строится по двум осям: уровень усилий, связанных с задачей, и уровень потенциального воздействия, которое может иметь завершение задачи. Квадранты уже нанесены на карту в нашем шаблоне, поэтому вам не нужно беспокоиться о создании его с нуля.
Шаг 4: Добавьте отдельные задачи в один из четырех квадрантов. Нанесите свои задачи на матрицу в зависимости от того, сколько усилий и влияния может иметь каждое действие. Внимательно изучите каждое место размещения со всей командой, чтобы убедиться, что все с ним согласны.
Шаг 5: Создайте план действий на основе ваших результатов.
Имея представление о влиянии и усилиях всех задач, вы можете определить, какие задачи заслуживают наибольшего времени и ресурсов в будущем.
Существует несколько ситуаций, когда полезно использовать матрицу усилия воздействия:
Распределение ресурсов: Если ваше время и ресурсы ограничены, матрица невероятно полезна. Например, если вам нужно рассмотреть несколько вариантов действий, вы можете использовать матрицу, чтобы найти наилучший вариант и соответствующим образом распределить ресурсы.
Для приоритизации задач: Матрица воздействия поможет вам приоритизировать задачи и найти наиболее эффективный путь к достижению ваших целей. Вы можете сосредоточиться на быстрых победах и увидеть результаты как можно быстрее.
Чтобы понять потребности клиентов: Использование матрицы поможет вам лучше понять, что ищут ваши клиенты.
Вы ставите себя на их место, чтобы увидеть, что они ценят, и включить это в свой план действий.
Вы ставите себя на их место, чтобы увидеть, что они ценят, и включить это в свой план действий.Матрица усилия воздействия является ценным инструментом для принятия решений. Это помогает командам оптимизировать ограниченное время и ресурсы, предоставляя визуальное руководство по всему, от ежедневных списков дел до более сложных стратегических планов. Рассмотрим некоторые из этих преимуществ более подробно.
Расставьте приоритеты задачМатрица воздействия заставляет вас расставлять приоритеты задач на основе того, что лучше для клиента и что поможет ему достичь своих целей. В результате вы определяете наиболее плодотворные способы провести время.
Максимальная эффективность и отдача Матрица результативных усилий анализирует, как вы тратите свое время. Обладая этой информацией, вы можете найти способы сократить количество отходов.