Как посчитать расстояние между точками по координатам: Расстояние между двумя точками

Содержание

Расчет расстояния между геокоординатами

У «Важных историй» вышел текст о том, как в 2021 году минимум 100 тысяч российских детей с трудом добираются до школ. Для части этого небольшого исследования мы считали радиусы доступности, то есть сколько километров от каждого населенного пункта России до ближайшей школы.

В этом уроке расскажем, как посчитать расстояния между объектами по прямой и затем выбирать ближайшие.

Важно, что расстояния в этом уроке считаются без учета дорог и естественных преград в виде гор, рек, болот и пр., поэтому дают общее представление о дальности объектов. Чтобы точно рассчитать дистанцию и время в пути по дорогам, можно воспользоваться API матрицы расстояний Яндекс.Карт (платно, либо можно попробовать попросить бесплатно в исследовательских и научных целях по индивидуальному запросу) или OSRM — Open Source Routing Machine (бесплатно).

Jupyter ноутбук с уроком доступен на странице Мастерской на GitHub.

Видео: Глеб Лиманский

1. Скачивание данных

Нам нужно два набора данных — с населенными пунктами и со школами.

1. Данные по населенным пунктам скачиваем на сайте ИНИД (Инфраструктура научно-исследовательских данных).

2. Данные по школам — с помощью парсинга с сайта https://schoolotzyv.ru/schools/9-russia/ (скачанные данные доступны в формате json по ссылке). По некоторым регионам на сайте есть не все школы. Можно дополнить данными с сайтов https://arhangelsk.fulledu.ru/, https://russiaedu.ru/, набора открытых данных с лицензиями Рособрнадзора (требуется парсинг xml) и других источников.

2. Загрузка библиотек

Загружаем 4 библиотеки: pandas для работы с датафреймами — данными в табличном виде, numpy и scikit-learn для математических операций, json для работы с файлами в формате json.

3. Загрузка и подготовка данных

Датасет со школами в формате json. Загружаем его в Pandas. В нем более 50 тысяч строк.

В файле есть геокоординаты (широта, долгота), ссылка на школу и ее название. Наименований регионов нет, а нам желательно для примера выбрать только один регион, иначе, если оставить всю Россию, это будет очень долго считаться. Регион можно узнать из ссылки. Например, в строке с индексом 1 школа из Камчатского края: в ссылке есть фрагмент «131-kamchatskij».

Выберем, например, Нижегородскую область. В ссылках она помечена как «146-nizhegorodskaya». С помощью метода contains («содержит»), выберем только те ссылки, в которых есть эта запись. Так у нас останутся только школы Нижегородской области. Подробнее о том, как фильтровать датафреймы — в первом уроке по Pandas.

Поскольку мы выбрали только некоторые строки, индексы датафрейма сбились и теперь идут не сначала:

Чтобы индексы сбросились и снова начинались с нуля, обновим их методом reset_index(). Drop = True означает, что старые индексы нам не нужны.

Далее загружаем файл с населенными пунктами. В нем есть регион, район, название, численность населения, сколько в них детей, координаты, код ОКТМО (Общероссийского классификатора территорий муниципальных образований).

Выберем тоже только Нижегородскую область, а чтобы все еще быстрее считалось, возьмем только один район, например, Воскресенский.

Снова обновляем индексы, чтобы шли с нуля.

4. Создание словарей

Прежде чем считать расстояния, нам понадобится создать два словаря — с населенными пунктами и со школами. Это нужно, чтобы в дальнейшем мы могли сопоставить разные датафреймы по какому-то уникальному параметру, доставать и добавлять нужные нам данные. Нам это пригодится на последних этапах.

Для населенных пунктов таким уникальным параметром, по которому можно будет объединять разные датафреймы, станет код ОКТМО (Общероссийского классификатора территорий муниципальных образований).

Перед этим нам нужно убедиться, что:

1) Во всех нужных нам столбцах указан правильный тип данных.

2) Удалены дубликаты в тех столбцах, которые будут уникальным ключом для словаря (для населенных пунктов это поле oktmo, для школ — url), поскольку ключи словаря не должны дублироваться.

Смотрим методом dtype, какой тип данных в столбце oktmo. Это float, число с плавающей точкой.

Удобнее будет в качестве уникального кода работать со строками, а не числами, поэтому поменяем тип данных сначала на integer, затем на string.

Смотрим, есть ли в столбце oktmo дубликаты.

Удаляем дубликаты и обновляем индексы.

Cобираем датафрейм с населенными пунктами в словарь, где ключом будет код ОКТМО, а значением — строка с информацией о соответствующем населенном пункте. Сначала мы создаем пустой словарь. Затем переменной i проходимся по всем индексам от 0 до последнего в нашем датафрейме. В переменную el записываем строку, которую получаем методом loc.

Переходим к датафрейму со школами. Сначала меняем тип данных в столбцах с широтой и долгой, потому что сейчас там строки, а нам для расчетов нужны числа (float).

Удаляем дубликаты и обновляем индексы.

И теперь для школ собираем такой же словарь, как и для населенных пунктов. Ключом будет url.

5. Расчет матрицы расстояний

Переходим к расчету расстояний между каждым населенным пунктом и каждой школой (матрица расстояний). За основу взят туториал Dana Lindquist.

Сначала переводим координаты из градусов в радианы, потому что математические формулы обычно требуют значения координат в радианах, а не в градусах. Делаем это с помощью библиотеки numpy.

Далее считаем расстояния с помощью формулы из библиотеки scikit-learn. Эта формула вычисляет гаверсинусное расстояние, то есть представляет форму Земли как идеальную сферу (а не геоид, как на самом деле) и за счет этого обеспечивает быстрые вычисления. Если требуется измерение в километрах, то в конце формулы нужно умоножать 6371, если в милях — на 3959. Мы получим расстояния от каждого населенного пункта до каждой школы в километрах.

Строим матрицу расстояний — таблицу, в которой индексами будут url школ, колонками — ОКТМО населенных пунктов, а в ячейках будет расстояние.

Но нам нужно расстояние от населенных пунктов до школ, а не наоборот, поэтому транспонируем таблицу — поменяем индексы и колонки местами.

6. Выбор ближайшего объекта

Выбираем ближайшую школу к каждому населенному пункту. Для этого сравниваем каждое значение в строке с предыдущим, чтобы проверить, больше оно или меньше. Меньшее записываем в переменную. Так проходим циклом по каждой строке, выбирая самое меньшее значение. И создаем словарь, в котором ключ — код ОКТМО населенного пункта, значения — url ближайшей школы и расстояние до нее.

Далее добавляем колонки с минимальным расстоянием и url школы в датафрейм places_voskresensk (с населенными пунктами). Для этого берем из созданного выше словаря schools_and_min_value_by_oktmo ссылку (url) и расстояние до школы (distns). Добавляем их в словари school_url_column и min_distance_column в том порядке, в каком соответствующие им коды ОКТМО расположены в датафрейме places_voskresensk. И добавляем соответствующие новые колонки к датафрейму.

Точно так же из словаря со школами достаем название школ и добавляем их к датафрейму.

В конце появились 3 новые колонки — url ближайшей школы, сколько до нее километров по прямой, название школы.

Сохраним полученный результат в csv.

7. Анализ данных

Дальше мы можем анализировать данные. Например, выбрать 15 наиболее удаленных от школ населенных пунктов методом nlarest. Подробнее об nlargest и nsmallest — в 3 уроке по Pandas.

Получили топ самых удаленных населенных пунктов. Или можем посчитать, сколько детей в Воскресенском районе Нижегородской области живут дальше 5 км от школы.

Или среднее расстояние от населенного пункта до школы.

Готово!

PostgreSQL : Документация: 9.5: F.12. earthdistance : Компания Postgres Professional

RU
EN
RU EN

F.12.1. Земные расстояния по кубам
F.12.2. Земные расстояния по точкам

Модуль earthdistance реализует два разных варианта вычисления ортодромии (расстояния между точками на поверхности Земли). Первый описанный вариант зависит от модуля cube. Второй вариант основан на встроенном типе данных point, в котором в качестве координат задаются широта и долгота.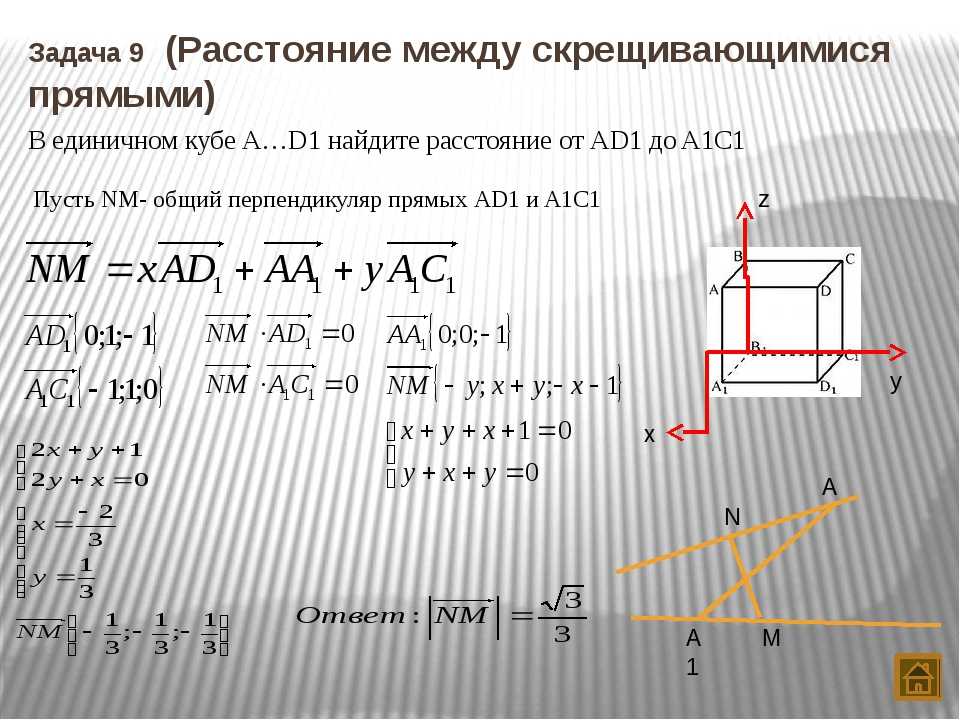

В этом модуле Земля считается идеальной сферой. (Если для вас это слишком грубо, обратите внимание на проект PostGIS.)

Прежде чем устанавливать earthdistance, вы должны установить модуль cube.

Внимание

Расширения earthdistance и cube настоятельно рекомендуется устанавливать в одну схему, и при этом в данной схеме недоверенные пользователи не должны в настоящем и будущем иметь право CREATE. В противном случае, если в схеме earthdistance окажутся объекты, созданные злонамеренным пользователем, возможна угроза безопасности. Более того, используя функции earthdistance после установки расширения, следует ограничивать путь поиска только доверенными схемами.

F.12.1. Земные расстояния по кубам

Данные хранятся в кубах, представляющих точки (оба угла куба совпадают) по 3 координатам, выражающим смещения x, y и z от центра Земли. Этот модуль предоставляет домен earth на базе cube, включающий проверки того, что значение соответствует этим ограничениям и представляет точку, достаточно близкую к сферической поверхности Земли.

Радиус Земли выдаёт функция earth() (в метрах). Изменив одну эту функцию, вы можете сделать так, чтобы модуль работал с другими единицами, либо выдать другое значение радиуса, которое кажется вам более подходящим.

Этот пакет может также применяться и для астрономических расчётов. Астрономы обычно меняют функцию earth(), чтобы она возвращала радиус, равный 180/pi(), и расстояния в результате выдавались в градусах.

В этом модуле реализованы функции для ввода данных, выражающих широту и долготу (в градусах), для вывода ширины и долготы, для вычисления ортодромии между двумя точками и простого указания окружающего прямоугольника, что полезно для поиска по индексу.

Предоставляемые этим модулем функции показаны в Таблица F.6.

Таблица F.6. Функции земных расстояний по кубам

Функция	Возвращает	Описание
`earth()`	`float8`	Возвращает предполагаемый радиус Земли.
`sec_to_gc(float8)`	`float8`	Переводит расстояние по обычной прямой (по секущей) между двумя точками на поверхности Земли в расстояние между ними по сфере.
`gc_to_sec(float8)`	`float8`	Переводит расстояние по сфере между двумя точками на поверхности Земли в расстояние по обычной прямой (по секущей) между ними.
`ll_to_earth(float8, float8)`	`earth`	Возвращает положение точки на поверхности Земли по заданной широте (аргумент 1) и долготе (аргумент 2) в градусах.
`latitude(earth)`	`float8`	Возвращает широту (в градусах) точки на поверхности Земли.
`longitude(earth)`	`float8`	Возвращает долготу (в градусах) точки на поверхности Земли.
`earth_distance(earth, earth)`	`float8`	Возвращает расстояние по сфере между двумя точками на поверхности Земли.
`earth_box(earth, float8)`	`cube`	Возвращает охватывающий куб, подходящий для поиска по индексу с применением оператора кубов `@>` точек в пределах заданной ортодромии от цели. Некоторые точки в этом кубе будут отстоять от цели дальше, чем на заданную ортодромию, поэтому в запрос нужно включить вторую проверку с функцией `earth_distance`.

F.12.2. Земные расстояния по точкам

Вторая часть этого модуля основана на представлении точек на Земле в виде значений типа point, в которых первый компонент представляет долготу в градусах, а второй — широту. Точки воспринимаются как (долгота, широта), а не наоборот, так как долгота ближе к интуитивному представлению как оси X, а широта — оси Y.

В модуле реализован один оператор, показанный в Таблице F.7.

Таблица F.7. Операторы земных расстояний по точкам

Оператор	Возвращает	Описание
`point` `<@>` `point`	`float8`	Выдаёт расстояние в сухопутных милях между точками на поверхности Земли.

Заметьте, что в этой части модуля, в отличие от части, построенной на cube, единицы зашиты жёстко: изменение функции earth() не повлияет на результат этого оператора.

Представление в виде долготы/широты плохо тем, что вам придётся учитывать граничные условия возле полюсов и в районе +/- 180 градусов долготы. Представление на базе cube лишено таких нарушений непрерывности.

Видео с вопросом

: нахождение расстояния между точкой и осью 𝑥 по координатам точки

Какое расстояние между точкой (19, 5, 5) и осью 𝑥?

Стенограмма видео

Какое расстояние между точка 19, пять, пять и ось 𝑥?

Любая точка, лежащая на оси 𝑥 будет иметь координаты 𝑥, ноль, ноль. И 𝑦-, и 𝑧-координаты должен быть равен нулю. Нам даны координаты пункт 19, пять, пять.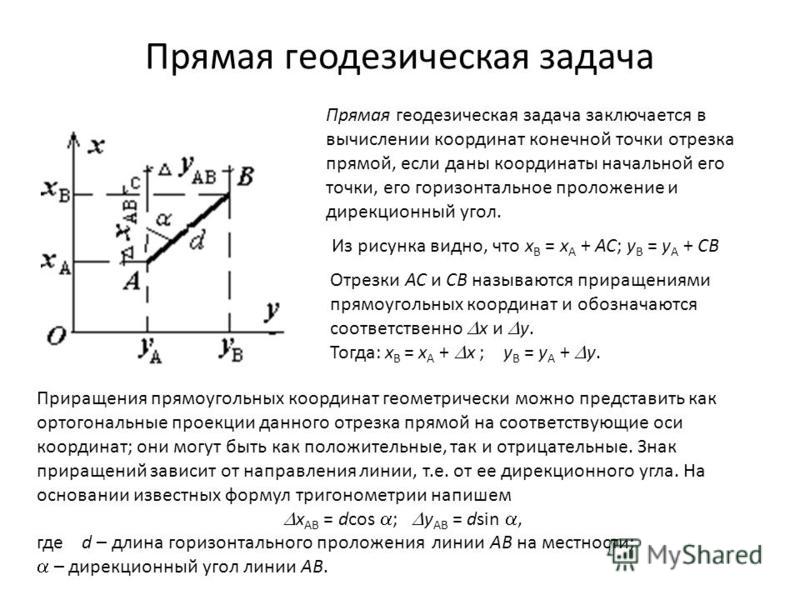 Точка на оси 𝑥, которая ближайший к этому будет иметь координаты 19, ноль, ноль. Кратчайшее расстояние будет до точка, где 𝑥-координата совпадает. Мы знаем, что можем вычислить расстояние между двумя точками в трех измерениях с использованием пифагорейской теории теорема. Если у нас есть две точки с координаты 𝑥 один, 𝑦 один, 𝑧 один и 𝑥 два, 𝑦 два, 𝑧 два, расстояние между равно квадратному корню из 𝑥 два минус 𝑥 один в квадрате плюс 𝑦 два минус 𝑦 один в квадрате плюс 𝑧 два минус 𝑧 один в квадрате.

Подставляем две наши координаты дает нам квадратный корень из 19 минус 19 в квадрате плюс ноль минус пять в квадрате плюс ноль минус пять в квадрате. 19 минус 19 равно нулю. Ноль минус пять равно минус пять. Итак, у нас остался квадратный корень минус пять в квадрате плюс минус пять в квадрате. Умножение отрицательного числа на отрицательное число дает нам положительный ответ.

Следовательно, минус пять в квадрате равно 25. Это означает, что наш ответ упрощается до квадратного корня из 50.

Стоит отметить, что мы мог бы вычесть координаты в другом порядке как пять минус ноль в квадрате также равно 25. Поскольку возведение числа в квадрат всегда дает положительный ответ, не имеет значения, в каком порядке мы вычтем наши координаты. На самом деле мы можем упростить наш ответ используя наши законы радикалов или сурдов. Квадратный корень из 50 равен квадратный корень из 25, умноженный на квадратный корень из двух. Поскольку квадратный корень из 25 равен пять, у нас осталось пять, умноженное на квадратный корень из двух или корень из пяти два. Квадратный корень из 50 равен пять корень два. Таким образом, мы можем сделать вывод, что расстояние между точками 19, пять, пять, а ось 𝑥 равна длине корня из пяти.

единицы измерения.

Мы могли бы заметить ярлык здесь. Чтобы найти расстояние между любым точка и ось, мы просто находим сумму квадратов двух других координаты, а затем квадратный корень ответ. Так как мы хотим вычислить расстояние до оси 𝑥, возводим в квадрат 𝑦- и 𝑧-координаты, находим их сумму и затем квадратный корень наш ответ. Если бы нам нужно было рассчитать расстояние между точкой и осью 𝑦, мы возвели бы 𝑥- и 𝑧-координаты, найдите их сумму и извлеките из этого ответа квадратный корень. Мы будем использовать тот же метод для найдите расстояние между точкой и осью 𝑧, на этот раз используя 𝑥- и 𝑦-координаты.

Как рассчитать расстояние между двумя точками. Урок YouTube, интерактивная демонстрация, с практическим рабочим листом

Рабочий лист формулы расстояния

Калькулятор формулы расстояния Просто введите свои уравнения, и пусть этот калькулятор сделает все остальное!

Апплет формулы расстояния

Формула расстояния и теорема Пифагора

Формула расстояния выводится из теоремы Пифагора.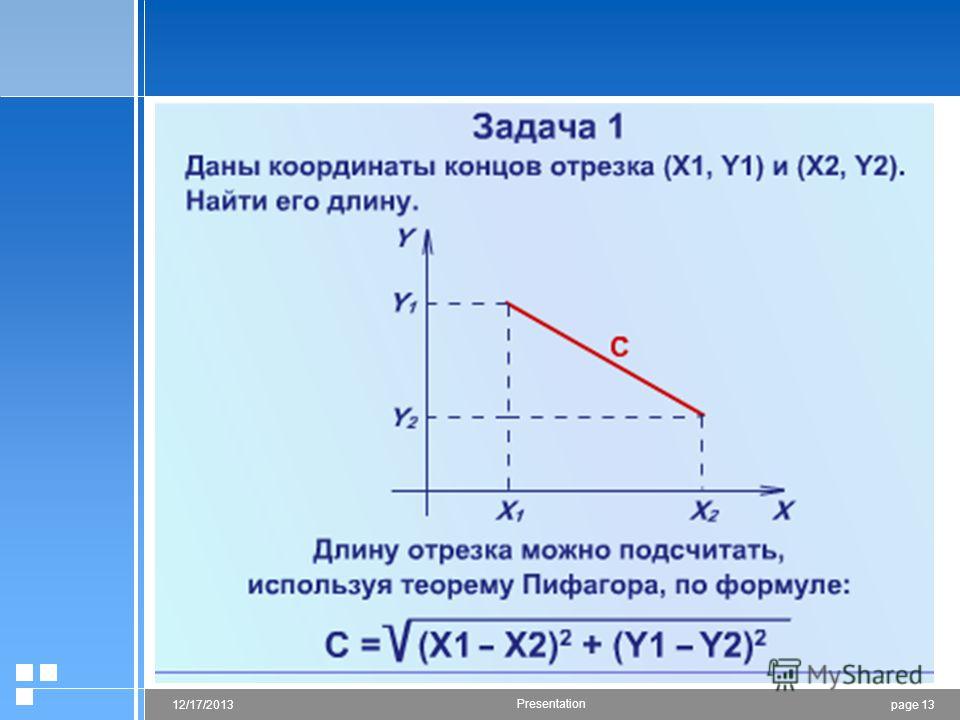 Чтобы найти расстояние между двумя точками ($$x_1, y_1$$) и ($$x_2, y_2$$), все, что вам нужно сделать, это использовать координаты этих упорядоченных пар и применить формулу, изображенную ниже.

Формула расстояния равна 92} $

Ниже приведена диаграмма формулы расстояния, примененная к изображению отрезка прямой

Видео Учебное пособие по формуле расстояния

Практика Проблемы

Проблема 1

Каково расстояние между точками $$(0,0)$$ и $$(6,8)$$, нанесенными на график?

Формула расстояния

Шаг 1

Соедините две точки и начертите прямоугольный треугольник. Установите теорему Пифагора 92} = с \\ \sqrt{100} = с \\ \fbox{с = 10} $

Обратите внимание: вы могли просто подставить координаты в формулу и прийти к тому же решению. Расстояние между точками 92} \\ \sqrt{36 + 64} = \sqrt{100} \\ \fbox{10} $

Имеет ли значение $$ \blue{x_1}$$ по сравнению с $$\blue{x_2}$$?

Вам может быть интересно, имеет ли значение, какое значение $$ \blue x $$ равно $$ \blue{ x_1} $$.

2 $$

Проблема 2

Каково расстояние между точками $$ (2, 4) $$ и $$ (26, 9)$$? Округлите ответ до десятых