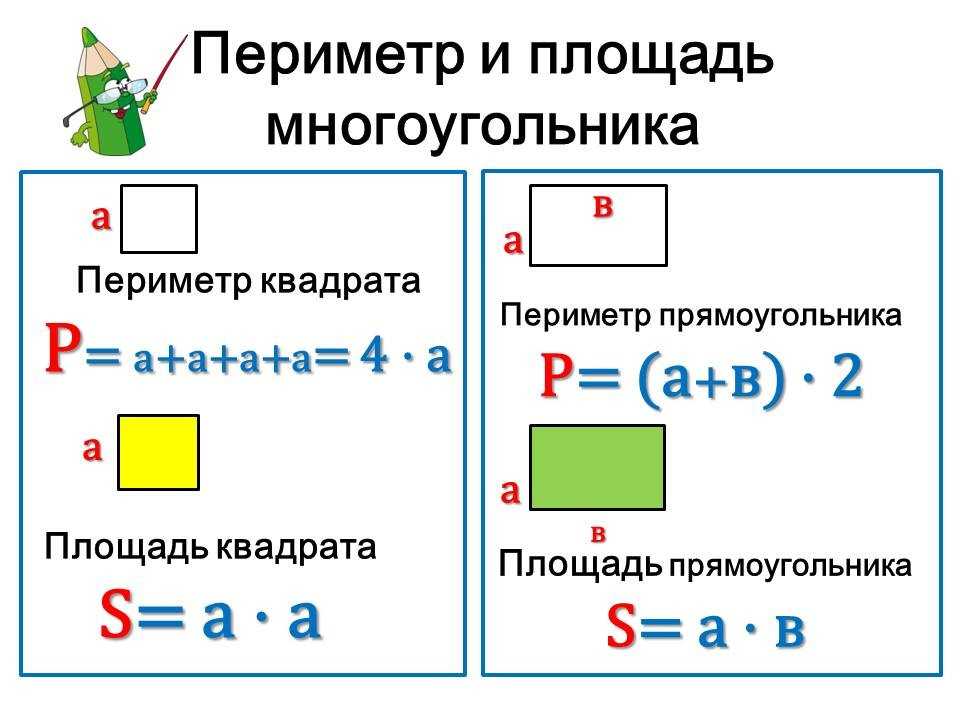
Урок математики «Площадь плоской фигуры»
Цели:
- Подготовить детей к введению понятия «площадь»; познакомить с мерами площади; Обеспечить усвоение детьми способа нахождения площади прямоугольника.
- Способствовать формированию ключевых компетенций: познавательной, информационной, коммуникативной, развивающей.
Задачи урока:
- Образовательные:
- вывести правило вычисления площади прямоугольника;
- актуализировать знания о признаках и свойствах геометрических фигур;
- способствовать совершенствованию вычислительных навыков.
- Развивающие:
- способствовать развитию основных операций
мышления (сравнение, обобщение, умение делать
выводы на основе полученной информации).

- формирование основных компонентов УУД (умение ставить учебную задачу, обобщать, делать выводы)
- способствовать развитию основных операций
мышления (сравнение, обобщение, умение делать
выводы на основе полученной информации).
- Воспитательные:
- формировать навыки самоанализа.
Планируемые результаты
- Личностные УУД:
- способность к самооценке на основе критерия успешности учебной деятельности.
- Метапредметные:
- Регулятивные УУД
- уметь определять и формулировать цель на уроке с помощью учителя;
- проговаривать последовательность действий на уроке;
- уметь высказывать своё предположение на основе работы с материалом учебника;
- уметь работать по коллективно составленному плану;
- оценивать правильность выполнения действия на уровне адекватной оценки;
- вносить необходимые коррективы в действие
после его завершения на основе его оценки и учёта
характера сделанных ошибок; планировать своё
действие в соответствии с поставленной задачей.

- Коммуникативные УУД
- уметь оформлять свои мысли в устной форме;
- слушать и понимать речь других;
- учиться работать в группе, формулировать собственное мнение и позицию.
- Познавательные УУД
- уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя;
- добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.
- Регулятивные УУД
- Предметные:
- уметь использовать в речи термины «длина», «ширина», «площадь».
- уметь вычислять площадь прямоугольника.
- знать основные понятия длина, ширина, площадь
Оборудование. Карта «Страна
Геометрия», нелинованные листы, ножницы,
геометрический материал, таблица «Меры
площади», «Справочное пособие для начальных
классов» (авт. Т.В. Шклярова, Л.И. Каржукова).
Карта «Страна
Геометрия», нелинованные листы, ножницы,
геометрический материал, таблица «Меры
площади», «Справочное пособие для начальных
классов» (авт. Т.В. Шклярова, Л.И. Каржукова).
ХОД УРОКА
I. Организационный момент
II. Повторение изученного материала
Учитель. Перед вами вновь страна
Геометрия. Сегодня на уроке мы побываем у жителей
некоторых замков этой страны. Хотите узнать, чем
занимаются жители замка «Повторяйка»
сегодня?
У. У них сейчас геометрическая разминка.
Подумаем вместе с ними над вопросами, которые
предлагает им царица Геометрия.
Перед вами круг, в нем проведены линии. Все они
называются по-разному. Как?
Д. Хорда, диаметр, радиус.
У. Как назвать все эти линии одним
словом?
Д. Отрезки.
У. Как называются геометрические фигуры
на следующем рисунке?
Как называются геометрические фигуры
на следующем рисунке?
Д. Квадрат, ромб, прямоугольник,
трапеция.
У. Чем являются стороны этих фигур?
У. Что мы называем отрезком?
Д. Часть прямой, ограниченная с двух сторон.
У. Как определить длину отрезка?
Д. Измерить с помощью линейки.
У. Можно ли измерить длину прямой? Луча?
Д. Нельзя.
У. Длину какой линии можно измерить на этом рисунке?
Д. Длину ломаной.
У. Какие вы знаете единицы меры длины?
Д. Миллиметр, сантиметр, дециметр, метр,
километр.
III. Подготовка к изучению нового материала
У. Узнаем, чем занимаются жители
второго замка – «Узнавайка». Само название
замка говорит о том, что они узнают что-то новое.
Давайте поработаем с ними по их программе.
Само название
замка говорит о том, что они узнают что-то новое.
Давайте поработаем с ними по их программе.
Д. Прямоугольник.
У. Имеет ли он ось симметрии?
Д. Да.
У. Проведем ось симметрии путем перегиба.
Дети складывают лист пополам.
– Еще одну – лист складывается еще раз. Сколько получилось частей?
Д. Четыре.
У. Одну вырежем. Проведем карандашом
диагональ. Сколько получили треугольников?
Д. Два.
У. Разрежем фигуру по диагонали.
Дети выполняют задание.
– Сравним треугольники. Что можно о них сказать?
Д. Треугольники равны.
У. Как вы это определили?
Д. Мы положили фигуры друг на друга, они
совместились.
У. Сложите из них всевозможные фигуры.
Дети выкладывают фигуры у себя на партах. Затем все образцы фигур выставляются на магнитной доске.
– Разделите все эти фигуры на группы по
признакам: симметричности, по количеству сторон
и углов.
Д. Симметричны фигуры 2, 3, 4. Фигуры 1, 4, 5, 6
– четырехугольники, 2, 3 – треугольники.
У. Найдите общее свойство всех фигур.
Дайте им общее название.
Д. Это многоугольники, все они сложены
из двух равных треугольников.
У. Посмотрите, дети, все эти фигуры
выстроились, как артисты на площади. А как вы
понимаете значение слова «площадь».
Д. Большое, открытое, ровное
пространство.
У.
IV. Физкультминутка
V. Работа над новым материалом
Работа над новым материалом
У. Откройте справочники на с. 82 и
прочитайте определение площади.
– Что же такое площадь в математике?
Д. Площадь – это внутренняя часть
какой-нибудь геометрической фигуры.
У. Когда сравнивают фигуры, говорят:
фигуры равной площади; площадь одной фигуры
больше площади другой фигуры.
Перед вами всевозможные геометрические фигуры.
Попробуйте сравнить их площади.
На доске – фигуры разного цвета и размера. Дети
на глаз сравнивают и пытаются определить,
площадь каких фигур больше или меньше.
– У вас у каждого на столе в коробочках
геометрические фигуры. Сравните площадь синего
квадрата с площадью красного квадрата и
прямоугольника.
– Перед вами наша помощница – доска. Как вы думаете, площадь какой ее части больше, меньше?
Д.
 Левое и правое «крыло» –
одинаковой площади. Центральная часть по площади
больше каждого «крыла».
Левое и правое «крыло» –
одинаковой площади. Центральная часть по площади
больше каждого «крыла».У. Определите на глаз, во сколько раз площадь квадратной доски меньше площади прямоугольной доски?
Д. Если мы закроем «крылья», они займут такую же площадь, как и прямоугольная доска. Значит, площадь «крыла» в 2 раза меньше центральной части.
У. Попробуйте теперь сравнить площади этих фигур.
На доске:
Д. Площади этих фигур одинаковы, равны.
Д. Посчитали количество клеточек. Их оказалось равное количество.
У. А теперь сравните площади этих прямоугольников с площадью квадрата.
На доску прикрепляется третья фигура:
– Я размышляю так: в прямоугольниках
поместилось по 10 клеток, значит, их площади
одинаковы.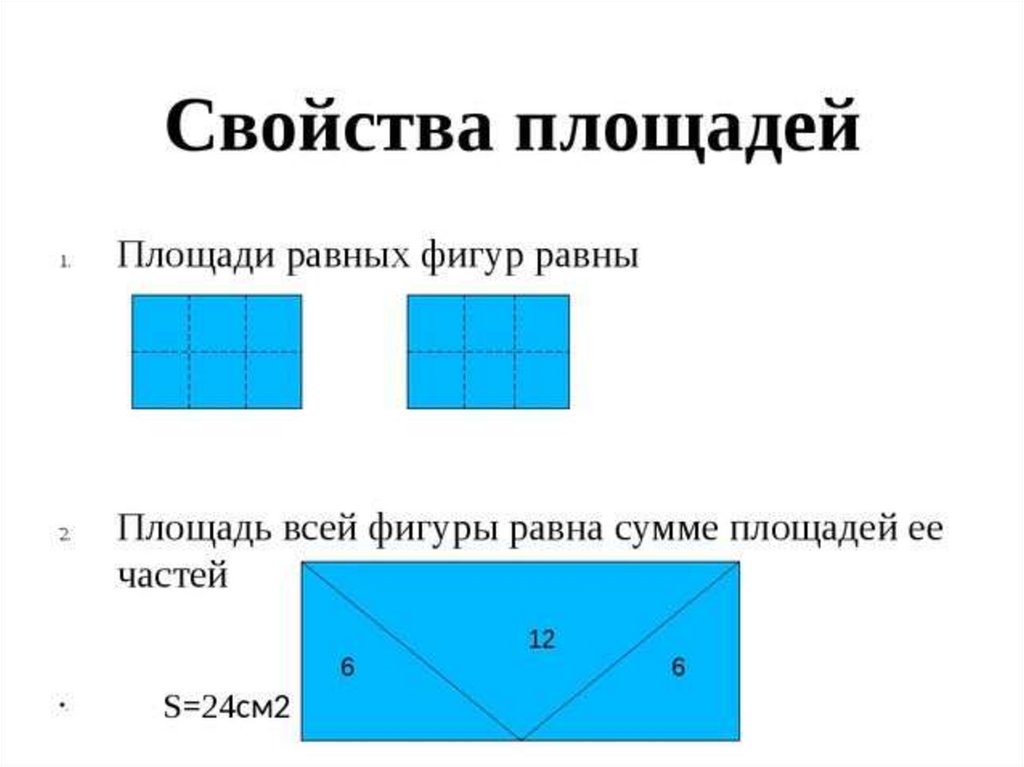 В квадрате 4 клетки, значит, он меньше
любого из этих прямоугольников. Правильно я
рассуждаю?
В квадрате 4 клетки, значит, он меньше
любого из этих прямоугольников. Правильно я
рассуждаю?
Д. Нет.
У. Почему вы со мной не согласны?
Д. Квадратики, на которые разделены
фигуры, разного размера, поэтому мы не можем так
рассуждать.
У. Для того чтобы сравнить две или
несколько геометрических фигур, надо измерить их
площадь. Как это сделать?
У. А что такое «мера площади»?
Д. Не знаем.
У. Мы в начале урока повторили меры длины. Мерами же площади являются квадратные сантиметр, метр, дециметр, километр.
Квадратным сантиметром называется квадрат со стороной один сантиметр. Это 4 клеточки нашей тетради.
Учитель показывает мерку квадратного сантиметра.

– Начертите в тетрадях квадратный сантиметр.
Дети выполняют задание.
– Как вы думаете, какую площадь имеет самый маленький квадрат?
Д. Квадратный миллиметр.
У. Правильно. Посмотрите на него.
Учитель передает по рядам лист миллиметровой бумаги, на которой отмечен квадратик со стороной 1 мм.
– Наша магнитная доска имеет форму квадрата. Какую она имеет площадь, если сторона ее равна 1 м?
Д. Квадратный метр.
У. Это тоже мера площади. А какую же меру площади надо выбрать, чтобы измерить площадь города, поля?
Д. Один квадратный километр.
У. Правильно. Все это единицы площади. Какая из них самая маленькая?
Д. Квадратный миллиметр.
У. Какая самая большая?
Д. Квадратный километр.
У. Молодцы! Теперь посмотрите, как эти единицы в математике принято обозначать.
На доске:
| Меры площади: 1 мм2 |
– Прочитаем их названия.
Дети называют все единицы площади.
VI. Закрепление нового материала
У. Наконец мы добрались до последнего
замка. Жители этого замка занимаются черчением.
Попробуем с ними начертить геометрические
фигуры.
Начертите при помощи линейки и карандаша
квадрат, площадь которого равна 1 кв. см.
Дети выполняют задание.
– Начертите прямоугольник со сторонами 3 см и 6
см.
Дети выполняют задание.
– Начертите квадрат со стороной 4 см.
Дети выполняют задание.
– Как вы считаете, площадь какой фигуры больше?
Д. Прямоугольника.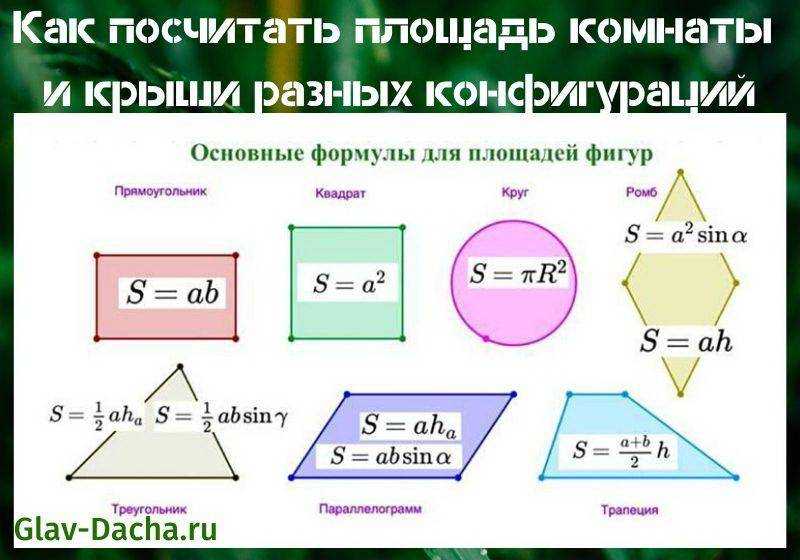
У. Как это проверить?
Д. Надо посчитать, сколько в каждой
фигуре квадратных сантиметров.
У. Разлинуйте прямоугольник и квадрат
на квадратные сантиметры и вычислите их площади.
Дети выполняют задание.
У. Что у вас получилось?
Д. В прямоугольнике – 18 квадратных
сантиметров, а в квадрате – 16. Значит, площадь
прямоугольника больше.
VII. Итог урока
У. Что такое «площадь фигуры»?
Д. Внутренняя часть фигуры.
У. С какими мерами площади вы
познакомились?
Д. Квадратные миллиметр, сантиметр,
дециметр, метр, километр.
У. Что такое один квадратный метр?
Д. Это квадрат со стороной 1 м.
У. Что такое один квадратный сантиметр?
Д. Это квадрат со стороной 1 см.
У. Подумайте, для чего нужно определять
площади различных фигур?
Подумайте, для чего нужно определять
площади различных фигур?
Д. Чтобы правильно вести строительство,
сажать растения, делать ремонт.
У. Жители страны Геометрии остались
вами очень довольны. Молодцы! Спасибо за
работу. Урок окончен.
Понятие площади
Площадь можно рассматривать как величину, по отношению к которой могут быть установлены критерии сравнения, то есть признаки равенства или неравенства. Главными свойствами площади являются:
- Независимость ее величины от положения фигуры в пространстве.
- Фигура, состоящая из нескольких фигур, имеет площадь, равную сумме площадей этих фигур.
Такой подход к понятию о площади и ее свойствах применим в начальной школе, тем более что он опирается на аналогичные свойства отрезков, уже изученные детьми, и найдет свое продолжение при изучении объемов. Частный случай измерения отрезков, когда одно из сравниваемых значений величины принимается за единицу, получит свое развитие и при измерении площади, а затем и объема. Надо, однако, иметь в виду известные трудности при переходе от измерения длины к измерению площади.
Надо, однако, иметь в виду известные трудности при переходе от измерения длины к измерению площади.
Трудности эти обусловлены усложнением наглядных пособий, введением косвенного приема измерения, а также тем, что здесь вводятся качественно новые величины, хотя названия мер сходны с названиями линейных мер. Поспешный переход к выводу правил для вычисления площадей и объемов нередко приводит к тому, что ученики смешивают понятия длины, площади, объема. Соблюдая последовательность этапов, опираясь на значительный опыт по непосредственному измерению площадей (объемов), можно перейти к выводу правил и добиться сознательного их применения.
При изучении площадей дети знакомятся: а) с понятием о площади как о величине; б) с квадратными мерами; в) производят непосредственное и косвенное измерение площадей; г) выводят правила для вычисления площади; д) решают практические задачи, в том числе такие, которые связаны с мерами земельных площадей. Сравнение площадей при помощи наложения (например, тетради на стол) создает понятие о площади как о величине (критерий больше, меньше, равно, то есть равенства или неравенства).
Попутно повторяется сравнение длин-отрезков при помощи наложения и измерения; особо подчеркивается, что для измерения длины служат единицы длины и что результат измерения выражается в линейных единицах.
На следующем этапе надо подвести учеников к мысли, что сравнение площадей при помощи наложения не всегда возможно. По заданию учителя ученики заготовляют по 3 равновеликих прямоугольника, например со сторонами 6 см и 8 см; 16 см и 3 см; 12 см и 4 см. Попытка сравнить их площади при помощи наложения приводит к полезной «дискуссии», в результате которой делается вывод, что наложение не дает ответа на поставленный вопрос. Вслед за этим проводится такая же работа с такими же фигурами, но разбитыми на квадратные сантиметры. Еще лучше, если ученики сами выполнят разбивку прямоугольников на квадратные сантиметры. Дети, пересчитав количество квадратов, приходят к выводу, что эти фигуры имеют одинаковую площадь (равновелики).
Итак, чтобы сравнить (узнать) площадь прямоугольников, надо их разбить на равные квадраты и подсчитать их количество. По аналогии с тем, как вводилось понятие о необходимости иметь стандартные единицы для измерения длины, устанавливается, что для измерения площадей берут не произвольные квадраты, а квадратные метры, дециметры, сантиметры.
По аналогии с тем, как вводилось понятие о необходимости иметь стандартные единицы для измерения длины, устанавливается, что для измерения площадей берут не произвольные квадраты, а квадратные метры, дециметры, сантиметры.
В классе вывешиваются образцы этих мер, а ученики самостоятельно изготовляют модели их. Выполняется ряд упражнений по непосредственному измерению площадей сначала путем наложения квадратных единиц, а затем расчерчиванием на равные квадраты (по 1 кв. см, а на доске по 1 кв. дм). Это задание выполняют на нелинованной бумаге.
Таким приемом вырабатывается понятие о площади и единицах измерения площади. Эти работы весьма полезны. Затраченное на них время вполне окупается, так как ученики получают конкретные представления о качественно новых единицах измерения. Вместе с тем дети на собственном опыте убеждаются, насколько труден и утомителен такой способ измерения площади.
Что такое площадь в математике?
Автор:
Малкольм МакКинзи
Проверено
Пол Маццола , круг или эллипс, занимает плоскость. Площадь фигуры всегда измеряется в квадратных единицах.
Как только вы узнаете, как квадратные единицы соотносятся с площадью, вы сможете найти площадь практически любой двумерной фигуры.
Как найти площадь фигуры
Плоские фигуры имеют два измерения:
Ширина
Длина
Квадрат, например, имеет ширину, равную его длине такой же. Эллипс также имеет ширину и длину.
Мы можем легко увидеть, как квадрат можно разделить на маленькие квадратные единицы, как на координатной плоскости. Вы не можете легко увидеть, как эллипс может быть составлен из маленьких квадратов, но это возможно.
Поскольку он имеет ширину и длину, он покрывает пространство, и это пространство, даже с изогнутыми сторонами эллипса, может быть разделено на квадратные единицы:
Подсчет площади квадрата и прямоугольника Подсчет квадратных единиц в квадрат легко: один, два, три и т.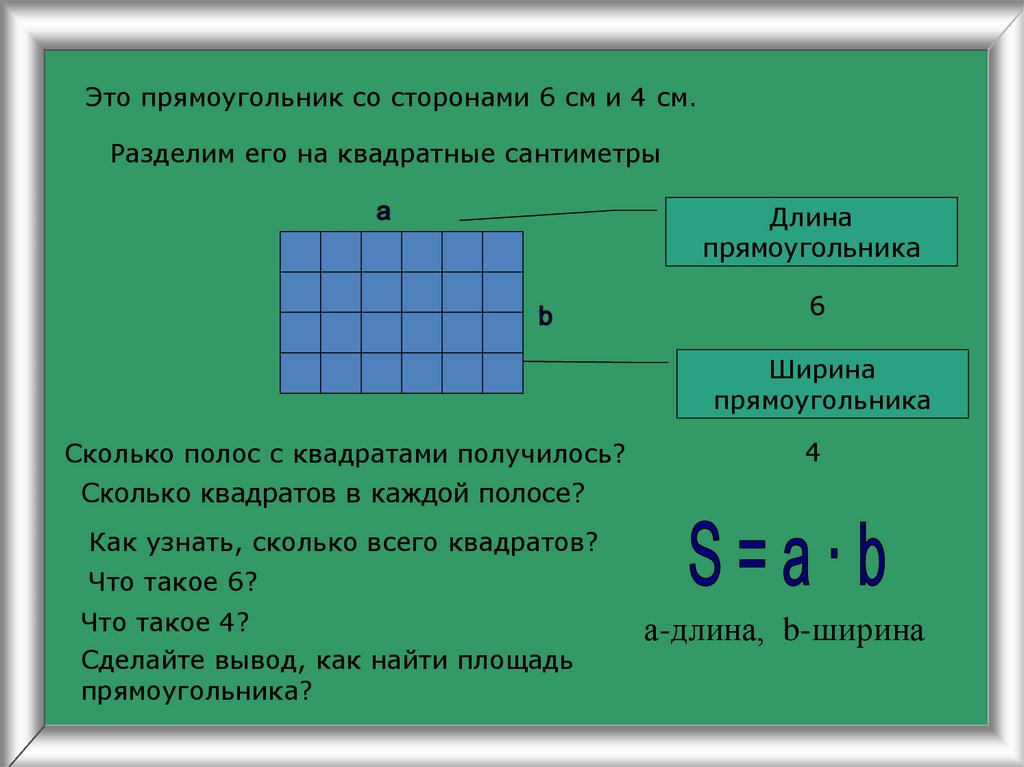 д. .
д. .
Но как посчитать все квадраты эллипса? Как определить, какая часть квадрата находится под верхней кривой? Как насчет кривых на левом и правом концах?
К счастью, у математиков есть быстрый способ сложить все квадратные единицы, не считая их. 9{2}mi2
Находите ли вы площадь четырехугольника, такого как трапеция и ромб, или любой другой замкнутой фигуры, площадь всегда будет возведена в квадрат.
Формула площади
Формула площади, которую вы используете, зависит от того, для какой фигуры вы пытаетесь найти площадь.
Площадь квадратов и прямоугольников
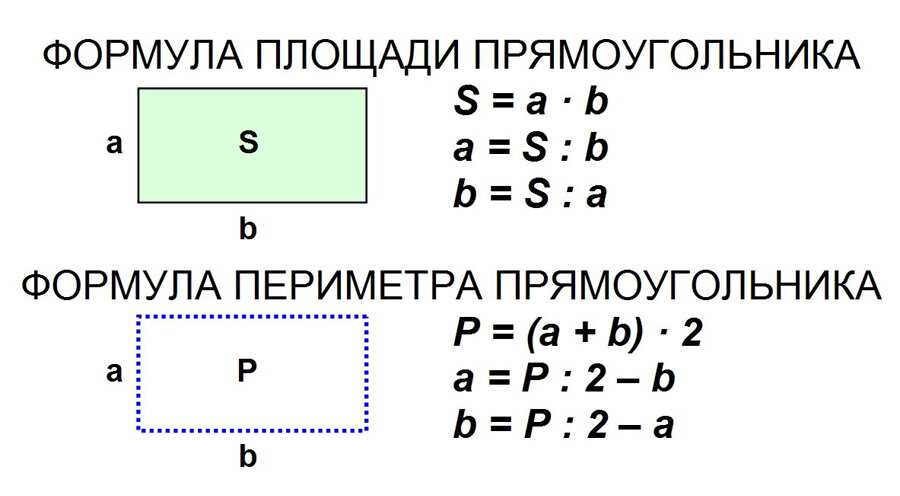
Чтобы найти площадь простых фигур, таких как квадрат или площадь прямоугольника, вам нужна только ширина w и длина l (или база, b ). Площадь равна длине, умноженной на ширину:
Площадь всегда возводится в квадрат. Вы всегда будете выражать площадь в квадратных единицах, полученных из линейных единиц.
Вот прямоугольник 90 метров в ширину и 120 метров в длину (самый большой размер футбольного поля ФИФА). Чему равна площадь этого прямоугольника?
Пример площади прямоугольникаПоскольку футбольное поле измеряется в погонных метрах, его площадь равна квадратным метрам. Площадь прямоугольника 10 800 метров в квадрате .
Формула площади квадрата на самом деле даже проще, чем запись длина × ширина , потому что все стороны равны:
Вот квадрат со сторонами 15 дюймов в длину, такой же размер, как основания на бейсбольном мяче MLB поле. Вычисление площади для этого квадрата выглядит следующим образом:
Пример площади квадратаПлощадь других фигур
Все остальные многоугольники нелегко разделить на квадратные единицы. Взгляните на параллелограмм.
Две стороны пересекают многие квадратные единицы. Конечно, параллелограмм — это просто опрокинутый прямоугольник.
Итак, математически, если бы мы могли отрезать один конец и присоединить его к другому, мы бы получили площадь в квадратных единицах. Мы можем сделать именно это, поскольку площадь параллелограмма с основанием b и шириной или высотой h находится по следующей формуле:
Мы можем сделать именно это, поскольку площадь параллелограмма с основанием b и шириной или высотой h находится по следующей формуле:
Это та же формула, что и для квадрата. или прямоугольник!
Если разделить параллелограмм по диагонали, что получится? Два треугольника. Это означает, что площадь любого треугольника равна половине площади параллелограмма с такой же длиной основания и высотой. Помните, что параллелограмм использует ту же формулу, что и прямоугольник.
Нахождение площади параллелограммаПлощадь треугольника тогда равна половине основания, b , умноженной на высоту, h :
Вот парус из прямоугольного треугольника 45-футовый парусник Morgan с базой 201420\frac{1}{4}2041 футов и высотой 441244\frac{1}{2}4421 футов. Какова его площадь?
Пример площади треугольникаДля удобства умножения можно изменить дроби на десятичные:
Площадь треугольного паруса приблизительно равна 450,6 квадратных футов .
Как насчет домашней пластины бейсбольного поля Главной лиги бейсбола? Мы можем рассчитать площадь плиты дома пятиугольника , рассматривая его как две формы:
Прямоугольник 17 дюймов × 8,5 дюймов
3 9{2}216,5 дюймов2
Пример площади пятиугольника — домашняя плитаНайдите площадь круга
Некоторые двумерные фигуры даже не являются многоугольниками, например наш эллипс или окружность. Площадь круга с радиусом ( r ) находится по следующей формуле:
Если у вас есть круг с радиусом 4 см , вы можете легко вычислить площадь круга по формуле вверху:
Площадь круга составляет приблизительно 50,24 квадратных сантиметра.
Найти площадь эллипса
Площадь эллипса находится с использованием двух его осей: большая ось (длина от центра), обычно обозначаемая как аа, и малая ось (ширина от центра), обычно обозначаемая как bb, с помощью этой формулы:
Площадь круга и эллипсаНезависимо от того, имеете ли вы дело с правильным многоугольником или неправильной плоской фигурой, вы можете найти площадь!
запрос ссылки — определение области
$\begingroup$
Я ищу привлекательное, но строгое определение площади; скажем, в евклидовой плоскости.
 Наверное, короткого определения нет. Можно сделать его еще длиннее, но можно ли его собрать из полезных деталей нескучным способом? Скажем так, что не все студенты будут спать на лекции?
Наверное, короткого определения нет. Можно сделать его еще длиннее, но можно ли его собрать из полезных деталей нескучным способом? Скажем так, что не все студенты будут спать на лекции?Комментарии.
Настоящая проблема заключается в том, чтобы доказать существование, уникальность несложна.
Использование интеграла не кажется хорошей идеей.
Есть подход, когда вы пишете формулу площади, а затем доказываете ее свойства. Мне это не нравится, так как оно перемещает вас к дискретной геометрии, которая совершенно не имеет значения, а идеи, используемые где-либо еще, почти бесполезны (поэтому нет причин изучать этот материал). [См., например, «Геометрия: метрический подход с моделями» Миллмана и Паркера.]
Метод с мерной сеткой (разрезание всего на квадратики и подсчет) выглядит намного лучше. Этот метод можно рассматривать как введение в интеграл. Есть только одно техническое утверждение, которое необходимо доказать: если вы повернете квадрат, его площадь не изменится.
 Единственная проблема в том, что нельзя обобщать, говоря, что абсолютная плоскость или сфера… 92\cdot N_\varepsilon$ для скажем полигонов. (Можно обменять лимит на ультралимит — так все работает гладко, но я не хочу продавать душу только за деф области…)
Единственная проблема в том, что нельзя обобщать, говоря, что абсолютная плоскость или сфера… 92\cdot N_\varepsilon$ для скажем полигонов. (Можно обменять лимит на ультралимит — так все работает гладко, но я не хочу продавать душу только за деф области…)
- запрос-справка
- mg.metric-геометрия
- евклидова геометрия
- плоскостная геометрия
- определения
$\endgroup$
15
$\begingroup$
Существует интуитивный подход к площади, основанный на том факте, что многоугольники $P, P’$ имеют одинаковую площадь тогда и только тогда, когда они равноразложимы (то есть один можно разрезать на части и собрать из другого) .
Первые три страницы этой заметки описывают «мотивированный» подход к определению площади полигонов. А именно, $K(\text{Poly})$ определяется как свободная абелева группа, порожденная плоскими многоугольниками $P$, при соблюдении следующих двух соотношений:
- $[P]=[P’]$, если $ P$ конгруэнтно $P’$
- $[P]=[P_1]+[P_2]$, если $P$ можно разрезать на многоугольники $P_1$ и $P_2$.

Простое упражнение (набросок приведен в примечании, на которое я ссылаюсь) показывает, что $[P]=[P’]$ тогда и только тогда, когда $P$ и $P’$ имеют одинаковую площадь, поэтому $K(Poly)\ simeq \mathbb{R}$. Но еще лучше, можно определить площадь многоугольника $P$ как его класс $[P]$ в $K(\text{Poly})$.
Действительно, для многих разумных классов подмножеств плоскости можно расширить это определение, чтобы присвоить такому множеству класс в $K(\text{Poly})$. Например, пусть последовательность классов $[P_i]$ в $K(\text{Poly})$ сходится к $[P]$, если существует представитель $[A]-[B]$ для $[P- P_i]$, где и $A$, и $B$ содержатся в $[0, \epsilon_i]\times [0, \epsilon_i]$, где $\epsilon_i\to 0$.
Предположим, что $X$ — подмножество плоскости, так что существует последовательность многоугольников $P_i$, такая что симметрическая разность $(X\cup P_i)-(X\cap P_i)$ содержится в многоугольнике $ Q_i$. Предположим далее, что $[Q_i]=[Q’_i]$ и $Q’_i\subset [0, \epsilon_i]\times [0,\epsilon_i]$, где $\epsilon_i\to 0$.
 n, n>2$. Действительно, Ден показал, что существует много многогранников с одинаковым объемом, которые не являются равноразложимыми.
n, n>2$. Действительно, Ден показал, что существует много многогранников с одинаковым объемом, которые не являются равноразложимыми.$\endgroup$
10
$\begingroup$
Если вас устраивают площади многоугольников, вы можете определить их а-ля K-теория.
Пусть $\mathcal A$ — свободная абелева группа, порожденная многоугольниками на плоскости по модулю соотношений, идентифицирующих пары конгруэнтных многоугольников, и такая, что $P=P_1+P_2$, если $P_1$ и $P_2$ являются результатом разрезая многоугольник $P$ линией на две части.
Можно показать, что $\mathcal A\cong\mathbb R$ как группа и что каноническое отображение $\mathrm{Polygons}\to\mathcal A$, переводящее многоугольник в его класс, является площадью.
$\endgroup$
3
$\begingroup$
Для студентов, наверное, самое элементарное, что нужно сделать, это ограничиться областями на плоскости, которые можно триангулировать конечным числом треугольников (с прямыми сторонами).
 Принимая площадь треугольника как известную, вы затем определяете площадь области, складывая площади треугольников в конечной триангуляции. Единственное, что вы должны проверить, это то, что это четко определено. Для этого я сначала доказал бы, что любые две конечные триангуляции области на плоскости имеют общее подразделение (если вы достаточно сообразительны, то это можно сделать очень быстро, уж точно на 3-5 страницах), а затем доказал бы что ваше понятие площади инвариантно относительно подразделений.
Принимая площадь треугольника как известную, вы затем определяете площадь области, складывая площади треугольников в конечной триангуляции. Единственное, что вы должны проверить, это то, что это четко определено. Для этого я сначала доказал бы, что любые две конечные триангуляции области на плоскости имеют общее подразделение (если вы достаточно сообразительны, то это можно сделать очень быстро, уж точно на 3-5 страницах), а затем доказал бы что ваше понятие площади инвариантно относительно подразделений.Самое приятное в этом то, что все основные свойства, которые вам нужны (например, правильное поведение областей при линейных картах и переводах), получаются бесплатно из аналогичных свойств треугольников, что легко.
$\endgroup$
7
$\begingroup$
Я не знаю, сколько областей вы хотите доказать, и насколько развита предыстория аудитории, но вот определение площади ограниченной плоской области.
 91$-функцию, то $D_1\cup D_2$ измерима и
91$-функцию, то $D_1\cup D_2$ измерима и$$\eA(D_1\cup D_2)=\eA(D_1)+\eA(D_2). $$
$\endgroup$
3
$\begingroup$
Честно говоря, я не уверен, что эта конструкция соответствует критерию нескучности, но она довольно короткая (обещаю вам, что все это займет меньше 40 страниц 😉 ) и работает во всех измерениях. Это связано с ответом Энди Путмана и последующими комментариями. Возможно, мне следовало продолжать комментировать, но места просто не хватило. 9n$ ), рассматривая счетные объединения замкнутых прямоугольников, ребра всех которых параллельны заданной системе декартовых координат (назовем их допустимыми). Объединение должно быть чистым, в том смысле, что прямоугольники аккуратно перекрываются, образуя, скажем, прямоугольник. Поскольку любое непустое пересечение двух допустимых прямоугольников снова является приемлемым прямоугольником, любое счетное объединение допустимых прямоугольников, очевидно, допускает чистую подпрямоугольность.
 Тот же самый аргумент работает также довольно хорошо для описания общего подпрямоугольника двух других, имеющих одно и то же изображение.
Тот же самый аргумент работает также довольно хорошо для описания общего подпрямоугольника двух других, имеющих одно и то же изображение.Сначала определите площадь для конечных объединений, начав с присвоения обычного значения площади одного прямоугольника (данного как аксиома) и расширив функционал площади, используя обычную аддитивность для квази-непересекающихся (пересекающихся не более чем по общему ребру) ) объединение допустимых прямоугольников (дано как аксиома). В этом случае вы получаете все обычные свойства области.
Теперь ограниченному счетному и чистому объединению $\bigcup_{n\in\mathbb{N}}R_n$ допустимых прямоугольников можно задать площадь в виде ряда $\sum_{n\in\mathbb{N}}\mathtt {Area}(R_n)$ (всегда сходится). Как указывалось выше, найти общий подпрямоугольник довольно просто, и предел не зависит от выбранного подпрямоугольника (коммутативно суммируемого ряда).
Поскольку любое открытое множество прямоугольно (в том смысле, что оно распадается на счетное чистое объединение приемлемых прямоугольников), мы можем измерить любое открытое множество.



 Наверное, короткого определения нет. Можно сделать его еще длиннее, но можно ли его собрать из полезных деталей нескучным способом? Скажем так, что не все студенты будут спать на лекции?
Наверное, короткого определения нет. Можно сделать его еще длиннее, но можно ли его собрать из полезных деталей нескучным способом? Скажем так, что не все студенты будут спать на лекции? Единственная проблема в том, что нельзя обобщать, говоря, что абсолютная плоскость или сфера… 92\cdot N_\varepsilon$ для скажем полигонов. (Можно обменять лимит на ультралимит — так все работает гладко, но я не хочу продавать душу только за деф области…)
Единственная проблема в том, что нельзя обобщать, говоря, что абсолютная плоскость или сфера… 92\cdot N_\varepsilon$ для скажем полигонов. (Можно обменять лимит на ультралимит — так все работает гладко, но я не хочу продавать душу только за деф области…)
 n, n>2$. Действительно, Ден показал, что существует много многогранников с одинаковым объемом, которые не являются равноразложимыми.
n, n>2$. Действительно, Ден показал, что существует много многогранников с одинаковым объемом, которые не являются равноразложимыми. Принимая площадь треугольника как известную, вы затем определяете площадь области, складывая площади треугольников в конечной триангуляции. Единственное, что вы должны проверить, это то, что это четко определено. Для этого я сначала доказал бы, что любые две конечные триангуляции области на плоскости имеют общее подразделение (если вы достаточно сообразительны, то это можно сделать очень быстро, уж точно на 3-5 страницах), а затем доказал бы что ваше понятие площади инвариантно относительно подразделений.
Принимая площадь треугольника как известную, вы затем определяете площадь области, складывая площади треугольников в конечной триангуляции. Единственное, что вы должны проверить, это то, что это четко определено. Для этого я сначала доказал бы, что любые две конечные триангуляции области на плоскости имеют общее подразделение (если вы достаточно сообразительны, то это можно сделать очень быстро, уж точно на 3-5 страницах), а затем доказал бы что ваше понятие площади инвариантно относительно подразделений. 91$-функцию, то $D_1\cup D_2$ измерима и
91$-функцию, то $D_1\cup D_2$ измерима и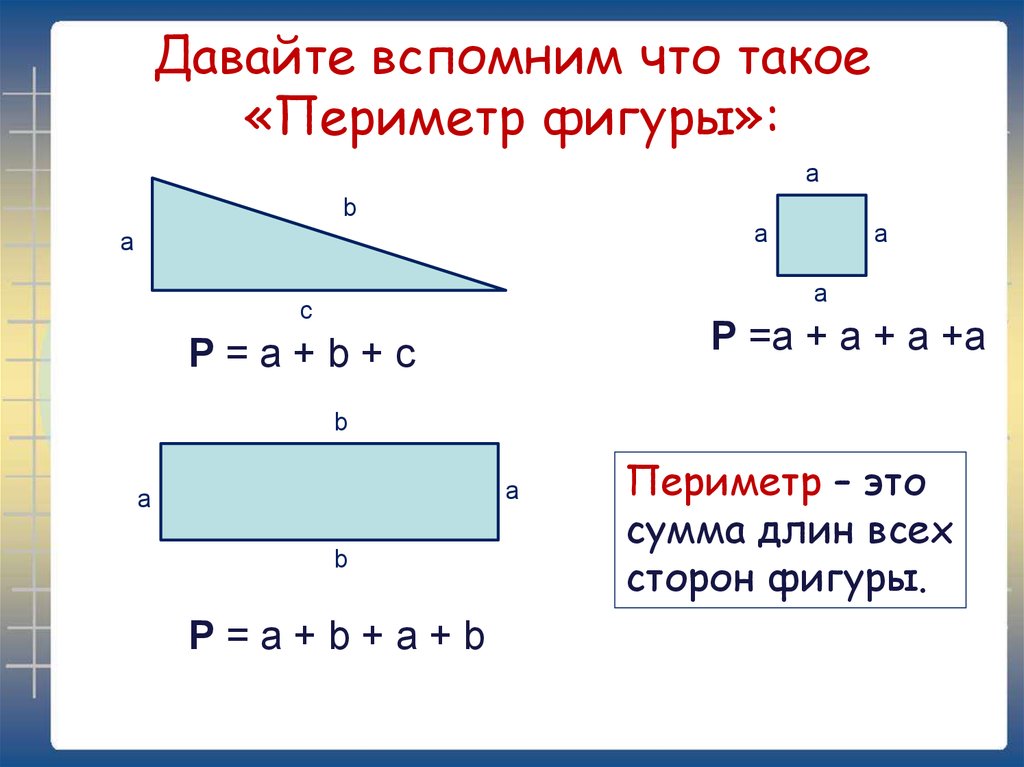 Тот же самый аргумент работает также довольно хорошо для описания общего подпрямоугольника двух других, имеющих одно и то же изображение.
Тот же самый аргумент работает также довольно хорошо для описания общего подпрямоугольника двух других, имеющих одно и то же изображение.