Арифметические действия с числами разных знаков.
 ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ГОРОДА МОСКВЫ
СТРОИТЕЛЬНЫЙ ТЕХНИКУМ №30
Предметная (цикловая) комиссия
«Общеобразовательная подготовка»
Арифметические действия
с числами разных знаков
У Ч Е Б Н О Е П О С О Б И Е — П Р А К Т И К У М
Рекомендуется для использования в качестве учебного пособия по учебной дисциплине «Математика» для обучающихся первых курсов
Москва 2015
22.130я722
Х24
Арифметические действия с числами разных знаков:учеб. пособие/ сост. Т. Г. Хасянова . – М: Изд-во ГБПОУ Строительный техникум №30, 2015 . – 15 с.
Учебное пособие-практикум «Арифметические действия с числами разных знаков» составлено Хасяновой Т.Г., преподавателем математики.
Учебное пособие-практикум рассмотрено и одобрено на заседании предметной (цикловой) комиссии «Общеобразовательная подготовка», протокол № 8 от 28 мая 2015 г.
Настоящее издание представляет собой часть базового курса дисциплины «Математика», который изучается обучающимися первых курсов техникума
ГБПОУ Строительный техникум №30, 2015
СОДЕРЖАНИЕ
Стр.
Введение …………………………………………………………………
31 Основные понятия, правила и действия с отрицательными и положительными числами…………………………………….………………
6
2 Практикум ……………………………………………………………….
8
3. Рефлексия ………………………………………………………………
13
4. Список использованных источников …………………………………
14
Введение
Современный уровень развития науки и техники требует глубоких и прочных математических знаний. Математические расчеты, основанные на использовании алгоритмов основных математических действий, являются составной частью трудовой деятельности рабочего, инженера и других. Одним из важнейших умений, которые обязано дать математическое образование, является сознательное, быстрое и безошибочное выполнение действий над числами. Однако, учение о действиях с отрицательными числами вызывает затруднения у учащихся. И не потому, что устанавливаемые правила действий сложны.
Напротив, они очень просты. Но неясными остаются два вопроса.
Зачем вводятся отрицательные числа?
Почему над ними совершаются действия по таким правилам, а не по иным? В частности, очень плохо понимается, почему при умножении и делении отрицательного числа на отрицательное результат есть положительное число.
Все эти вопросы возникают потому, что с отрицательными числами учащихся обычно знакомят до того, как они начали решать уравнения, и больше не возвращаются к правилам действий с отрицательными числами. Между тем лишь в связи с решением уравнений выясняется ответ на оба поставленных выше вопроса. Исторически отрицательные числа возникли именно в этой связи. Не будь уравнений, не было бы нужды и в отрицательных числах.
На два выше поставленных вопроса нужно ответить следующим образом:
Отрицательные числа вводятся затем, чтобы устранить ряд трудностей, возникающих прежде всего при решении уравнений.
Правила действий над ними вытекают из необходимости согласовать результаты, полученные с помощью отрицательных чисел, с теми результатами, которые могли быть получены и без них.
Опираясь на свой многолетний опыт, в учебном пособии-практикуме предельно просто изложена задача изучения этой темы: в примерах использованы только целые числа с целью сознательного усвоения именно законов и свойств арифметических действий с числами разных знаков, не отвлекая внимание на сложную работу с самими числами.
Особое внимание уделено необходимости применять теоретические знания (правила) в практике вычислений.
Первое время рекомендуется проговаривать выполняемое действие , так как это позволяет не торопиться и помогает добиться осознанных умений рациональной организации вычислений. Таким образом, у обучающихся быстрее развивается числовая наблюдательность, помогающая им проникнуть в особенности чисел и правил действий над ними. Сами приемы должны быть как можно однообразнее.
Полезно напомнить обучающимся, что цифры надо писать четко, располагать при соответствующих вычислениях по вертикали одну под другой, не пропускать математические знаки. Обучающимся следует напоминать о том, что скорость и точность вычисления зависят от того, как ведется оформление вычислительных работ на бумаге. Письменные вычисления являются основным видом вычислительной работы на уроках физики, химии и других учебных дисциплин.
В настоящем учебном пособии-практикуме изложены рекомендации, разработанные автором в помощь преподавателям математики, родителям и обучающимся с целью повышения вычислительной культуры и формирования сознательных и прочных навыков вычисления чисел с разными знаками.
1.Основные понятия, правила и действия с отрицательными и положительными числами
1.1.Абсолютная величина (модуль)
Абсолютная величина (модуль ). Для отрицательного числа – это положительное число, получаемое от перемены его знака с « – » на « + »; для положительного числа и нуля – само это число. Для обозначения абсолютной величины (модуля) числа используются две прямые черты, внутри которых записывается это число.
П р и м е р ы : | – 5 | = 5, | 7 | = 7, | 0 | = 0.
1.2. Сложение
при сложении двух чисел с одинаковыми знаками складываются их абсолютные величины и перед суммой ставится общий знак.
П р и м е р ы :
( + 6 ) + ( + 5 ) = 11 ;
( – 6 ) + ( – 5 ) = – 11 .
при сложении двух чисел с разными знаками их абсолютные величины вычитаются ( из большей меньшая ) и ставится знак числа с большей абсолютной величиной.
П р и м е р ы :
( – 6 ) + ( + 9 ) = 3 ;
( – 6 ) + ( + 3 ) = – 3 .
1.3. Вычитание
Можно заменить вычитание двух чисел сложением, при этом уменьшаемое сохраняет свой знак, а вычитаемое берётся с противоположным знаком.
П р и м е р ы :
( + 8 ) – ( + 5 ) = ( + 8 ) + ( – 5 ) = 3;
( + 8 ) – ( – 5 ) = ( + 8 ) + ( + 5 ) = 13;
( – 8 ) – ( – 5 ) = ( – 8 ) + ( + 5 ) = – 3;
( – 8 ) – ( + 5 ) = ( – 8 ) + ( – 5 ) = – 13;
1.4. Умножение
При умножении двух чисел их абсолютные величины умножаются, а произведение принимает знак « + » , если знаки сомножителей одинаковы, и знак « – » , если знаки сомножителей разные.
Полезна следующая схема (правила знаков при умножении):
+ · + = +
+ · – = –
– · + = –
– · – = +
При умножении нескольких чисел ( двух и более ) произведение имеет знак « + » , если число отрицательных сомножителей чётно, и знак « – » , если их число нечётно.
П р и м е р :
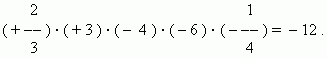
1.5. Деление
При делении двух чисел абсолютная величина делимого делится на абсолютную величину делителя, а частное принимает знак « + » , если знаки делимого и делителя одинаковы, и знак « – » , если знаки делимого и делителя разные.
Здесь действуют те же правила знаков, что и при умножении:
+ : + = +
+ : – = –
– : + = –
– : – = +
П р и м е р : ( – 12 ) : ( + 4 ) = – 3 .
2. Практикум
2.1. Сложение отрицательных чисел
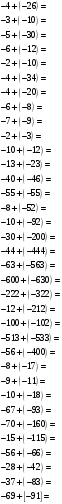
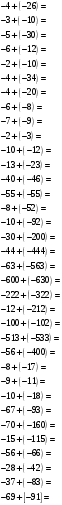
2.2. Сложение чисел с разными знаками
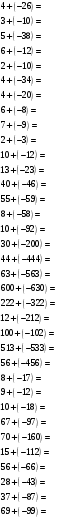
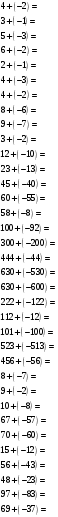
2.3. Вычитание чисел с разными знаками
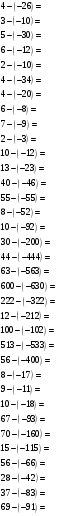
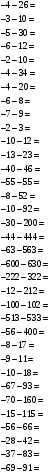
2.4. Умножение и деление чисел с разными знаками
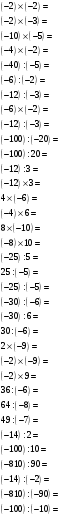
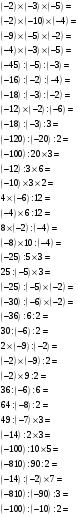
2.5. Примеры на все действия
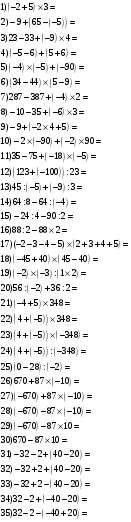
3. Рефлексия
Для закрепления данной темы, рекомендуется ответить на вопросы:
Что называют модулем числа?
Какие числа называют противоположными?
Сформулируйте правило сложения чисел с разными знаками.
Сформулируйте правило сложения отрицательных чисел.
Сформулируйте правило умножения отрицательных чисел.
Сформулируйте правило умножения чисел с разными знаками.
Чему равна сумма противоположных чисел?
Какое число противоположно нулю?
Какие числа называют взаимно обратными?
Как умножить смешанные числа?
Сформулируйте правило деления отрицательных чисел.
Сформулируйте правило деления чисел, имеющих разные знаки
Список используемых источников
1.http://www.bymath.net/ «Средняя математическая интернет школа»
2. «Справочник по элементарной математике», Москва, 1986г.
Учебное издание
Арифметические действия
с числами разных знаков
Ответственный за выпуск С.В. Михайлов
Верстка – А. Фадеев
______________________________
Подписано в печать 22.06.2015.
Формат 60х90/16. Бумага офсетная мелованная.
Печ. л. 1,8. Тираж 60 экз.
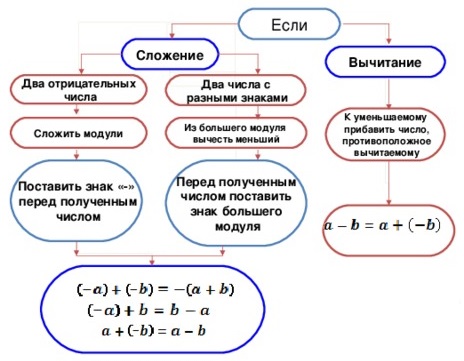
Сложение и вычитание целых чисел с разными знаками
Сложение
При сложении двух целых чисел с одинаковым знаком складываются их абсолютные величины и перед суммой ставится их общий знак.
Примеры:
(+3) + (+7) = 10
(-3) + (-7) = -10
Из данных примеров следует, что в результате сложения двух положительных чисел получится положительное число, а в результате сложения двух отрицательных чисел – отрицательное число.
При сложении двух целых чисел с разными знаками нужно взять их абсолютные величины и из большей вычесть меньшую, в результате ставится знак того числа, у которого абсолютная величина больше.
Другими словами, можно просто, не обращая внимания на знаки, вычесть из большего числа меньшее и у получившегося результата поставить знак большего числа:
Примеры:
(-4) + (+11) = 7, так как 11 — 4 = 7
(-5) + (+2) = -3, так как 5 — 2 = 3
Из данных примеров следует, что в результате сложения двух чисел с разными знаками может получится как положительное, так и отрицательное число.
Сумма двух противоположных чисел равна нулю:
(-7) + 7 = 0
Вычитание
Вычитание одного целого числа из другого можно заменить сложением, при этом уменьшаемое берётся со своим знаком, а вычитаемое с противоположным:
(+6) — (+5) = (+6) + (-5) = 1
(+6) — (-5) = (+6) + (+5) = 11
(-6) — (-5) = (-6) + (+5) = -1
(-6) — (+5) = (-6) + (-5) = -11
Из данных примеров следует, что, чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.
При решении выражений, содержащих и сложение, и вычитание, можно сначала заменить вычитание сложением, затем отдельно сложить положительные и отрицательные слагаемые, а потом найти сумму получившихся чисел.
Пример:
12 — 18 + 41 — 9
Заменим вычитание на сложение:
12 + (-18) + 41 + (-9)
сгруппируем слагаемые по их знакам и сложим отдельно положительные и отрицательные числа:
(12 + 41) + ((-18) + (-9)) = 53 + (-27)
Теперь осталось только найти сумму двух получившихся результатов:
53 + (-27) = 26, значит 12 — 18 + 41 — 9 = 26
Урок 10: Действия с отрицательными числами
План урока:
Сложение отрицательных чисел
Сложение чисел с разными знаками
Вычитание отрицательных чисел и чисел с разными знаками
В субботу, ученики 6 класса договорились встретиться и погулять в парке. Утром Юля выглянула в окошко, ярко светит солнышко, но при этом морозно. Девочка взглянула на термометр. Он показывал -10˚C. Мама попросила Юлю пойти на улицу немного позже, когда на улице потеплеет. Юля расстроилась и стала ждать. Через два часа девочка снова взглянула на термометр. Он показал -3. Ого! Всего два часа, а так потеплело – обрадовалась девочка и стала одеваться, чтобы идти гулять. В это время в комнату вошла мама и удивленно спросила «Уже потеплело? На сколько градусов?» Дочь не знала, что сказать и как правильно узнать, на сколько градусов стало теплее. Мама пришла на помощь и сообщила, что достаточно от -10 отнять -3, и мы узнаем, на сколько градусов изменилась температура воздуха за окном. Иначе, можно сказать, что шкала термометра поднялась вверх на 7 делений, значит, на улице стало теплее на 7 градусов. Запомнив все, что рассказала мама, Юля побежала в парк делиться новыми знаниями с друзьями.

Источник
Сложение и вычитание отрицательных чисел
Давайте вспомним любимую многими сказку «Буратино» и разберем задачу с участием любимых персонажей.
В театре Карабаса-Барабаса актерам жилось очень сложно, все куклы мечтали жить на свободе. Актеры тяжело работали, но долги перед хозяином росли с каждым днем. Злой владелец пообещал отпустить Буратино и Мальвину из своего театра только тогда, когда кукольные герои вернут ему долг. Сколько монет нужно собрать героям, чтобы оказаться на свободе, если у Буратино было -15 монет, а у Мальвины -6?

Источник
Чтобы ответить на главный вопрос задачи, нам нужно понимать, о чем идет речь. Изучив условие, возникает вопрос «Как может быть -15 и -6 монет?». В данном случае выходит, что Буратино и Мальвина должны вернуть Карабасу-Барабасу 15 и 6 монет, поэтому перед данными числами и стоит знак «минус». Получается, кукольные персонажи смогут покинуть театр, когда полностью вернут долг. Для этого необходимо узнать общий размер долга Буратино и Мальвины. Чтобы узнать размер долга, суммируем монеты персонажей -15 и -6. Но как их сложить, когда перед слагаемыми стоит «минус»? В подобных ситуациях применяют правило сложения отрицательных чисел.

Возвращаемся к решению задачи.
Теперь, правильно запишем и суммируем известные данные.

Получается, что герои имеют -21 монету, следовательно, они должны собрать 21 монету и вернуть долг, только тогда появится возможность покинуть театр Карабаса-Барабаса.

Источник
Рассмотрим еще одно задание.
Найдите результат сложения -24 и -16.
Чтобы вычислить сумму двух значений со знаком «минус», достаточно суммировать их модули, и перед полученной цифрой записать «-».
-24+(-16)=-(24+16)=-40.
Запомни! Если складываем два отрицательных числа, то суммируем их модули, а перед результатом сложения записываем «-».
Сложение чисел с разными знаками
Рассмотрим ситуацию.
Мишин папа навещал бабушку в деревне, обещал привезти гостинец сыну – яблоки. Во дворе Миша рассказал мальчишкам про папино обещание, и решил угостить яблоком, каждого из трех друзей, то есть, у него уже стало -3 яблока. Папа привез сыну 10 яблок и мальчик с радостью поделился фруктами с друзьями. Сколько яблок осталось у мальчика?

Источник
Чтобы найти количество яблок у мальчика, нам нужно узнать, чему равна сумма яблок –тех которые были у мальчика(-3), и тех, которые дал папа(10). То есть, чтобы ответить на главный вопрос задачи, достаточно сложить -3 и 10. Но слагаемые имеют разные знаки «+» и «-». Как же выполнить сложение положительного и отрицательного чисел? Запомнив алгоритм сложения положительных и отрицательных чисел сделать это, будет очень просто.

Используем рассмотренный алгоритм при выполнении действий.
Суммируем-3 и 10. Для этого:
- определяем модули: -3=|3|, 10=|10|;
- сравниваем модули, определяя больший: |3|<|10|;
- от большего отнимаем меньший: 10 – 3=7;
- так как по условию 10 – число положительное, то и результат будет числом положительным.
Записывается в таком виде:
-3+10=10 – 3=7.
Выходит, у мальчика стало 7 яблок.

Источник
Рассмотрим еще один пример сложения чисел с разными знаками.
Вычислите сумму -28 и 11.
Известные слагаемые имеют разные знаки, то есть -28 является значением отрицательным, а 11–положительным. Чтобы суммировать слагаемые, необходимо воспользоваться ранее рассмотренным алгоритмом. Вначале, определяем модули и сравниваем их.
-28=|28|;
11=|11|;
28>11.
Помним, что большее значение модуля имеет отрицательное слагаемое (-28), поэтому перед результатом нужно будет поставить знак «минус». Теперь, находим разность большего и меньшего значения модуля (28-17) и записываем математическое выражение:
-28+11=-(28-11)=-17.
Учитывая рассмотренные примеры, можно сказать, что:
любое числовое значение от прибавления к нему положительного числа, всегда становится больше, а от прибавления отрицательного числа только меньше.
Докажем справедливость данного правила, вычислив выражение и сравнив уменьшаемое с полученной суммой:-150+50.
Чтобы найти значение выражения нужно определить модули (150 и 50), оставив знак«-» модуля большего слагаемого, от большего значения отнимаем меньшее:
-150+50=-(150-50)=-100.
Сравним найденное значение выражения (-100) с уменьшаемым (-150), используя правило сравнения чисел с отрицательным знаком:
При сравнении цифровых значений со знаком «минус», меньшим будет то, чей модуль больше.
-150=|150|;
-100=|100|.
150>100;
-150<-100.
Действительно, при сложении с отрицательным числом уменьшаемое стало только меньше.
Вычитание отрицательных чисел и чисел с разными знаками
Мы уже знаем, как выполнять сложение и вычитание положительных и отрицательных чисел, но хочется сказать, что именно в этом разделе математики, большую роль играют противоположные числа. Для тех, кто забыл, напоминаем, какие числовые значения называются противоположными:
Если два числа отличаются только знаком, то они являются противоположными:-13 и 13, 141 и -141, 1000 и -1000.
Чтобы понять, какие правила необходимо соблюдать при выполнении вычитания чисел с разными знаками, давайте разберем задание.
Определите, чему будет равно значение выражения: от -510 отнять +210.
На первый взгляд задание очень простое и не вызывает никаких проблем. Но стоит записать разность в виде выражения:
-510-(+210)
сразу возникает вопрос «Как вычитать, если уменьшаемое со знаком «минус», а вычитаемое со знаком «плюс»?».Чтобы решение подобных выражений не вызывало у вас трудностей, возьмите на заметку правило:
Чтобы выполнить вычитание чисел с разными знаками, нужно уменьшаемое оставить без изменений и прибавить к нему число, противоположное вычитаемому.
Например: -5-(+2).
Минус пять оставляем без изменений. Вычитаемое +2, а противоположное ему -2. Складываем уменьшаемое(-5) и число противоположное вычитаемому(-2): -5+(-2).
По правилу сложения отрицательных чисел, складываем модули(5+2) и ставим знак «-»:
-5+(-2)=-(5+2)=-7
Учитывая данное правило, получается, что к уменьшаемому(-510) необходимо прибавить значение,противоположное вычитаемому(210), таким числом будет -210:
Запишем выражение:
-510-(+210)=-510+(-210). Чтобы вычислить полученное выражение нужно сложить отрицательные значения, согласно правилу сложения отрицательных чисел:
-510-(+210)=-510+(-210)=-(510+210)=-720.
Вычисления окончены.

Источник
Рассмотрим следующее задание.
Найдите значение выражения: -248+248.
Используем правило сложения значений с разными знаками.
-248=|248|;
248=|248|;
248 – 248=0.
Следовательно,
при сложении противоположных числовых значений в результате всегда будет 0.
Зная правило вычитания отрицательных чисел, можем сделать вывод, что знаки, стоящие перед скобками, могут менять знак числа, находящегося в скобках.
К примеру, в выражении 19-(-4), при вычислении используем правило, согласно которого, к уменьшаемому прибавляем, число противоположное вычитаемому, то есть знак вычитаемого «-» меняем на противоположный «+». Получим:

Запомни! Если перед скобкой в математическом выражении стоит знак «минус», то знак числа в скобках меняется на противоположный.

Ну а сейчас, разберем задание, в котором перед скобкой стоит знак «плюс».
Вычисли: -36+(-7).
В этом задании воспользуемся правилом сложения отрицательных чисел– сложим модули числовых значений, а перед суммой поставим знак «минус»:

Мы видим, что «плюс» перед скобкой никак не повлиял на знак числа, стоящего в скобках. Запомни! Если перед скобками стоит «плюс», то знак числового значения, стоящего в скобках никак не меняется.
В выполнении рассматриваемых действий нет ничего сложного. Главное запомнить основные требования и придерживаться их в процессе любых вычислений! Если сразу запомнить все правила не получается, заходи на сайт 100уроков.ru и мы всегда с удовольствием напомним нужное правило или алгоритм.
Минутка истории
История математики утверждает, что человечество длительное время не принимало ряд отрицательных числовых значений. Данный вид чисел, казался непонятным и ненужным. Привычных нам знаков «плюс» и «минус» просто не существовало. Если возникала необходимость в записи отрицательно числа, то его записывали следующим образом «долг в 30 монет». И лишь математики Древней Индии и Китая, выполняли записи отрицательных чисел без употребления слова «долг», а просто использовали черные чернила, вместо синих.
Только в 3 веке греческий ученый Диофант, стал обозначать знак «минус» вот таким символом .
Привычные нам знаки «+» и «-» появились в Германии в конце 15 века. Чешский ученый Ян Видман, отразил данные знаки в своей книге-пособии, помогающей подсчитывать прибыль и убытки чешским купцам. Стоит заметить, что данная книга была написана от руки и имела огромную популярность среди богатых людей того времени.
Сложение чисел с разными знаками. Видеоурок. Математика 6 Класс
Посмотрите на эту шестеренку (см. рис. 1).

Рис. 1. Шестеренка часов
Это не стрелка, которая непосредственно показывает время и не циферблат (см. рис. 2). Но без этой детали часы не работают.

Рис. 2. Шестеренка внутри часов
А что обозначает буква Ы? Ничего, кроме звука Ы. Но без нее не будут «работать» многие слова. Например, слово «мЫшь». Так и отрицательные числа: они не показывают никакого количества, но без них механизм вычислений был бы существенно труднее.
Мы знаем, что сложение и вычитание равноправные операции, и их можно выполнять в любом порядке. В записи 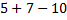 в прямом порядке мы можем посчитать:
в прямом порядке мы можем посчитать: 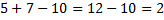 , а начать с вычитания нет, так как мы не договорились еще, а что же такое
, а начать с вычитания нет, так как мы не договорились еще, а что же такое 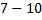 .
.
Понятно, что увеличить число на 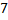 , а потом уменьшить на
, а потом уменьшить на 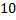 означает в итоге уменьшение на три. Почему бы так и не обозначить этот объект
означает в итоге уменьшение на три. Почему бы так и не обозначить этот объект 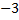 и так и считать: прибавить
и так и считать: прибавить 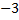 – значит вычесть
– значит вычесть 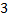 . Тогда
. Тогда 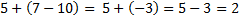 .
.
Число 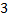 может означать, например,
может означать, например, 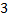 яблока. Новое число
яблока. Новое число 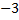 не обозначает никакого реального количества. Само по себе оно ничего не означает, как буква Ы. Это просто новый инструмент для упрощения вычислений.
не обозначает никакого реального количества. Само по себе оно ничего не означает, как буква Ы. Это просто новый инструмент для упрощения вычислений.
Назовем новые числа отрицательными. Теперь мы можем вычитать из меньшего числа большее. Технически всё равно нужно вычесть из большего числа меньшего, но в ответе поставить знак минус: 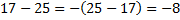 .
.
Рассмотрим ещё один пример: 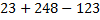 . Можно сделать все действия подряд:
. Можно сделать все действия подряд: 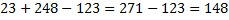 .
.
Однако из первого числа легче вычесть третье, а потом прибавить второе число:

Отрицательные числа можно определить и по-другому.
Для каждого натурального числа, например 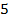 , введем новое число, которое обозначим
, введем новое число, которое обозначим 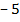 , и определим, что оно обладает следующим свойством: сумма числа
, и определим, что оно обладает следующим свойством: сумма числа 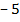 и
и 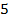 равна
равна  :
: 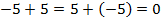 .
.
Число 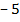 будем называть отрицательным, а числа
будем называть отрицательным, а числа 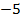 и
и 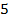 – противоположными. Таким образом, мы получили бесконечное количество новых чисел, например:
– противоположными. Таким образом, мы получили бесконечное количество новых чисел, например:
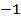 – противоположное для числа
– противоположное для числа 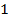 ;
; 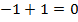
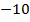 – противоположное числу
– противоположное числу 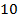 ;
; 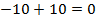
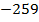 – противоположное числу
– противоположное числу 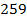 ;
; 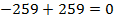
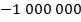 – противоположное числу
– противоположное числу 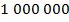 ;
; 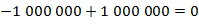
Вычтем из меньшего числа большее: 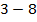 . Прибавим к данному выражению
. Прибавим к данному выражению 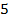 :
: 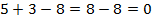 . Получили ноль. Однако согласно свойству: число, которое в сумме с пятью дает ноль, обозначается минус пять
. Получили ноль. Однако согласно свойству: число, которое в сумме с пятью дает ноль, обозначается минус пять 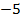 :
: 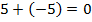 . Следовательно, выражение
. Следовательно, выражение 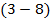 можно обозначить как
можно обозначить как 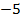 .
.
То есть теперь мы можем вычитать из меньшего числа большее. Результатом будет отрицательное число: 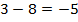
У каждого положительного числа существует число-близнец, которое отличается только тем, что перед ним стоит знак минус Такие числа называются противоположными (см. рис. 3).

Рис. 3. Примеры противоположных чисел
Свойства противоположных чисел
1. Сумма противоположных чисел равна нулю: 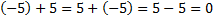 .
.
2. Если из нуля вычесть положительное число, то результатом будет противоположное отрицательное число: 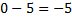 .
.
1. Оба числа могут быть положительными, и складывать их мы уже умеем: 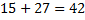 .
.
2. Оба числа могут быть отрицательными.
Мы уже прошли сложение таких чисел на предыдущем уроке, но убедимся, что понимаем, что с ними делать. Например: 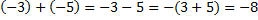 .
.
Чтобы эту сумму найти, складываем противоположные положительные числа 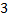 и
и 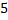 и ставим знак минус.
и ставим знак минус.
3. Одно число может быть положительным, а другое – отрицательным.
Прибавление отрицательного числа мы, если это нам удобно, можем заменять на вычитание положительного: 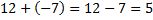 .
.
Ещё один пример: 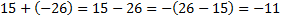 . Опять сумму записываем как разность. Вычесть из меньшего большее число можно, вычитая из большего меньшее, но поставив знак минус.
. Опять сумму записываем как разность. Вычесть из меньшего большее число можно, вычитая из большего меньшее, но поставив знак минус.
Слагаемые можем менять местами: 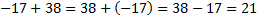 .
.
Ещё один аналогичный пример: 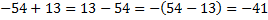 .
.
Во всех случаях в итоге получается вычитание.
Чтобы коротко сформулировать эти правила, давайте вспомним еще один термин. Противоположные числа, конечно, не равны друг другу. Но было бы странно не заметить у них общего. Это общее мы назвали модулем числа. Модуль у противоположных чисел одинаковый: у положительного числа он равен самому числу, а у отрицательного – противоположному, положительному. Например: 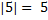 ,
, 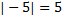 .
.
Чтобы сложить два отрицательных числа, нужно сложить их модули и поставить знак минус:
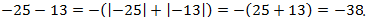
Чтобы сложить отрицательное и положительное число, нужно из большего модуля вычесть меньший модуль и поставить знак числа с большим модулем: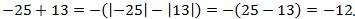
1. 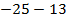
Оба числа отрицательные, следовательно, складываем их модули и ставим знак минус: 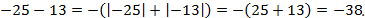
2. 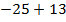
Два числа с разными знаками, следовательно, из модуля числа 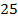 (больший модуль) вычитаем модуль числа
(больший модуль) вычитаем модуль числа 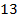 и ставим знак минус (знак числа с большим модулем):
и ставим знак минус (знак числа с большим модулем):
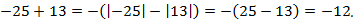
3. 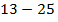
Два числа с разными знаками, следовательно, из модуля числа 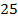 (больший модуль) вычитаем модуль числа
(больший модуль) вычитаем модуль числа 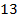 и ставим знак минус (знак числа с большим модулем):
и ставим знак минус (знак числа с большим модулем): 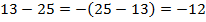 .
.
4. 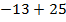
Два числа с разными знаками, следовательно, из модуля числа 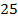 (больший модуль) вычитаем модуль числа
(больший модуль) вычитаем модуль числа 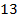 и ставим знак плюс (знак числа с большим модулем):
и ставим знак плюс (знак числа с большим модулем): 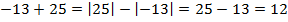 .
.
У положительных и отрицательных чисел исторически разная роль.
Сначала мы ввели натуральные числа для счета предметов: 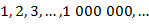
Потом мы ввели другие положительные числа – дроби, для счета нецелых количеств, частей: 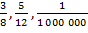 .
.
Отрицательные же числа появились как инструмент для упрощения расчетов. Не было такого, чтобы в жизни были какие-то количества, которые нам было не посчитать, и мы изобрели отрицательные числа.
То есть отрицательные числа не возникли из реального мира. Просто они оказались настолько удобными, что кое-где им нашлось применение и в жизни. Например, мы часто слышим про отрицательную температуру. При этом мы никогда не сталкиваемся с отрицательным количеством яблок. В чем же разница?
Разница в том, что в жизни отрицательные величины используют только для сравнения, но не для количеств. Если в гостинице оборудовали подвал и туда пустили лифт, то, чтобы оставить привычную нумерацию обычных этажей, может появиться минус первый этаж. Этот минус первый означает всего лишь на этаж ниже уровня земли (см. рис. 1).

Рис. 4. Минус первый и минус второй этажи
Отрицательная температура отрицательна только по сравнению с нулем, который выбрал автор шкалы Андерс Цельсий. Есть другие шкалы, и та же самая температура уже может не быть там отрицательной.
При этом мы понимаем, что невозможно поменять точку отсчета так, чтобы яблок стало не пять, а шесть. Таким образом, в жизни положительные числа используются для определения количеств (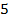 яблок,
яблок,  торта).
торта).
Еще мы их используем вместо имен. Каждому телефону можно было бы дать свое имя, но количество имен ограничено, а чисел нет. Поэтому мы используем номера для телефонов. Также для упорядочивания ( век идет за
век идет за  веком).
веком).
Отрицательные числа в жизни используются в последнем смысле (минус первый этаж ниже нулевого и первого этажей)
Список рекомендованной литературы
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. М.: Мнемозина, 2012.
- Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. «Гимназия», 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. М.: Просвещение, 1989.
- Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5–6 класс. М.: ЗШ МИФИ, 2011.
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5–6. Пособие для учащихся 6 классов заочной школы МИФИ. М.: ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5–6 классов средней школы. М.: Просвещение, Библиотека учителя математики, 1989.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Math-prosto.ru (Источник).
- Youtube (Источник).
- School-assistant.ru (Источник).
- Allforchildren.ru (Источник).
Домашнее задание
- Вопросы в конце раздела 33 (§6), задание 1066, 1073 (стр. 181-182) – Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6 класс (Источник).
- Сложите положительное число
 и отрицательное число
и отрицательное число  .
. - Температура плавления ртути
 . При изменении ее температуры на
. При изменении ее температуры на  она закипит. Определите температуру кипения ртути.
она закипит. Определите температуру кипения ртути.
Сложение и вычитание отрицательных и положительных чисел. Решение примеров.
Существуют разные типы чисел — четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов — положительные числа и отрицательные числа. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны — положительные.
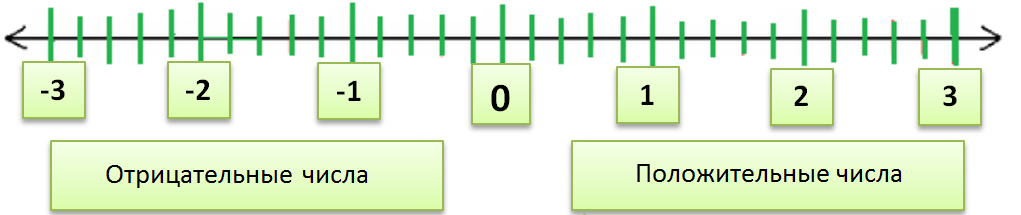
Ноль — это нейтральный элемент относительно сложения целых чисел. В основном в этой статье мы будем изучать операции сложения и вычитания с отрицательными числами. Существуют определенные правила для знаков при сложении и вычитании:
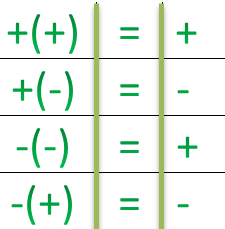
- Для того чтобы сложить два отрицательных числа, надо сложить два числа и поставить знак минус.
\((-2)+(-3)=-5\)
- Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:
\((-8)+4=4-8=-4\)
\(9+(-4)=9-4=5\)
Для каждого числа кроме \(0\) существует противоположный элемент, при сумме с ним образуется ноль:
\(-9+9=0\) \(7,1+(-7,1)=0\)
- При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.
\((-7)-(-6)=(-7)+6=(-1)\)
- Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.
\(7-9=-2\) так как \(9>7\)
- Также не стоит забывать минус на минус дает плюс:
\(7-(-9)=7+9=16\)
Задача 1. Вычислите:
- \(4+(-5)\)
- \(-36+15\)
- \((-17)+(-45)\)
- \(-9+(-1)\)
Решение:
- \(4+(-5)=4-5=-1\)
- \(-36+15=-21\)
- \((-17)+(-45)\) \(=-17-45=-62\)
- \(-9+(-1)=-9-1=-10\)
Задача 2. Вычислите:
- \(3-(-6)\)
- \(-16-35\)
- \(-27-(-5)\)
- \(-94-(-61)\)
Решение:
- \(3-(-6)=3+6=9\)
- \(-16-35=-51\)
- \(-27-(-5)=-27+5=-22\)
- \(-94-(-61)=-94+61=-33\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Сложение и вычитание отрицательных и положительных чисел ℹ️ правило сложения чисел с разными знаками и действия с ними, как складывать и вычитать числа с разными знаками, онлайн-калькулятор
Впервые знакомство с отрицательными числами происходит в школьном курсе в 6 классе, иногда раньше. Число со знаком «+» называется положительным, противоположное — отрицательным.
Чтобы понять, что такое сложение и вычитание положительных и отрицательных чисел, достаточно воспользоваться координатной прямой. Например, сумма чисел -18 и 2. Сначала отмечаем на координатном отрезке число (-18), откладываем от него вправо, соответствующие масштабу, 2 единичных отрезка, и получаем на координатном луче число -16.
Правило сложения отрицательных чисел и чисел с разными знаками
Для суммирования двух отрицательных чисел, необходимо:
Например, сложение чисел -9 и -6 будет выглядеть следующим образом:
-9 + (-6) = -15
В данном случае, складываем модули 9 и 6, и перед получившимся натуральным числом 15 ставим знак «-«.
Сложение рациональных или дробных чисел выполняется аналогичным способом:
-26,35 + (-25,35) = -(26,35 + 25,35) = -51,75
К 26,35 прибавляем 25,35 (т. е. мы складываем модули), в итоге получаем 51,75 с отрицательным значением. Перед ним ставим знак «минус».
Для суммирования натуральных чисел со знаками «+» и «-», надо:
-
из слагаемого с большим значением модуля вычесть слагаемое с меньшим значением;
-
перед полученным результатом поставить знак того слагаемого, которое имело большее значение.
Пример:
61,2 + (-31,5) = + (61,2 — 31,5) = 30,5
Модуль большего числа со знаком «+», соответственно, сумма получилась положительная:
-81 + 35 = -(81 — 35) = 46
Большее число со знаком «-», поэтому заменяем плюс на минус и получаем отрицательный ответ.
Как вычитать отрицательные и положительные числа
Для нахождения разности противоположных чисел, надо к уменьшаемому прибавить вычитаемое с противоположным знаком, то есть заменить разность суммой.
Наглядно данное действие лучше представить в виде формулы:
a — b = a + (-b)
То есть любое выражение, содержащее знаки сложения и вычитания, следует решать как сумму чисел.
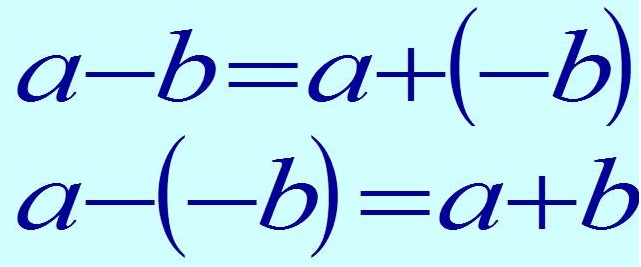
Примеры:
-20 — 14 = -20 + (-14) = -34;
-6,1 + 5,6 = 5,6 + (-6,3) = 0,5.
Разность выражения будет положительной, если уменьшаемое больше вычитаемого, и отрицательной, если значение модуля уменьшаемого меньше вычитаемого. В случае, когда уменьшаемое и вычитаемое одинаковые, их разность будет равна нулю.
Примеры:
-
15 — 6 = 15 + (-6) = 9 — уменьшаемое 15, больше вычитаемого, поэтому ответ положительный;
-
-15 — 6 = -15 + (-6) = -21 — уменьшаемое -15, меньше вычитаемого, следовательно, ответ отрицательный.
Если нужно отнять отрицательное число, то два знака «минус» подряд дают знак «плюс».
Пример:
10 — (-5) = 10 + 5 = 15;
— 10 — (-5) = -10 + 5 = 5 — 10 = -5.
Все вышеперечисленные действия возможно выполнить на калькуляторе. Для этого достаточно ввести сначала модуль числа, потом нажать кнопку изменения знака «+/-».
Например, чтобы задать число -81,73, надо в следующем порядке нажать кнопки: «8», «1», «,», «7». «3», «+/-». А решать пример с отрицательными числами следует в том же порядке, что и с положительными.
Заключение
Для закрепления изученных правил можно использовать различные методы проверки знаний. На первом этапе лучшим вариантом будет тренажер, с помощью которого решение подобных примеров можно довести до автоматизма.
Так же для закрепления материала подойдет тестирование. Его можно провести в виде самостоятельной работы. В конце изучения всех правил применяется контрольная работа, задания для которой можно подобрать из различных дидактических материалов.
правило, примеры, как складывать числа с разными знаками
В этом материале мы расскажем, как правильно выполнять сложение отрицательного и положительного числа. Сначала мы приведем основное правило такого сложения, а потом покажем, как оно применяется при решении задач.
Основное правило сложения положительных и отрицательных чисел
Мы уже говорили ранее, что положительное число можно рассматривать как доход, а отрицательное – как убыток. Чтобы узнать величину дохода и расхода, надо смотреть на модули этих чисел. Если в итоге окажется, что наши расходы превышают доходы, то после их взаимного учета мы останемся должны, а если наоборот, то мы останемся в плюсе. Если же расходы равны доходам, то у нас будет нулевой остаток.
Используя приведенные выше рассуждения, можно вывести основное правило сложения чисел с разными знаками.
Определение 1Для сложения положительного числа с отрицательным необходимо найти их модули и выполнить сравнение. Если значения окажутся равны, то мы имеем два слагаемых, которые являются противоположными числами, и их сумма будет нулевой. Если же они не равны, то нам надо учесть, что результат будет иметь тот же знак, что и большее число.
Таким образом, сложение в данном случае сводится к вычитанию из большего числа меньшего. Итог этого действия может быть разным: мы можем получить как положительное, так и отрицательное число. Нулевой результат тоже возможен.
Это правило распространяется на целые, рациональные и действительные числа.
Задачи на сложение положительного числа с отрицательным
Разберем, как применять на практике правило, озвученное выше. Возьмем для начала простой пример.
Пример 1Вычислите сумму 2+(-5).
Решение
Выполним последовательно шаги, которые мы изучили до этого. Найдем для начала модули исходных чисел, которые будут равны 2 и 5. Больший модуль – 5, поэтому запоминаем минус. Далее вычитаем из большего модуля меньший и получаем: 5−2=3.
Ответ: (−5)+2=−3.
Если в условиях задачи стоят рациональные числа с разными знаками, не являющиеся при этом целыми, то для удобства расчетов нужно представить их в виде десятичных или обыкновенных дробей. Возьмем такую задачу и решим ее.
Пример 2Вычислите, ско

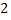 и отрицательное число
и отрицательное число 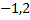 .
.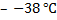 . При изменении ее температуры на
. При изменении ее температуры на 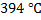 она закипит. Определите температуру кипения ртути.
она закипит. Определите температуру кипения ртути.