Чему равен cos1
Чтобы понять, чему равны cos 1,cos 2 и т.д., начертим единичную окружность и приблизительно отметим на ней точки 1, 2, 3, 4, 5, 6.
Небольшая справка:cos 1 — это косинус угла в 1 радиан.
1 радиан − это угол, соответствующий дуге, длина которой равна ее радиусу.
Кроме того, вспомним, что π≈3,14 рад, тогда π/3≈3,14/3≈1,047 рад.
Значит, точка 1 лежит на дуге чуть ниже точки π/3 Аналогично отмечаем на окружности точки 2, 3, 4, 5, 6.
По рисунку можно определить, что: cos 6 > cos 1 > cos 5 > cos 2 > cos 4 > cos 3
xn--80adc1aphnvc.xn--p1ai
cos 2
Единичная окружность помогает разобраться, чему равны cos 1, cos 2, cos 3, cos 4, cos 5 и cos 6, без калькулятора и таблиц.

Чтобы найти углы в 1, 2, 3, 4 5 и 6 радиан на единичной окружности, можно вспомнить, что п приближенно равно 3,14, и привязать их местонахождение к п, п/2, 3п/2 и 2п. Можно пойти другим путем: угол в 1 радиан соответствует длине дуги, равной радиусу окружности. Соответственно, отмечаем 6 раз на окружности длину радиуса. Конечно, рисунок получается очень приблизительным, но наглядным.
Итак, косинус 1, косинус 2, косинус 3, косинус 4, косинус 5 и косинус 6 — это абсциссы (x) отмеченных точек. С помощью единичной окружности можно легко сравнивать косинусы. Мы видим, cos 1>0, cos 5>0 и cos 6>0, а cos 2<0, cos 3<0, cos 4<0. Соответственно, вопрос сравнения косинусов с разными знаками решается элементарно: любое положительное число больше любого отрицательного: например, cos1 > cos3. При сравнении косинусов с одинаковыми знаками можно использовать геометрическую интерпретацию. Таким образом получаем, например: cos2 > cos4, cos5 < cos1.
Если нужны более точные значения cos 1, cos 2, cos 3, cos 4, cos 5 и cos 6, можно воспользоваться калькулятором либо таблицами:
При оценке приблизительных значений углов, больших 6 радиан, геометрическая интерпретация тоже работает, но с увеличением угла накапливается погрешность вычислений.
www.uznateshe.ru
Косинус
Примеры:
\(\cos{30^°}=\)\(\frac{\sqrt{3}}{2}\)
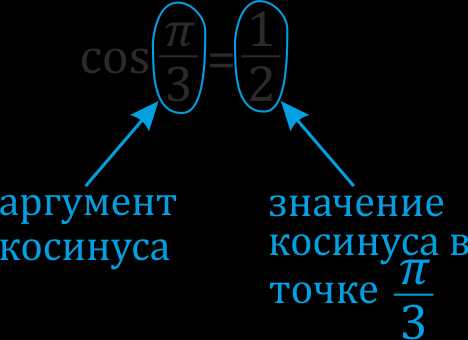
\(\cos\)\(\frac{π}{3}\)\(=\)\(\frac{1}{2}\)
\(\cos2=-0,416…\)
Содержание:
Аргумент и значение
Косинус острого угла
Косинус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к гипотенузе.
Пример:
1) Пусть дан угол и нужно определить косинус этого угла.

2) Достроим на этом угле любой прямоугольный треугольник.
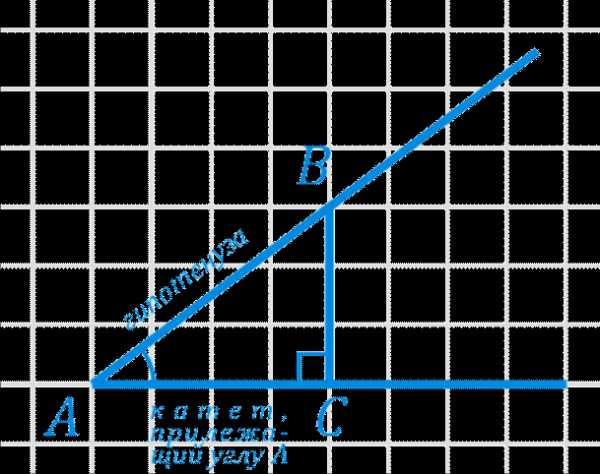
3) Измерив, нужные стороны, можем вычислить косинус.
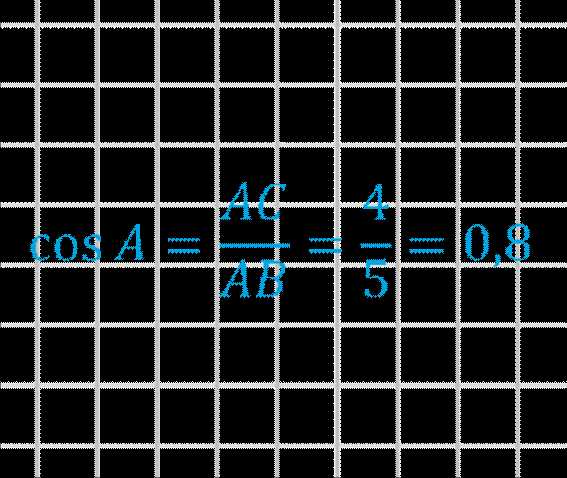
Косинус острого угла больше \(0\) и меньше \(1\)
Если при решении задачи косинус острого угла получился больше 1 или отрицательным, то значит где-то в решении есть ошибка.
Косинус числа
Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с Пи: \(\frac{π}{2}\), \(\frac{3π}{4}\), \(-2π\).
Например, для числа \(\frac{π}{6}\) — косинус будет равен \(\frac{\sqrt{3}}{2}\). А для числа \(-\)\(\frac{3π}{4}\) он будет равен \(-\)\(\frac{\sqrt{2}}{2}\) (приблизительно \(-0,71\)).
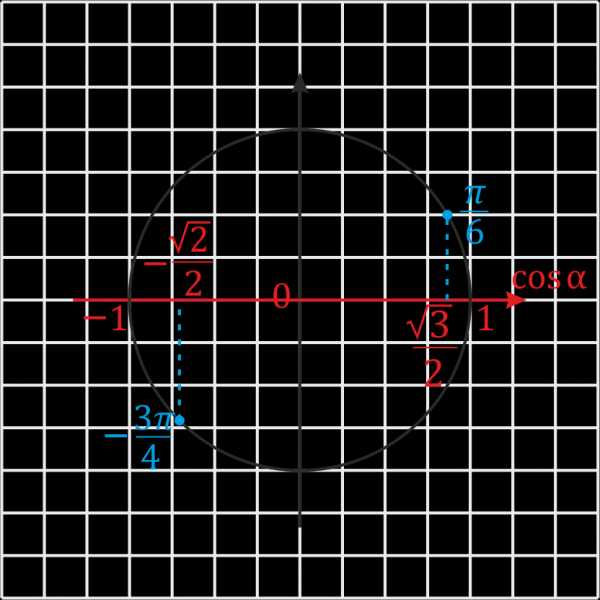
Косинус для других часто встречающихся в практике чисел смотри в тригонометрической таблице.
Значение косинуса всегда лежит в пределах от \(-1\) до \(1\). При этом вычислен косинус может быть для абсолютно любого угла и числа.
Косинус любого угла
Благодаря числовой окружности можно определять косинус не только острого угла, но и тупого, отрицательного, и даже большего, чем \(360°\) (полный оборот). Как это делать — проще один раз увидеть, чем \(100\) раз услышать, поэтому смотрите картинку.
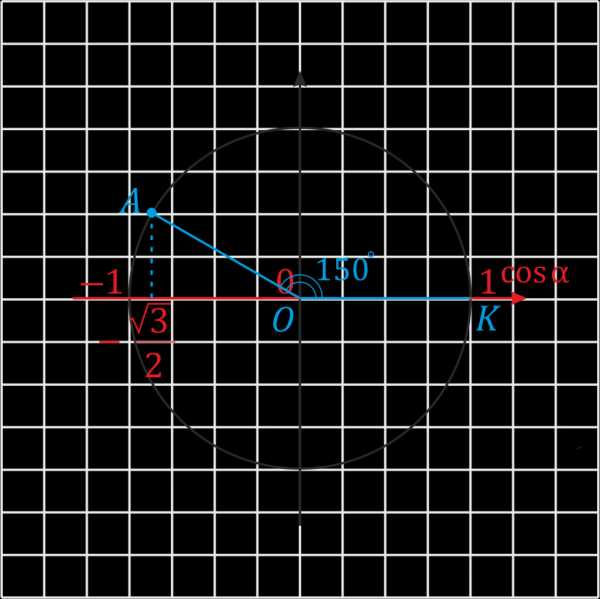
Теперь пояснение: пусть нужно определить косинус угла КОА с градусной мерой в \(150°\). Совмещаем точку О с центром окружности, а сторону ОК – с осью \(x\). После этого откладываем \(150°\) против часовой стрелки. Тогда ордината точки А покажет нам косинус этого угла.
Если же нас интересует угол с градусной мерой, например, в \(-60°\) (угол КОВ), делаем также, но \(60°\) откладываем по часовой стрелке.
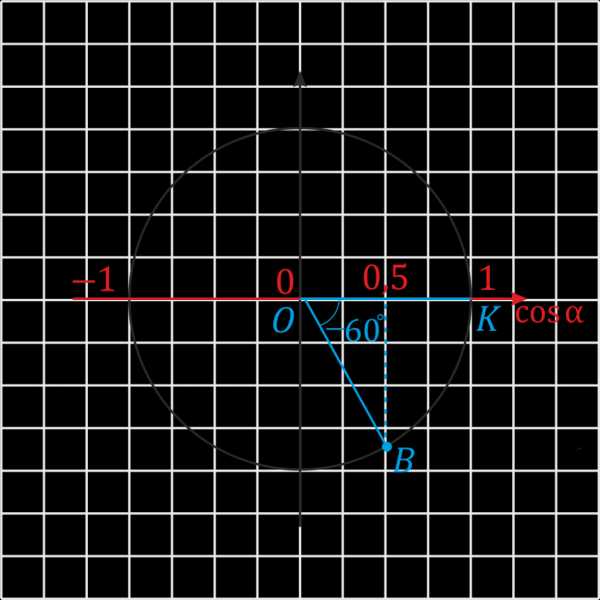
И, наконец, угол больше \(360°\) (угол КОС) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол \(405°\) отложен как \(360° + 45°\).

Несложно догадаться, что для откладывания угла, например, в \(960°\), надо сделать уже два оборота (\(360°+360°+240°\)), а для угла в \(2640°\) — целых семь.
Стоит запомнить, что:
Косинус прямого угла равен нулю. Косинус тупого угла — отрицателен.
Знаки косинуса по четвертям
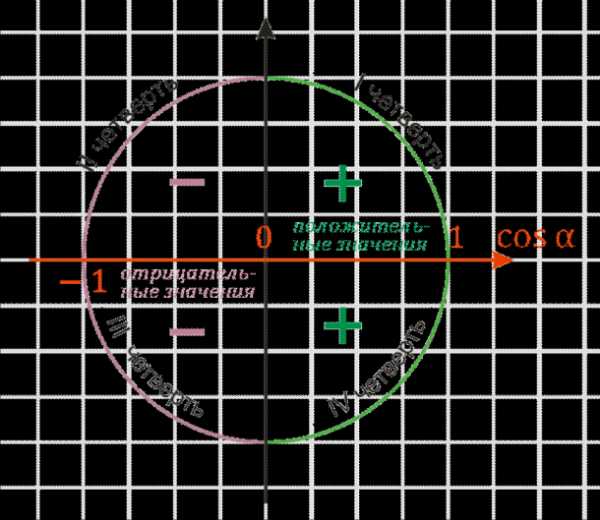
С помощью оси косинусов (то есть, оси абсцисс, выделенной на рисунке красным цветом) легко определить знаки косинусов по четвертям числовой (тригонометрической) окружности:
— там, где значения на оси от \(0\) до \(1\), косинус будет иметь знак плюс (I и IV четверти – зеленая область),
— там, где значения на оси от \(0\) до \(-1\), косинус будет иметь знак минус (II и III четверти – фиолетовая область).
Пример. Определите знак \(\cos 1\).
Решение: Найдем \(1\) на тригонометрическом круге. Будем отталкиваться от того, что \(π=3,14\). Значит единица, примерно, в три раза ближе к нулю (точке «старта»).
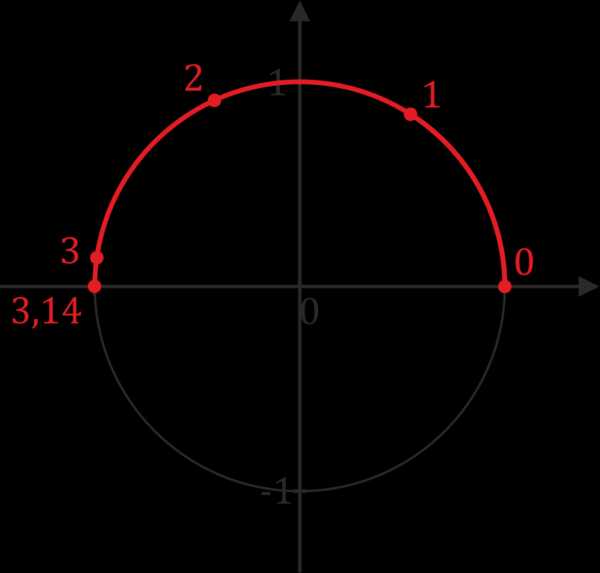
Если провести перпендикуляр к оси косинусов, то станет очевидно, что \(\cos1\) – положителен.
Ответ: плюс.
Связь с другими тригонометрическими функциями:
— синусом того же угла (или числа): основным тригонометрическим тождеством \(\sin^2x+\cos^2x=1\)— тангенсом того же угла (или числа): формулой \(1+tg^2x=\)\(\frac{1}{\cos^2x}\)
— котангенсом и синусом того же угла (или числа): формулой \(ctgx=\)\(\frac{\cos{x}}{\sinx}\)
Другие наиболее часто применяемые формулы смотри здесь.
Функция \(y=\cos{x}\)
Если отложить по оси \(x\) углы в радианах, а по оси \(y\) — соответствующие этим углам значения косинуса, мы получим следующий график:
График данной функции называется косинусоида и обладает следующими свойствами:
— область определения – любое значение икса: \(D(\cos{x} )=R\)
— область значений – от \(-1\) до \(1\) включительно: \(E(\cos{x} )=[-1;1]\)
— четная: \(\cos(-x)=\cos{x}\)
— периодическая с периодом \(2π\): \(\cos(x+2π)=\cos{x}\)
— точки пересечения с осями координат:
ось абсцисс: \((\)\(\frac{π}{2}\)\(+πn\),\(;0)\), где \(n ϵ Z\)
ось ординат: \((0;1)\)
— промежутки знакопостоянства:
функция положительна на интервалах: \((-\)\(\frac{π}{2}\)\(+2πn;\) \(\frac{π}{2}\)\(+2πn)\), где \(n ϵ Z\)
функция отрицательна на интервалах: \((\)\(\frac{π}{2}\)\(+2πn;\)\(\frac{3π}{2}\)\(+2πn)\), где \(n ϵ Z\)
— промежутки возрастания и убывания:
функция возрастает на интервалах: \((π+2πn;2π+2πn)\), где \(n ϵ Z\)
функция убывает на интервалах: \((2πn;π+2πn)\), где \(n ϵ Z\)
— максимумы и минимумы функции:
функция имеет максимальное значение \(y=1\) в точках \(x=2πn\), где \(n ϵ Z\)
функция имеет минимальное значение \(y=-1\) в точках \(x=π+2πn\), где \(n ϵ Z\).
Смотрите также:
Синус
Тангенс
Котангенс
Решение уравнения \(\cosx=a\)
cos-cos.ru
cos x = 1 / 3
Задание.
Решить уравнение:
Решение.
Исходное уравнение относят к простым видам тригонометрических уравнений, для которых существует специальная формула, согласно которой легко найти все корни данного уравнения.
Разберемся, что значит — решить уравнение. Это значит, что нужно найти такие аргументы для заданной функции, при которых косинус будет равен . Сразу можно обратиться к таблице значений тригонометрических функций, в частности косинуса. В таблице ищем среди значений косинуса число . Таких чисел для косинуса нет, это значит, что косинус может быть равен этому значению от каких-либо других углов, отличных от тех, которые представлены в таблице.
Что такой угол существует, говорит тот факт, что значение лежит между —1 и 1. Только на этом промежутке могут находиться значения функции косинус.
Для таких случаев используется специальная формула, которая использует обратную функцию к косинусу — арккосинус. Запишем решение согласно этой формуле:
, переменная z может быть любым целым числом.
Ответ. , z —целое число.
Также о существовании корней любого уравнения можно узнать из графика функции. Или с помощью тригонометрической окружности.
ru.solverbook.com
