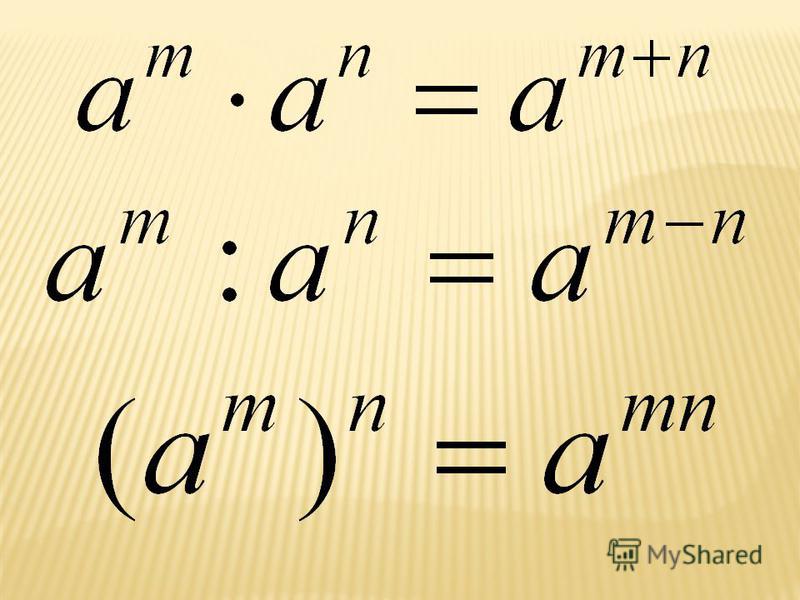Калькулятор высот
Этот калькулятор высот определяет и выражает четырьмя различными способами уклон земной поверхности. Она может быть выражена в единицах угла возвышения от горизонтальной плоскости, в процентах отклонения от горизонтальной линии или просто в единицах отношения ее «подъема к разбегу» или «единицы подъема в запустить» . Чтобы рассчитать наклон линии и узнать больше о наклонах в целом, вы можете воспользоваться нашим калькулятором уклонов. Чтобы узнать больше о том, как найти склон местности (или земли в целом), продолжайте читать.
Что такое отметка высоты?
Отметка (или уклон ) — это крутизна или степень наклона определенного участка земли. Это может быть просто крутизна между двумя конкретными точками в данной области, среднее значение постепенного изменения крутизны области или беспорядочное изменение высоты земли.
Обычно мы измеряем высоту земли как ее высоту над уровнем моря. Геодезисты и инженеры обычно измеряют и записывают эти высоты, используя геодезическое оборудование и инструменты.
Зачем нам знать высотную отметку конкретной местности?
Знание уклона местности дает много преимуществ по сравнению с полным его незнанием. Также может потребоваться продолжение других видов деятельности, таких как строительство или ирригация . Вот несколько примеров того, как важно и полезно знать степень в той или иной области:
- Знание высоты местности помогает в строительстве дорог . Мы используем его, например, в формуле вертикальной кривой. Очень крутая местность может потребовать, чтобы дороги были проложены зигзагом для более безопасного подъема и спуска. Инженеры могут разработать процедуру резки и заполнения менее крутой местности, чтобы уменьшить уклон. Выемка и засыпка — это когда почва из верхней части склона перемещается в нижнюю часть для уменьшения ее уклона.
- Определение уровня высот также помогает при строительстве подпорных стен.
Если вы хотите узнать больше о подпорных стенах, воспользуйтесь нашим калькулятором подпорных стен. - Знание угла возвышения местности также помогает при оценке способности земли поддерживать строение. Строительные конструкции на наклонной площадке могут потребовать дополнительного фундамента, чтобы избежать обрушения.
- Уровень высоты также помогает при исследовании потока воды с более высоких отметок, чтобы увидеть, можно ли орошать землю без насосов.
- и многое другое. 🙂
Как рассчитать уклон и угол возвышения?
Мы вычисляем уклон местности так же, как мы вычисляем наклон линии. Наклон данной линии требует координат ее конечных точек.
наклон=y2-y1x2-x1 \footnotesize \text{slope} = \frac{y_2 — y_1}{x_2 — x_1}slope=x2−x1y2−y1
В математическом сообществе эти изменения значений x и y имеют прозвища. Мы называем изменение значений y «подъемом» , так как оно происходит по вертикальной оси. С другой стороны, мы называем изменение значений x «пробегом» , поскольку оно проходит вдоль горизонтальной оси. Это соотношение дает нам популярное уравнение, которое вы, возможно, уже слышали раньше: «уклон равен подъему над пробегом». Или:
уклон=поднятие\размер сноски \text{откос} = \frac{\text{подъем}}{\text{пробег}}slope=поднятие
Помимо этого, мы также можем выразить уклон в терминах углов . При этом нам понадобится помощь тригонометрии, чтобы получить угол. Нас интересует угол между горизонтальной плоскостью и плоскостью наклона.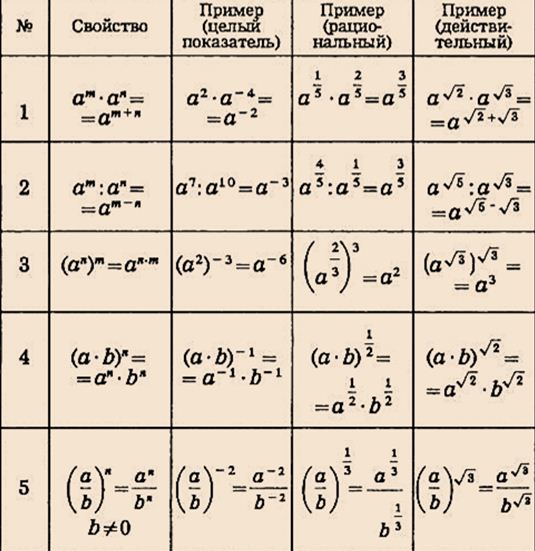
Уровень (угол)=arctanriserun\footnotesize \text{Угол (угол)} = \arctan{\frac{\text{подъем}}{\text{пробег}}}Уровень (угол)=arctanrunrise
Если у вас нет калькулятора с этой тригонометрической функцией, не волнуйтесь, мы уже включили ее в наш калькулятор высот выше. Если вы хотите узнать больше о других важных тригонометрических функциях, вы можете проверить наш калькулятор тригонометрических функций и поиграть с углами.
Помимо выражения класса с помощью отношений и углов, мы также можем определить его в процентах — нам нужно только умножить значение отношения на 100, чтобы получить его. Вот откуда берется приведенное ниже уравнение. Стопроцентная оценка означает, что подъем склона равен его длине.
Оценка (в процентах)=нарастание⋅100%\footnotesize \text{Уровень (в процентах)} = \frac{\text{подъем}}{\text{пробег}} \cdot 100\%Уровень (в процентах)=нарастание ⋅100%
Мы оснастили наш калькулятор высот всеми этими уравнениями, поэтому он может давать вам все ответы, которые вам нужны, каждый раз, когда вы вводите значение для любой переменной. Вы можете установить уклон и определить расстояние по горизонтали, необходимое для получения требуемого изменения расстояния по вертикали, а также получить угол возвышения.
Понимание значений уклона
Значения уклона довольно легко понять. Уровни рельефа менее 1 (уровень рельефа <1) означают, что склон пологий. С другой стороны, уровень рельефа больше единицы (уровень рельефа > 1) означает, что рельеф крутой. С точки зрения угла возвышения, углы выше 45 градусов являются крутыми, тогда как углы ниже 45 градусов относительно пологими.
Как определить «подъем» и «бег».
Мы можем получить «пробег» или изменение горизонтального расстояния, используя измерительная лента . Нам придется натянуть ленту, чтобы получить точное измерение. Однако, если не натягивать ее слишком сильно, значение будет выше, чем это фактическое значение, потому что лента провиснет под действием силы тяжести.
С другой стороны, мы можем получить вертикальное расстояние с помощью оптических устройств, таких как геодезический переход в паре с нивелирной рейкой . Транзит геодезиста имеет встроенный телескоп, который можно поворачивать вбок или вертикально над штативом. Сфокусировав его на нивелирной рейке (которая похожа на огромную линейку), вы получите показание. Мы можем перевести это показание в высоту между выравнивающей рейкой и переходом. Транзит геодезиста также имеет отличительную маркировку в поле зрения, которая позволяет ему также измерять горизонтальные расстояния в сочетании с нивелирной рейкой.
Мы также можем использовать такой инструмент, как клинометр, который может напрямую определить угол возвышения между двумя точками. Клинометр похож на мини-телескоп с транспортиром, прикрепленным к его боку. Другие, более сложные цифровые гаджеты теперь могут помочь получить наклон той или иной поверхности. Смартфон , если он оснащен соответствующим оборудованием, таким как гироскопические датчики , может точно определить наклон поверхности, когда вы кладете ее на склон.
Подробнее о местности
Мы можем нанести на график средние оценки местности, чтобы составить контурную карту. Контурная карта — это топографическая карта, которая дает зрителям представление о том, на что похожа местность в определенной области. Вертикальное преувеличение часто необходимо, чтобы подчеркнуть определенные особенности рельефа, например высоту гор или вулканов.
Чтобы узнать больше о вертикальном преувеличении, воспользуйтесь нашим калькулятором вертикального преувеличения.
Часто задаваемые вопросы
Какой уклон самой крутой дороги в мире?
Baldwin Street, Новая Зеландия, имеет впечатляющий уклон около 0,35 , что соответствует горизонтальной длине 2,86 м на каждый метр по вертикали. Короткая 350-метровая длинная улица — это настоящий вызов!
Класс 0,35 соответствует углу:
угол = арктангенс(1/2,86) = 19,27° .
В чем разница между наклоном в виде угла и уклоном в процентах?
Формула дает наклон, определяемый как угол:
уклон (угол) = арктангенс (подъем/угол)
Где подъем — это расстояние по вертикали, а уклон — горизонтальное расстояние откоса.
Чтобы вычислить уклон в процентах, возьмите аргумент функции арктангенса и умножьте его на 100 :
уклон (в процентах) = рост/уклон × 100
Какой угол соответствует наклону 100%?
Парадоксально, но наклон 100% соответствует углу 45°.
уклон = подъем/спуск Где
-
подъем— расстояние по вертикали; и -
пробег— горизонтальный.
Уклон, в котором каждый горизонтальный метр соответствует вертикальному метру, имеет уклон 1 , который умножается на 100 и возвращает значение 100% .
Как рассчитать уклон дороги?
Предположим, что дорога имеет 12 метров подъема на каждые 200 метров пробега. Оценка будет 0,06 . Для расчета уклона дороги:
-
подъем = 12 м; и -
пробег = 200 м:
- Вычислите соотношение между подъемом и уклоном:
уклон = подъем/уклон = 12/200 = 0,06 - Если вы хотите узнать угол наклона, введите значение в функцию арктангенса:
наклон (угол) = арктангенс (подъем/наклон) = арктангенс (12/200) = 3,43° - Если вы хотите узнать наклон в процентах, умножьте соотношение на
100:
уклон (в процентах) = 100 × подъем/спуск = 6%.
Калькулятор траектории движения снаряда
Используйте этот калькулятор траектории, чтобы найти траекторию полета снаряда . Введите три значения: скорость , угол и начальная высота , и очень скоро вы найдете формулу траектории и ее форму. Продолжайте читать, если вы хотите проверить определение траектории, а также простой пример вычислений.
Пока вы здесь, обязательно ознакомьтесь с нашим калькулятором движения снаряда.
Определение траектории
Траектория, также называемая траекторией полета, представляет собой траекторию движения движущегося объекта под действием силы тяжести . Обычно мы используем этот термин, когда говорим о снарядах или спутниках (где регулярно повторяющаяся траектория называется орбитой). Если вам нужно бросить объект на короткое расстояние, то парабола является хорошим приближением к форме траектории.
Некоторые примеры движения снаряда:
- Хоккейная шайба, бейсбольный мяч или мяч для гольфа в полете ⚾.{\!2} \end{split}yyy=h+Vy×t−2g×t2=h+Vy×Vxx−2g×(Vxx)2=h+x×V0×cos( α)V0×sin(α)−g×21×(V0×cos(α)x)2 92(\альфа)} \end{split}y=h+x×tan(α)−g×2×V02×cos2(α)x2
Если вас интересуют различные аспекты движения снаряда, ознакомьтесь с другими нашими инструментами. :
- Калькулятор времени полета;
- Калькулятор максимальной высоты;
- Вычислитель дальности полета снаряда; и
- Горизонтальное движение снаряда.
Калькулятор траектории: как пользоваться
Давайте проверим траекторию движения воды из фонтана:
- Введите скорость . Предположим, что оно равно 5 футам/с5\ \mathrm{фут/с}5 футов/с.
- Введите угол . Например, 60°60\градус60°.
- Выберите начальную высоту . Давайте выберем 5 дюймов5\ \mathrm{in}5 дюймов
- Вот ты где! Калькулятор траектории отображает формулу и траекторию полета!
Важно отметить возможную разницу в масштабировании осей, поэтому угол может выглядеть не так, как должен на графике.
Помните, что во всех расчетах сопротивлением воздуха пренебрегают.FAQ
Как найти максимальный угол движения снаряда?
Чтобы найти угол, который максимизирует горизонтальное расстояние при движении снаряда, выполните следующие шаги:
- Возьмите выражение для пройденного горизонтального расстояния:
x = sin(2θ) × v²/g. - Дифференцируйте выражение относительно угла:
2 × cos(2θ) × v²/g. - Приравняйте выражение к
0и найдитеθ: угол, который дает0, равен2θ = π/2; следовательно,θ = π/4 = 45°.
Какова траектория снаряда, запущенного под углом 30° со скоростью 10 м/с?
При запуске с нулевой начальной высоты траектория снаряда соответствует следующему уравнению: °))
Какова форма траектории снаряда?
Траектория полета снаряда равна
Помните, что во всех расчетах сопротивлением воздуха пренебрегают.