Деление функции на функцию онлайн: Калькулятор онлайн — Деление многочлена на многочлен (двучлен) столбиком (уголком) (с подробным решением)

Содержание

Деление многочленов онлайн

Онлайн калькулятор осуществляет деление многочленов двумя различными способами: делением в столбик и методом неопределенных коэффициентов. Для работы калькулятора введите исходные данные своей задачи.

Метод деления в столбик рассмотрим на следующем примере. Пусть нам требуется разделить многочлен

на многочлен

Сразу необходимо отметить, что:

деление многочленов возможно только в том случае, если степень многочлена делимого больше или равна степени многочлена делителя.

В нашем случае указанное условие выполняется т.к. степень многочлена делимого равна трём, а степень многочлена делителя — двум.

Чтобы осуществить деление многочленов, запишем многочлен делимое слева от вертикальной черты, а многочлен делитель — справа:

Далее, разделим слагаемое со старшей степенью многочлена делителя на слагаемое со старшей степенью многочлена делимого :

Запишем полученный результат (частное от деления) справа под чертой:

Теперь, умножаем на многочлен делитель , получаем:

Записываем полученный результат слева под многочленом делимым:

Вычитаем из многочлена делимого полученный результат:

Записываем полученный многочлен в столбик:

Далее, процедура повторяется, т. е. мы делим слагаемое со старшей степенью полученного многочлена ( ) на слагаемое со старшей степенью многочлена делителя ( ), и т.д., в результате получаем:

Процесс деления останавливается, когда степень многочлена остатка меньше степени многочлена делителя. Это условие описано выше.

Записываем полученный результат следующим образом. Сначала записываем частное (многочлен справа под чертой) равное , затем прибавляем к нему дробь, числителем которой является многочлен остаток равный (тот многочлен, который остался после всех вычитаний слева снизу в столбике) а знаменателем — многочлен делитель . В результате получаем:

Таким образом:

Другим способом деления многочленов является метод неопределенных коэффициентов. Рассмотрим его на том же самом примере.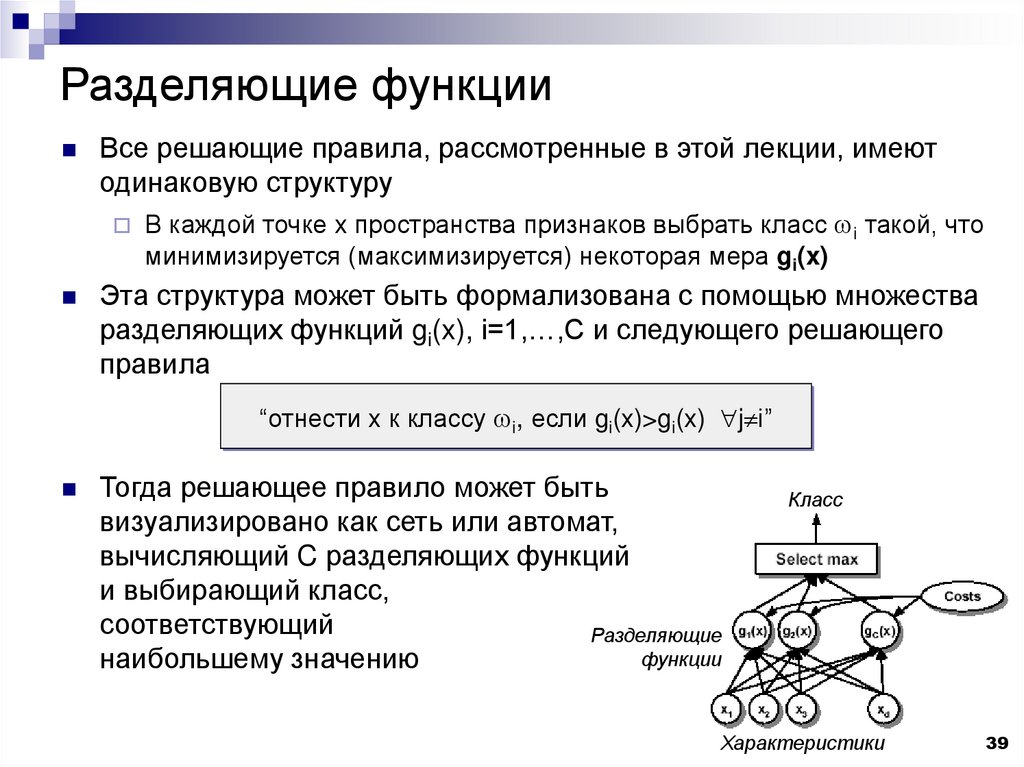 В общем случае, результат деления многочленов можно записать в следующем виде:

где — многочлен частное, степень которого равна разности степеней многочлена делимого и многочлена делителя, т.е. в нашем случае — единице. — многочлен остаток, степень которого не больше степени многочлена делителя, т.е. в нашем случае — не больше единице.

Теперь, запишем многочлен в общем виде:

— неизвестные пока коэффициенты.

Тоже самое для многочлена :

— неизвестные пока коэффициенты.

Таким образом, получаем следующее равенство:

Итак, нам нужно определить неизвестные коэффициенты и . Для этого домножаем обе части приведенного выше равенства на знаменатель — многочлен делитель , получаем:

Раскрываем скобки, приводим подобные слагаемые:

Для того, чтобы сохранить верное равенство, нам нужно приравнять коэффициенты при одинаковых степенях . В результате получаем следующую систему линейных уравнений:

В результате решения этой системы, получаем следующие значения коэффициентов:

Подставляем значения полученных коэффициентов и исходное равенство:

Как видно, данный результат полностью совпадает с результатом, полученным методом деления в столбик.

Решение систем уравнений онлайн
Калькулятор метода подстановки
Метод Крамера онлайн

Длинное Деление Многочленов — Mathcracker.Com

Инструкции: Используйте этот калькулятор для вычисления длинного деления многочлена, показывая все шаги. Пожалуйста, введите два многочлена, которые вы хотите разделить, в поле формы ниже.

Калькулятор длинного деления полинома

Данный калькулятор поможет вам в процессе выполнения длинного деления между двумя заданными многочленами. Для этого вам необходимо предоставить два правильных выражения многочлена. Эти многочлены могут быть уже упрощенными или нет, и калькулятор упростит их, если это необходимо.

Когда

деление многочленов вам нужно предоставить два многочлена, один из которых вы будете делить, который называется делителем, а другой — делимым.

Как только вы предоставите два действительных полиномы следующим шагом будет нажатие на кнопку «Рассчитать», которая покажет все соответствующие вычисления, необходимые для желаемого длинного деления между указанными многочленами.

Процесс проведения деления многочленов с использованием

Метод Длинного Деления это относительно простой метод, но он требует очень организованного подхода, чтобы не заблудиться. Обычно лучше всего работает табличный подход, показывающий соответствующие шаги.

Более простой подход используется с Синтетическое подразделение но это применимо только в том случае, если делитель имеет степень один, поэтому имеет более ограниченный охват

Что такое многочлен?

Многочлен — это тип простого выражения, которое объединяет с помощью сумм и вычитаний целые степени определенной переменной x (или какое бы имя переменной ни было выбрано), возможно, умноженные на константы. 2+8x+3\]

Деление немного сложнее, поскольку в нем задействована идея о том, что один полином не может делиться на другой именно другой многочлен. Математически, когда у нас есть два многочлена $p(x)$ и $s(x)$, и мы хотим разделить $p(x)$ на $s(x)$, мы ищем коэффициент $q(x)$ и остаток $r(x)$ (оба многочлена), которые обладают тем свойством, что $p(x)= q(x)\cdot s(x) + r(x)$, с условием степень полинома $r(x)$ меньше, чем степень $s(x)$. Обычно это называется

Разложение Евклида .

Метод длинного деления

Итак, метод длинного деления — это один из систематических способов начать с двух многочленов, которые мы хотим разделить $p(x)$ и $s(x)$, и найти коэффициент $q(x)$ и остаток $r(x)$ таким образом, чтобы

\[p(x)= q(x)\cdot s(x) + r(x)\]

Этот алгоритм чрезвычайно полезен, и хотя задача кажется простой на вид, в ней нетрудно заблудиться, если не использовать систематический подход, который гарантированно приведет к требуемому коэффициенту и остатку.

Каковы этапы выполнения длинного деления?

Шаг 1: Определите два многочлена p(x) и s(x), которые вы хотите разделить, и определите p(x) как делитель и s(x) как делимое

Шаг 2: Сверьте степень дивиденда p(x) со степенью s(x). Если степень s(x) больше степени p(x), то остаток равен самому дивиденду p(x), а коэффициент равен нулю: q(x) = 0, и все готово
Шаг 3: В данном случае мы предполагаем, что степень дивиденда p(x) больше или равна степени дивиденда s(x), иначе мы бы остановились на шаге 2
Шаг 4: Нам нужно провести итерационный процесс нахождения временного остатка, пока мы не придем к остатку, степень которого меньше степени s(x)
Шаг 5: Временный или промежуточный остаток обновляется каждый раз, сначала находится отношение между старшим членом текущего временного остатка и делителем s(x). Затем это отношение (которое является сильным членом) умножается на s(x), и результат этого умножения вычитается из текущего временного остатка, что приводит к обновленному остатку
Шаг 6: Этот процесс продолжается до тех пор, пока степень остатка не станет меньше степени s(x). На каждом шаге итерации степень временного остатка уменьшается по крайней мере на 1, так что процесс гарантированно завершится

В конце концов, процесс деление двух многочленов сводится к вычислению умножений — сумм многочленов, что в основном и происходит с числами. Метод длинного деления для многочленов — это распространение способа деления чисел на многочлены.

Как длинное деление связано с нахождением корней полиномиального уравнения

Предположим, что p(x) — это делитель, который вы хотите разделить, а s(x) — делимое. Согласно методу длинного деления, вы сможете найти делитель q(x) и остаток r(x) так, чтобы:

\[\displaystyle p(x) = q(x)s(x) + r(x) \]

Но иногда случается, что остаток равен r(x) = 0, и тогда мы говорим, что s(x) делит p(x) (или в точности делит p(x)). Итак, когда r(x) = 0

\[\displaystyle p(x) = q(x)s(x) \]

Это говорит о том, что для нахождения корней p(x) = 0 мы можем получить решение q(x) = 0 и s(x) = 0, по отдельности, которые являются более простыми уравнениями для решения.

Преимущества этого калькулятора для деления на длинные отрезки

Как я уже говорил, деление на длинные отрезки не слишком сложно, но требует систематического подхода. Большое преимущество использования калькулятор деления как этот, заключается в том, что вы получите все этапы процесса, показанные на рисунке

Возможно, не обязательно знать, как выполнять эти действия самостоятельно, но этот калькулятор позволяет увидеть, как это делается, с объяснением каждого шага, устраняя загадку получения остатка и коэффициента, скажем, от цифрового калькулятора, который выдаст вам ответ, не показывая шагов. 2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \end{array}\]

Шаг 3: В этом случае ведущий член текущего остатка $\displaystyle \frac{17}{4}x-\frac{5}{6}$ равен $\displaystyle \frac{17}{4}x$, и мы знаем, что ведущий член делителя равен $\displaystyle x$.

Итак, член, который нам нужно умножить $x$, чтобы получить ведущий член текущего остатка — $\displaystyle \frac{ \frac{17}{4}x}{ x} = \frac{17}{4}$, поэтому мы прибавляем этот член к квантору. Также мы умножаем его на делитель, чтобы получить $\displaystyle \frac{17}{4} \cdot \left(x+3\right) = \frac{17}{4}x+\frac{51}{4}$, который нам нужно вычесть из текущего остатка:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle -x & \displaystyle +\frac{17}{4}&\\[0. 2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle & \displaystyle -\frac{17}{4}x & \displaystyle -\frac{51}{4}\\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle & \displaystyle -\frac{163}{12}\\[0.8em] \end{array}\]

который завершает это вычисление, так как степень текущего остатка $r(x) = -\frac{163}{12}$ меньше степени делителя $s(x) = x+3$.

Заключение: Therefore, we conclude that for the given dividend $\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}$ and divisor $\displaystyle s(x) = x+3$, we get that the quotient is $\displaystyle q(x) = \frac{1}{3}x^2-x+\frac{17}{4}$ and the remainder is $\displaystyle r(x) = -\frac{163}{12}$, and that

Калькулятор деления полиномов с шагами

Онлайн-калькулятор деления полиномов с шагами поможет вам выполнить деление заданного делимого и делителя в длину. Вы можете найти остаток и частное с помощью калькулятора полиномиального деления с шагами, которые обеспечивают подробные вычисления для длинного полиномиального деления. Вы можете изучить и понять всю концепцию деления многочленов в длинное и многое другое.

Что такое полиномиальное длинное деление?

В алгебре длинное деление многочленов — это алгоритм деления многочлена, при котором один многочлен делится на другой многочлен той же или меньшей степени. Поэтому обобщенная версия знакомого арифметического метода называется многочленами от деления в длину.
Это можно легко сделать с помощью калькулятора делящих многочленов с шагами, потому что он разделяет сложные задачи деления на более мелкие.

Как выполнить полиномиальное длинное деление? 9{2} – 13 x + 78+\dfrac{(-395)}{x + 5}} \)
Однако онлайн-калькулятор синтетического деления для поиска нулей позволит вам определить напоминание и частное полиномов с помощью метод синтетического деления.
Типы полиномиального деления:
Существует четыре различных типа полиномиального деления:
Полиномиальное деление на другой одночлен
Деление многочлена на номинал
Полиномиальное деление на бином 92} {10 x} = 4x $$
Деление полинома на номинал:
Когда многочлен делится на номинал, каждый член полинома отдельно делится на моном, а частное каждого деления заменяется для получения результатов. Когда вы используете калькулятор деления полинома деления для деления полинома на номинал, он использует метод длинного деления. Вы можете выполнить деление многочлена на любой номинал вручную разными способами. Давайте проверим это на примере: 92 – 4y + 3 $$
Для проверки приведенного выше результата попробуйте воспользоваться нашим бесплатным делением с использованием полиномов калькулятора деления в длину абсолютно бесплатно.
Деление многочлена на двучлен:
Деление многочлена на двучлен может быть выполнено легко, поскольку двучлен представляет собой выражение с двумя членами. Если мы используем бесплатный онлайн-калькулятор многочлена с длинным делением с переменными для деления многочлена на двучлен, то он отображает многочлен в стандартной форме. Теперь используйте калькулятор полиномов методом длинного деления, как показано ниже: 9{2} – 3 х) = 5 – 5 х $$
Без сомнения, эти расчеты немного сложны. Вот почему, чтобы уменьшить сложность, вы можете воспользоваться бесплатной помощью этого калькулятора деления многочленов на длинное деление.
Шаг 3:
Разделить старший член делимого на старший член делителя:
$$ \space \dfrac{- 5 x}{x} = -5 $$
Умножить на делитель :
$$ \space -5(x – 1) = 5 – 5 x $$
Из полученного результата вычесть делимое: 9{2} + 3 x – 5} $$
Например, и перекрестная проверка, вы можете использовать этот бесплатный многочлен калькулятора длинного деления алгебры, чтобы помочь вам.
Тем не менее, онлайн-калькулятор теоремы об остатках позволяет определить остаток заданных полиномиальных выражений по теореме об остатках.
Деление многочлена на другой многочлен:
Для деления многочлена на длинное деление с помощью калькулятора многочленов запишите многочлен в стандартной форме и используйте метод деления на длинное. Возьмем пример: 9{2} + 2 x + 1}} $$
Как работает калькулятор полиномиального деления?
Онлайн-калькулятор деления многочленов с решением позволяет разделить два многочлена, выполнив следующие действия:
Ввод:
Сначала введите делимое и делитель в данные поля.
Нажмите кнопку «Рассчитать».
Вывод:
Калькулятор полиномов деления с шагом сначала отображает специальный формат заданных значений. 92 \) для заданного полиномиального выражения xy / x + y.
Как лучше и проще всего делить длинные многочлены?
Метод длинных полиномов деления — лучший способ разделить два длинных полинома.
Вывод:
Используйте этот онлайн-калькулятор деления многочленов в длину с переменными для деления многочленов в длину с подробными решениями. Инженеры в основном используют полиномы для моделирования пути американских горок. Итак, калькулятор деления длинных полиномов с шагом точно предоставляет таблицу результатов с полными вычислениями для заданных значений.
Ссылка:
Из источника Википедии: Полиномиальное длинное и короткое деление, Псевдокод, Евклидово деление, Разложение многочленов на множители, Нахождение касательных к полиномиальным функциям.
Из источника Purple Math: деление длинного многочлена, деление многочлена, деление одночлена на другой одночлен, деление многочлена на одночлен.
Из источника Lumen Learning: Алгоритм деления, деление многочленов, теорема о рациональном корне, теорема об остатке, синтетическое деление, рациональные корни и многочлены деления с использованием калькулятора деления. 92+2x-3}{x+3}}$$
РЕКЛАМА
РЕКЛАМА
Содержание:
Калькулятор полиномиального длинного деления
Что такое полиномиальное длинное деление?
Как решать задачи на полиномиальное деление?
Дайте нам отзыв
✎
✉
Калькулятор полиномов с длинным делением
Калькулятор полиномов с длинным делением используется для деления полиномиальных функций путем получения делителя и делимого. Этот калькулятор деления многочленов находит частное и остаток заданных функций.
Что такое полиномиальное длинное деление?
Полиномиальное длинное деление похоже на длинное деление целых чисел, используемое для разложения на множители или определения касательных линий функции. В этом методе деления многочлен более высокой степени является делимым, а многочлен более низкой степени — делителем.
Как решать задачи на полиномиальное деление?
Задачи на полиномиальное деление в длину легко решаются как с помощью калькулятора, так и вручную. Давайте возьмем пример, чтобы понять эту концепцию.
Пример
Найдите длинное деление многочлена, если делимое многочлена равно 2×4 + 6×3 + x2 + 12x + 20, а делитель равен x+1.
Решение
Шаг 1: Разделите старший член делимого многочлена на старший член делителя, чтобы получить первый член частного.
2x ⁴ /x = 2x ³
Это означает, что вам нужно умножить делитель на 2x ³, чтобы получить первый шаг.
No related posts.