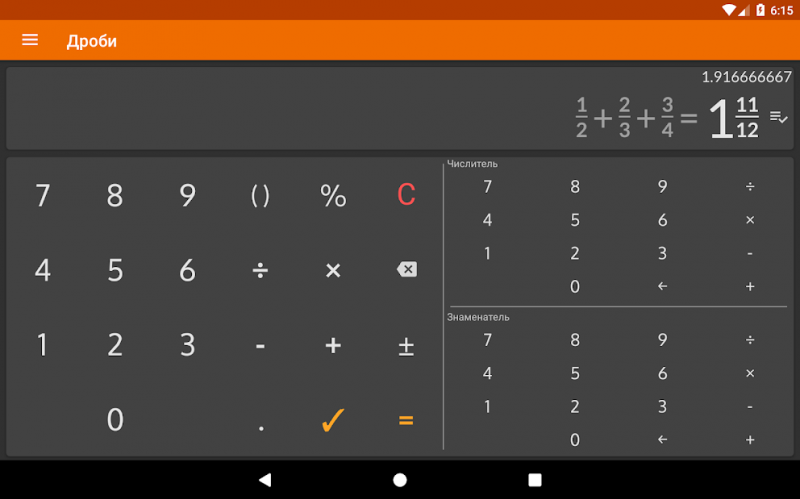
Деления дробей калькулятор: Калькулятор рациональных выражений

Содержание

Деление дробей через онлайн-калькулятор — Calculators.by

Дроби – это такие числа, при помощи которых можно выполнять самые разные математические операции, доступные и для натуральных чисел. Например, можно выполнять сложение, вычитание или умножение. Особого внимания заслуживает деление дробей, которое требует учитывать определенные особенности со стороны пользователя. Здесь необходимо обратить внимание на базовые правила. Также следует учитывать определенные рекомендации, рассмотреть множество примеров, что позволит сложить общее впечатление о процедуре.

Деление самых простых дробей выполняется по простым правилам. Базовые правила отличаются относительной простотой и понятностью для каждого. при этом нужно учитывать особенности деления дробей на обычные натуральные числа. Также следует внимательно рассмотреть примеры работы со смешанными числами. Каждая операция обладает своими характеристиками и преимуществами, которые требуется обязательно учитывать.

Правила деления дробей

Деление дробей – это достаточно непростая процедура, которая требует понимания определенных особенностей и механик действий. Для того, чтобы получить результат, необходимо перемножить противоположные числители и знаменатели. Чтобы лучше понимать механику процедуры, рекомендуется рассмотреть следующий пример:

4/5 / 3/5 = 4 х 5 / 3 х 5 = 20 / 15 = 4/3 = 1 1/3.

Как видно, если понимать особенности проведения математической операции, а также учитывать определенные особенности в каждом случае, то выполнение данной процедуры возможно всего в несколько кликов. Следует обратить внимание на такие базовые правила деления дробей:

Если планируется делить обычные дроби, тогда необходимо просто перемножить противоположные числители и знаменатели. В результате получается дробь, которую можно сократить при необходимости.
Если необходимо поделить дробь на натуральное число, то необходимо умножить знаменатель на число, но при этом числитель остается без каких-либо изменений.
Если натуральное число делят на дробь, действует немного другое правило. Необходимо умножать число на обратную дробь. Это означает, что числитель и знаменатель дроби нужно поменять местами.
При делении двух обычных дробей нужно перемножить дроби. При этом во второй дроби необходимо числитель и знаменатель поменять местами для того, чтобы получить искомый результат.

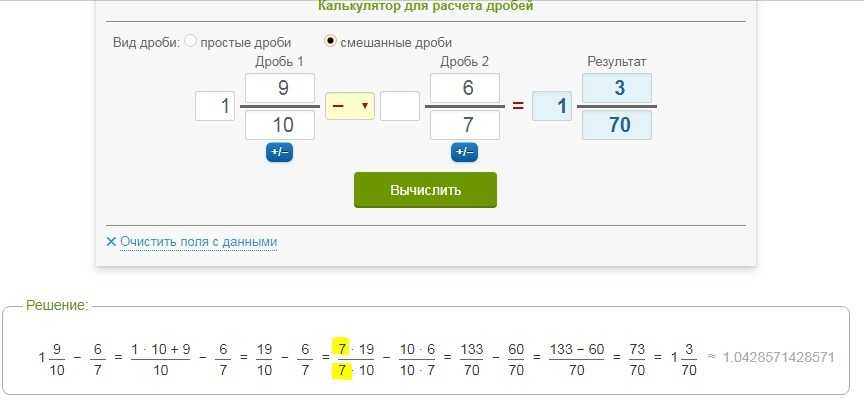
Если проводится процедура деления смешанных дробей, правила немного отличаются, что следует учитывать. Сейчас не требуется обязательно знать все правила наизусть, но понимать базовые принципы проведения описанных операций рекомендуется, чтобы достичь поставленных задач намного быстрее и избежать возможных ошибок. С помощью специального онлайн-калькулятора, вы можете разделить дробь онлайн всего в несколько кликов, получив максимально точное число, которое можно использовать для выполнения прочих математических операций.

Как делить обыкновенные дроби?

Деление обыкновенной дроби – это самая простая операция. Это обратная операция умножения, которое не требует соблюдения особенно сложных правил. Для этого достаточно учитывать определенные особенности проведения процедуры. Например, в процессе деления множители сохраняются при проведении произведения. Это позволяет получить корректный результат при проведении процедуры.

Если говорить проще, то числитель первого числа нужно умножить на знаменатель второго, а с другим числом выполнить такую же манипуляция. В результате сохраняется требуемый результат, который не требует особых усилий. Базовое правило выполнения деления выглядит следующим образом: для деления самой обычной дроби, необходимо произвести умножение на число, которое является обратным делимому. В результате операция деления – это действительно умножение, которое выполнено в обратной форме. Далее процедура проводится с учетом правил обычного умножения.

Ниже приведен пример для того, чтобы лучше понимать особенности проведения данной процедуры:

9/7 / 5/3 = 9/7 х 3/5 = 27/35.

Как видно, процедура выглядит максимально просто.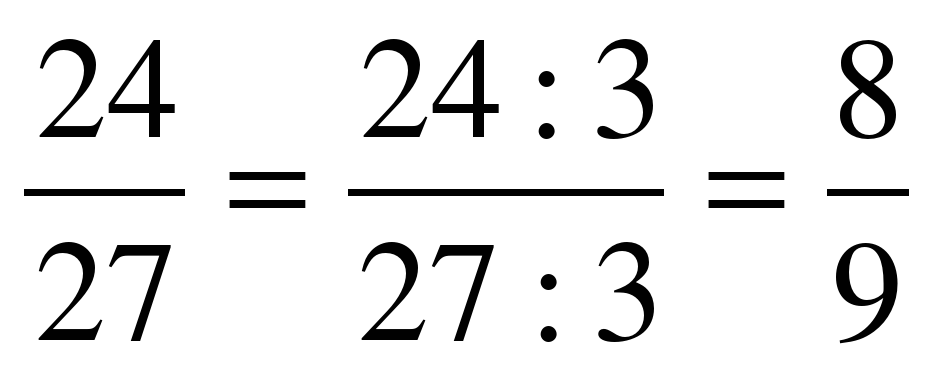 Если позволяет пример, можно провести сокращение дробей, что поможет сделать ответ более простым, понятным и лаконичным, а также упростить проведение дальнейших возможных манипуляций с числами.

Как разделить число на дробь?

Если необходимо выполнить операцию деления числа на дробь, то тогда нужно следовать простым рекомендациям. Необходимо обычно число умножить на обратную дробь. Обычно эта процедура выполняется по формуле. Для этого достаточно следовать простым рекомендациям, а также рассмотреть несколько базовых примеров, если возникают какие-либо трудности. В качестве примера можно рассмотреть следующую операцию:

3/(2/3) = 3 х 3/2 = 9/2 = 4 1/2.

Как видно, сама операция достаточно простая, поэтому выполнить ее можно очень легко с минимальными затратами и усилиями. Вы можете выполнить операцию при помощи онлайн-калькулятора. Это может упростить задачу для каждого, кому нужно выполнить расчет.

Как разделить смешанную дробь на число?

Если необходимо поделить смешанную дробь на обычное число, тогда достаточно выполнить несколько простых манипуляций. Для начала нужно преобразовать дробь в неправильную, а после этого воспользоваться правилом, которое касается перемножения обычных дробей. Это достаточно простая, но эффективная операция, которая позволяет быстро выполнить поставленную задачу с минимальными усилиями и затратами. В качестве примера можно рассмотреть следующее:

1 1/3 / 3 = 4/3 / 3 = 9/4 = 2 1/4.

Как видно, операция также выполняется достаточно быстро, поэтому не потребует каких-либо усилий со стороны пользователя, позволяя максимально быстро выполнить операцию с минимальными затратами. Также можно воспользоваться онлайн-калькулятором, что позволит намного быстрее выполнить задачу, а также использовать полученное значение для того, чтобы получить результат намного быстрее и эффективнее.

Как разделить смешанную дробь на смешанную дробь?

Если необходимо выполнить операцию, которая касается классических смешанных дробей, тогда необходимо следовать таким базовым рекомендациям:

для начала необходимо преобразовать обычные смешанные числа в неправильные дроби – обычно это не требует много времени, достаточно следовать базовому правилу;
далее нужно умножить перевернутые дроби по базовому правилу деления дробей;
далее нужно сократить полученную дробь по правилам, если это позволяет конкретная ситуация;
если нужно преобразовать неправильные дроби, тогда остается только сделать из него смешанное число по правилу.

Как видно, процедура выполняется по алгоритму. Для получения результатов достаточно воспользоваться базовой формулой. Базовый пример выглядит следующим образом:

1 1/2 / 2 2/3 = 3/2 / 8/3 = 9/16.

Этот дробь сократить не получится, поэтому результат остается таким же. Как видно, данная операция выполняется максимально просто.

С помощью онлайн-калькулятора разделить дроби не составит труда. Эта операция не потребует много времени и усилий, что предоставит отличную возможность для выполнения других операций.

Калькулятор дробей и смешанных чисел

Введите дроби ниже:

Как работает калькулятор дробей и смешанных чисел?

Учитывая (неправильные дроби, правильные дроби, смешанные числа или целые числа), он выполняет следующие операции:
* Сложение (сложение)
* Вычитание (вычитание)
* Положительная разность (Абсолютное значение разности)
* Умножение (Умножение)
* Деление (Деление: деление сложной дроби включено)
* Сравнение дробей
* Упрощение правильных и неправильных дробей, а также смешанных чисел.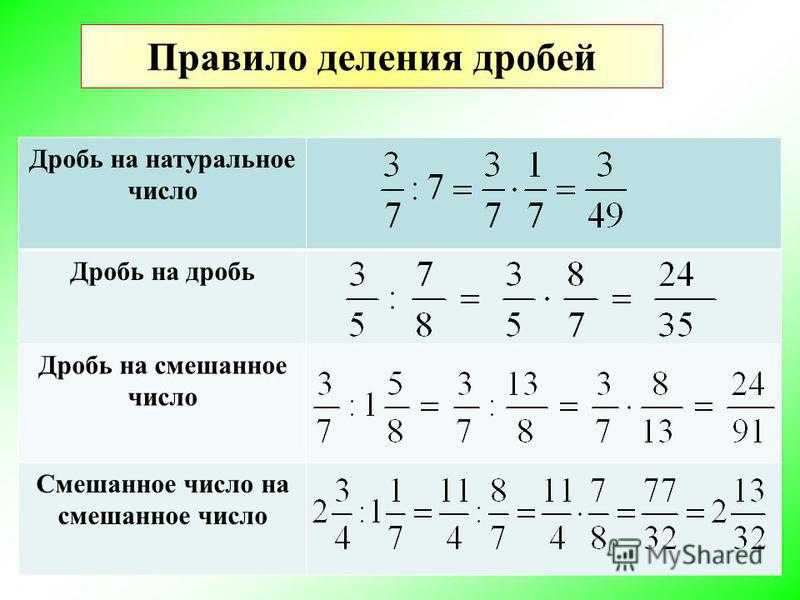 Фракции будут максимально сокращены (Сокращение фракций).
* Обратная дробь
* Найти все дроби между двумя дробями
* уменьшить дробь
Этот калькулятор имеет 2 входа.

Какие 7 формул используются в калькуляторе дробей и смешанных чисел?

а/с + b/с = (а + b)/с
а/с — b/с = (а — b)/с
a/c * b/c = ab/c * c

a/b/c/d = ad/bc
Обратная величина a/b = b/a другие математические формулы см. в нашем досье по формулам
Какие 10 понятий используются в калькуляторе дробей и смешанных чисел?
сложение
математическая операция с суммой элементов
знаменатель
Нижняя часть дроби. Для a/b b является знаменателем
деление
разделить число на части
дробь
сколько существует частей определенного размера
a/b где a числитель и b знаменатель
смешанное число правильная дробь.
умножение
математическая операция с произведением элементов
числитель
число над чертой в обыкновенной дроби
обратное
число, которое при умножении на х дает мультипликативное тождество, 1
упрощает
сокращение выражения/дроби/задачи в более простой форме.

вычитание
математическая операция с разностью элементов
Каковы некоторые примеры расчетов для калькулятора дробей и смешанных чисел?
1. 1/5+6/7
2. 3/4-1/2
3. 8/9*5/6
4. 2/3/5/7
5. 1&5/8
6. 4 и 3/7
7. 1/2 и 5/9
8. 2/9 от 3
9. обратное от 9/4
10. 195/6/4
11. Упрощение 15/20
12. 1/2–3/4 90234
Видео калькулятор дробей и смешанных чисел
- Электронная почта: [email protected]
- Тел: 800-234-2933
- Математическая тревога
- Судоку
- Раздор
- Информационный бюллетень о недобросовестном преимуществе
- Биографии математиков
- Подкаст цены за клик
- Математические Мемы
- Глоссарий по математике
- Предметы
- бейсбольная математика
- Друзья
- Спонсоры
- Связаться с нами
- Вакансии учителя математики
- Политика в отношении файлов cookie
- политика конфиденциальности
- Политика возврата
Как получить остаток в калькуляторе
••• wutwhanfoto/iStock/GettyImages
Обновлено 27 октября 2020 г.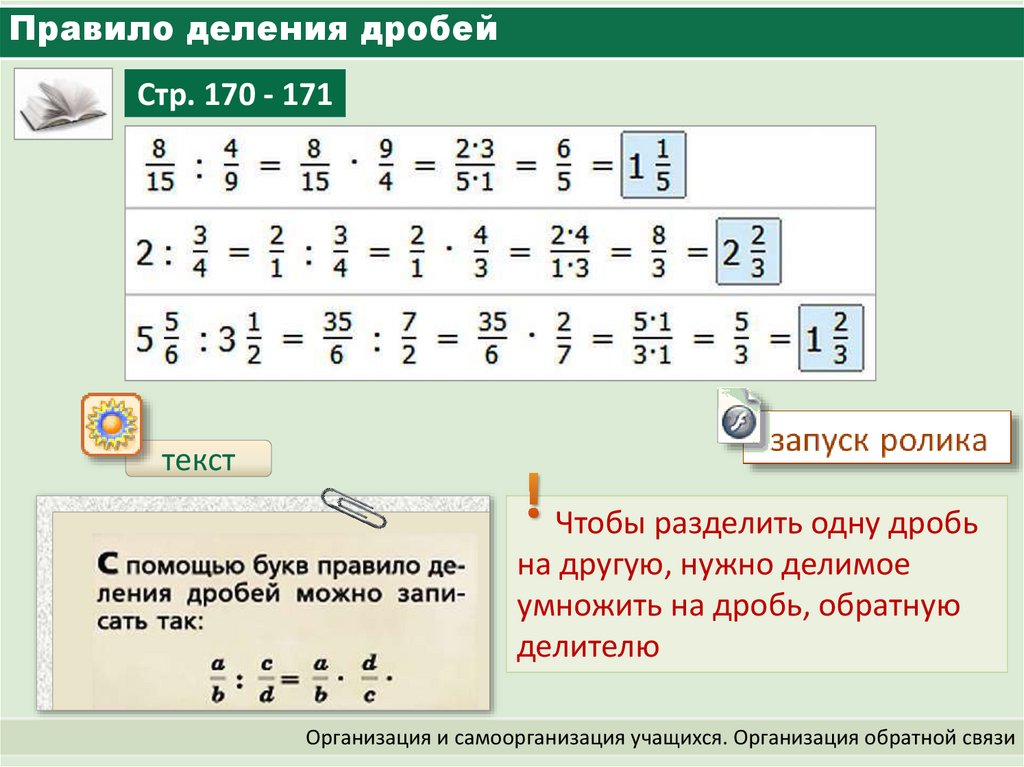
Автор Lisa Maloney вам результат как целое число, за которым следует десятичная дробь с числами после десятичной дроби. Но в зависимости от контекста задачи на деление вам может потребоваться ответ в виде целого числа с остатком. В то время как большинство научных калькуляторов имеют функцию остатка, которую вы можете найти либо на клавиатуре, либо прокручивая их меню, этот быстрый трюк позволяет вам вычислить остаток с помощью любого калькулятора.
TL;DR (слишком длинно, не читал)
Выполните деление в калькуляторе как обычно. Получив ответ в десятичной форме, вычтите целое число, а затем умножьте оставшееся десятичное значение на делитель исходной задачи. Результат — ваш остаток.
Например, разделите 346 на 7, чтобы получить 49,428571. Округлите это число до целого числа 49. Умножьте 49 на 7, чтобы получить 343, выраженное как 49 × 7 = 343. Вычтите это из исходного числа 346, чтобы получить остаток 3,9.0019
Прежде чем решать задачу на деление с помощью калькулятора, полезно разобраться с некоторыми основными терминами. Число, на которое делится, — это делимое, число, на которое вы делите его, — это делитель, а ответ — это частное. Часто вы увидите, что задачи на деление написаны так: Делимое ÷ делитель = частное. Если бы вы записали свою задачу на деление в виде дроби, число сверху (также называемое числителем) было бы делимым, а число внизу (также называемым знаменателем) — делителем.