Y cos3x четная или нечетная: Четная или нечётная f(x)=x^5*cos3x — ответ на Uchi.ru

alexxlab / / Разное

Функции

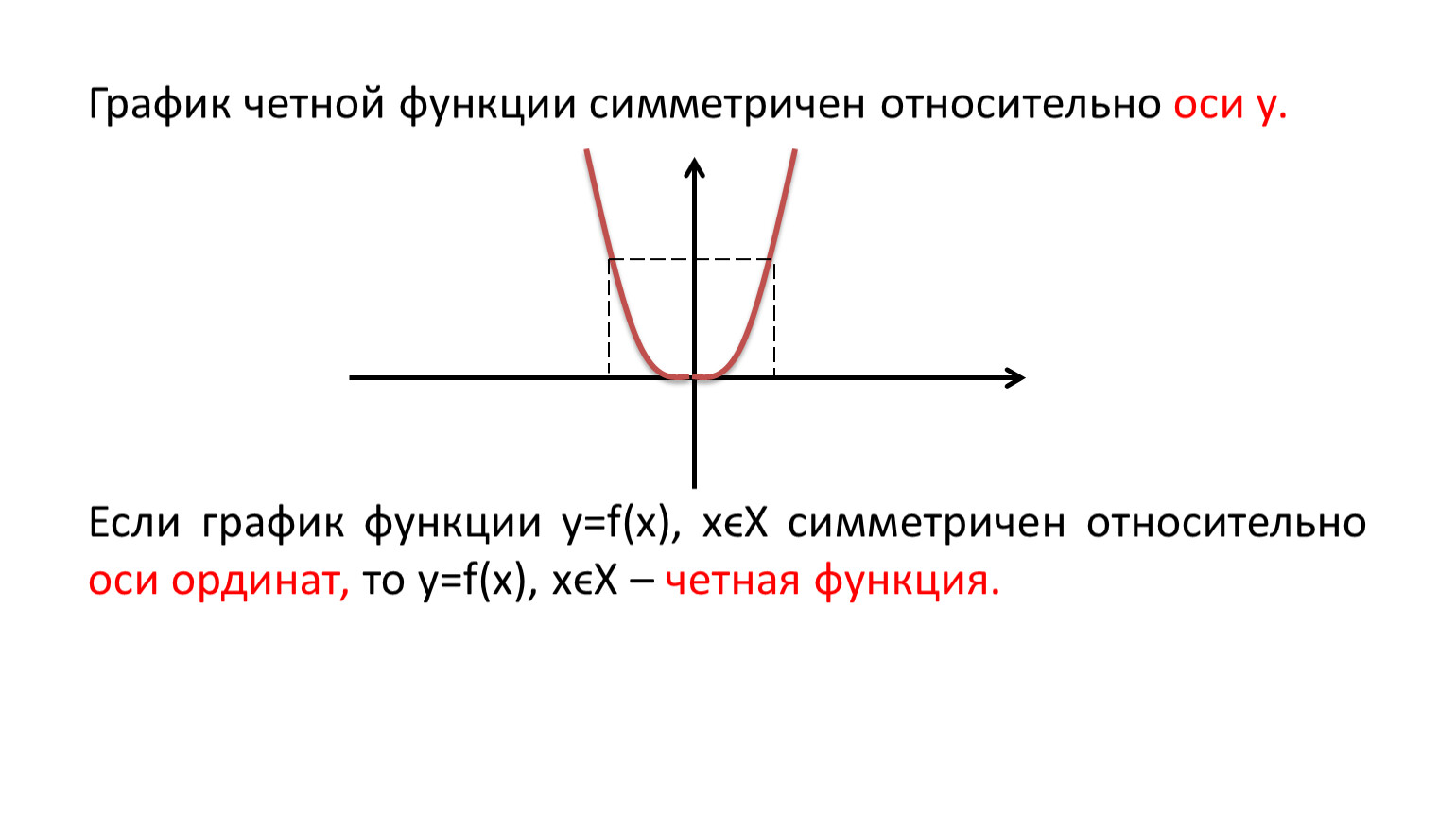
Четность и нечетность функции

  1. Если f(-x)= f(x),то функция f(x) четная

  2. Если f(-x)= — f(x),то функция нечетная

Возрастающая и убывающая функции

Пусть x1<x2 (x1,x2 ϵ X):

  1. Если,то функциявозрастает н сножестве Х.

  2. Если,то функцияубывает на Х.

  3. Если,то функциянеубывающая на Х.

  4. Если,то функцияневозрастающая на Х.

Виды функции

Линейная функция

Линейной называется функция вида y=kx+b, где kиbR.

Некоторые свойства линейной функции:

  1. Область определения R

  2. Функция ни четная, ни нечетная.

  3. При k>0 функция возрастает,а при k<0 убывает на всей числовой прямой

  4. График линейной функция прямая

Квадратичная функция

Квадратичной функцией называется функция вида

Координаты вершины параболы

Свойства квадратичных функций:

  1. Область определения R

  2. Множества значений

При a>0 промежуток.

При a<0 промежуток.

  1. График функций пересекает ось абсцисс при D≥0 в точках с абсциссами ;приD<0парабола не имеет общих точек с осью абсцисс. Это точки называются нулями функции.

  2. Функция ы точке a<0и наименьшее значения при a>0,равное

Рациональная функция

Рациональные функция делятся на целые рациональные и дробно – рациональные функции.

Область определения функции

R, кроме значении, при которых знаменатель равен нулю (g(x)).

Иррациональные функции:

–область определения

  1. R ,еслиn– нечетное.

  2. Решение неравенства g(x)≥0, если n — четное.

Элементы тригонометрии

Основные тригонометрические тождества

  1. sin2x + cos2x = 1

  1. tgx

 =  

sinx

cosx

  1. ctgx

 =  

cosx

sinx

  1. tgxctgx = 1

  1. tg2x + 1

=  

1

cos2x

  1. 1+ctg2x=

Формулы суммы/разности двух углов

  1. sin(α + β) = sinα cosβ + cosα sinβ cos(α + β) = cosα cosβ — sinα sinβ

    1. tg(α + β)

      =  

    tgα + tgβ1

    1 — tgα tgβ

ctg(α + β)

  =  

ctgα ctgβ — 1

ctgα + ctgβ

  1. sin(α — β) = sinα cosβ — cosα sinβ cos(α — β) = cosα cosβ + sinα sinβ

    1. tg(α — β)

      =  

    tgα — tgβ

    1 + tgα tgβ

ctg(α — β)

  =  

ctgα ctgβ + 1

ctgα — ctgβ

Формулы тригонометрических функций двойного, тройного, и половинного углов

  1. sin2x = 2sinxcosx;

  1. tg2x

  =  

2tgx

  = 

2ctgx

  = 

2

1 — tg2x

ctg2x — 1

ctgx — tgx

  1. sin2  =  

;

  1. sin3x = 3sinx — 4sin3x;

  2. tg3x  =  ;

  3. cos2x = cos2x — sin2x;

  4. ctg2x  =   ;  

  5. cos2  =  

;

  1. cos3x = 4cos3x — 3cosx;

  2. ctg3x  =  ;

    1. sinα + sinβ

 =  2sin

α + β

 ∙ cos

α — β

2

2.

sinα — sinβ

  =  2sin

α — β

 ∙ cos

α + β

2

2

  1. cosα + cosβ

  =  2cos

α + β

 ∙ cos

α — β

2

2

5. tgα + tgβ

  =  

sin(α + β)

cosα cosβ

  1. cosα — cosβ

  =  -2sin

α + β

 ∙ sin

α — β

2

2


  1. tgα + ctgβ

  =  

sin(α + β)

sinα sinβ

  1. tgα — tgβ

  =  

sin(α — β)

cosα cosβ

  1. ctgα — ctgβ

  =  – 

sin(α — β)

sinα sinβ

Функциональный метод решения уравнений — HintFox

Учеба  ->  Среднее образование  | Автор: | Добавлено: 2015-03-23

В стандартном курсе школьной математике свойства функций применяются в основном для построения их графиков. Функциональный метод решения уравнений применяют тогда и только тогда, когда уравнение F(x) = G(x) в результате преобразований или замены переменных не может быть приведено к тому или иному стандартному уравнению, имеющему определенный алгоритм решения.

В отличие от графического метода, знание свойств функций позволяет находить точные корни уравнения, при этом не требуется построения графиков функций. Использование свойств функций способствует рационализации решения уравнений.

В работе рассмотрены следующие свойства функции: область определения функции; область значений функции; свойства монотонности функции; свойства выпуклости функции; свойства четности и нечетности функции.

Цель работы: провести некоторую классификацию нестандартных уравнений по использованию общих свойств функций, описать суть каждого свойства, дать рекомендации по его использованию, указания к применению.

Вся работа сопровождается решением конкретных задач, предлагавшихся на ЕГЭ различных лет.

Глава 1. Использование понятия области определения функции.

Введем несколько ключевых определений.

Областью определения функции y = f(x) называется множество значений переменной х, при которых функция имеет смысл.

Пусть дано уравнение f(x) = g(x), где f(x) и g(x)- элементарные функции, определенные на множествах D1, D2. Тогда областью D допустимых значений уравнения будет множество, состоящее из тех значений х, которые принадлежат обоим множествам, то есть D = D1∩ D2. Ясно, что когда множество D пустое (D= ∅), то уравнение решений не имеет. (Приложение № 1).

Примеры.

1. arcsin (x+2) +2x- x2 = x-2.

ОДЗ:-1 =0⇔-3

Ответ: решений нет.

2. (х2-4х+3 +1)log5х5 + 1х(8х-2х2-6 + 1) = 0.

ОДЗ: х2-4х+3>=0,х>0,8х-2х2-6>=0⇔х∈(-infinity;1∪ 3;infinity),х>01

Проверка: х = 1.

(1-4+3 +1)log515 + (8-2-6 + 1) = 0,

0 = 0 — верно.

х = 3. (9-12+3+1)log535 +13(24-18-6+1) = 0, log535 +13 = 0 — неверно.

Ответ: 1.

Часто оказывается достаточным рассмотреть не всю область определения функции, а лишь ее подмножество, на котором функция принимает значения, удовлетворяющие некоторым условиям (например, только неотрицательные значения).

Примеры.

1. x+27-x(x-9 +1) = 1.

ОДЗ: x-9>=0, x>=9.

При x>=9 x+2>0, 7-x0, таким образом, произведение трех сомножителей, стоящих в левой части уравнения отрицательно, а правая часть уравнения положительна, значит, уравнение решений не имеет.

Ответ: ∅.

2. 3-x2+ x+2 = x-2.

ОДЗ: 3-x2>=0,x+2>=0,⇔ 3-x(3+x)>=0,x>=-2,⇔ -3=-2,⇔

⇔ -3

На множестве допустимых значений левая часть уравнения — положительна, а правая — отрицательна, значит, уравнение решений не имеет.

Ответ: решений нет.

Глава 2. Использование понятия области значений функции.

Областью значений функции y = f(x) называется множество значений переменной y при допустимых значениях переменной x.

Функция y = f(x) называют ограниченной снизу (соответственно сверху) на множестве Х, если существует такое число М, что на Х выполняется неравенство fx>=М (соответственно fx

Функция y = f(x) называется ограниченной на данном промежутке (содержащемся в области ее определения), если существует такое число М >0, что при всех значениях аргумента, принадлежащих данному промежутку, имеет место неравенство f(x)

Пусть дано уравнение f(x) = g(x), где g(x) — элементарные функции, определенные на множествах D1, D2. Обозначим область изменения этих функций соответственно E1 и E2. Если х1 является решением уравнения, то будет выполняться числовое равенство f(x1) = g(x1), где f(x1) значение функции f(x) при х = х1, а g(x1) — значение функции g(x) при х = х1. Значит, если уравнение имеет решение, то области значений функций f(x) и g(x) имеют общие элементы (Е1∩Е2 !=∅). Если же таких общих элементов множества Е1 и Е2 не содержат, то уравнение решений не имеет.

Для оценки выражений используются базовые неравенства. (Приложение №2).

Примеры:

Пусть дано уравнение f(x) = g(x). Если f(x)>=0 и g(x)

Примеры.

1. x2+2xsinxy+1=0.

Решение. В левой части есть единица, значит, можно воспользоваться основным тригонометрическим тождеством: x2+ 2xsinxy+ sin2xy+cos2xy=0.

Сумма первых трех членов представляет собой полный квадрат:

(x+sinxy)2+cos2xy =0.

Следовательно, в левой части сумма квадратов, она равна нулю тогда, когда одновременно равны нулю выражения, стоящие в квадратах. Запишем систему: cosxy=0,x+sinxy=0.

Если cosxy=0, то sinxy= +-1, поэтому эта система равносильна совокупности двух систем: x+1=0,cosxy=0 или x-1=0,cosxy=0.

Их решениями являются пары чисел х=1, у = PI 2 + PIm, m∈Z, и x=-1, y = = PI 2 + PIm, m∈Z.

Ответ: х=1, у = PI 2 + PIm, m∈Z, и x=-1, y = = PI 2 + PIm, m∈Z.

Если на промежутке Х наибольшее значение одной из функций y = f(x), y = g(x) равно А и наименьшее значение другой функции тоже равно А, то уравнение f(x) = g(x) равносильно на промежутке Х системе уравнений fx=А,gx=А.

Примеры.

1. Найдите все значения a, при которых имеет решение уравнение

2cos222x-x2=a+3sin(22x-x2+1).

Решение.

После замены t= 22x-x2 приходим к уравнению cos(2t+PI3)=a-12.

Функция t=2mвозрастает, значит, она достигает своего наибольшего значения при наибольшем значении m. Но m=2х — х[2] имеет наибольшее значение, равное 1. Тогда tнаиб = 22·1-1=2. Таким образом, множеством значений функции t= 22x-x2является промежуток (0;2, а функции cos(2t+PI3)- промежуток -1;0,5). Следовательно, исходное уравнение имеет решение для тех и только тех значений a, которые удовлетворяют неравенствам -1

Ответ: -1

2. Решить уравнение (log23)x+a+2 = (log94)x2+a2-6a-5.

Решение.

Воспользовавшись очевидными неравенствами

1

Ответ: x= — 5+32, если a=1+32 и x=-5+32, если a= 1-32.

Можно подробнее рассмотреть и другие уравнения. (Приложение №3).

Глава 3. Использование свойства монотонности функции.

Функцию y = f(x) называют возрастающей (соответственно убывающей) на множестве Х, если на этом множестве при увеличении аргумента увеличиваются (соответственно уменьшаются) значения функции.

Иными словами, функция y = f(x) возрастает на множестве Х, если из х1∈Х, х2∈Х и х1

Она убывает на этом множестве, если из х1∈Х, х2∈Х и х1 f(x2).

Функцию y = f(x) называют нестрого возрастающей (соответственно нестрого убывающей) на Х, если из х1∈Х, х2∈Х и х1=f(x2)).

Функции, возрастающие и убывающие на Х, называют монотонными на Х, а функции, нестрого возрастающие или нестрого убывающие на Х, называют нестрого монотонными на Х.

Для доказательства монотонности функций используются следующие утверждения:

1. Если функция f возрастает на множестве Х, то для любого числа С функция f+С тоже возрастает на Х.

2. Если функция f возрастает на множестве Х и С > 0, то функция Сf тоже возрастает на Х.

3. Если функция f возрастает на множестве Х, то функция — f убывает на этом множестве.

4. Если функция f возрастает на множестве Х и сохраняет знак на множестве Х, то функция 1f убывает на этом множестве.

5. Если функции f и g возрастают на множестве Х, то их сумма f+g тоже возрастает на этом множестве.

6. Если функции f и g возрастают и неотрицательны на множестве Х, то их произведение fg тоже возрастает на Х.

7. Если функция f возрастает и неотрицательна на множестве Х и n — натуральное число, то функция fn тоже возрастает на Х.

8. Если обе функции f(x) и g(x) возрастающие или обе убывающие, то функция h(x) = f(g(x)) — возрастающая функция. Если одна из функций возрастающая. А другая убывающая, то h(x) = f(g(x)) — убывающая функция.

Сформулируем теоремы об уравнениях.

Теорема 1.

Если функция f(x) монотонна на промежутке Х, то уравнение f(x) = С имеет на промежутке Х не более одного корня.

Теорема 2.

Если функция f(x) монотонна на промежутке Х, то уравнение f(g(x)) = f(h(x)) равносильно на промежутке Х уравнению g(x) = h(x).

Теорема 3.

Если функция f(x) возрастает на промежутке Х, а g(x) убывает на промежутке Х, то уравнение g(x) = f(x) имеет на промежутке Х не более одного корня.

Теорема 4.

Если функция f(x) возрастает на промежутке Х, то уравнение f(f(x)) = x равносильно на промежутке Х уравнению f(x) = х.

Примеры.

1. Найдите все значения a, при которых имеет ровно три корня уравнение

4-x-alog3(x2-2x+3)+2-x2+2xlog13(2x-a+2)=0.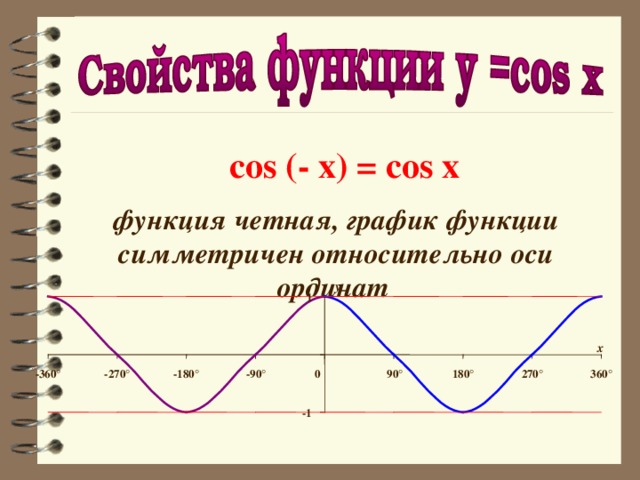

Решение. Преобразуем данное уравнение к виду

2×2-2xlog3(x2-2x+3)= 22x-a-1log3(2x-a+2).

Если положить u = x2-2x, v=2x-a-1, то придем к уравнению

2ulog3(u+3)= 2vlog3(v+3).

Функция f (t) = 2tlog3(t+3) монотонно возрастает при t >-2, поэтому от последнего уравнения можно перейти к равносильному u = v, x2-2x = 2x-a-1⇔(x-1)2=2x-a.

Это уравнение, как видно из рисунка, имеет ровно три корня в следующих случаях:

1. Вершина графика функции у = 2x-a располагается в вершине параболы у = (x-1)2, что соответствует a = 1;

2. Левый луч графика у = 2x-a касается параболы, а правый пересекает ее в двух точках; это возможно при a=12;

3. Правый луч касается, а левый — пересекает параболу, что имеет место при a=32.

Поясним второй случай. Уравнение левого луча у = 2a-2x, его угловой коэффициент равен -2. Следовательно, угловой коэффициент касательной к параболе равен

2(х -1) = -2 ⇒ х = 0 и точка касания имеет координаты (0; 1). Из условия принадлежности этой точки лучу находим a=12.

Третий случай можно рассмотреть аналогично или привлечь соображения симметрии.

Ответ: 0,5; 1;1,5.

Можно рассмотреть подробнее и другие уравнения. (Приложение №4).

Глава 4. Использование свойств выпуклости.

Пусть функция f(x) определена на промежутке Х она называется строго выпуклой вниз (вверх) на Х, если для любых u и v из Х, u!=v и 0λf(u) + (1 — λ)f(v)).

Геометрически это означает, что любая точка хорды ВС (то есть отрезка с концами в точках B(u;f(u)) и C(v;f(v)), отличная от точек В и С, лежит выше (ниже) точки А графика функции f(x), соответствующей тому же значению аргумента. (Приложение №5).

Функции строго выпуклые вверх и вниз называются строго выпуклыми.

Справедливы следующие утверждения.

Теорема 1.

Пусть функция f(x) является строго выпуклой вниз на промежутке Х, u ,v ∈X, u

Из теоремы 1 вытекает следующее утверждение.

Теорема 2.

Если функция f(x) является строго выпуклой на промежутке Х, функции u = u(x), v = v(x), u1=u1(x), v1 = v1(x) такие, что при всех х из ОДЗ уравнения f(u)+f(v) = f(u1) + f(v1) (1) их значения u(x), v(x), u1(x), v1(x) содержатся в Х и выполнено условие u+v = u1 +v1, то уравнение f(u)+f(v) = f(u1) + f(v1) (2) на ОДЗ равносильно совокупности уравнений u (x) = u1(x), u(x) = v1(x) (3).

Примеры.

1. 41-sin4x+41-cos4x=412.

Решение. Если положим fx= 41-x2, u=cos2x, v=sin2x, u1=v1=12, то данное уравнение запишется в виде (1). Поскольку f’x= -x24(1-x2)3, f»x=-2+x244(1-x2)7, то функция fx является строго выпуклой вверх на сегменте -1;1. Очевидно, что выполнены остальные условия теоремы 2 и, следовательно, уравнение равносильно уравнению cos2x = 0,5, х = PI4 +PIk2, где k∈Z.

Ответ: х = PI4 +PIk2, где k∈Z.

Теорема 3.

Пусть функция fx является строго выпуклой на промежутке Х и u,v, λv+(1-λ)u∈X. Тогда равенство f (λv+(1-λ)u) = λf(v)+(1-λ)f(u) (4) справедливо в том и только и том случае, если либо u=v, либо λ=0, либо λ=1.

Примеры: sin2xcos3x+cos2xsin3x∙1+sin2xcos3x+cos2xsin3x= sin2xcos3x1+cos3x+cos2xsin3x1+sin3x.

Решение.

Уравнение имеет вид (4), если fx=x1+x= x+x2, u=sin3x, v= cos3x, λ=sin2x.

Очевидно, что функция fx является строго выпуклой вниз на R. Следовательно, по теореме 3 исходное уравнение равносильно совокупности уравнений sinx=0, sin2x=1, cos3x=sin3x.

Отсюда получаем, что его решениями будут PIk2, PI12+PIn3, где k,n∈Z.

Ответ: PIk2, PI12+PIn3, где k,n∈Z.

Использование свойств выпуклости применяется при решении и более сложных уравнений. (Приложение № 6).

Глава 5. Использование свойств четности или нечетности функций.

Функция fx называется четной, если для любого значения х, взятого из области определения функции, значение — х также принадлежит области определения и выполняется равенство f-x= fx. Функция fx называется нечетной, если для любого значения х, взятого из области определения функции, значение — х также принадлежит области определения и выполняется равенство f-x=- fx.

Из определения следует, что области определения четной и нечетной функций симметричны относительно нуля (необходимое условие).

Для любых двух симметричных значений аргумента из области определения четная функция принимает равные числовые значения, а нечетная — равные по абсолютной величине, но противоположного знака.

Теорема 1.

Сумма, разность, произведение и частное двух четных функций являются четными функциями.

Теорема 2.

Произведение и частное двух нечетных функций представляют собой четные функции.

Пусть имеем уравнение F(x)=0, где F(x) — четная или нечетная функция.

Чтобы решить уравнение F(x) = 0, где F(x) — четная или нечетная функция, достаточно найти положительные (или отрицательные) корни, симметричные полученным, и для нечетной функции корнем будет х = 0, если это значение входит в область определения F(x). Для четной функции значение х = 0 проверяется непосредственной подстановкой в уравнение.

Примеры.

1. 8x=2x+2+x-2.

Решение.

В обеих частях уравнения имеем четные функции. Поэтому достаточно найти решения для x>=0. Так как x=0 не является корнем уравнения, рассмотрим два промежутка: (0;2, 2;infinity.

а) На промежутке (0;2 имеем:

8x= 2x+2-x+2, 23x=24, x= 43.

b) На промежутке 2;infinity имеем:

8x= 2x+2+x-2,23x=22x, x=0.

Но так как х = 0 не является корнем уравнения, то для х>0 данное уравнение имеет корень x= 43. Тогда x=- 43 также является корнем уравнения.

Ответ: 43; — 43.

Автор полагает, что работа может быть использована учителями и учащимися общеобразовательных типов на факультативных занятиях, при подготовке к математическим олимпиадам, сдаче ЕГЭ, вступительным экзаменам в технические учебные заведения.

тригонометрия — решить $\sin(3x)\cos(6x)-\cos(3x)\sin(6x)=-.9$ — Mathematics Stack Exchange

Альтернативная точка зрения:
Интуитивный подход.

Вы хотите найти все значения $x$ такие, что $\sin(3x) = 0,9$, при этом $0 \leq x < 2\pi.$

Предположим, что $\theta = 3x$.

Тогда отправной точкой будет выявление всех значений $\theta$ таких, что $0 \leq \theta < 2\pi$ и $\sin(\theta) = 0,9.$

Вместо изучения графика $ y = \sin(x)$, я считаю полезным визуализировать единичный круг и рассмотреть, что происходит, когда $\theta$ вращается от $0$ до $2\pi$ вокруг этого единичного круга.

Ясно, что в первом квадранте будет ровно одно значение $\theta$, такое что $\sin(\theta) = 0,9.$

Обозначим этот угол как $\theta_1$.

Далее, по симметрии у вас будет ровно одно значение $\theta$ во 2-м квадранте, такое что $\sin(\theta) = 0,9$.

Обозначьте этот угол как $\theta_2$.

Из визуализации функции синуса на фоне единичного круга вы знаете, что для любого угла $\theta$, такого что $\pi \leq \theta < 2\pi$, вы получите $\sin (\тета) < 0.$

Следовательно, $\theta_1$ и $\theta_2$ являются единственными $2$ углами в пределах модуля $2\pi$, такими что $\sin(\theta) = 0,9. $

Итак, прежде чем продолжить, необходим некоторый метод, чтобы иметь возможность явно ссылаться на $\theta_1$ и $\theta_2$.

Диапазон функции арксинуса $-\pi/2 \leq \theta \leq \pi/2,$ в пределах модуля $2\pi.$ Таким образом, диапазон функции арксинуса находится в диапазоне от квадранта 4 до квадранта 1.

Следовательно, $\theta_1 = \text{Арксинус}(0,9).$

Затем либо с помощью симметричной визуализации, либо с учетом формулы:
$\sin(\pi — \theta_1) = \sin(\pi)\cos(\theta_1) — \sin(\theta_1)\cos (\pi) = \sin(\theta_1)$

вы можете интуитивно что

$\theta_2 = \pi — \theta_1 = \pi — \text{Arcsine}(0.9).$

Итак, теперь у вас есть $2$ подходящих углов в пределах модуля $2\pi$

  • $\theta_1 = \text{Arcsine}(0.9).$
  • $\theta_2 = \pi — \text{арксинус}(0,9).$

Теперь вам нужно найти все углы $x$ так, чтобы:

  • $(3x) \equiv \theta_1 \pmod{2\pi}. $
  • $(3x) \эквив\тета_2 \pmod{2\pi}.$

Я понимаю, что так как ответ ищется 3 раза, то я должен пройти по кругу три раза. В книге говорится: «Всякий раз, когда мы решаем задачу в виде sin(nx)=c, мы должны пройти по кругу n раз».

Это правда, но сбивает с толку. Попытка запомнить такое правило не принесет вам много пользы. Вместо этого вам нужно проанализировать правило и напрячь свою интуицию, чтобы понять, что стоит за таким правилом. 9+}.$

Это означает, что вы хотите, чтобы $(nx — \alpha)$ было кратно $2\pi$. Следовательно, вы хотите, чтобы существовало некоторое целое число $k$, такое что

$\displaystyle nx = (\alpha + 2k\pi) \ подразумевает x = \frac{\alpha + 2k\pi}{n}.$

Так что забудьте об элегантности.
Забудьте о запоминании и слепом следовании формуле.

Вместо этого просто поэкспериментируйте.

Если $k = 0$, то $~\displaystyle x = \frac{\alpha}{n}.$

Если $k = 1$, то $~\displaystyle x = \frac{\alpha}{ n} + \frac{2\pi}{n}. $

Если $k = 2$, то $~\displaystyle x = \frac{\alpha}{n} + \frac{4\pi}{n}.$

Если $k = 3$, то $~ \displaystyle x = \frac{\alpha}{n} + \frac{6\pi}{n}.$

$\cdots$

Если $k = (n-2)$, то $~\displaystyle x = \frac{\alpha}{n} + \frac{2(n-2)\pi}{n}.$

Если $k = (n-1)$, то $~\displaystyle x = \ frac{\alpha}{n} + \frac{2(n-1)\pi}{n}.$

Если $k = (n)$, то $~\displaystyle x = \frac{\alpha} {n} + \frac{2(n)\pi}{n}.$

Если $k = (n+1)$, то $~\displaystyle x = \frac{\alpha}{n} + \ frac{2(n+1)\pi}{n}.$

В этот момент, напрягая свою интуицию, вы понимаете, что позволили $k$ пройтись по всем элементам в $\{0,1,2,\cdots,(n-2),(n-1),n,(n+1)\}$, и вы могли бы продолжить.

Это момент AHA .
Ваша интуиция подсказывает, что и при $k = 0$, и при $k = n$ повторяется один и тот же угол. Это связано с тем, что

$\displaystyle \frac{\alpha}{n}~$ эквивалентно $~\displaystyle \frac{\alpha}{n} + \frac{2n\pi}{n},~$ в модуль $(2\pi).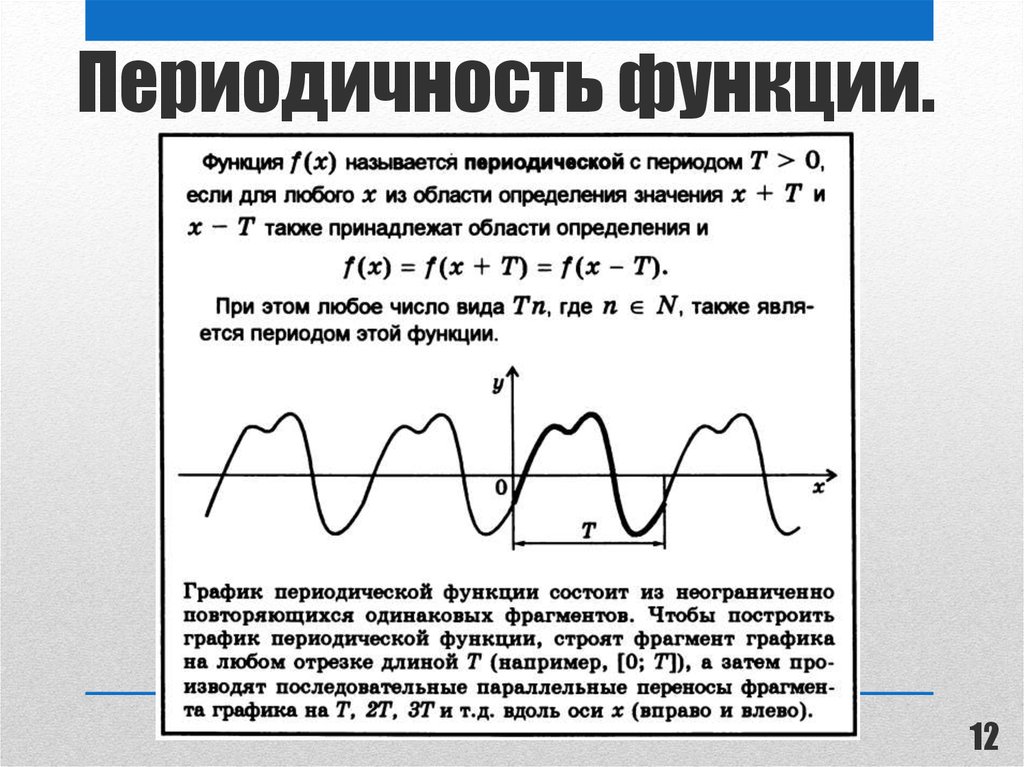

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *