Делимость чисел – определение (5 класс, математика)
4.7
Средняя оценка: 4.7
Всего получено оценок: 171.
4.7
Средняя оценка: 4.7
Всего получено оценок: 171.
Большая часть признаков делимости чисел не имеет под собой доказательной базы. Это набор наблюдений, которые помогают в быстром счете. Имеющие доказательства слишком сложны для понимания обычных людей, но использовать формулировки признаков сможет каждый в рамках математики 5 класса.
Что такое делимость?
Делимостью зовут возможность поделить одно число на другое без остатка.
Встречаются задачи, где не требуется выполнять саму операцию деления. Достаточно доказать, что число поделится нацело, с помощью признаков делимости это можно сделать без расчетов.
Отдельно оговорим, что деление без остатка подразумевает получение в результате деления целого числа. Это важно, поскольку очень часто ученики делят число, получая в итоге десятичную дробь. Такое деление тоже происходит без остатка, но не может считаться делением нацело.
Признаки делимости
Рассмотрим основные признаки делимости.
Делимость на 2
На 2 может делиться любое четное число. Четным числом считается любое число, у которого на позиции единиц стоит любая из следующих цифр:
- 0
- 2
- 4
- 6
- 8
Цифр всего 10: от 0 до 9. Чисел же бесконечное множество. Числа это слова, которые составляют из цифр-букв.
Делимость на 5 и 10
На 5 делятся только числа, которые оканчиваются на 5 и 0. Это легко проверить, если посмотреть на таблицу умножения. В столбце с умножением числа 5, все результаты оканчиваются на 5 или 0. Конечно, в таблице показано умножение на числа от 1 до 10, то тенденция сохраняется и дальше, вплоть до бесконечности. Так число 50000995 будет делиться на 5 нацело.
Число 10 представляет собой произведение чисел 2 и 5. При нахождении признака делимости на это число пользуются следующими рассуждениями: число 10 это произведение 2 и 5.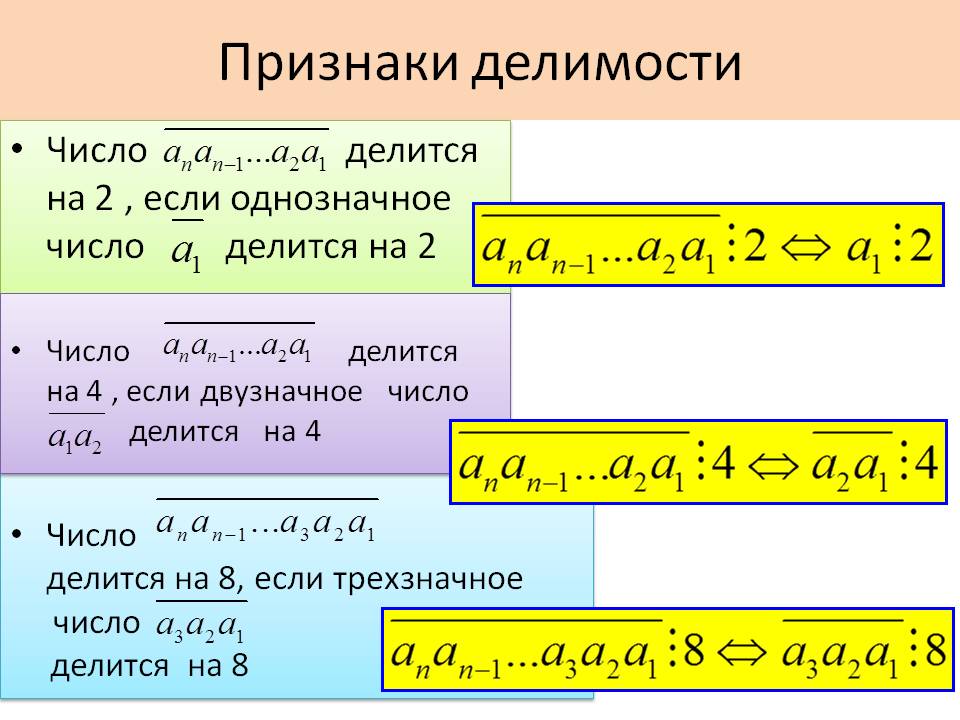
Делимость на 3 и 9
Признак делимости на 3 уникален в своем роде. Для того, чтобы убедиться в возможности поделить число на 3, нужно сложить все цифры числа. Если получившаяся сумма делится на 3, то и все число делится на 3. Конечно, в итоге все равно придется проверять какое-то число на делимость. Но сумма цифр всегда в разы меньше самого числа, поэтому этот признак облегчает определение делимости числа.
Делимость числа на 9 определяется по тому же признаку. Если сумма цифр числа делится на 9, то и все число делится на 9.
Делимость на 6
Число 6 представляет собой произведение чисел 2 и 3. Поэтому, чтобы число делилось на 6 необходимо выполнение двух условий:
- Число должно быть четным
- Сумма цифр числа должна делиться на 3.
Что мы узнали?
Мы поговорили о делимости чисел. Рассказали, что такое делимость и как определяется делимость чисел. Выделили основные признаки делимости. Оговорили некоторые способы вывода признака делимости.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Оценка статьи
4.7
Средняя оценка: 4.7
Всего получено оценок: 171.
А какая ваша оценка?
Виленкин: §1 Делимость чисел | Частная школа. 6 класс
Математика 6 класс УЧЕБНИК 2021 в 2-х частях (УМК Виленкин и др.) §1 Делимость чисел (Делители и кратные. Признаки делимости на 10, на 5 и на 2. Признаки делимости на 9 и на 3. Простые и составные числа. Разложение на простые множители. Наибольший общий делитель. Взаимно простые числа. Наименьшее общее кратное).
Перейти в ОГЛАВЛЕНИЕ
Ознакомительная версия перед покупкой.
Цитаты из учебного пособия использованы в учебных целях.
Математика 6 класс (УМК Виленкин)
§ 1. Делимость чисел.
1. Делители и кратные.
2. Признаки делимости на 10, на 5 и на 2.
3. Признаки делимости на 9 и на 3.
4. Простые и составные числа.
5. Разложение на простые множители.
6. Наибольший общий делитель. Взаимно простые числа.
7. Наименьшее общее кратное.
Задания для самопроверки.
Проектные задачи.
1. Делители и кратные.
20 яблок можно разделить поровну между 4 ребятами. Каждый получит по 5 яблок. А если надо разделить (не разрезая) 20 яблок между 6 ребятами, то каждый получит по 3 яблока, а ещё 2 яблока останутся.
Говорят, что число 4 является делителем числа 20, а число 6 не является делителем числа 20.
Делитель натурального числа. Делителем натурального числа а называют натуральное число, на которое а делится без остатка.
Число 12 имеет шесть делителей: 1, 2, 3, 4, 6 и 12.
Число 1 является делителем любого натурального числа.
Пусть на столе лежат пачки, в каждой из которых по 8 печений. Не раскрывая пачек, можно взять 8 печений, 16 печений, 24 печенья, а 18 печений так взять нельзя. Числа 8, 16, 24 делятся на 8, а 18 на 8 не делится. Говорят, что числа 8, 16, 24 кратны числу 8, а число 18 не кратно числу 8.
Кратное натурального числа. Кратным натурального числа а называют натуральное число, которое делится без остатка на а.
Любое натуральное число имеет бесконечно много кратных. Например, первые пять чисел, кратных 8, такие: 8, 16, 24, 32, 40.
Наименьшим из кратных натурального числа является само это число.
ВОПРОСЫ:
Какое число называют делителем данного натурального числа?
Какое число называют кратным натуральному числу а?
Какое число является делителем любого натурального числа?
Какое число и кратно n, и является делителем n?
2. Признаки делимости на 10, на 5 и на 2.
Всякое натуральное число, запись которого оканчивается цифрой 0, делится без остатка на 10. Чтобы получить частное, достаточно отбросить эту цифру 0.
Например, 280 делится без остатка на 10, так как 280 : 10 = 28.
При делении же числа 283 на 10 получаем неполное частное 28 и остаток 3 (т. е. последнюю цифру записи этого числа). Поэтому если последняя цифра в записи натурального числа отлична от нуля, то это число не делится без остатка на 10.
Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10.
Если запись натурального числа оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа.
Число 10 = 2 • 5. Поэтому число 10 делится без остатка и на 2, и на 5. Отсюда и любое число, запись которого оканчивается цифрой 0, делится без остатка и на 5, и на 2.
Например, 60 = 6 • 10 = 6 • (2 • 5) = (6 • 2) • 5 = 12 • 5, значит, 60 : 5 = 12. А из того, что 60 = 6 • (5 • 2) = (6 • 5) • 2 = = 30-2, получаем, что 60 : 2 = 30.
Каждое число можно представить в виде суммы полных десятков и единиц, например: 246 = 240 + 6, 1435 = = 1430 + 5. Так как полные десятки делятся на 5, то и всё число делится на 5 лишь в том случае, когда на 5 делится число единиц. Это возможно только тогда, когда в разряде единиц стоит цифра 0 или 5.
Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5. Если же запись числа оканчивается иной цифрой, то число без остатка на 5 не делится.
Например, числа 870 и 875 делятся без остатка на 5, а числа 872 и 873 на 5 без остатка не делятся.
Числа, делящиеся без остатка на 2, называют чётными, а числа, которые при делении на 2 дают остаток 1, называют нечётными. Из однозначных чисел числа 0, 2, 4, 6 и 8 чётны, а числа 1, 3, 5, 7 и 9 нечётны. Поэтому и цифры О, 2, 4, 6, 8 называют чётными, а цифры 1, 3, 5, 7, 9 — нечётными. Все полные десятки делятся на 2 без остатка (т. е. они чётны). Значит, любое натуральное число чётно лишь в случае, когда в разряде единиц стоит чётная цифра, и нечётно, когда в разряде единиц стоит нечётная цифра.
Если запись натурального числа оканчивается чётной цифрой, то это число чётно (делится без остатка на 2), а если запись числа оканчивается нечётной цифрой, то это число нечётно.
Например, числа 2, 60, 84, 96, 308 чётные, а числа 3, 51, 85, 97, 509 нечётные.
ВОПРОСЫ:
Как по записи натурального числа определить, делится оно без остатка на 10 или не делится на 10?
Как по записи натурального числа узнать, делится оно без остатка на 5 или не делится на 5?
Как по записи натурального числа узнать, делится оно без остатка на 2 или не делится на 2?
3.
Признаки делимости на 9 и на 3.4. Простые и составные числа.
5. Разложение на простые множители.
Число 210 является произведением чисел 21 и 10. Значит, 210 = 21 • 10. Числа 21 и 10 составные. Их тоже можно представить в виде произведений: 21 = 3 • 7, 10 = 2 • 5. Получаем: 210 = 3 • 7 • 2 • 5. Теперь в произведении 3 • 7 • 2 • 5 все множители — простые числа.
6. Наибольший общий делитель. Взаимно простые числа.
7. Наименьшее общее кратное.
Задания для самопроверки.
Проектные задачи.
Вы смотрели: Математика 6 класс УЧЕБНИК 2021 в 2-х частях (УМК Виленкин и др.) §1 Делимость чисел (Делители и кратные. Признаки делимости на 10, на 5 и на 2. Признаки делимости на 9 и на 3. Простые и составные числа.
Разложение на простые множители. Наибольший общий делитель. Взаимно простые числа. Наименьшее общее кратное).
Перейти в ОГЛАВЛЕНИЕ
Просмотров: 34 802
Правила делимости чисел от 2 до 10 (делится ли число на 2? на 3? на 4? и т. д.) — Криста Кинг Математика
Что означает, что число «делится» на другое число?
Когда мы говорим о «делимости» целого числа, мы как раз говорим о целых числах, которые делятся на него без остатка. Например, ???5??? делится поровну на ???15??? три раза, так как ???15\div5=3???, значит, мы можем сказать, что ???15??? «делится» на ???5???.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Прочитайте больше.
Если мы хотим быть техническими, ???15??? делится на ???5??? потому что, когда мы делаем деление ???15\div5???, ответ, который мы получаем (???3???), является целым числом.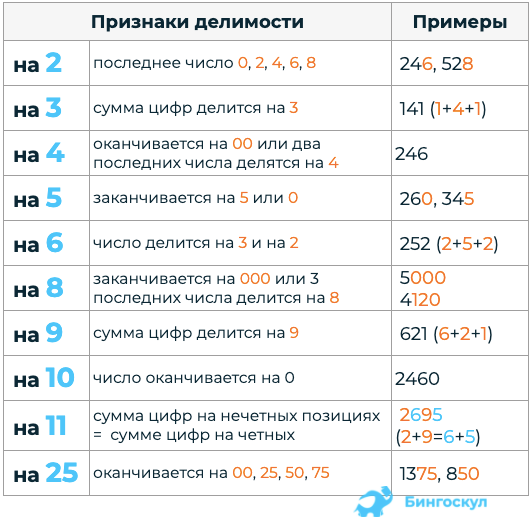
Это техническое определение делимости: результатом деления должно быть целое число.
Другими словами, мы должны получить остаток от ???0???. Поскольку мы часто думаем о ???0??? как «ничего», мы иногда говорим, что остатка нет, когда остаток равен ???0???. Итак, третий способ сказать, что одно целое число делится на другое, состоит в том, что мы не получаем остатка при делении.
Вот контрпример. ???9??? делится на ???4???? Если мы разделим???9??? по ???4???, мы знаем ???4??? переходит в ???9??? два раза, и это доводит нас до ???8???, но тогда у нас есть остаток ???1???. Другими словами, поскольку у нас есть остаток (кроме ???0???), наш ответ не является целым числом. Мы получаем целое число в качестве ответа на ???8\div4??? (ответ целое число ???2???), и мы получаем целое число как ответ для ???12\div4??? (ответ целое число ???3???), но мы не получаем целое число как ответ для ???9\дел4???. Следовательно, мы можем сказать, что ???9??? не делится на ???4???. Но как мы только что видели, ???8??? и ???12??? оба делятся на ???4???.
Следующий список правил делимости представляет собой сокращенный способ определения, делится ли конкретное целое число на другое, без фактического выполнения деления.
Делится на ???2??? если последняя цифра ???0,\2,\4,\6,\8???
Делится на ???3??? если сумма цифр делится на ???3???
Делится на ???4??? если последние две цифры делятся на ???4???Делится на ???5??? если последняя цифра ???0,\5???
Делится на ???6??? если делится на ???2??? и ???3???
Делится на ???7??? если ???5\раз??? последняя цифра + остаток числа делится на ???7???
Делится на ???8??? если последние три цифры делятся на ???8???
Делится на ???9??? если сумма цифр делится на ???9???
Делится на ???10??? если последняя цифра ???0???
Правила кратности на 2, 3, 4 и т. д. до 10
Пройти курс
Хотите узнать больше о Pre-Algebra? У меня есть пошаговый курс для этого.
🙂Учить больше
Пример, где мы определяем делимость на конкретное число
Пример
???56??? делится на ???8????
Если поделить, то получится???56\div8=7???. С ???7??? это целое число, мы можем сказать, что ???56??? делится на ???8???.
Получить доступ к полному курсу Pre-Algebra
Начать
Изучение математикиКриста Кинг математика, выучить онлайн, онлайн-курс, онлайн-математика, преалгебра, преалгебра, основы, основы математики, основы, основы математики, делимость, правила делимости, правила делимости, делимое, делится на, делится ли число?
0 лайков12 правил делимости, которые нужно знать
Существует ряд правил делимости, которые могут быть очень полезны при решении математических задач. Правила делимости помогают определить, делится ли целое число на делитель, без необходимости выполнять полное вычисление деления.
Здесь мы представляем 12 правил делимости, которые должен знать каждый студент, изучающий математику.
Что такое правила делимости?
Правила делимости — это правила, которые помогают узнать, можно ли разделить целое число на другое целое число полностью (с полученным числом без десятичных знаков), без необходимости выполнять процедуру деления, такую как деление в большую сторону или другие методы деления.
Зачем нужны правила делимости?
Правила делимости очень полезны для проверки того, является ли число кратным другому, или для проверки простых чисел. Они полезны при попытке упростить дроби или решить другие задачи, связанные с большими числами.
Когда вы изучаете правила делимости
В соответствии с Едиными базовыми стандартами штата правила делимости вводятся в 4-м классе, и они постоянно применяются в 5-м классе. Для школ, которые следуют Техасским знаниям и навыкам, вы можете ожидать, что они будут представлены в 5-м классе.
В старших классах начальной школы нужно выучить больше правил деления, и многие из них по-прежнему очень важны в средней школе и за ее пределами.
Здесь мы перечислим самые важные правила делимости, которые должен знать каждый студент, и некоторые из них, которые не так хорошо известны, но очень полезны. Позже мы также увидим, почему они важны во взрослой жизни!
Некоторые правила делимости основаны на проверке того, что числа делятся на множители этого числа, поэтому иногда может потребоваться более одного теста делимости.
Каждое целое число делится на единицу, поэтому мы это пропустим!
См. также: Что такое наибольший общий делитель и Наименьшее общее кратное
Правило делимости на 2
Число делится на 2, если оно четное.
Все четные числа имеют цифры 0, 2, 4, 6 или 8 в разряде единиц.
Примеры делимости на 2:
478 оканчивается цифрой 8, поэтому 478 четно и делится на 2.
386 519 оканчивается на цифру 9, поэтому 386 519 нечетно и не делится на 2.
Правило делимости числа 3
Чтобы проверить, делится ли целое число на 3, нам нужно найти сумму цифр целого числа мы тестируем. Если сумма его цифр кратна 3, то исходное целое число также кратно 3.
Если сумма цифр не является очевидным кратным 3, мы можем многократно складывать цифры сумм, пока не получим можно проверить, кратно ли число 3.
Примеры делимости на 3
126;
1+2+6=9. 9 кратно 3, поэтому 126 делится на 3.
76 887 694 143 612;
7+6+8+8+7+6+9+4+1+4+3+6+1+2=72,
7+2=9. 9 кратно 3, поэтому 76 887 694 143 612 делится на 3.
46736;
4+6+7+3+6=26.
2+6=8. 8 не делится на 3, поэтому 46736 не делится на 3.
Правило делимости числа 4
Чтобы целое число делилось на 4, первое, что нужно сделать, это проверить, является ли последняя цифра числа четной, поскольку 4 — четное число, любое число, кратное 4, всегда будет четным.
Если последняя цифра четная, теперь мы должны посмотреть на две последние цифры.
Достаточно проверить, делятся ли две последние цифры на 4, чтобы узнать, делится ли какое-либо целое число на 4. Почему?
Ну, любое целое число, превышающее две цифры, будет состоять как минимум из сотен.
100 равно 4, умноженному на 25, поэтому любое число, кратное 100, будет делиться на 4.
Таким образом, если оставшиеся две цифры кратны 4, все число также должно быть кратно 4.
Если вы знаете число 4 таблицу умножения, вы можете использовать это, чтобы проверить последние две цифры
4, 8, 12, 16, 20, 24, 28, 32, 36, …
Если вы не уверены в таблице умножения на 4 после 48, то вы можете попробовать разделить последние две цифры пополам, чтобы увидеть, соответствует ли это число тогда четно. Если половина числа четная, то исходное число должно быть кратным 4.
Примеры делимости для 4
4736 оканчивается на 36. 36=4×9, поэтому делится на 4, поэтому 4736 делится на 4
52 678 заканчивается на 78. 78÷2=39. 39 нечетно, поэтому 78 не делится на 4, поэтому 52 678 не делится на 4.
Правило делимости числа 5
Таблица умножения на пять дает значения с повторяющимся шаблоном в разряде единиц.
5, 10, 15, 20, 25, 30, 35, …
Число, кратное 5, всегда оканчивается на 0 или 5. 5.
6430 оканчивается на 0, поэтому 6430 делится на 5.
783451 оканчивается на 1, поэтому 783451 не делится на 5.
Правило делимости числа 6
Чтобы проверить, делится ли заданное число на 6, нам нужно проверить, проходит ли оно проверку на делимость на 2 и 3, поскольку 2 и 3 являются простыми множителями числа 6.
Примеры делимости числа 6
456;
456 оканчивается на 6, что является четным, поэтому 456 делится на 2.
4+5+6=15. 15 делится на 3, поэтому 456 делится на 3.
456 делится и на 2, и на 3, поэтому 456 делится на 6.
5,372;
5,372 оканчивается на 2, поэтому 5,372 делится на 2.
5+3+7+2=17. 17 не делится на 3, следовательно, 5,372 не делится на 3.
5,372 делится на 2, но не на 3, следовательно, 5,372 не делится на 6.
Правило делимости 7 – старое правило и бренд новый!
До недавнего времени основной признак делимости на 7 был следующим:
Умножьте последнюю цифру на 2, а затем вычтите из остального числа. Если это значение кратно 7, исходное число было кратно 7. При необходимости процесс удвоения и вычитания можно повторить для большего количества шагов.
Примеры делимости на 7 с помощью вычитания
1,659;
9×2=18, 165-18=147.
7×2=14, 14-14=0.
0 кратно 7, поэтому 1659 делится на 7.
Новое правило делимости для 7
Новое правило делимости открыла в 2019 году 12-летняя Чика Офили.
Чика открыла для себя это правило во время работы на летних каникулах.
Умножьте последнюю цифру на 5 и прибавьте к остальным цифрам. При необходимости этот процесс можно повторить. Если это значение кратно 7, исходное число делится на 7.
Примеры делимости 7 при умножении на 5
8,743;
3×5=15, 874+15=889.
9×5=45, 88+45=133.
3×5=15, 13+15=28.
28 кратно 7, следовательно, 8743 делится на 7.
Чика не только открыл правило, но и придумал алгебраическое доказательство — какой же он многообещающий молодой математик!
Правило делимости числа 8
Чтобы любое целое число делилось на 8, опять же мы знаем, что оно должно быть четным.
8 = 4 × 2 = 2 × 2 × 2, поэтому мы могли бы разделить число вдвое и проверить, делится ли это значение на 4, или мы могли бы разделить число дважды и посмотреть, является ли это число четным. Эти методы будут хорошо работать для чисел в сотню или меньше, но как насчет гораздо больших чисел?
Метод для больших целых чисел состоит в том, чтобы использовать процесс, аналогичный тесту делимости на 4.
100 не делится на 8, но 1000 делится на 8, потому что 1000 = 8 × 125.
Итак, чтобы проверить, является ли большее число делится на 8, нам нужно проверить только последние три цифры.
Примеры делимости 8
245 768 оканчивается на 768.
Половина 768 равна 384, 84=4×21. Итак, 384 делится на 4, что означает, что 768 делится на 8, следовательно, 245 768 делится на 8. 892 не делится на 8, а значит, и 67 892 не делится.
Правило делимости числа 9
Проверка делимости числа 9 аналогична проверке числа 3.
Чтобы проверить, делится ли число на 9нам нужно проверить, кратна ли сумма его цифр 9.
Как и в случае с тестом на делимость на 3, мы можем продолжать повторять процесс для каждой суммы цифр, пока число не станет меньше.
Примеры делимости на 9
59 364;
5+9+3+6+4=27. 27 кратно 9, поэтому 59 364 делится на 9.
358 256;
3+5+8+2+5+6=29. 29 не делится на 9, поэтому 358 256 не делится на 9.
Правило делимости 10
Число, кратное 10, всегда будет иметь ноль в качестве единицы измерения.
10, 20, 30, 40, 50, …..
Примеры делимости для 10
495,430 оканчивается на 0, поэтому 495,430 делится на 10
6,590 0 оканчивается на 7, поэтому на 1 не делится 0.
Правило делимости числа 11
Правило делимости числа 11 немного сложнее, чем предыдущие тесты, которые мы видели.
Чтобы проверить числа, которые делятся на 11, нам нужно найти переменная сумма цифр. Переменная сумма начинается с вычитания, за которым следует сложение, затем вычитание, сложение и так далее.
переменная сумма цифр числа 23 456 будет равна 2-3+4-5+6=4.
Если сумма переменных чисел кратна 11 (положительному, отрицательному или нулю), исходное число кратно 11.
Примеры делимости на 11
40,194;
4-0+1-9+4=0. 0 кратно 11, поэтому 40,194 делится на 11.
5 978 321;
5-9+7-8+3-2+1=-1. -1 не делится на 11, поэтому 5 978 321 не делится на 11.
Правило делимости 12
проверьте на 4, потому что 12 составное число.
Примеры делимости на 12
42,816;
4+2+8+1+6=21. 21 кратно 3, поэтому 42 816 делится на 3.
42 816 оканчивается на 16.
16 делится на 4, поэтому 42 816 делится на 4.
Следовательно, 42 816 делится на 12.
Как найти другие правила делимости?
Мы видели, что тесты на делимость 6 и 12 состоят из тестов на 2, 3 и 4. Это потому, что 6 и 12 являются составными числами, то есть они состоят из более чем одного простого делителя.
6=2×3
12=2²×3
Итак, тесты на делимость других составных чисел могут состоять из тестов простых множителей в их наибольшей степени.
Примеры делимости
15=3×5, поэтому, чтобы проверить делимость на 15, мы можем проверить на 3 и 5.
18= 2×3²=2×9, поэтому, чтобы проверить делимость на 18, мы можем проверить на 2 и 9.
24= 2³×3=8×3, значит, чтобы проверить делимость на 24, мы можем проверить на 3 и 8.
45= 3²×5=9×5, значит, чтобы проверить делимость на 45, мы можем проверить на 9 и 5.
84=2²×3×7=4×3×7, поэтому, чтобы проверить делимость на 84, мы можем проверить на 4, 3 и 7.
делимости на число N, нужно проверить на делимость на наивысшую степень каждого из простых множителей числа N.
А как насчет правил делимости для других больших простых чисел?
Проверка делимости некоторых больших простых чисел может быть довольно сложной, но процесс аналогичен правилу делимости числа 7. Существует также общее правило, которое применяется для проверки всех других простых чисел, оканчивающихся на 1, 3, 7 или 9.
Индивидуальное онлайн-обучение Third Space Learning помогает учащимся определять числовые закономерности и применять свои знания для решения математических задач.
Слайд из урока 9 повторного онлайн-обучения в школе Third Space Learning0108 Вот несколько интересных правил для больших простых чисел:Правило делимости на 29 – Умножьте последнюю цифру на 3 и прибавьте ее к оставшемуся усеченному числу. При необходимости повторите этот шаг. Если результат делится на 29, исходное число также делится на 29.
Правило делимости на 41 – Умножьте последнюю цифру на 4 и вычтите из оставшегося усеченного числа. При необходимости повторите этот шаг.
Если результат делится на 41, исходное число также делится на 41.
Правила делимости имеют значение только в школе?
Простые числа и делимость составляют большую часть математической области теории чисел. Существует много важных теорем, и огромное количество исследований проводится в этой области математики, которая имеет жизненно важное значение для таких приложений, как криптография, безопасность в Интернете и устройствах и электронная коммерция, которые являются очень прибыльными отраслями для работы.
Заинтересовать учащихся в теории чисел в раннем возрасте могли настроить их на всю жизнь! 9{2}.
1-7+2-7=-11. Сумма переменных кратна 11.
661-25=651, 65-21=63. 63 кратно 7, значит 6615 делится на 7 a 0 и 6 + 9 + 3 + 0 = 18, поэтому оно делится на 2, 5 и 9.
92 делится на 4. 492 не делится на 8.
Часто задаваемые вопросы о правилах делимости
Что такое формула делимости?
Если число x делится на число y без остатка, то говорят, что y делится на x.
Что такое делимость в математике?
Делимость в математике означает, что целое число, деленное на другое число, дает целое число без остатка.
Что такое правило делимости на 4 с примером?
Чтобы проверить, делится ли число на 4, сначала проверьте, является ли последняя цифра четным числом. Если оно четное, то посмотрите на две последние цифры, если они делятся на 4, то и все число делится на 4.
Например: 87492: 2 — четное число, 92 делится на 4, поэтому 87492 делится на 4.
Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Предоставьте учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.
Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а организованное обучение гарантирует, что каждый учащийся учится в нужном темпе.