Как делить отрицательные числа на положительные
Как разделить отрицательные числа?
Деление отрицательных. Как делить два отрицательных числа. Как разделить, если одно число отрицательное. И разделим отрицательные числа на калькуляторе!
Для деления отрицательных чисел существует только два пункта правил!
О делении отрицательных.
Правило деления отрицательных чисел.
Правила деления отрицательных аналогично умножению, только отличие в знаке.
1). Когда делимое и делить отрицательные
Первый пункт правил деления отрицательных чисел звучит так : «если делимое a и делитель b » отрицательные, то минус на минус дает плюс, т.е. результат(частное с) будет положительным:
2). Когда при делении только одно число отрицательное
Второй пункт правил деления отрицательных чисел звучит так : «если, либо делимое a , либо делитель b » отрицательные, то частное будет отрицательным (-с):
Как разделить отрицательные числа.
Заменяем наши буквы на числа и получим пример деления отрицательных чисел.
(-15) : (-12) = 15 : 12 = 1.25
Как разделить отрицательные числа на калькуляторе.
Как и в предыдущем пункте заменяем буквенные значения на числовые.
(-15) : 12 = -(15 : 12) = -1.25
Как разделить отрицательные числа на калькуляторе.
Следующим пунктом, мы разделим два отрицательных числа на калькуляторе
Набираем делимое 12.
Меняем знак на отрицательный, кнопкой плюс/минус -«±».
Набираем делитель : 15.
Меняем знак на отрицательный, кнопкой плюс/минус : «±».
Нажимаем равно » http://calc.dwweb.ru/__img/0115_delenie_otritsatelnyih_2020_10_18_09_15.png» alt=»Как разделить отрицательные числа на калькуляторе.» title=»Как разделить отрицательные числа на калькуляторе.»>
Получаем результат деления двух отрицательных чисел.
Как разделить отрицательное на положительное на калькуляторе.
Делим отрицательные на калькуляторе, когда только одно число отрицательное:
Набираем делимое 12.
Меняем знак на отрицательный, кнопкой плюс/минус -«±».
Набираем делитель : 15.
Нажимаем равно » http://calc.dwweb.ru/__img/0115_delenie_otritsatelnyih_2020_10_18_09_22.png» alt=»Как разделить отрицательное на положительное на калькуляторе.» title=»Как разделить отрицательное на положительное на калькуляторе.»>
Получаем результат деления двух отрицательных чисел, когда лишь одно число отрицательное.
Урок по математике в 5-м классе. Тема: «Деление положительных и отрицательных чисел»
Оборудование: ПК, мультимедийный проектор.
Ход урокаУчитель: Здравствуйте, садитесь. Сегодня мы будем изучать с вами новый материал, но с начала мы с вами повторим ранее изученный материал. Для этого нам нужно будет решить примеры.
1. Устные упражнения| а) |
| б) |
| в) |
| г) |
| д) |
| е) |
| ж) |
 Работа по теме урока
Работа по теме урока1. Деление отрицательных чисел имеет тот же смысл, что и деление положительных чисел, т.е. по данному произведению и одному из множителей находят второй множитель.
Кто может назвать компоненты деления?
Что значит -10 : (-5) ? (Значит, найти такое число х, что при -5 · х = -10)
Теперь найдем знак числа х.
Как вы думаете, как это можно сделать?
Так как при умножении -5 на х получается отрицательное число -10 следовательно множители должны иметь разные знаки. Следовательно, х – положительное число.
Теперь найдем модуль числа х.
Как вы думаете, чему он будет равен?
Так как модуль произведения равен произведению модулей множителей, следовательно . Следовательно , так как х – положительное число, то х = следователь х = 2
Это записывается так:
Правило: чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.
2.2. Теперь разделим отрицательное число на положительное.
Что значит -24 : 4 ? (Значит, найти такое число х, что при 4 · х = -24)
Теперь найдем знак числа х.
Как это можно сделать?
Так как при умножении 4 на х получается отрицательное число -24 следовательно х – отрицательное число.
Теперь найдем модуль числа х.
Как вы думаете, чему он будет равен?
так как х – отрицательное число с модулем 6 , то тогда х будет равен -6
Умножение и деление целых чисел
Ниже представлена схема (правило знаков при умножении):
Из данных примеров следует, что в результате умножения двух чисел с разными знаками получится отрицательное число, а результате умножения двух чисел с одинаковыми знаками – положительное.
При умножении любого числа на -1 получится число противоположное данному.
Деление
При делении одного целого числа на другое делят абсолютную величину первого на абсолютную величину второго. Перед частным ставится знак плюс, если знаки делимого и делителя одинаковы, и минус, если они разные.
Перед частным ставится знак плюс, если знаки делимого и делителя одинаковы, и минус, если они разные.
При делении используется то же правило, что и для умножения. Ниже представлена схема (правило знаков при делении):
Из данных примеров следует, что частное двух чисел с разными знаками – отрицательное число, а частное двух чисел с одинаковыми знаками – положительное число.
При делении любого числа на -1 получится число противоположное данному.
Возведение в степень
При возведении в степень целого числа в результате может получится как положительное число, так и отрицательное.
Степень положительного числа всегда будет положительным числом.
Степень отрицательного числа может быть как положительным, так и отрицательным числом.
Нечётный показатель степени:
| (-3) 3 = | (-3) · (-3) | · (-3) = |
| + |
Чётный показатель степени:
| (-4) 4 = | (-4) · (-4) | · | (-4) · (-4) | = |
| + | + |
следовательно, степень отрицательного числа положительна, если показатель степени чётный, и отрицательна, если показатель степени нечётный.
Выполнение арифметических операций в Go
15 июня, 2019 12:02 пп 4 285 views | Комментариев нетLinux | Amber | Комментировать запись
Операции с числами – неотъемлемая часть программирования. Числа используются для представления многих вещей: размеров экрана, географического положения, суммы денег, продолжительности видео, позиции игровых аватаров, цвета при назначении числовых кодов и т. д.
Эффективное выполнение математических операций в программировании – это важный навык, который необходимо развивать, потому что с числами вы будете работать часто. Хорошие знания математики, безусловно, пригодятся вам, чтобы стать хорошим программистом, но это условие не является обязательным. Если в математике вы не так сильны, как хотелось бы, постарайтесь думать о математике как о инструменте для достижения вашей цели и как о способе улучшить ваше логическое мышление.
В этом мануале мы будем работать с двумя наиболее используемыми числовыми типами данных Go, целыми числами и числами с плавающей точкой:
- Целые числа – это числа, которые могут быть положительными, отрицательными или 0 (…, -1, 0, 1,…).
- Числа с плавающей точкой – это действительные числа, содержащие десятичную точку, например 9,0 или -2,25.
Читайте также: Основные типы данных в Go
В этом руководстве рассматриваются операторы, которые мы можем использовать с числовыми типами данных в Go.
Операторы
Оператор – это символ или функция, обозначающая операцию. Например, в математике знак плюс или + – это оператор, который выполняет сложение.
В Go вы встретите некоторые знакомые операторы из математики. Однако другие операторы, которые мы будем использовать, специфичны для компьютерного программирования.
Вот краткая справочная таблица математических операторов в Go. Мы рассмотрим в этом руководстве все следующие операции.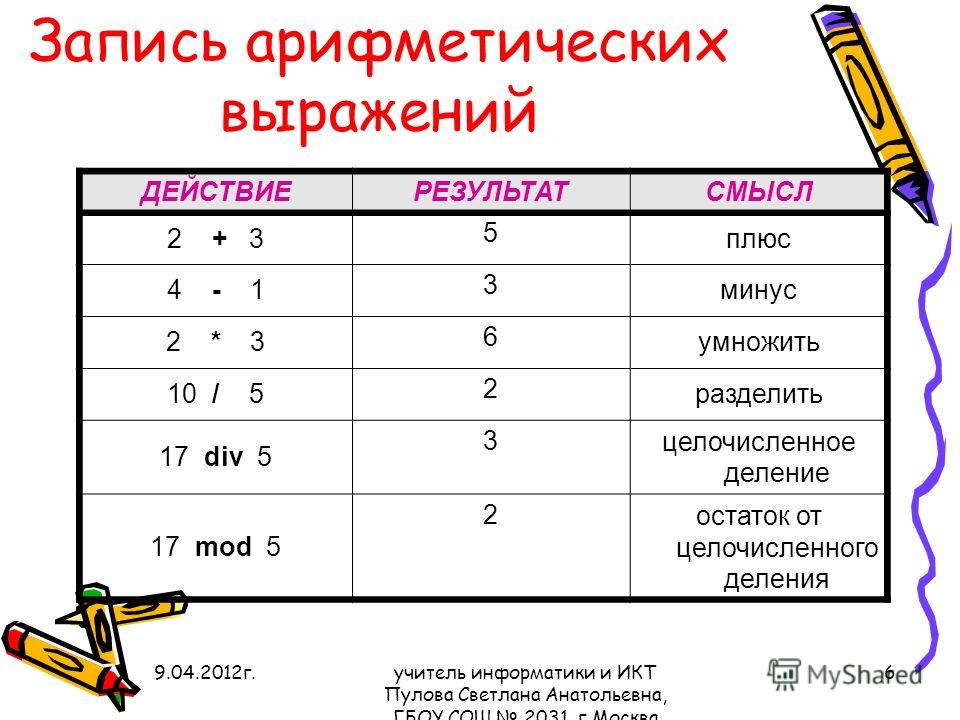
| Операция | Результат |
| x + y | Сумма х и у |
| x – y | Разница между х и у |
| -x | Меняет знак х |
| +x | Преобразование значения х в число |
| x * y | Произведение х и у |
| x / y | Отношение х к у |
| x % y | Остаток х / у |
Мы также рассмотрим составные операторы присваивания, включая += и *=, которые объединяют арифметический оператор с оператором =.
Сложение и вычитание
В Go операторы сложения и вычитания работают так же, как и в математике. Фактически вы можете использовать язык программирования Go в качестве калькулятора.
Давайте рассмотрим несколько примеров, начиная с целых чисел:
fmt.Println(1 + 5)
6
Вместо того чтобы передавать целые числа непосредственно в fmt.Println, мы можем инициализировать переменные для обозначения целочисленных значений, используя подобный синтаксис:
a := 88
b := 103
fmt. Println(a + b)
Println(a + b)
191
Поскольку целые числа могут быть как положительными, так и отрицательными числами (и 0 тоже), мы можем добавить отрицательное число к положительному:
c := -36
d := 25
fmt.Println(c + d)
-11
Сложение аналогично происходит и с числами с плавающей точкой:
e := 5.5
f := 2.5
fmt.Println(e + f)
8
Поскольку мы сложили два числа с плавающей точкой, Go вернул значение с плавающей точкой, с десятичным знаком. Но поскольку в этом случае десятичный знак равен нулю, fmt.Println отбрасывает его. Чтобы правильно отформатировать вывод, можно использовать fmt.Printf и оператор %.2f, которые будут форматировать вывод до сотых, как в этом примере:
fmt.Printf("%.2f", e + f)
8.00
Синтаксис вычитания такой же, как и сложения, нужно только изменить оператор плюс (+) на минус (-):
g := 75.67
h := 32.0
fmt.Println(g - h)
43.67
В Go использовать операторы можно только с одинаковыми типами данных. То есть нельзя складывать или вычитать int и float64:
То есть нельзя складывать или вычитать int и float64:
i := 7
j := 7.0
fmt.Println(i + j)
i + j (mismatched types int and float64)
Попытка выполнить операцию с разными типами данных приведет к ошибке компилятора.
Унарные арифметические операции
Унарное математическое выражение состоит только из одного компонента или элемента. В Go можно использовать знаки плюс и минус как один элемент в сочетании со значением, чтобы: вернуть модуль значения (+) или изменить его знак (-).
Хотя унарный плюс обычно не используется, иногда он применяется для преобразования значения в число. Мы можем использовать знак плюс с положительными значениями:
i := 3.3
fmt.Println(+i)
3.3
Когда мы используем знак плюс с отрицательным значением, он также возвращает число, и в этом случае оно тоже будет отрицательным:
j := -19
fmt.Println(+j)
-19
При отрицательном значении знак плюс возвращает такое же отрицательное число.
А унарный минус меняет знак значения. Итак, если мы передадим положительное значение, то знак минус перед значением вернет отрицательное значение:
k := 3.3
fmt.Println(-k)
-3.3
Если же использовать унарный оператор минус с отрицательным значением, будет возвращено положительное значение:
j := -19
fmt.Println(-j)
19
Унарные арифметические операторы плюс и минус возвращают число и меняют знак на противоположный.
Умножение и деление
Как и сложение с вычитанием, умножение и деление в Go очень похожи на обыкновенные математические операции. Знак, который мы будем использовать для умножения – это *, а для деления используется /.
Вот пример умножения двух значений с плавающей запятой:
k := 100.2
l := 10.2
fmt.Println(k * l)
1022.04
В Go деление имеет разные характеристики в зависимости от числового типа, который мы делим.
При делении целых чисел оператор / выполняет деление floor, где для частного x возвращается наибольшее целое число, меньшее или равное x.
Если вы попробуете разделить 80/6, вы получите 13, а тип данных будет int:
package main
import (
"fmt"
)
func main() {
m := 80
n := 6
fmt.Println(m / n)
}
13
Если в выводе вы хотите получить число с плавающей точкой, вы должны явно преобразовать значения перед делением.
Вы можете сделать это, заключив значения в float32() или float64():
package main
import (
"fmt"
)
func main() {
s := 80
t := 6
r := float64(s) / float64(t)
fmt.Println(r)
}
13.333333333333334
Модуль
Оператор % — это модуль, который возвращает остаток от деления. К примеру, это позволяет найти числа, кратные одному и тому же числу.
Давайте посмотрим на пример модуля:
o := 85
p := 15
fmt. Println(o % p)
Println(o % p)
10
При делении 85 на 15 получается 5 и 10 в остатке. Наша программа возвращает здесь значение 10, потому что оператор модуля возвращает остаток от деления.
Чтобы выполнить деление по модулю с данными float64, нужно использовать функцию Mod из пакета math:
package main
import (
"fmt"
"math"
)
func main() {
q := 36.0
r := 8.0
s := math.Mod(q, r)
fmt.Println(s)
}
4
Приоритет операций
Как и в математике, в Go нужно помнить о том, что операции выполняются в порядке их приоритета, а не по порядку справа налево.
К примеру:
u = 10 + 10 * 5
Сначала выполняется умножение (10*5=50), а затем сложение (10+50). Потому результат будет такой:
60
Чтобы сначала выполнить операцию сложения, а затем умножить полученный результат на 5, нужно взять сложение в скобки:
u = (10 + 10) * 5
print(u)
Математические операции имеют такой приоритет:
| Порядок | Буква | Значение |
| 1 | P | Parentheses (выражение в скобках) |
| 2 | E | Exponent (экспоненты) |
| 3 | M | Multiplication (умножение) |
| 4 | D | Division (деление) |
| 5 | A | Addition (сложение) |
| 6 | S | Subtraction (вычитание) |
Его можно запомнить по акрониму PEMDAS.
Возможно, вы знаете другие аббревиатуры для запоминания порядка операций, например, BEDMAS или BODMAS. Какой бы аббревиатурой вы ни пользовались, постарайтесь помнить о порядке при выполнении математических операций в Go, иначе результат может вас сильно удивить.
Операторы присваивания
Наиболее распространённым оператором присваивания является знак равенства (=). Он присваивает переменной слева значение справа. К примеру, в выражении v = 23 переменной v было присвоено значение 23.
В программировании часто используются составные операторы присваивания, которые выполняют операцию со значением переменной, а затем присваивают этой переменной полученное новое значение. Составные операторы объединяют арифметический оператор с оператором =. Поэтому для сложения мы будем комбинировать + с =, чтобы получить составной оператор +=. Давайте посмотрим, как это выглядит:
w := 5
w += 1
fmt.Println(w)
6
Сначала мы присваиваем переменной w значение 5, затем мы используем составной оператор присваивания +=, чтобы добавить правильное число к значению переменной слева, а затем присваиваем переменной w полученный результат.
Составные операторы присваивания часто используются в циклах for, которые позволяют программе повторить процесс несколько раз:
package main
import "fmt"
func main() {
values := []int{0, 1, 2, 3, 4, 5, 6}
for _, x := range values {
w := x
w *= 2
fmt.Println(w)
}
}
0
2
4
6
8
10
12
Используя цикл for для итерации по срезу values, вы смогли автоматизировать процесс оператора *=, который умножил переменную w на 2, а затем снова присвоил результат переменной w. Это позволяет автоматизировать процесс умножения чисел в заданном диапазоне.
В Go есть составные операторы присваивания для каждой математической операции:
- y += 1 (сложение и присваивание)
- y -= 1 (вычитание и присваивание)
- y *= 2 (умножение и присваивание)
- y /= 3 (деление и присваивание)
- y %= 3 (вывод остатка и присваивание)
Составные операторы присваивания могут быть полезны, когда значения нужно постепенно увеличивать или уменьшать или если вам нужно автоматизировать определенные процессы в программе.
Заключение
В этом мануале рассматриваются многие операторы, которые можно использовать с числовыми типами данных.
Читайте также:
- Основные типы данных в Go
- Преобразование типов данных в Go
Плюс-минус математика – Картина дня – Коммерсантъ
Школьная математика становится предметом ожесточенных споров не только среди педагогов и ученых, но и в обществе в целом. Все больше учеников не справляются со школьной программой, и правительства разных стран вынуждены искать пути выхода из ситуации. В США призывают программу упростить, во Франции убеждены, что само математическое знание потеряло престиж, и нужно срочно вкладываться в популяризацию. В России же математический курс пока только делают более сложным, несмотря на то что в прошлом году дети массово получили по ОГЭ двойки.
Фото: Алексей Танюшин, Коммерсантъ
Фото: Алексей Танюшин, Коммерсантъ
Перед математикой не все равны
«Подвергать детей нашего крупнейшего государства такому эксперименту — верх безответственности»,— говорится в открытом письме, под которым поставили подпись уже более полутора тысяч ученых, включая нескольких лауреатов самой престижной премии в математике — премии Филдса. Письмо направлено против одной из крупнейших реформ математического образования, которую планируют провести в Калифорнии в наступившем году. Главная ее цель — сделать школьную математику привлекательной, в частности, чтобы ею хотели активнее заниматься национальные меньшинства и девочки, которые традиционно представлены в этом секторе меньше. Для этого авторы идеи предлагают убрать из программы наиболее сложные разделы алгебры, заменив их дисциплинами под общим названием «большие данные», упразднить существующее разделение классов в соответствии с математическими способностями и отменить экзамены в государственные математические школы, заменив их распределением мест по квотам.
Письмо направлено против одной из крупнейших реформ математического образования, которую планируют провести в Калифорнии в наступившем году. Главная ее цель — сделать школьную математику привлекательной, в частности, чтобы ею хотели активнее заниматься национальные меньшинства и девочки, которые традиционно представлены в этом секторе меньше. Для этого авторы идеи предлагают убрать из программы наиболее сложные разделы алгебры, заменив их дисциплинами под общим названием «большие данные», упразднить существующее разделение классов в соответствии с математическими способностями и отменить экзамены в государственные математические школы, заменив их распределением мест по квотам.
Математик, профессор Калифорнийского университета в Ирвайне Светлана Житомирская
Фото: The Centre de Recherches Math?matiques, The Centre de Recherches Mathematiques
Математик, профессор Калифорнийского университета в Ирвайне Светлана Житомирская
Фото: The Centre de Recherches Math?matiques, The Centre de Recherches Mathematiques
«В Америке, особенно в последние полтора года, очень сильно движение за расовое и другие равенства, которое суперпрогрессивными левыми понимается как пропорциональное населению представительство во всем,— комментирует ситуацию математик, профессор Калифорнийского университета в Ирвайне Светлана Житомирская (в этом году Светлана приглашена в качестве пленарного докладчика на Международный конгресс математиков — крупнейшее и самое значимое научное мероприятие в этой сфере, что является признанием заслуг ученого. —“Ъ”).— А представительство в продвинутых математических школах и классах часто очень непропорциональное. Зачастую здесь доминируют дети азиатского происхождения, а мальчиков традиционно намного больше, чем девочек. Нет нужды объяснять, что квоты для одних означают дискриминацию других. Мы все это проходили в Советском Союзе, где отвратительную дискриминацию в отношении евреев при приеме, скажем, на мехмат МГУ некоторые объясняли стремлением к пропорциональному представительству. Этому нет морального оправдания».
—“Ъ”).— А представительство в продвинутых математических школах и классах часто очень непропорциональное. Зачастую здесь доминируют дети азиатского происхождения, а мальчиков традиционно намного больше, чем девочек. Нет нужды объяснять, что квоты для одних означают дискриминацию других. Мы все это проходили в Советском Союзе, где отвратительную дискриминацию в отношении евреев при приеме, скажем, на мехмат МГУ некоторые объясняли стремлением к пропорциональному представительству. Этому нет морального оправдания».
По словам эксперта, основная проблема предлагаемой калифорнийской реформы — значительное ослабление алгебраического фундамента, фактически его предлагают заменить на довольно пустой с математической точки зрения материал, якобы приближенный к современным нуждам «анализа данных». Также предполагается, что все, даже самые сильные, дети будут изучать алгебру только начиная с 9-го класса (с 14 лет), и в итоге у них просто не будет достаточно времени чтобы приобрести фундамент, необходимый для основ анализа, и пройти начала анализа, а последнее крайне желательно для тех, кто выберет технические специальности. Вторая существенная проблема состоит в том, что предлагаемая программа игнорирует существование математических способностей.
Вторая существенная проблема состоит в том, что предлагаемая программа игнорирует существование математических способностей.
«Хотя массовое математическое образование в Америке поставлено в целом из рук вон плохо и отстает от многих других стран, до сих пор был один очень хороший момент,— говорит Светлана Житомирская.— Во многих местах детей довольно рано на основании разных экзаменов делят на уровни и обучают раздельно. Большинство детей, у которых отмечаются способности, идут потом на технические специальности. Если новая программа будет утверждена, все они могут оказаться отброшенными назад по крайней мере на два года. При этом пострадают как раз дети из не самых обеспеченных семей, потому что остальные перейдут в частные школы, где математику будут преподавать так, как и прежде».
Отдельное опасение вызывает то, что Калифорния, как самый большой и наиболее густонаселенный штат, является законодателем мод в образовательной сфере, поэтому опыт в дальнейшем может быть экстраполирован на всю страну.
Долой Евклида!
Конечно, это не первый эксперимент радикальной реформы преподавания математики в школе. После Второй мировой войны во всех странах думали, как преподавать эффективнее. В США мощные преобразования начались в конце 1950-х годов. Президенту Кеннеди приписывают слова о том, что Америка проиграла космос русским «за школьной партой», которые Кеннеди якобы произнес после полета Гагарина в космос. С тех пор в США, а вслед за ними и в других западных странах начали внедрять «новую математику», которая должна была сделать науку более актуальной, понятной и доступной большинству учеников. При этом из школьного курса выкинули, например, Евклидову геометрию. «Евклид должен уйти» — так сформулировал постулат новой системы образования выдающийся французский математик Жан Дьёдонне. «Новая математика» продержалась вплоть до 1980-х годов, после чего этот опыт признали неудачным.
Предыдущая фотография
Математик, вице-президент Академии педагогических наук РСФСР Алексей Маркушевич
Фото:
Н. Максимов / РИА Новости
Максимов / РИА Новости
Академик АН СССР и Академии педагогических наук СССР Андрей Николаевич Колмогоров
Фото: РИА Новости
Следующая фотография
1 / 2
Математик, вице-президент Академии педагогических наук РСФСР Алексей Маркушевич
Фото:
Н. Максимов / РИА Новости
Максимов / РИА Новости
Академик АН СССР и Академии педагогических наук СССР Андрей Николаевич Колмогоров
Фото: РИА Новости
В СССР, как известно, реформа школьного математического образования стартовала чуть позже (до этого учились, например, по учебникам Киселева, написанным еще до революции) и была связана с именами математика Алексея Маркушевича и академика Андрея Колмогорова. Последний был председателем Комиссии по математическому образованию при Академии наук и лично написал учебник по алгебре, который переиздается до сих пор, а вот его учебник по геометрии скоро был изъят из обращения.
«У нас до сих пор жив миф о том, что советское математическое образование было лучшим в мире,— говорит педагог-математик, директор Центра непрерывного математического образования в РФ Иван Ященко. — Оно действительно было блестящим, но это касалось специализированных физмат школ, куда со всей страны собирали одаренных детей. При этом говорить о хорошем массовом математическом образовании не приходится. В школах давали огромный объем знаний, который приходилось зазубривать и решать механистически. В итоге те, кто умудрялся продраться сквозь этот поток, действительно становились прекрасными специалистами, но огромное количество школьников получали прививку против математики, не любили и не понимали ее всю жизнь. В итоговом контроле царила имитация, выпускные экзамены помогали выполнять учителя, а билеты устного экзамена по геометрии (кстати, замечательная по сути идея) массово зубрились наизусть без понимания».
— Оно действительно было блестящим, но это касалось специализированных физмат школ, куда со всей страны собирали одаренных детей. При этом говорить о хорошем массовом математическом образовании не приходится. В школах давали огромный объем знаний, который приходилось зазубривать и решать механистически. В итоге те, кто умудрялся продраться сквозь этот поток, действительно становились прекрасными специалистами, но огромное количество школьников получали прививку против математики, не любили и не понимали ее всю жизнь. В итоговом контроле царила имитация, выпускные экзамены помогали выполнять учителя, а билеты устного экзамена по геометрии (кстати, замечательная по сути идея) массово зубрились наизусть без понимания».
Директор Центра непрерывного математического образования в РФ Иван Ященко
Фото: Дмитрий Лебедев, Коммерсантъ
Директор Центра непрерывного математического образования в РФ Иван Ященко
Фото: Дмитрий Лебедев, Коммерсантъ
По словам Ивана Ященко, когда в 2000-х годах в России ввели ЕГЭ, при всех его плюсах и минусах, появилась возможность реально увидеть то, о чем все знали и так: общий срез образования по стране, по математике в первую очередь, оказался очень слабым. Аттестационный порог составлял три простейших задания, да еще и с выбором ответа. Особенно провальной оказалась геометрия, которую формально из российской программы никто не удалял, но в обязательном экзамене в 11-м классе ее не было.
Аттестационный порог составлял три простейших задания, да еще и с выбором ответа. Особенно провальной оказалась геометрия, которую формально из российской программы никто не удалял, но в обязательном экзамене в 11-м классе ее не было.
Жертвы математики
Русский и советский педагог, «законодатель» школьной математики Андрей Киселев
Русский и советский педагог, «законодатель» школьной математики Андрей Киселев
Незнание математики современными школьниками лишь следствие общей нелюбви к точным наукам у большой части общества, считают эксперты. С тех пор как появились доступные информационные технологии и гаджеты, сложные математические умозаключения многим кажутся ненужными для жизни. Кризис интереса к математике в последнее время остается в центре новостной повестки газет во Франции. Здесь математику для изучения выбрало рекордно низкое количество студентов-первокурсников. Аналитики уже заявляют о том, что через несколько лет в стране не будет хватать инженеров и других высококлассных специалистов для воплощения технологической революции 4. 0, которая связана с информационными и цифровыми направлениями.
0, которая связана с информационными и цифровыми направлениями.
«Для большинства математика самый трудный школьный предмет, и очень многие ее усваивают совсем плохо, часто не столько в силу лени и отсутствия способностей или упорства, сколько в силу плохих программ или плохого преподавания,— комментирует Светлана Житомирская.— Поэтому желание эту ситуацию изменить совершенно естественно. Если те, кто принимает решения, сами математику не любят и не понимают, страдали от нее в детстве, то им, конечно, нравится идея внедрить курс, который будет даваться без труда. Действительно, на нашей памяти из школьных программ исчезли некоторые распространенные раньше вещи, например алгоритм извлечения квадратных корней. Кажется, что можно отказаться и от запоминания таблицы умножения, от алгоритма длинного деления или навыков строить графики вручную. Но опыт показал, что этого делать нельзя. Когда калькуляторами начинают пользоваться слишком рано, получаются очень плохие результаты в дальнейшем, так как отсутствует фундамент».
Математик Андрей Окуньков
Фото: Евгений Гурко, Коммерсантъ
Математик Андрей Окуньков
Фото: Евгений Гурко, Коммерсантъ
«Мои дети учились на Западе в начале 2000-х, и уже тогда меня поразило, что им преподавали физику без формул — только ее описательную часть,— комментирует профессор Колумбийского университета, Принстона, Калифорнийского университета в Беркли и Высшей школы экономики, профессор Сколтеха, лауреат премии Филдса Андрей Окуньков.— Сейчас такие тенденции доходят и до математики, ее пробуют превратить в описательную, почти гуманитарную науку. Мне очень странно слышать о повсеместных нападках на математику, на попытки изгнать ее из университетов, колледжей или школ, потому что сегодня именно эта наука лежит в основе технологического благополучия каждой страны. В наше время не пища, не энергия и уже даже не информация, а способность обрабатывать и понимать информацию стала самым стратегическим ресурсом. А этого невозможно сделать без большого количества специалистов с математическим образованием».
А этого невозможно сделать без большого количества специалистов с математическим образованием».
По словам экспертов, сегодня математически неграмотный человек постоянно становится жертвой более образованных. Огромное количество людей оказываются обманутыми именно потому, что не знают элементарных азов теории вероятности, которые лежат в основе многих финансовых операций на рынке.
«Конечно, преподавание математики на базовом уровне должно быть понятным, доступным и актуальным,— говорит Иван Ященко.— Например, сейчас в школьных программах много времени уделяется такой теме, как “оценивание порядка величин”. Оказывается, это знание очень важно в эпоху, когда мы во всем привыкли доверять гаджетам и компьютерам. Они сильно облегчают нам жизнь, но параллельно увеличивают опасность больших ошибок. В прошлом году газеты написали про забавный случай, когда жительница Австралии покупала туалетную бумагу в интернет-магазине и перепутала рулоны и коробки. Тот факт, что высветилась огромная сумма, в десятки раз больше той, которая должна была быть, ее не смутила. И в итоге ей привезли грузовик туалетной бумаги. Это было действительно смешно, а теперь представьте, если порядок величин перепутал врач, рассчитывающий дозу химиотерапии, или архитектор, проектирующий мосты. Другой важный предмет, который, кстати, с сентября 2022 года будет реализовываться в рамках ФГОС в России наравне с алгеброй и геометрией,— это статистика и теория вероятности,— за отсутствие которой уже много лет критиковалось наше школьное математическое образование. Чтобы продемонстрировать важность подобных знаний, достаточно вспомнить знаменитый исторический пример времен Второй мировой войны, который вошел в науку под названием “систематическая ошибка выжившего”. Когда открыли второй фронт, многие американские бомбардировщики возвращались на базу с пробоинами от зениток. Тогда было решено укрепить броню, выбрав места, куда снаряды попадали чаще всего. На ошибку такого подхода указал математик Абрахам Вальд, который сказал, что инженеры учли только те самолеты, которые вернулись, и, значит, получили некритические поражения, а укреплять нужно те места, повреждение которых вело к крушению самолета.
И в итоге ей привезли грузовик туалетной бумаги. Это было действительно смешно, а теперь представьте, если порядок величин перепутал врач, рассчитывающий дозу химиотерапии, или архитектор, проектирующий мосты. Другой важный предмет, который, кстати, с сентября 2022 года будет реализовываться в рамках ФГОС в России наравне с алгеброй и геометрией,— это статистика и теория вероятности,— за отсутствие которой уже много лет критиковалось наше школьное математическое образование. Чтобы продемонстрировать важность подобных знаний, достаточно вспомнить знаменитый исторический пример времен Второй мировой войны, который вошел в науку под названием “систематическая ошибка выжившего”. Когда открыли второй фронт, многие американские бомбардировщики возвращались на базу с пробоинами от зениток. Тогда было решено укрепить броню, выбрав места, куда снаряды попадали чаще всего. На ошибку такого подхода указал математик Абрахам Вальд, который сказал, что инженеры учли только те самолеты, которые вернулись, и, значит, получили некритические поражения, а укреплять нужно те места, повреждение которых вело к крушению самолета. Так что современный человек просто обязан обладать навыками математического мышления, логикой, умением соотносить данные и так далее».
Так что современный человек просто обязан обладать навыками математического мышления, логикой, умением соотносить данные и так далее».
Страшно далека она от народа
Основную проблему российского школьного математического образования эксперты видят как раз в его оторванности от жизни. Известно, что российские школьники год за годом побеждают в самых престижных международных математических олимпиадах и при этом показывают невысокие результаты при оценке так называемой функциональной математической грамотности. По сути, это способность школьника применять в жизни полученные в школе знания. Она оценивается раз в три года в рамках Международной программы по оценке образовательных достижений учащихся — PISA (Program for International Student Assessment). В 2018-м по математике Россия заняла 30-е место (на первых пяти — школьники Азиатского региона). Два года назад в рамках ОГЭ по математике ввели задачи как раз на функциональную грамотность: например, нужно было посчитать, какое оборудование выгоднее провести в дом — газовое или электрическое. Именно из-за таких заданий в прошлом году школьники получили рекордное количество двоек.
Именно из-за таких заданий в прошлом году школьники получили рекордное количество двоек.
«Сейчас в России идет очень тяжелый переход от обязаловки и от зубрежки к осознанному подходу к предмету,— говорит Иван Ященко.— Но при этом мы наблюдаем среди школьников бум интереса к математике, которая сегодня стала социальным лифтом — в России постоянно фиксируется нехватка специалистов в сфере цифровых технологий, и есть крупные компании, которые готовы трудоустраивать выпускников. В России, в частности в Москве и Санкт-Петербурге, Татарстане уже реализуется все то лучшее, что хотят оставить в школьной программе те, кто выступает против нынешней реформы в Калифорнии. Уже несколько лет в школах Москвы введена так называемая Математическая вертикаль, когда практически в каждой школе дети могут учиться по разным программам — базу, причем современную, получают все; те, кому это интересно, могут освоить углубленный курс. А те, кто хочет еще большего,— учатся в ведущих математических школах, которые получают специальную поддержку».![]() Реальную доступность качественного математического образования и развития таланта по всей стране обеспечивают массовые, разумеется бесплатные, математические олимпиады (такие, как проходящий онлайн школьный этап Всероссийской олимпиады школьников на платформе «Сириус», Математический праздник, «Я люблю математику»).
Реальную доступность качественного математического образования и развития таланта по всей стране обеспечивают массовые, разумеется бесплатные, математические олимпиады (такие, как проходящий онлайн школьный этап Всероссийской олимпиады школьников на платформе «Сириус», Математический праздник, «Я люблю математику»).
Правда, одновременно в стране год за годом отмечается самый большой дефицит учителей именно по математике — особенно в регионах. То есть программы хорошие, но учить по ним пока некому.
Математика с акцентом
«Российская математика внесла и, очень надеюсь, будет вносить гигантский вклад в развитие мировой математики. У нас много замечательной талантливой молодежи, очень живо интересующейся математикой, так что основания для такой надежды есть,— говорит Андрей Окуньков.— Но есть и волнение, потому что в последнее время связи между российской и мировой наукой во многих областях математики заметно ослабевают, и где-то уже наметилось, увы, некоторое отставание».
Чтобы не дать этому процессу зайти слишком далеко, несколько лет назад было решено провести Международный конгресс математиков в России, где молодежь сможет услышать самых ярких звезд математического олимпа. В последний раз столь значимое и масштабное математическое мероприятие проводилось у нас более полувека назад — в 1966 году.
«Когда конгресс замышлялся, никто и помыслить не мог, каков будет размер проблем на нашем пути. Разумеется, пандемия смешала все карты, многие международные мероприятия уже пали ее жертвой,— говорит Андрей Окуньков.— Но столь же трудно было предположить, что мы, организаторы конгресса, подвергнемся настоящей травле со стороны большого числа как отдельных коллег, так и целых профессиональных сообществ, неоднократно поднимавших вопрос о бойкоте конгресса. Очень нелегко сталкиваться с сознательным стремлением нанести вред, весьма вероятно подогреваемым подсознательным отторжением целой страны. Это особенно удивительно потому, что невозможно представить себе более универсального и объединяющего предмета, чем математика. Население Земли говорит на тысячах очень разных языков, а язык математики один для всех, один для всех стран, для всех категорий граждан, просто один. Он совершенно аполитичен, не знает авторитетов, минимально подвержен моде и выражает собой правду и истину настолько аккуратно, насколько человечество вообще способно об истине говорить. Поэтому каждый раз обидно, когда математика становится разменной монетой в общественных или политических спорах».
Население Земли говорит на тысячах очень разных языков, а язык математики один для всех, один для всех стран, для всех категорий граждан, просто один. Он совершенно аполитичен, не знает авторитетов, минимально подвержен моде и выражает собой правду и истину настолько аккуратно, насколько человечество вообще способно об истине говорить. Поэтому каждый раз обидно, когда математика становится разменной монетой в общественных или политических спорах».
Елена Кудрявцева
Плюс минус умножить разделить математические символы векторное изображение
Плюс минус умножить разделить математические символы векторное изображение- лицензионные векторы
- символы векторов
ЛицензияПодробнее
Стандарт Вы можете использовать вектор в личных и коммерческих целях. Расширенный
Вы можете использовать вектор на предметах для перепродажи и печати по требованию.
Расширенный
Вы можете использовать вектор на предметах для перепродажи и печати по требованию.Тип лицензии определяет, как вы можете использовать этот образ.
| Станд. | Расшир. | |
|---|---|---|
| Печатный/редакционный | ||
| Графический дизайн | ||
| Веб-дизайн | ||
| Социальные сети | ||
| Редактировать и изменить | ||
| Многопользовательский | ||
| Предметы перепродажи | ||
| Печать по требованию |
Способы покупкиСравнить
Плата за изображение $ 14,99 Кредиты $ 1,00 Подписка $ 0,69 Оплатить стандартные лицензии можно тремя способами. Цены составляют долларов США долларов США.
Цены составляют долларов США долларов США.
| Оплата с помощью | Цена изображения |
|---|---|
| Плата за изображение $ 14,99 Одноразовый платеж | |
| Предоплаченные кредиты $ 1 Загружайте изображения по запросу (1 кредит = 1 доллар США). Минимальная покупка 30р. | |
| План подписки От 69 центов Выберите месячный план. Неиспользованные загрузки автоматически переносятся на следующий месяц. | |
Способы покупкиСравнить
Плата за изображение $ 39,99 Кредиты $ 30,00Существует два способа оплаты расширенных лицензий. Цены составляют долларов США долларов США.
| Оплата с помощью | Стоимость изображения |
|---|---|
Плата за изображение $ 39,99 Оплата разовая, регистрация не требуется. | |
| Предоплаченные кредиты $ 30 Загружайте изображения по запросу (1 кредит = 1 доллар США). | |
Дополнительные услугиПодробнее
Настроить изображение Доступно только с оплатой за изображение $ 85,00Нравится изображение, но нужны лишь некоторые модификации? Пусть наши талантливые художники сделают всю работу за вас!
Мы свяжем вас с дизайнером, который сможет внести изменения и отправить вам изображение в выбранном вами формате.
Примеры
- Изменить текст
- Изменить цвета
- Изменение размера до новых размеров
- Включить логотип или символ
- Добавьте свою компанию или название компании
файлов включены
Загрузка сведений…
- Идентификатор изображения
- 10085753
- Цветовой режим
- RGB
- Художник
- крафикс
Как делить отрицательные числа
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- MCAT Репетиторство
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский диалект
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочее
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все математические ресурсы ACT
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept
ACT Math Help » Арифметика » Целые числа » Отрицательные числа » Как разделить отрицательные числа
Что такое ?
Возможные ответы:
Правильный ответ:
Объяснение:
Отрицательное число, деленное на отрицательное число, всегда дает положительное число. разделить на равно . Поскольку ответ положительный, ответ не может быть или любым другим отрицательным числом.
разделить на равно . Поскольку ответ положительный, ответ не может быть или любым другим отрицательным числом.
Сообщить об ошибке. Объяснение:
Начните с выделения вашей переменной.
Вычесть с обеих сторон:
, или
Затем вычтите из обеих частей:
или
Затем разделите обе части на :
Вспомните, что деление отрицательного числа на отрицательное дает положительное значение, поэтому:
01 или 1 9010 Сообщить об ошибке
Решите следующее уравнение:
Возможные ответы:
Правильный ответ:
Объяснение:
Правило деления отрицательных чисел такое же, как и для умножения отрицательных чисел.
Если оба числа отрицательные, вы получите положительный ответ.
Если одно число положительное, а другое отрицательное, вы получите отрицательный ответ.
Следовательно:
Отчет о ошибке
Выберите ответ, который наилучшим образом решает следующее уравнение:
Возможные ответы:
Правильный ответ:
1502. Объяснение:
Чтобы решить, сначала поставьте уравнение в терминах :
Сначала умножьте x на обе стороны.
Теперь разделите на 12, чтобы найти x.
Здесь, поскольку одно из чисел в уравнении положительное, а другое отрицательное, ответ должен быть отрицательным числом:
Сообщить об ошибке Уильям
Сертифицированный преподаватель
Салезианский колледж Дона Боско, бакалавр естественных наук. Universidad Rafael Landívar, бакалавр искусств, бизнес-реклама…
View ACT Math Tutors
Ann
Сертифицированный преподаватель
Главный кампус государственного университета Райта, бакалавр наук, математики и компьютерных наук. Университет Вестерн Губернатор, Массачусетс…
Университет Вестерн Губернатор, Массачусетс…
Просмотр ACT Репетиторы по математике
Чандрика
Сертифицированный репетитор
Университет Кина, бакалавриат, клеточная и молекулярная биология.
Все математические ресурсы ACT
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Учитесь по концепции
Сложение, суммирование, вычитание, умножение, деление, возведение в квадрат
Одной из самых полезных вещей, которые вы можете делать с помощью Google Таблиц, является математика. Независимо от того, хотите ли вы просто решить простые математические задачи или у вас есть расчеты, которые необходимо выполнить с набором данных, выполнять математические операции в электронной таблице Google очень легко, если вы знаете, какие символы использовать.
Чтобы выполнить математические вычисления в электронной таблице Google, выполните следующие действия:
- Введите в ячейку знак равенства (=)
- Введите число или ссылку на ячейку (ячейку, содержащую число)
- Затем используйте один из следующих математических операторов: + (плюс), – (минус), * (умножение), / (Разделить)
- Введите другое число или ссылку на ячейку
- Нажмите Enter
В этой статье я покажу вам, как выполнять математические операции в электронной таблице Google, используя обычные числа и ссылки на ячейки… и я также показать вам разницу между математическими функциями и математическими операторами.
Формалы добавления в Google Sheets
ADD с использованием ссылок на ячейки
- = A1+A2
- = A1+A2 9
- = A1+A2 9
- . =100+200
Сложить с помощью функции ДОБАВИТЬ0403
Формулы вычитания в Google Sheets
Вычитание с использованием ячеек. Функция МИНУС
- = МИНУС(700,300)
Формулы умножения в Google Таблицах
Умножение с использованием ссылок на ячейки
- =A1*B1
Умноженные номера, без ячеек. Разделить, используя ссылки на ячейки
- =A1/B1
2
Квадратные числа с использованием функции СТЕПЕНЬ
- =СТЕПЕНЬ(2,2)
- =СЛС(2,2)
- =SQRT(A1)
Square root numbers, without cell references
- =SQRT(9)
Get your free Google Sheets cheat sheet
Spreadsheet math: Functions Vs.
 Операторы
ОператорыЕсли вы новичок в использовании формул Google Таблиц, может возникнуть соблазн использовать математические функции, такие как =Добавить, =Вычесть, =Минус, =Разделить… и эти функции действительно работают… но это намного проще и больше обычно используются операторы электронных таблиц при выполнении сложения, вычитания, умножения и деления в Google Sheets (а также возведения в квадрат).
Некоторые из этих математических операторов (перечислены ниже) очень интуитивно понятны, например, плюс (+) и минус (-), однако не все они суперочевидны, например символ/оператор умножения, который, как вы можете подумать, будет буквой «x»… но на самом деле это звездочка (*). 9) ~ Указатель
Функции математической таблицы
- = Добавить ( ~ Дополнение
- = MANUS ( ~ Suptraction
- = MULTYLLY ( ~ SUBTRACTION
- = MULTYLLY ( ~ ~
- = MUNUSLEL ( ~ ~
- .
 =СУММ( ~ Суммирование
=СУММ( ~ Суммирование - =СТЕПЕНЬ( ~ Экспонента / Степень
- = SQRT( ~ Квадратный корень
Порядок операций в электронной таблице
Порядок операций, который преподается на обычных уроках математики, также применяется в электронных таблицах Google. Самый простой способ убедиться, что ваши математические формулы решаются в том порядке, в котором вы ожидаете, это использовать больше круглых скобок, чтобы изолировать нужные числа/термины
Порядок операций в электронной таблице следующий:
- P (круглые скобки)
- E (экспоненты)
- M (умножение)
- 92/4*4-1
- =(3)+4/4*4-1
- =(3)+1*4-1
- =(3)+4-1
- =7-1
- =6
Использование простых чисел вместо ссылок на ячейки
При настройке математических формул в электронной таблице Google вы можете вводить числа непосредственно в формулу или ссылаться на ячейку, в которой есть число внутри Это…. или вы можете использовать смесь двух, где это необходимо.
или вы можете использовать смесь двух, где это необходимо.
Большим преимуществом использования ссылок на ячейки в ваших формулах является то, что вы можете легко изменить число внутри ячейки и, следовательно, число в вашей формуле… без необходимости изменять саму формулу. Это становится еще более полезным, когда у вас есть несколько формул, использующих одну и ту же ссылку на ячейку.
Следует ли вводить числа непосредственно в формулу или вводить числа в ячейки, а затем ссылаться на эти ячейки в формуле… все зависит от конкретной задачи. Если вы планируете довольно часто менять номер, то лучше всего использовать ссылку на ячейку. Но если вы применяете в своей формуле константу, которая не изменится, может быть лучше просто ввести число в формуле.
Ниже показано несколько примеров этого с включенными изображениями, но вот краткое объяснение использования ссылок на ячейки вместо простых чисел в математических формулах электронных таблиц.
Расчеты с электронными таблицами с использованием только чисел
Например, если вы хотите решить простую математическую задачу, используя Google Sheets как калькулятор, вы можете ввести в ячейку что-то вроде следующего:
= 27/3
Это отобразит ответ «9» в ячейке.
Математические вычисления в электронных таблицах с использованием ссылок на ячейки
Но при желании вы также можете вводить числа в ячейки и выполнять математические операции, ссылаясь на эти ячейки. Ссылка на ячейку — это буква, за которой следует число… буква относится к столбцу, а число — к строке. Так, например, если вы хотите «сослаться» на ячейку в своей формуле, вы должны ввести ссылку или адрес ячейки, который снова представляет собой букву столбца, за которой следует номер строки. Итак, самая первая ячейка в электронной таблице, в столбце A и строке 1, как ячейка A1.
Если вы ввели число «27» в ячейку A1 и число «3» в ячейку B1, вы можете использовать следующую формулу в любой другой ячейке:
=A1/B1
. ответ «9» в ячейке.
Использование сочетания чисел и ссылок на ячейки для выполнения математических операций
Во многих случаях вам потребуется использовать ссылки на ячейки и числа, как здесь.
=A1/3
Это также даст ответ «9», если предположить, что число «27» введено в ячейку A1.
Быстрое применение формул к нескольким ячейкам
Вероятно, вы захотите иметь возможность легко и быстро применять вычисления в своей электронной таблице к нескольким ячейкам, поэтому я хочу показать вам два способа сделать это. (Последние примеры этого урока продемонстрируют оба этих метода с включенным изображением).
Вариант 1: После ввода математической формулы в ячейку скопируйте и вставьте ячейку/формулу в ячейки ниже, и формула будет скопирована в каждую отдельную ячейку. Если в вашей формуле есть ссылки на ячейки, они будут скорректированы автоматически при копировании в строки ниже.
Щелкните здесь, чтобы узнать, как быстро копировать формулы вниз по всему столбцу.
Вариант 2: Вы также можете использовать функцию ФОРМУЛА МАССИВА, чтобы ваши математические формулы применялись к нескольким ячейкам. С помощью ARRAYFORMULA вы можете применить одну формулу к нескольким ячейкам или ко всему столбцу.
С помощью ARRAYFORMULA вы можете применить одну формулу к нескольким ячейкам или ко всему столбцу.
Как добавить в Google Sheets
Начнем с различных способов добавления в Google Sheets. Я покажу вам, как складывать, используя обычные числа, а также используя ссылки на ячейки, а затем я покажу вам, как складывать более двух ячеек вместе.
Чтобы добавить в Google Таблицы, просто введите знак равенства в ячейке (=), затем введите числа или ячейки (ссылку), которые вы хотите добавить, разделенные знаком плюс (+), а затем нажмите клавишу ввода. Вот три примера формул сложения:
- =25+25
- =A1+25
- =A1+B1
Добавление чисел
простые числа для выполнения математических операций в Google Sheets, вроде использования калькулятора.
Выберите любую ячейку на листе, введите приведенную ниже формулу и десять раз нажмите клавишу ввода.
=100+200
В ячейке должен отображаться ответ «300», как показано ниже.
Добавление ячеек с номерами
Теперь давайте добавим, используя ссылки на ячейки. Вместо того, чтобы вводить числа непосредственно в нашу формулу, на этот раз мы обращаемся к ячейкам, внутри которых есть числа, и сообщаем формуле о добавлении чисел, которые находятся в этих ячейках.
Выполните следующие действия, чтобы добавить в Google Sheets:
- Щелкните ячейку A1, затем введите число «100» и нажмите клавишу ВВОД
- Щелкните ячейку A2, затем введите число «200» и нажмите клавишу ВВОД
- Щелкните ячейку A3, затем введите « =A1+A2″, а затем нажмите клавишу ввода
- Теперь ячейка A3 должна отображать ответ «300»
Формула, показанная ниже: =A1+A2
Добавление нескольких ячеек
Вы также можете добавить более двух ячейки вместе в электронной таблице. Просто продолжайте вводить ссылки на ячейки, которые вы хотите добавить, разделенные знаком плюс, а затем нажмите клавишу ВВОД, когда ваша формула будет завершена.
После ввода знака плюс или любого другого математического оператора, если на то пошло, вы также можете щелкнуть ячейку, на которую хотите сослаться, вместо того, чтобы вводить ссылку.
Формула, показанная ниже: =A1+A2+A3+A4+A5+A6+A7
Добавление нескольких несмежных ячеек
Если складываемые ячейки находятся в одном столбце или строке, самый простой способ добавить их — «суммировать», что я покажу вам через мгновение… но когда добавляемые ячейки не являются смежными, это когда добавление нескольких отдельных ячеек становится чрезвычайно полезным.
Если на вашем листе есть числа, введенные в разных местах, которые вы хотите сложить, вы можете сделать это, используя формулу, подобную той, что показана в примере ниже.
Формула, используемая в примере: =A1+B2+C3
Использование функции ДОБАВИТЬ для сложения
Использование функции ДОБАВИТЬ для сложения гораздо менее распространено и менее полезно, чем использование оператора со знаком плюс, но вот пример который показывает, как использовать его в случае, если вам это нужно.
Формула, показанная ниже: =ДОБАВИТЬ(100,200)
Как суммировать в Google Таблицах
Функция СУММ — чрезвычайно полезная формула, которая позволит вам суммировать целые строки, столбцы или указанные диапазоны.
Чтобы просуммировать в Google Sheets, начните с ввода «=Sum(«, затем введите диапазон ячеек, которые вы хотите просуммировать, например, «B1:B100», введите закрывающие круглые скобки «)», а затем нажмите Enter .
Допустим, у вас есть столбец чисел, который вы хотите добавить, но вам не нужна длинная формула, добавляющая множество отдельных ячеек. Здесь вы должны использовать функцию СУММ.
Чтобы суммировать весь столбец в электронной таблице Google, выполните одно из следующих действий:
- Используйте ячейку в верхней части столбца, чтобы ввести формулу, подобную этой, которая суммирует все ячейки под ней: =СУММ (C1:C)
- Или используйте ячейку, которая находится ниже диапазона, который вы хотите суммировать, и введите формулу, содержащую диапазон ячеек, которые находятся над ней.
 Другими словами, например, если ваша формула СУММ находится в ячейке C100, то для суммирования чисел в столбце А, которые находятся над вашей формулой, убедитесь, что вы указали конечную строку в диапазоне, который меньше 100, например: =СУММ (С1:С99)
Другими словами, например, если ваша формула СУММ находится в ячейке C100, то для суммирования чисел в столбце А, которые находятся над вашей формулой, убедитесь, что вы указали конечную строку в диапазоне, который меньше 100, например: =СУММ (С1:С99)
Формула, показанная в примере на изображении ниже: =СУММ(A1:A7)
Примечание. Если диапазон в вашей формуле суммы содержит ячейку, в которую введена ваша формула, это вызовет циклическую ошибку зависимости.
Как вычитать в Google Sheets
Теперь давайте рассмотрим различные способы вычитания в электронной таблице. Я снова покажу вам, как вычитать, используя только числа, и я также покажу вам, как вычитать со ссылками на ячейки.
Чтобы вычесть в Google Sheets, введите знак равенства в ячейке (=), затем введите числа или ячейку (ссылки, например A1), которые вы хотите вычесть, со знаком минус (-) между ними, а затем нажмите клавишу ввода . Вот три примера:
- = 100-50
- = A1-50
- = A1-B1
Вычитание чисел
формула.
Формула, показанная в примере ниже: =700-300
После ввода приведенной выше формулы в ячейку электронной таблицы, ячейка отобразит ответ «400».
Вычитание ячеек с числами
Вы также можете использовать ссылки на ячейки для вычитания… когда числа, которые вы хотите вычесть друг из друга, вводятся в ячейки, а затем вы обращаетесь к этим ячейкам в формуле для выполнения вычислений. Использование ссылок на ячейки для вычитания позволит вам очень быстро и легко изменить числа, на которые ссылается ваша формула, без необходимости изменять формулу.
Выполните следующие действия, чтобы вычесть в Google Таблицах:
- Нажмите на ячейку A1, затем введите число «3000», а затем нажмите клавишу ввода
- Нажмите на ячейку A2, затем введите число «1000», а затем нажмите Enter
- Нажмите на ячейку A3, затем введите «=A1-A2», а затем нажмите Enter
- Теперь ячейка A3 должна отображать ответ «2000»
Пример формулы: =A1-A2
Используя функция МИНУС для вычитания
Вот пример, который показывает, как вычитать с помощью функции МИНУС.
Формула, показанная ниже: =МИНУС(700,300)
Как умножать в Google Таблицах
Теперь давайте рассмотрим, как умножать в электронной таблице. Как и в случае сложения и вычитания, вы можете выбрать, хотите ли вы использовать обычные числа в своей формуле, хотите ли вы использовать ссылки на ячейки… или их сочетание.
Чтобы умножить в электронной таблице Google, сначала введите знак равенства в ячейке (=), затем введите числа или ссылки на ячейки, которые вы хотите умножить, со звездочкой (*), разделяющей их, а затем нажмите клавишу ввода. Вот три кратких примера формул умножения:
- =10*10
- =A1*10
- =A1*A2
Умножение чисел
Если вы хотите, чтобы умножить, вы можете использовать электронную таблицу, как калькулятор, и просто ввести формулу, подобную этой показано ниже, в котором не используются ссылки на ячейки, а числа вводятся непосредственно в строку формул.
Формула, показанная в примере: =10*7
Введите приведенную выше формулу в ячейку на листе, и ячейка отобразит ответ «70».
Умножение ячеек с числами
Опять же, как и при сложении и вычитании, вы можете использовать ссылки на ячейки в формулах умножения, где числа, которые вы хотите умножить, вводятся в отдельные ячейки, и где ваша формула ссылается на эти ячейки для обозначения значения, которые нужно умножить.
Выполните следующие действия, чтобы умножить в Google Sheets:
- Нажмите на ячейку A1, затем введите число «7», а затем нажмите клавишу ввода
- Щелкните на ячейке B1, затем введите число «7», а затем нажмите ввод
- Нажмите на ячейку C1, затем введите «=A1*B1», а затем нажмите клавишу ввода. Функция УМНОЖЕНИЕ для умножения
В приведенном ниже примере показано, как умножать с помощью функции УМНОЖЕНИЕ. Однако гораздо более распространенным и простым в использовании является операторный метод, показанный выше.
Формула, показанная ниже: =УМНОЖИТЬ(10,7)
Как делить в Google Sheets
Теперь я покажу вам, как делить в электронной таблице! Еще раз я покажу вам разницу между использованием обычных чисел и использованием ссылок на ячейки для деления… и я также покажу вам разницу между использованием оператора и функции для деления.

Чтобы разделить в электронной таблице Google, начните с привязки знака равенства в ячейке (=), затем введите числа (или ссылки на ячейки с числами), которые вы хотите разделить, разделив их косой чертой (/) , а затем нажмите клавишу ВВОД. Вот три простых примера формул деления:
- =75/3
- =A1/3
- =A1/A2
Обратите внимание, что, как и при использовании калькулятора, вы не можете успешно разделить на 0 в электронная таблица. Если ваш знаменатель (число «внизу» или после косой черты) равен 0, ваша формула деления будет отображать ошибку #DIV/0. Эту ошибку можно обработать с помощью функции ЕСЛИОШИБКА, которая позволит вам указать, какое значение должно отображаться, если в формуле есть ошибка.
Вот два примера обработки ошибки #DIV/0:
- =ЕСЛИОШИБКА(C1/C2,0)
- =ЕСЛИОШИБКА(C1/C2,»Ошибка»)
Разделение чисел
Вот пример, который показывает, как делить только числа, не обращаясь к каким-либо ячейкам листа.

Формула, показанная ниже: =100/5
Введите приведенную выше формулу в любую ячейку на вашем листе, и ячейка должна отображать ответ «20».
Разделить ячейки с цифрами
Если вы хотите, вы можете ввести числа, которые вы хотите разделить на отдельные ячейки электронной таблицы, а затем ссылаться на эти ячейки в формуле деления. Это будет особенно полезно, если вы планируете со временем изменить одно или несколько значений в формуле.
Выполните следующие действия, чтобы разделить в Google Sheets:
- Нажмите на ячейку A1, затем введите число «99», а затем нажмите клавишу ввода
- Щелкните на ячейке B1, затем введите число «11», а затем нажмите ввод
- Щелкните ячейку C1, затем введите «=A1/B1» и нажмите клавишу ввода
- Теперь в ячейке C1 должно отображаться значение «9»
Формула, показанная ниже: =A1/B1
Использование Функция DIVIDE для деления
Этот пример покажет вам, как разделить в электронной таблице Google с помощью функции DIVIDE.

Формула, показанная ниже: =ДЕЛИТЬ(100,5)
Этот контент был первоначально создан и написан SpreadsheetClass.com 92
Введите приведенную выше формулу в любую ячейку электронной таблицы, и ячейка должна показать ответ «4».
Квадратные ячейки с числами
Как и в случае с другими математическими операциями, вы можете ввести число, которое хотите возвести в квадрат, в ячейку, а (в другой ячейке) обратиться к ячейке с числом внутри нее с/в вашем формула квадрата, как показано ниже.
Выполните следующие действия, чтобы возвести в квадрат числа в Google Sheets:
- Щелкните ячейку A1, затем введите число «2» и нажмите клавишу ввода 9.2
Возведение в квадрат с использованием функции POWER
Существует также функция, которую можно использовать для возведения в квадрат, и она называется POWER. Эта функция также может быть записана просто как POW. Вот пример использования этой функции.

Формула, показанная ниже: =POWER(2,2)
Альтернатива формулы: =POW(2,2)
вашей электронной таблицы, вы можете использовать функцию SQRT.
Чтобы получить квадратный корень в Google Таблицах, в любой ячейке просто введите «=SQRT(», затем введите число по вашему выбору, введите закрывающие скобки «)» и нажмите клавишу ввода. Вот два примера формул квадратного корня. просто введите обычное число непосредственно в формулу SQRT, как показано ниже.
Формула, используемая в приведенном ниже примере: =КОРЕНЬ(9)
Введите формулу, показанную выше, в ячейку электронной таблицы, после чего ячейка должна отобразить ответ «3».
Ячейки квадратного корня с числами
Если вы хотите использовать ссылку на ячейку для обозначения значения, которое вы хотите извлечь из квадратного корня, чтобы при изменении числа в ячейке также менялся ваш ответ… вы можете сделать это с помощью Функция SQRT также выполняется простым вводом адреса/ссылки ячейки в функцию.

Выполните следующие действия, чтобы получить квадратный корень в Google Таблицах:
- Нажмите на ячейку A1, затем введите число «9», а затем нажмите Enter
- Нажмите на ячейку B1, затем введите = SQRT (A1) и нажмите ввод
- Теперь ячейка B1 должна отображать ответ «3»
Формула, используемая в примере ниже: =SQRT(A1)
Как вычислять уравнения в Google Sheets
Google Sheets может делать гораздо больше, чем просто простые математические задачи с двумя значениями. Вы также можете настроить математические уравнения, чтобы ваш лист автоматически решал уравнение при вводе/изменении переменных.
Ниже показано, как рассчитать длину окружности и площадь в электронной таблице при заданном радиусе.
Обратите внимание, что в формулах этих уравнений используются числа и ссылки на ячейки. Числа, введенные непосредственно в формулу, такие как 3,14 (пи), что является константой… и ссылки на ячейки представляют собой радиус, который является переменной, и мы хотим, чтобы ее можно было легко изменить.

Окружность Окружность Табличное уравнение (где A2 — радиус)
92На изображении выше вы можете видеть, что формулы окружности вводятся в столбец B, а формулы площади вводятся в столбец C.
В каждой синей ячейке на изображении есть формула… и каждая формула ссылается до радиуса, который указан рядом с ним. Это было сделано путем копирования и вставки формул вверху (строка 2) в ячейки ниже.
При копировании и вставке подобных формул ссылка на ячейку будет автоматически корректироваться по мере вставки формулы в следующую строку. Таким образом формулы окружности и площади относятся к радиусу, указанному в одной и той же строке, потому что каждый раз, когда формулы вставляются в следующую ячейку ниже, ссылка на ячейку также корректируется на одну строку.
Ниже вы можете увидеть, как будут выглядеть формулы, когда они будут скопированы в строки ниже строки 2 в приведенном выше примере.
Копирование формулы длины окружности вниз по столбцу:Строка 3: =2*3,14* A3
Строка 4: =2*3,14* 92)
Как создавать уравнения с несколькими операторами
Теперь давайте рассмотрим использование уравнения, в котором используется несколько типов операторов в одной формуле.

Ниже приведен пример, который показывает расчет и сравнение двух разных услуг и их стоимость в зависимости от количества часов обслуживания.
Допустим, вы собираетесь нанять фотографа. У них разная базовая стоимость и другая почасовая ставка, и вы хотите знать, какой из них будет стоить меньше всего… опять же, в зависимости от того, на сколько часов вам нужно будет их нанять.
Чтобы рассчитать общую стоимость услуги для данной почасовой ставки, базовой стоимости и количества часов… мы сделаем следующее:
Возьмем почасовую ставку (столбец C), умноженную на количество часов (столбец D ), а затем добавьте базовую стоимость (столбец B).
Как видно из примера изображения, первая формула вводится в ячейку E2:
=B2+(C2*D2)
Затем эта формула копируется и вставляется в ячейки ниже, чтобы сделать такой же расчет для каждой отдельной строки данных.
Из-за различий в базовой стоимости и почасовой ставке, одна услуга будет стоить в целом меньше при найме на короткий период времени, а другая услуга будет стоить меньше при найме на более длительный период времени.


 =СУММ( ~ Суммирование
=СУММ( ~ Суммирование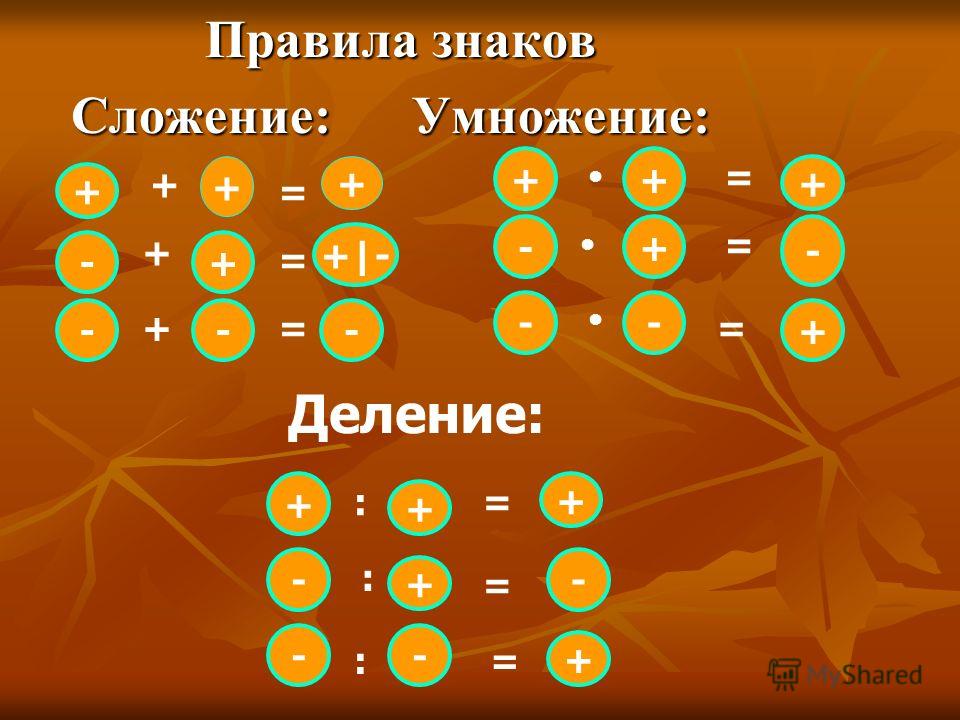 Другими словами, например, если ваша формула СУММ находится в ячейке C100, то для суммирования чисел в столбце А, которые находятся над вашей формулой, убедитесь, что вы указали конечную строку в диапазоне, который меньше 100, например: =СУММ (С1:С99)
Другими словами, например, если ваша формула СУММ находится в ячейке C100, то для суммирования чисел в столбце А, которые находятся над вашей формулой, убедитесь, что вы указали конечную строку в диапазоне, который меньше 100, например: =СУММ (С1:С99)