Составить математическую модель задачи: Построение математических моделей задач линейного программирования

Содержание

Составление математической модели задачи и её решение симплекс-методом и графическим методом. Расчет оптимальной стратегии и цены игры, заданной платежной матрицей

Экономика и менеджмент \ Экономико-математическое моделирование

Страницы работы

14 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

1-20. Составить математическую модель задачи и решить ее двумя способами: симплекс-методом и графически. Для полученной задачи составить двойственную и проверить оптимальность плана исходной задачи с помощью критериев оптимальности планов двойственных задач.

Решение: Составить математическую модель по данной таблице:

Виды ресурсов	Технолог. Способы I II		Запасы ресурсов
Виды ресурсов	Технолог. Способы I II		Запасы ресурсов
Сырье	3	1	18
Трудовые ресурсы	1	3	14
Накладные расходы	1	2	6
Прибыль	4	2

Составить план использования технологических способов в производстве, обеспечивающих максимальную прибыль.

Математическая модель задачи:

(I)

(II)

— целевая функция. (III)

Задача (I)-(III) является общей задачей, т.к. система ограничений (I) состоит из неравенств.

Введем дополнительные неизвестные и прибавим их к левым частям неравенств (I), тогда получим основную задачу:

(IV)-(VI)

Основная задача (IV)-(VI) является канонической и поэтому ее можно решить симплекс-методом.

1. Симплекс-метод.

Составим таблицу

								Табл. 1
		0	4	2	0	0	0
	Базис	x₀	x₁	x₂	x₃	x₄	x₅
0	x₃	18	3	1	1	0	0
0	x₄	14	1	3	0	1	0
0	x₅	6	3	2	0	0	1
	f	0	-4	-2	0	0	0

Последняя строка называется индексной строкой, значения в которой находятся из следующих уравнений:

Обозначим: ключевая строка: s=3

ключевой столбец: r=1

Задача считается решенной, если все элементы индексной строки неотрицательны. У нас это условие не выполнено, это означает, что исходный базис можно улучшить, построив новую таблицу. По табл.1 базисный план X₁=(0,0,18,14,6), для которого значение целевой функции f(X₁)=0.

Чтобы построить новую таблицу, среди элементов индексной строки выберем наименьший элемент. В нашем случае он равен -4, который находится в столбце x

1. Это означает, что неизвестный x₁вводится в базис. Осталось определить ключевую строку по формуле:

Поэтому,

Это означает, что нас интересует 3 строка, поэтому строка с неизвестным x₅ выводится из базиса. На пересечении ключевого столбца и ключевой строки стоит элемент 3 (в табл.1 выделен зеленым цветом).

Составим таблицу 2:

								Табл. 2
		0	4	2	0	0	0
	Базис	x₀	x₁	x₂	x₃	x₄	x₅
0	x₃	12	0	-1	1	0	-1
0	x₄	12	0		0	1
4	x₁	2	1		0	0
	f	8	0		0	0

Найдем значения:

3 строка: элементы 3-й строки из табл.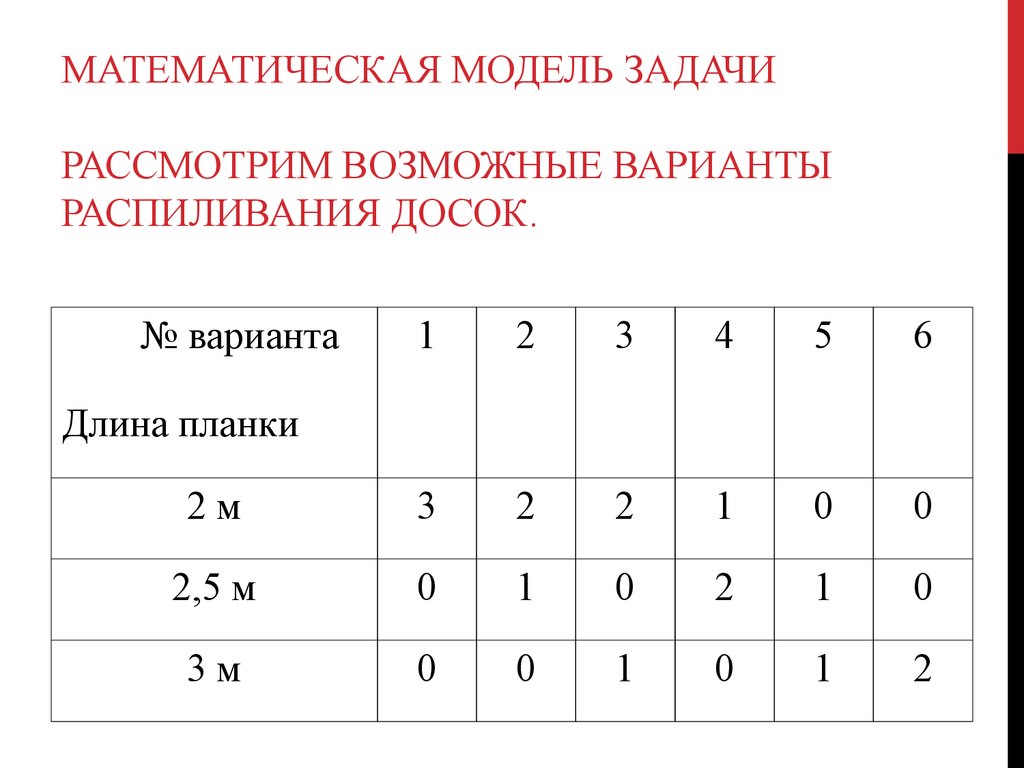 1 разделили на ключевой элемент=3.

1 и 2 строки: вычисляются по следующим формулам, где s=3, r=1.

Например, покажем для элемента a₁₂, остальные вычисляются аналогично, подставляя в формуле нужные индексы.

Значение индексной строки вычисляются аналогично Табл.1.

Получилось, что в индексной строке все элементы неотрицательны, значит, задача решена. Базисный план X₂=(2,0,12,12,0), для которого f(X₂)=8 – есть максимальное значение целевой функции. Значит, X₂=(2,0,12,12,0) является оптимальным планом основной задачи (IV)-(VI). Обозначим его X₂*=(2,0,12,12,0), тогда f(X₂*)=8- максимальное значение целевой функции (VI).

Отбросив значение дополнительных переменных, получим:

Ответ: оптимальный план X*=(2,0) общей задачи (I)-(III), а значение целевой функции останется прежним f(X*)=8.

Таким образом, для того, чтобы получить максимальную прибыль, равную 8 ед., следует использовать 2ед. ресурсов I вида. Значения дополнительных неизвестных x₃*=x₄*=12 и x₅*=0 показывают, что ресурсы I, II видов используются не полностью, а III вида – полностью.

2.Графический способ.

Общая задача (I)-(III) содержит 2 неизвестных, поэтому может быть решена графически.

Введем систему декартовых координат на плоскости x₁Ox₂ и построим множество планов задача (I)-(III). Каждое линейное неравенство системы определяет полуплоскость по одну сторону от граничной прямой, заданной соответствующим равенством. Множество планов задачи есть пересечение полуплоскостей, представляющих собой выпуклый многоугольник.

Построим каждую из граничных прямых :

Определим направление полуплоскостей: так как каждое из неравенств (I) содержит точку О(0,0):

Поэтому полуплоскости обращены к началу координат. Так как , то множество планов задачи (I)-(III) представляет собой пересечение трех полуплоскостей, попавшее в I-ую координатную четверть, т. е многоугольник.

Информация о работе

Скачать файл

Выбери свой ВУЗ

АлтГТУ 419
АлтГУ 113
АмПГУ 296
АГТУ 267
БИТТУ 794
БГТУ «Военмех» 1191
БГМУ 172
БГТУ 603
БГУ 155
БГУИР 391
БелГУТ 4908
БГЭУ 963
БНТУ 1070
БТЭУ ПК 689
БрГУ 179
ВНТУ 120
ВГУЭС 426
ВлГУ 645
ВМедА 611
ВолгГТУ 235
ВНУ им. Даля 166
ВЗФЭИ 245
ВятГСХА 101
ВятГГУ 139
ВятГУ 559
ГГДСК 171
ГомГМК 501
ГГМУ 1966
ГГТУ им. Сухого 4467
ГГУ им. Скорины 1590
ГМА им. Макарова 299
ДГПУ 159
ДальГАУ 279
ДВГГУ 134
ДВГМУ 408
ДВГТУ 936
ДВГУПС 305
ДВФУ 949
ДонГТУ 498
ДИТМ МНТУ 109
ИвГМА 488
ИГХТУ 131
ИжГТУ 145
КемГППК 171
КемГУ 508
КГМТУ 270
КировАТ 147
КГКСЭП 407
КГТА им. Дегтярева 174
КнАГТУ 2910
КрасГАУ 345
КрасГМУ 629
КГПУ им. Астафьева 133
КГТУ (СФУ) 567
КГТЭИ (СФУ) 112
КПК №2 177
КубГТУ 138
КубГУ 109
КузГПА 182
КузГТУ 789
МГТУ им. Носова 369
МГЭУ им. Сахарова 232
МГЭК 249
МГПУ 165
МАИ 144
МАДИ 151
МГИУ 1179
МГОУ 121
МГСУ 331
МГУ 273
МГУКИ 101
МГУПИ 225
МГУПС (МИИТ) 637
МГУТУ 122
МТУСИ 179
ХАИ 656
ТПУ 455
НИУ МЭИ 640
НМСУ «Горный» 1701
ХПИ 1534
НТУУ «КПИ» 213
НУК им. Макарова 543
НВ 1001
НГАВТ 362
НГАУ 411
НГАСУ 817
НГМУ 665
НГПУ 214
НГТУ 4610
НГУ 1993
НГУЭУ 499
НИИ 201
ОмГТУ 302
ОмГУПС 230
СПбПК №4 115
ПГУПС 2489
ПГПУ им. Короленко 296
ПНТУ им. Кондратюка 120
РАНХиГС 190
РОАТ МИИТ 608
РТА 245
РГГМУ 117
РГПУ им. Герцена 123
РГППУ 142
РГСУ 162
«МАТИ» — РГТУ 121
РГУНиГ 260
РЭУ им. Плеханова 123
РГАТУ им. Соловьёва 219
РязГМУ 125
РГРТУ 666
СамГТУ 131
СПбГАСУ 315
ИНЖЭКОН 328
СПбГИПСР 136
СПбГЛТУ им. Кирова 227
СПбГМТУ 143
СПбГПМУ 146
СПбГПУ 1599
СПбГТИ (ТУ) 293
СПбГТУРП 236
СПбГУ 578
ГУАП 524
СПбГУНиПТ 291
СПбГУПТД 438
СПбГУСЭ 226
СПбГУТ 194
СПГУТД 151
СПбГУЭФ 145
СПбГЭТУ «ЛЭТИ» 379
ПИМаш 247
НИУ ИТМО 531
СГТУ им. Гагарина 114
СахГУ 278
СЗТУ 484
СибАГС 249
СибГАУ 462
СибГИУ 1654
СибГТУ 946
СГУПС 1473
СибГУТИ 2083
СибУПК 377
СФУ 2424
СНАУ 567
СумГУ 768
ТРТУ 149
ТОГУ 551
ТГЭУ 325
ТГУ (Томск) 276
ТГПУ 181
ТулГУ 553
УкрГАЖТ 234
УлГТУ 536
УИПКПРО 123
УрГПУ 195
УГТУ-УПИ 758
УГНТУ 570
УГТУ 134
ХГАЭП 138
ХГАФК 110
ХНАГХ 407
ХНУВД 512
ХНУ им. Каразина 305
ХНУРЭ 325
ХНЭУ 495
ЦПУ 157
ЧитГУ 220
ЮУрГУ 309

Полный список ВУЗов

МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ТЕКСТОВЫХ ЗАДАЧАХ.

Авторы
Руководители
Файлы работы
Наградные документы

Суслова Д.А. 1

1МОУ «Темповская средняя общеобразовательная школа Ртищевского района Саратовской области»

Кравцов В.В. 1

1 МОУ

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение.

Текстовые задачи – одни из самых сложных задач в школьном курсе математики. Алгебраический метод решения не всегда бывает удобным для решения задач подобного типа — нередко бывает сложным выбрать нужную неизвестную величину так, чтобы решение было максимально простым и понятным.

С каждым годом текстовые задачи в школьном курсе математики усложняются, причем времени на совершенствование решений этих задач практически не выделяется. И если раньше их решение не вызывало особых затруднений, то теперь с этим могут возникнуть некоторые трудности. Поэтому решить задачу стандартным способом вряд ли получится. Решая одну из текстовых задач, я решила обратиться к математическому моделированию.

Для того чтобы устранить эти трудности, я решила рассмотреть другие возможные методы решения этих задач, а в частности задач на движение по окружности. Предметом моего исследования является математическое моделирование, как процесс, без которого, на мой взгляд, решение подобных задач будет наиболее трудоемким или даже невозможным.

Цель моей работы – рассмотреть основные виды математических моделей, применяемых к решению математических задач, и выбрать наиболее оптимальные к конкретной из них. К постановке этой цели меня привела следующая проблема: в современном мире, насыщенном информацией, необходимо умение представлять информацию в доступном (упрощенном) виде с целью достижения результата (решения задачи).

Исходя из цели, были поставлены следующие задачи:

Проанализировать научно-учебную литературу по теме работы.
Рассмотреть процесс математического моделирования и этапы создания модели для конкретной задачи.
Рассмотреть этапы создания математической модели.
Научиться составлять математические модели различного типа.
Выявить оптимальный метод математического моделирования для решения конкретной задачи (подобрать оптимальные модели для решения определённого типа задач).

Гипотеза: Существует универсальная математическая модель, с помощью которой можно решить любую текстовую задачу.

Объект исследования: текстовые задачи различного типа.

Методы исследования: анализ, аналогия, обобщение, прогнозирование, эксперимент.

Основная часть.

Глава I. Что такое математическая модель?

1.1 Краткая теоретическая справка.

Заинтересовавшись математическим моделированием, я проанализировала литературу, подробно описывающую данный метод. Существуют различные трактовки и классификации этого понятия. Я остановилась на учебном пособии [1] И.А. Печерских и А.Г. Семенова, которые дают следующее определение математической модели:

Математическая модель представляет собой формализованное описание системы на некотором абстрактном языке, например, в виде совокупности математических соотношений, т. е. такое математическое описание, которое обеспечивает имитацию работы систем или устройств на уровне, достаточно близком к их реальному поведению. Любая математическая модель описывает реальный объект, явление или процесс с некоторой степенью приближения к действительности. Целью математического моделирования является анализ реальных процессов математическими методами.

1.2 Этапы математического моделирования.

Постановка задачи.

На этом этапе требуется четкое понимание поставленной задачи.

Изучение теоретических основ и сбор информации об объекте оригинала.

На этом этапе подбирается или разрабатывается подходящая теория

Формализация.

Заключается в выборе системы условных обозначений.

Выбор метода решения.

На этом этапе устанавливаются окончательные параметры моделей с учетом условия функционирования объекта.

Реализация модели.

Выполнятся построение математической модели (строится график, таблица, рисунок или эскиз, граф) и решается задача исходя из новых условий.

Анализ полученной информации.

Сопоставляется полученное и предполагаемое решение.

7. Проверка адекватности реальному объекту.

Результаты, полученные по модели, сопоставляются с условиями исходной задачи.

Глава II. Применение моделирования к решению задачи.

Для достижения поставленной цели я составила несколько математических моделей, и постаралась к решению одной задачи (на движение по окружности) применить этот метод.

Задача.

Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 18 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 25 км/ч больше скорости другого?

Данную задачу решим с помощью математических моделей:

1. Таблица.

2. «Математический маятник».

3. Графическая модель.

2.1 Таблица – математическая модель, которая помогает упорядочить все данные в задаче для более удобного восприятия.

(Приложение 1. Таблица. Стр. 14.)

Решение.

Пусть x кмч – скорость первого мотоциклиста, тогда скорость 2-го мотоциклиста (x + 25) км/ч. Пусть первый раз мотоциклисты поравняются через t часов. Для того, чтобы мотоциклисты поравнялись, более быстрый (то есть второй ) должен преодолеть изначально разделяющее их расстояние, равное половине длины всей трассы ( т.к. мотоциклисты расположены в диаметрально противоположных точках )

( x + 25 )t — xt = 9

tx + 25t – tx = 9

25t = 9

t = 21,6 (минут)

Ответ: 21,6 минут.

2.2 «Математический маятник».

Математическим маятником [2] называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. Математический маятник имеет следующие характеристики: период, частота колебаний, количество колебаний и длина нити, но для решения этой задачи я остановилась на двух из них: период частота. Если связать эти величины со скоростью, временем и расстоянием, то задачу на движение по окружности можно будет решать с помощью формул, которые свойственны математическому маятнику.

T – период — это время, затраченное на один круг.

ʋ – частота колебаний – это величина обратная периоду.

Составим математическую модель.

(Приложение 2. «Математический маятник». Стр.14).

Пусть х км/ч – скорость первого мотоциклиста, тогда скорость второго мотоциклиста (х+25) км/ч. Длина всей трассы 18 км.

Т₁ = время, затраченное 1-ым мотоциклистом на прохождение полного круга (период).

Т₂ = время, затраченное 2-ым мотоциклистом на прохождение полного круга (период).

Для того чтобы мотоциклисты поравнялись в первый раз их частоты должны совпасть, значит:

– частота первого мотоциклиста.

– частота второго мотоциклиста.

Тогда разность – частота с которой будут происходить встречи при старте из одной точки.

Так как мотоциклисты расположены в диаметрально противоположных точках, то частота увеличится в 2 раза:

Тогда (ч) = 21,6 (мин. )

Ответ: 21,6 мин.

2.3 Графическая модель.

Графики законов, которые описывают зависимость S от t, строятся в системе координат SOt. Поскольку t > 0 и S > О, то построения выполняются в первой координатной четверти.

График движения тела по окружности можно заменить графиком движения по прямой. Обход телом окружности и возвращение в исходную точку равносильны достижению телом на прямой точки, удаленной от начальной на расстояние S₀, равное длине окружности.

Изобразим схематически в системе SOt движение мотоциклистов.

Так как все величины положительны, то достаточно рассмотреть графики в первой четверти.

Пусть x ч – время, за которое первый мотоциклист догнал второго, y км – путь, пройденный вторым мотоциклистом до момента встречи с первым. Решение сводится к решению геометрической задачи.

(Приложение 3. Графическая модель. Стр. 15)

Ответ: 21, 6 минуты.

На примере решения данной задачи были выявлены следующие преимущества решения задач с помощью геометрической модели: наглядность, оперативность, простота решения.

Глава 3. Выявление оптимальных моделей для решения конкретных

задач.

3.1 Задачи на совместную работу.

Задачи подобного типа удобнее всего решать с помощью таблицы, потому что производительность, объем работы и время на выполнение всей работы можно легко связать со скоростью, временем и расстоянием. Роль скорости выполняет производительность труда, роль расстояния – вся работа, время выполняет свою роль.

Задача.

Двое рабочих, работая вместе, могут выполнить производственное задание за 40 дней. За сколько дней может выполнить задание каждый из них, работая самостоятельно, если одному из них для этого надо на 18 дней больше, чем другому?

Решение:

Примем весь объем работы за единицу. Пусть 2-ой рабочий, работая самостоятельно, может выполнить все задание за x дней, тогда 1-ый — за (x+18) дней.

(Приложение 4. Таблица. Стр. 15)

Вместе за 1 день рабочие выполняют задания. За 40 дней рабочие выполнят всю работу. Составим уравнение:

40× ( ) = 1

→

Второй корень не подходит по смыслу задачи (так как время не может быть отрицательным числом). Значит, 2-ой рабочий, работая самостоятельно, может выполнить всю работу за 10 дней, а 1-ый — за 10+9=19 дней.

Ответ: 10 дней, 19 дней.

3.2 Задачи на движение.

Задачи на движение по прямой удобнее всего решать с помощью графической модели.

Задача: Два пешехода вышли одновременно из своих сел W и C навстречу друг другу. После встречи первый шел 25 минут до села C, а второй шел 16 минут до села W. Сколько минут они шли до встречи?

(Приложение 5. Графическая модель. Стр. 16)

Решение:

Пусть ОЕ расстояние между сёлами W и C. OD — график движения первого пешехода ( который шёл медленнее), а EF – график движения второго. М – место встречи.

1) ∆ MND~∆MPO,

_{2) ∆}MNE~∆MPF,

4) => что t = 20 (мин.)

Ответ: 20 мин.

3.3 Задачи на движение по окружности.

Два велосипедиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?

Решение:

Используя модель «математического маятника», описанного выше, задача решается практически устно. — частота с которой будут происходить встречи при старте из одной точки.

Так как мотоциклисты расположены в диаметрально противоположных точках, то частота увеличится в 2 раза:

Тогда (ч) = (ч) = 20 (мин.)

Ответ: через 20 минут.

С помощью этой модели можно также быстро решать задачи, в которых отставание составляет не половину трассы, а конкретное расстояние. Решим эту же задачу, изменив в ней условие.

Два велосипедиста стартуют одновременно в одном направлении из двух точек круговой трассы, расстояние между которыми равно 3 км. Длина трассы равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?

Решение: Задача будет иметь 2 решения в зависимости от направления

движения по круговой трассе.

Составим математическую модель (для данной задачи их будет две).

(Приложение 6. «Математический маятник». Стр. 16)

В первом случае решение будет таким:

— частота, с которой будут происходить встречи при старте из одной точки. – часть периода (отставание), тогда

∙ = 7; тогда Т = (ч).

Во втором случае

— частота, с которой будут происходить встречи при старте из одной точки. – часть периода (отставание), тогда

=∙ = ; тогда Т = (ч).

Ответ: через часа; или через часа.

Таким образом, модель «Математический маятник» подходит для решения задач на движение по окружности. Применение такого способа решения значительно сокращает время на решение задачи, что позволит при выполнении контрольных работ и на экзамене увеличить время на решение более трудных задач.

Заключение.

В результате исследования были получены следующие результаты:

Был изучен процесс математического моделирования и этапы создания модели для конкретной задачи.
В ходе исследования была опровергнута гипотеза, о существовании универсальной математической модели для решения всех типов задач.
Я научилась составлять математические модели различного типа.
Были выявлены оптимальные математические модели для решения конкретной задачи.

Я думаю, что за моделированием – будущее. Умение составлять математические модели сможет помочь в решении задач из различных отраслей науки, а также жизненных задач. Хочется отметить, что решение задач с применением моделирования активизирует мыслительную деятельность, помогает лучше понять задачу, самостоятельно найти рациональный путь ее решения, установить подходящий способ проверки, определить условия, при которых задача имеет (или не имеет) решения. Работа с моделью позволяет яснее увидеть зависимости между данными и искомыми величинами, оценить задачу в целом, продемонстрировать разные варианты решения.

Библиографический список.

1. Рецензенты Черкасов В.С., кандидат физ.-мат. наук, доцент;

Чуешев А.В., кандидат физ.-мат. наук, доцент; Печерских, И. А. П 31 Математические модели в экономике: учебное пособие / И.А. Печерских, А.Г. Семенов; Кемеровский технологический институт пищевой промышленности. – Кемерово, 2011. – 191 с.

2. Перышкин, А. В.

П27 Физика. 9 кл. : учебник для общеобразоват. учреждений / А. В.

Перышкин, Е. М. Гутник. – 14-е изд., стереотип. – М. : Дрофа, 2009, – 300,

с, : ил, ; 1 л, цв. Вкл.

3. http://www.pedsovet.info/info/pages/referats/inf_00002.htm

Приложения

Приложение 1. Таблица

	V (км/ч)	t (ч)	S (км)
1-ый мотоциклист	X	t	xt
2-ой мотоциклист	(х+25)	t	( x + 25 )t

Приложение 2. «Математический маятник».

Приложение 3. Графическая модель.

Приложение 4. Таблица.

	Производительность труда	Время работы	Работа
1-ый рабочий	ч/день	(x+18) дней	1часть
2-ой рабочий	ч/день		1часть

Приложение 5. Графическая модель.

25 минут

Приложение 6. «Математический маятник».

1) 2)

х+21

Просмотров работы: 7439

что это, понятие, классификация, какие параметры нужны для построения

Что такое математическая модель

Определение 1

Математическая модель — концепция представления реальности математическим способом, вариант схемы как комплекса, изучение которого позволяет человеку обрести знания о некой другой системе.

Пример

Простой пример: график зависимости среднесуточной температуры от времени.

Математическая модель также была создана для того, чтобы проанализировать и предугадать поведение материального объекта. Однако у математической модели есть проблема, от которой не избавиться — идеализация.

Определение 2

Математическое моделирование — процесс создания, а также приемы построения и исследования математических моделей.

Все науки, которые используют для решения своих задач математический аппарат, практикуют математическое моделирование. То есть, заменяют объект своего исследования математической моделью и занимаются исследованием последней.

При помощи совокупности математических методов можно описать образцовый объект или процесс, который построен на стадии содержательного моделирования.

Как осуществляется связь математической модели и реальности?

Эмпирические законы.
Гипотезы.
Идеализация.
Упрощения.

Самые важные математические модели всегда обладают качеством универсальности. То есть, совершенно разные феномены могут быть описаны одной математической моделью.

Однако стоит помнить, что модель — объект, она может иметь собственные качества и свойства, которые могут не относиться к реальному моделируемому объекту.

Часто математические модели представляют в виде:

Графика. Получить данные для решения задачи мы можем, посмотрев на данные графика.
Уравнения. Данные для решения задачи зашифрованы в виде уравнения, под буквами x и y.

Представим основные понятия, которые важны для изучения данной темы:

Реальный объект — исследуемый объект. Им может быть явление, система, либо процесс.
Модель — нематериальный или материальный объект исследования, который является заменителем настоящего процесса\явления\системы.
Моделирование — способ исследования предметов с помощью прототипов.

Виды математических моделей, классификация

Существует несколько классификаций математических моделей. Рассмотрим некоторые из них.

Формальная типология

Основа данной классификации — какие математические средства используются для создания модели. Для создания схем в формальной классификации часто используется прием дихотомии.

Примечание 1

Дихотомия — раздвоение, разделение чего-то на две части. Например, графиков.

К известным типам дихотомии относятся:

Линейные	Нелинейные
Сосредоточенные	Распределенные
Детерминированные	Стохастические
Статические	Динамические
Дискретные	Непрерывные

Типология по методу представления объекта

В рамках данной классификации выделяют структурные и функциональные модели.

Структурная модель показывает объект как комплекс с механизмом и устройством функционирования.
Функциональные модели могут отражать поведение объекта, которое мы можем воспринимать внешне.

Эти парадигмы также имеют название «черные ящики».

Содержательные, а также формальные модели

Многие авторы, которые описывают процесс моделирования в математике, отмечают, что для начала нужно построить специальную образцовую конструкцию, так называемую содержательную модель.

Примечание 2

В разных учебных изданиях идеальный объект называется по-разному. Встречаются такие примеры как умозрительная модель, концептуальная модель, а также предмодель.

Конечная математическая схема будет назваться формальной моделью (математическая модель). Она получается в результате представления предмодели с помощью формального языка.

Построить умозрительную модель можно с помощью уже готового набора идеализаций. Например, в механике существуют идеальные пружины, маятники, твердые тела и тд, которые представляют собой готовые заготовки для построения содержательной модели.

Однако есть научные области, в которых сложно построить содержательные модели, потому что в них нет полноценных формализованных доктрин. К таким дисциплинам относятся биология, физика, психология, экономика и многие другие).

Содержательная типология

В работах английского физика Рудольфа Эрнста Пайерлса можно найти некоторые типологии математических моделей, которые используются в физике и других естественных науках. Советские ученые Александр Горбань и Рэм Хлебопрос расширили классификацию Пайерлса. Данная типология акцентирует свое внимание на процессе выстраивания содержательной модели. Итак, существуют следующие типы математических моделей:

Гипотеза. Это пробное описание феноменов, автор которых либо верит в возможность их существования, либо считает это явление истинным. Такой, по мнению Пайерлса, является макет Солнечной системы от Птолемея, атомная модель Резерфорда, прототип Большого взрыва.
Феноменологическая модель. Этот тип содержит систему для описания феномена. Эта система обычно не особенно убедительна, не имеет достаточную аргументационную базу, плохо соотносится с существующими теориями. У феноменологических моделей временный статус. Ответ на вопрос феноменологической модели неизвестен, поэтому продолжается поиск истинных решений проблемы. К этому типу относятся макет теплорода.
Приближение. Если возможно построение уравнения, которое могло бы описать систему, это не значит, что его можно найти решения уравнения с помощью компьютерных программ. К таким уравнения относятся модели линейного отклика. Просто пример приближения — закон Ома.
Упрощение. В рамках данной модели убираются детали, которые могли бы повлиять на результат исследования (заметно и не контролируемо). Примером данного типа являются уравнения состояния Вандер-Ваальса, а также модели из физики жидкостей, твердого тела и т.д.
Эвристическая модель. Данная модель сохраняет подобие реальности, метод «слепого поиска» (через ошибки и пробы). Примером данной модели может быть измерение средней длины свободного пробега в кинетической теории.
Аналогия. Этот тип учитывает лишь некоторые особенности систем. Примером аналогии может быть исследование Гейзенберга о происхождении ядерных сил.
Мысленный эксперимент. Основа данного типа — предположение не на практике, не в результате реального эксперимента, а в опровержении какой-либо возможности в теории. Мысленный эксперимент часто использовал в своей работе Эйнштейн. В результате одного из мысленных экспериментов была выведена специальная теория относительности.
Демонстрация возможности. Основа данного типа — показать непротиворечивость возможности. Это своеобразные мысленные эксперименты, которые демонстрируют, что явление может согласоваться с базовыми теориями и непротиворечиво само по себе. Модель демонстрации возможности был использован для эксперимента геометрии Лобачевского.

Сложность моделируемой системы

Выделяются три уровня систем по сложности:

простые физические;
сложные физические;
биологические системы.

Советский академик Александр Андронов выделил три типа неустойчивых моделей:

Неустойчивые к преобразованию начальных требований.
Неустойчивые к небольшим преобразованиям условий, которые не вызывают никаких изменений в числе степеней свободы системы.
Неустойчивые к небольшим преобразованиям условий, которые вызывают изменения в числе степеней свободы системы.

Неустойчивые модели называют негрубыми. Устойчивые модели — мягкие.

Какие еще бывают модели?

Игровые (игры).
Учебные (тренажеры).
Опытные (уменьшенные копии чего-то).
Исследовательские (для исследования процессов).
Имитационные (представляют явления реальности).

Это ряд прототипов, которые выделяются по принципу применения.

Также выделяют материальные и информационные модели. Натуральные — муляжи, макеты. А информационные — прототипы, которые заменяют реальность формально (то есть словесно, графически и т. д.).

Какие параметры нужны для построения математической модели

Рассмотрим принципы построения математических моделей:

Информационная достаточность. Невозможно построить схему без исследуемой информации. А при полноценном информационном обеспечении (когда все известно), построение не имеет никакого смысла. Поэтому для разработки математической модели важно иметь достаточное количество информации (не избыточное или недостаточное).
Осуществимость проекта. Схема обязана гарантировать достижение определенной цели исследования.
Множественность модели. Модель обязана отражать свойства реальных явлений, которые сказываются на эффективности исследования. Должны исследоваться лишь некоторые части реального объекта. Для полноценного исследования необходимо проанализировать некоторое множество (ряд) моделей.
Агрегирование. Создание в рамках большой и сложной системы несколько подсистем, которые могут помочь решить задачу, поставленную в исследовании.
Параметризация. Подсистема с определенным параметром выражается в числовой величине. Они не описывают процесс функционирования. Зависимость величины может быть задано таблицей, формулой, графиком. Служит для сокращения объема.

Также все математические модели должны отличаться следующими признаками адекватностью, конечностью, полнотой, упрощенностью, гибкостью.

Алгоритм составления, основные моменты

Для того чтобы составить математическую модель необходимо перевести данные задачи в вид математической формы. То есть переделать слова в формулу, уравнение и т.д. Необходимо установить математические связи между всеми условиями задачи.

Стоит помнить, что формула, уравнение математической модели должно полностью соответствовать тексту задачи, потому что иначе цель исследования изменится, а значит и задачу мы будем решать другую.

Представим алгоритм решения математической модели:

Определяем цель исследования.
Выделяем свойства системы.
Выбираем средства, с помощью которых будем исследовать систему.
Проводим исследование.
Анализируем получившиеся результаты.
Корректируем прототип.

Попробуем составить математическую модель на примере простой задачи:

Задача

Иван Федорович вернулся с охоты и показал своей семье добычу. Оказалось, что он принес 10 тушек зайцев, которые живут в тайге, 50 % всей добычи — из тундры, а из местного леса, где охотился Иван Федорович нет ни одного животного. Сколько всего дичи купил Иван Федорович в магазине «Мясо диких животных?».

Данный текст нужно представить в виде уравнения. Для этого необходимо установить математические связи между всеми условиями задачи.

Обращаем внимание на главные математические данные. 10 тушек и 50%.
Найдем скрытую информацию. Под 50% имеется в виду 50% от всего количества дичи.
Представим главный вопрос — сколько дичи — в виде X. То есть, X — количество всей дичи, что есть у Ивана Федоровича.
Процентное соотношение дичи из тундры нужно перевести в штуки, потому что в математических задачах важно все составлять в одинаковых значениях.
Число дичи из тундры невозможно посчитать в штуках, поэтому переводим в уравнение 50% = 0,5*X. Данное уравнение верно для вычисления количества дичи из тундры.
Какие данные у нас есть? 10 штук тушек зайцев из тайги, 0,5*X — дичи из тундры, а также X общее количество дичи.
То есть, общее количество дичи будет равно сумме дичи из тайги и дичи из тундры. То есть, уравнение X = 10 + 0,5X.
X = 10 + 0,5X — математическая модель.
Далее решаем линейное уравнение и получаем, что дичи всего 20 штук.
Ответ: 20.

Обобщение — для того, чтобы построить математическую модель, нужно выбросить всю ненужную информацию из задачи, оставить только нужное и заменяем на математический объект.

4.5: Создание собственного уравнения модели

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 7786

Хироки Саяма
Бингемтонский университет, Университет штата Нью-Йорк через OpenSUNY

Теперь, когда вы знаете, как моделировать динамику разностных уравнений, вы можете попробовать построить собственное модельное уравнение и проверить его поведение. Тогда возникает вопрос: как построить собственное модельное уравнение?

Математика — это язык, который используется для описания мира. Точно так же не существует единственно правильного способа описать идею на английском языке, как нет и единственно правильного способа построить уравнение математической модели. Это сильно зависит от вашей личной грамотности, творчества и выразительности на языке математики. В конечном счете, вам просто нужно продолжать «читать» и «писать» математику каждый день, чтобы совершенствоваться в построении математических моделей. Сказав это, я могу предложить несколько практических советов, которые помогут вам построить собственные модельные уравнения. Вот они:

Практические советы по построению математической модели

1. Если вы не знаете, с чего начать, просто возьмите существующую модель и настройте ее.
2. Реализуйте каждое допущение модели одно за другим. Не пытайтесь добраться до финальной модели одним прыжком.
3. Чтобы реализовать новое предположение, сначала определите, какая часть уравнения модели представляет величину, которую вы собираетесь изменить, замените ее неизвестной функцией, а затем спроектируйте функцию.
4. По возможности используйте простейшую математическую форму.
5. Закончив уравнение, проверьте, работает ли оно так, как вы хотели. Часто бывает полезно протестировать его поведение с экстремальными значениями, присвоенными переменным и/или параметрам.

Позвольте мне проиллюстрировать каждый из этих советов на примере. Рассмотрите возможность построения другой модели роста популяции, которая может показать не только экспоненциальный рост, но и конвергенцию к определенному пределу популяции. Любые идеи о том, с чего начать? Как следует из первого совета, вы можете использовать существующую модель, похожую на то, что вы хотите смоделировать, а затем изменить ее для своих нужд. Поскольку этот пример касается роста населения, мы уже знаем одну такую модель: модель экспоненциального роста. Итак, начнем с этого:

\[x_{t}=ax_{t-1}\метка{(4.19)} \]

Эта модель очень проста. Он состоит всего из двух компонентов: коэффициента роста $a$ и численности населения $x_{t−1}$.

Второй совет говорит о том, что вам следует применять пошаговый подход. Итак, давайте подумаем, что нам дополнительно нужно реализовать в этой модели. Наша новая модель должна демонстрировать следующие два поведения:

Экспоненциальный рост
Конвергенция к определенному лимиту населения

Сначала нужно проверить первую. Исходная модель уже сама по себе показывает экспоненциальный рост, так что это уже сделано. Итак, переходим ко второму. Очевидно, исходная модель не показывает такой сходимости, поэтому это то, что нам нужно будет реализовать в модели. Третий совет говорит, что вам нужно сосредоточиться на конкретном компоненте, который нужно пересмотреть. Здесь есть много вариантов. Вы можете пересмотреть $a$, $x_{t−1}$ или даже добавить еще один член в правую часть. Но в данном конкретном случае сходимость к определенному пределу означает, что коэффициент роста $а$ должен стремиться к 1 (т.е. нет чистого роста). Итак, мы можем сосредоточиться на части a и заменить ее неизвестной функцией размера популяции $f(x_{t−1})$. Уравнение модели теперь выглядит так:

\[x_{t}=f(x_{t-1})x_{t-1}\метка{(4.20)} \]

Теперь ваша задача стала проще: просто сконструируйте функцию $f(x)$. Подумайте об ограничениях, которым он должен удовлетворять. $f(x)$ должно быть близко к исходной константе $a$, когда популяция мала, т. е. когда ресурсов окружающей среды достаточно, чтобы показать экспоненциальный рост. Между тем, $f(x)$ должно приближаться к 1, когда популяция приближается к пропускной способности окружающей среды (давайте пока назовем это $K$). С математической точки зрения эти ограничения означают, что функция $f(x)$ должна пройти через следующие две точки: $(x,f(x)) = (0,a)$ и $(K, 1)$.

И тут на помощь приходит четвертый совет. Если у вас нет дополнительной информации о том, как должна выглядеть модель, следует выбрать максимально простую форму, удовлетворяющую требованиям. В данном конкретном случае прямая линия, соединяющая две указанные выше точки, является простейшей (рис. 4.5.1), которая задается числом

\[f(x)= -\frac{a-1}{K}x+a.\label{(4.21)} \]

Вы можете вставить эту форму в исходное уравнение, чтобы завершить новое математическое уравнение:

\[x_{t} =-(\frac{a-1}{K} x_{t-1} +a) x_{t-1}\label{(4.22)} \]

Похоже, построение вашей модели завершено. Следуя пятому совету, давайте проверим, ведет ли себя новая модель так, как вы задумали. Как следует из подсказки, тестирование с экстремальными значениями часто помогает выявить возможные проблемы в модели. Что происходит, когда $x_{t−1} = 0$?

Рисунок $\PageIndex{1}$: Простейший пример того, как коэффициент роста $a = f(x)$ от численности населения должен вести себя как $x$.

В этом случае уравнение принимает вид $x_{t = 0}$, поэтому роста нет. Это имеет смысл; если организмов не осталось, не должно быть и роста. Другой крайний случай: что происходит, когда $x_{t−1} = K$? В этом случае уравнение принимает вид $x_{t} = x_{t−1}$, т. е. система поддерживает тот же размер популяции. Это новое конвергентное поведение, которое вы хотели реализовать, так что это тоже хорошая новость. Теперь вы можете проверить поведение новой модели с помощью компьютерного моделирования.

Упражнение $\PageIndex{1}$

Смоделируйте поведение новой модели роста населения для нескольких различных значений параметра $a$ и начального условия $x_{0}$, чтобы увидеть, какое поведение возможны.

\[x_{t} = -(\frac{a-1}{K} x_{t-1} +a)x_{t-1}\label{(4.23)} \]

Для информации , уравнение новой модели, которое мы только что вывели выше, на самом деле имеет особое имя; в математической биологии и некоторых других дисциплинах она называется моделью логистического роста . Вы можете применить замену параметра $r = a−1$, чтобы привести уравнение к более известной форме:

\[x_{t} = -(\frac{a-1}{K} x_{t-1} +a)x_{t-1}\label{(4.24)} \]

\[=-(\frac{r}{K}x_{t-1} +r+1)x_{t-1}\label{ (4.25)} \]

\[=x_{t-1}+rx_{t-1}(1- \frac{x_{t-1}}{K})\метка{(4. 26)} \]

В правой части этой формулы два члена: текущая численность населения $(x_{t−1})$ и количество новорожденных $(rx_{t−1}(···))$ . Если $x$ намного меньше, чем $K$, значение в скобках становится ближе к 1, и, таким образом, модель приближается к

\[x_{t} \ приблизительно x_{t-1} +rx_{t-1}.\метка{(4.27)} \]

Это означает, что в $r$ раз текущая популяция добавляется к популяции на каждом временном шаге, что приводит к экспоненциальному росту. Но когда $x$ приближается к $K$, внутри скобок приближается к 0, так что чистого роста не будет.

Упражнение $\PageIndex{2}$

Создайте математическую модель роста популяции, в которой коэффициент роста максимален при определенном оптимальном размере популяции, но снижается по мере отклонения численности популяции от оптимального. Затем смоделируйте его поведение и посмотрите, чем оно отличается от поведения модели логистического роста.

Эта страница под названием 4.5: Построение собственного уравнения модели распространяется под лицензией CC BY-NC-SA 3. 0 и была создана, изменена и/или курирована Хироки Саямой (OpenSUNY) с помощью исходного содержимого, отредактированного в соответствии со стилем. и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
Хироки Саяма
Лицензия
CC BY-NC-SA
Версия лицензии
3,0
Показать страницу TOC
нет
Теги
1. source@https://milneopentextbooks. org/introduction-to-the-modeling-and-analysis-of-complex-systems

Математические модели

Математику можно использовать для «моделирования» или представления того, как устроен реальный мир.

Пример: сколько места внутри этой картонной коробки?

Мы знаем три измерения:

л (длина),
ш (ширина) и
ч (высота),

, а формула объема прямоугольного параллелепипеда:

Объем = l × w × h

Итак, у нас есть (очень простая) математическая модель пространства в этом ящике.

Точно?

Модель не такая, как настоящая.

В нашем примере мы не учли толщину картона и многие другие вещи из «реального мира».

Но будем надеяться, что он достаточно хорош, чтобы быть полезным .

Если мы платим за объем отправляемой коробки, мы можем сделать несколько измерений и узнать, сколько платить.

Это также может быть полезно при выборе коробки, когда нам нужно упаковать вещи.

Значит модель полезная!

Но, может быть, нам нужно больше точности, нам может понадобиться отправлять сотни коробок каждый день, и толщина картона имеет значение. Итак, давайте посмотрим, сможем ли мы улучшить модель :

Картон имеет толщину «t», и мы измеряем снаружи коробки. Сколько места внутри?

Внутренние размеры должны быть уменьшены на толщину каждой стороны:

Внутренняя длина л-2т
Внутренняя ширина w-2t ,
Внутренняя высота h-2t

и теперь формула:

Внутренний объем = (л-2т) × (ш-2т) × (ч-2т)

Теперь у нас есть лучшая модель . Все еще не идеально (учитывали ли мы потраченное впустую пространство, потому что мы не могли аккуратно упаковать вещи и т. д.), но лучше.

Итак, модель не является реальностью, но должна быть достаточно хороша, чтобы быть полезной.

Игра с моделью

Теперь у нас есть модель, мы можем использовать ее по-разному:

Пример: Ваша компания использует коробки размером 200x300x400 мм, толщина картона 5 мм.

Кто-то предлагает использовать картон толщиной 4 мм… насколько это лучше?

Сравним два объема:

Текущий объем = (200-2×5) × (300-2×5) × (400-2×5) = 21 489 000 мм ³
Новый объем = (200-2×4) × (300-2×4) × (400-2×4) = 21,977 088 мм ³

Это изменение:

(21 977 088-21 489 000)/21 489 000 ≈ 2% больше объема

Значит модель полезная . Это дает нам понять, что мы получим на 2% больше места внутри коробки (при тех же внешних размерах).

Но есть еще вещи «реального мира», о которых нужно подумать, например, «достаточно ли он силен?»

Мыслить ясно

Чтобы построить математическую модель, мы также должны ясно мыслить о фактах!

Пример: на нашей улице собак вдвое больше, чем кошек.

Как мы запишем это в виде уравнения?

Пусть D = количество собак
Пусть C = количество кошек

Теперь… это: 2D = C

или должно быть: D = 2C

Теперь хорошенько подумайте!

Правильный ответ: D = 2C

( 2D = C — распространенная ошибка, так как вопрос написан «дважды… собаки… кошки»)

Вот еще один:

Пример: Вы начальник восьмичасовых сменных рабочих. Недавно они сократили время перерыва на 10 минут, но общая производительность не улучшилась.

На первый взгляд моделировать нечего, так как изменений в производстве не было.

Но подождите минутку… они работают на 10 минут больше, но производят столько же, так что производительность в час , должно быть, упала!

Допустим, они работали 7 часов (420 минут):

Изменение производительности в час = 410/420 = 0,976…

сокращение более чем на 2%

время перерыва, так что это может быть сокращение на 4 или 5% позже в течение смены.

Вы могли бы порекомендовать:

просмотр производительности за каждый час смены
попробовать изменить время перерыва, чтобы увидеть, как это повлияет на производительность

Большой пример: самый экономичный размер

Хорошо, давайте попробуем построить и использовать математическую модель для решения реального вопроса.

Ваша компания собирается делать коробки своими руками!

Было решено, что ящик должен вмещать 0,02 м ³ (0,02 кубических метра, что соответствует 20 литрам) гаек и болтов.

Коробка должна иметь квадратное основание и двойную толщину сверху и снизу.

Картон стоит 0,30 $ за квадратный метр.

Вы сами выбираете наиболее экономичный размер.

Шаг первый: нарисуйте эскиз!

Это помогает набросать то, что мы пытаемся решить!

Основание квадратное, поэтому мы будем использовать букву «w» для обеих длин

Коробка имеет 4 стороны, двойные верх и низ.

Коробку можно вырезать вот так (но это, вероятно, сложнее):

Шаг второй: создание формул.

Игнорирование толщины для этой модели:

Объем = w × w × h = w ² ч

А нам говорят, что объем должен быть 0.02м ³ :

ш ² ч = 0,02

Площадь:

Площадь четырех сторон = 4 × ширина × в = 4wh

Площадь двойных вершин и оснований = 4 × w × w = 4w ²

Всего необходимо картона:

Площадь картона = 4wh + 4w ²

Шаг третий: создайте единую формулу стоимости

Нам нужна единая формула стоимости:

Стоимость = 0,30 $ × площадь картона

= 0,30 долл. США × (4wh + 4w ² )

И это стоимость, когда мы знаем ширину и высоту .

С этим может быть сложно работать… функция с двумя переменными.

Но мы можем сделать проще! Потому что ширина и высота уже связаны с объемом:

Объем = w ² ч = 0,02

… который можно переставить на …

ч = 0,02/ш ²

… и это можно ввести в формулу стоимости …

Стоимость = 0,30 долл. США × (4w× 0,02/w ² + 4w ² )

А сейчас стоимость напрямую связана с шириной только .

С небольшим упрощением получаем:

Стоимость = 0,30 долл. США × (0,08/нед. + 4 нед. ² )

Шаг четвертый: начертите и найдите минимальную стоимость

Что чертить? Что ж, формула имеет смысл только для ширины больше нуля, и я также обнаружил, что для ширины больше 0,5 стоимость становится все больше и больше.

Итак, вот график этой формулы стоимости для ширины от 0,0 м до 0,55 м :

Участок y= 0,3(0,08/x+4x ² )
x — ширина, а y — стоимость

Просто на глаз вижу, что стоимость достигает минимума примерно на (0,22, 0,17) . Другими словами:

при ширине около 0,22 м (значение x),
минимальная стоимость около 0,17 $ за коробку (значение Y).

На самом деле, глядя на график, ширина может быть где угодно между 0,20 и 0,24 без существенного влияния на минимальную стоимость.

Шаг пятый: рекомендации

Используя эту математическую модель, теперь вы можете рекомендовать:

Ширина = 0,22 м
Высота = 0,02/ш ² = 0,02/0,22 ² = 0,413 м
Стоимость = 0,30 долл. США × (0,08/нед. + 4 нед. ² ) = 0,30 долл. США × (0,08/0,22+ 4 × 0,22 ² ) = 0,167 долл. США

Или около 16,7 цента за коробку

Но подойдет любая ширина от 0,20 м до 0,24 м.

Вы также можете предложить улучшения для этой модели:

Включая стоимость клея/скоб и сборки
Учитывайте отходы при вырезании формы коробки из картона.
Подходит ли эта коробка для упаковки, транспортировки и хранения?
Любые другие идеи!

Предсказание будущего

Математические модели также можно использовать для прогнозирования будущего поведения.

Пример. Компания по производству мороженого отслеживает, сколько мороженого продается в разные дни.

Сравнивая это с погодой в каждый день, они могут построить математическую модель продаж по сравнению с погодой .

Затем они могут прогнозировать будущие продажи на основе прогноза погоды и решать, сколько мороженого им нужно приготовить … заранее!

Компьютерное моделирование

Математические модели могут быть очень сложными, поэтому математические правила часто записываются в компьютерные программы для создания компьютерной модели.

Поиграйте с простой компьютерной моделью отражения внутри эллипса
или с анимацией одиночного маятника или двойного маятника.

Более сложные примеры включают:

Прогноз погоды
Экономические модели (прогнозирование процентных ставок, безработицы и т. д.)
Общественное здравоохранение и инфекционные заболевания
Модели того, как большие конструкции ведут себя под нагрузкой (мосты, небоскребы и т. д.)
Еще много…

Если вы станете экспертом в любой из них, у вас будет работа на всю жизнь!

Полное руководство по математическому моделированию — академическое письмо EaseMyPhD

6 сентября 2020 г. 22 сентября 2020 г.

Философия моделирования

Моделирование — это умственная деятельность, которая позволяет нам думать и создавать модели для описания того, как ведут себя различные объекты, люди и устройства. Затем эти модели используются для извлечения более сложной информации. Модель — это перевод идеи или явления в форму, облегчающую понимание. Например, в школах учителя показывают муляж скелета человеческого тела для обучения анатомии человека. С помощью скелета в качестве модели становится легче находить ребра, пояса и другие части тела, которые иначе были бы скрыты в мире за нашей кожей. Пластическая модель дыхательной системы человека, арбузная аналогия атомов Томсона, ядро в виде капли жидкости — все это прекрасные примеры усилий человека по упрощению сложных проблем.

Математика — это точный и четкий язык природы. Это помогает нам сформулировать наши убеждения и идеи и доказать предположения. Он действует как цемент между нашими убеждениями или идеями и реальными явлениями.
Математика — это краткий язык с четко определенными правилами манипулирования.
Математика — это наука, изучающая логику формы, количества и качественного распределения.
Чистые математики доказывают теоремы, а прикладная математика строит теории.
Идея прикладной математики в создании методов решения научных задач. Современные области прикладной математики включают математическую физику, математическую биологию и математические финансы.
Обычная методология в прикладной математической науке состоит в том, чтобы создать научную модель подлинного чуда, изучить модель и внести предложения по улучшению исполнения.

Математическая модель — это способ представления экспериментальных результатов и природных явлений на математическом языке для описания поведения системы. Он широко используется в естественных науках и инженерных дисциплинах (физика, химия, биология и вся инженерия), а также в науках о социальном развитии, таких как социология, наука об окружающей среде и экономика. Представление доказательств реальных явлений имеет много преимуществ.

Теперь давайте перейдем к нашему девизу математического моделирования. Процесс разработки модели с использованием математических инструментов называется математическим моделированием. Чтобы создать математическую модель, мы должны пройти определенную процедуру, которая сделает нашу модель правильной.

Чтобы построить точную и достижимую математическую модель, мы должны следовать следующей процедуре.

1. Решение проблемы

Основная задача при построении любой математической модели состоит в том, чтобы решить вашу проблему. Проблема — это сложная задача, потому что, если вы решите свою проблему, вы пройдете почти 30% пути математического моделирования. Так что тщательно запишите основные ключевые факторы, на которых вы должны сосредоточиться.

Просмотрите краткую литературу

Прежде всего, вы знаете все о явлениях или экспериментах. Укажите некоторые важные детали наблюдений. Попытайтесь найти какие-либо выводы, о которых сообщалось до вас. Собираем все вместе и обдумываем свои наблюдения.

Найдите то, что вы хотите знать

После обзора литературы вы должны решить, чего вы не будете знать. Это означает, что вы хотите знать некоторые мелкие детали о ваших наблюдениях. Эти мелкие детали приводят к вашей проблеме.

Уже то, что вы знаете

Постарайтесь указать, что вы знаете о своих наблюдениях из своего прошлого учебного опыта и недавнего обзора литературы. Потому что это играет важную роль в решении проблемы.

после выполнения всех трех шагов. Собирает все знания, которые вы получили в результате трех предыдущих шагов, в одном месте. И теперь решить проблему немного проще. Потому что без этих трех шагов вы одалживаете в другом месте. Скажем, вы решили, не выполнив эти шаги, в промежуточном путешествии вы обнаружите, что это невозможно или уже сделано. Так что идите шаг за шагом.

2. Сделайте предположения

Следующим важным шагом после решения вашей проблемы будет создание предположения для вашей модели. Потому что в природе все идеально, а в наших экспериментах все не идеально. Таким образом, чтобы увидеть вашу модель в реальном мире, вы должны сделать предположения, которые отображают вашу модель в определенных границах.