Делитель и делимое что это: Деление чисел. Делимое, делитель, частное

правила, примеры, как делить целые числа, деление нуля на число

Данная статья рассказывает о том, как делить без остатка целые числа, то есть нацело. Будут введены термины и обозначения для дальнейшего описания чисел, деление положительных и отрицательных чисел. В итоге произведем проверку вычислений.

Термины и обозначения

При делении целых чисел используются те же термины, что и при описании натуральных чисел.

Определение 1

Делимое – это число, над которым совершают деление.

Делитель – число, на которое делят.

Частное – результат деления.

Знак деления обозначают двоеточием «:» или знаком ÷. Его расположение после делимого и перед делителем. Запись с использованием символов выглядит так: a:b. Результат записывается после знака равно «=». Если при делении числа а на b получаем с, тогда запись выглядит в виде равенства a:b=c. Деление иначе называют частным.

Деление целых чисел

Между умножением и делением натуральных чисел существует связь. Это связано с тем, что при делении можно найти частное, которое при обратном действии будет считаться множителем. Иначе можно записать, что деление целых чисел служит нахождением одного из целых множителей.

Отсюда делаем вывод, что произведение целых чисел a и b с частным, равным с, можно представить обратным действием деления с на b  с частным равным а. Если произведение чисел 5 и -7 равна -35, отсюда имеем, что частное (−35):5 равняется -7, а (−35):(−7) с результатом 5.

Частное от деления считается целым тогда, когда получается результат без остатка, то есть целое число a должно делиться на число b с целым частным в результате.

Правила деления целых чисел

Смысл деления необходим для утверждения того, что одним из двух множителей является частным, а другой просто множителем. Таким образом не найти неизвестный множитель, имея известный множитель  и произведение. Равенство 6·(−7)=−42 говорит о том, что результаты  (−42):6 и (−42):(−7) равняются -7 и 6 соответственно. При известном произведении 45, а одного из множителей -5, то смысл деления не даст прямого результата другого множителя.

Можно сделать вывод, что необходимо использовать правила, которые позволяют производить деление целых чисел. Они позволят делить целые и натуральные числа.

Деление целых положительных чисел

Целыми положительными числами называют натуральные числа, поэтому деление целых положительных чисел производится, исходя из правил деления натуральных чисел. Рассмотрим несколько примеров для детального просмотра деления целых положительных чисел.

Пример 1

Произвести деление целого положительного 104 на целое положительное 8.

Решение

Для упрощения процесса деления можно представить число 104 в виде суммы 80+24,теперь необходимо применить правило деления суммы на данное число. Получим 104:8=(80+24):8=80:8+24:8=10+3=13.

Ответ: 104:8=13.

Пример 2

Найти частное от деления 308 716:452.

Решение

Когда имеем большое число, деление лучше всего производить в столбик:

Ответ: 308 716:452=683.

Правило деления целых отрицательных чисел, примеры

Для формулировки правила необходимо применить рассуждения. Если необходимо поделить целые отрицательные числа a на b, то искомое частное получится равным с. Форма записи: a:b=c. После чего можно выяснить, чему равна абсолютная величина с.

Исходя из смысла деления равенство b·c=a справедливо. Значит, b·c=a. Благодаря свойствам модуля, можно записать равенство b·c=b·c, значит, и b·c=a. Отсюда получаем, что c=a:b. Абсолютная величина частного от деления равняется частному от деления модулей делимого и делителя.

Для определения знака числа с необходимо выяснить, какие знаки находятся перед делимым и делителем.

Исходя из смысла деления целых чисел, равенство b·c=a справедливо. Правило умножения целых чисел говорит о том, что частное должно быть положительным. Иначе, b·c будет производиться по правилам целых отрицательных чисел. Частное с от деления целых отрицательных целых чисел является положительным числом.

Объединить в правило деления: чтобы разделить целое отрицательное число на отрицательное, необходимо разделить делимый на делитель по модулю. Эта запись будет выглядеть так a:b=a:b, при а и b равными отрицательным числам.

Рассмотрим несколько примеров деления отрицательных чисел.

Пример 3

Разделить -92 на -4.

Решение

Используя правила деления целых отрицательных чисел, получим, что следует делить по модулю. Получим, что -92:-4=-92:-4=92:4=23

Ответ: (−92):(−4)=23.

Пример 4

Вычислить -512: (-32).

Решение

Для решения необходимо разделить числа по модулю. Деление производится столбиком.

Ответ: (−512):(−32)=16.

Правило деления целых чисел с разными знаками, примеры

Выделим правило деления целых чисел, содержащих разные знаки.

Если делим целое числа a и b с разными знаками, то получаем число с.  Необходимо определить знак получаемого числа. Следует записать c=a:b.

Чтобы определить смысл деления равенства b·c=a, необходимо рассмотреть два варианта. Предположительно существует вариант, когда а – отрицательное, b – положительное или а – положительное, а b – отрициательное. Любой из случаев в итоге имеет отрицательный результат. Следуя из правил умножения, имеем, что b и с отрицательные, тогда произведение будет являться положительным. Если b положительное, с – отрицательное, тогда произведение является отрицательным числом.

Для формулировки применимо правило деления целых чисел с разными знаками. Отсюда получим: чтобы разделить целые числа с разными знаками, необходимо разделить делимое на делитель по модулю, перед полученным результатом поставить «-». Получаем, что a и b являются целыми числами с разными знаками. Это запишем, как a:b=-a:b.

Детально разберем примеры, где необходимо применить правило деления целых чисел с разными знаками.

Пример 5

Разделить 56 на -4.

Решение

Исходя из правила, имеем, что 56 необходимо разделить на 4 по модулю. Значит, получим, что 56:4=14. Для определения знака результата необходимо посмотреть наличие «-» перед делителем и делимым. Если имеется только один знак минуса, то результат запишем как отрицательное значение. То есть, -14.

Ответ: 56:(−4)=−14.

Пример 5

Выполнить деление -1625 на 25.

Решение

Данный пример показывает правильное деление целых чисел с разными знаками. Для этого необходимо применить правило 

-1625:25=—1625:25=-1625:25=-65

Деление числа 1625 можно производить в столбик или с помощью представления его в виде суммы 1500+125, применив правило деления полученной суммы на число.

Ответ: (−1 625):25=−65.

Деление нуля на целое число

Деление нуля на любое целое число рассматривается как отдельная тема, так как имеет свои нюансы. По правилу частное от деления на любое целое число, отличное от нуля, равно нулю. Иначе можем записать, что 0:b=0, где значение числа b отлично от нуля.

Для углубления в правило рассмотрим некоторые пояснения.

Допустим, что результат деления нуля на целое число равен с, тогда равенство b·c=0 считается верным. Произведение в итоге дает ноль тогда, когда хотя бы один из них равен нулю. Если по условию b не равно нулю, тогда множитель с=0. Отсюда следует, что  частное, полученное делением нуля на целое число, отличное от нуля, равняется нулю.

Например, при делении нуля на целое число, частное получаем равное нулю: 0:4 или 0:-908. Оба результаты будут равны нулю.

Не делить на нуль

Деление целого числа на нуль не определяется, поэтому и запрещено производить деление на 0.

Например, если при делении целого числа а на ноль получим число с, то из смысла деления должно быть справедливо равенство c·0=a. Правило умножения на нуль говорит о том, что c·0=0 при любом значении с. Сравнивая оба равенства, получим, что, если делимое анне равно нулю, тогда равенство c·0=a считается неверным. Поэтому можно делать вывод о том, что деление на нуль производить нельзя.

Возможно ли деление нуля на самого себя? Допустим, что при делении получаем целое число с, тогда равенство c·0=0 должно быть верным. Оно считается действительным при любом значении с. Результат деления 0 на 0 принимается любое значение. Для уменьшения многозадачности данный вариант не рассматривается.

Проверка результата деления целых чисел

Проверку осуществляют умножением. Чтобы произвести проверку деления, нужно полученное частное умножить на делитель, если  в результате получается число, равное делимому, тогда результат считается правильным.

Рассмотрим на примере решение с проверкой результата.

Пример 6

Результат деления 72 на -9 равен -7. Произвести проверку данного выражения.

Решение

Выполняем проверку деления. Необходимо произвести умножение полученного частного и делителя, то есть (−7)·(−9)=63. Проверка показала, что 63 отлично от 72, значит действие выполнено неверно.

Ответ: деление выполнено неверно.

что такое, чем отличаются друг от друга, как найти, примеры решения

Что такое делители и кратные числа

Определение 1

Деление — математическое действие, которое определяет, сколько раз одно число содержится в другом. Обратной операцией является умножение.

Выделяют следующие компоненты деления:

• делимое;
• делитель;
• частное.

Определение 2

Делимое — число, которое делят на несколько частей.

Делитель — число, которое показывает, на сколько частей нужно разделить делимое.

Частное — число, которое является результатом деления.

a:b=c, где a — делимое, b — делитель, c — частное.

Умножение частного на делитель дает делимое.

Чтобы получить делитель, нужно делимое разделить на частное.

Делимое = частное * делительДелитель = делимое / частное

Пример 1

Например, нужно поровну разделить 16 мандаринов между двумя детьми. Для этого 16:2=8. Таким образом, каждый ребенок получит по 8 мандаринов.

16 в этом примере является делимым, 2 — делителем, 8 — частным. Шестнадцать поделили на две части, по восемь в каждой. Или восемь содержится в 16 два раза. Или 2 содержится в 16 восемь раз. Деление прошло без остатка — нацело. Тогда число 2 является делителем числа 16.

Определение 3

Делителем числа a называется такое число b, на которое a делится нацело.

Пример 2

Например, 9:4=2 (остаток 5).

В примере 9 — делимое, 4 — делитель, 2 — неполное частное, 5 — остаток.

Остаток от деления — число, которое меньше делителя. Образуется при делении с остатком. Значит, в примере 9:4=2 (остаток 5) — число 4 не является делителем числа 9.

Упражнение 

Задание: найдите такую пару делителей числа 144, если один из делителей равен 2.

Объяснение:

Пусть неизвестный делитель равен x. Чтобы найти еще один делитель, если какой-то известен, нужно данное нам число разделить на известный делитель.

Тогда представим решение данной задачи в виде уравнения:

144:x=2;x=144:2;x=72.

72 — целое число, без остатка.

Проверка:

Произведение делителей должно дать в результате 144:

72*2=144 — верно, значит, 72 — корень уравнения и делитель 144.

Ответ: числа 2 и 72 — делители 144.

Определение 4

Число называют кратным, если оно делится на данное число нацело, без остатка.

Пример 3

Например, 15:3 нацело.

15:3=5.

Тогда число 15 является кратным 3.

Пишут: 15 кратно 3.

Слово «кратно» синонимично слову «делится».

Фразу «15 кратно 3» можно в уме заменить на «15 делится на 3 нацело».

Примечание 1

15 делится накратно 3.

Основные понятия и определения

Определение 5

Делитель — это число, на которое данное число делится нацело. Делитель всегда меньше или равен числу.

Делится нацело = без остатка.

Наименьшим делителем любого числа является единица.

Наибольшим делителем числа является само число.

Делителем нуля будет любое число, но сам 0 делителем не будет.

При делении нуля на любое число получаем 0. А делить на ноль нельзя.

У единицы только один делитель — единица.

Другие числа, кроме 1, имеют не меньше двух делителей.

Определение 6

Кратное — число, которое делится на данное число нацело. Всегда больше или равно числу.

Наименьшее кратное числа является равным самому числу.

Наибольшее кратное подобрать нельзя, потому что ряд натуральных чисел бесконечен. У любого натурального числа бесконечное множество кратных.

Ноль является кратным для любого числа. При умножении на ноль всегда получается ноль.

Когда одно число делится нацело на другое, то первое число — кратное второго, а второе — делитель первого.

Примечание 2

a:b=c, где a — кратное b и b — делитель a.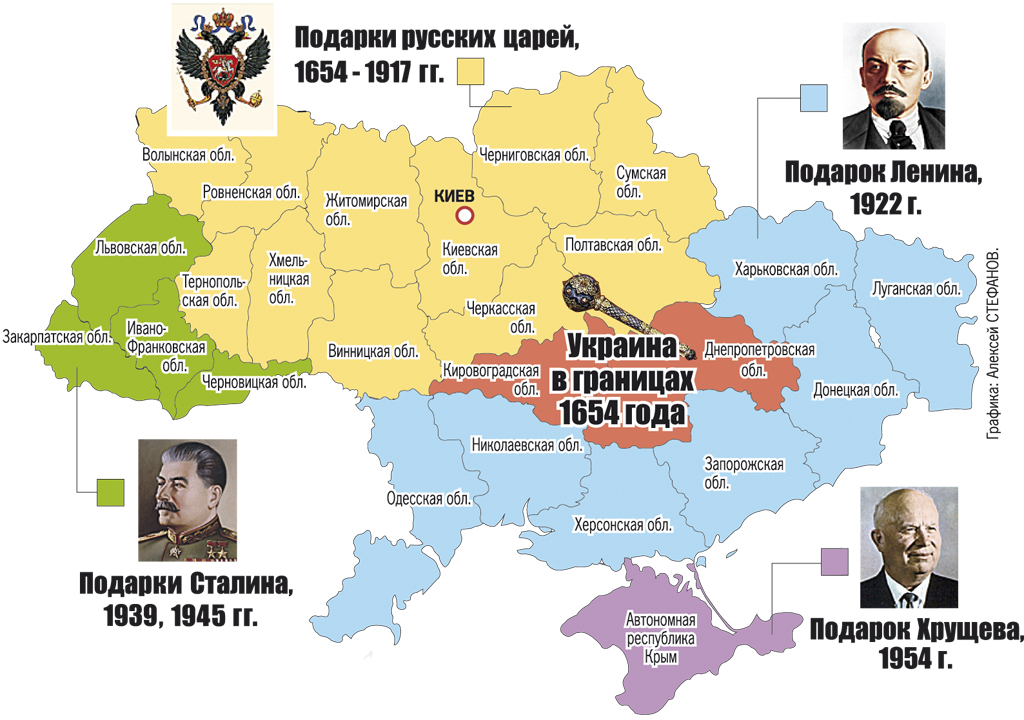

Чем отличаются друг от друга, как найти

Делитель отличается от кратного тем, что:

• делитель — это число, НА которое делится заданное число;
• кратное — это число, которое само ДЕЛИТСЯ НА заданное число.

Чтобы найти делители числа, нужно данное число разложить на множители.

Разложить на множители — представить число в виде произведения целых чисел.

Чтобы проверить, является ли одно число делителем другого, нужно разделить число на данное нам.

Для нахождения кратного числа заданному числу, нужно это число последовательно умножать на натуральные числа. Каждое полученное число будет кратно — будет делиться — заданному.

Делители и кратные связаны между собой. Например, делителем числа 15 является 3 и число, кратное 3, равно 15.

Примеры решения задач

Задача 1

Необходимо найти делители числа 14.

Решить задание можно двумя способами.

Способ 1:

Последовательно делим 14 на натуральные числа от 1 до 14. Помним, что делитель всегда меньше или равен заданному числу.

14:1=14;14:2=7;14:3=4 (остаток 2);14:4=3 (остаток 2);14:5=2 (остаток 4);14:6=2 (остаток 2);14:7=2;14:8=1 (остаток 6);14:9=1 (остаток 5);14:10=1 (остаток 4;)14:11=1 (остаток 3);14:12=1 (остаток 2);14:13=1 (остаток 1);14:14=1.

Выбираем такие числа в качестве делителя, при делении на которые мы не получили остаток: 1, 2, 7, 14.

Ответ: делители числа 14: 1, 2, 7, 14.

Способ 2:

Представим 14 в виде произведения чисел:

14=14*1=2*7

Делителями будут множители, так как можем разделить 14 нацело на каждый из них.

Ответ: делители 14: 1, 2, 7, 14.

Задача 2

Найдите три числа, кратных 7.

Решение:

Чтобы найти число, кратное данному, нужно это число умножить на любое натуральное число.

7*1=7  — семь кратно семи;

7*2=14 — 14 кратно 7;

7*3=21  — 21 кратно 7.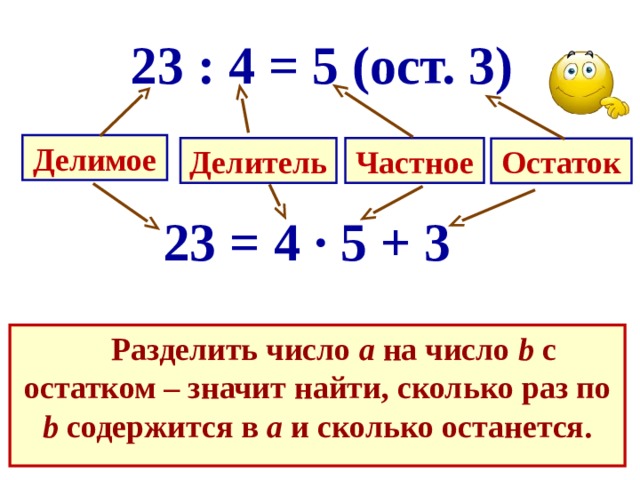

Ответ: числа, кратные 7: 7, 14, 21.

Задача 3

Самостоятельно проверьте, 225 кратно 3 или нет.

Чтобы проверить, кратно ли одно число другому, нужно разделить числа друг на друга.

225:3=75.

75 — целое число, при делении нет остатка. Тогда 225 кратно 3.

Задача 4

Найдите любое число, делителями которого являются числа 7 и 8.

Самый простой способ, если в задании не оговорены еще какие-либо условия, просто перемножить эти делители:

7*8=56.

Ответ: 56.

Делитель, делимое, частное и остаток

Формула делимого-частного показывает соотношение между делимым, делителем, частным и остатком, что является одним из основных аспектов деления. Деление — это процесс деления числа на равные части с сохранением остатка, если число нельзя разделить дальше. Формула частного остатка от деления является важным правилом при делении. Давайте узнаем больше об этих концепциях впереди!

Части подразделения

Что такое остаток от делителя дивиденда?

• Делитель

Делитель — это число, на которое при расчете делится другое число. Определение делителя гласит, что это термин, выполняющий операцию деления делимого. Например, когда мы делим число 28 на число 7, 7 называется делителем, а число 28 называется делимым.

Формула для делителя = (дивиденд — остаток) ÷ частное

• Дивиденд

Дивиденд – это целое число или количество вещей, которые необходимо разделить на определенные равные части. Делимое – это число, которое нужно разделить на делитель.

Формула для Делимого = Делитель x Частное + Остаток

• Частное

При делении двух чисел результат их деления, называемый частным, будет целым числом. Если два числа не имеют остатка при делении, они называются «совершенными» делителями, а их частное является их «произведением».

Формула Частное = Дивиденд ÷ Делитель.

• Остаток

В математике остаток — это сумма, «оставшаяся» после выполнения некоторых вычислений. В арифметике остаток — это целое число, «оставшееся» после деления одного целого числа на другое для получения целочисленного частного.

Формула для Остаток = делимое — (делитель × частное)

Например, 75 разделить на 9 дает 8 в частном и 3 в остатке.

Делитель, делитель, частное и остаток

Где в математике используются делитель, делитель, частное и остаток?

Делитель используется в десятичной системе для преобразования десятичного числа в дроби. Частное используется при умножении двух целых чисел: например, 4×5=20, которое было упрощено из $4 \times 5=20\Rightarrow \dfrac{(4 \times 10)}{2}$.

Решенные примеры

Q 1 Разделите 217 на 4.

Ответ: $\dfrac{217}{4}$

Здесь, Делимое = 217

Делитель = 4

Частное = 54

Остаток = 1

Q 2 Найдите остаток, если делимое равно 75, делитель равен 5, а частное равно 15.

s

делимое = 75, делитель = 5, частное = 15 и пусть остаток равен х

75 = 5 × 15 + х

75 = 75 + х

х = 75 — 75

х = 0

Следовательно, используя формулу, мы получили остаток, который равен 0. Остаток = 0

Q 3 Найдите остаток, если делимое равно 63, делитель равен 2, а частное равно 31.

Ответ: Дано, делимое = 63, делитель = 2, частное = 31 и пусть остаток равен x

63 = 2 × 31 + x

63 = 62 + x

x = 63 — 62

x = 1

Q 4 Разделите 5679 на 7.

Ответ: $\dfrac{5679}{7}$

3, 9 Делимое = 5679

Делитель = 7

Частное = 811

Остаток = 2

Q 5 Найдите остаток, если делимое равно 57, делитель равен 8, а частное равно 7.

Ответ: Дано, делимое = 75, делитель = 5, частное = 15 и пусть остаток равен х

57 = 8 × 7 + х

57 = 56 + х

х = 57 -56

х = 1

Следовательно, используя формулу, мы получили остаток, равный 1. Остаток =1

Практические вопросы

Q 1 Разделите 120 на 5 и найдите частное и остаток.

Ответ: Частное = 24

Остаток = 0

Q 2 Найдите делимое, если остаток равен 1, делитель равен 3, а частное равно 31.

Ответ: Делимое = 94

Q 3 Найдите остаток, если делимое равно 55, делитель равен 3, а частное 18.

Ответ: Остаток = 1

Суммарно разделенное здесь называется дивидендом. Число, которое делит данное число, является делителем. Кроме того, число, которое мы получаем в результате, известно как частное. Делитель, который не делит число полностью, дает число, которое называется остатком. Теперь мы надеемся, что у вас есть четкое представление о

делитель, делимое, частное и остаток .

Узнать определение, формулу и примеры

0

 Сохранить

Скачать публикацию в формате PDF

Делимое, делитель и частное — три компонента операции деления. Начальное делимое число называется делимым, делимое число — делителем, а результат — частным.

В этой статье по математике мы подробно рассмотрим делимое, делитель, частное, остаток и соответствующий решенный пример.

Частное делителя делителя

Фразы делимое, делитель, частное и остаток используются при делении одного целого числа на другое.

Дивиденд: значение, которое делится на другое значение для получения результата, называется дивидендом.

Делитель: Делитель — это число, которое полностью или частично делится на другое число.

Частное: результатом деления двух чисел является частное.

На приведенном выше рисунке 20 — делимое, 4 — делитель и 5 — частное.

Остаток делителя делителя

Число, разделенное на делитель, называется делимым. Элемент, который делит делимое, называется делителем. Число, оставшееся после деления, называется остатком, а результат, полученный в процессе деления, известен как частное. Метод деления дает формулу остатка частного делителя делимого.

Связь между делителем делимого и остатком

Связь между делимым, делителем, частным и остатком — один из ключевых компонентов деления показана формулой делителя делителя и остатка.

Формула объясняет, как эти четыре члена операции деления соотносятся друг с другом.

\( Делимое = делитель \умножить на частное + остаток\)

Когда указаны только делитель, частное и остаток, делимое может быть определено с использованием этого соотношения или может использоваться для подтверждения процесса деления.

Вывод формулы остатка от делителя дивиденда

Результат метода деления можно проверить с помощью формулы остатка от делителя дивиденда. Обычно, когда мы делим одно число на другое, мы получаем такой ответ:

\( \frac{a}{b} = c\)

Где a = делимое

b = делитель

c = частное

Это также может быть выражено следующим образом:

\( \frac{Dividend }{Делитель} = Частное\)

\( Дивиденд = Делитель \множить Частное\)

А если после операции деления что-то осталось, то записывается так:

\( Делимое = Делитель \кратное Частное + Остаток\)

Узнайте больше о теореме об остатках.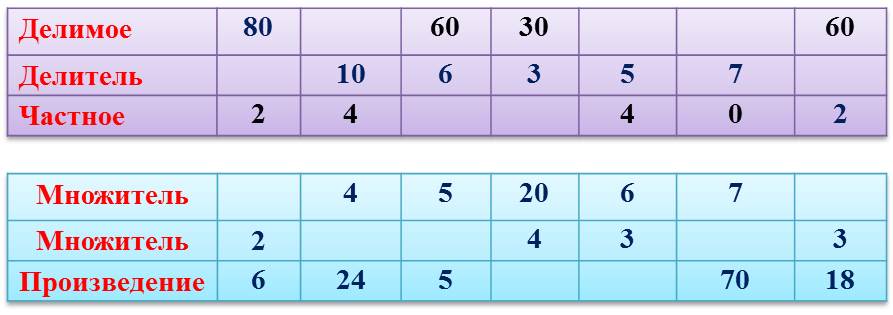

Запомнить

Важно помнить следующее:

• Целое число делится на части делителем.
• Термин «делитель» также используется для обозначения числа, на которое без остатка делится целое число.
• Делимое можно разделить полностью или частично на делитель. При делении числа пополам в остатке получается целое число, отличное от нуля, а при полном делении — в остатке ноль.

Узнайте больше о правиле частных.

Решенные примеры

Задача: 1 Если делитель равен 4, а частное равно 0,5, найдите делимое.

Решение:

Делитель = 4 , Частное = 0,5, Остаток = 0

\( Делимое = Делитель \умноженное на частное + остаток\)

\( Делимое = 4 \умноженное на 0,1 + 10 9 + 0,2 = 2

Задача: 2 Когда частное равно 15, делитель равен 5, а делимое равно 75, найдите остаток.

Решение:

Делимое = 75, Делитель = 5, Частное = 15

Остаток = 75 -75

Остаток = 0

Если вы хотите хорошо сдать экзамен по математике, то вы попали по адресу. Здесь вы получите еженедельную подготовку к тестам, живые уроки и серию экзаменов. Загрузите приложение Testbook прямо сейчас, чтобы подготовить умную и высокорейтинговую стратегию к экзамену.

Часто задаваемые вопросы о делителях и частных

В.1 Что происходит, когда в формуле остатка для делителей дивидендов используется ноль?

Ответ 1 Существует три результата использования нуля в формуле остатка частного делителя: Частное равно нулю, когда 0 делится на число. Ноль нельзя использовать в качестве оператора деления числа. Остаток равен нулю, если делимое можно разделить без остатка на делитель.

Q.2 Что означает формула остатка делителя дивиденда?

Ответ 2 Делимое, делитель, частное и остаток — это четыре ключевых компонента, которые составляют формулу остатка делителя делителя. \( Делимое = делитель \умножить на частное + остаток\)

Q.3 Является ли 1 простым делителем?

Ответ 3 1 не является простым делителем.