Дроби на координатной прямой. Задачи на дроби презентация, доклад
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Страхование
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация на тему Презентация на тему Дроби на координатной прямой. Задачи на дроби, предмет презентации: Математика. Этот материал содержит 14 слайдов. Красочные слайды и илюстрации помогут Вам заинтересовать свою аудиторию. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций ThePresentation.ru в закладки!
Задачи на дроби, предмет презентации: Математика. Этот материал содержит 14 слайдов. Красочные слайды и илюстрации помогут Вам заинтересовать свою аудиторию. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций ThePresentation.ru в закладки!
Дроби на координатной прямой.
Задачи на дроби.
Урок 92
Новости науки. Какие?
Что такое координатная прямая?
Начертите прямую.
Что нужно на ней обозначить?
Групповая работа:
На выданных координатных прямых выберите подходящее деление единицы на части в соответствии с указанным для вашей группы знаменателем .
Изобразите все возможные дроби с указанным для вашей группы знаменателем.
Лист с вашей координатной прямой закрепите на доске в указанном в задании порядке.
Сделаем выводы:
Из дробей выберите ту,
Объясните ваш выбор:
а) по правилу сравнения долей;
б) с помощью расположения этих дробей на координатной прямой.
Охарактеризуйте понятия правильной и неправильной дроби:
с помощью сравнения числителя со знаменателем у этих дробей;
с помощью расположения таких дробей на координатной прямой.
НАХОЖДЕНИЕ ДРОБИ ОТ ЧИСЛА
1. Найдите долю:
2.
Сформулируйте правило нахождения дроби от целого:
Сначала нужно найти…
то есть поделить…
Затем взять…
то есть умножить…
нужную долю от целого,
целое на знаменатель.
столько долей, каков числитель,
полученное число на числитель.
Самостоятельная работа в тетради с взаимопроверкой:
Вариант 1
Вариант 2
Решение задач на нахождение дроби от числа:
№ 485 (б)
№ 488
Самостоятельная работа на листочках…
…с которой вы, конечно, справитесь! ☺
Домашнее задание:
1) РТ — № 248, 249, 252, 253;
2) учебник — № 487;
3) тетради с домашними заданиями завтра принести!
Скачать презентацию
Обратная связь
Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: Нажмите что бы посмотреть
Что такое ThePresentation.
 ru?
ru?Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.
Для правообладателей
Десятичные дроби презентация, доклад
Метапредмет – Знак
ДЕСЯТИЧНЫЕ ДРОБИ.
Цель нашего урока
целеполагание
Мы продолжаем записывать дробные числа по-новому.
Но не ко всем обыкновенным дробям можно применить новую запись. Кто-нибудь догадался, к каким?
Эти дроби перед вами.
Полюбуйтесь ими сами.
В знаменателе, смотри –
Единица и нули.
Обсуждаем домашнее задание 117, 119, 120*
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.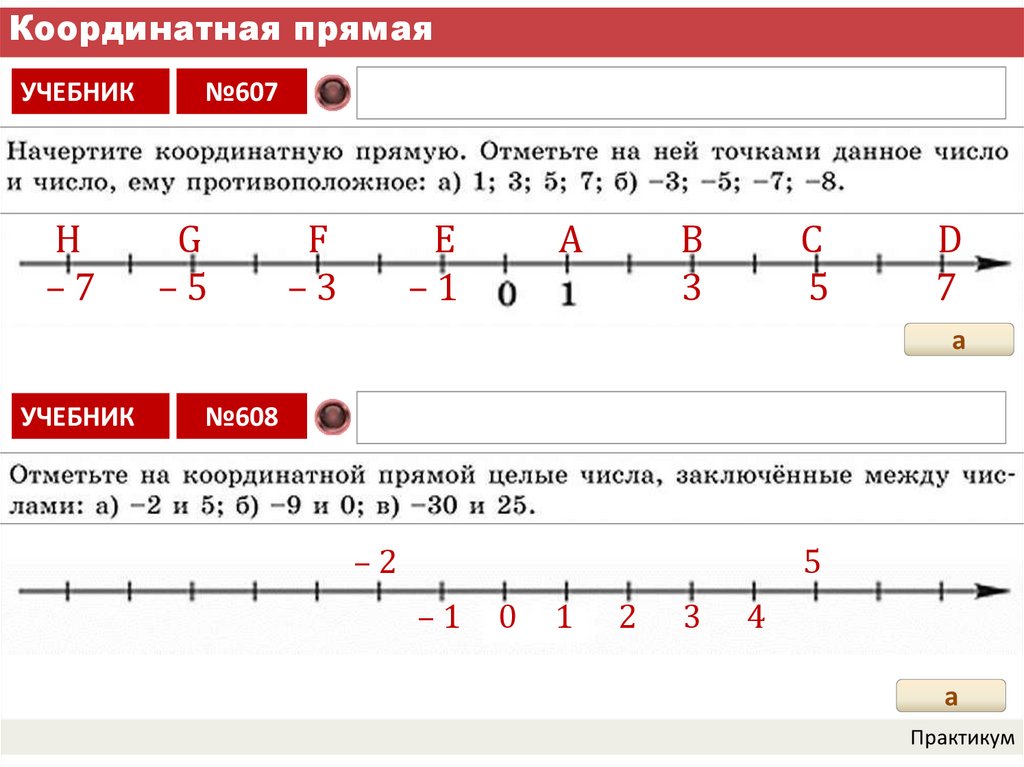
?
?
?
а) 0,1; 0,03; 0,007; 0,0002
б) 0,11; 0,027; 0, 0139; 0,00907.
?
а) 2,18; 5,03; 1,238; 8,008
б) 3,9; 18,7; 3,41; 1,002.
Группе гамма
Практикум
1,3;
1,03;
1,003;
0,11;
1,25;
10,08;
5,047;
7,105;
20,002;
Одна целая три десятых
Одна целая три сотых
Одна целая три тысячных
Ноль целых одиннадцать сотых
Одна целая двадцать пять сотых
Десять целых восемь сотых
Пять целых сорок семь тысячных
Семь целых сто пять тысячных
Двадцать целых две тысячных
Математическая разминка
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.
Почитайте десятичные дроби:
3,7
2,18
35,025
702,00032
0,00304
100,01002
0,008
Запишите ответы в тетрадь
Вхождение в тему урока и создание условий для осознанного восприятия нового материала.
Запишите десятичную дробь в виде обыкновенной дроби:
а) 0,3 =
0,33 =
0,333 =
0,033 =
б) 1,9 =
1,93 =
19,3 =
0,193 =
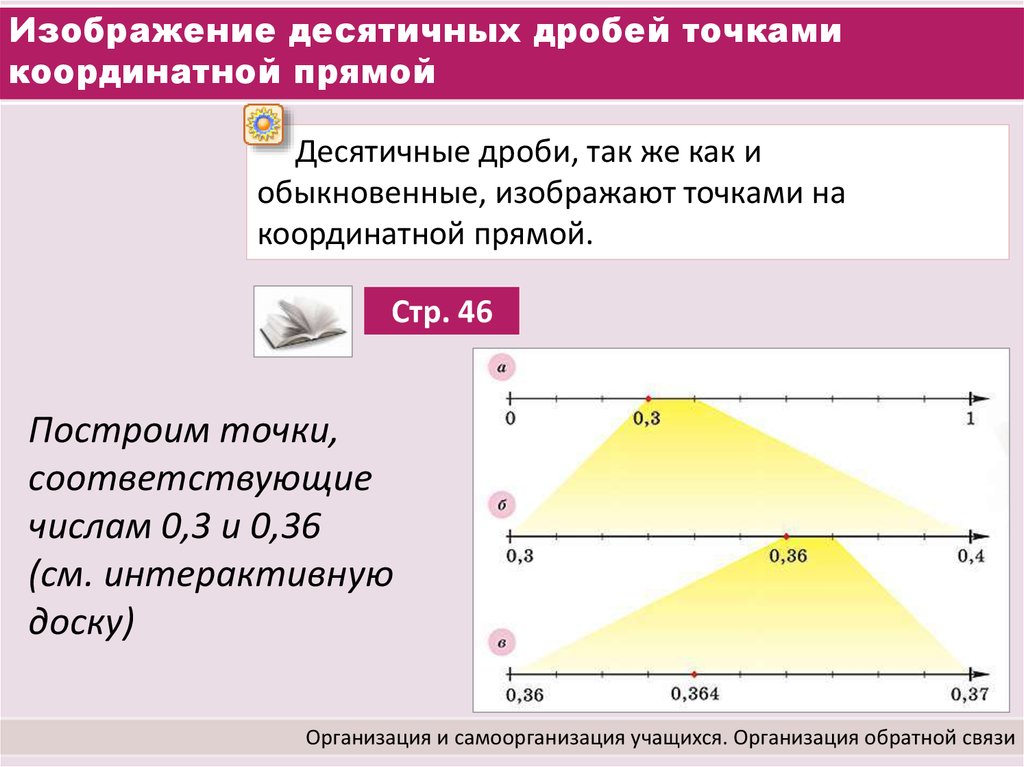
Изображение десятичных дробей точками координатной прямой
Организация и самоорганизация учащихся. Организация обратной связи
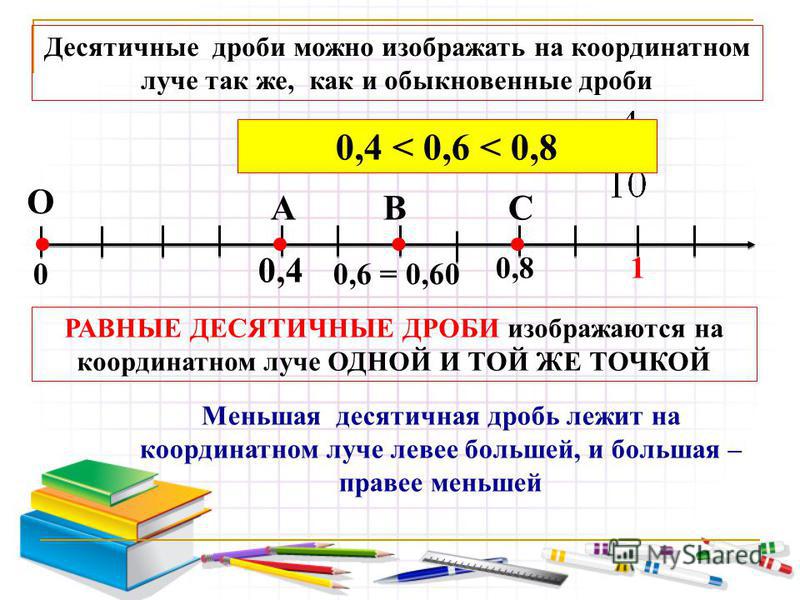
Десятичные дроби, так же как и обыкновенные, изображают точками на координатной прямой.
Построим точки, соответствующие числам 0,3 и 0,36
(см. интерактивную доску)
Работаем с моделями
Практикум
Работаем с моделями
Практикум
Работаем с моделями
Практикум
Работаем с моделями
Практикум
Домашнее задание
Подведение итогов, рефлексия, домашнее задание.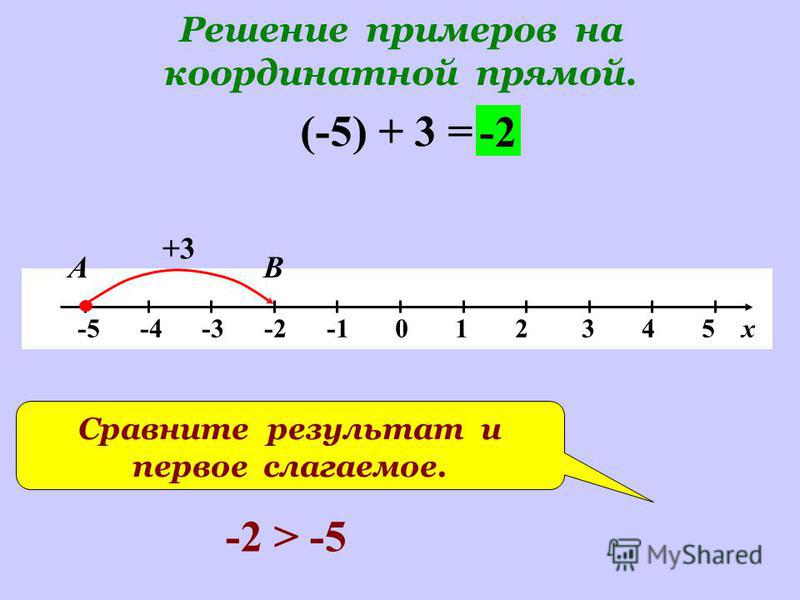
Домашнее задание
1) стр. 46, фрагмент 3 – читать;
2) № 121, 122, 123*, 120*.
Прямоугольная система координат и построение точек — Подготовка к оценке TSI
Прямоугольная система координат также известна как декартова система координат в честь Рене Декарта.
Прямоугольная система координат основана на сетке, и каждая точка на плоскости может быть идентифицирована уникальными координатами x и y , так же как любая точка на Земле может быть идентифицирована по ее широте и долготе.
Оси
Положения на сетке измеряются относительно фиксированной точки, называемой началом координат , и измеряются в соответствии с расстоянием вдоль пары осей.
Оси x и y подобны числовой прямой, с положительными расстояниями вправо и отрицательными влево в случае оси x , и положительными расстояниями вверх и отрицательными вниз для у ось.
Любое смещение от начала координат можно построить, переместив заданное расстояние в направлении x , а затем еще одно расстояние в направлении y .
Думайте об этом так, как если бы вы давали кому-то указания, говоря что-то вроде «Иди три квартала на восток, а затем 2 квартала на север».
Координаты, графические точки
Мы указываем местоположение точки, сначала задавая ее координату x (смещение влево или вправо от начала координат), а затем y координата (смещение вверх или вниз от начала координат). Таким образом, каждая точка на плоскости может быть идентифицирована парой чисел ( x , y ), называемых ее координатами .
Квадранты
Иногда мы просто хотим знать, о какой общей части графика мы говорим. Оси естественным образом делят плоскость на четверти. Мы называем эти квадрантов и нумеруем их от одного до четырех. Обратите внимание, что нумерация начинается в верхнем правом квадранте и продолжается против часовой стрелки. Заметьте также, что каждый квадрант можно идентифицировать по уникальной комбинации положительных и отрицательных знаков для координат точки в этом квадранте.
Обратите внимание, что нумерация начинается в верхнем правом квадранте и продолжается против часовой стрелки. Заметьте также, что каждый квадрант можно идентифицировать по уникальной комбинации положительных и отрицательных знаков для координат точки в этом квадранте.
Выше показана прямоугольная система координат , также называемая декартовой системой координат
Обратите внимание, что прямоугольная система координат состоит из 4 квадрантов , горизонтальной оси , вертикальной оси и начала координат . Горизонтальную ось обычно называют x – ось , а вертикальную ось обычно называют 9.0077 y – ось . Исходная точка — это точка пересечения двух осей.
Пример :
Нанесите на график каждую из следующих точек. А(-3,-1), В(0,4) и С(2,0).
Решение :
A(–3, –1): От исходной точки идите на 3 единицы влево, затем на 1 единицу вниз. Затем нанесите точку.
Затем нанесите точку.
B(0, 4) От исходной точки идите прямо вверх на 4 единицы.
C(2, 0) От начала координат пройдите на 2 единицы вправо и нанесите точку.
В каком квадранте находится точка (-2, 4)?
Найти расстояние от (-6, 1) до (-3, 5).
а. 6
б. 4
в. 5
д. 7
Из точек (-6, 1) и (-3, 5) составьте прямоугольный треугольник.
Найдите расстояние между горизонтальными и вертикальными отрезками.
Применим теорему Пифагора:0143 2
16 + 9 = c 2
25 = c 2
Расстояние от (-6, 1) до (-3, 5) равно 5 единицам.
Правильный ответ: c
В плоскости координат xy, в каком квадранте xy < 0?
a) II квартал
b) III квартал
c) IV квартал
d) II и IV квартал
а.
б. б
в. с
д. д
Квадранты нумеруются сверху слева против часовой стрелки.
В квадранте I значения x и y положительны. Следовательно, в Q I xy > 0.
Квадрант II: x отрицательный, y положительный, xy < 0
Квадрант III: x отрицательный, y отрицательный, xy > 0
Квадрант IV: x положительный, y отрицателен, xy < 0
xy < 0 в Q II и Q IV
Правильный ответ: d
0 из 0 верно.
Общий тест GRE. Количественное мышление. Обзор
.
Общий тест GRE ®
Один тест для выпускников, бизнес- и юридических школ
Выберите шаг, чтобы узнать больше о своем путешествии по общему тесту GRE ® .
Количественное мышление общего теста GRE оценивает ваши:
- базовые математические навыки
- понимание элементарных математических понятий
- способность рассуждать количественно, а также моделировать и решать задачи количественными методами.
Охватываемые области содержания
Некоторые из вопросов количественного мышления задаются в реальных условиях, тогда как другие задаются в чисто математических условиях. Многие из вопросов представляют собой «словные задачи», которые необходимо перевести и смоделировать математически. Навыки, концепции и способности оцениваются в четырех областях содержания, указанных ниже.
Многие из вопросов представляют собой «словные задачи», которые необходимо перевести и смоделировать математически. Навыки, концепции и способности оцениваются в четырех областях содержания, указанных ниже.
- Темы арифметики, в том числе:
- свойства и типы целых чисел, такие как делимость, факторизация, простые числа, остатки, нечетные и четные целые числа
- арифметические операции, показатели степени и корни
- такие понятия, как оценка, процент, отношение, скорость, абсолютное значение, числовая линия, десятичное представление и последовательность чисел
- Темы по алгебре, в том числе:
- операции с показателями
- разложение на множители и упрощение алгебраических выражений
- отношения, функции, уравнения и неравенства
- решение линейных и квадратных уравнений и неравенств
- решение одновременных уравнений и неравенств
- составление уравнений для решения текстовых задач
- координатная геометрия, включая графики функций, уравнения и неравенства, точки пересечения и наклоны линий
- Темы геометрии, в том числе:
- параллельные и перпендикулярные линии
- круга
- треугольники, включая равнобедренные, равнобедренные и треугольники с углами 30°-60°-90°
- четырехугольники
- другие полигоны
- конгруэнтные и подобные фигуры
- Трехмерные фигуры
- район
- периметр
- том
- теорема Пифагора
- измерение угла в градусах
Способность конструировать доказательства не проверяется.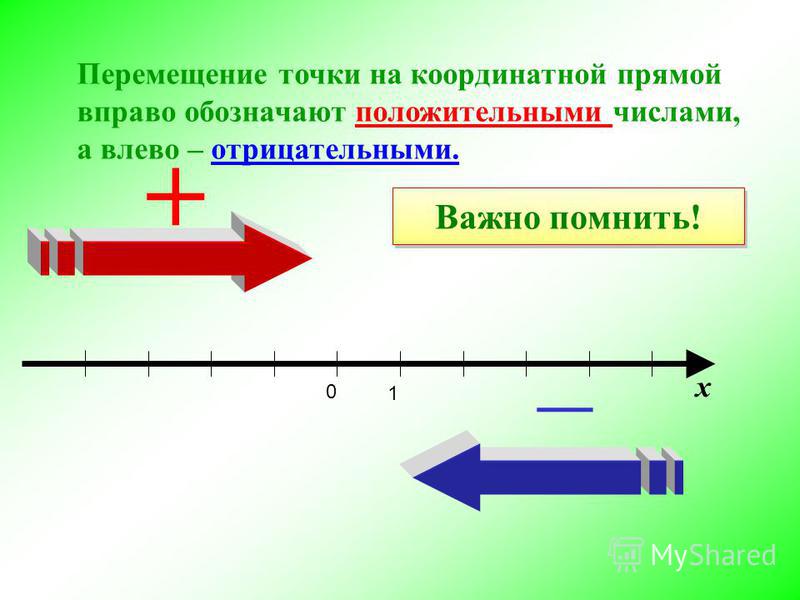
- Темы анализа данных , включая:
- основные описательные статистические данные, такие как среднее значение, медиана, мода, диапазон, стандартное отклонение, межквартильный диапазон, квартили и процентили
- интерпретация данных в таблицах и графиках, таких как линейные графики, гистограммы, круговые диаграммы, ящичные диаграммы, диаграммы рассеяния и частотные распределения
- элементарная вероятность, такая как вероятности составных событий и независимых событий
- условная вероятность
- случайные величины и распределения вероятностей, включая нормальные распределения
- методы подсчета, такие как комбинации, перестановки и диаграммы Венна
Эти темы обычно преподаются на курсах алгебры в средней школе или на вводных курсах статистики.
Логическая статистика не проверена.
Содержание в этих областях включает математику и статистику средней школы на уровне, который обычно не выше второго курса алгебры.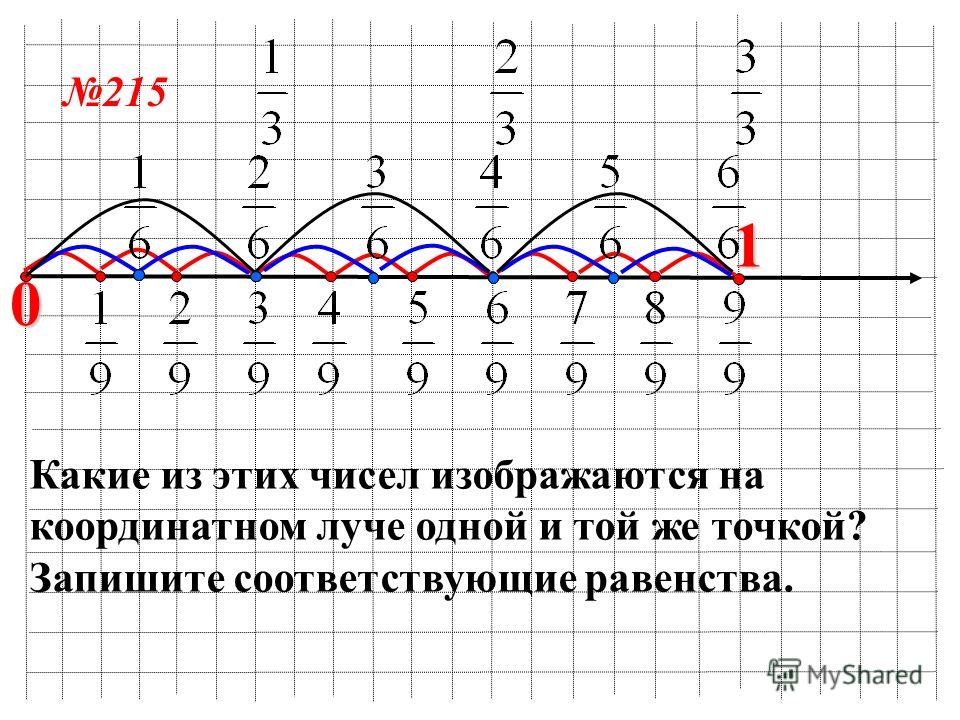 Он не включает тригонометрию, исчисление или другую математику более высокого уровня. В Math Review (PDF) предоставляется подробная информация о содержании меры количественного рассуждения.
Он не включает тригонометрию, исчисление или другую математику более высокого уровня. В Math Review (PDF) предоставляется подробная информация о содержании меры количественного рассуждения.
Символы, терминология, условные обозначения и допущения
Математические символы, терминология и условные обозначения, используемые в измерении количественного мышления, являются стандартными для старшей школы. Например, положительное направление числовой прямой — вправо, расстояния неотрицательны, а простые числа больше 1. Всякий раз, когда в вопросе используются нестандартные обозначения, они явно вводятся в вопросе.
Помимо условных обозначений, существуют некоторые важные предположения о числах и цифрах, которые перечислены в указаниях раздела «Количественное рассуждение»:
- Все используемые числа действительны.
- Предполагается, что все фигуры лежат в плоскости, если не указано иное.
- Геометрические фигуры, такие как линии, окружности, треугольники и четырехугольники, не обязательно изображаются в масштабе .
 Не предполагайте, что такие величины, как длины и угловые меры, представлены на рисунке. Однако следует исходить из того, что:
Не предполагайте, что такие величины, как длины и угловые меры, представлены на рисунке. Однако следует исходить из того, что:- линии, показанные прямыми, на самом деле являются прямыми
- точки на линии расположены в указанном порядке
- все геометрические объекты находятся в показанных относительных положениях
Ответы на вопросы с геометрическими фигурами следует основывать на геометрических рассуждениях, а не на оценке или сравнении величин визуально или путем измерения.
- Следующие являются нарисованными в масштабе. Вы можете считывать, оценивать или сравнивать количества и значения данных визуально или путем измерения:
- системы координат, такие как xy -плоскости и числовые линии
- графические представления данных, такие как гистограммы, круговые диаграммы и линейные диаграммы
Чтобы узнать больше об соглашениях и допущениях, загрузите Mathematical Conventions (PDF).
Типы вопросов и наборы для интерпретации данных
Мера количественного рассуждения включает четыре типа вопросов:
- Вопросы количественного сравнения
- Вопросы с несколькими вариантами ответов — выберите один вариант ответа
- Вопросы с несколькими вариантами ответов — выберите один или несколько вариантов ответа
- Числовые вопросы ввода
Каждый вопрос появляется либо независимо как отдельный вопрос, либо как часть набора вопросов, который называется набором интерпретации данных. Все вопросы в наборе интерпретации данных основаны на одних и тех же данных, представленных в таблицах, графиках или других формах отображения данных.
В этих вопросах вам предлагается сравнить две величины — количество A и количество B — и затем определить, какое из следующих утверждений описывает сравнение.
- Количество A больше.
- Количество B больше.
- Две величины равны.

- Отношение не может быть определено из предоставленной информации.
Советы по ответам на вопросы
- Ознакомьтесь с вариантами ответов . Вопросы количественного сравнения всегда имеют один и тот же вариант ответа, поэтому изучите их, особенно последний вариант: «Отношения не могут быть определены на основе предоставленной информации». Никогда не выбирайте этот последний вариант, если ясно, что значения двух величин могут быть определены вычислением. Кроме того, если вы определили, что одна величина больше другой, убедитесь, что вы тщательно выбрали соответствующий вариант и не меняете местами первые два варианта.
- Избегайте ненужных вычислений . Не тратьте время на ненужные вычисления для сравнения двух величин. Упростите, преобразуйте или оцените одну или обе заданные величины только по мере необходимости, чтобы сравнить их.
- Помните, что геометрические фигуры не обязательно рисуются в масштабе . Если какой-либо аспект данной геометрической фигуры не определен полностью, попытайтесь перерисовать фигуру, оставив фиксированными те аспекты, которые полностью определяются данной информацией, но изменив аспекты фигуры, которые не определены.
 Изучите результаты. Какие вариации возможны в относительных длинах отрезков или мер углов?
Изучите результаты. Какие вариации возможны в относительных длинах отрезков или мер углов? - Вставьте номера . Если одна или обе величины являются алгебраическими выражениями, вы можете заменить переменные простыми числами и сравнить полученные величины в своем анализе. Рассмотрите все виды подходящих чисел, прежде чем давать ответ: например, ноль, положительные и отрицательные числа, маленькие и большие числа, дроби и десятичные дроби. Если вы видите, что количество A больше количества B в одном случае, а количество B больше количества A в другом случае, выберите «Отношение не может быть определено на основе предоставленной информации».
- Упростить сравнение . Если обе величины являются алгебраическими или арифметическими выражениями, и вы не можете легко увидеть взаимосвязь между ними, попробуйте упростить сравнение. Попробуйте выполнить пошаговое упрощение, аналогичное шагам, которые выполняются при решении уравнения для x , или аналогичным шагам, которые необходимо выполнить, когда вы определяете, что неравенство эквивалентно более простому неравенству Начните с настройки сравнения, включающего две величины:
, где – это заполнитель, который может обозначать отношение больше (>), меньше (<) или равно (=) или может обозначать тот факт, что отношение невозможно определить на основе предоставленной информации. Затем попытайтесь упростить сравнение, шаг за шагом, пока не сможете определить взаимосвязь между упрощенными величинами. Например, вы можете сделать вывод после последнего шага, который представляет собой равенство (=). Основываясь на этом выводе, вы, возможно, сможете сравнить количества A и B. Чтобы лучше понять эту стратегию, см. примеры вопросов 6–9..
Затем попытайтесь упростить сравнение, шаг за шагом, пока не сможете определить взаимосвязь между упрощенными величинами. Например, вы можете сделать вывод после последнего шага, который представляет собой равенство (=). Основываясь на этом выводе, вы, возможно, сможете сравнить количества A и B. Чтобы лучше понять эту стратегию, см. примеры вопросов 6–9..
В этих вопросах с несколькими вариантами ответов вам предлагается выбрать только один вариант ответа из списка из пяти вариантов.
Советы по ответу
- Используйте тот факт , что ответ есть . Если ваш ответ не входит ни в один из пяти предложенных вариантов ответа, предположите, что ваш ответ неверен, и сделайте следующее:
- Внимательно перечитайте вопрос — возможно, вы упустили важную деталь или неверно истолковали какую-то информацию.
- Проверьте свои вычисления — возможно, вы допустили ошибку, например, неправильно набрали число на калькуляторе.
- Пересмотрите свой метод решения — у вас может быть изъян в рассуждениях.

- Просмотрите варианты ответов . В некоторых вопросах вас прямо спрашивают, какой из вариантов имеет определенное свойство. Возможно, вам придется рассмотреть каждый вариант отдельно или вы сможете увидеть взаимосвязь между вариантами, что поможет вам быстрее найти ответ. В других вопросах может быть полезно работать в обратном направлении от вариантов, например, заменяя варианты в уравнении или неравенстве, чтобы увидеть, какой из них работает. Однако будьте осторожны, так как этот метод может занять больше времени, чем использование рассуждений.
- Для вопросов, требующих приближения, просмотрите варианты ответов, чтобы увидеть, насколько точное приближение необходимо . (Это может быть полезно и для других вопросов, так как поможет вам лучше понять, о чем идет речь.) Для некоторых вопросов вам, возможно, придется выполнить все вычисления точно и округлить только ваш окончательный ответ, чтобы получить необходимая степень точности. В других случаях оценки достаточно, и это поможет вам не тратить время на долгие вычисления.

В этих вопросах с несколькими вариантами ответов вам предлагается выбрать один или несколько вариантов ответа из списка вариантов. Вопрос может указывать или не указывать количество вариантов для выбора.
Советы по ответу
- Обратите внимание, просят ли вас указать определенное количество вариантов ответа или все варианты, которые применимы . В последнем случае обязательно рассмотрите все варианты, определите, какие из них правильные, и выберите все эти и только эти варианты. Обратите внимание, что правильный выбор может быть только один.
- В некоторых вопросах, которые включают условия, ограничивающие возможные значения числовых вариантов ответа, может оказаться эффективным определить наименьшее и/или максимально возможное значение . Зная наименьшее и/или максимально возможное значение, вы сможете быстро определить все правильные варианты.
- Избегайте длинных вычислений, распознавая и продолжая числовые шаблоны .

Эти вопросы требуют, чтобы вы либо ввели свой ответ в виде целого числа или десятичной дроби в одно поле для ответа, либо в виде дроби в двух отдельных полях — одно для числителя и одно для знаменателя. Вы будете использовать компьютерную мышь и клавиатуру, чтобы ввести свой ответ.
Советы по ответу
- Убедитесь, что вы ответили на заданный вопрос . Поскольку нет вариантов ответов, которые могли бы вам помочь, внимательно прочитайте вопрос и убедитесь, что вы даете требуемый тип ответа. Иногда перед или после поля для ответа будут метки, указывающие на соответствующий тип ответа. Обратите особое внимание на такие единицы, как футы или мили, на порядки величин, такие как миллионы или миллиарды, и на проценты по сравнению с десятичными дробями.
- Если вас попросят округлить ответ, убедитесь, что вы округлили до требуемой степени точности . Например, если ответ 46,7 должен быть округлен до ближайшего целого числа, вам нужно ввести число 47.
 Если ваша стратегия решения включает промежуточные вычисления, выполните все вычисления точно и округлите только ваш окончательный ответ, чтобы получить требуемое степень точности. Если инструкции по округлению не указаны, введите точный ответ.
Если ваша стратегия решения включает промежуточные вычисления, выполните все вычисления точно и округлите только ваш окончательный ответ, чтобы получить требуемое степень точности. Если инструкции по округлению не указаны, введите точный ответ. - Изучите свой ответ, чтобы убедиться, что он разумен с учетом предоставленной информации . Вы можете использовать оценку или другой путь решения, чтобы перепроверить свой ответ.
Вопросы интерпретации данных сгруппированы вместе и относятся к одной и той же таблице, графику или другому представлению данных. Эти вопросы просят вас интерпретировать или анализировать данные. Типы вопросов могут быть с множественным выбором (оба типа) или числовым вводом.
Советы по ответу
- Кратко просмотрите презентацию данных, чтобы понять, о чем она, но не тратьте время на подробное изучение всей информации . Сосредоточьтесь на тех аспектах данных, которые необходимы для ответа на вопросы.
 Обратите внимание на:
Обратите внимание на:- оси и шкалы графиков
- единицы измерения или порядки величины (например, миллиарды), указанные в заголовках, метках и легендах
- любые примечания, уточняющие данные
- Когда графические представления данных, такие как гистограммы и линейные графики, отображаются с помощью масштабов, вы должны считывать, оценивать или сравнивать величины визуально или путем измерения в соответствии с соответствующими шкалами . Например, используйте относительные размеры столбцов или секторов для сравнения величин, которые они представляют, но имейте в виду сломанные шкалы и столбцы, которые не начинаются с 0.
- Отвечайте на вопросы только на основе представленных данных, повседневных фактов (таких как количество дней в году) и ваших знаний по математике . Не используйте специализированную информацию, которую вы можете вспомнить из других источников о конкретном контексте, на котором основаны вопросы, за исключением случаев, когда эта информация может быть получена из представленных данных.

Этапы решения проблем
В дополнение к советам по ответам в разделах типов вопросов выше, есть также некоторые общие шаги и стратегии решения проблем, которые вы можете использовать. Вопросы из измерения «Количественное мышление» требуют моделирования и решения проблем с использованием количественных или математических методов. Как правило, решение математических задач состоит из трех основных шагов:
Внимательно прочитайте формулировку задачи, чтобы убедиться, что вы понимаете предоставленную информацию и задачу, которую вам предлагается решить.
- Некоторая информация может описывать определенные количества.
- Количественная информация может быть представлена словами или математическими выражениями, или их комбинацией.
- Вам может понадобиться читать и понимать количественную информацию в представлениях данных, геометрических фигурах или системах координат.
- Другая информация может иметь форму формул, определений или условий, которым должны удовлетворять величины.
 Например, условия могут быть уравнениями или неравенствами, или могут быть словами, которые можно перевести в уравнения или неравенства.
Например, условия могут быть уравнениями или неравенствами, или могут быть словами, которые можно перевести в уравнения или неравенства.
Помимо понимания предоставленной вам информации, убедитесь, что вы понимаете, что вам нужно сделать, чтобы решить проблему. Например, какие неизвестные величины необходимо найти? В какой форме они должны быть выражены?
Решение математической задачи требует большего, чем понимание описания задачи (количеств, данных, условий, неизвестных и всех других математических фактов, связанных с задачей). Это также требует определения какие математические факты использовать и когда и как использовать эти факты для разработки решения задачи. Это требует стратегии.
Математические задачи решаются с использованием самых разных стратегий, и могут быть разные способы решения данной задачи. Разработайте репертуар стратегий решения проблем и понимание того, какие стратегии, вероятно, будут работать лучше всего при решении конкретных проблем. Попытка решить проблему без стратегии может привести к большой работе без получения правильного решения.
Попытка решить проблему без стратегии может привести к большой работе без получения правильного решения.
После того, как вы определите стратегию, выполните ее. Если вы застряли, проверьте свою работу, чтобы увидеть, не допустили ли вы ошибку в своем решении. Сохраняйте гибкий и открытый образ мышления. Если вы проверяете свое решение и не можете найти ошибку, или если ваша стратегия решения просто не работает, поищите другую стратегию.
Когда вы получите ответ, убедитесь, что он разумен и корректен с точки зрения вычислений.
- Вы ответили на заданный вопрос?
- Является ли ваш ответ обоснованным в контексте вопроса? Проверить правильность ответа можно так же просто, как вспомнить базовый математический факт и проверить, согласуется ли ваш ответ с этим фактом. Например, вероятность события должна быть от 0 до 1 включительно, а площадь геометрической фигуры должна быть положительной. Возможно, вы сможете использовать оценку, чтобы проверить, является ли ваш ответ разумным.
 Например, если ваше решение включает сложение трех чисел, каждое из которых находится в диапазоне от 100 до 200, оценка суммы говорит вам, что сумма должна быть в диапазоне от 300 до 600.
Например, если ваше решение включает сложение трех чисел, каждое из которых находится в диапазоне от 100 до 200, оценка суммы говорит вам, что сумма должна быть в диапазоне от 300 до 600. - Вы допустили вычислительную ошибку при получении ответа или ошибку при вводе ключа с помощью калькулятора? Проверьте наличие ошибок на каждом этапе вашего решения. Или вы можете напрямую проверить правильность вашего решения. Например, если вы решаете уравнение относительно x, подставьте свой ответ в уравнение, чтобы убедиться, что он правильный.
Стратегии
Не существует установленных правил, применимых ко всем математическим задачам, для определения наилучшей стратегии. Способность определить стратегию, которая будет работать, растет по мере того, как вы решаете все больше и больше проблем. Загрузите примеры вопросов, чтобы получить список из 14 полезных стратегий, которые вы можете использовать, а также один или два примера вопросов, которые иллюстрируют, как использовать каждую стратегию.
Скачать PDF
Использование калькулятора
Вам предоставляется базовый экранный калькулятор для меры количественного рассуждения. Иногда вычисления, которые вам нужно сделать, чтобы ответить на вопрос в показателе количественного рассуждения, требуют много времени, например, деление в длинную сторону, или они включают в себя квадратные корни. Хотя калькулятор может сократить время, необходимое для выполнения вычислений, имейте в виду, что калькулятор дает результаты, которые дополняют, но не заменяют ваши знания математики. Вам нужно будет использовать свои математические знания, чтобы определить, являются ли результаты калькулятора разумными и как результаты можно использовать для ответа на вопрос.
Вот некоторые общие рекомендации по использованию калькулятора в измерении количественного мышления:
- Большинство вопросов не требуют сложных вычислений, поэтому не используйте калькулятор только потому, что он доступен.


 Не предполагайте, что такие величины, как длины и угловые меры, представлены на рисунке. Однако следует исходить из того, что:
Не предполагайте, что такие величины, как длины и угловые меры, представлены на рисунке. Однако следует исходить из того, что: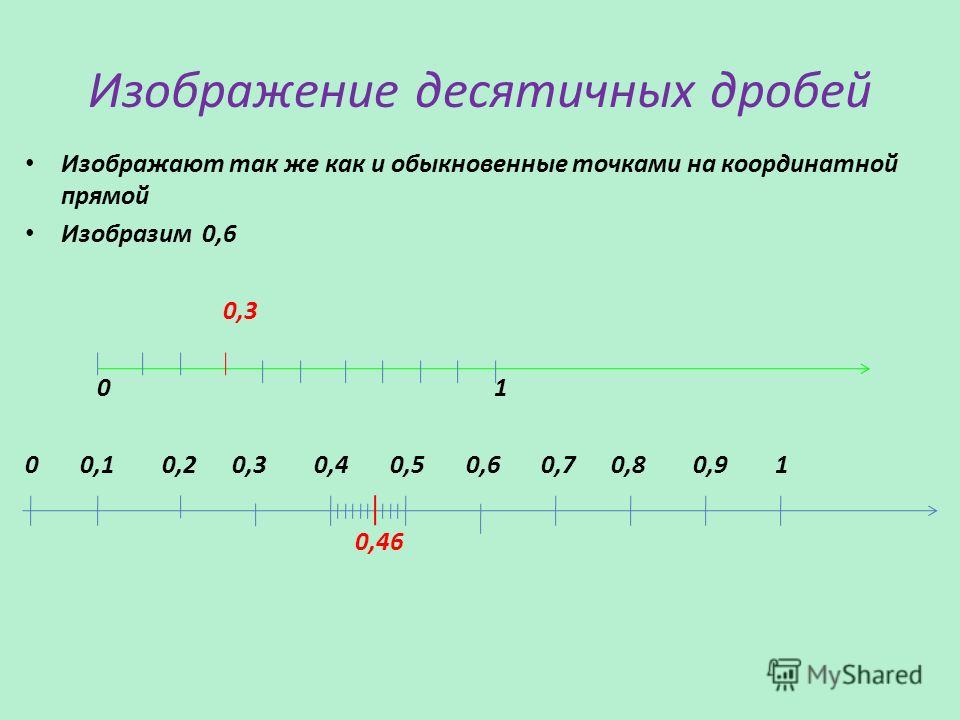
 Изучите результаты. Какие вариации возможны в относительных длинах отрезков или мер углов?
Изучите результаты. Какие вариации возможны в относительных длинах отрезков или мер углов?

 Если ваша стратегия решения включает промежуточные вычисления, выполните все вычисления точно и округлите только ваш окончательный ответ, чтобы получить требуемое степень точности. Если инструкции по округлению не указаны, введите точный ответ.
Если ваша стратегия решения включает промежуточные вычисления, выполните все вычисления точно и округлите только ваш окончательный ответ, чтобы получить требуемое степень точности. Если инструкции по округлению не указаны, введите точный ответ. Обратите внимание на:
Обратите внимание на:
 Например, условия могут быть уравнениями или неравенствами, или могут быть словами, которые можно перевести в уравнения или неравенства.
Например, условия могут быть уравнениями или неравенствами, или могут быть словами, которые можно перевести в уравнения или неравенства. Например, если ваше решение включает сложение трех чисел, каждое из которых находится в диапазоне от 100 до 200, оценка суммы говорит вам, что сумма должна быть в диапазоне от 300 до 600.
Например, если ваше решение включает сложение трех чисел, каждое из которых находится в диапазоне от 100 до 200, оценка суммы говорит вам, что сумма должна быть в диапазоне от 300 до 600.