Диаметр свойства: Радиус и диаметр окружности — определения, свойства, формулы

определение, основные свойства, как построить

Определения и свойства окружности

Определение 1

Окружностью называют кривую на плоскости, которая состоит из точек, находящихся на равном расстоянии от центра этой окружности.

 

Источник: microexcel.ru

Введем несколько определений, связанных с темой окружности. Данные термины можно встретить на уроках в седьмом классе и других курсах по алгебре и геометрии.

Определение 2

Радиус окружности (R) является отрезком, один конец которого расположен в центре окружности, а второй находится на окружности.

Определение 3

Диаметр окружности (d) представляет собой линию, или хорду, которая пересекает центральную точку окружности и соединяет две противоположные точки, расположенные на окружности.

 

1 Примечание 1

В распространенных случаях возникает путаница в понятиях окружности и круга. Заметим, что кругом может называться множество точек на плоскости, которые при построении ограничены окружностью, то есть данные точки расположены во внутренней области окружности.

Окружность обладает рядом свойств:

1. Если три точки на плоскости не принадлежат общей прямой, то через них допустимо построить единственную окружность.
2. Точка (С), в которой касаются две окружности, расположена на общей с центрами этих окружностей прямой (АВ).
3. Изопериметрическое неравенство: из всех замкнутых кривых на графике, имеющих одинаковую длину, окружность ограничивает область с максимальной площадью.

Источник: microexcel.ru

При решении самостоятельных работ и задач на некоторые окружности пригодятся следующие формулы, чтобы находить ключевые параметры:

Диаметр окружности можно высчитать таким образом:

d=2*R  или  d=cπ 

Длина окружности в теории:

C=2*π*R=d*π 

Радиус окружности можно узнать с помощью формулы:

R=d2  или  R=c2*π 

Источник: microexcel.ru.

Виды окружностей — вписанные и описанные окружности

Определение 4

Описанная вокруг многоугольника окружность представляет собой такую окружность, на которой расположена каждая из вершин этого многоугольника. При этом многоугольник является вписанным в данную окружность.

Какой-либо без ограничений многоугольник, являющийся правильным, допустимо вписать в окружность. На рисунке изображена описанная около шестиугольника окружность, которая проходит через все его вершины:

Источник: spadilo.ru

Запишем свойства, которые характерны для описанной около треугольника окружности:

1. Около какого-либо треугольника допустимо описать единственную окружность.
2. Если окружность описана около прямоугольного треугольника, то ее центральная точка располагается на середине гипотенузы.
3. Окружность, описанная около треугольника, имеет радиус, который определяют, как отношение произведения сторон a, b, c треугольника к его учетверенной площади: R=abc4S.
4. Окружность, описанная около треугольника, имеет радиус, который определяют, как отношение стороны треугольника к удвоенному синусу противолежащего угла: R=AB2sin∠C=AC2sin∠B=BC2sin∠A.

В том случае, когда окружность описана около четырехугольника, она обладает следующими свойствами:

1. Около какого-либо четырехугольника допустимо описать окружность при условии, что его противоположные углы в сумме дают 180°.
2. Вписанный в окружность четырехугольник имеет диагонали, произведение которых соответствует сумме произведений противоположных сторон.
3. Если четырехугольник вписан в окружность, то его площадь определяют с помощью формулы Брахмагупты: S=(p-a)(p-b)(p-c)(p-d).

Определение 5

Вписанная в многоугольник окружность представляет собой такую окружность, которая касается каждой из сторон этого многоугольника. При этом многоугольник называют описанным около окружности.

Заметим, что в какой-либо многоугольник, который является правильным, допустимо вписать окружность. Продемонстрируем это с помощью рисунка, на котором изображена окружность, вписанная в правильный многоугольник с шестью углами и касающаяся каждой его стороны:

Источник: spadilo. ru

Вписанная окружность обладает следующими свойствами:

1. Центральная точка окружности, вписанной в многоугольник, совпадает с точкой пересечения биссектрис внутренних углов данного многоугольника.
2. В какой-либо треугольник допустимо вписать единственную окружность.
3. Вписанная окружность имеет радиус, равный отношению площади треугольника к половине его периметра: r=Sp.
4. Вписать окружность в четырехугольник допустимо при условии, что данный четырехугольник является выпуклым.
5. Окружность допустимо вписать в выпуклый четырехугольник в том случае, когда соблюдается равенство сумм его противолежащих сторон.

Взаимное отношение хорд и их расстояний от центров

Теорема 1

В том случае, когда радиус окружности расположен перпендикулярно относительно хорды, данный радиус делит хорду и дугу на две равные части.

Изобразим окружность и ее элементы, согласно теореме:

 

Источник: maths-public.ru

Заметим, что радиус, обозначенный, как OC, расположен перпендикулярно к хорде AB, как показано на рисунке:

CO⊥AB.

Попробуем доказать следующее:

AD = BD

⏝AC=⏝CB.

Проведем прямую через точки А и В, которая соединит их с центральной точкой О. Заметим, что наклонные ОА и ОВ равны и удалены от перпендикулярной прямой ОС. В результате:

AD = DB.

Предположим, что перпендикулярная прямая CD выходит из середины АВ. В таком случае, точка С равноудалена относительно концов перпендикуляра. Из этого следует равенство хорд AC и CB. Таким образом:

⏝AC=⏝CB.

Получаем, что перпендикуляр ОС делит на две равные части дугу АВ, что и требовалось доказать.

Следствие 1

Перпендикуляр, который опущен из середины хорды, пересекает центр окружности.

Начнем доказательство данного утверждения с того, что центральная точка равноудалена от концов хорды. В таком случае, она будет расположена на перпендикуляре, который восстановлен из середины хорды, что и требовалось доказать.

Теорема 2

При условии равенства хорд они равноудалены от центральной точки окружности.

Перенесем данные на рисунок:

 

Источник: maths-public. ru

Запишем равенство двух хорд AB и CD:

AB = CD.

Представим доказательство того, что данные хорды расположены на одинаковом расстоянии от центральной точки:

OE = OF.

Если соединить между собой точки А и С, а также центральную точку О, получим пару треугольников AEO и COF, которые равны и являются прямоугольными. Объясним это равенством радиусов:

OA = OC.

Заметим также, что половины одинаковых хорд будут равны друг другу:

AE = CF.

В результате получим доказательство теоремы:

OE = OF.

Теорема 3

На одинаковых расстояниях от центральной точки окружности расположены хорды, которые равны друг другу.

Воспользуемся предыдущим рисунком. Запишем, что хорды AB и CD равноудалены от центра:

OE = OF.

Попробуем подтвердить справедливость следующего равенства:

AB = CD.

Рассмотрим пару прямоугольных треугольников AEO и COF. Данные треугольники равны, исходя из равенства гипотенуз и катетов. Согласно условию:

OE = OF.

Равенство радиусов:

OA = OC.

В результате получим, что:

AE = CF

½AB = ½CD

Таким образом, теорема доказана:

AB = CD.

Теорема 4

Хорда, которая является большей, находится ближе к центру по сравнению с меньшей хордой.

 

Источник: maths-public.ru

Заметим, что хорда AB больше по сравнению с хордой AC:

AB > AC.

Требуется доказать следующее:

OD < OE.

Заметим, что OD расположен перпендикулярно относительно АВ. Линия OF является наклонной. В таком случае:

OD < OF.

Запишем, что:

OF < OE.

В результате теорема доказана:

OD < OE.

Формулы длины окружности и площади круга

Формула 1

Длину окружности определяют, зная радиус или диаметр, по формуле:

L=2πr=πd

 

Формула 2

При известном радиусе или диаметре площадь круга определяют с помощью формулы:

S=πr2=πd24

Касательная к окружности

Определение 6

Касательная к окружности представляет собой прямую, которая обладает с окружностью единственной общей точкой.

 

Источник: mypresentation.ru

Касательная к окружности характеризуется следующими свойствами:

1. Касательная расположена перпендикулярно по отношению к радиусу окружности, проведенному в точку касания: AC⊥OA.
2. Отрезки касательных, которые проведены из одинаковой точки, являются равными: AC=BC.

Углы в окружности

Определение 7

Вписанный в окружность угол представляет собой угол с вершиной, принадлежащей окружности, и сторонами, которые эту окружность пересекают.

 

Источник: kornev-school.ru

На рисунке ∠BAC является вписанным.

Вписанные углы обладают следующими свойствами:

1. Вписанный угол соответствует ½ дуги, на которую данный угол опирается.
2. Вписанный угол соответствует ½ центрального угла, опирающегося на аналогичную дугу: ∠BAC=12∠BOC.
3. Вписанные углы, которые опираются на общую дугу, считают равными.
4. Вписанный угол, опирающийся на диаметр, равен 90°.
5. Какая-либо пара вписанных углов, которые опираются на одинаковую хорду и обладают вершинами, расположенными с разных сторон хорды, в сумме дают 180°.

Примеры решения задач

Задача 1

Точкой пересечения хорд AB и CD является точка О. Отрезок OD на 5 см больше по сравнению с OB, AO=12 см, CO=6 см. Требуется вычислить, чему равны OB и OD.

Решение

 

Исходя из свойства, которым обладает хорда, получим, что:

AO·OB=CO·OD

Подставим в формулу значения:

12·x=6·(x+5)

В результате:

x=5

OB=5 см

OD=10 см.

Ответ: OB=5 см, OD=10 см.

Задача 2

Некий четырехугольник ABCD вписан в окружность. Даны следующие условия:

AB=AD

∠A=80°.

Требуется определить, чему равен ∠ACD.

Решение

 

Начнем решение с изучения треугольника ABD. Данный треугольник является равнобедренным, согласно условию:

AB=AD.

В таком случае, допустимо равенство углов при BD. В результате:

∠ABD=∠ADB=180°-∠A2=180°-80°2=50°

Заметим, что опорой для углов ∠ABD и ∠ACD является одинаковая хорда, что говорит о равенстве данных углов. Таким образом:

∠ACD=50°

Ответ: ∠ACD=50°.

Задача 3

Дана окружность, диаметр которой равен 1,5 см. Требуется найти длину этой окружности.

Решение

Обратимся к формуле:

l=πd.

Путем подстановки значения диаметра определим, что:

l=1,5·π=1,5π(см)

Допустим, что:

π≈3,14

Тогда:

l=1,5π≈1,5·3,14=4,71(см)

Ответ: окружность имеет длину l=1,5πсм или l≈4,71см.

Задача 4

В правильный треугольник вписана некая окружность. Сторона треугольника равна 43см. Нужно определить, чему равна длина вписанной окружности.

Решение

Согласно условию:

a=43см.

Существует связь между стороной правильного треугольника и радиусом окружности, которая в него вписана:

r=a23

Выполним подстановку:

r=4323=2

Определим длину окружности:

l=2πr

l=2·2·π=4π(см)

При условии, что π≈3,14, получим:

l=4π≈4·3,14=12,56(см)

Ответ: l=4πсм или l≈12,56см.

Задача 5

Задан круг, радиус которого составляет 4 м. Требуется вычислить площадь этого круга.

Решение

Применим следующую формулу:

S=πr2

Путем подстановки значения радиуса из условия задания преобразуем формулу:

S=π·42⇒S=16π(м2)

Ответ: S=16πм2.

Задача 6

Правильный треугольник вписан в некий круг. Сторона треугольника равна 3 дм. Требуется определить, чему равна площадь круга.

Решение

Воспользуемся следующим соотношением:

R=a3

Путем подстановки получим:

R=33

Площадь круга определим с помощью формулы:

S=πr2

В результате:

S=π32=3π(дм2)

Ответ: S=3πдм2.

Задача 7

На плоскости с помощью окружности ограничили определенный участок. Радиус этой окружности равен 2см. Нужно вычислить площадь ограниченного участка.

Решение

Плоскость частично ограничена окружностью с определенным радиусом. В результате образован круг с аналогичным радиусом 2. Воспользуемся формулой:

S=πr2.

Путем подстановки получим:

S=π·22=2π(см2)

Ответ: S=2πсм2.

Задача 8

Сторона квадрата равна 22см. Данный квадрат вписан в окружность. Требуется определить, какова площадь круга, ограниченного этой окружностью.

Решение

 

Диагональ AC вписанного квадрата ABCD равна диаметру окружности, которая описана около квадрата. Определим, чему равна диагональ AC.

Исходя из того, что фигура ABCD является квадратом, треугольник ACD является прямоугольным. Согласно теореме Пифагора, получим:

AC=AD2+CD2

Путем подстановки преобразуем выражение:

AC=222+222=8+8=16=4(см)

Площадь круга можно рассчитать с помощью формулы:

S=πd24

Путем подстановки получим:

S=π424=4πсм2

Ответ: S=4πсм2.

Задача 9

Построены две касательные к окружности, которые берут начало в точке С. Точками касания являются A и B. Угол AOB составляет 105°. Нужно определить градусную меру угла ACB.

Решение

В полученном четырехугольнике:

∠A=∠B=90°

Данное равенство справедливо, так как OA и OB обозначают радиусы, которые проведены в точку касания.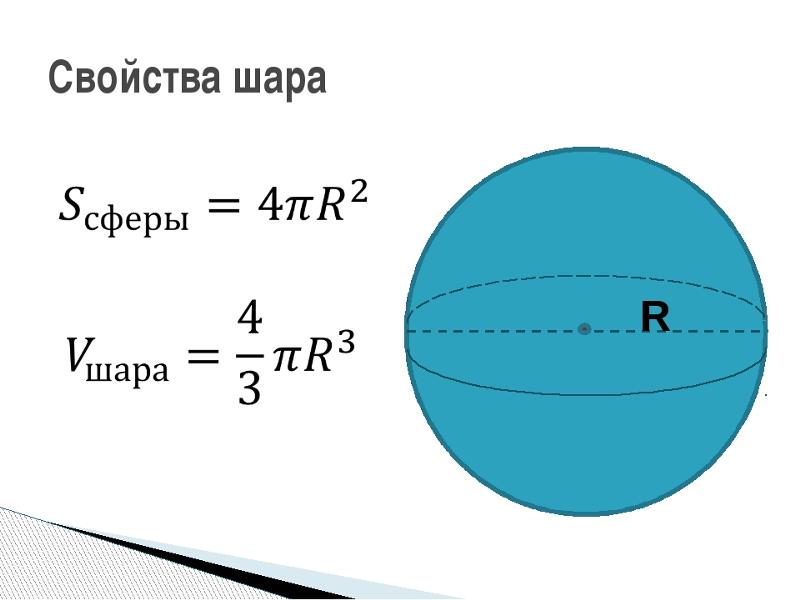  В сумме углы четырехугольника составляют 360°. Таким образом:

∠C=360°-∠A-∠B-∠O=360°-90°-90°-105°=75°

Ответ: ∠C=75°.

Задача 10

С помощью хорды AC стянута дуга окружности в 80°. Точка A является точкой касания. Требуется определить угол, расположенный между касательной и хордой.

Решение

Исходя из условия задачи, центральный угол, опирающийся на хорду, составляет:

∠AOC=80°.

Заметим, что OA и OC являются радиусами. Таким образом, треугольник AOC является равнобедренным. В результате:

∠OAC=∠OCA=180°-80°2=50°

С помощью радиуса OA и касательной образован угол в 90°, согласно свойству касательной. Тогда:

∠CAB=180°-90°-50°=40°

Ответ: ∠CAB=40°.

Задача 11

Треугольник АВС является прямоугольным. Его катеты равны:

AB=3 см

AC=4 см.

Около данного треугольника описана окружность, радиус которой требуется вычислить.

Решение

Исходя из того, что треугольник является прямоугольным, центральная точка описанной окружности расположена на середине гипотенузы. Таким образом, радиус окружности можно определить как половину гипотенузы. С помощью теоремы Пифагора вычислим, чему равна гипотенуза:

BC=AB2+AC2=9+16=5 cm

В результате:

R=12BC=2,5см.

Ответ: R=2,5 см.

Задача 12

Четырехугольник ABCD вписан в окружность. Угол A меньше по сравнению с углом B в 2 раза. Угол C больше по сравнению с углом D в три раза. Нужно вычислить градусные меры углов данного многоугольника.

Решение

Обозначим углы, которые требуется найти с помощью переменных:

∠A=x

∠B=2x

∠D=y

∠C=3y.

Во вписанном четырехугольнике противоположные углы в сумме дают 

Корнями данной системы являются:

x=72,  y=36.

В результате:

∠A=72°, ∠B=2·72°=144°, ∠D=36°, a ∠C=3·36°=108°

Ответ: ∠A=72°, ∠B=144°, ∠C=108°, ∠D=36°

Задача 13

Гипотенуза в равнобедренном прямоугольном треугольнике равна 6 см. Обозначим ее за А. Данный треугольник описан около окружности, радиус которой необходимо определить.

Решение

Формула радиуса вписанной окружности имеет следующий вид:

r=Sp.

Исходя из того условия, что прямоугольный треугольник является равнобедренным, запишем:

AB=BC.

Введем переменную х и применим теорему Пифагора:

x2+x2=36

Тогда:

x=32

AB=BC=32см.

Запишем формулу для вычисления площади треугольника:

S=12AB·BC=9 cm2

Определим, чему равен периметр треугольника:

p=AB+BC+AC2=32+32+62=32+3=3(2+1) cm

Далее вычислим радиус окружности:

r=Sp=93(2+1)=32+1 cm

Ответ: r=32+1см.

Задача 14

Задан некий четырехугольник ABCD. Сторона этого многоугольника CD больше по сравнению со стороной AD в три раза, AB=4 см, BC=10 см. Нужно определить, чему равны стороны CD и AD, если этот четырехугольник описан около окружности.

Решение

Исходя из того, что в четырехугольник вписана окружность, запишем равенство сумм его противолежащих сторон:

AB+CD=BC+AD

Введем обозначение:

AD = x.

В таком случае:

CD=3x.

Преобразуем записанное ранее соотношение:

4+3x=10+x

Таким образом:

х=3.

В результате:

AD=3 cm,  CD=3·3=9 cm

Ответ: AD=3 см, CD=9 см.

Задача 15

В окружности построили хорду АВ. С разных сторон от этой хорды отметили точки С и D. Данные точки соединили с концами хорды. В результате получился угол АСВ, который больше по сравнению с углом ADB в два раза. Требуется определить градусную меру полученных углов.

Решение

Заметим, что опорой углов ACB и ADB является единственная хорда. Так как эти углы расположены по разные стороны относительно хорды, в сумме они составляют 180°. Предположим, что:

∠ADB=x

В таком случае:

∠ACB=2x

x+2x=180

x=60

Таким образом:

∠ADB=60°, a ∠ACB=120°

Ответ: ∠ADB=60°, ∠ACB=120°.

Задача 16

Дано два треугольника. Эти треугольники вписаны в окружность. Угол D составляет 35°, сторона BC пересекает центральную точку описанной окружности. Требуется определить, чему равен угол ABC.

Решение           

Заметим, что у треугольников есть общая сторона АВ. Этот отрезок служит опорой для углов C и D. В результате:

∠C=∠D=35°

Треугольник ABC имеет прямой угол А, так как его опорой является диаметр BC. В результате:

∠ABC=180°-∠A-∠C=180°-90°-35°=55°

Ответ: ∠ABC=55°.

Что такое окружность: определение, свойства, формулы

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Что такое окружность: определение, свойства, формулы

В данной публикации мы рассмотрим определение и свойства одного из основных геометрических объектов – окружности. Также приведем формулы, с помощью которых можно найти ее радиус, диаметр и длину.

• Определение окружности
• Свойства окружности
  • Свойство 1
  • Свойство 2
  • Свойство 3
• Формулы

Определение окружности

Окружность – это замкнутая кривая на плоскости, состоящая из точек, равноудаленных от определенной точки. Данная точка называется центром окружности.

Радиус окружности (R) – это отрезок, соединяющий любую точку, лежащую на окружности, с ее центром.

Диаметр  окружности (d) – это линия (хорда), проходящая через центр окружности и соединяющая две противоположные точки, лежащие на ней.

Примечание: Не стоит путать окружность с кругом, т.к. круг – это множество точек плоскости, ограниченных окружностью (т.е. лежащих внутри окружности).

Свойства окружности

Свойство 1

Через три точки на плоскости, не лежащие на одной прямой, можно провести окружность, причем только одну.

Свойство 2

Точка касания двух окружностей (C) лежит на одной прямой (AB), которая проходит через их центры.

Свойство 3

Изопериметрическое неравенство: Из всех замкнутых кривых одинаковой длины окружность ограничивает область с самой большой площадью.

Формулы

1. Диаметр окружности (d):

2. Длина окружности (С):

3. Радиус окружности (R):

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Свойства документа — Размеры диаметра — 2020

Для размеров диаметра можно указать параметры чертежа на уровне документа. Доступно для всех типов документов.

Чтобы открыть эту страницу:

При открытом чертеже нажмите «Параметры» (панель инструментов «Стандартная»), выберите «Свойства документа», а затем выберите «Размеры» > «Диаметр».

Общий чертежный стандарт

---

Общий стандарт оформления

Унаследовано от выбранных настроек страницы «Чертежный стандарт».

---

Стандартный размер диаметра основания

Стандартный размер диаметра основания

Выберите стандарт: ANSI ИСО ДИН ДЖИС БСИ ГОСТ ГБ

Стиль выноски/размерной линии

---

Стиль выноски	Выберите: стиль.
Толщина выноски	Выберите: толщину или выберите Пользовательский размер и введите толщину.

---

Стиль выносной линии

---

Стиль выносной линии	Выберите: стиль.
Толщина выносной линии	Выберите: толщину или выберите Пользовательский размер и введите толщину.
То же, что и стиль выноски/размерной линии	Выберите, чтобы сохранить стиль линии.

---

Текст

---

Шрифт

Нажмите, чтобы изменить шрифт.

---

---

Горизонтальный выравнивание текста	Левый
	Центр
	Справа
Вертикальный выравнивание текста	Топ
	Средний
	Низ

---

Два размера

---

Двойной дисплей	Выберите для отображения размеров в двойных единицах измерения.
Единицы измерения для двойного дисплея	Выберите для отображения единиц измерения для второго набора измерений.
Разделить, если положение текста «Сплошная выноска, выровненный текст»	Выберите, чтобы задать новые линейные размеры с двойными размерами для отображения разделения над и под сплошной размерной линией.
Позиция значения размера	Топ
	Низ
	Справа
	Левый

---

Основная точность

---

Единица точности	Выберите количество цифр после запятой для значения.
Допуск Точность	Выберите количество цифр после запятой для допуска.

---

Двойная точность

---

Единичная точность	Выберите количество знаков после запятой из списка для значения во вторичных единицах.
Допуск Точность	Выберите количество знаков после запятой для допуска значения для второстепенных единиц.

---

Ракурс

	Двойная стрела
	Зигзаг

Если размер диаметра слишком велик для вида чертежа, размер автоматически укорачивается в ракурсе.

Слой

---

Слой	Выберите слой. Сначала необходимо создать слои для чертежа, прежде чем их можно будет выбрать для свойств документа.

---

Чтобы применить эти настройки слоя, необходимо выбрать «По стандарту» для «Слой» (панель инструментов «Слой») в документе вида чертежа.

Положение текста

Сплошная выноска, выровненный текст
Сломанная выноска, горизонтальный текст
Сломанная выноска, выровненный текст

Опции

Отображение второй внешней стрелки	Выберите для отображения двух внешних стрелок.
Дисплей со сплошной выноской	Для стандартов, отличных от ANSI, выноска отображается по центру, а не по окружности.
Допуск	Нажмите, чтобы установить допуск.

Плотность волос, диаметр, эллиптичность, пористость

Последнее обновление: 27 сентября 2022 г. , Verna Meachum

Знаете ли вы свои физические свойства волос? Правильный уход за волосами начинается с понимания каждого фактора, влияющего на ваши уникальные пряди, и того, как за ними ухаживать.

Пористость также является важным фактором, поскольку она влияет на степень повреждения волос. Если ваши волосы особенно пористые, они могут быть более склонны к повреждению и ломкости. Если вы не уверены, что означает какой-либо из этих терминов, не беспокойтесь! Мы разберем их для вас.

Зная эти свойства, вы сможете лучше адаптировать свой уход за волосами к вашим конкретным потребностям.

Волосы являются основным компонентом нашей внешности. Это определяет наш стиль, отношение и существенно влияет на то, как мы выглядим в глазах окружающих.

Несмотря на важность волос в нашей жизни, мы часто воспринимаем их как должное, не задумываясь о том, как они растут и какие факторы влияют на их внешний вид.

С научной точки зрения, волосы — это белковый придаток, предназначенный для защиты нашей кожи (кожи головы и тела) от внешних факторов, таких как тепло или механическое воздействие. Его белковая природа обеспечивает теплоизоляцию, помогая нам поддерживать температуру тела.

У всех нас немного разные волосы, потому что мы можем принадлежать к разным этническим группам. Они отличаются своим цветом, рисунком завитка, плотностью и механической прочностью. Они также могут различаться по своей структуре и морфологии.

Эти факторы сильно влияют на повседневную укладку и укладку волос. Они также влияют на наш подход к выбору средств по уходу за волосами для повседневного использования.

Все мы знаем, что волосы афроамериканцев чрезмерно вьются и отличаются от волос европейцев или европеоидов.

Точно так же слегка вьющиеся или волнистые волосы демонстрируют другой стиль стиля. Из-за их различий им требуются специальные средства по уходу за волосами для очищения, кондиционирования и укладки.

Каждый должен знать свои волосы. Чем больше мы понимаем науку о наших волосах, тем лучше мы подготовлены к тому, чтобы успешно управлять ими и укладывать их. Это может помочь нам в выборе продуктов, которые лучше всего подходят для наших волос.

Итак, о каких характеристиках и особенностях нам следует знать, чтобы лучше понять наши волосы? О каких качествах мы должны знать?

Мы рассмотрим все основные функции и характеристики и то, как они могут повлиять на наш уход за волосами, чтобы вы могли стать экспертом по своим волосам в кратчайшие сроки!

Тип завитка

Тип завитка относится к форме отдельных прядей ваших волос. Это может варьироваться от прямого до туго свернутого.

Существует несколько всесторонних стратегий для классификации моделей завитков волос, чтобы обсудить общие черты, рекомендации по продуктам и лучше понять наши волосы.

Одной из наиболее широко используемых и общепринятых является система типирования волос Андре Уокера. Система типирования волос была впервые представлена ​​в 1990-х годах знаменитым парикмахером Андре Уокером на шоу Опры Уинфри для продвижения своей коллекции средств по уходу за волосами.

Система классифицирует волосы по четырем основным категориям:

• Тип 1: прямые волосы
• Тип 2: волнистые волосы
• Тип 3: вьющиеся волосы
• Тип 4: курчавые волосы

Толщина определяется другим размером волос.

• Уровень a для тонких волос
• Уровень b для средних волос
• Уровень c для густых волос

Таким образом, при объединении двух векторов волосы 2c будут волнистыми густыми волосами, так далее и тому подобное.

Также возможно иметь более одного типа завитка. У вас могут быть локоны 2b на макушке головы и локоны 3a в нижней половине. Это совершенно нормально!

Понимание типов завитков может помочь вам определить лучшие продукты для ваших волос и то, как ваши волосы реагируют на укладку.

Например, для прямых или волнистых от природы волос можно использовать спреи и средства для укладки, которые помогают сохранить форму и завить волосы, такие как гели и лаки для волос.

С другой стороны, если у вас курчавые волосы, ваши пряди могут нуждаться в дополнительном увлажнении, и им могут помочь масла для завивки и несмываемые кондиционеры.

Также важно отметить, что, поскольку эта система устанавливает ожидания относительно здоровья волос, важно не путать тип волос и здоровье.

Как определить характер завитка ваших волос?

Возьмите от 1 до 3 прядей волос с расчески и положите их на белую бумагу или бумажное полотенце. Попробуйте оценить степень завитка и его диаметр.

Увеличенное изображение может помочь улучшить зрение наблюдения. Если ваши волосы находятся между двумя типами завитков, то это смесь обоих.

Как подобрать изделие к определенному типу локонов?

Прямые волосы (1a, b или c) сильно отличаются от кудрявых (3 a, b или c). Их реакция на различные прически и уровень влажности наружного воздуха (влажность) существенно различается.

Каждый уровень имеет разное содержание кожного сала и влаги, поэтому требуются разные средства по уходу за волосами.

Прямые волосы обычно легко утяжеляются. Чтобы избежать налипания и растекания, в средствах по уходу за прямыми волосами требуется меньше масел и полимеров.

Волнистые и кудрявые волосы (уровень 3) предпочитают объем и форму и поэтому ищут больше продуктов для покрытия, которые могут покрыть стержень волоса, удерживать их в определенном стиле в течение желаемого времени.

Кудрявые/кудрявые волосы (уровень 4) сухие и ломкие и поэтому нуждаются в глубоко увлажняющих ингредиентах, таких как натуральные масла (карите, манго, какао) и натуральные масла. Чтобы было понятнее, когда мы говорим здесь об «увлажняющих» ингредиентах, мы имеем в виду ингредиенты, которые удерживают влагу.0003

Плотность

Одним из наиболее важных аспектов, которые следует учитывать при укладке волос, является густота волос. Плотность волос определяется как «количество волосяных волокон на единицу площади кожи головы». ¹

Высокая густота волос свидетельствует об обильном росте волос на небольшой площади, в то время как низкая густота волос указывает на то, что на той же площади растет меньше волос. Как правило, если у вас много волос (то есть они густые), у вас высокая плотность волос. И наоборот, если у вас тонкие волосы, скорее всего, у вас низкая густота волос.

Обычно густота волос запрограммирована генетически. В случае выпадения волос могут быть разные причины низкой густоты волос.

Наиболее распространенными являются экологические проблемы, чрезмерное использование химической обработки волос и важные изменения гормонов в нашем организме.

Как измерить густоту волос?

Точный метод определения густоты волос требует помощи друга. Отметьте область кожи головы и подсчитайте количество волосяных волокон в этой области.

Например, вы отмечаете площадь 1 см x 1 см, и у вас есть 250 волокон, плотность волос будет:

Плотность волос = 250/см путем выбора новой области на коже головы. Чтобы провести эксперимент с тремя измерениями, продублируйте его и возьмите среднее значение. Чем выше число, тем больше волос (плотность).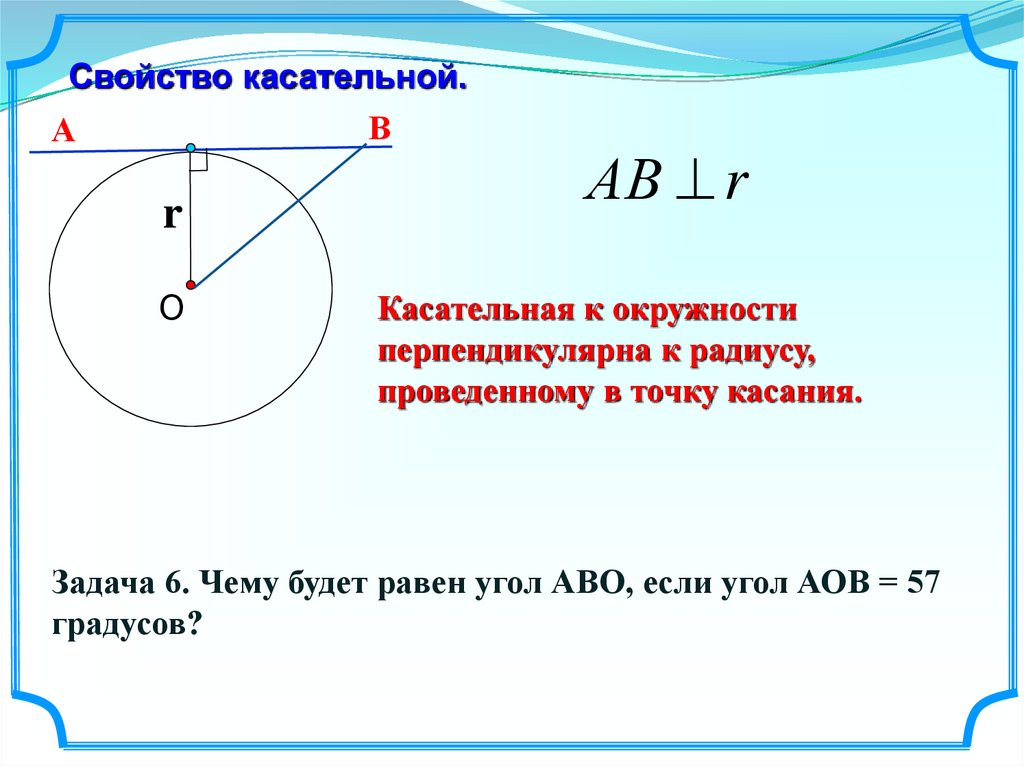

Какое значение имеет густота волос?

Густота волос имеет решающее значение, так как некоторые волосы нуждаются в разном уходе за волосами. Например, если у вас много волос, вам понадобится концентрированный состав.

Из-за большого количества волосяных волокон на единицу площади их может быть трудно расчесать, когда они влажные или сухие. Поэтому им требуется состав, богатый полимерами и смягчающими средствами, чтобы облегчить расчесывание и облегчить расчесывание.

Для низкой густоты волос вам понадобится более легкая формула. Поэтому лучше избегать составов, содержащих полимеры с высокой молекулярной массой, такие как поликватерниум 7 и 10 или хлорид гуаргидроксипропилтримония.

Эллиптичность волос

Эллиптичность определяет форму волосяного волокна. Простыми словами, у вас волосы круглые (круглые) или эллиптические (овальные)?

Определяется как изменение диаметра волосяного волокна по двум осям (ось X и ось Y).

Отношение двух осей дает нам числовое значение эллиптичности. Идеально круглый круг имеет это значение 1. Для измерения эллиптичности нам нужно рассчитать диаметр волос. ^2-3

Что говорит нам эллиптичность? Правильный выбор продукта

Волосы с высокой эллиптичностью более хрупкие и легко ломаются. В этом случае курчавые вьющиеся волосы попадают в эту категорию и поэтому требуют особого ухода.

Средства по уходу за очень вьющимися и вьющимися волосами нуждаются в большем количестве увлажняющих, смягчающих и распутывающих средств. Такой состав должен содержать натуральное масло, масла, воски и полимеры с высоким содержанием катионов, т.е. polyquaternium 7 или 10.

С другой стороны, для кавказских волос с низкой эллиптичностью требуется относительно менее концентрированный состав. Как упоминалось ранее, такие волосы, если на них наносится большое количество масел и полимеров, могут привести к жирным и жирным проблемам с волосами и кожей головы.

Диаметр

Диаметр также известен как ширина волоса; это ширина пряди волос. Поскольку человеческий волос различается по диаметру, это измерение не является точным. Он колеблется от 17 мкм до 181 мкм (миллионных долей метра).

Диаметр может быть разным для каждого человека в зависимости от генетической структуры. Кроме того, важен и цвет волос. Черные волосы толще рыжих. Меланин — это пигмент, который придает цвет нашим волосам, коже и глазам. Чем выше содержание меланина, тем толще волосы.

Необходимо понимать диаметр, поскольку он связан с другими важными факторами, такими как прочность, гибкость и эластичность.

Как измеряется диаметр волос?

Диаметр можно измерить с помощью микроскопа, который представляет собой устройство для измерения небольших объектов. Разные этнические группы имеют разный диаметр.

Обзор литературы показывает, что волосы группы 1а (прямые тонкие кавказские волосы) имеют средний диаметр 30-100 микрометров, а 4с (густые черные волосы) имеют средний диаметр 45-120 микрометров. Тем не менее, этнические группы показывают изменение диаметра одного и того же диаметра в определенных точках вдоль стержня волоса.

Например, чрезмерно вьющиеся волосы имеют некоторые точки, где волосы довольно тонкие, а волокна кажутся уплощенными.

Эти наконечники хрупкие, и волосы могут даже сломаться, даже если приложить очень небольшое усилие. В этих точках отношение двух осей меняется, и это дает значение эллиптичности, как показано на рисунке.

Волосы европеоидной расы имеют эллиптичность 1,40, в то время как чрезмерно вьющиеся имеют высокую эллиптичность 1,89.

Пористость

Пористость волос — это большая проблема, с которой мы сталкиваемся каждый день. Волосы состоят из белка кератина и содержат миллионы пор по всей длине стержня.

Поврежденные и химически обработанные волосы более пористые и имеют больший размер пор. Микроскопически пористость волоса означает, что в его кутикулярных слоях имеется большое пустое пространство.

Пористые волосы впитывают больше воды, химикатов и сильно реагируют на внешнюю влажность. Они тусклые, без блеска и жизни, а также вьющиеся.

Как определяется пористость волос?

Два разных типа подходов к испытаниям в домашних условиях: «испытание на плаву» и «испытание на мокрой воде». Оба теста не дают точных результатов и не дают истинной картины состояния волос. Оба теста дают очень эмпирический результат и имеют технические недостатки.

Например, в плавающем тесте волосы помещаются на поверхность воды, и если они тонут, то они пористые, а если они плавают на поверхности воды, они не пористые. Техническим недостатком здесь является смачиваемость.

Волосы могут быстро тонуть из-за pH водного раствора, температуры или присутствия соли в воде. Эти факторы влияют на смачиваемость и, следовательно, должны поддерживаться.

С научной точки зрения мы определяем пористость волос, используя метод набора веса. Волосы калибруются при постоянной относительной влажности 65% в течение 24 часов. Предварительно взвешенные образцы волос погружают в отмеренное количество воды постоянной температуры и без присутствия солей.

Через определенный период волосы удаляют, высушивают полотенцем и центрифугируют для удаления поверхностно-абсорбированной воды. Прибавка в весе (вес до погружения и вес после) рассчитывается и указывается в виде % возрастной пористости. ⁴

Как ухаживать за пористыми волосами

Сильно пористые волосы повреждаются и требуют тщательного ухода. Шампуни для пористых волос готовятся с использованием мягких поверхностно-активных веществ, смешанных с катионными полимерами и другими смягчающими средствами.

Кондиционеры для пористых волос должны содержать увлажнители, протеины, смягчающие вещества и смягчители волокон. Хлорид бегентримония, хлорид стеартримония и хлорид цетримония являются предпочтительным выбором для катионных.

Увлажнители жизненно необходимы, а глицерин является лучшим выбором для доставки столь необходимых молекул воды к пористым волосам.

Пористые волосы трудно расчесывать и укладывать. Поэтому масла действительно важны для обеспечения смазывающей способности, легкости расчесывания и блеска. Масло какао, манго и ши предпочтительнее из-за их уникальных уровней углеродной цепи.

Характеристики здоровых волос

Здоровые волосы являются важной частью общего состояния здоровья и благополучия человека.

Здоровые волосы сильные, гибкие и блестящие. Отдельные пряди гладкие и без повреждений. Волосы должны хорошо впитывать и удерживать влагу.

Эластичность ваших волос должна позволять им возвращаться к своей первоначальной форме после того, как их вытягивали или растягивали. Если у вас здоровые волосы, вам, вероятно, не нужно беспокоиться о том, что они ломаются, секутся или легко изнашиваются. Здоровые волосы также хорошо питаются и, как правило, не имеют налета.

Волосяные фолликулы не закупорены, что позволяет прядям беспрепятственно расти. Кожа головы чистая, без мусора.

Правильный уход за волосами, такой как использование мягких шампуней и кондиционеров, а также защита волос от теплового повреждения, может помочь сохранить здоровье волос.

Регулярное подравнивание также может предотвратить появление секущихся кончиков и других повреждений. Заботясь о своих волосах, люди могут помочь им выглядеть наилучшим образом.

Часто задаваемые вопросы

В чем разница между тонкими и тонкими волосами?

Тонкие волосы и тонкие волосы могут показаться одинаковыми, но на самом деле между ними есть некоторые ключевые различия. Тонкие волосы не означают, что волосы тонкие.

Под тонкими волосами понимается диаметр (ширина) отдельных прядей, а под тонкими волосами подразумевается густота волос на голове.

Тонкие волосы также более склонны к ломкости, что может привести к более тонкому внешнему виду.

Как правило, тем, у кого тонкие волосы, необходимо проявлять осторожность при укладке или распутывании и использовать средства, придающие объем и густоту.

Людям с тонкими волосами могут быть полезны продукты, которые покрывают пряди и создают иллюзию более густых и полных волос.

Оба типа волос требуют особого ухода и внимания, чтобы сохранить здоровый и блестящий вид.

Что такое жесткие волосы?

Жесткие волосы — это густые, крепкие волосы большего диаметра. Часто его трудно укладывать, потому что он плохо удерживает влагу. Это может сделать его непослушным и трудным в управлении.

Людям с жесткими волосами часто приходится использовать специальные кондиционеры и средства для укладки, чтобы держать их под контролем. Жесткие волосы обычно сухие и ломкие, поэтому важно использовать продукты, которые увлажняют и питают их.

Глубокие кондиционеры часто необходимы для поддержания здоровья и послушности жестких волос. В целом, людям с жесткими волосами следует избегать использования средств для укладки с нагреванием и следует сосредоточиться на использовании продуктов, которые помогут смягчить и увлажнить волосы.

Что означает состояние или состояние волос?

Состояние ваших волос может многое сказать о вашем здоровье в целом. Например, если у вас сухие и ломкие волосы, это может быть признаком того, что вы не получаете достаточного количества незаменимых жирных кислот в своем рационе.

С другой стороны, если ваши волосы жирные, а кожа головы шелушится, это может быть признаком повышенной активности сальных желез.

Хотя это всего лишь два примера, состояние ваших волос может дать вам представление о ваших пищевых привычках и общем состоянии здоровья.

Если вас беспокоит состояние ваших волос, обязательно поговорите со своим врачом или квалифицированным диетологом. Они смогут помочь вам определить, не хватает ли вашему рациону необходимых питательных веществ.

Ваши волосы сухие и поврежденные?

Да! Сухие, поврежденные волосы — распространенная проблема, которая может быть вызвана целым рядом факторов, в том числе чрезмерным мытьем, горячей укладкой и воздействием окружающей среды.

Хотя поврежденные волосы могут выглядеть безжизненными и тусклыми, на самом деле они более подвержены ломкости, чем здоровые волосы.

Лучший способ восстановить сухие, поврежденные волосы — это подвергнуть их дополнительной термической обработке. Начните с использования шампуня и кондиционера, специально разработанных для сухих волос.

Кроме того, по возможности старайтесь избегать горячей укладки и используйте средство глубокого кондиционирования хотя бы раз в неделю.

Выполняя эти действия, вы поможете восстановить естественный баланс влаги в волосах и защитите их от дальнейшего повреждения.

Ссылки

1. Zviak, C., The Science of Hair Care . Taylor & Francis: 2005.
2. Сайед, А. Н.; ТЕЛЕВИЗОР.; Н, С. М., Этническая принадлежность и эллиптичность волос: предварительное исследование. Косметика и труды. 2013.
3. Robbins, C.R., Химическое и физическое поведение человеческих волос . 4-е изд.; Springer-Verlag: Нью-Йорк, 2002 г.; стр. 311-343.
4. Сайед А. Н.; Аюб, Х., Корреляция пористости и прочности на разрыв химически модифицированных волос.