Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений.
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | ||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Решение уравнений и неравенств. Поделиться:
1966 Поиск в инженерном справочнике DPVA. Введите свой запрос: | |||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www. | |||
Системы уравнений. Формулы. Методы. / / Решение дифференциальных уравнений (диффуров). Дифференциальные уравнения, порядок дифференциального уравнения. Системы дифференциальных уравнений.
Введите свой запрос:Решение системы дифуравнений по формуле Коши
Образовательные онлайн сервисы: теория и практика
- Главная
- Примеры
- Математический анализ
- Векторная алгебра и аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование
Методы оптимизации - Математика в экономике
Экономическая статистика
- Видео-уроки
- Математический анализ
- Векторная алгебра и Аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование.
Методы оптимизации
- Готовые работы
- Математический анализ
- Векторная алгебра и аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование
Методы оптимизации - Математика в экономике
Экономическая статистика - Другое
- Контакты
Методы оптимизации
Полезные материалы:
- Учебники
- Справочники
- Онлайн калькуляторы
- Помощь в решении
- Онлайн занятия в Zoom
Решение системы дифуравнений по формуле Коши
Пример использования формулы КошиРассмотрим дифференциальное уравнение с дополнительными условиями: Сведем его к задаче Коши для следующей системы дифференциальных уравнений:
Перепишем систему в матричном виде:
Решим ее по формуле Коши.
Для этого подсчитаем матрицу
— составлено из векторов ФСР.
Общее решение вычисляется через собственные числа и
соответствующие им векторы матрицы А. Получаем:
Отсюда:
Найдем собственный вектор. соответствующий собственному значению.
Для этого решаем систему линейных алгебраических уравнений
Получаем Для второго вектора аналогично:
Выписываем общее решение соответствующей однородной дифференциальной системы: .
Переписываем в матричной форме относительно и получаем:
.
Поскольку то получаем
Таким образом, матрица Коши (Грина) построена и можно применить формулу Коши
С учетом того что окончательно получаем формульное решение задачи Коши:
Решить систему дифференциальных уравнений по формуле Коши
Задать вопрос
Заказать помощь
Отзывы
+7-911-7987704
vk.
com/id286009794
Написать в Whatsapp
Написать в Viber
@matem96
Skype: matem96.ru
Дифференциальное уравнение – определение, типы, применение и примеры
Дифференциальное уравнение – это математическое уравнение, включающее одну или несколько функций и их производные. Скорость изменения функции в точке определяется ее производными. Он в основном используется в таких областях, как физика, инженерия и биология. Анализ решений, удовлетворяющих уравнениям, и свойства решений являются основной целью дифференциальных уравнений. Использование явных формул — один из самых простых способов решения дифференциального уравнения. В этой статье давайте обсудим значение дифференциального уравнения, типы, методы решения дифференциального уравнения, порядок и степень дифференциального уравнения, формулы дифференциальных уравнений и несколько решенных задач.
Определение дифференциального уравнения
Дифференциальное уравнение имеет один или несколько членов, а также производные одной переменной (зависимой переменной) по отношению к другой переменной (т.
е. независимой переменной)
\[\frac{dy}{dx }\] = f(x)
Здесь «x» — независимая переменная, а «y» — зависимая переменная.
Например, \[\frac{dy}{dx}\] = 5x
Частные производные и обыкновенные производные также присутствуют в дифференциальном уравнении. Дифференциальное уравнение определяет связь между величиной, которая непрерывно изменяется по отношению к изменению другой величины, и производной, представляющей скорость изменения.
Что такое дифференциальное уравнение?
Уравнение, включающее неизвестную функцию y=f(x) и одну или несколько ее производных, называется дифференциальным уравнением. Иными словами, это уравнение, в которое входят производные одной или нескольких зависимых переменных по отношению к одной или нескольким независимым переменным. Дифференциальные уравнения важны для математического описания природы и лежат в основе многих физических теорий.
Порядок дифференциального уравнения 9{3}\] + 3x)y = 9
В этом случае старший порядок производной равен 2.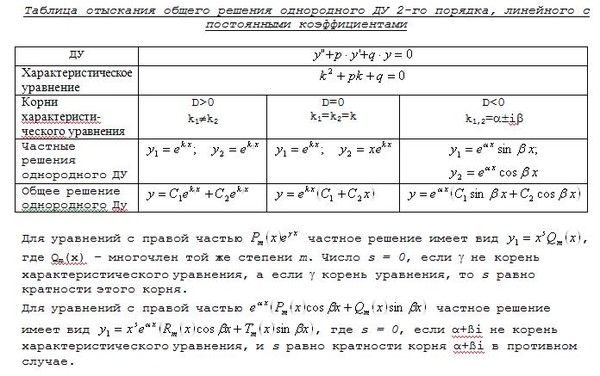
В результате уравнение является дифференциальным уравнением второго порядка.
Типы дифференциальных уравнений
Дифференциальные уравнения подразделяются на множество категорий. Это:
Обыкновенные дифференциальные уравнения
Дифференциальные уравнения в частных производных
Линейные дифференциальные уравнения
Нелинейные дифференциальные уравнения
Однородные дифференциальные уравнения
Неоднородные дифференциальные уравнения
Решения дифференциальных уравнений
Решение дифференциального уравнения можно найти одним из двух способов.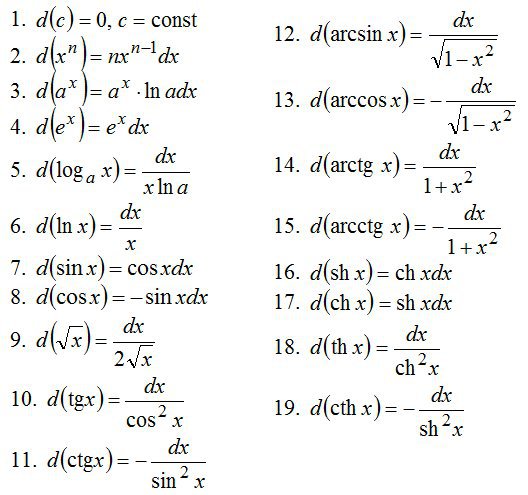
Переменная изолирована, когда дифференциальное уравнение может быть записано в форме dy/dx = f(y)g(x), где f — функция только y, а g — функция только x. Перепишите задачу как 1/f(y)dy=g(x)dx, а затем проинтегрируйте с обеих сторон, используя начальное условие.
Когда дифференциальное уравнение имеет вид dy/dx + p(x)y = q(x), где p и q являются функциями только от x, используется метод интегрирующих коэффициентов.
y’+ P(x)y = Q — дифференциальное уравнение первого порядка (x). P и Q являются функциями x и первой производной y соответственно. Уравнение, содержащее частные или обыкновенные производные неизвестной функции, называется дифференциальным уравнением высшего порядка. Это можно изобразить в любом порядке. 9{2}}\] + 2(\[\frac{dy}{dx}\]) + y = 0 является дифференциальным уравнением, и в этом случае степень этого уравнения равна 1. Вот еще несколько примеров:
dy/dx + 1 = 0, степень равна 1
(y”’)3 + 3y” + 6y’ – 12 = 0, в этом уравнении степень равна 3.
Обыкновенное дифференциальное уравнение
Функция и его производные входят в обыкновенное дифференциальное уравнение. Используется только одна независимая переменная и одна или несколько ее производных по переменной. 9{3}\] = 0 — обыкновенное дифференциальное уравнение.
Линейные дифференциальные уравнения
Дифференциальное уравнение вида: \[\frac{dy}{dx}\] + My = N
Линейное дифференциальное уравнение первого порядка, где M и N — константы или функции только x. Ниже приведен пример линейных дифференциальных уравнений первого порядка: \[\frac{dy}{dx}\] + y = sinx
Линейные дифференциальные уравнения Реальный пример
Найдите этот базовый пример, чтобы лучше понимать дифференциальные уравнения. Вы когда-нибудь задумывались, почему горячая чашка кофе остывает, если ее подержать при комнатной температуре? Согласно Ньютону, охлаждение горячего тела пропорционально разности температур между его температурой T и температурой T\[_{0}\] его окружения.
С точки зрения математики это предложение можно записать так:
dT/dt ∝ (T – T\[_{0}\])…………(1)
Такую форму принимает линейное дифференциальное уравнение.
С добавлением константы пропорциональности k приведенное выше уравнение принимает следующий вид: , а t — время в этом уравнении.
T\[_{0}\] — температура окружающей среды,
Скорость охлаждения тела dT/dt.
Приложения дифференциальных уравнений:
1) Дифференциальные уравнения используются для объяснения роста и убывания различных экспоненциальных функций.
2) Их также можно использовать для объяснения того, как рентабельность инвестиций меняется с течением времени.
3) Они используются в медицине для моделирования роста рака и распространения болезни по всему телу.
4) Может также использоваться для объяснения движения электричества.
5) Они помогают экономистам в определении наиболее эффективных инвестиционных стратегий.
6) Эти уравнения также могут быть использованы для объяснения движения волн или маятника.
Примеры дифференциальных уравнений
1. Составьте дифференциальное уравнение y=mx, где m — произвольная постоянная, для описания семейства кривых.
Sol: Здесь мы удалим константу путем дифференцирования y,
Учитывая y=mx
Сначала вычислим значение \[\frac{du}{dx}\]
\[\frac{dy}{dx }\] = \[\frac{d(mx)}{dx}\]
⇒ \[\frac{dy}{dx}\] = m
Или m = \[\frac{dy}{dx }\]
Теперь данное уравнение имеет вид y=mx 9{-1}\]
IF = \[\frac{1}{x}\]
Следовательно, множитель интегрирования = \[\frac{1}{x}\]
Вывод:
Из приведенного выше обсуждения мы Можно сказать, что дифференциальное уравнение определяется как уравнение, содержащее производную или производные зависимой переменной по независимой переменной.
Мы обсудили формулы дифференциальных уравнений и различные методы решения дифференциальных уравнений с использованием основных формул дифференциальных уравнений.
Элементарные дифференциальные уравнения
Математика 340 Дом, Содержание учебника, Домашнее задание онлайн Домашний номер
Предупреждение: MathJax
требует JavaScript для обработки математики на этой странице.
Если ваш браузер поддерживает JavaScript, убедитесь, что он включен.
Уравнения Эйлера
Обсуждение
Сейчас мы начнем работать над решениями
дифференциальные уравнения вблизи особых точек. Самые простые примеры мы
могут быть легко решены, называются уравнениями Эйлера. Дифференциальное уравнение
называется 9{я\лог х}$. (На самом деле, логарифмируя
в сложной плоскости может быть опасной вещью, но мы не будем волноваться
об этом сейчас.
Вы должны взять вводные комплексные переменные
хотя бы когда-нибудь на занятиях и узнайте об этом все.) Но что, если корни
повторяются? В этом случае у нас нет очевидной догадки о том, как найти
второй корень. Есть несколько способов справиться с этим. Как мы
будет использовать, чтобы сделать замену переменных, чтобы уменьшить исходный
уравнение к уравнению с постоянными коэффициентами. Эта техника будет работать
в любом уравнении Эйлера, а не только в уравнениях с повторяющимися корнями. Но
первая парадигма более эффективна, когда она работает.
9з$.
Важнейшие вычисления здесь заключаются в том, как производные от $y$ с
по $x$ преобразуются в производные от $y$ по $z$. Мы
первое вычисление
$$
\frac{dy}{dx}=\frac{dy}{dz}\frac{dz}{dx}=\frac1x\frac{dy}{dz}
$$
где мы использовали цепное правило. Итак, $xdy/dx=dy/dz$. Далее мы занимаемся
вторая производная. Здесь мы должны помнить, что мы хотим написать
производная по $x$ от производной по $x$
через производную по $z$ от производной с
относительно $z$.