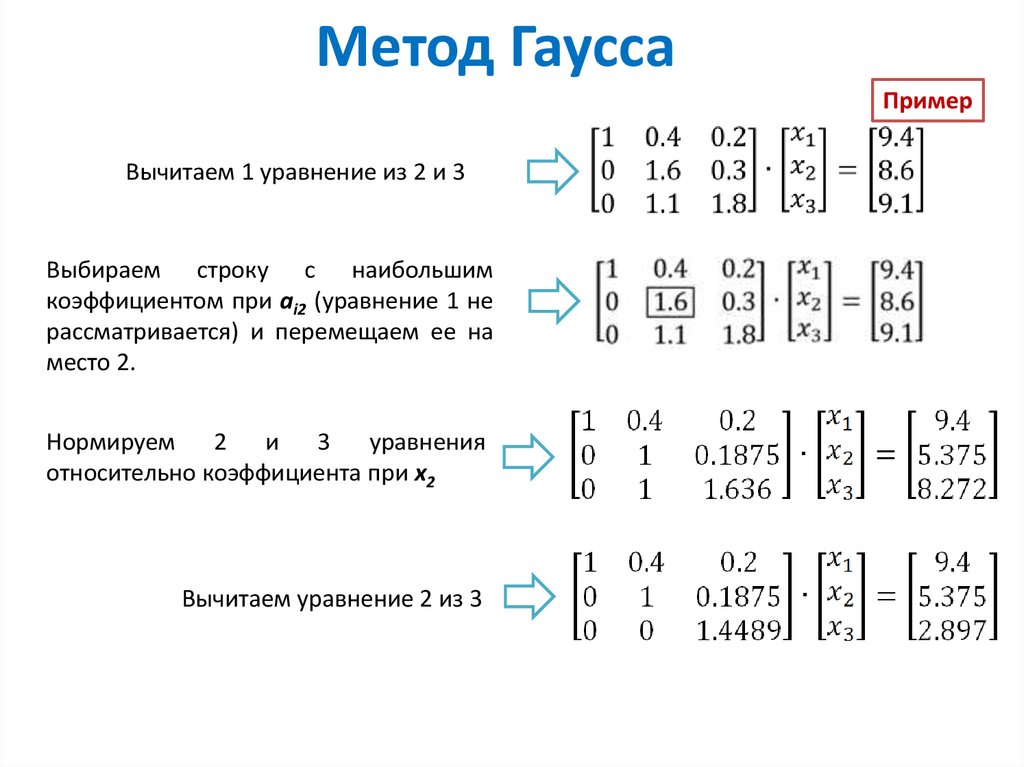
Решение системы уравнений
1. Решение системы уравнений методом Гаусса и с помощью встроенной функции
Задание: Решить систему уравнений методом Гаусса и с помощью встроенной функции: описать теоретический материал соответствующего метода решения, алгоритм применения данного метода для решения системы уравнений, сделать проверку правильности решения
Условие системы уравнений
1.1 Решение системы уравнений методом Гаусса
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно находятся все переменные системы.
Матрица А называется основной матрицей системы, В-столбцом свободных членов.
Достоинства метода:
для матриц ограниченного размера менее трудоёмкий по сравнению с другими методами;
позволяет однозначно установить, совместна система или нет, и если совместна, найти её решение;
позволяет найти максимальное число линейно независимых уравнений — ранг матрицы системы.
Метод Гаусса применим для решения системы линейных алгебраических уравнений c невырожденной матрицей системы. Идея метода Гаусса состоит в том, что систему n линейных алгебраических уравнений относительно n неизвестных x1, x2,…, xn
приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей
решение, которой находят по рекуррентным формулам:
xn =dn, xi = di — S nk=i+1cikxk, i=n-1, n-2,…, 1.
Матричная запись метода Гаусса.
Прямой ход метода Гаусса: приведение расширенной матрицы системы
к ступенчатому виду
с помощью элементарных операций над строками матрицы (под элементарными операциями понимаются следующие операции:
перестановка строк;
умножение строки на число, отличное от нуля;
сложение строки матрицы с другой строкой, умноженной на отличное от нуля число).
Составим матрицу системы и векторов свободных членов с помощью соответствующей пиктограммы на панели «Матрица»:
Производим слияние матриц с помощью функции augment:
Приводим полученную матрицу к ступенчатому виду функцией rref:
Та часть матрицы, полученная в результате вышеуказанных преобразований, в которой ранее находился вектор правых частей, даёт нам вектор неизвестных.
Выделим нужную часть матрицы с помощью оператора SUBMATRIX и получим ответ:
Проведём проверку:
Полученный результат сходится с правой частью, значит система уравнений решена верно.
1.2 Решение систему уравнений с использованием встроенной функции
Для решения систем линейных алгебраических уравнений в программе «MathCad» имеется встроенная функция «lsolve». Рассмотрим решение СЛАУ с её помощью.
Составим матрицу системы:
Выполняем функцию lsolve (Вставка — Функция — lsolve) и получаем ответ:
2. Решение системы уравнений матричным методом и с помощью вычислительного блока Given/Find
Задание: Решить систему уравнений матричным методом и с помощью вычислительного блока Given и функции Find. Описать теоретический материал соответствующего метода решения, алгоритм применения данного метода, сделать проверку правильности решения.
Условие системы уравнений:
.1 Решение системы уравнений матричным методом
Матричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.
Пусть дана система линейных уравнений с n неизвестными (над произвольным полем):
Тогда её можно переписать в матричной форме AX=B, где А — основная матрица системы, В и Х — столбцы свободных членов и решений системы соответственно:
Умножим это матричное уравнение слева на А-1 — матрицу, обратную к матрице А: А-1(АХ) = А-1В.
Так как А-1А = Е, получаем Х = А-1 В. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A, det ?0.
Для однородной системы линейных уравнений, то есть когда вектор В=0, действительно обратное правило: система АХ=0 имеет нетривиальное (то есть ненулевое) решение только если det А=0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
Составим матрицу системы:
Перед нахождением обратной матрицы находим определитель, если он равен нулю, то обратной матрицы не существует:
Получаем решение матрицы:
2.2 Решение системы с помощью блока Given/Find
Решающий блок Given — Find можно применять для решения систем нелинейных уравнений, как в численном, так и в символьном виде. Для численного решения с помощью решающего блока нужно задать начальные значения для неизвестных величин и заключить уравнения в ключевые слова, начинающиеся со слова Given и заканчивающиеся словом Find (var1, var2,…) со знаком =. Для символьного решения системы не надо вводить начальные значения, а вместо знака равно, поставить знак символьного равенства.
Задаём начальные приближённые значения для всех неизвестных, входящих в систему:
Открываем блок Given и записываем уравнения:
С помощью функции Find получает результат:
3. Нахождение производных функций
Задание: Найти производные данных функций.
) Дана функция у, равная:
Введём её в рабочую область программы и отметим курсором переменную х, по которой производится дифференцирование. Затем выполним команды меню: Символьные операции — Переменная — Дифференцировать. В результате получим производную:
) Дана функция у, равная:
Вычислим производную с помощью оператора дифференцирования. Для этого необходимо нажать знак «производная» на панели «математический анализ», затем символьный знак равенства и щёлкнуть левой кнопкой мыши в любом свободном месте документа. На экране появится результат вычисления. Производная исходной функции равна:
3) Дана функция у, равная:
С помощью данного выражения зададим переменную f(x):
Далее вычислим производную с помощью пиктограммы на панели «математический анализ»:
Преимущество данного способа вычисления производной заключается в автоматическом обновлении результата при изменении исходного выражения.
4. Полное исследование функции и построение её графика
Задание: Провести полное исследование функции f(x)= x2 — 2*ln(x) и построить её график.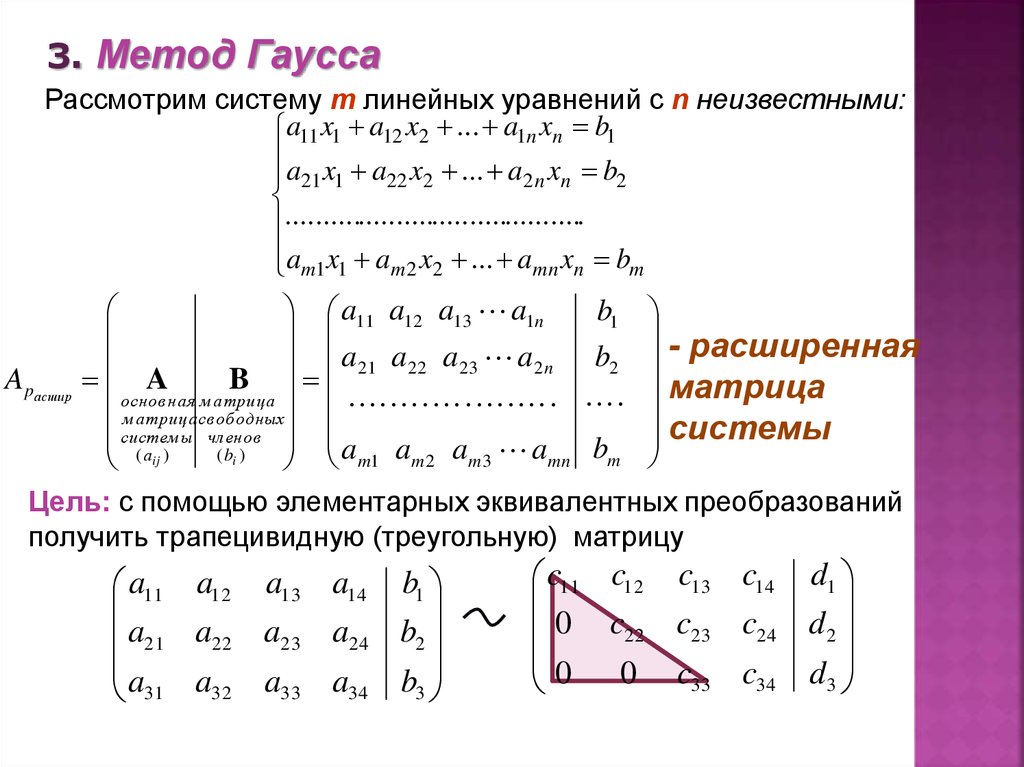
Исследование функции начинают с поиска области определения. Под областью определения понимается множество всех значений аргумента, при которых функция определена, то есть может быть вычислена. Особое внимание следует обратить на логарифмы, входящие в выражение. Если функция содержит логарифм, то на область определения накладываются ограничения исходя из неравенств:
Далее исследуем общие свойства функции: чётность; нечётность; периодичность. Функция f(x) называется чётной, если f(-x)=f(x). График чётной функции симметричен относительно оси ординат. Функция называется нечётной, если f(-x)=-f(x). График функции симметричен относительно начала координат (центральная симметрия). Если функция ни чётная, ни нечётная, то говорят, что функция имеет график общего положения.
Находим точки пересечения графика функции с осями координат.
Абсцисса пересечения с осью OX ищется исходя из уравнения y=f(x)=0. Ордината пересечение с осью OY ищется подстановкой значения в выражение функции y=f(x).
Если пересечение с осью OX найти не удаётся, то обходятся без него. Обычно поиск пересечения с осью OY не представляет труда.
Исследуется непрерывность функции, находятся точки разрыва. Функция f(x) называется непрерывной в точке x0, если она определена в этой точке и существует предел, который равен значению функции.
Функция называется непрерывной на промежутке (отрезке), если она непрерывна в каждой точке этого промежутка (отрезка). Точка x0 является точкой разрыва функции, если функция определена и непрерывна в окрестности точки x0, а в самой точке не является непрерывной (хотя может быть определённой). В этом случае говорят, что функция терпит разрыв в точке x0.
Aсимптоты графика функции.
Прямая называется асимптотой графика функции, если расстояние от точек графика до этой прямой стремится к нулю при бесконечном удалении от начала координат вдоль графика функции. Асимптоты бывают вертикаль-ные, наклонные и горизонтальные. Вертикальные асимптоты ищутся по точкам разрыва второго рода.
Если в точке x0 функция терпит бесконечный разрыв, то вертикальная прямая x= x0 является вертикальной асимптотой. График функции имеет наклонную асимптоту при x?+? (соответственно при x?-?), если существуют конечные пределы . При этом уравнение наклонной асимптоты y=kx+b. Если хотя бы один из двух пределов не существует (или бесконечен), то соответствующей наклонной асимптоты нет.
Критические точки и интервалы монотонности.
Функция y=f(x) имеет максимум в точке x0, если её значение в этой точке больше, чем её значения во всех точках некоторой окрестности, содержащей точку x0. Функция y=f(x) имеет минимум в точке x0, если её значение в этой точке меньше, чем её значения во всех точках некоторой окрестности, содержащей точку x0. Для определения критических точек находим производную по соответствующим правилам и используя таблицу производных. В критических точках производная равна нулю или не существует. Определяем знак производной в интервалах между критическими точками. Если на некотором интервале производная положительна, то функция возрастает.
Если производная отрицательна, то на данном интервале функция убывает.
Tочки перегиба и интервалы выпуклости.
Для определения точек перегиба находят вторую производную. В точке перегиба вторая производная равна нулю или не существует. По знаку второй производной в интервалах между точками перегиба определяют направление выпуклости графика функции. Если вторая производная положительна, то график функции выпуклый вниз. Если вторая производная отрицательная, то график функции выпуклый вверх.
На основании проведённого исследования строим график.
Проверим функцию на чётность / нечётность:
уравнение производный гаусс система
Из этого делаем вывод, что данная функция ни чётная, ни нечётная или общего вида.
Область определения задана на промежутке
График функции имеет вид:
— Точек разрыва нет.
Точки пересечения с осями X и Y:
Значит, график функции не пересекает оси координат.
Интервалы монотонности и точки экстремума функции:
Значение х=-1 не входит в область определения.
Точка с координатами (1; 1) будет являться точкой минимального значения функции, так как выполняется условие f(x) ? f(x0). Функция убывает на промежутке (0; 1), возрастает на промежутке (1;+?).
Выпуклость и вогнутость функции:
Решений нет, оси не пересекает. Функция вогнута.
Асимптоты:
Т.к. функция логарифмическая, то она имеет вертикальную асимптоту, совпадающую с осью ОУ.
Уравнение наклонных асимптот ищут в виде у=kх+b. Находим коэффициент k:
Поскольку k=?, то наклонных асимптот не существует.
5. Построение графика функции
Задание: Построить график функции на промежутке [-10; 10] с шагом 0,5. Функция задана выражением:
Зададим область определения функции на оси х:
С помощью встроенной функции «if» (Вставка — Функция) зададим выражение:
Затем, в меню программы выбираем последовательно команды: Вставка — График — График Х-У, получаем график функции на заданном интервале:
6. Построение графика функции на заданном промежутке и нахождение корней уравнения
Задание: Построить график функции f(x) на заданном промежутке с шагом 0,1 и найти корни уравнения.
Зададим функцию и промежуток, на котором будем искать её значения:
Зададим точность функцией TOL:
Построим график данной функции: Вставка — График — График Х-У:
Так как данное выражение является многочленом n-ой степени, то для его решения применим функцию «polyroots». Запишем коэффициенты поли-нома в вектор, начиная с коэффициента, стоящего у неизвестного низшей степени:
Выполнив последовательно команды меню Вставка — Функция, выбираем функцию «polyroots»:
Значения, полученные в скобках, являются корнями уравнения.
7. Нахождение пределов
Задание: Найти пределы данных выражений
Для нахождения пределов воспользуемся кнопкой «Двухсторонний предел» на панели «Математический анализ». Затем зададим предел для переменной и выражение, предел которого вычисляем. После этого выделим всё выражение и нажмём значок символьного вычисления. Получим искомое значение предела:
8. Нахождение неопределенных и определённых интегралов
Задание: Найти неопределённый и определённый интегралы
Для нахождения неопределённого и определённого интегралов воспользуемся соответствующими операторами интегрирования, выбрав их на панели «Математический анализ».
После ввода оператора интегрирования введём подынтегральную функцию и переменную интегрирования, затем выделим всё выражение и нажмём знак равенства (для неопределённого интеграла — символьного равенства). Получим ответ.
Литература
1 Шушкевич Г.Ч., Шушкевич С.В.: «Введение в MathCad», учебное пособие, издательство ГрГУ им Я. Купалы, Гр. — 2001 г.
Бугров Я.С. Никольский С.М.: «Высшая математика: Учебник для вузов», Дрофа-2004 г.
w
Теги:
Решение системы уравнений
Контрольная работа
Математика
Просмотров: 16338
Найти в Wikkipedia статьи с фразой: Решение системы уравнений
Гауссовский метод исключения — Уроки Византа
Метод решения систем уравнений методом исключения также известен как метод исключения Гаусса
, потому что он приписывается Карлу Фридриху Гауссу как изобретателю метода
.
Исключение или включает в себя манипулирование данной системой уравнений таким образом, что одна
или более переменных исключается, оставляя уравнение с одной переменной, которое затем может быть легко решено.
Оттуда обратная замена используется, чтобы найти другие
переменных.
Решение систем уравнений методом исключения
При решении систем уравнений с двумя переменными метод исключения включает в себя
манипулирование одним уравнением путем умножения его на константу таким образом, что когда это
уравнение добавляется к другому уравнению в системе, одна переменная удаляется
и все такое. осталось уравнение с одной переменной, которое мы можем легко решить. После того, как
получили решение этой переменной, мы подставляем это значение в любое из
уравнений, чтобы найти другую переменную.
Учитывая систему уравнений ниже;
Процесс исключения позволяет нам умножить уравнение (1) или (2) таким образом, что при сложении двух уравнений одна из переменных будет исключена.
Например, если бы мы хотели исключить переменную x , мы бы получили это число
, умножив уравнение (1) или (2) на некоторую константу, которая гарантирует, что
уравнение (1) + уравнение (2) равно уравнению (3), которое имеет только одну переменную
y .
Если мы умножим уравнение (2) на константу -a ⁄ c , мы
получим следующий результат
что упрощается до
Тогда, если бы мы добавили новое уравнение (2n) выше к уравнению (1), мы бы наблюдали
следующее:
будет
Это уравнение с одной переменной для y , и мы можем перейти к решению для
y . После получения значения y мы можем подставить его либо в
уравнение (1), либо в уравнение (2), из которого мы можем вычислить значение x .
Давайте попробуем несколько примеров, чтобы увидеть, как все это работает.
Пример 1
Решите следующую систему уравнений
Шаг 1
Для того, чтобы отслеживать, о каком уравнении мы говорим, первым шагом всегда должна быть маркировка уравнений в системе.
Этап 2
Следующим шагом является проверка уравнений, чтобы увидеть, как мы можем манипулировать ими, чтобы получить
избавиться от одной из переменных. Этот пример довольно прост, чтобы избавиться от
переменной y , нам не нужно умножать какое-либо уравнение на какую-либо константу,
мы можем просто сложить два уравнения, и переменная y просто исчезнет.
Это связано с тем, что в обоих уравнениях коэффициент y в уравнении (1) равен
, что противоположно коэффициенту в уравнении (2), т.е. .
Этап 3
Вышеупомянутое уравнение представляет собой уравнение с одной переменной для x , и мы можем легко решить для x
, разделив на 5
Этап 4
Теперь, когда у нас есть решение для x , мы можем заменить x в уравнении (1)
, чтобы получить уравнение с одной переменной, которое мы можем использовать для решения для y .
замена х
Следовательно, мы имеем решение системы уравнений как x = 5 и y = -1 .
Пример 2
Решите следующую систему уравнений
Шаг 1
Первый шаг — пометить уравнения, чтобы мы знали, какое уравнение мы имеем в виду.
Этап 2
Затем мы исследуем систему уравнений, чтобы увидеть, как мы можем эффективно исключить
одну из переменных.
Изучив систему, мы можем заметить, что мы можем умножить уравнение (1) на
-3, так что, сложив два уравнения, мы можем исключить x .
что приводит к
Этап 3
Далее мы продолжаем добавлять новое уравнение к уравнению (2)
Что упрощается до
Этап 4
Значение y было получено как -1 . Мы продолжаем использовать это значение
для решения x , подставляя y в любое из приведенных выше уравнений.
Подставим y в исходное уравнение (1)
Решение системы уравнений: {x,y} = {-1,-1} .
Пример 3
Найдите значения x и y в системе уравнений, приведенной ниже
Шаг 1
Когда вам дана система уравнений в неорганизованном виде, как указано выше,
всегда лучше начать с перестановки уравнений таким образом, чтобы переменные
0003 совпадает. Это облегчит работу с уравнениями. Затем вы можете продолжить
, чтобы пометить уравнения.
Этап 2
При рассмотрении приведенной выше системы не так очевидно, на какую константу умножить
на уравнение (1) или (2), чтобы исключить одну из переменных. Когда возникает такая
ситуация, вы выбираете одну переменную и решаете, что хотите исключить
что, затем вы выбираете одно уравнение и умножаете его на дробь, числитель которой равен
отрицательному значению коэффициентной переменной, которую мы исключаем из другого уравнения,
а знаменатель является коэффициентом переменной для уравнения, которое мы умножаем .
Для этого примера удалим переменную x и сначала поработаем с уравнением (2):
что упрощает как
Этап 3
Добавление вышеуказанного к уравнению (2) приводит к следующим
Шаг 4
Теперь, когда у нас есть значение y , мы можем подставить и найти x
следующим образом;
Решение системы уравнений: {x,y} = { 148 ⁄ 95 , -43 ⁄ 19 }
Решение систем уравнений с тремя переменными методом исключения
Решение систем уравнений с тремя переменными мало чем отличается от решения этих
с двумя переменными.
Основная концепция остается той же, только в этом случае мы
пойдем немного дальше, чтобы учесть третью переменную.
Подобно тому, как мы решали для двух переменных, когда дело доходит до трех переменных,
мы начинаем с манипулирования двумя из трех уравнений таким образом, что когда они добавляются к другому уравнению, одна из переменных полностью исчезает. Затем мы фокусируемся на этих новых уравнениях с двумя переменными, а также манипулируем ими таким образом, чтобы
0003 остаются с уравнением с одной переменной.
Учитывая систему уравнений ниже
Мы можем найти переменные x , y и z следующим образом:
Сначала мы выбираем уравнение (1) и используем его для исключения переменной x из
других уравнений.
Мы можем добиться этого в уравнении (2), умножив уравнение на константу, такую
, что, когда мы добавляем уравнение (2) к уравнению (1), x переменная исчезает.
Умножение вышеприведенного на константу a ⁄ d
Добавляя вышеуказанное к уравнению (1):
результат:
Выше приведено новое уравнение (2).
Мы также исключаем переменную x из уравнения (3) аналогичным образом:
умножение на константу
Добавляя вышеуказанное к уравнению (1)
что приводит к
Выше приведено новое уравнение (3)
Итак, теперь у нас есть два уравнения с двумя переменными, мы можем решить эти уравнения с двумя переменными
, используя то, что мы узнали в разделе о системах уравнений с двумя переменными выше.
Давайте посмотрим на примере, как работает приведенный выше алгоритм
. Пример 4
Решите следующую систему уравнений
Шаг 1
Мы начнем с того, что пометим наши уравнения, чтобы было легче обращаться к ним
.
Этап 2
Затем мы выбираем переменную y уравнения (2), мы проверяем это уравнение вместе
с уравнением (1), чтобы найти способ исключить это уравнение.
Этап 3
Из проверки вы можете видеть, что простое добавление уравнения (1) к уравнению (2) вы
эффективно исключите переменную y из уравнения (2)
результаты в
Выше приведено новое уравнение (2)
Этап 4
Делаем то же самое для уравнения (3)
Но обратите внимание, что в этом случае нам повезло, что уравнение (3) уже является уравнением с двумя переменными
в z и x .
Этап 5
Таким образом, мы можем перейти к обработке уравнений (2) и (3) как системы уравнений с двумя переменными
Изучив приведенную выше систему, мы можем выбрать любую переменную для исключения, поскольку
все они будут относительно простыми, но давайте возьмем x .
Шаг 6
Мы можем исключить x, умножив уравнение (3) на -1, а затем добавив результат
к уравнению 2 следующим образом:
что дает
что приводит к
Шаг 7
Выше приведено относительно простое уравнение с одной переменной, из которого мы можем решить для
x , разделив обе части на 3:
Затем, используя обратную замену, мы можем найти x и y , начиная с
x .
Чтобы найти x , мы подставляем значение z в уравнение (2)
Шаг 8
Теперь, когда у нас есть значения для x и z , мы можем найти y , подставив
этих значений в уравнение (1)
Решением системы уравнений является {х, у, г} = {1, 2, 3}
Пример 5
Найдите x, y и z из системы уравнений ниже
Шаг 1
Как всегда, мы начинаем с маркировки уравнений, чтобы на них было легче ссылаться.
Этап 2
Далее рассмотрим уравнения (1) и (2) так, чтобы исключить одну из переменных;
в данном случае x
Этап 3
Мы можем видеть, что если мы умножим уравнение (2) на -1 ⁄ 3 ,
, а затем добавим результат к уравнению (1), мы можем получить новое уравнение (2), в котором
будет двумя уравнение переменной в y и z .
что приводит к:
Этап 4
Добавление приведенного выше результата к уравнению (1)
результат:
Приведенное выше становится нашим новым уравнением (2).
Этап 5
Затем мы выполняем ту же процедуру для уравнения (3):
Изучая приведенную выше систему, мы можем видеть, что если мы умножим уравнение (3) на
-1 ⁄ 6
результат:
Шаг 6
Затем мы добавляем вышеуказанное к уравнению (1)
что приводит к:
Приведенный выше результат становится нашим новым уравнением (3)
Шаг 7
Теперь мы получили новую систему уравнений, которая имеет только две переменные:
Шаг 8
Мы можем исключить y из приведенной выше системы, умножив уравнение (3) на
-2 ⁄ 3 , а затем добавив результат к уравнению (2).
Результирующее уравнение
будет уравнением с одной переменной в z , и мы можем решить
для z из этого.
результат:
Шаг 9
Добавляя вышеуказанное к уравнению (2):
что приводит к;
Мы можем решить z из приведенного выше:
Шаг 10
Используя обратную замену, теперь мы можем найти и , затем x .
Сначала мы находим y , подставляя значение z в уравнение (2):
Шаг 11
Получив y , мы можем найти х , подставив y и z
в уравнение (1):
Решение системы уравнений: {x, y, z} = { 1 ⁄ 14 , 4 ⁄ 21 , 8 ⁄ 7 1 1 1 1 7 2} Квантовый алгоритм играет заметную роль в решении линейных систем уравнений с экспоненциальным ускорением по сравнению с классическим алгоритмом. Здесь мы демонстрируем метод исключения Гаусса для решения системы уравнений с использованием хорошо известного алгоритма квантового поиска Гровера. Метод исключения в основном включает в себя элементарные операции со строками, которые можно выполнить, применяя определенные матрицы, которые можно получить из алгоритма Гровера. Мы явно проиллюстрируем весь процесс, взяв… View PDF on arXiv Эта работа направлена на улучшение существующих подходов к объяснению алгоритма поиска Гровера и предлагает новую методологию его обучения, которая позволяет избежать сложных описаний и использует простой прикладной пример, а именно классическое деление. Информатика Компьютеры, материалы и непрерывность Кратко описаны три репрезентативных квантовых алгоритма, а именно алгоритмы Дойча-Йожа, Гровера и Шора, а затем представлены схемы их реализации, соответственно. показать реализуемость этих алгоритмов и оценить функциональные возможности этих устройств. Информатика 7-кубитная квантовая схема, основанная на более ранней работе Сао и др., чтобы решить задачу регрессии с тремя переменными, используя только базовые квантовые вентили, обсуждаются результаты моделирования схемы с помощью Qiskit и исследуются некоторые возможные обобщения. Информатика, физика количество вентилей и количество уровней) для большого количества схем Clifford+T, которые уже реализованы в квантовых компьютерах IBM. Физика Квантовое скремблирование, измеренное вневременно-упорядоченным коррелятором понимания физики (ОТОС) играет важную роль в понимании физики дыры и оценка квантового хаоса. Известно, что атом Ридберга имеет… Предлагается новая квантовая схема для проектирования квантового маршрутизатора с использованием квантового компьютера IBM с пятью кубитами, и запутанность между управляющим кубитом и двумя сигнальными кубитами проиллюстрировано, и хорошее сохранение информации о сигнале в любом из двух путей после процесса маршрутизации. Physics, Computer Science IET Quantum Communication An код обнаружения ошибок для (2n+1)-кубитного запутанного состояния с использованием двух синдромных кубитов представлен и смоделирован на 16-кубитном квантовом компьютере IBM для 13-кубитной запутанной системы, чтобы проложить путь к разработке кодов обнаружения ошибок для общего высшего количество запутанных систем кубитов. Информатика, физика Квантовая инф. Процесс. Представленный здесь квантовый робот демонстрирует поведение «страха», его движение носит детерминированный характер и может быть успешно смоделировано в игре, где он всегда может избежать несчастного случая. Информатика Рассчитывается шумовой порог бит-фазового шума для требуемой вероятности успеха, и результат показывает, что GSA с шумом в пределах порог по-прежнему превосходит свой классический аналог. Предлагается квантовый алгоритм поиска со сдвигом фазы π/18 для поиска мультипликативного обратного уравнения в несортированной базе данных с временной сложностью с лучшей производительностью, чтобы найти матч. ПОКАЗАНЫ 1-10 ИЗ 41 ССЫЛОК СОРТИРОВАТЬ ПОРелевантность Наиболее влиятельные статьиНедавность Информатика, математика Письма с физическим обзором (—>), время выполнения которого является полиномом от log(N) и каппа, и доказывает, что любой классический алгоритм для этой задачи обычно требует экспоненциально больше времени, чем этот квантовый алгоритм. Этот специальный выпуск журнала Mathematical Structures in Computer Science содержит несколько статей, связанных с современной областью квантовой информации и квантовых вычислений. Первые две статьи касаются… Физика, химия Природохимия Применение новейшей фотонной квантовой компьютерной технологии для расчета свойств наименьшей молекулярной системы: сообщается о молекуле водорода в минимальном базисе, а полный энергетический спектр рассчитывается с точностью до 20 бит. Компьютерные науки, физика Эта работа показывает здесь для n-кубитного случая, что алгоритм квантовой перестановки может быть упрощен, так что он требует только O(n) квантовых вентилей, которые теоретически снижает сложность реализации. Physics, Computer Science [PDF] Решение линейных систем уравнений методом исключения Гаусса с использованием алгоритма поиска Гровера: опыт IBM Quantum
@article{Srinivasan2017SolvingLS,
title={Решение линейных систем уравнений методом исключения Гаусса с использованием алгоритма поиска Гровера: квантовый опыт IBM},
автор = {Картик Шринивасан и Бикаш К.
Бехера и Прасанта К. Паниграхи},
журнал={arXiv: квантовая физика},
год = {2017}
} ПОНИМАНИЕ АЛГОРИТМА ПОИСКА ГРОВЕРА НА ПРОСКОМ ПРИМЕРЕ ИССЛЕДОВАНИЯ
Квантовые алгоритмы и реализации экспериментов на основе IBM Q
Демонстрация методологии проектирования квантовых схем для множественной регрессии
Оптимизация схемы для процессоров IBM: способ получить более высокую точность и более высокие значения неклассичности свидетелей
Применение квантового скремблирования в ридберговском атоме на квантовом компьютере IBM
Проектирование квантового маршрутизатора в квантовом компьютере IBM
Демонстрация общего отказоустойчивого квантового кода обнаружения ошибок для (2
н
+ 1)‐qubit entangled state on IBM 16‐qubit quantum computer
Квантовые роботы умеют летать; играть в игры: квантовый опыт IBM
Производительность алгоритма поиска Гровера с диагонализируемым шумом
Мультипликативный обратный алгоритм с квантовым алгоритмом поиска при повороте фазы π/18
Квантовый алгоритм для линейных систем уравнений.
Harrow, Avinatan Hassidim, S. Lloyd Квантовые вычисления и квантовая информация
На пути к квантовой химии на квантовом компьютере.
Оптимизация и экспериментальная реализация алгоритма квантовой перестановки
Моделирование ферми-систем многих тел на универсальном квантовом компьютере
Быстрый квантово-механический алгоритм для поиска в базе данных
- Лов К. Гровер
Информатика
STOC ’96
- 1996
эффективный алгоритм с использованием классических компьютеров, то есть проверка того, является ли заданное целое число N простым или нет, за время, которое является конечной степенью o (logN) .
Быстрое решение задач с помощью квантовых вычислений
Описан класс задач, которые могут быть решены с помощью квантовых вычислений более эффективно, чем с помощью любого классического или стохастического метода. Квантовые вычисления уверенно решают проблему в…
Приближенные квантовые сумматоры с генетическими алгоритмами: квантовый опыт IBM
- Руи Ли, У. Альварес-Родригес, Л. Ламата, Э. Солано
Физика, информатика
- 2017
В данной работе анализируются теоретические предложения по реализации приближенных квантовых сумматоров и их оптимизация с помощью генетических алгоритмов, улучшающих предыдущие протоколы с точки зрения эффективности и точности.
Аппаратно-эффективный вариационный квантовый собственный решатель для малых молекул и квантовых магнитов
- А. Кандала, А. Меццакапо, Дж. Гамбетта
Физика
Природа
- 2017 9 до шести кубитов и более ста членов Паули, определяя энергию основного состояния для молекул увеличивающегося размера, вплоть до Beh3.
