Дискретное распределение: Дискретное распределение | это… Что такое Дискретное распределение?

Дискретное распределение | это… Что такое Дискретное распределение?

ТолкованиеПеревод

Дискретное распределение

Фу́нкция вероя́тности в теории вероятностей — наиболее часто используемый способ охарактеризовать дискре́тное распределение.

Содержание 1 Определения 1.1 Функция произвольной вероятности 1.2 Функция вероятности случайной величины 2 Свойства функции вероятности 3 Примеры дискретных распределений 4 См. также

Определения

Функция произвольной вероятности

Пусть является вероятностной мерой на , то есть определено вероятностное пространство , где обозначает борелевскую σ-алгебру на .

Определение 1. Вероятностная мера называется дискретной, если её носитель не более, чем счётен, то есть существует не более, чем счётное подмножество такое, что .

Определение 2. Функция , определённая следующим образом:

называется функцией вероятности .

Функция вероятности случайной величины

Определение 3. Пусть — случайная величина (случайный вектор). Тогда она индуцирует вероятностную меру на , называемую распределением. Случайная величина называется дискретной, если её распределение дискретно. Функция вероятности p_X случайной величины X имеет вид:

.

или короче

,

где .

Свойства функции вероятности

Из свойств вероятности очевидно следует:

• .
• .
• Функция распределения случайной величины может быть выражена через её функцию вероятности:

.

• Если X = (X₁,X₂), то

,

,

где — функция вероятности вектора (X₁,X₂), а — функция вероятности величины .

Это свойство очевидно обобщается для случайных векторов размерности n > 2.

• Математическое ожидание функции от дискретной величины, когда оно существует, имеет вид:

,

при условии что ряд в правой части абсолютно сходится.

Примеры дискретных распределений

• Распределение Бернулли;
• Биномиальное распределение;
• Геометрическое распределение;
• Гипергеометрическое распределение;
• Логарифмическое распределение;
• Отрицательное биномиальное распределение;
• Распределение Пуассона;
• Дискретное равномерное распределение;
• Мультиномиальное распределение.

См. также

• Плотность вероятности.

Wikimedia Foundation. 2010.

Игры ⚽ Поможем сделать НИР

• Дискретное топологическое пространство
• Дискретный фильтр

Полезное

Дискретное распределение | это.

.. Что такое Дискретное распределение?

ТолкованиеПеревод

Дискретное распределение

Фу́нкция вероя́тности в теории вероятностей — наиболее часто используемый способ охарактеризовать дискре́тное распределение.

Содержание 1 Определения 1.1 Функция произвольной вероятности 1.2 Функция вероятности случайной величины 2 Свойства функции вероятности 3 Примеры дискретных распределений 4 См. также

Определения

Функция произвольной вероятности

Пусть является вероятностной мерой на , то есть определено вероятностное пространство , где обозначает борелевскую σ-алгебру на .

Определение 1. Вероятностная мера называется дискретной, если её носитель не более, чем счётен, то есть существует не более, чем счётное подмножество такое, что .

Определение 2. Функция , определённая следующим образом:

называется функцией вероятности .

Функция вероятности случайной величины

Определение 3. Пусть — случайная величина (случайный вектор). Тогда она индуцирует вероятностную меру на , называемую распределением. Случайная величина называется дискретной, если её распределение дискретно. Функция вероятности p_X случайной величины X имеет вид:

.

или короче

,

где .

Свойства функции вероятности

Из свойств вероятности очевидно следует:

• .
• .
• Функция распределения случайной величины может быть выражена через её функцию вероятности:

.

• Если X = (X₁,X₂ ), то

,

,

где — функция вероятности вектора (X₁,X₂), а — функция вероятности величины . Это свойство очевидно обобщается для случайных векторов размерности n > 2.

• Математическое ожидание функции от дискретной величины, когда оно существует, имеет вид:

,

при условии что ряд в правой части абсолютно сходится.

Примеры дискретных распределений

• Распределение Бернулли;
• Биномиальное распределение;
• Геометрическое распределение;
• Гипергеометрическое распределение;
• Логарифмическое распределение;
• Отрицательное биномиальное распределение;
• Распределение Пуассона;
• Дискретное равномерное распределение;
• Мультиномиальное распределение.

См. также

• Плотность вероятности.

Wikimedia Foundation. 2010.

Игры ⚽ Поможем сделать НИР

• Дискретное топологическое пространство
• Дискретный фильтр

Полезное

Дискретное распределение вероятностей: определение и примеры

Вероятностные распределения > Дискретное распределение вероятностей

Вы можете сначала прочитать эту статью:
Дискретные и непрерывные переменные

Что такое дискретное распределение вероятностей?

В статистике вы встретите десятки различных типов вероятностных распределений, таких как биномиальное распределение, нормальное распределение и распределение Пуассона.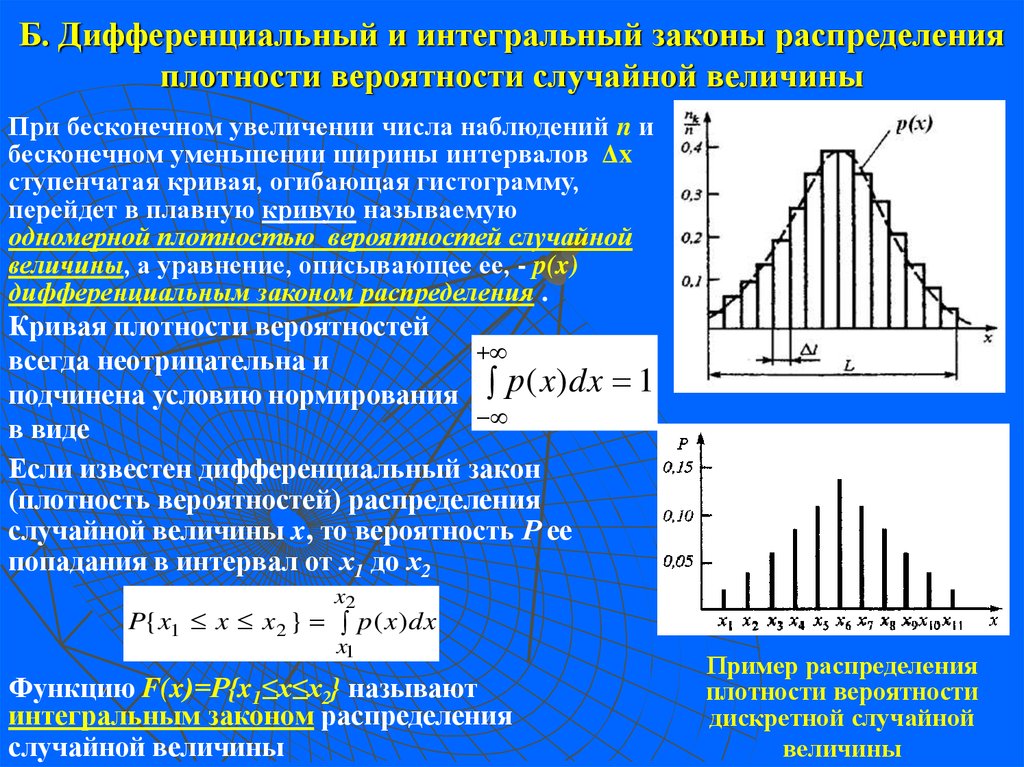 Все эти распределения можно классифицировать как непрерывное или дискретное распределение вероятностей.
Дискретное распределение вероятностей состоит из дискретных переменных. В частности, если случайная величина является дискретной, то она будет иметь дискретное распределение вероятностей.

Примеры дискретного распределения вероятностей

Например, предположим, что у вас есть выбор сыграть две азартные игры на ярмарке.
Игра 1: Бросьте кубик. Если выпадет шестерка, вы выиграете приз.
Игра 2: Угадай вес человека. Если вы угадаете в пределах 10 фунтов, вы выиграете приз.
Одна из этих игр представляет собой дискретное распределение вероятностей, а другая — непрерывное распределение вероятностей. Какой какой?

В игре 1 вы можете выбросить 1, 2, 3, 4, 5 или 6. Все броски кубиков имеют равные шансы выпадения (один из шести, или 1/6). Это дает вам дискретное распределение вероятности из:

Рулон	1	2	3	4	5	6
Шансы	1/6	1/6	1/6	1/6	1/6	1/6

Альберт Харрис | Wikimedia Commons
В игре «Угадай вес» можно предположить, что среднее значение весит 150 фунтов.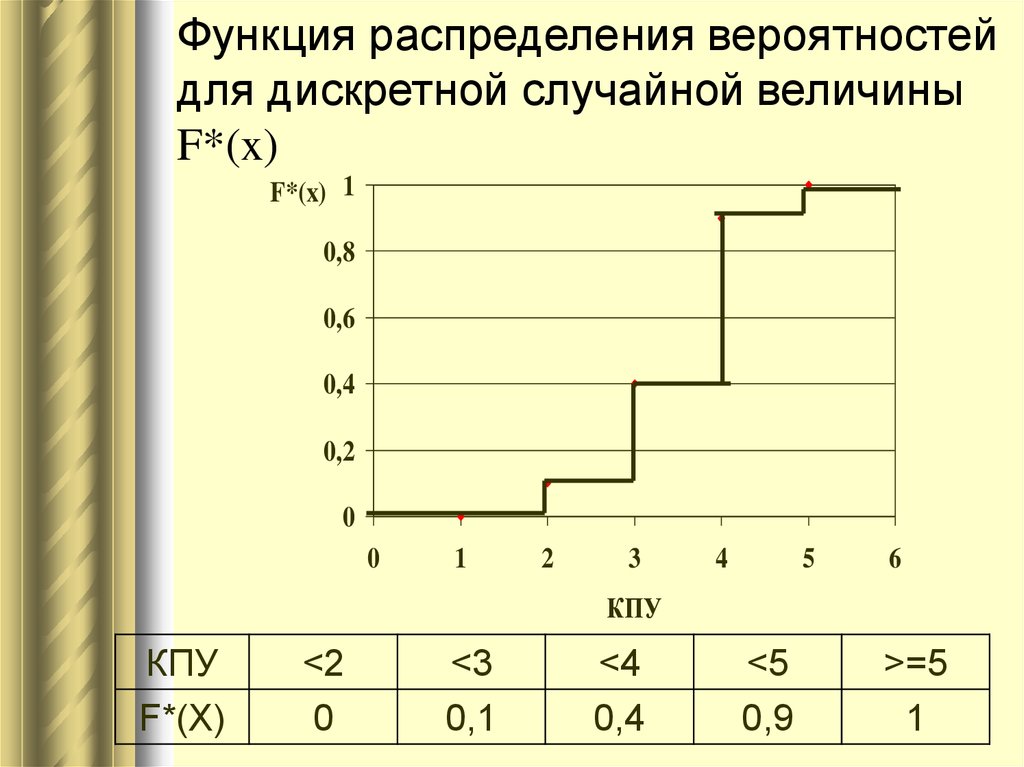 Или 210 фунтов. Или 185,5 фунтов. Или любая часть фунта (172,566 фунта). Даже если вы придерживаетесь, скажем, между 150 и 200 фунтами, возможности безграничны:

• 160,1 фунта.
• 160,11 фунта.
• 160,111 фунтов.
• 160,1111 фунтов.
• 160,111111 фунтов.

В действительности вы, вероятно, не догадались бы, что 160,111111 фунтов… это кажется немного смешным. Но это не меняет того факта, что вы могли бы (если бы захотели), поэтому это непрерывное распределение вероятностей

.

Ниже приведены примеры дискретных вероятностных распределений, обычно используемых в статистике:

• Биномиальное распределение.
• Геометрическое распределение
• Гипергеометрическое распределение.
• Полиномиальное распределение.
• Отрицательное биномиальное распределение.
• Распределение Пуассона.

Посетите наш канал статистики YouTube, где вы найдете сотни видео со статистикой.

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Дискретное распределение вероятностей: определение и примеры» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/discrete-probability-distribution/

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .

Дискретное распределение вероятностей — примеры, определение, типы

Дискретное распределение вероятностей — это тип распределения вероятностей, который показывает все возможные значения дискретной случайной величины вместе с соответствующими вероятностями.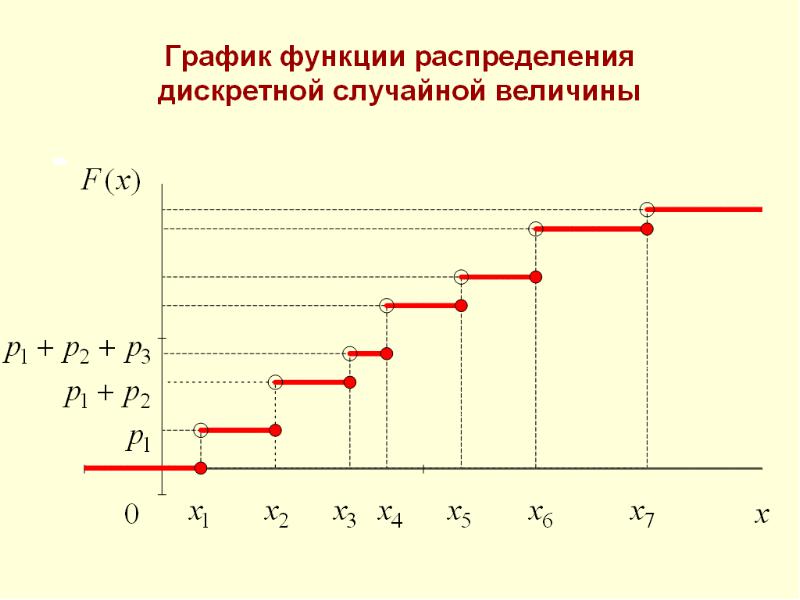 Другими словами, дискретное распределение вероятностей дает вероятность появления каждого возможного значения дискретной случайной величины.

Геометрические распределения, биномиальные распределения и распределения Бернулли являются одними из наиболее часто используемых дискретных распределений вероятностей. Эта статья проливает свет на определение дискретного распределения вероятностей, его формулы, типы и различные связанные примеры.

1.	Что такое дискретное распределение вероятностей?
2.	Дискретная формула распределения вероятностей
3.	Типы дискретного распределения вероятностей
4.	Как найти дискретное распределение вероятностей?
5.	Часто задаваемые вопросы о дискретном распределении вероятностей

Что такое дискретное распределение вероятностей?

Дискретное распределение вероятностей и непрерывное распределение вероятностей — это два типа распределений вероятностей, которые определяют соответственно дискретные и непрерывные случайные величины.

Распределение вероятностей можно определить как функцию, описывающую все возможные значения случайной величины, а также связанные с ней вероятности.

Дискретное распределение вероятностей Определение

Дискретное распределение вероятностей можно определить как распределение вероятностей, дающее вероятность того, что дискретная случайная величина будет иметь заданное значение. Такое распределение будет представлять данные, имеющие конечное счетное число результатов. Есть два условия, которым должно удовлетворять дискретное распределение вероятностей. Они задаются следующим образом:

• 0 ≤ P(X = x) ≤ 1. Это означает, что вероятность того, что дискретная случайная величина X примет точное значение x, лежит в пределах от 0 до 1,9.0069
• ∑P(X = x) =1. Сумма всех вероятностей должна быть равна 1.

Пример дискретного распределения вероятностей

Предположим, что подброшены игральные кости и необходимо создать дискретное распределение вероятностей.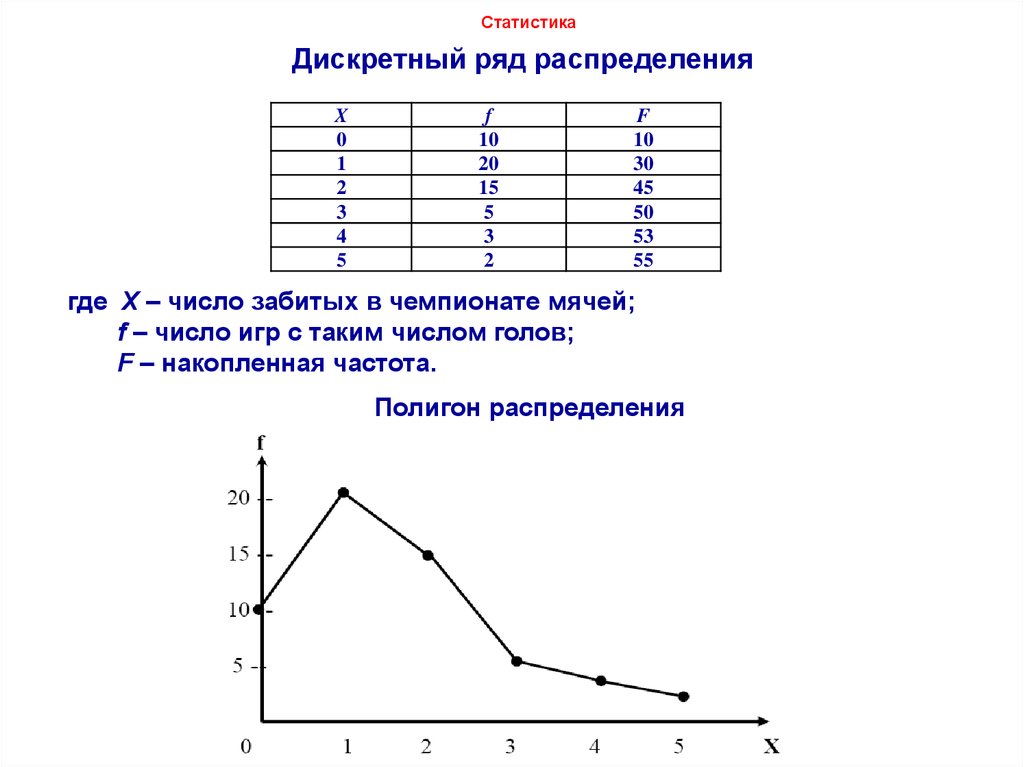 Возможные исходы: {1, 2, 3, 4, 5, 6}. Таким образом, общее количество исходов будет равно 6. Все числа имеют равные шансы выпасть. Это означает, что вероятность выпадения любого числа равна 1/6. Используя эти данные, таблица дискретного распределения вероятностей для броска костей может быть представлена ​​следующим образом:

х	1	2	3	4	5	6
Р(Х = х)	1 / 6	1 / 6	1 / 6	1 / 6	1 / 6	1 / 6

Дискретная формула распределения вероятностей

Дискретная случайная величина используется для моделирования дискретного распределения вероятностей. Есть две основные функции, связанные с такой случайной величиной. Это функция массы вероятности (PMF) и функция распределения вероятностей или кумулятивная функция распределения (CDF).

Дискретное распределение вероятностей PMF

Функция массы вероятности может быть определена как функция, которая дает вероятность того, что дискретная случайная величина X точно равна некоторому значению x. Эта функция требуется при создании дискретного распределения вероятностей. Формула дается следующим образом:

f(x) = P(X = x)

Дискретное распределение вероятностей CDF

Кумулятивная функция распределения дает вероятность того, что дискретная случайная величина будет меньше или равна определенному значению. Значение CDF можно рассчитать, используя дискретное распределение вероятностей. Его формула выглядит следующим образом:

F(x) = P(X ≤ x)

Среднее значение дискретного распределения вероятностей

Среднее значение дискретного распределения вероятностей дает средневзвешенное значение всех возможных значений дискретной случайной величины. Его также называют ожидаемым значением. Формула среднего значения дискретной случайной величины выглядит следующим образом:

E[X] = ∑x P(X = x)

Дисперсия дискретного распределения вероятностей

Дисперсия дискретного распределения вероятностей дает дисперсию распределения относительно среднего. Его можно определить как среднее квадратов отличий распределения от среднего \(\mu\). Формула приведена ниже:

Var[X] = ∑(x — \(\mu\)) ² P(X = x)

Дискретные типы распределения вероятностей

Дискретное распределение вероятностей используется в моделировании методом Монте-Карло для определения вероятностей различных исходов. Ниже приведены наиболее часто используемые типы дискретных распределений вероятностей.

Распределение Бернулли

Распределение Бернулли — это тип дискретного распределения вероятностей, в котором случайная величина может быть либо равна 0 (неудача), либо равна 1 (успех). Вероятность успеха равна p, а вероятность неудачи равна 1-p. Он обозначается как X ∼ Бернулли (p). PMF выражается следующим образом:

P(X = x) = \(\left\{\begin{matrix} p &,if \: x = 1 \\ 1-p & , if \: x = 0 \ end{matrix}\right.\)

Биномиальное распределение 9{n-x}\)

Геометрическое распределение

Геометрическое распределение — это еще один тип дискретного распределения вероятностей, который представляет вероятность получения ряда последовательных неудач до получения первого успеха. Он задается X ∼ G(p). Формула для PMF дается следующим образом:

P(X = x) = (1 — p) ^x p, где p — вероятность успеха испытания.

Распределение Пуассона

Распределение Пуассона — это дискретное распределение вероятностей, которое широко используется в области финансов. Он дает вероятность того, что заданное количество событий произойдет в течение фиксированного периода времени. Обозначение записывается как X ∼ Pois(\(\lambda\)), где \(\lambda>0\). PMF определяется по следующей формуле: 9{-\лямбда}}{х!}\)

Как найти дискретное распределение вероятностей?

Дискретное распределение вероятностей может быть представлено либо в виде таблицы, либо с помощью графика. Чтобы найти дискретное распределение вероятностей, требуется функция массы вероятности. Другими словами, для построения дискретного распределения вероятностей требуются все значения дискретной случайной величины и связанные с ними вероятности. Предположим, что честная монета подбрасывается дважды. Скажем, дискретное распределение вероятностей должно быть определено для количества наблюдаемых орлов. Шаги следующие:

• Шаг 1: Определите пространство выборки для эксперимента. Когда честная монета подбрасывается дважды, пространство выборки равно {HH, HT, TH, TT}. Здесь H обозначает голову, а T представляет хвост. Таким образом, общее количество исходов равно 4.
• Шаг 2: Задайте дискретную случайную величину X. Например, пусть X будет количеством наблюдаемых голов.
• Шаг 3: Определите возможные значения, которые может принимать переменная. Существует 3 возможных значения X. Это 0 (орел не наблюдается), 1 (наблюдается ровно один орел) и 2 (монета дважды падает орлом).
• Шаг 4: Рассчитайте вероятность каждого исхода. В данном примере вероятность можно рассчитать по формуле количество благоприятных исходов / общее количество возможных исходов.
• Шаг 5: Чтобы получить дискретное распределение вероятностей, представьте вероятности и соответствующие исходы в табличной или графической форме. Это выражается следующим образом:

х	0 {ТТ}	1 {HT, TH}	2 {ЧЧ}
Р(Х = х)	1/4 = 0,25	2/4 = 0,5	1/4 = 0,25

Гистограмму можно использовать для представления дискретного распределения вероятности для этого примера.

Статьи по теме:

• Отрицательное биномиальное распределение
• Вероятность и статистика
• Вероятностные правила

Важные замечания по дискретному распределению вероятностей

• Дискретное распределение вероятностей используется для моделирования результатов дискретной случайной величины, а также связанных с ней вероятностей.
• Дискретное распределение используется для расчета вероятности того, что случайная величина будет точно равна некоторому значению.
• 0 ≤ P(X = x) ≤ 1 и ∑P(X = x) =1 — два условия, которым должно удовлетворять дискретное распределение вероятностей.
• Примерами дискретного распределения вероятностей являются распределение Бернулли, биномиальное распределение, распределение Пуассона и геометрическое распределение.

Часто задаваемые вопросы о дискретном распределении вероятностей

Что такое дискретное распределение вероятностей в теории вероятностей?

Дискретное распределение вероятностей используется для моделирования вероятности каждого результата дискретной случайной величины. Это распределение используется, когда случайная величина может принимать только конечные счетные значения.

Каковы два ключевых требования для дискретного распределения вероятностей?

Два ключевых требования для достоверности дискретного распределения вероятностей:

• 0 ≤ P(X = x) ≤ 1.
• ∑P(X = x) =1.

Как построить дискретное распределение вероятностей?

Шаги построения дискретного распределения вероятностей следующие:

• Определите пространство выборки или общее количество возможных результатов.
• Задайте дискретную случайную величину и значения, которые она может принимать.
• Найдите вероятность появления каждого значения.
• Представьте значения случайных величин вместе с соответствующими вероятностями в табличной или графической форме, чтобы получить дискретное распределение вероятностей.

Как найти среднее значение дискретного распределения вероятностей?

Среднее значение случайной величины X после дискретного распределения вероятностей можно определить по формуле E[X] = ∑x P(X = x).

Как найти дисперсию дискретного распределения вероятностей?

Чтобы найти переменную случайной величины, следуя дискретному распределению вероятностей, примените формулу Var[X] = ∑(x — \(\mu\)) ² P(X = x). Здесь \(\mu\) — среднее значение распределения.

Может ли ожидаемое значение дискретного распределения вероятностей быть отрицательным?

Ожидаемое значение случайной величины после дискретного распределения вероятностей может быть отрицательным.