8.2. Числовые характеристики непрерывных случайных величин
Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством
Где Р(Х) — плотность распределения случайной величины Х. Предполагается, что интеграл сходится абсолютно. В частности, если все возможные значения принадлежат интервалу , то
Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох определяется равенством
Если интеграл сходится, или равносильным равенством
В частности, если все возможные значения Х принадлежат интервалу , то
Или
Все свойства математического ожидания и дисперсии для дискретных случайных величин справедливы и для непрерывных величин.
Среднее квадратическое отклонение непрерывной случайной величины определяется равенством
.
Модой непрерывной случайной величины Х называется ее наиболее вероятное значение (для которого плотность вероятности
Медианой непрерывной случайной величины Х называется такое ее значение, для которого
.
Вертикальная прямая , проходящая через точку с абсциссой, равной , геометрически делит площадь фигуры под кривой распределения на две равные части (рис. 8.7).
Рис. 8.7
Очевидно, что .
Начальный теоретический момент порядка k непрерывной случайной величины Х определяется равенством
.
Центральный теоретический момент порядка K непрерывной случайной величины Х определяется равенством
.
Если все возможные значения Х принадлежат интервалу , то
, .
Очевидно, что ; ; ; ; . Центральные моменты выражаются через начальные моменты по формулам:
,
,.
Математическое ожидание М(Х), или первый начальный момент, характеризует среднее значение распределения случайной величины Х; второй центральный момент, или дисперсия , — степень рассеяния распределения Х относительно М(Х).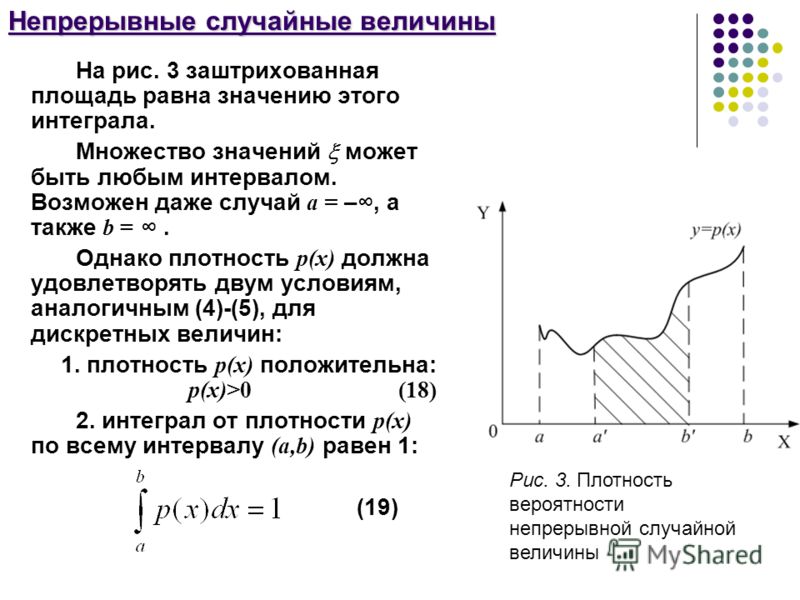
Третий центральный момент служит для характеристики асимметрии распределения.
Величина называется Коэффициентом асимметрии случайной величины.
А = 0, если распределение симметрично относительно математического ожидания.
Четвертый центральный момент характеризует крутость распределения.
Эксцессом случайной величины называется число
.
Кривые более островершинные, чем кривая для нормального распределения, обладают положительным эксцессом, более плосковершинные — отрицательным эксцессом.
Пример 8.7. Дана функция
При каком значении параметра
Решение. Для того чтобы Р(Х) была плотностью вероятности некоторой случайной величины Х, она должна быть неотрицательна, т. е. , откуда и она должна удовлетворять свойству 4 плотности вероятности.
Следовательно,
Откуда
.
Найдем интеграл , применив метод интегрирования по частям
Таким образом,
И плотность распределения имеет вид
Следовательно,
Дисперсия
Вначале найдем
Теперь
Пример 8.8. Случайная величина Х распределена по «закону прямоугольного треугольника» в интервале (рис. 8.8).
1. Написать выражение плотности распределения.
2. Найти функцию распределения F(Х).
3. Найти вероятность попадания случайной величины Х на участок от до А.
4. Найти характеристики величины Х: М(Х), D(Х), , .
Решение. Так как площадь прямоугольного треугольника есть площадь фигуры, ограниченной кривой распределения и осью абсцисс, то она равна единице: И, следовательно, .
Уравнение прямой АВ в отрезках имеет вид , откуда , то есть функция плотности распределения имеет вид
Найдем функцию распределения F(Х):
Если , то
Если , то
Если , то
Таким образом,
Вероятность попадания случайной величины
.
Найдем математическое ожидание:
Следовательно,
,
.
Так как , а , ,
,
То .
Пример 8.9. По данным задачи 8.5 найти математическое ожидание М(Х), дисперсию D(Х), моду М0(Х) и медиану Ме(Х).
Решение. Так как
То .
Дисперсия
Вначале найдем
.
Следовательно,
График плотности вероятности Р(Х) имеет вид (рис. 8.9)
Рис. 8.9
Плотность вероятности р(Х) максимальна при х = 2, это означает, что М0(Х) = 2.
Из условия Найдем медиану Ме(Х): ; откуда
Пример 8.10. Дана функция
Найти коэффициент асимметрии и эксцесс случайной величины Х.
Решение. Плотность распределения случайной величины Х равна
Так как асимметрия , эксцесс , то найдем начальные моменты первого, второго, третьего и четвертого порядков:
Тогда
Так как то Следовательно,
Пример 8.11. Плотность случайной величины Х задана следующим образом:
Найти моду, медиану и математическое ожидание Х.
Решение. Найдем математическое ожидание Х:
.
Так как плотность распределения достигает максимума при Х = 1, то М0(Х) =1. Медиану Ме(Х) найдем из условия . Для этого вначале найдем функцию распределения :
Если , то
Если , то
Если , то
Таким образом,
Уравнение равносильно уравнению , откуда .
Пример 8.12. Случайная величина Х задана плотностью распределения
Найти математическое ожидание функции (не находя предварительно плотности распределения ).
Решение. Воспользовавшись формулой для вычисления математического ожидания функции от случайного аргумента Х
Где А и B — концы интервала, в котором заключены возможные значения Х, получим
Пример 8.13. Случайная величина Х задана плотностью распределения
Найти моду, математическое ожидание и медиану величины Х.
Решение. Так как , то отсюда видно, что при Х = 4 плотность распределения достигает максимума и, следовательно, М0(Х) = 4 (можно было найти максимум методами дифференциального исчисления).
Кривая распределения симметрична относительно прямой Х = 4, поэтому М(Х) = Ме(Х) = 4.
| < Предыдущая | Следующая > |
|---|
Error
Sorry, the requested file could not be found
More information about this error
Jump to.
..
Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.
Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.
Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2. Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.
2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1.2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1.3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture.
Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.
3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson.
Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.
1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2.
Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1.
Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.
2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2.
Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2.
Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие.
Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Тест 3.2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2.
Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.4.2. (данное тестирование по теме 1)Видеолекция.
Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.
5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.
6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2.
Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)4.2: Ожидаемое значение и дисперсия непрерывных случайных величин
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3268
- Кристин Кутер
- Колледж Святой Марии
Теперь рассмотрим математическое ожидание и дисперсию для непрерывных случайных величин.
{\infty}_{-\infty}\! х\cdot f(x)\, dx.\notag$$
Формула для ожидаемого значения непрерывной случайной величины является непрерывным аналогом ожидаемого значения дискретной случайной величины, где вместо суммирования по всем возможным значениям мы интегрируем (вспомните разделы 3.6 и 3.7).
Для дисперсии непрерывной случайной величины определение такое же, и мы по-прежнему можем использовать альтернативную формулу, данную теоремой 3.7.1, только теперь мы интегрируем для вычисления значения: 92\notag$$
Пример \(\PageIndex{1}\)
Рассмотрим снова контекст примера 4.1.1, где мы определили непрерывную случайную величину \(X\) для обозначения времени, в течение которого человек ожидает прибытия лифта. PDF \(X\) был задан как
$$f(x) = \left\{\begin{array}{l l}
x, & \text{for}\ 0\leq x\leq 1 \\
2-x, & \text{for}\ 1< x\leq 2 \\
0, & \text{иначе}
\end{array}\right.\notag$$
Применяя определение 4.
2.1, мы вычислить ожидаемое значение \(X\): 92 = \frac{7}{6} — 1 = \frac{1}{6} \\
\Rightarrow\ \text{SD}(X) &= \sqrt{\text{Var}(X)} = \frac{1}{\sqrt{6}} \приблизительно 0,408
\end{align*}
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Кристин Кутер
- Показать оглавление
- да
- Теги
Непрерывная случайная величина — определение, формулы, среднее значение, примеры
Непрерывная случайная величина — это случайная величина, которая может принимать континуум значений.
Другими словами, случайная величина называется непрерывной, если она принимает значение, попадающее в определенный интервал.
Непрерывные случайные величины используются для обозначения таких измерений, как рост, вес, время и т. д. Площадь под кривой плотности используется для представления непрерывной случайной величины. В этой статье мы узнаем об определении непрерывной случайной величины, ее среднем значении, дисперсии, типах и связанных примерах.
| 1. | Что такое непрерывная случайная величина? |
| 2. | Непрерывные формулы случайных величин |
| 3. | Среднее значение и дисперсия непрерывной случайной величины |
| 4. | Типы непрерывных случайных величин |
| 5. | Непрерывная случайная величина против дискретной случайной величины |
| 6. | Часто задаваемые вопросы о непрерывной случайной величине |
Что такое непрерывная случайная величина?
Непрерывная случайная величина и дискретная случайная величина — это два типа случайных величин.
Случайная величина — это переменная, значение которой зависит от всех возможных исходов эксперимента. Непрерывная случайная величина определяется в диапазоне значений, а дискретная случайная величина определяется точным значением.
Определение непрерывной случайной величины
Непрерывная случайная величина может быть определена как случайная величина, которая может принимать бесконечное число возможных значений. Благодаря этому вероятность того, что непрерывная случайная величина примет точное значение, равна 0. Для описания характеристик непрерывной случайной величины используются кумулятивная функция распределения и функция плотности вероятности.
Пример непрерывной случайной величины
Предположим, что функция плотности вероятности непрерывной случайной величины X задана как 4x 3 , где x ∈ [0, 1]. Необходимо определить вероятность того, что X примет значение от 1/2 до 1. Это можно сделать, интегрируя 4x 3 между 1/2 и 1. Таким образом, требуемая вероятность равна 15/16.
Непрерывные формулы случайных величин
Функция плотности вероятности (PDF) и кумулятивная функция распределения (CDF) используются для описания вероятностей, связанных с непрерывной случайной величиной. Формулы непрерывных случайных величин для этих функций приведены ниже.
PDF непрерывной случайной величины
Функцию плотности вероятности непрерывной случайной величины можно определить как функцию, которая дает вероятность того, что значение случайной величины попадет в диапазон значений. Пусть X — непрерывная случайная величина, тогда формула для PDF f(x) задается следующим образом:
f(x) = \(\frac{\mathrm{d} F(x)}{\mathrm {d} x}\) = F'(x)
, где F(x) — кумулятивная функция распределения.
Чтобы PDF непрерывной случайной величины была достоверной, она должна удовлетворять следующим условиям: 9{\ infty} е (х) dx = 1 \). Это означает, что общая площадь под графиком PDF должна быть равна 1,.
Отсюда следует, что функция плотности вероятности непрерывной случайной величины не может быть отрицательной.CDF непрерывной случайной величины
Кумулятивную функцию распределения непрерывной случайной величины можно определить путем интегрирования функции плотности вероятности. Его можно определить как вероятность того, что случайная величина X примет значение, меньшее или равное определенному значению x. Формула для cdf непрерывной случайной величины, оцененной между двумя точками a и b, приведена ниже: 9{b}f(x)dx\)
Среднее значение и дисперсия непрерывной случайной величины
Среднее значение и дисперсию непрерывной случайной величины можно определить с помощью функции плотности вероятности f(x).
Среднее значение непрерывной случайной величины
Среднее значение непрерывной случайной величины можно определить как средневзвешенное значение случайной величины X. Оно также известно как математическое ожидание непрерывной случайной величины.
Формула дается следующим образом: 9{2}f(x)dx\)
Типы непрерывных случайных величин
Непрерывная случайная величина обычно используется для моделирования ситуаций, связанных с измерениями. Например, возможные значения температуры в любой день. Поскольку температура может быть любым действительным числом в заданном интервале, для ее описания требуется непрерывная случайная величина. Ниже приведены некоторые важные непрерывные случайные величины, связанные с определенными распределениями вероятностей.
Равномерная случайная величина
Непрерывная случайная величина, которая используется для описания равномерного распределения, называется равномерной случайной величиной. Такое распределение описывает события, которые происходят с одинаковой вероятностью. PDF равномерной случайной величины выглядит следующим образом:
\(f(x) = \left\{\begin{matrix} \frac{1}{ba} & a\leq x\leq b\\ 0 & в противном случае \end{matrix}\right.\)
Нормальная случайная величина
Непрерывная случайная величина, используемая для моделирования нормального распределения, называется нормальной случайной величиной.
{2})\), то формула для PDF задается следующим образом: 9{2}}{2}}\)
Экспоненциальная случайная величина
Экспоненциальные распределения — это непрерывные распределения вероятностей, которые моделируют процессы, в которых определенное количество событий происходит непрерывно с постоянной средней скоростью, \(\lambda\geq0\) . Таким образом, непрерывная случайная величина, используемая для описания такого распределения, называется экспоненциальной случайной величиной. PDF-файл имеет следующий вид:
f(x) = λe −λx
Непрерывная случайная величина против дискретной случайной величины
Для моделирования случайного явления используются как дискретные, так и непрерывные случайные величины. Различия между непрерывной случайной величиной и дискретной случайной величиной приведены в таблице ниже:
| Непрерывная случайная величина | Дискретная случайная величина |
|---|---|
Значение непрерывной случайной величины попадает в диапазон значений. {\infty}xf(x)dx\) 9{2}f(x)dx\) | Дисперсия дискретной случайной величины равна Var[X] = ∑(x − μ) 2 P(X = x) |
| Примерами непрерывной случайной величины являются равномерная случайная величина, экспоненциальная случайная величина, нормальная случайная величина и стандартная нормальная случайная величина. | Примерами дискретной случайной величины являются биномиальная случайная величина, геометрическая случайная величина, случайная величина Бернулли и случайная величина Пуассона. |
Статьи по теме:
- Вероятность и статистика
- Вероятностные правила
- Калькулятор функции плотности вероятности
Важные примечания о непрерывной случайной переменной
- Непрерывная случайная величина — это переменная, используемая для моделирования непрерывных данных, и ее значение попадает в интервал значений.
- Функция плотности вероятности непрерывной случайной величины задается как f(x) = \(\frac{\mathrm{d} F(x)}{\mathrm{d} x}\) = F'(x).
9{2}f(x)dx\). - Равномерная случайная величина, экспоненциальная случайная величина, нормальная случайная величина и стандартная нормальная случайная величина являются примерами непрерывных случайных величин.
9{2}f(x)dx\).Часто задаваемые вопросы о непрерывной случайной величине
Что такое непрерывная случайная величина в теории вероятностей?
Непрерывная случайная величина может быть определена как переменная, которая может принимать любое значение в заданном интервале. Обычно это такие измерения, как рост, вес, время и т. д. 9{2}f(x)dx\).
Какие существуют типы непрерывной случайной величины?
Существует три наиболее часто используемых непрерывных распределения вероятностей, таким образом, существует три типа непрерывных случайных величин. Они даны следующим образом:
- Однородная случайная величина
- Стандартная нормальная случайная величина
- Экспоненциальная случайная величина.
Как найти CDF непрерывной случайной величины?
Чтобы найти кумулятивную функцию распределения непрерывной случайной величины, проинтегрируйте функцию плотности вероятности между двумя пределами.