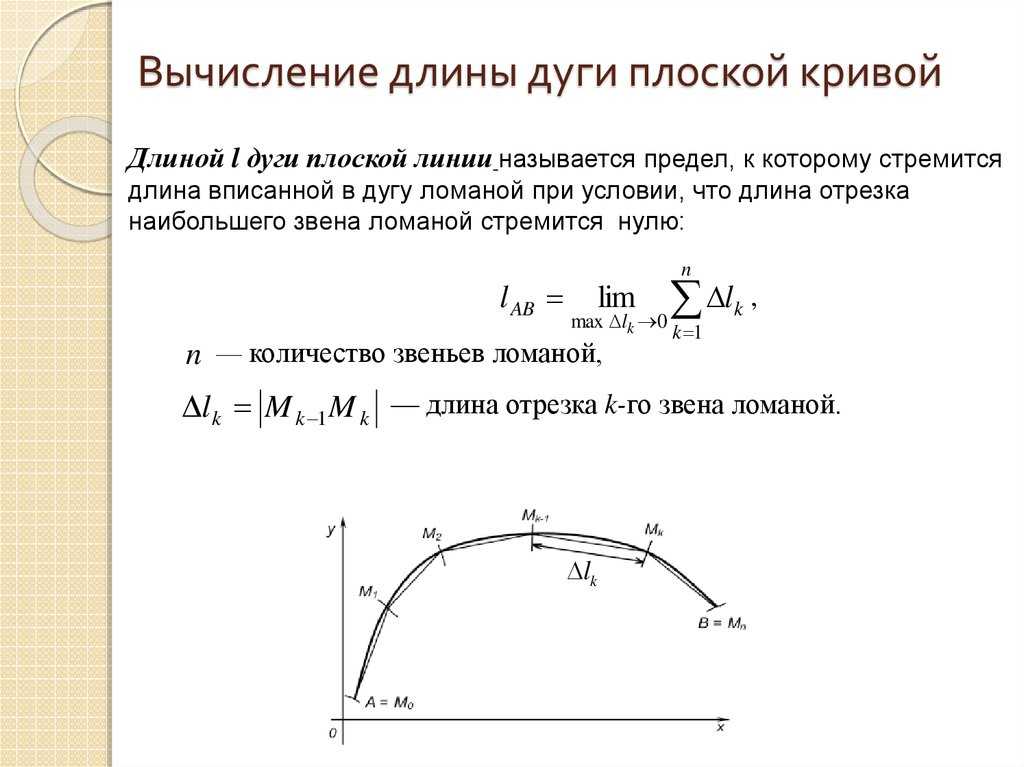
Длина дуги кривой заданной параметрически
Если кривая C задана уравнениями x=x(t), y=y(t) (t[t0;T]), где x(t) и y(t) непрерывные на [t0;T] функции, то длина дуги кривой С равняется определенному интегралу
Из формулы длины дуги кривой, заданной параметрически видим, что здесь нужно хорошо знать производные элементарных функций и иметь отличные знания c интегрирования. Как это выглядит на практике Вы можете увидеть с готовых ответов до заданий.
Примеры подобрано из учебной программы для студентов механико-математического факультета Львовского национального университета имени Ивана Франко.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича).
Для изучения основных моментов схема интегрирования и формулы вычисления дуги кривой, заданной в параметрической форме будут повторяться из примера в пример.
Часть заданий обязательно проиллюстрируем графиками кривых.
Пример 2.127-2443 Найти длину дуги кривой, заданной в параметрическом виде
x=a(t-sin(t)), y=a(1-cos (t)), tє[0;2pi].
(См. 2.100)
Вычисление: Найдем производные по переменной t функций:
Пределы интегрирования берем из условия: [0;2pi].
Выражаем подинтегральную функцию:
Интегрированием находим длину дуги кривой на заданном отрезке:
Для выведения формулы использовали известные тригонометрические формулы.
Длина дуги равна 8a единиц.
Пример 2.128 (2444) Найти длину дуги кривой, заданной параметрически
x=a(cos(t)+t*sin(t)), y=a(sin(t)-t*cos(t)), tє[0;2*Pi]. (См. 2.103)
Вычисление: Вычисляем производную по переменной t от параметрических уравнений координат функции:
Пределы интегрирования записываем из начального условия: [0;2*Pi].
Складываем подинтегральную функцию:
Ее вид чрезвычайно прост, а длина дуги параметрической кривой через интеграл вычисляется быстро:
Пример 2. 129 (2442) Найти длину дуги кривой, заданной параметрически
129 (2442) Найти длину дуги кривой, заданной параметрически
x=cos4(t), y=sin4(t).
Вычисление: Найдем производные по переменной t от параметрически заданных координат:
Имеем пределы интегрирования:
[0;Pi/2], поскольку функция принимает только положительные значения.
График кривой приведен на рисунку
Складываем уравнение подинтегральной функции:
Однократно применив замену переменных и метод интегрирования частями находим длину дуги кривой:
Интеграл достаточно распространен для такого сорта примеров, поэтому вспомните все формулы интегрирования, которые в результате дают логарифм.
Пример 2.130 Найти длину дуги кривой, заданной параметрически
x=t2,y=t-t3,
Вычисление: Первым делом находим производные параметрически заданных координат по переменной t:
x’=2t; y’=1-t2.
Крайние точки известны:
, отсюда нужно определить чему равен параметр:
из условия y=0 определяем
Функция симметрична относительно оси Ox, поэтому принимаем и результат интегрирования умножаем на 2.
График кривой на положительной части оси абсцисс изображен ниже
Составим уравнение подинтегральной функции:
Последним шагом находим длину дуги кривой на заданном отрезке:
Интеграл достаточно быстро вычисляется.
Пример 2.131 (2445.1) Найти длину дуги кривой, заданной в параметрическом виде
x=ch3(t), y=sh3(t), [0;T]
Вычисление: Найдем производные от гиперболичного косинуса и синуса по t:
Пределы интегрирования известны: [0;T].
График кривой приведен на рисунке
Вычислим подинтегральную функцию:
Учитывая формулы для гиперболичных функций при вычислении интеграла синус гиперболический от двойного угла вносим под дифференциал.
В результате придем к формуле, которую и без замены переменных можем проинтегрировать.
Пример 2441 Найти длину дуги эволюты эллипса, заданной параметрически
Вычисление: Найдем производные параметрически заданных координат эволюты эллипса:
Пределы интегрирования: [0;Pi/2] (оси координат являются осями симметрии).
График эволюты эллипса имеет вид
Складываем уравнение подинтегральной функции:
Чтобы найти длину дуги эволюты эллипса придется превратить подинтегральную функцию, потом свести ее под известные интегралы.
Чтобы облегчить чтение формул на середине вычислений выполняем замену переменных и, соответственно, пересчет пределов интегрирования.
Также последние строки показывают, что умение работать с дробями Вам тоже пригодятся.
Если не упрощать, то получим тяжелую для чтения формулу с иррациональными слагаемыми.
Пример 2445 Найти длину дуги кривой, заданной параметрически
x=a(sh(t)-t), x=a(ch(t)-1, tє[0;T].
Вычисление: Вычислим производные от параметрических координат кривой:
x’=a(ch(t)-1;
y’=a*sh(t).
Пределы интегрирования заданы: [0;T].
Подносим к квадрату производные параметрических координат линии:
За формулой находим длину дуги кривой:
для этого превращаем подынтегральную функцию, а дальше методом замены переменных вычисляем интеграл:
Конечная формула длины дуги кривой содержит зависимости от косинуса гиперболического.
22. Вычисление длины дуги плоской кривой
1 случай. Пусть в прямоугольных координатах на плоскости дана кривая . Вычислим длину дуги кривой, заключенной между точкамии(рис. 12).
Возьмем на дуге точкис абсциссамии проведем хорды, длины которых обозначим соответственно. Тогда получим ломанную, вписанную в дугу. Длина ломанной равна
.
Определение. Длиной дугиназывается тот предел, к которому стремится длина вписанной ломанной, когда длина ее наибольшего звена стремится к нулю:
.
Длина всей дуги , заключенной между точкамии, вычисляется по формуле
.
Пример 16. Найти длину окружности .
Решение. Вычислим сначала длину четверти окружности, расположенной в 1 четверти.
Из уравнения окрежности ,.
Тогда .
Длина всей окрежности
Ответ: (лин.ед).
23. Вычисление объема тела, образованного вращением плоской фигуры вокруг оси
Пример 1
Вычислить
объем тела, полученного вращением
фигуры, ограниченной линиями ,вокруг
оси.
Решение: Как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. То есть, на плоскости необходимо построить фигуру, ограниченную линиями,, при этом не забываем, что уравнениезадаёт ось. Как рациональнее и быстрее выполнить чертёж, можно узнать на страницахГрафики и свойства Элементарных функцийи Определенный интеграл. Как вычислить площадь фигуры. Это китайское напоминание, и на данном моменте я больше не останавливаюсь.
Чертёж здесь довольно прост:
Искомая плоская фигура заштрихована синим цветом, именно она и вращается вокруг оси В результате вращения получается такая немного яйцевидная летающая тарелка, которая симметрична относительно оси. На самом деле у тела есть математическое название, но по справочнику что-то лень уточнять, поэтому едем дальше.
Как вычислить объем тела вращения?
Объем тела вращения можно вычислить по формуле:
В
формуле перед интегралом обязательно
присутствует число . Так повелось – всё, что в жизни крутится,
связано с этой константой.
Так повелось – всё, что в жизни крутится,
связано с этой константой.
Как расставить пределы интегрирования «а» и «бэ», думаю, легко догадаться из выполненного чертежа.
Функция … что это за функция? Давайте посмотрим на чертеж. Плоская фигура ограничена графиком параболысверху. Это и есть та функция, которая подразумевается в формуле.
В практических заданиях плоская фигура иногда может располагаться и ниже оси . Это ничего не меняет – подынтегральная функция в формуле возводится в квадрат:, таким образоминтеграл всегда неотрицателен, что весьма логично.
Вычислим объем тела вращения, используя данную формулу:
Как я уже отмечал, интеграл почти всегда получается простой, главное, быть внимательным.
Ответ:
В ответе нужно обязательно указать размерность – кубические единицы . То есть, в нашем теле вращения примерно 3,35 «кубиков». Почему именно кубические
 д.,
это уж, сколько зеленых человечков ваше
воображение поместит в летающую тарелку.
д.,
это уж, сколько зеленых человечков ваше
воображение поместит в летающую тарелку.24. Определение двойного интеграла
Понятие интеграла может быть расширено на функции двух и большего числа переменных. Рассмотрим, например, функцию двух переменных z = f (x,y). Двойной интеграл от функции f (x,y) обозначается как
где R — область интегрирования в плоскости Oxy. Если определенный интеграл от функции одной переменнойвыражает площадь под кривойf (x) в интервале от x = a до x = b, то двойной интеграл выражает объем под поверхностью z = f (x,y) выше плоскости O xy в области интегрирования R (рисунок 1).
Рис.1 |
25. Геометрический
смысл двойного интеграла. Если f(x,y)
?0 в области D, то двойной интеграл (1)
равен объему “цилиндрического” тела,
изображенного на рис.1:
Если f(x,y)
?0 в области D, то двойной интеграл (1)
равен объему “цилиндрического” тела,
изображенного на рис.1:
V = (2)
Пояснение. Цилиндрическое тело ограничено снизу областью D, сверху — частью поверхности z=f(x,y), с боков — вертикальными отрезками прямых, соединяющих границы этой поверхности и области D.
26. Основные свойства двойного интеграла:
1. Постоянный множитель выносится за знак интегр.
2. Интеграл от суммы равен сумме интегралов
3. Если область D разбить на 2 части, то
27. Вычисление двойного интеграла в декартовых координатах
Пусть требуется вычислить двойной интегр. Где ф-ция f(x;y) непрерывна в области D
Пусть область D представляет собой криволин. Трапецию ограниченную кривыми и прямыми D: ;x=a; x=b
Такая область правильная в направлении оси OY, то есть любая прямая параллельная OY пересекает границу области на более чем в 2-х точках
Если
область правильная, тогда вычисление
2-го интегр. сводится к вычислению
двукратного (повторного) интеграла.
сводится к вычислению
двукратного (повторного) интеграла.
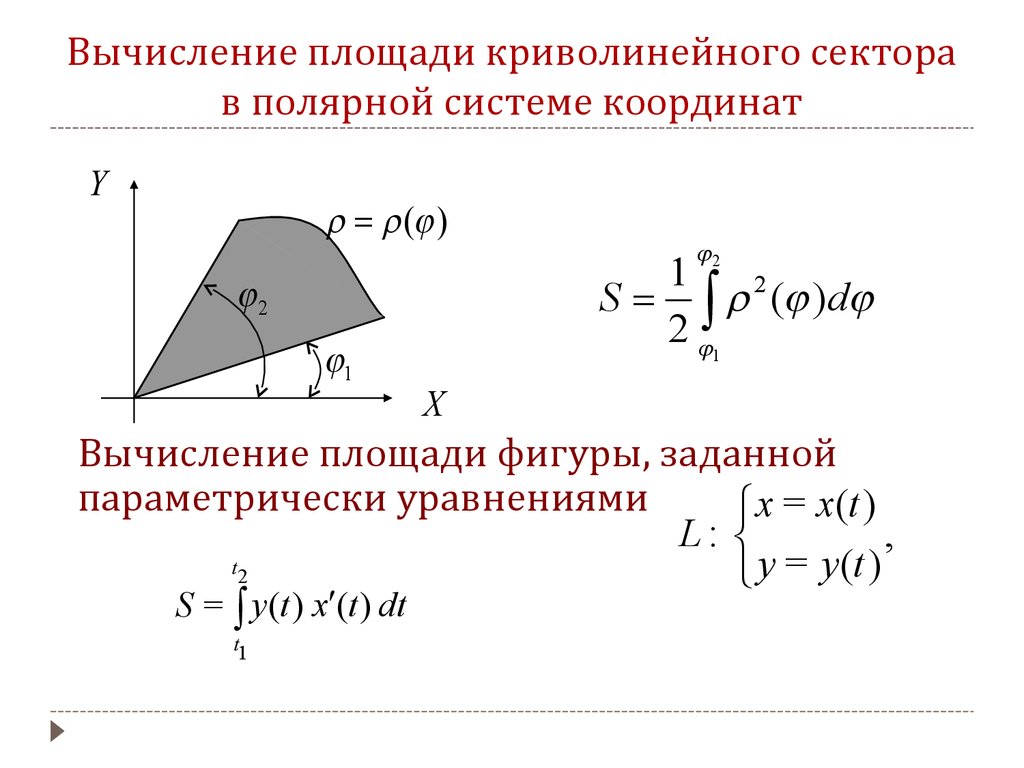
28. Замена переменной в двойном интеграле. Вычисление двойного интеграла в полярных координатах
Заменим независимые переменные х и у через функцию ;, если эти функции имеют в некоторой областинепрерывные частные производные и отличный от нуля определитель
А f(x;y) интегрируема в области D, тогда имеет место замена переменных
I(u;v) – определитель Якоби (якобиан)
Пусть в полярных координатах
x=rcosφ
y=rsinφ
I(φ;r)=-r
Пусть область ограничена лучами,и кривыми
29. Физические приложения двойного интеграла
Физический смысл двойного интеграла заключен в нахождении массы плоской пластины
30. Определение криволинейного интеграла 1 рода
Если существует предел интегральной суммы, который не зависит ни от способа разбиения кривой на части, ни от выбора в них точек, то он называется криволинейный интеграл от ф-ции f(x;y) по длине кривой AB
31.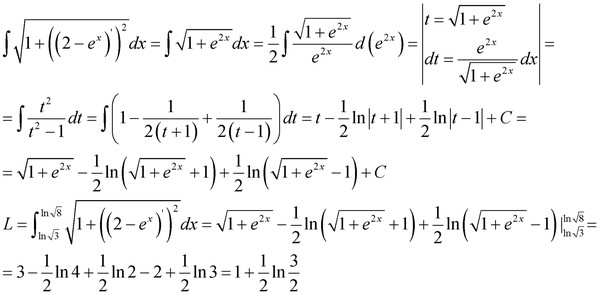 Основные свойства криволинейного
интеграла 1 рода
Основные свойства криволинейного
интеграла 1 рода
1. Постоянный множитель выносится за знак интегр.
2. Интеграл от суммы равен сумме интегралов
3. Если кривую АВ разбить на части такие, что их объединение = АВ и они имеют только 1 общую точку разделяющую их, тогда
4. Криволинейный интеграл 1-го порядка не зависит от направления пути направления кривой
32. Вычисление криволинейного интеграла 1 рода
а. Параметрическое представление кривой
б. Явно заданная функция
33. Приложения криволинейного интеграла 1 рода
1. Длина кривой
2. Площадь цилиндрической поверхности
Если направляющей цилиндрической поверхности служит кривая АВ, а образующая параллельна оси OZ, то площадь такой поверхности z=f(x;y) вычисляется по формуле
3. Масса плоской кривой (провод)
4. Статические моменты
5. Координаты центра тяжести
6. Момент инерции
34. Определение криволинейного интеграла 2 рода
Предположим,
что кривая C задана векторной
функцией ,
где переменная s − длина дуги
кривой. Тогда производная векторной
функции
Тогда производная векторной
функции
представляет собой единичный вектор, направленный вдоль касательной к данной кривой. В приведенной выше формуле α, β и γ − углы между касательной и положительными направлениями осей Ox, Oy и Oz, соответственно.
Введем векторную функцию F(P;Q;R), определенную на кривой C, так, чтобы для скалярной функции
существовал криволинейный интеграл . Такой интеграл называетсякриволинейным интегралом второго рода от векторной функции вдоль кривойC и обозначается как
35. Основные свойства криволинейного интеграла 2 рода
1. Если в КИ2 изменить направление интегрирования, то он поменяет знак на противоположный
2. Если кривая АВ разбита точкой С на части, то
3. Если кривая лежит в плоскости перпендикулярной ОХ, то
Аналогично для OY
4. Криволинейный интеграл по замкнутой кривой не зависит от выбора начальной точки, а зависит только от направления обхода прямой
36. Вычисление криволинейного интеграла
2 рода
Вычисление криволинейного интеграла
2 рода
а. Параметрическое представление кривой
б. Явно заданная функция
37. Приложения криволинейного интеграла 2 рода
C помощью криволинейных интегралов вычисляются:
— Масса кривой
— Центр масс и моменты инерции кривой
— Работа при перемещении тела в силовом поле
— Магнитное поле вокруг проводника с током (Закон Ампера)
— Электромагнитная индукция в замкнутом контуре при изменении магнитного потока (Закон Фарадея)
38. Формула Остроградского-Грина
Пусть на плоскости OXY задана область D, ограниченная кривой пересекающейся с прямыми параллельными координатным осям не более чем в 2-х точках то есть, область D правильная.
Если ф-ции P(x;y) и Q(x;y) непрерывны вместе со своими частными производными в области D, то имеет место формула:
39. Основные понятия о дифференциальных уравнениях (определение, решение, порядок, обыкновенные ДУ, ДУ в общих производных, вид, общее решение, частные решения, начальные условия, задача Коши)
40. ДУ с разделяющимися переменными
ДУ с разделяющимися переменными
Среди обыкновенных дифференциальных уравнений первого порядка существуют такие, в которых возможно переменные x и y разнести по разные стороны знака равенства. В уравнениях вида переменные уже разделены, а в ОДУпеременные разделяются посредством преобразований. Кроме того, некоторые дифференциальные уравнения сводятся к уравнениям с разделяющимися переменными после введения новых переменных.
41. Однородные ДУ 1-го порядка
ДУ вида – однородныеn-го порядка, если при умножении каждого элемента функции на множитель t вся функция умножится на
42. Линейные ДУ 1-го порядка. Метод вариации произвольной постоянной
Линейные ДУ 1-го порядка имеют такой вид
Характерная особенность – функция и ее производные входят в уравнение в 1 степени и между собой не перемножаются
Метод Лагранжа (Метод вариаций произвольной постоянной)
Метод вариации произвольной постоянной состоит в том, что постоянную С в полученном решении заменяем С=с(x), тогда решение исходного уравнения будем искать в виде
После находим производную и подставляем в исходное уравнение
43. Линейные ДУ 1-го порядка. Метод Бернулли
Линейные ДУ 1-го порядка. Метод Бернулли
Линейные ДУ 1-го порядка имеют такой вид
Характерная особенность – функция и ее производные входят в уравнение в 1 степени и между собой не перемножаются
Метод Бернулли
Решение данного уравнения ищется в виде производной 2-х функция то, есть с помощью подстановки
y=U*V, где U=u(x) и V=v(x)
Подставим выражение для y и в исходное уравнение
Сгруппируем 1 и 3 слогаемые, или 2 и 3 и вынесем общий множитель за скобки
(*)
Функцию v подберём таким образом, чтобы выражение в скобках было равно нулю
–уравнение с разд. переменными, получаем:
Подставляем полученное в уравнение (*), учитывая, что выражение в скобках равно нулю
Ответ:
44. ДУ высших порядков, допускающие понижения порядка. ДУ вида
Рассмотрим
дифференциальное уравнение вида ,
где–
производная «энного» порядка, а правая
частьзависиттолько
от «икс».
В простейшем случае может
быть константой.
Данное дифференциальное уравнение решается последовательным интегрированием правой части. Причём интегрировать придется ровно раз.
На практике наиболее популярной разновидность является уравнение второго порядка: . Дважды интегрируем правую часть и получаем общее решение. Уравнение третьего порядканеобходимо проинтегрировать трижды, и т.д.
45. ДУ высших порядков, допускающие понижения порядка. ДУ вида
Порядок такого уравнения можно понизить на единиц заменой. Тогда уравнение примет вид
Из последнего уравнения, если это возможно, определяем , а затем находимиз уравненияk-кратным интегрированием.
46. ДУ высших порядков, допускающие понижения порядка. ДУ вида
Отличительная особенность данного диффура состоит в том, что в нём в явном виде отсутствует независимая переменная «икс». То есть, в исходном дифференциальном уравнении нет «икса».
Подстановка позволяет
понизить порядок уравнения на единицу.
При этомрассматривается
как новая неизвестная функция от. Все производныевыражаются
через производные от новой неизвестной
функциипо
Все производныевыражаются
через производные от новой неизвестной
функциипо
Подставив эти выражения вместо в уравнение, получим дифференциальное уравнение (n–1)-го порядка
47. Линейные однородные ДУ второго порядка. Определитель Вронского. Структура общего решения
Рассмотрим линейное дифференциальное уравнение вида
где p, q − постоянные коэффициенты. Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение:
Общее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие случаи:
Дискриминант характеристического квадратного уравнения положителен: D > 0. Тогда корни характеристического уравнения k1 и k2 действительны и различны. В этом случае общее решение описывается функцией
где C1 и C2 −
произвольные действительные числа.
Дискриминант характеристического квадратного уравнения равен нулю: D = 0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k1 второго порядка. Общее решение однородного дифференциального уравнения имеет вид:
Дискриминант характеристического квадратного уравнения отрицателен: D < 0. Такое уравнение имеет комплексно-сопряженные корни k1 = α + βi, k1 = α − βi. Общее решение записывается в виде
48. Интегрирование ЛОДУ второго порядка с постоянными коэффициентами
Эйлер предложил искать частные решения в виде:
k – некоторое число
–характеристическое уравнение
Случ.1 D>0 =>
Общее решение записываем в виде
Случ.2 D=0 =>
Случ.3 D<0 =>
49. Интегрирование ЛНДУ второго порядка с
постоянными коэффициентами. Случай
Интегрирование ЛНДУ второго порядка с
постоянными коэффициентами. Случай
Общее решение ЛНДУ выглядит так:
Для ЛНДУ с правой частью специального вида частное решение можно найти пользуясь методом неопределённых коэффициентов. Суть метода: по виду правой части уравнения запишем ожидаемую форму частного решения с неопределённым коэффициентом, затем дважды её продифференцируем и полученные выражения подставим в исходное уравнение после чего найдём неопределённые коэффициенты
Частное для такого уравнения будет находиться в виде
r – число равное кратности α, как корня характеристического уравнения
а. Если
б. Если
в. Если
50. Интегрирование ЛНДУ второго порядка с постоянными коэффициентами. Случай
Общее решение ЛНДУ выглядит так:
Для ЛНДУ с правой частью специального вида частное решение можно найти пользуясь методом неопределённых коэффициентов. Суть метода: по виду правой части уравнения запишем ожидаемую форму частного решения с неопределённым коэффициентом, затем дважды её продифференцируем и полученные выражения подставим в исходное уравнение после чего найдём неопределённые коэффициенты
l = max (n;m)
r – число равное кратности как корень характеристического уравнения
Длина дуги кривой в прямоугольных координатах
Контрольная работа
По дисциплине:
«Высшая математика»
Тема:
«Длина дуги кривой в прямоугольных координатах»
1. Производная определенного интеграла по переменному верхнему пределу
Производная определенного интеграла по переменному верхнему пределу
Сформулируем следующее свойство определенных интегралов:
Пусть функция непрерывна на . Составим для нее определенный интеграл . Пусть для определенности на всем отрезке. Тогда с геометрической точки зрения составленный интеграл не что иное, как площадь криволинейной трапеции с основанием , которая ограничена линией .
Если в рассматриваемом интеграле заменить переменную интегрирования на , то величина его, очевидно, не изменится. Поэтому в дальнейшем для удобства будем считать, что площадь трапеции определяется интегралом .
Величина определенного интеграла зависит от значений верхнего и нижнего пределов интегрирования, то есть от длины основания криволинейной трапеции. Рассмотрим поэтому теперь случай, когда нижний предел интеграла фиксирован и равен , а верхний может меняться, принимая значения , где . В этом случае определенный интеграл будет соответствовать площади криволинейной трапеции, величина которой меняется. Зависеть эта площадь будет от значения , то есть . Если будет меняться непрерывно, то и площадь трапеции будет меняться непрерывно, то есть – непрерывная функция, которую можно дифференцировать.
Зависеть эта площадь будет от значения , то есть . Если будет меняться непрерывно, то и площадь трапеции будет меняться непрерывно, то есть – непрерывная функция, которую можно дифференцировать.
Теорема. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, у которой переменная интегрирования заменена этим верхним пределом, то есть или .
Для вычисления производной проделаем все стандартные операции. Зададим приращение аргументу: , что, в свою очередь, приведет к приращению функции: . Так как , а , то приращение функции определяется выражением:
.
Применим к полученному выражению теорему о среднем в определенном интеграле:
, где .
Составим отношение . Чтобы получить производную , перейдем в составленном отношении к пределу: . Так как , то при стремлении точка будет стремиться к . Следовательно, вычисление предела приведет к выражению: .
Из доказанной теоремы следует, что – это первообразная от , следовательно, определенный интеграл также является первообразной от , и вычислять его, очевидно, необходимо с помощью тех же приемов, что и неопределенный интеграл.
2. Формула Ньютона–Лейбница
Вычисление определенного интеграла как предела интегральной суммы представляет собой довольно сложную задачу и может быть выполнено лишь в некоторых наиболее простых случаях. Однако полученная в п. 1 связь между определенным интегралом и первообразной позволяет получить простой метод для вычисления этих интегралов.
Теорема. Если какая-либо первообразная от непрерывной функции , то справедлива формула: .
В предыдущем пункте было показано, что – это первообразная от функции . Но как было показано при изучении неопределенного интеграла, любая непрерывная функция имеет бесконечное множество первообразных, отличающихся друг от друга на постоянное слагаемое. Поэтому, если какая-то другая первообразная от той же функции , то .
Оказывается, что в случае определенного интеграла постоянную можно вычислить. Действительно, так как может принимать любые значения между и (п. 1), то пусть . Тогда: . Но определенный интеграл с равными пределами равен нулю, следовательно, . Значит,
Тогда: . Но определенный интеграл с равными пределами равен нулю, следовательно, . Значит,
.
Положим теперь, что , тогда
.
Полученное выражение называется формулой Ньютона – Лейбница. Другая форма записи этого выражения следующая:
.
Обычно в полученных выражениях переменная интегрирования обозначается буквой .
Таким образом, чтобы вычислить определенный интеграл, необходимо найти любую первообразную от и вычислить разность ее значений в верхнем и нижнем пределах интегрирования. Полученная простая формула позволяет легко находить решения многих математических и прикладных задач, связанных с вычислением определенного интеграла.
3. Замена переменной в определенном интеграле
При изучении неопределенного интеграла было показано (п. 5.4), что одним из наиболее часто встречающихся методов его вычисления является замена переменных. Так как вычисление определенного интеграла, согласно формуле Ньютона – Лейбница, также связано с нахождением первообразной, то метод замены переменной применим и в нем, однако при этом имеются некоторые особенности. В неопределенном интеграле замена переменной приводила в конце вычислений к обратной замене, в определенном же, оказывается, можно обойтись без этого.
В неопределенном интеграле замена переменной приводила в конце вычислений к обратной замене, в определенном же, оказывается, можно обойтись без этого.
Теорема. Если в определенном интеграле , где непрерывна на , сделать замену переменной и при этом:
1) , ;
2) и непрерывны на ;
3) непрерывна на и при изменении от до не выходит за пределы отрезка ,
то .
Пусть – какая-то первообразная от , тогда . Согласно формуле Ньютона – Лейбница, получим соответствующий определенный интеграл: . Но, как было показано в п. 5.4, в неопределенном интеграле можно сделать замену переменной , тогда . В этом случае соответствующий определенный интеграл будет иметь вид:
.
У обоих определенных интегралов правые части равны, следовательно, равны и левые части:
,
что и требовалось доказать.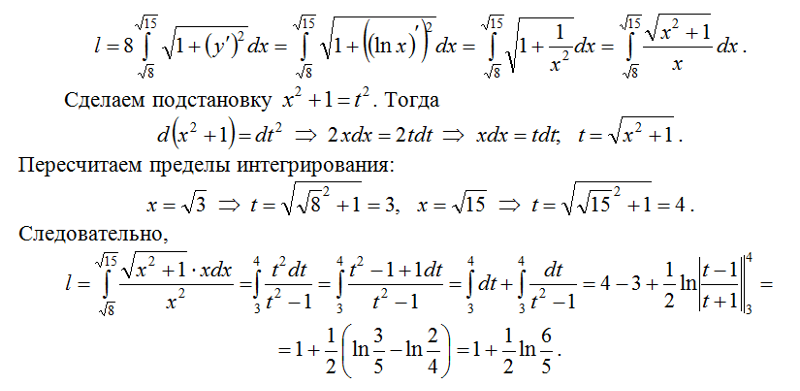
Из доказанной теоремы следует, что при замене переменной в определенном интеграле должны поменяться пределы интегрирования, и обратная замена здесь уже не нужна, так как и при старой и при новой переменной в ответе получается одно и то же число.
4. Интегрирование по частям в определенном интеграле
Пусть даны функции и , которые непрерывны со своими производными на . Составим их произведение и продифференцируем его:
.
Возьмем от обеих частей полученного равенства определенные интегралы:
.
Но , , . Следовательно, , откуда: . Так же как и в неопределенном интеграле, данная формула требует правильного выбора множителей и .
5. Длина дуги кривой в прямоугольных координатах
При вычислении длины кривой линии может быть использована та же методика, что и при вычислении площадей криволинейных трапеций, то есть кривую разбивают на такие малые участки, длину которых можно посчитать геометрическими методами.
Определение. Длиной дуги кривой линии называют предел, к которому стремится длина вписанной в нее ломаной линии при неограниченном увеличении числа ее звеньев и при стремлении длины наибольшего звена к нулю.
Итак, пусть кривая линия описывается функцией на отрезке . При этом пусть непрерывна на этом отрезке вместе со своей производной . Разобьем кривую на частичных дуг точками . Соединив начало и конец каждой частичной дуги хордой, получим в результате вписанную ломаную линию, длина которой равна сумме длин ее звеньев:
.
Обозначим: , ,…, ,…, . Кроме того, , ,…, ,…, . В таком случае можно рассматривать как гипотенузу прямоугольного треугольника и поэтому
.
Согласно теореме Лагранжа о среднем
, где ,
следовательно,
.
Отсюда длина ломаной линии равна
.
Переходя к пределу в данной интегральной сумме, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю, получаем длину кривой линии в прямоугольной системе координат:
.
Данный интеграл существует, поскольку по условию производная непрерывна.
Из полученной формулы можно получить выражение для дифференциала дуги, которое используется как в математике, так и в некоторых задачах теоретической механики. Пусть положение правого конца кривой линии является переменной величиной, тогда ее длина будет функцией точки, в которой она заканчивается, то есть
.
Возьмем производную данного интеграла по переменному верхнему пределу (п. 1.):
.
Отсюда следует, что
.
6. Длина дуги кривой при ее параметрическом задании
Рассмотрим теперь случай, когда кривая, длину которой необходимо вычислить, задана параметрически, то есть при этом изменение от до приводит к изменению от до . Пусть функции и непрерывны вместе со своими производными на отрезке и при этом . Тогда , а . Подставим значение данной производной и дифференциала в формулу для длины дуги в прямоугольной системе координат (п. 5):
5):
.
В случае пространственной кривой ее параметрическое задание будет выглядеть следующим образом:
Если указанные функции непрерывны вместе со своими производными на отрезке , то можно доказать, что длина данной кривой вычисляется по формуле
.
7. Длина дуги в полярной системе координат
Если кривая задана в полярной системе координат, то она описывается функцией , где . Пусть непрерывна вместе со своей производной на отрезке .
Перейдем от полярной к прямоугольной системе координат: . Но так как , то получаем, что . Иначе говоря, и выражены через параметр , поэтому можно воспользоваться формулой для длины дуги при ее параметрическом задании (п. 6.):
Возведя в квадрат выражения в скобках и выполнив элементарные преобразования, получаем:
.
Обычно данную формулу записывают следующим образом:
.
8. Вычисление объемов тел по известным площадям поперечных сечений
Определенный интеграл в некоторых случаях может быть использован и для вычисления объемов тел. Это можно сделать, когда известны площади всех их поперечных сечений.
Это можно сделать, когда известны площади всех их поперечных сечений.
Пусть некоторое тело, объем которого необходимо определить, расположено вдоль оси между точками и . Пусть это тело обладает тем свойством, что известна площадь его любого поперечного сечения плоскостью , то есть плоскостью, перпендикулярной оси . Так как в общем случае величина этого сечения будет меняться, то . В случае, если поверхность тела является гладкой, а тело сплошным, то будет непрерывной функцией.
Разобьем отрезок точками на частичные отрезки и в каждой полученной точке проведем плоскость, перпендикулярную оси . Все тело при этом разобьется на слои, а его объем будет равен сумме объемов всех полученных слоев: .
Найдем приближенно величину объема -ого слоя . Для этого рассмотрим отрезок , длина которого равна . Возьмем некоторую точку и проведем в ней секущую плоскость, перпендикулярную оси . Если достаточно мало, то слой, соответствующий объему , можно практически считать прямым цилиндром с поперечным сечением равным . Но в этом случае, как и у кругового цилиндра, . Отсюда следует, что
Но в этом случае, как и у кругового цилиндра, . Отсюда следует, что
.
Полученное выражение является интегральной суммой. Так как функция по условию непрерывна, то предел этой суммы при и существует и равен определенному интегралу:
.
Итак, объем тела с известными поперечными сечениями равен:
.
9. Объем тела вращения
Рассмотрим теперь тело, полученное в результате вращения криволинейной трапеции вокруг оси . Пусть основанием этой трапеции является отрезок , расположенный на оси , и она ограничена непрерывной кривой . В этом случае в любом сечении полученного тела плоскостью, перпендикулярной оси , будет круг, радиус которого совпадает со значением функции в данной конкретной точке. Поэтому площадь сечения будет равна .
Подставив данное выражение в формулу для объема тела с известными площадями поперечных сечений, приведенную в предыдущем параграфе, получим:
.
Если трапеция вращается вокруг оси , то должна быть задана функция на отрезке . В этом случае объем тела вращения равен:
В этом случае объем тела вращения равен:
.
Литература
Крищенко Александр, Канатников Анатолий Аналитическая геометрия: Учебное пособие для студентов высших учебных заведений. Изд-во «Академия», 2009. – 208c.
Макарычев Юрий Тригонометрия. Издательство: ПРОСВЕЩЕНИЕ, 2004. – 360 с.
Потапов Михаил Задачи по алгебре, тригонометрии и элементарными функциями. Издательство: ЭКЗАМЕН XXI, 2008. – 160 с.
Тоом А., Гельфанд И., Львовский С. Тригонометрия. МЦМНО, 2003. – 200 с.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования… Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает. Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности… Интересное: Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления… Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом… Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 4 из 6Следующая ⇒
Рассмотрим плоскую кривую, уравнение которой имеет вид Если функция является гладкой (т. . Пример. Вычислить длину дуги параболы , заключенной между точками (0,0) и (4,8). Так как кривая задана неявно, то необходимо сначала выделить явно y относительно x, получим . Отсюда . Абсцисса текущей точки параболы меняется в пределах от 0 до 4, т.е. , поэтому формула для вычисления длины дуги кривой примет вид . Возьмем этот определенный интеграл
Случай кривой, заданной параметрически.
Рассмотрим плоскую кривую, уравнение которой имеет вид , где функции и — непрерывно дифференцируемы на , причем . Тогда длина кривой вычисляется по формуле Пример. Найти длину одной арки циклоиды Найдем точки пересечения циклоиды с осью ОХ, для этого приравняем ординату y к нулю и решим уравнение . Следовательно, первой арке циклоиды соответствует изменение параметра в пределах Найдем производные от абсциссы и ординаты этой кривой .
Случай кривой, заданной в полярных координатах.
Если гладкая кривая задана уравнением в полярных координатах , то длина дуги этой кривой определяется по формуле , где и — значения полярного угла в крайних точках дуги, причем . Пример. Найти длину кривой . Текущая точка обойдет всю кривую, если полярный угол будет меняться в пределах . Найдем производную функции
. Тогда подкоренное выражение примет вид: Для вычисления длины дуги кривой, заданной в полярных координатах, применим соответствующую формулу .
Вычисление объема тела. Формула объема тела по площади параллельных сечений.
Пусть требуется найти объем тела V, причем известны площади S сечений этого тела, плоскостями, перпендикулярными координатным осям, например оси OX. Искомая величина V находится путем интегрирования площади заданного сечения, т.е. . Пример. Найти объем сферы радиуса с центром в начале координат О(0,0,0) Рассмотрим сечение этой сферы плоскостью , перпендикулярной оси ОХ, где . Для этого подставим в уравнение сферы вместо и приведем полученное уравнение к каноническому виду: . Таким образом, сечения представляет собой новую окружность радиуса с центром в точке . Используя формулу площади круга, известную из школьного курса . Используя формулу объема тела по площади параллельных сечений, получаем
Объем тела вращения.
Пусть задана непрерывная кривая . Рассмотрим фигуру, полученную вращением криволинейной трапеции вокруг оси ОХ. Фигура, полученная в результате вращения кривой вокруг любой из координатных осей, называется телом вращения . Так как сечением тела вращения вокруг оси ОХ плоскостью является окружность радиуса , то площадь этого сечения будет равна . Для нахождения объема тела вращения применим формулу объема тела по площади параллельных сечений: Если та же кривая вращается вокруг оси OY, то необходимо найти функцию, обратную к заданной и в качестве интервала интегрирования рассмотреть область значения исходной функции, т.е. . Тогда формула объема тела вращения вокруг оси OY примет вид: . Пример 1. Найти объем тела, образованного вращением фигуры, ограниченной линиями , вокруг оси ОХ. Применяя соответствующую формулу, получим Пример 2. В условиях предыдущего примера найти объем тела вращения той же кривой вокруг оси OY. Рассмотрим ту ветвь параболы, которая располагается в первой координатной четверти, и найдем функцию, обратную к заданной . Для этого выразим через . Искомая функцию будет иметь вид , при этом, если x изменялся в пределах от 1 до 2, то y будет принимать значения из промежутка [2,8]. Тогда, используя формулу для вычисления объема тела вращения вокруг оси OY, получим: .
⇐ Предыдущая123456Следующая ⇒ Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… |
Длина дуги кривой в прямоугольных координатах (стр. 1 из 3)
Контрольная работа
По дисциплине:
«Высшая математика»
Тема:
«Длина дуги кривой в прямоугольных координатах»
1. Производная определенного интеграла по переменному верхнему пределу
Производная определенного интеграла по переменному верхнему пределу
Сформулируем следующее свойство определенных интегралов:
Пусть функция
непрерывна на
. Составим для нее определенный интеграл
. Пусть для определенности
на всем отрезке. Тогда с геометрической точки зрения составленный интеграл не что иное, как площадь криволинейной трапеции с основанием
, которая ограничена линией
.
Если в рассматриваемом интеграле заменить переменную интегрирования
на
, то величина его, очевидно, не изменится. Поэтому в дальнейшем для удобства будем считать, что площадь трапеции определяется интегралом
.
Величина определенного интеграла зависит от значений верхнего и нижнего пределов интегрирования, то есть от длины основания криволинейной трапеции. Рассмотрим поэтому теперь случай, когда нижний предел интеграла фиксирован и равен
Рассмотрим поэтому теперь случай, когда нижний предел интеграла фиксирован и равен
, а верхний может меняться, принимая значения
, где
. В этом случае определенный интеграл будет соответствовать площади криволинейной трапеции, величина которой меняется. Зависеть эта площадь будет от значения
, то есть
. Если
будет меняться непрерывно, то и площадь трапеции будет меняться непрерывно, то есть
– непрерывная функция, которую можно дифференцировать.
Теорема. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, у которой переменная интегрирования заменена этим верхним пределом, то есть или .
Для вычисления производной проделаем все стандартные операции. Зададим приращение аргументу:
, что, в свою очередь, приведет к приращению функции:
. Так как
Так как
, а
, то приращение функции определяется выражением:
.
Применим к полученному выражению теорему о среднем в определенном интеграле:
, где
.
Составим отношение
. Чтобы получить производную
, перейдем в составленном отношении к пределу:
. Так как
, то при стремлении
точка
будет стремиться к
. Следовательно, вычисление предела приведет к выражению:
.
Из доказанной теоремы следует, что
– это первообразная от
, следовательно, определенный интеграл
также является первообразной от
, и вычислять его, очевидно, необходимо с помощью тех же приемов, что и неопределенный интеграл.
2. Формула Ньютона–Лейбница
Вычисление определенного интеграла как предела интегральной суммы представляет собой довольно сложную задачу и может быть выполнено лишь в некоторых наиболее простых случаях. Однако полученная в п. 1 связь между определенным интегралом и первообразной позволяет получить простой метод для вычисления этих интегралов.
Теорема. Если какая-либо первообразная от непрерывной функции , то справедлива формула: .
В предыдущем пункте было показано, что
– это первообразная от функции
. Но как было показано при изучении неопределенного интеграла, любая непрерывная функция имеет бесконечное множество первообразных, отличающихся друг от друга на постоянное слагаемое. Поэтому, если
какая-то другая первообразная от той же функции
, то
.
Оказывается, что в случае определенного интеграла постоянную
можно вычислить. Действительно, так как
Действительно, так как
может принимать любые значения между
и
(п. 1), то пусть
. Тогда:
. Но определенный интеграл с равными пределами равен нулю, следовательно,
. Значит,
.
Положим теперь, что
, тогда
.
Полученное выражение называется формулой Ньютона – Лейбница. Другая форма записи этого выражения следующая:
.
Обычно в полученных выражениях переменная интегрирования обозначается буквой
.
Таким образом, чтобы вычислить определенный интеграл, необходимо найти любую первообразную от
и вычислить разность ее значений в верхнем и нижнем пределах интегрирования. Полученная простая формула позволяет легко находить решения многих математических и прикладных задач, связанных с вычислением определенного интеграла.
Полученная простая формула позволяет легко находить решения многих математических и прикладных задач, связанных с вычислением определенного интеграла.
3. Замена переменной в определенном интеграле
При изучении неопределенного интеграла было показано (п. 5.4), что одним из наиболее часто встречающихся методов его вычисления является замена переменных. Так как вычисление определенного интеграла, согласно формуле Ньютона – Лейбница, также связано с нахождением первообразной, то метод замены переменной применим и в нем, однако при этом имеются некоторые особенности. В неопределенном интеграле замена переменной приводила в конце вычислений к обратной замене, в определенном же, оказывается, можно обойтись без этого.
Теорема. Если в определенном интеграле , где непрерывна на , сделать замену переменной и при этом:
Длина дугиОбщий подход а также Определение гладкой кривой
Длина дуги — это расстояние между двумя точками на участке кривой .
После исправления кривая дает отрезок прямой, длина которого равна длине дуги кривой.
Длина дуги ˙s из логарифмической спирали в зависимости от ее параметра & thetas .
Определение длины сегмента неправильной дуги также называется исправлением кривой. Появление исчисления бесконечно малых привело к общей формуле, которая в некоторых случаях дает решения в замкнутой форме .
Общий подход
Аппроксимация несколькими линейными отрезками
Кривые в плоскости может быть аппроксимировано путем подключения конечного числа точек на кривом с использованием отрезков , чтобы создать многоугольный путь . Так как длину каждого линейного сегмента легко вычислить (например, используя теорему Пифагора в евклидовом пространстве), общую длину приближения можно найти, суммируя длины каждого линейного сегмента;это приближение известно как (кумулятивное) хордовое расстояние . [1]
Если кривая еще не является многоугольной траекторией, использование все большего числа сегментов меньшей длины приведет к лучшему приближению. {b} {\ Big |} f ‘(t) {\ Big |} \ dt.}
{b} {\ Big |} f ‘(t) {\ Big |} \ dt.}
Последнее равенство верно по следующим причинам: (i) по теореме о среднем значении , ж ( т я ) — ж ( т я — 1 ) Δ т знак равно ж ′ ( т я — 1 + θ я ( т я — т я — 1 ) ) , {\ displaystyle {\ frac {f (t_ {i}) — f (t_ {i-1})} {\ Delta t}} = f ‘(t_ {i-1} + \ theta _ {i} (t_ {i} -t_ {i-1})),} где 0 < θ я < 1 {\ Displaystyle 0 <\ theta _ {я} <1} [ сомнительно — обсудить ] . (ii) функция | ж ′ | {\ Displaystyle \ влево | е ‘\ вправо |} непрерывна, следовательно, она равномерно непрерывна , поэтому существует положительная действительная функция δ ( ϵ ) {\ displaystyle \ delta (\ epsilon)} положительного реального ϵ {\ displaystyle \ epsilon} такой, что Δ т < δ ( ϵ ) {\ Displaystyle \ Дельта т <\ дельта (\ эпсилон)} подразумевает | | ж ′ ( т я — 1 + θ я ( т я — т я — 1 ) ) | — | ж ′ ( т я ) | | < ϵ . {\ displaystyle \ left | {\ Big |} f ‘(t_ {i-1} + \ theta _ {i} (t_ {i} -t_ {i-1})) {\ Big |} — {\ Big |} f ‘(t_ {i}) {\ Big |} \ right | <\ epsilon. {{\ sqrt {2}} / 2} = {\ frac {\ pi} { 2}}}
{{\ sqrt {2}} / 2} = {\ frac {\ pi} { 2}}}
от 1,3 × 10 −11 и 16-точечная оценка квадратурного правила Гаусса1.570 796 326 794 727 отличается от истинной длины только1,7 × 10 −13 . Это означает, что можно оценить этот интеграл почти с машинной точностью с помощью всего 16 вычислений подынтегрального выражения.
Кривая на поверхности
Позволять Икс ( ты , v ) {\ Displaystyle \ mathbf {х} (и, v)} отображение поверхности и пусть C ( т ) знак равно ( ты ( т ) , v ( т ) ) {\ Displaystyle \ mathbf {С} (т) = (и (т), v (т))} — кривая на этой поверхности. Подынтегральное выражение интеграла длины дуги равно | ( Икс ∘ C ) ′ ( т ) | . {\ displaystyle \ left | \ left (\ mathbf {x} \ circ \ mathbf {C} \ right) ‘(t) \ right |.} Для вычисления производной требуется цепное правило для векторных полей:
- D ( Икс ∘ C ) знак равно ( Икс ты Икс v ) ( ты ′ v ′ ) знак равно Икс ты ты ′ + Икс v v ′ .
 {2} = v} ).
{2} = v} ).Другие системы координат
Позволять C ( т ) знак равно ( р ( т ) , θ ( т ) ) {\ Displaystyle \ mathbf {С} (т) = (г (т), \ тета (т))} быть кривой, выраженной в полярных координатах. Отображение, которое преобразует полярные координаты в прямоугольные координаты, выглядит следующим образом:
- Икс ( р , θ ) знак равно ( р потому что θ , р грех θ ) . {\ displaystyle \ mathbf {x} (r, \ theta) = (r \ cos \ theta, r \ sin \ theta).}
Подынтегральное выражение интеграла длины дуги равно | ( Икс ∘ C ) ′ ( т ) | . {\ displaystyle \ left | \ left (\ mathbf {x} \ circ \ mathbf {C} \ right) ‘(t) \ right |.} Цепное правило для векторных полей показывает, что D ( Икс ∘ C ) знак равно Икс р р ′ + Икс θ θ ′ . {\ displaystyle D (\ mathbf {x} \ circ \ mathbf {C}) = \ mathbf {x} _ {r} r ‘+ \ mathbf {x} _ {\ theta} \ theta’.} Таким образом, квадрат подынтегральной функции интеграла длины дуги равен
- ( Икс р ⋅ Икс р ) ( р ′ ) 2 + 2 ( Икс р ⋅ Икс θ ) р ′ θ ′ + ( Икс θ ⋅ Икс θ ) ( θ ′ ) 2 знак равно ( р ′ ) 2 + р 2 ( θ ′ ) 2 .
 {2} \,}} d \ theta.}
{2} \,}} d \ theta.}
Теперь позвольте C ( т ) знак равно ( р ( т ) , θ ( т ) , ϕ ( т ) ) {\ Displaystyle \ mathbf {С} (т) = (г (т), \ тета (т), \ фи (т))} — кривая в сферических координатах, где θ {\ displaystyle \ theta} полярный угол, отсчитываемый от положительного z {\ displaystyle z} ось и ϕ {\ displaystyle \ phi} азимутальный угол. Отображение, которое преобразует сферические координаты в прямоугольные координаты:
- Икс ( р , θ , ϕ ) знак равно ( р грех θ потому что ϕ , р грех θ грех ϕ , р потому что θ ) . {\ displaystyle \ mathbf {x} (r, \ theta, \ phi) = (r \ sin \ theta \ cos \ phi, r \ sin \ theta \ sin \ phi, r \ cos \ theta).}
Повторное использование цепного правила показывает, что D ( Икс ∘ C ) знак равно Икс р р ′ + Икс θ θ ′ + Икс ϕ ϕ ′ . {\ Displaystyle D (\ mathbf {x} \ circ \ mathbf {C}) = \ mathbf {x} _ {r} r ‘+ \ mathbf {x} _ {\ theta} \ theta’ + \ mathbf {x} _ {\ phi} \ phi ‘.
 {2} \,}} dt.}
{2} \,}} dt.}
Простые случаи
Дуги окружностей
Длины дуги обозначаются буквой s , так как латинское слово для обозначения длины (или размера) — это пространство .
В следующих строках р {\ displaystyle r} представляет собой радиус от в окружности , d {\ displaystyle d} его диаметр , C {\ displaystyle C} это его окружность , s {\ displaystyle s} — длина дуги окружности, а θ {\ displaystyle \ theta} — угол, под которым дуга проходит в центре круга. Расстояния р , d , C , {\ displaystyle r, d, C,} а также s {\ displaystyle s} выражены в тех же единицах.
- C знак равно 2 π р , {\ Displaystyle С = 2 \ пи г,} который совпадает с C знак равно π d . {\ Displaystyle C = \ pi d.} Это уравнение является определением π . {\ displaystyle \ pi.}
- Если дуга — полукруг , то s знак равно π р . {\ displaystyle s = \ pi r.}
- Для произвольной дуги окружности:
- Если θ {\ displaystyle \ theta} в радианах, тогда s знак равно р θ .
 {\ circ}}}.}
{\ circ}}}.} - Если θ {\ displaystyle \ theta} находится в градациях (100 градаций, или оценок, или градианов — один прямой угол ), то s знак равно π р θ 200 град , {\ displaystyle s = {\ frac {\ pi r \ theta} {200 {\ text {grad}}}},} который совпадает с s знак равно C θ 400 град . {\ displaystyle s = {\ frac {C \ theta} {400 {\ text {grad}}}}.}
- Если θ {\ displaystyle \ theta} находится в поворотах (один оборот — полный оборот, или 360 °, или 400 градусов, или 2 π {\ displaystyle 2 \ pi} радианы), то s знак равно C θ / 1 повернуть {\ displaystyle s = C \ theta / 1 {\ text {turn}}} .
- Если θ {\ displaystyle \ theta} в радианах, тогда s знак равно р θ .
Дуги больших кругов на Земле
Две единицы длины, морская миля и метр (или километр), были изначально определены таким образом, чтобы длины дуг больших окружностей на поверхности Земли были просто численно связаны с углами, которые они образуют в ее центре. Простое уравнение s знак равно θ {\ displaystyle s = \ theta} применяется в следующих случаях:
- если s {\ displaystyle s} находится в морских милях, и θ {\ displaystyle \ theta} в угловых минутах ( 1 ⁄ 60 градусов), или
- если s {\ displaystyle s} находится в километрах, и θ {\ displaystyle \ theta} в градусах Цельсия ( 1 ⁄ 100 град ).

Длины единиц расстояния были выбраны так, чтобы окружность Земли была равна 40 000 километров, или21 600 морских миль. Это количество соответствующих угловых единиц за один полный оборот.
Эти определения метра и морской мили были заменены более точными, но исходные определения все еще достаточно точны для концептуальных целей и некоторых расчетов. Например, они подразумевают, что один километр равен точно 0,54 морской мили. Используя официальные современные определения, одна морская миля составляет ровно 1,852 километра [3], что означает, что 1 километр составляет примерно0,539 956 80 морских миль. [4] Это современное соотношение отличается от рассчитанного по исходным определениям менее чем на одну часть из 10 000.
Длина дуги параболы
Исторические методы
Античность
На протяжении большей части истории математики даже величайшие мыслители считали невозможным вычислить длину неправильной дуги. Хотя Архимед первым изобрел способ нахождения площади под кривой с помощью своего « метода истощения », мало кто верил, что кривые могут иметь определенную длину, как и прямые линии. Первые шаги в этой области, как это часто бывает в расчетах , были сделаны путем приближения . Люди начали вписывать многоугольники в кривые и вычислять длину сторон для некоторого точного измерения длины. Используя больше сегментов и уменьшая длину каждого сегмента, они смогли получить все более и более точное приближение. В частности, вписав в круг многоугольник с множеством сторон, они смогли найти приблизительные значения π . [5] [6]
Первые шаги в этой области, как это часто бывает в расчетах , были сделаны путем приближения . Люди начали вписывать многоугольники в кривые и вычислять длину сторон для некоторого точного измерения длины. Используя больше сегментов и уменьшая длину каждого сегмента, они смогли получить все более и более точное приближение. В частности, вписав в круг многоугольник с множеством сторон, они смогли найти приблизительные значения π . [5] [6]
17 век
В 17 — м века, метод исчерпывания привели к выпрямлению геометрических методами нескольких кривых трансцендентных : логарифмическая спираль по Торричелли в 1645 году (некоторые источники говорят , Валлис в 1650 — х годах), то циклоида от Кристофера Рена в 1658 году, и цепная линия от Готфрида Лейбница в 1691 году.
В 1659 году Уоллис приписал Уильяму Нейлу открытие первого выпрямления нетривиальной алгебраической кривой — полукубической параболы . [7] Сопутствующие рисунки приведены на странице 145. На странице 91 Уильям Нейл упоминается как Гулиельмус Нелиус .
На странице 91 Уильям Нейл упоминается как Гулиельмус Нелиус .
Интегральная форма
До полного формального развития исчисления основа современной интегральной формы для длины дуги была независимо открыта Хендриком ван Хойраетом и Пьером де Ферма .
В 1659 году ван Хойрает опубликовал конструкцию, показывающую, что задача определения длины дуги может быть преобразована в задачу определения площади под кривой (т. Е. Интеграла). В качестве примера своего метода он определил длину дуги полукубической параболы, что потребовало нахождения области под параболой . [8] В 1660 году Ферма опубликовал более общую теорию, содержащую тот же результат, в своей работе De linearum curvarum cum lineis rectis comparatione dissertatio geometry (Геометрическая диссертация о кривых линиях в сравнении с прямыми линиями). [9]
Метод Ферма определения длины дуги
Основываясь на своей предыдущей работе с касательными, Ферма использовал кривую
- у знак равно Икс 3 2 {\ Displaystyle у = х ^ {\ гидроразрыва {3} {2}} \,}
которого касательной при х = имела наклон в
- 3 2 а 1 2 {\ displaystyle {3 \ over 2} а ^ {\ frac {1} {2}}}
так что касательная линия будет иметь уравнение
- у знак равно 3 2 а 1 2 ( Икс — а ) + ж ( а ) .
 {2} \ left (1+ {9 \ over 4} a \ right) \ end {align}}}
{2} \ left (1+ {9 \ over 4} a \ right) \ end {align}}}
что, когда решено, дает
- А C знак равно ε 1 + 9 4 а . {\ displaystyle AC = \ varepsilon {\ sqrt {1+ {9 \ over 4} a \,}}.}
Чтобы приблизиться к длине, Ферма суммировал бы последовательность коротких отрезков.
Кривые бесконечной длины
Кривая Коха.
График x sin (1 / x ).
Как упоминалось выше, некоторые кривые нельзя исправить. То есть не существует верхней границы длин полигональных аппроксимаций; длину можно сделать сколь угодно большой . Неформально говорят, что такие кривые имеют бесконечную длину. Существуют непрерывные кривые, на которых каждая дуга (кроме одноточечной) имеет бесконечную длину. Примером такой кривой является кривая Коха . Другим примером кривой бесконечной длины является график функции, определяемой формулой f ( x ) = x sin (1 / x ) для любого открытого множества с 0 в качестве одного из его разделителей и f (0) = 0. {1} {\ sqrt {\ pm g \ left (\ gamma ‘(t), \ gamma’ (t) \ right) \,}} dt,}
{1} {\ sqrt {\ pm g \ left (\ gamma ‘(t), \ gamma’ (t) \ right) \,}} dt,}
где γ ′ ( т ) ∈ Т γ ( т ) M {\ Displaystyle \ гамма ‘(т) \ в Т _ {\ гамма (т)} М} является касательным вектором γ {\ displaystyle \ gamma} в т . {\ displaystyle t.} Знак квадратного корня выбирается один раз для данной кривой, чтобы гарантировать, что квадратный корень является действительным числом. Положительный знак выбран для пространственноподобных кривых; в псевдоримановом многообразии отрицательный знак может быть выбран для времениподобных кривых. Таким образом, длина кривой — неотрицательное действительное число. Обычно не рассматриваются кривые, частично пространственноподобные, а частично времениподобные.
В теории относительности длина дуги времениподобных кривых ( мировых линий ) — собственное время, прошедшее вдоль мировой линии, а длина дуги пространственноподобной кривой — собственное расстояние вдоль кривой.
Смотрите также
- Дуга (геометрия)
- Длина окружности
- Формула Крофтона
- Эллиптический интеграл
- Геодезические
- Внутреннее уравнение
- Интегральные приближения
- Линейный интеграл
- Дуга меридиана
- Многопараметрическое исчисление
- Извилистость
Рекомендации
- ^ Альберг; Нильсон (1967).
 MPEAS (псевдоним Ферма) (1660). De Linearum Curvarum cum Lineis Rectis Comparatione Dissertatio Geometrica . Тулуза: Арно Коломер.
MPEAS (псевдоним Ферма) (1660). De Linearum Curvarum cum Lineis Rectis Comparatione Dissertatio Geometrica . Тулуза: Арно Коломер.
Источники
- Фаруки, Рида Т. (1999). «Кривые от движения, движение от кривых». В Laurent, P.-J .; Sablonniere, P .; Шумакер, LL (ред.). Кривая и дизайн поверхностей: Сен-Мало 1999 . Vanderbilt Univ. Нажмите. С. 63–90. ISBN 978-0-8265-1356-4.
Внешние ссылки
- «Спрямляемая кривая» , Энциклопедия математики , EMS Press , 2001 [1994]
- История искривления
- Вайсштейн, Эрик В. «Длина дуги» . MathWorld .
- Длина дуги , Эд Пегг младший , Демонстрационный проект Вольфрама , 2007.
- Учебное пособие по исчислению — Длина дуги (исправление)
- Указатель известных кривых Архив истории математики MacTutor
- Аппроксимация длины дуги, сделанная Чадом Пирсоном, Джошем Фрицем и Анжелой Шарп, The Wolfram Demonstrations Project .

- Длина кривой Эксперимент. Иллюстрирует численное решение нахождения длины кривой.
Исчисление II — Длина дуги с полярными координатами
Онлайн-заметки Пола
Главная
/
Исчисление II
/
Параметрические уравнения и полярные координаты
/ Длина дуги с полярными координатами
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 3-9: Длина дуги с полярными координатами
Теперь нам нужно перейти к применению интегралов в исчислении II и к тому, как мы их вычисляем в полярных координатах. В этом разделе мы рассмотрим длину дуги кривой, заданной выражением
. \[r = f\left(\theta\right)\hspace{0.5in}\alpha\le\theta\le\beta\]
, где мы также предполагаем, что кривая трассируется ровно один раз. Как и в случае с касательными линиями в полярных координатах, мы сначала запишем кривую в терминах набора параметрических уравнений
\[\begin{align*}x & = r\cos \theta & \hspace{0.75in} y & = r\sin \theta \\ & = f\left( \theta \right)\cos \theta & \ hspace{0.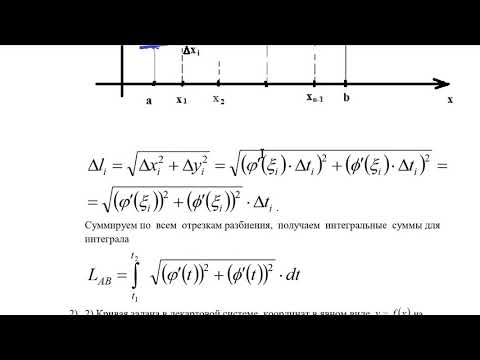 75in} & = f\left(\theta\right)\sin\theta\end{align*}\]
75in} & = f\left(\theta\right)\sin\theta\end{align*}\]
и теперь мы можем использовать параметрическую формулу для нахождения длины дуги.
Для этих вычислений нам понадобятся следующие производные.
\[\begin{align*}\frac{{dx}}{{d\theta }} & = f’\left( \theta \right)\cos \theta — f\left( \theta \right)\sin \theta & \hspace{0.75in}\frac{{dy}}{{d\theta}} & = f’\left( \theta \right)\sin \theta + f\left( \theta \right)\ cos \ theta \\ & = \ frac {{dr}} {{d \ theta }} \ cos \ theta — r \ sin \ theta & \ hspace {0,75 дюйма} & = \ frac {{dr}} {{d \ тета }} \ грех \ тета + r \ соз \ тета \ конец {выравнивание *} \] 9{\ frac {\ pi} {4}} \\ & = \ frac {1} {2} \ left ( {\ sqrt 2 + \ ln \ left ( {1 + \ sqrt 2 } \ right)} \ right) \конец{выравнивание*}\]
В качестве отступления перед тем, как мы закончим эту главу. Полярное уравнение \(r = \theta\) является уравнением спирали. Вот краткий набросок \(r = \theta\) для \(0 \le \theta \le 4\pi \).
8.1: Длина дуги — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4492
Цели обучения
- Определить длину кривой \(y=f(x)\) между двумя точками.
- Определите длину кривой \(x=g(y)\) между двумя точками.
- Найдите площадь поверхности тела вращения.
В этом разделе мы используем определенные интегралы, чтобы найти длину дуги кривой. Мы можем думать о длине дуги как о расстоянии, которое вы прошли бы, если бы шли по пути кривой. Во многих реальных приложениях используется длина дуги. Если ракета запускается по параболической траектории, мы можем захотеть узнать, как далеко пролетит ракета. Или, если кривая на карте представляет собой дорогу, мы можем захотеть узнать, какое расстояние нам нужно проехать, чтобы добраться до пункта назначения.
Или, если кривая на карте представляет собой дорогу, мы можем захотеть узнать, какое расстояние нам нужно проехать, чтобы добраться до пункта назначения.
Мы начнем с вычисления длины дуги кривых, определенных как функции \(x\), затем исследуем тот же процесс для кривых, определенных как функции \(y\). (Процесс идентичен, но роли \(x\) и \(y\) поменялись местами.) Методы, которые мы используем для определения длины дуги, можно расширить, чтобы найти площадь поверхности вращения, и мы замыкаем раздел с рассмотрением этого понятия.
Длина дуги кривой y = f(x)
В предыдущих приложениях интегрирования мы требовали, чтобы функция \( f(x)\) была интегрируемой или, самое большее, непрерывной. Однако для расчета длины дуги у нас есть более строгие требования к \(f(x)\). Здесь мы требуем, чтобы \(f(x)\) было дифференцируемым, и, кроме того, мы требуем, чтобы его производная, \( f′(x),\), была непрерывной. Такие функции, которые имеют непрерывные производные, называются гладкими. (Это свойство снова появляется в следующих главах.)
(Это свойство снова появляется в следующих главах.)
Пусть \(f(x)\) — гладкая функция, определенная над \([a,b]\). Мы хотим вычислить длину кривой от точки \( (a,f(a))\) до точки \( (b,f(b))\). Начнем с использования линейных сегментов для аппроксимации длины кривой. Для \(i=0,1,2,…,n\) пусть \(P={x_i}\) будет обычным разделом \([a,b]\). Затем для \( i=1,2,…,n\) построить отрезок от точки \( (x_{i−1},f(x_{i−1}))\) до точки \ ((x_i,f(x_i))\). Хотя может показаться логичным использовать либо горизонтальные, либо вертикальные сегменты линий, мы хотим, чтобы наши сегменты линий как можно точнее аппроксимировали кривую. На рисунке \(\PageIndex{1}\) показана эта конструкция для \( n=5\).
Рисунок \(\PageIndex{1}\): Мы можем аппроксимировать длину кривой, добавляя отрезки. Чтобы помочь нам найти длину каждого сегмента линии, мы смотрим на изменение расстояния по вертикали, а также изменение расстояния по горизонтали на каждом интервале. Поскольку мы использовали регулярное разбиение, изменение расстояния по горизонтали на каждом интервале определяется выражением \(Δx\). Однако изменение расстояния по вертикали варьируется от интервала к интервалу, поэтому мы используем \( Δy_i=f(x_i)−f(x_{i−1})\) для представления изменения расстояния по вертикали за интервал \([x_ {i−1},x_i]\), как показано на рисунке \(\PageIndex{2}\). Обратите внимание, что некоторые (или все) \( Δy_i\) могут быть отрицательными. 9{3/2}\). Вычислите длину дуги графика \(f(x)\) на интервале \([0,1]\). Округлите ответ до трех знаков после запятой.
Однако изменение расстояния по вертикали варьируется от интервала к интервалу, поэтому мы используем \( Δy_i=f(x_i)−f(x_{i−1})\) для представления изменения расстояния по вертикали за интервал \([x_ {i−1},x_i]\), как показано на рисунке \(\PageIndex{2}\). Обратите внимание, что некоторые (или все) \( Δy_i\) могут быть отрицательными. 9{3/2}\). Вычислите длину дуги графика \(f(x)\) на интервале \([0,1]\). Округлите ответ до трех знаков после запятой.
- Подсказка
Используйте процесс из предыдущего примера. Не забудьте изменить пределы интегрирования.
- Ответить
\[ \dfrac{1}{6}(5\sqrt{5}−1)≈1,697 \номер\]
Хотя хорошо иметь формулу для вычисления длины дуги, эта конкретная теорема может генерировать выражения, которые трудно интегрировать. Мы изучаем некоторые методы интеграции во Введении в методы интеграции. В некоторых случаях нам, возможно, придется использовать компьютер или калькулятор для аппроксимации значения интеграла. 92}\,dx ≈ 8,26815. \nonumber \]
92}\,dx ≈ 8,26815. \nonumber \]
Упражнение \(\PageIndex{2}\)
Пусть \( f(x)=\sin x\). Вычислите длину дуги графика \(f(x)\) на интервале \([0,π]\). Используйте компьютер или калькулятор, чтобы приблизить значение интеграла.
- Подсказка
Используйте процесс из предыдущего примера.
- Ответить
\[ \text{Длина дуги} ≈ 3,8202 \номер\]
Длина дуги кривой \(x = g(y)\)
Мы только что видели, как аппроксимировать длину кривой с помощью отрезков. Если мы хотим найти длину дуги графика функции \(y\), мы можем повторить тот же процесс, за исключением того, что мы разделяем ось y вместо оси x. На рисунке \(\PageIndex{3}\) показан репрезентативный сегмент линии.
Рисунок \(\PageIndex{3}\): репрезентативный отрезок линии на интервале \([y_{i−1},y_i].\)Тогда длина отрезка равна 94}dy≈21.0277.\номер \]
Упражнение \(\PageIndex{3}\)
Пусть \(g(y)=1/y\). Вычислите длину дуги графика \(g(y)\) на интервале \([1,4]\). Используйте компьютер или калькулятор, чтобы приблизить значение интеграла.
Вычислите длину дуги графика \(g(y)\) на интервале \([1,4]\). Используйте компьютер или калькулятор, чтобы приблизить значение интеграла.
- Подсказка
Используйте процесс из предыдущего примера.
- Ответить
\[\text{Длина дуги} =3,15018 \номер\]
Площадь поверхности вращения
Понятия, которые мы использовали для определения длины дуги кривой, можно расширить, чтобы найти площадь поверхности вращения. Площадь поверхности — это общая площадь внешнего слоя объекта. Для таких объектов, как кубы или кирпичи, площадь поверхности объекта равна сумме площадей всех его граней. Для криволинейных поверхностей ситуация немного сложнее. Пусть \(f(x)\) — неотрицательная гладкая функция на отрезке \([a,b]\). Мы хотим найти площадь поверхности вращения, созданной вращением графика \(y=f(x)\) вокруг оси \(x\), как показано на следующем рисунке.
Как мы делали много раз раньше, мы собираемся разбить интервал \([a,b]\) и аппроксимировать площадь поверхности, вычислив площадь поверхности более простых форм. Мы начнем с использования линейных сегментов для аппроксимации кривой, как мы делали ранее в этом разделе. Для \(i=0,1,2,…,n\) пусть \(P={x_i}\) будет обычным разделом \([a,b]\). Затем для \(i=1,2,…,n,\) построить отрезок от точки \((x_{i−1},f(x_{i−1}))\) до точки \ ((x_i,f(x_i))\). Теперь вращайте эти отрезки вокруг оси \(x\), чтобы создать аппроксимацию поверхности вращения, как показано на следующем рисунке.
Рисунок \(\PageIndex{5}\): (a) Аппроксимация \(f(x)\) отрезками. (b) Поверхность вращения, образованная вращением отрезков вокруг \(оси x\). Обратите внимание, что когда каждый сегмент линии вращается вокруг оси, образуется полоса. Эти полосы на самом деле представляют собой кусочки рожков (представьте себе рожок мороженого с отрезанным заостренным концом). Часть такого конуса называется усеченным конуса.
Часть такого конуса называется усеченным конуса.
Чтобы найти площадь поверхности полосы, нам нужно найти площадь боковой поверхности \(S\) усеченного конуса (площадь только наклонной наружной поверхности усеченного конуса, не включая площади вершины или нижние грани). Пусть \(r_1\) и \(r_2\) — радиусы широкого и узкого концов усеченного конуса соответственно, а \(l\) — наклонная высота усеченного конуса, как показано на следующем рисунке.
Рисунок \(\PageIndex{6}\): Усеченный конус может аппроксимировать небольшую часть площади поверхности.Мы знаем, что площадь боковой поверхности конуса равна
\[\text{Площадь боковой поверхности } =πrs, \nonumber \]
, где \(r\) — радиус основания конуса, а \ (s\) — это наклонная высота (рисунок \(\PageIndex{7}\)).
Рисунок \(\PageIndex{7}\): площадь боковой поверхности конуса определяется выражением \(πrs\). Поскольку усеченный конус можно рассматривать как часть конуса, площадь боковой поверхности усеченного конуса равна площади боковой поверхности всего конуса за вычетом площади боковой поверхности меньшего конуса (заостренного кончика), который был срезан. выключено (рис. \(\PageIndex{8}\)).
выключено (рис. \(\PageIndex{8}\)).
Сечения малого конуса и большого конуса представляют собой подобные треугольники, поэтому мы видим, что
\[ \dfrac{r_2}{r_1}=\dfrac{s−l}{s} \nonumber \]
Находя \(s\), получаем =s−ls
\[\begin{align*} \dfrac{r_2}{r_1} &=\dfrac{s−l}{s} \\ r_2s &=r_1 (s−l) \\ r_2s &=r_1s−r_1l \\ r_1l &=r_1s−r_2s \\ r_1l &=(r_1−r_2)s \\ \dfrac{r_1l}{r_1−r_2} =s \end{align *}\] 92_2)l}{r_1−r_2}=\dfrac{π(r_1−r+2)(r1+r2)l}{r_1−r_2} \\[4pt] &= π(r_1+r_2)l. \label{eq20} \end{align*} \]
Теперь воспользуемся этой формулой для расчета площади поверхности каждой из полос, образованных вращением отрезков линии вокруг \(оси x\). Репрезентативная полоса показана на следующем рисунке.
Рисунок \(\PageIndex{9}\): репрезентативная полоса, используемая для определения площади поверхности. Обратите внимание, что наклонная высота этой усеченной пирамиды равна длине отрезка, использованного для ее создания. Итак, применяя формулу площади поверхности, мы имеем 92}) \end{align*}\]
Итак, применяя формулу площади поверхности, мы имеем 92}) \end{align*}\]
Как и в случае с длиной дуги, мы можем провести аналогичное развитие для функций \(y\), чтобы получить формулу для площади поверхностей вращения вокруг \(y- ось\). Эти выводы резюмируются в следующей теореме.
Площадь поверхности вращения
Пусть \(f(x)\) — неотрицательная гладкая функция на интервале \([a,b]\). Тогда площадь поверхности вращения, образованной вращением графика \(f(x)\) вокруг оси x, равна 92}dy \nonumber \]
Пример \(\PageIndex{4}\): Расчет площади поверхности вращения 1.
Пусть \(f(x)=\sqrt{x}\) над интервал \([1,4]\). Найдите площадь поверхности, образованной вращением графика \(f(x)\) вокруг оси \(x\). Округлите ответ до трех знаков после запятой.
Решение
График \(f(x)\) и поверхность вращения показаны на рисунке \(\PageIndex{10}\).
Рисунок \(\PageIndex{10}\): (a) График \(f(x)\). (б) Поверхность вращения. 9{17/4}_{5/4} \\[4pt] &=\dfrac{π}{6}[17\sqrt{17}−5\sqrt{5}]≈30,846 \end{align*}\ ]Упражнение \(\PageIndex{4}\)
Пусть \( f(x)=\sqrt{1−x}\) на интервале \([0,1/2]\). 3\). График \(g(y)\) и поверхность вращения показаны на следующем рисунке. 92}\) на интервале \( y∈[0,2]\). Найдите площадь поверхности, образованной вращением графика \(g(y)\) вокруг оси \(y\).
3\). График \(g(y)\) и поверхность вращения показаны на следующем рисунке. 92}\) на интервале \( y∈[0,2]\). Найдите площадь поверхности, образованной вращением графика \(g(y)\) вокруг оси \(y\).
- Подсказка
Используйте процесс из предыдущего примера.
- Ответить
\( 12π\)
Ключевые понятия
- Длину дуги кривой можно рассчитать с помощью определенного интеграла.
- Длина дуги сначала аппроксимируется с помощью отрезков прямой, в результате чего получается сумма Римана. Принятие предела дает нам формулу определенного интеграла. Тот же процесс можно применить к функциям \(y\).
- Понятия, используемые для расчета длины дуги, можно обобщить, чтобы найти площадь поверхности вращения.
- Интегралы, полученные по формулам длины дуги и площади поверхности, часто трудно вычислить. Может потребоваться использование компьютера или калькулятора для аппроксимации значений интегралов.
 92})dx\)
92})dx\)Глоссарий
- длина дуги
- длину дуги кривой можно рассматривать как расстояние, которое человек пройдет по пути кривой
- усеченный конус
- часть конуса; усеченный конус строится путем разрезания конуса плоскостью, параллельной основанию
- площадь поверхности
- площадь поверхности твердого тела – это общая площадь внешнего слоя объекта; для таких объектов, как кубы или кирпичи, площадь поверхности объекта равна сумме площадей всех его граней
8.1: Длина дуги распространяется по незаявленной лицензии и была создана, изменена и/или курирована LibreTexts.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Показать страницу TOC
- нет
- Включено
- да
- Теги
- длина дуги
Длина дуги (расчет)
Использование вычислений для определения длины кривой .

(Сначала прочтите о производных и интегралах)Представьте, что мы хотим найти длину кривой между двумя точками. И кривая гладкая (производная непрерывна).
Сначала мы разбиваем кривую на маленькие отрезки и используем формулу расстояния между 2 точками для каждого отрезка, чтобы получить приблизительный ответ:
Расстояние от x 0 до x 1 составляет:
S 1 = √ (х 1 − х 0 ) 2 + (у 1 − у 0 ) 2
И давайте использовать Δ (дельта) для обозначения разницы между значениями, так что это будет:
S 1 = √ (Δx 1 ) 2 + (Δy 1 ) 2
Теперь нам нужно намного больше:
S 2 = √(Δx 2 ) 2 + (Δy 2 ) 2
S 3 = √(Δx 3 ) 2 + (ΔY 3 ) 2
. ..
..
…
S N = √ (Δx N ) 2 + (Δx N ) 2 00 + (Δx 4) 484848484848484848484848484848484) (Δx n )Мы можем написать все эти строки всего за одной строкой используя Sum:
С ≈
√(Δx i ) 2 + (Δy i ) 2
Но мы все равно обречены на большое количество вычислений!
Может быть, мы можем сделать большую электронную таблицу или написать программу для вычислений… но давайте попробуем что-нибудь еще.
У нас есть хитрый план:
- все Δx i будут одинаковыми , поэтому мы можем извлечь их из квадратного корня
- , а затем превратить сумму в интеграл.
Поехали:
Сначала разделите и , умножьте Δy i на Δx i :
С ≈
√(Δx i ) 2 + (Δx i ) 2 (Δy i /Δx i ) 2
Теперь вычтите (Δx i ) 2 :
С ≈
√(Δx i ) 2 (1 + (Δy i /Δx i ) 2 )
Возьмем (Δx i ) 2 из квадратного корня:
С ≈
√1 + (Δy i /Δx i ) 2 Δx i
Теперь, когда n приближается к бесконечности (поскольку мы движемся к бесконечному количеству срезов, и каждый срез становится меньше), мы получаем:
С =
lim
n→∞
√1 + (Δy i /Δx i ) 2 Δx i
Теперь у нас есть интеграл, и мы пишем dx , чтобы обозначить Δx .
 срезы приближаются к нулю по ширине (аналогично для dy) :
срезы приближаются к нулю по ширине (аналогично для dy) :С =
√1+(dy/dx) 2 dx
И dy/dx является производной функции f(x), которую также можно записать как f’(x) :
С =
√1+(f’(x)) 2 dx
Формула длины дугиА теперь вдруг мы в гораздо лучшем месте, нам не нужно складывать множество срезов, мы можем вычислить точный ответ (если мы сможем решить дифференциал и интеграл).
Примечание: интеграл также работает по y, полезно, если мы знаем x=g(y):
С =
√1+(g’(y)) 2 dy
Итак, наши шаги:
- Найдите производную от f’(x)
- Решите интеграл от √1 + (f’(x)) 2 dx
Несколько простых примеров для начала:
Пример: Найдите длину f(x) = 2 между x=2 и x=3
f(x) — это просто горизонтальная линия, поэтому ее производная равна f’(x) = 0
Начните с:
S =
√1+(f’(x)) 2 dx
Введите f’(x) = 0 :
S =
√1+0 2 дх
Упрощение:
S =
dx
Вычислить интеграл:
S = 3 − 2 = 1
Таким образом, длина дуги между 2 и 3 равна 1.
 Конечно, это так, но приятно, что мы нашли правильный ответ!
Конечно, это так, но приятно, что мы нашли правильный ответ!Интересный момент: «(1 + …)» часть формулы длины дуги гарантирует, что мы получим по крайней мере расстояние между значениями x, например, в этом случае, когда f’(x) равно нулю.
Пример: Найдите длину f(x) = x между x=2 и x=3
Производная f’(x) = 1
Начните с:S =
√1+(f’(x)) 2 dx
Введите f’(x) = 1 :
S =
√1+(1) 2 дх
Упрощение:
S =
√2 дх
Вычислить интеграл:
S = (3−2)√2 = √2
А диагональ единичного квадрата действительно равна квадратному корню из 2, верно?
Хорошо, теперь о более сложном.
 Пример реального мира.
Пример реального мира.Пример: Металлические столбы установлены
на расстоянии 6 м друг от друга через ущелье.Найдите длину висячего моста, следующего за кривой:
f(x) = 5 ch(x/5)
Вот реальная кривая:
Сначала решим общий случай!
Висячий трос образует кривую, называемую контактной сетью :
f(x) = a ch(x/a)
Большие значения a имеют меньший прогиб в середине
функция косинуса.Производная равна f'(x) = sh(x/a)
Кривая симметрична, поэтому легче работать только с половиной контактной сети, от центра до конца в точке «b»:
Начать с:
S =
√1+(f’(x)) 2 dx
Введите f’(x) = sh(x/a) :
S =
√1 + sin 2 (x/a) dx
Используйте идентификатор 1 + sinh 2 (x/a) = cosh 2 (x/a):
S =
√кош 2 (х/а) дх
Упрощение:
S =
кош(х/а) дх
Вычислить интеграл:
S = a sh(b/a)
Теперь, помня о симметрии, перейдем от −b к +b:
S = 2a sh(b/a)
В нашем конкретном случае a=5 и 6-метровый пролет изменяется от −3 до +3
S = 2×5 sinh(3/5)
= 6,367 м (с точностью до миллиметра)Это важно знать! Если мы построим его ровно 6 м в длину, то 90 568 никоим образом не 90 569 мы могли бы тянуть его достаточно сильно, чтобы он соответствовал столбам.
 Но на 6,367 м он будет работать прекрасно.
Но на 6,367 м он будет работать прекрасно.Пример: Найдите длину y = x
(3/2) от x = 0 до x = 4.)
Начните с:
S =
√1+(f’(x)) 2 dx
Вставить (3/2)x (1/2) :
S =
√1+((3/2)x (1/2) ) 2 дх
Упрощение:
S =
√1+(9/4)х дх
Мы можем использовать интегрирование путем замены:
- u = 1 + (9/4)x
- du = (9/4)dx
- (4/9)ду = дх
- Границы: u(0)=1 и u(4)=10
И получаем:
S =
(4/9)√у ду
Интегрировать:
S = (8/27) u (3/2) от 1 до 10
Рассчитать:
S = (8/27) (10 (3/2) − 9 1 9055 (3/2) ) = 9,073.
 ..
.. Формула длины дуги для функции f(x):
С =
√1+(f’(x)) 2 dx
шагов:
- Взять производную f(x)
- Запись формулы длины дуги
- Упростить и решить интеграл
13.3 Длина дуги и кривизна
Иногда полезно вычислить длину кривой в пространстве; за Например, если кривая представляет путь движущегося объекта, длина кривой между двумя точками может быть расстоянием, пройденным объект между двумя временами.
Напомним, что если кривая задана вектор-функцией $\bf r$, то вектор $\Delta {\bf r}= {\bf r}(t+\Delta t)-{\bf r}(t)$ точек из одной позиции на кривой к другой, как показано на рисунке 13.2.1. Если точки расположены близко друг к другу, длина $\Delta {\bf r}$ близка к длине кривая между двумя точками. Если мы сложим длины многих таких крошечных векторов, расположенных лицом к хвосту вдоль сегмента кривой, мы получаем приближение к длине кривой на этом сегменте.
 b|{\bf r}'(t)|\,dt.$$
(Ну, иногда. Это работает, если между $a$ и $b$ отрезок кривой
трассируется ровно один раз.)
92}\,дх.$$
К сожалению, такие интегралы часто невозможно вычислить точно и
должны быть приближены.
b|{\bf r}'(t)|\,dt.$$
(Ну, иногда. Это работает, если между $a$ и $b$ отрезок кривой
трассируется ровно один раз.)
92}\,дх.$$
К сожалению, такие интегралы часто невозможно вычислить точно и
должны быть приближены.Одним из полезных применений длины дуги является параметризация длины дуги . Вектор функция ${\bf r}(t)$ задает положение точки с точки зрения параметр $t$, который часто является временем, но не обязательно. Предположим, что $s$ расстояние вдоль кривой от некоторой фиксированной начальной точки; если мы используем $s$ для переменной, мы получаем ${\bf r}(s)$, позицию в пространстве в с точки зрения расстояния по кривой. Мы все еще можем представить себе, что кривая представляет положение движущегося объекта; теперь мы получаем положение объекта в зависимости от того, насколько далеко объект путешествовал.
Пример 13.3.3 Предположим, что ${\bf r}(t)=\langle \cos t,\sin t,0\rangle$. Мы знаем что эта кривая представляет собой окружность радиуса 1. Хотя $t$ может представлять время, он также может в этом случае представлять собой обычный угол между положительная ось $x$ и ${\bf r}(t)$.
 2(s/\sqrt2)\over2}+{1\over2}}=
\sqrt{{1\over2}+{1\over2}}=1.$$
Таким образом, в общем случае ${\bf r}’$ является единичным касательным вектором.
2(s/\sqrt2)\over2}+{1\over2}}=
\sqrt{{1\over2}+{1\over2}}=1.$$
Таким образом, в общем случае ${\bf r}’$ является единичным касательным вектором.Имея кривую ${\bf r}(t)$, мы хотели бы иметь возможность измерить при различные точки, как резко он изогнут. Очевидно, это связано с насколько «быстро» касательный вектор меняет направление, поэтому первое предположение может быть, мы можем измерить кривизну с помощью $|{\bf r}»(t)|$. Немного мысль показывает, что это ошибочно; если мы думаем о $t$ как о времени, для например, мы могли бы отслеживать кривую более или менее быстро по прошествии времени. Вторая производная $|{\bf r}»(t)|$ включает это понятие времени, так что оно зависит не только от геометрического свойств кривой, а от того, как быстро мы движемся по кривой.
Пример 13.3.5. Рассмотрим ${\bf r}(t)=\langle \cos t,\sin t,0\rangle$ и ${\bf s}(t)=\langle \cos 2t,\sin 2t,0\rangle$. Оба эти вектора функции представляют единичную окружность в плоскости $x$-$y$, но если $t$ интерпретируется как время, вторая описывает движение объекта в два раза быстрее быстрый как первый.
 Вычисляя вторые производные, находим
$|{\bf r}»(t)|=1$, $|{\bf s}»(t)|=4$.
$\квадрат$
Вычисляя вторые производные, находим
$|{\bf r}»(t)|=1$, $|{\bf s}»(t)|=4$.
$\квадрат$Для снятия зависимости от времени используем длину дуги параметризация. Если кривая задается ${\bf r}(s)$, то первая производная ${\bf r}'(s)$ является единичным вектором, т.е. ${\bf r}'(s)={\bf T}(s)$. Теперь вычисляем вторую производную ${\bf r}»(s)={\bf T}'(s)$ и использовать $|{\bf T}'(s)|$ в качестве «официальная» мера кривизна , обычно обозначаемая как $\kappa$.
Пример 13.3.6. Мы видели, что параметризация длины дуги конкретная спираль ${\bf r}(s)= \langle \cos(s/\sqrt2),\sin(s/\sqrt2),s/\sqrt2\rangle$. Вычисление второй производной дает $ {\ bf г} » (с) = \langle -\cos(s/\sqrt2)/2,-\sin(s/\sqrt2)/2,0\rangle$ длины $1/2$. $\квадрат$
Что если нам дана кривая как вектор-функция ${\bf r}(t)$, где $t$ не является длиной дуги? Мы видели, что длина дуги может быть сложной вычислить; к счастью, нам не нужно преобразовывать в длину дуги параметризация для вычисления кривизны.
 Вместо этого давайте представим, что у нас есть
сделали это, поэтому мы нашли $t=g(s)$ и затем сформировали
$\шляпа{\bf r}(s)={\bf r}(g(s))$. Первая производная $\hat{\bf r}'(s)$
является единичным касательным вектором, поэтому он совпадает с единичным касательным вектором
${\bf T}(t)={\bf T}(g(s))$. Взяв производную от этого, мы получим
$${d\over ds}{\bf T}(g(s))= {\bf T}'(g(s)) g'(s)={\bf T}'(t){dt\ над
дс}.$$
Кривизна — это длина этого вектора:
$$\каппа = |{\bf T}'(t)||{dt\over ds}|={|{\bf T}'(t)|\over|ds/dt|}=
{|{\bf T}'(t)|\over|{\bf r}'(t)|}.$$
(Вспомним, что мы видели, что $ds/dt=|{\bf r}'(t)|$.) Таким образом, мы можем
вычислить кривизну, вычислив только производные по
$т$; нам не нужно делать преобразование в длину дуги.
Вместо этого давайте представим, что у нас есть
сделали это, поэтому мы нашли $t=g(s)$ и затем сформировали
$\шляпа{\bf r}(s)={\bf r}(g(s))$. Первая производная $\hat{\bf r}'(s)$
является единичным касательным вектором, поэтому он совпадает с единичным касательным вектором
${\bf T}(t)={\bf T}(g(s))$. Взяв производную от этого, мы получим
$${d\over ds}{\bf T}(g(s))= {\bf T}'(g(s)) g'(s)={\bf T}'(t){dt\ над
дс}.$$
Кривизна — это длина этого вектора:
$$\каппа = |{\bf T}'(t)||{dt\over ds}|={|{\bf T}'(t)|\over|ds/dt|}=
{|{\bf T}'(t)|\over|{\bf r}'(t)|}.$$
(Вспомним, что мы видели, что $ds/dt=|{\bf r}'(t)|$.) Таким образом, мы можем
вычислить кривизну, вычислив только производные по
$т$; нам не нужно делать преобразование в длину дуги.Пример 13.3.7 Возвращаясь к спирали, предположим, что мы начинаем с параметризации ${\bf r}(t)=\langle \cos t,\sin t,t\rangle$. затем ${\bf r}'(t)=\langle -\sin t,\cos t,1\rangle$, $|{\bf r}'(t)|=\sqrt2$ и ${\bf T}(t)=\langle -\sin t,\cos t,1\rangle/\sqrt2$.
 затем
${\bf T}'(t)=\langle -\cos t,-\sin t,0\rangle/\sqrt2$ и
$|{\bf T}'(t)|=1/\sqrt2$. Наконец, $\kappa=1/\sqrt2/\sqrt2=1/2$,
как прежде.
$\квадрат$
затем
${\bf T}'(t)=\langle -\cos t,-\sin t,0\rangle/\sqrt2$ и
$|{\bf T}'(t)|=1/\sqrt2$. Наконец, $\kappa=1/\sqrt2/\sqrt2=1/2$,
как прежде.
$\квадрат$Пример 13.3.8 Рассмотрим эту окружность радиуса $a$: ${\bf r}(t)=\langle a\cos t,a\sin t,1\rangle$. затем ${\bf r}'(t)=\langle -a\sin t,a\cos t,0\rangle$, $|{\bf r}'(t)|=a$ и ${\bf T}(t)=\langle -a\sin t,a\cos т,0\угл/а$. В настоящее время ${\bf T}'(t)=\langle -a\cos t,-a\sin t,0\rangle/a$ и $|{\bf T}'(t)|=1$. Наконец, $\kappa=1/a$: кривизна круга везде обратна радиусу. Это иногда полезно думать о кривизне как описывающей окружность кривая больше всего напоминает точку. Кривизна спирали в предыдущий пример — $1/2$; это означает, что небольшой кусочек спирали очень похоже на круг радиусом $2$, как показано на рисунок 13.3.1. $\квадрат$ 9{3/2}}.$$ Нарисовав это, мы получим
Высший кривизна возникает там, где кривая имеет самую высокую и самую низкую точки, и действительно на картинке они кажутся наиболее резко изогнутыми части кривой, в то время как кривая представляет собой почти прямую линию посередине между этими точками.
 3$ дает нужную формулу.
3$ дает нужную формулу.Здесь мы использовали тот факт, что ${\bf T}’$ перпендикулярна ${\bf T}$; вектор ${\bf N}={\bf T}’/|{\bf T}’|$, таким образом, является единичным вектором перпендикулярно ${\bf T}$, называемому блок нормальный к кривой. Иногда используется единица бинормаль ${\bf B}={\bf T}\times{\bf N}$, а единичный вектор перпендикулярен как ${\bf T}$, так и ${\bf N}$.
Sage может помочь с несколько утомительным вычислением кривизны.
Пример 13.3.1 Найдите длину $\langle 3\cos t,2t,3\sin t\rangle$, $t\in[0,2\pi]$. (отвечать) 94$ по $(1,1)$. (отвечать)
Длина дуги | Brilliant Math & Science Wiki
Содержание
- Объяснение
- Доказательство
- Параметрическая форма
- Полярная форма
- Смотрите также
92}w2+(wm)2=w1+m2.

Следующие разделы призваны показать, что (1)(1)(1) можно аппроксимировать функцию кусочно-линейными функциями и (2)(2)(2) независимо от того, как функция моделируется кусочно-линейными функциями. -линейные функции, длина дуги остается неизменной.
(1)(1)(1) Первый подход заключается в выборе множества точек, распределенных по функции, и проведении в этих точках касательных к функции. Выбрав достаточное количество точек, всегда можно сделать так, чтобы последующие касательные пересекались (т. Е. Не были параллельны). Сегменты линий между пересечениями касательных линий затем обеспечивают грубую оценку самой функции и, следовательно, ее длины (и ее легко вычислить!). 92} \cdot w_i.i=1∑n1+(mi)2⋅wi. Если вспомнить, что каждый mim_imi равен dydx\tfrac{dy}{dx}dxdy для функции, а каждый wiw_iwi представляет собой разность xxx, эта формула очень похожа на приведенную выше формулу (только с суммированием вместо интеграла). На самом деле, когда nnn становится очень большим, они становятся равными.

Интуитивно понятно. Касательные линии служат для моделирования функции вблизи их точки касания, поэтому их длина также должна хорошо моделировать длину дуги функции. Основная трудность при формализации этого метода заключается в том, что для того, чтобы оставаться «рядом» с функцией, последующие касательные линии должны пересекаться между своими точками касания (это также допускает более естественный перевод между wiw_iwi и xix_ixi). ). Эта проблема решается путем выбора большего количества точек вдоль кривой везде, где касательные линии не находятся «рядом» с функцией.
(2)(2)(2) Второй подход состоит в том, чтобы выбрать точки, равномерно распределенные по функции, и соединить их отрезками. Если интервал имеет длину W=b−aW = b — aW=b−a, то n+1n+1n+1 точек можно выбрать по правилу xk=a+k⋅(b−an)x_k = a + k \cdot \left( \frac{b-a}{n} \right)xk=a+k⋅(nb−a) и yk=f(xk)y_k = f(x_k)yk=f(xk ). Затем линия, соединяющая (xk, yk)(x_k, \, y_k)(xk,yk) и (xk+1, yk+1)(x_{k+1}, \, y_{k+1} )(xk+1,yk+1) является как аппроксимацией самой функции, так и, по мере увеличения nnn, аппроксимацией касательной к функции в точке x=xkx = x_kx=xk.
 92} \cdot (x_{k+1} — x_k),k=1∑n1+(xk+1−xkyk+1−yk)2⋅(xk+1−xk ), дает выражение, очень похожее на сумму Римана (еще один способ выражения интеграла). Вспоминая, что yk+1−ykxk+1−xk\frac{y_{k+1} — y_k}{x_{k+1} — x_k}xk+1−xkyk+1−yk аппроксимация производной функции (наклон ее касательной), результат очень похож на приведенную выше формулу. При увеличении nnn значения фактически становятся равными.
92} \cdot (x_{k+1} — x_k),k=1∑n1+(xk+1−xkyk+1−yk)2⋅(xk+1−xk ), дает выражение, очень похожее на сумму Римана (еще один способ выражения интеграла). Вспоминая, что yk+1−ykxk+1−xk\frac{y_{k+1} — y_k}{x_{k+1} — x_k}xk+1−xkyk+1−yk аппроксимация производной функции (наклон ее касательной), результат очень похож на приведенную выше формулу. При увеличении nnn значения фактически становятся равными.Интуитивно этот метод аппроксимации является очень прямым и геометрическим. Он пытается аппроксимировать функцию набором отрезков на основе значений самой функции (без дополнительной информации). Он предполагает, что длина функции действительно может быть хорошо смоделирована множеством маленьких отрезков 9.2 — \frac{1}{2} \ln x }y=41x2−21lnx для 4≤x≤8,4 \leq x \leq 8,4≤x≤8. Если L=a+12lnb,L = a+\frac{1}{2}\ln{b} ,L=a+21lnb, где aaa и bbb — положительные целые числа, каково значение a+b ?а+б?а+б?
444 555 666 777 888 Ничего из вышеперечисленного
Пусть f(n)f(n)f(n) обозначает длину дуги кривой y=ln(x)y=\ln\left(x\right)y=ln(x) в интервале x∈ [1,n]x\in\left [1,n\right ]x∈[1,n].
 Находить
limn→∞(n−f(n)).\lim_{n\to\infty}\big(n-f(n)\big).n→∞lim(n−f(n)).
Если ваш ответ имеет форму ln(a−b)+c−d\ln\left(\sqrt{a}-b\right)+\sqrt{c}-dln(a−b)+c −d, где aaa, bbb, ccc и ddd — целые неотрицательные числа, а aaa и ccc — неполные квадраты, найти a+b+c+da+b+c+da+b+c+d.
Находить
limn→∞(n−f(n)).\lim_{n\to\infty}\big(n-f(n)\big).n→∞lim(n−f(n)).
Если ваш ответ имеет форму ln(a−b)+c−d\ln\left(\sqrt{a}-b\right)+\sqrt{c}-dln(a−b)+c −d, где aaa, bbb, ccc и ddd — целые неотрицательные числа, а aaa и ccc — неполные квадраты, найти a+b+c+da+b+c+da+b+c+d.Основное доказательство этого результата имеет элементы, общие с обоими вышеупомянутыми подходами, но по своей сути является развитием второго подхода.
Предположим, что кривая CCC задана уравнением y=f(x),y=f(x),y=f(x), где функция fff непрерывна в a≤x≤b,a \leq x \leq b,a≤x≤b, и разобьем интервал [a,b][a,b][a,b] на nnn подынтервалов с концами x0,x1,…,xnx_0, x_1, \ldots , x_nx0, x1,…,xn и равной ширины Δx.\Delta x.Δx. Поскольку yi=f(xi),y_i=f(x_i),yi=f(xi), точка Pi=(xi,yi)P_i=(x_i,y_i)Pi=(xi,yi) лежит на CCC, а отрезки, соединяющие две соседние точки P0,P1,…,Pn,P_0,P_1, \ldots, P_n,P0,P1,…,Pn, показанные выше, являются приближением к C.
 C.C. 92} \, д\тета.
L=∫abr2+(dθdr)2dθ.
C.C. 92} \, д\тета.
L=∫abr2+(dθdr)2dθ.Эта формула следует непосредственно из параметрической формы, если учесть, что параметр равен θ\thetaθ и x′(θ)=ddθ(r(θ)cosθ)=r′(θ)cosθ−r(θ )sinθ,y′(θ)=ddθ(r(θ)sinθ)=r′(θ)sinθ+r(θ)cosθ. x'(\theta) = \frac{d}{d\theta} \left( r(\theta) \cos \theta \right) = r'(\theta) \cos \theta — r(\theta) \ sin \theta, \\ y'(\theta) = \frac{d}{d\theta} \left( r(\theta) \sin \theta \right) = r'(\theta) \sin \theta + г (\ тета) \ соз \ тета. x′(θ)=dθd(r(θ)cosθ)=r′(θ)cosθ−r(θ)sinθ,y′(θ)=dθd(r(θ)sinθ)=r′(θ) sinθ+r(θ)cosθ.
- Рог Габриэля
- Параметрическая длина дуги
- Длина полярной дуги
- Объем при вращении (метод диска и метод оболочки)
Цитировать как: Длина дуги. Brilliant.org . Извлекаются из https://brilliant.org/wiki/arc-length/
Длина дуги кривой и площадь поверхности · Исчисление
Длина дуги кривой и площадь поверхности · Расчет- Определить длину кривой,
y=f(x),
между двумя точками.

- Определить длину кривой,
x=g(y),
между двумя точками.
- Найдите площадь поверхности тела вращения.
В этом разделе мы используем определенные интегралы, чтобы найти длину дуги кривой. Мы можем думать о длины дуги как о расстоянии, которое вы прошли бы, если бы шли по пути кривой. Во многих реальных приложениях используется длина дуги. Если ракета запускается по параболической траектории, мы можем захотеть узнать, как далеко пролетит ракета. Или, если кривая на карте представляет собой дорогу, мы можем захотеть узнать, какое расстояние нам нужно проехать, чтобы добраться до пункта назначения.
Начнем с вычисления длины дуги кривых, определенных как функции x,
, то мы исследуем тот же процесс для кривых, определенных как функции y.
(Процесс идентичен, с ролями х
и у
наоборот.) Методы, которые мы используем для определения длины дуги, можно расширить, чтобы найти площадь поверхности вращения, и мы завершаем раздел рассмотрением этой концепции.

Длина дуги кривой
y = ф ( х )В предыдущих приложениях интеграции нам требовалась функция f(x)
, чтобы быть интегрируемым или, самое большее, непрерывным. Однако для расчета длины дуги у нас есть более строгие требования к f(x).
Здесь нам требуется f(x)
, чтобы быть дифференцируемым, и, кроме того, мы требуем, чтобы его производная, f′(x),
, чтобы быть непрерывным. Такие функции, которые имеют непрерывные производные, называются гладкими . (Это свойство снова появится в последующих главах.)
Пусть f(x)
— гладкая функция, определенная над [a,b].
Мы хотим рассчитать длину кривой от точки (a,f(a))
до точки (b,f(b)).
Мы начнем с использования отрезков для аппроксимации длины кривой. Для i=0,1,2,…,n,
пусть P={xi}
— обычный раздел [a,b].
Тогда для i=1,2,…,n
построить отрезок из точки (xi−1,f(xi−1))
до точки (xi,f(xi)).

Хотя может показаться логичным использовать как горизонтальные, так и вертикальные сегменты линий, мы хотим, чтобы наши сегменты линий как можно точнее аппроксимировали кривую. [ссылка] изображает эту конструкцию для n = 5.
Чтобы помочь нам найти длину каждого сегмента линии, мы смотрим на изменение расстояния по вертикали, а также изменение расстояния по горизонтали на каждом интервале. Поскольку мы использовали регулярное разбиение, изменение горизонтального расстояния на каждом интервале определяется как Δx.
Однако изменение вертикального расстояния варьируется от интервала к интервалу, поэтому мы используем Δyi=f(xi)−f(xi−1)
для представления изменения расстояния по вертикали в интервале [xi−1,xi],
, как показано в [ссылка]. Обратите внимание, что некоторые (или все) Δyi
может быть отрицательным.
По теореме Пифагора длина отрезка равна (Δx)2+(Δyi)2.
Мы также можем записать это как Δx1+((Δyi)/(Δx))2.

Теперь по теореме о среднем значении существует точка xi*∈[xi−1,xi]
, такое что f′(xi*)=(Δyi)/(Δx).
Тогда длина отрезка равна ∆x1+[f′(xi*)]2.
Складывая длины всех отрезков, получаем
Длина дуги≈∑i=1n1+[f′(xi*)]2Δx.
Это сумма Римана. Беря предел при n→∞,
у нас есть
Длина дуги=limn→∞∑i=1n1+[f′(xi*)]2∆x=∫ab1+[f′(x)]2dx.
Мы суммируем эти выводы в следующей теореме.
Длина дуги для *y* = *f*(*x*)
Пусть f(x)
— гладкая функция на интервале [a,b].
Тогда длина дуги части графика f(x)
от точки (a,f(a))
до точки (b,f(b))
равна
Длина дуги=∫ab1+[f′(x)]2dx.
Обратите внимание, что мы интегрируем выражение, включающее f′(x),
, поэтому мы должны быть уверены, что f′(x)
является интегрируемым. Вот почему нам нужно f(x)
., чтобы было гладко. В следующем примере показано, как применить теорему.
Вычисление длины дуги функции *x*
Пусть f(x)=2×3/2.

Вычислить длину дуги графика функции f(x)
на интервале [0,1].
Ответ округлить до трех знаков после запятой.
У нас есть f′(x)=3×1/2,
, поэтому [f′(x)]2=9x.
Тогда длина дуги равна
Длина дуги=∫ab1+[f′(x)]2dx=∫011+9xdx.
Заменить u=1+9x.
Тогда du=9dx.
Когда x=0,
тогда u=1,
и когда x=1,
тогда u=10.
Таким образом,
Длина дуги=∫011+9xdx=19∫011+9x9dx=19∫110udu=19·23u3/2\|110=227[1010−1]≈2,268 ед.
Пусть f(x)=(4/3)x3/2.
Вычислить длину дуги графика функции f(x)
на интервале [0,1].
Ответ округлить до трех знаков после запятой.
16(55−1)≈1,697
Подсказка
Используйте процесс из предыдущего примера. Не забудьте изменить пределы интегрирования.
Хотя хорошо иметь формулу для вычисления длины дуги, эта конкретная теорема может генерировать выражения, которые трудно интегрировать. Мы изучаем некоторые методы интеграции во Введении в методы интеграции.
 В некоторых случаях нам, возможно, придется использовать компьютер или калькулятор для аппроксимации значения интеграла.
В некоторых случаях нам, возможно, придется использовать компьютер или калькулятор для аппроксимации значения интеграла.Использование компьютера или калькулятора для определения длины дуги функции *x*
Пусть f(x)=x2.
Вычислить длину дуги графика функции f(x)
на интервале [1,3].
У нас есть f′(x)=2x,
, поэтому [f′(x)]2=4×2.
Тогда длина дуги определяется как
Длина дуги=∫ab1+[f′(x)]2dx=∫131+4x2dx.
Используя компьютер для аппроксимации значения этого интеграла, мы получаем
∫131+4x2dx≈8,26815.
Пусть f(x)=sinx.
Вычислить длину дуги графика f(x)
на интервале [0,π].
С помощью компьютера или калькулятора приблизительно вычислите значение интеграла.
Длина дуги≈3,8202
Подсказка
Используйте процесс из предыдущего примера.
Длина дуги кривой
x = г ( y )Мы только что видели, как аппроксимировать длину кривой отрезками.
 Если мы хотим найти длину дуги графика функции y,
Если мы хотим найти длину дуги графика функции y,мы можем повторить тот же процесс, за исключением того, что мы разделим ось Y
вместо оси x.
[ссылка] показывает репрезентативный сегмент линии.
Тогда длина отрезка равна (Δy)2+(Δxi)2,
, что также можно записать как Δy1+((Δxi)/(Δy))2.
Если мы теперь будем следовать тому же развитию, что и ранее, мы получим формулу для длины дуги функции x=g(y).
Длина дуги для *x* = *g*(*y*)
Пусть g(y)
— гладкая функция на интервале [c,d].
Тогда длина дуги графика g(y)
от точки (c,g(c))
до точки (d,g(d))
равно
Длина дуги = ∫cd1+[g′(y)]2dy.
Вычисление длины дуги функции *y*
Пусть g(y)=3y3.
Вычислить длину дуги графика g(y)
на интервале [1,2].
У нас есть g′(y)=9y2,
, поэтому [g′(y)]2=81y4.
Тогда длина дуги равна
Длина дуги=∫cd1+[g′(y)]2dy=∫121+81y4dy.

Используя компьютер для аппроксимации значения этого интеграла, мы получаем
∫121+81y4dy≈21,0277.
Пусть g(y)=1/y.
Вычислить длину дуги графика g(y)
на интервале [1,4].
С помощью компьютера или калькулятора приблизительно вычислите значение интеграла.
Длина дуги=3,15018
Подсказка
Используйте процесс из предыдущего примера.
Площадь поверхности вращения
Понятия, которые мы использовали для определения длины дуги кривой, можно расширить, чтобы найти площадь поверхности вращения. Площадь поверхности — это общая площадь внешнего слоя объекта. Для таких объектов, как кубы или кирпичи, площадь поверхности объекта равна сумме площадей всех его граней. Для криволинейных поверхностей ситуация немного сложнее. Пусть f(x)
— неотрицательная гладкая функция на интервале [a,b].
Мы хотим найти площадь поверхности вращения, созданной вращением графика y=f(x)
вокруг оси x
, как показано на следующем рисунке.

Как мы уже делали много раз, мы собираемся разбить интервал [a,b]
и аппроксимируйте площадь поверхности, рассчитав площадь поверхности более простых форм. Мы начнем с использования линейных сегментов для аппроксимации кривой, как мы делали ранее в этом разделе. Для i=0,1,2,…,n,
пусть P={xi}
— обычный раздел [a,b].
Тогда для i=1,2,…,n
построить отрезок из точки (xi−1,f(xi−1))
до точки (xi,f(xi)).
Теперь поверните эти отрезки вокруг оси x
, чтобы создать аппроксимацию поверхности вращения, как показано на следующем рисунке.
Обратите внимание, что когда каждый сегмент линии вращается вокруг оси, образуется полоса. Эти полосы на самом деле представляют собой кусочки рожков (представьте себе рожок мороженого с отрезанным заостренным концом). Часть такого конуса называется усеченным конусом .
Чтобы найти площадь поверхности ленты, нам нужно найти площадь боковой поверхности, S,
усеченного конуса (площадь только наклонной наружной поверхности усеченного конуса, не включая площади верхней или нижней граней).
 Пусть r1
Пусть r1и р2
— радиусы широкого и узкого концов усеченного конуса соответственно, и пусть l
— наклонная высота усеченного конуса, как показано на следующем рисунке.
Мы знаем, что площадь боковой поверхности конуса равна
.Площадь боковой поверхности = πrs,
где р
— радиус основания конуса, а s
.— высота наклона (см. следующий рисунок).
Поскольку усеченный конус можно рассматривать как часть конуса, площадь боковой поверхности усеченного конуса равна площади боковой поверхности всего конуса за вычетом площади боковой поверхности меньшего конуса (заостренного кончика), который был срезан. выключено (см. следующий рисунок).
Сечения малого конуса и большого конуса представляют собой подобные треугольники, поэтому мы видим, что
r2r1=s−ls.
Решение для s,
получаем
r2r1=s-lsr2s=r1(s-l)r2s=r1s-r1lr1l=r1s-r2sr1l=(r1-r2)sr1lr1-r2=s.

Тогда площадь боковой поверхности (SA) усеченного конуса равна
S=(Боковая СА большого конуса)−(Боковая СА малого конуса)=πr1s−πr2(s−l)=πr1(r1lr1−r2)−πr2(r1lr1−r2−l)=πr12lr1−r2−πr1r2lr1− r2+πr2l=πr12lr1−r2−πr1r2lr1−r2+πr2l(r1−r2)r1−r2=πr12lr1−r2−πr1r2lr1−r2+πr1r2lr1−r2−πr22lr1−r2=π(r12−r22)lr1−r2=π( r1−r2)(r1+r2)lr1−r2=π(r1+r2)l.
Теперь воспользуемся этой формулой для расчета площади поверхности каждой из полос, образованных вращением отрезков линии вокруг оси x.
Репрезентативная полоса показана на следующем рисунке.
Обратите внимание, что наклонная высота этой усеченной пирамиды равна длине отрезка, использованного для ее создания. Итак, применяя формулу площади поверхности, мы имеем
S=π(r1+r2)l=π(f(xi−1)+f(xi))Δx2+(Δyi)2=π(f(xi−1)+f(xi))Δx1+(ΔyiΔx)2 .
Теперь, как и при разработке формулы длины дуги, мы применяем теорему о среднем значении, чтобы выбрать xi*∈[xi−1,xi]
, такое что f′(xi*)=(Δyi)/Δx.
Это дает нам
S=π(f(xi−1)+f(xi))∆x1+(f′(xi*))2.

Кроме того, поскольку f(x)
непрерывно, по теореме о промежуточном значении существует точка xi**∈[xi−1,xi]
таких, что f(xi**)=(1/2)[f(xi−1)+f(xi)],
получаем
S=2πf(xi**)∆x1+(f′(xi*))2.
Тогда приблизительная площадь всей поверхности вращения равна
Площадь поверхности≈∑i=1n2πf(xi**)Δx1+(f′(xi*))2.
Это почти выглядит как сумма Римана, за исключением того, что у нас есть функции, вычисляемые в двух разных точках, xi*
и xi**,
на интервале [xi−1,xi].
Хотя мы не рассматриваем здесь детали, оказывается, что поскольку f(x)
будет гладким, если мы позволим n→∞,
предел работает так же, как сумма Римана, даже с двумя разными точками оценки. Это интуитивно понятно. Оба xi*
и xi**
находятся в интервале [xi−1,xi],
, поэтому логично, что при n→∞
оба xi*
и xi**
подход х.
Тем из вас, кто интересуется подробностями, следует обратиться к учебнику по продвинутому исчислению.

Принимая предел при n→∞,
получаем
Площадь поверхности = limn→∞∑i=1n2πf(xi**)∆x1+(f′(xi*))2=∫ab(2πf(x)1+(f′(x))2)dx.
Как и в случае с длиной дуги, мы можем провести аналогичную разработку для функций y
, чтобы получить формулу площади поверхностей вращения вокруг оси Y.
Эти результаты резюмируются в следующей теореме.
Площадь поверхности вращения
Пусть f(x)
— неотрицательная гладкая функция на интервале [a,b].
Тогда площадь поверхности вращения, образованная вращением графика f(x)
вокруг оси x , равна
Площадь поверхности=∫ab(2πf(x)1+(f ′(х))2)дх.
Аналогично, пусть g(y)
— неотрицательная гладкая функция на интервале [c,d].
Тогда площадь поверхности вращения, образованная вращением графика g(y)
вокруг оси y
, равна
Площадь поверхности=∫cd(2πg(y)1+(g ′(у))2)ды.
Расчет площади поверхности вращения 1
Пусть f(x)=x
на интервале [1,4].

Найдите площадь поверхности, полученной путем вращения графика f(x)
вокруг оси x.
Ответ округлить до трех знаков после запятой.
График f(x)
и поверхность вращения показаны на следующем рисунке.
Имеем f(x)=x.
Тогда f′(x)=1/(2x)
и (f′(x))2=1/(4x).
Тогда
Площадь поверхности=∫ab(2πf(x)1+(f′(x))2)dx=∫14(2πx1+14x)dx=∫14(2πx+14)dx.
Пусть u=x+1/4.
Тогда du=dx.
Когда x=1,
u=5/4,
и когда x=4,
u=17/4.
Это дает нам
∫01(2πx+14)dx=∫5/417/42πudu=2π[23u3/2]\|5/417/4=π6[1717−55]≈30,846.
Пусть f(x)=1−x
на интервале [0,1/2].
Найдите площадь поверхности, полученной путем вращения графика f(x)
вокруг оси x.
Ответ округлить до трех знаков после запятой.
π6(55−33)≈3,133
Подсказка
Используйте процесс из предыдущего примера.

Расчет площади поверхности вращения 2
Пусть f(x)=y=3×3.
Рассмотрим часть кривой, где 0≤y≤2.
Найдите площадь поверхности, полученной путем вращения графика f(x)
вокруг оси y.
Обратите внимание, что мы вращаем кривую вокруг оси y,
, а интервал выражен в единицах y,
, поэтому мы хотим переписать функцию как функцию y . Получаем x=g(y)=(1/3)y3.
График g(y)
и поверхность вращения показаны на следующем рисунке.
Имеем g(y)=(1/3)y3,
, поэтому g'(y)=y2
и (g'(y))2=y4.
Затем
Площадь поверхности=∫cd(2πg(y)1+(g′(y))2)dy=∫02(2π(13y3)1+y4)dy=2π3∫02(y31+y4)dy .
Пусть u=y4+1.
Тогда du=4y3dy.
Когда y=0,
u=1,
и когда y=2,
u=17.
Тогда
2π3∫02(y31+y4)dy=2π3∫11714udu=π6[23u3/2]\|117=π9[(17)3/2−1]≈24,118.
Пусть g(y)=9−y2
на интервале y∈[0,2].

Найдите площадь поверхности, полученной путем вращения графика g(y)
вокруг оси Y.
12π
Подсказка
Используйте процесс из предыдущего примера.
Ключевые понятия
- Длину дуги кривой можно рассчитать с помощью определенного интеграла.
- Длина дуги сначала аппроксимируется с помощью отрезков прямой, в результате чего получается сумма Римана. Принятие предела дает нам формулу определенного интеграла. Тот же процесс может быть применен к функциям у.
- Понятия, используемые для расчета длины дуги, можно обобщить, чтобы найти площадь поверхности вращения.
- Интегралы, полученные по формулам длины дуги и площади поверхности, часто трудно вычислить. Может потребоваться использование компьютера или калькулятора для аппроксимации значений интегралов.
Ключевые уравнения
- Длина дуги функции x
Длина дуги=∫ab1+[f′(x)]2dx - Длина дуги функции y
Длина дуги=∫cd1+[g′(y)]2dy - Площадь поверхности функции x
Площадь поверхности=∫ab(2πf(x)1+(f′(x))2)dx
Для следующих упражнений найдите длину функций на заданном интервале.

y=5xfromx=0tox=2
226
y=−12x+25fromx=1tox=4
x=4yfromy=−1toy=1
217
Выберите произвольную линейную функцию x=g(y)
на любом интервале по вашему выбору (y1,y2).
Определите длину функции, а затем докажите правильность длины с помощью геометрии.
Найдите площадь поверхности объема, образованного, когда кривая y=x
вращается вокруг оси x
от (1,1)
до (4,2),
, как показано здесь.
π6(1717−55)
Найдите площадь поверхности объема, образованного, когда кривая y=x2
вращается вокруг оси y
от (1,1)
до (3,9).
Для следующих упражнений найдите длины функций x
за указанный интервал. Если вы не можете точно вычислить интеграл, используйте технологию для его аппроксимации.
y=x3/2
от (0,0) до (1,1)
1313−827
y=x2/3
от (1,1) до (8,4)
y=13(x2+2)3/2
от x=0tox=1
43
y=13(x2−2)3/2
от x=2
до x=4
[T] y=ex
при x=0
до x=1
2,0035
y=x33+14x
из x=1tox=3
y=x44+18×2
из x=1tox=2
12332
y=2×3/23−x1/22
из x=1tox=4
y=127(9×2+6)3/2
от x=0tox=2
10
[T] y=sinx
на x=0tox=π
Для следующих упражнений найдите длины функций y
за указанный интервал.
 Если вы не можете точно вычислить интеграл, используйте технологию для его аппроксимации.
Если вы не можете точно вычислить интеграл, используйте технологию для его аппроксимации.y=5−3×4
от y=0
до y=4
203
x=12(ey+e-y)
от y=-1toy=1
x=5y3/2
от y=0
до y=1
1675(229229−8)
[T] x=y2
от y=0
до y=1
x=y
от y=0toy=1
18(45+ln(9+45))
x=23(y2+1)3/2
от y=1
до y=3
[Т] х = любой
от y=0
до y=34
1,201
[T] x=cos2y
от y=−π2
до y=π2
[T] x=4y
от y=0toy=2
15,2341
[T] x=ln(y)
при y=1e
до y=e
В следующих упражнениях найдите площадь поверхности объема, полученного при вращении следующих кривых вокруг оси x.

Если вы не можете точно вычислить интеграл, воспользуйтесь калькулятором, чтобы аппроксимировать его.
y=x
от x=2
до x=6
49π3
y=x3
от x=0
до x=1
y=7x
от x=−1tox=1
70π2
[T] y=1×2
из x=1tox=3
y=4−x2
из x=0tox=2
8π
y=4−x2
из x=−1tox=1
y=5x
от x=1tox=5
120π26
[Т] у=tanx
из x=−π4tox=π4
В следующих упражнениях найдите площадь поверхности объема, полученного при вращении следующих кривых вокруг оси Y.
Если вы не можете точно вычислить интеграл, воспользуйтесь калькулятором, чтобы аппроксимировать его.
y=x2
из x=0tox=2
π6(1717−1)
y=12×2+12
от x=0tox=1
y=x+1
от x=0tox=3
92π
[Т] у=1x
от х=12
до х=1
y=x3
из x=1tox=27
1010π27(7373−1)
[T] y=3×4
от x=0
до x=1
[T] y=1x
от x=1
до x=3
25,645
[T] y=cosx
от x=0
до x=π2
Основание лампы состоит из вращения четверти окружности y=2x−x2
вокруг оси y
от x=1
до x=2,
как показано здесь.
 Создайте интеграл для площади поверхности этой кривой и вычислите его.
Создайте интеграл для площади поверхности этой кривой и вычислите его.2π
Лампочка — это сфера радиусом 1/2
дюйма с отрезанным дном, чтобы точно соответствовать цилиндру радиусом 1/4
дюйма и длиной 1/3
дюйма, как показано здесь. Нижняя сфера обрезана так, чтобы точно соответствовать цилиндру, поэтому радиус разреза равен 1/4
дюйма. Найдите площадь поверхности (не включая верх и низ цилиндра).
[T] Абажур создается путем вращения y=1/x
вокруг оси x
от y=1
до y=2,
, как показано здесь. Определите, сколько материала вам понадобится для изготовления этого абажура, то есть площадь поверхности, с точностью до четырех знаков после запятой.
10,5017
[T] Якорь тянется за лодкой в соответствии с функцией y=24e−x/2−24,
, где y
представляет глубину под лодкой, а x
— горизонтальное расстояние от якоря до задней части лодки.
 Если якорь находится на 23
Если якорь находится на 23фута ниже лодки, за сколько веревки вам придется тянуть, чтобы добраться до якоря? Округлите ответ до трех знаков после запятой.
[T] Вы строите мост длиной 10
фута. Вы собираетесь добавить декоративную веревку в форме y=5\|sin((xπ)/5)\|,
, где x
— расстояние в футах от одного конца моста. Узнайте, сколько веревки вам нужно купить, округлив до ближайшего фута.
Для следующих упражнений найдите точную длину дуги для следующих задач за заданный интервал.
y=ln(sinx)
от x=π/4
до x=(3π)/4.
( Подсказка: Вспомнить тригонометрические тождества.)
Нарисуйте графики y=x2,
y=x6,
и y=x10.
Для y=xn,
при увеличении n
сформулируйте прогноз длины дуги от (0,0)
до (1,1).
Теперь вычислите длины этих трех функций и определите, верен ли ваш прогноз.

2
Сравните длины параболы x=y2
и прямой x=by
от (0,0) до (b2,b)
при увеличении b
. Что ты заметил?
Найдите длину x=y2
от (0,0) до (1,1).
Покажите, что x=(1/2)y2
от (0,0)
до (2,2)
в два раза длиннее. Нарисуйте график обеих функций и объясните, почему это так.
Ответы могут отличаться
[T] Что больше из (1,1)
и (2,1/2):
гипербола y=1/x
или график x+2y=3?
Объясните, почему площадь поверхности бесконечна, когда y=1/x
вращается вокруг оси x
при 1≤x<∞,
, но объем конечен.
Для получения дополнительной информации найдите Рог Габриэля.
Глоссарий
- длина дуги
- длину дуги кривой можно представить как расстояние, которое человек прошел бы по пути кривой
- усеченный конус
- часть конуса; усеченный конус строится путем разрезания конуса плоскостью, параллельной основанию
- площадь поверхности
- площадь поверхности твердого тела – это общая площадь внешнего слоя объекта; для таких объектов, как кубы или кирпичи, площадь поверхности объекта равна сумме площадей всех его граней
Эта работа находится под лицензией Creative Commons Attribution 4.

 ..
.. е. непрерывно дифференцируемой) на , то длина дуги этой кривой вычисляется по формуле
е. непрерывно дифференцируемой) на , то длина дуги этой кривой вычисляется по формуле Используя формулу вычисления длины дуги для кривой, заданной параметрически, получим
Используя формулу вычисления длины дуги для кривой, заданной параметрически, получим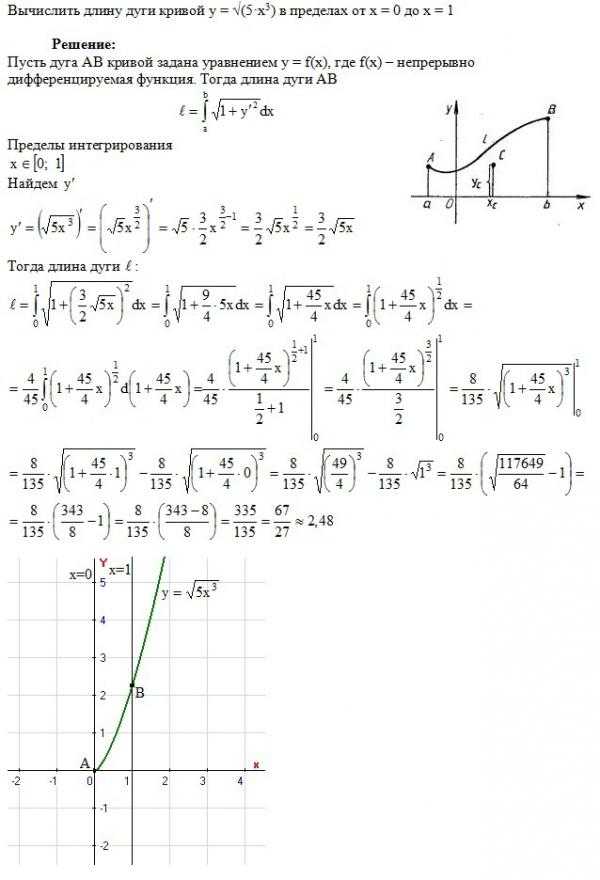 Тогда площадь сечения является функцией от аргумента x: .
Тогда площадь сечения является функцией от аргумента x: .

 {2} = v} ).
{2} = v} ). {2} \,}} d \ theta.}
{2} \,}} d \ theta.} {2} \,}} dt.}
{2} \,}} dt.} {\ circ}}}.}
{\ circ}}}.}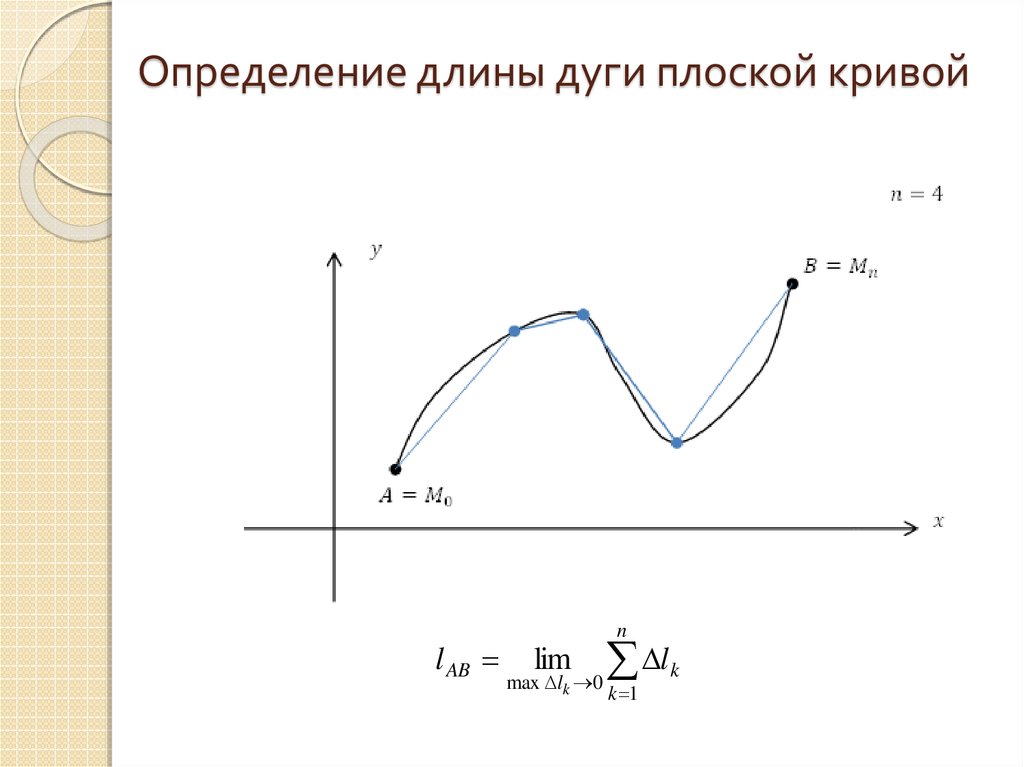
 {2} \ left (1+ {9 \ over 4} a \ right) \ end {align}}}
{2} \ left (1+ {9 \ over 4} a \ right) \ end {align}}} MPEAS (псевдоним Ферма) (1660). De Linearum Curvarum cum Lineis Rectis Comparatione Dissertatio Geometrica . Тулуза: Арно Коломер.
MPEAS (псевдоним Ферма) (1660). De Linearum Curvarum cum Lineis Rectis Comparatione Dissertatio Geometrica . Тулуза: Арно Коломер.
 92})dx\)
92})dx\)
 ..
.. 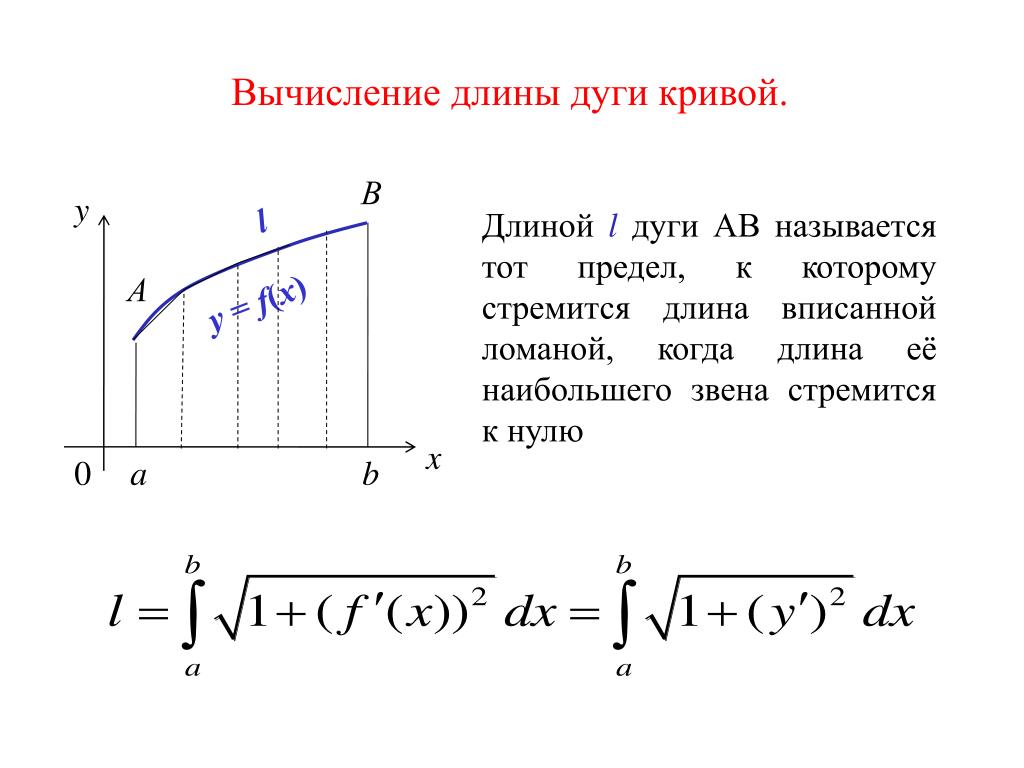 срезы приближаются к нулю по ширине (аналогично для dy) :
срезы приближаются к нулю по ширине (аналогично для dy) : Конечно, это так, но приятно, что мы нашли правильный ответ!
Конечно, это так, но приятно, что мы нашли правильный ответ! Пример реального мира.
Пример реального мира. Но на 6,367 м он будет работать прекрасно.
Но на 6,367 м он будет работать прекрасно. ..
..  b|{\bf r}'(t)|\,dt.$$
(Ну, иногда. Это работает, если между $a$ и $b$ отрезок кривой
трассируется ровно один раз.)
92}\,дх.$$
К сожалению, такие интегралы часто невозможно вычислить точно и
должны быть приближены.
b|{\bf r}'(t)|\,dt.$$
(Ну, иногда. Это работает, если между $a$ и $b$ отрезок кривой
трассируется ровно один раз.)
92}\,дх.$$
К сожалению, такие интегралы часто невозможно вычислить точно и
должны быть приближены.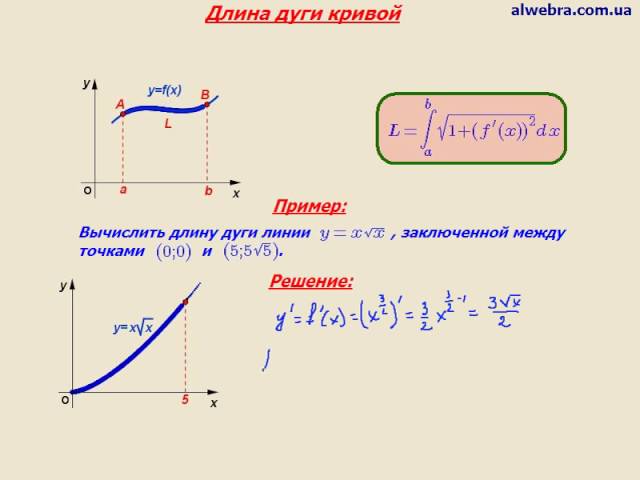 2(s/\sqrt2)\over2}+{1\over2}}=
\sqrt{{1\over2}+{1\over2}}=1.$$
Таким образом, в общем случае ${\bf r}’$ является единичным касательным вектором.
2(s/\sqrt2)\over2}+{1\over2}}=
\sqrt{{1\over2}+{1\over2}}=1.$$
Таким образом, в общем случае ${\bf r}’$ является единичным касательным вектором. Вычисляя вторые производные, находим
$|{\bf r}»(t)|=1$, $|{\bf s}»(t)|=4$.
$\квадрат$
Вычисляя вторые производные, находим
$|{\bf r}»(t)|=1$, $|{\bf s}»(t)|=4$.
$\квадрат$ Вместо этого давайте представим, что у нас есть
сделали это, поэтому мы нашли $t=g(s)$ и затем сформировали
$\шляпа{\bf r}(s)={\bf r}(g(s))$. Первая производная $\hat{\bf r}'(s)$
является единичным касательным вектором, поэтому он совпадает с единичным касательным вектором
${\bf T}(t)={\bf T}(g(s))$. Взяв производную от этого, мы получим
$${d\over ds}{\bf T}(g(s))= {\bf T}'(g(s)) g'(s)={\bf T}'(t){dt\ над
дс}.$$
Кривизна — это длина этого вектора:
$$\каппа = |{\bf T}'(t)||{dt\over ds}|={|{\bf T}'(t)|\over|ds/dt|}=
{|{\bf T}'(t)|\over|{\bf r}'(t)|}.$$
(Вспомним, что мы видели, что $ds/dt=|{\bf r}'(t)|$.) Таким образом, мы можем
вычислить кривизну, вычислив только производные по
$т$; нам не нужно делать преобразование в длину дуги.
Вместо этого давайте представим, что у нас есть
сделали это, поэтому мы нашли $t=g(s)$ и затем сформировали
$\шляпа{\bf r}(s)={\bf r}(g(s))$. Первая производная $\hat{\bf r}'(s)$
является единичным касательным вектором, поэтому он совпадает с единичным касательным вектором
${\bf T}(t)={\bf T}(g(s))$. Взяв производную от этого, мы получим
$${d\over ds}{\bf T}(g(s))= {\bf T}'(g(s)) g'(s)={\bf T}'(t){dt\ над
дс}.$$
Кривизна — это длина этого вектора:
$$\каппа = |{\bf T}'(t)||{dt\over ds}|={|{\bf T}'(t)|\over|ds/dt|}=
{|{\bf T}'(t)|\over|{\bf r}'(t)|}.$$
(Вспомним, что мы видели, что $ds/dt=|{\bf r}'(t)|$.) Таким образом, мы можем
вычислить кривизну, вычислив только производные по
$т$; нам не нужно делать преобразование в длину дуги. затем
${\bf T}'(t)=\langle -\cos t,-\sin t,0\rangle/\sqrt2$ и
$|{\bf T}'(t)|=1/\sqrt2$. Наконец, $\kappa=1/\sqrt2/\sqrt2=1/2$,
как прежде.
$\квадрат$
затем
${\bf T}'(t)=\langle -\cos t,-\sin t,0\rangle/\sqrt2$ и
$|{\bf T}'(t)|=1/\sqrt2$. Наконец, $\kappa=1/\sqrt2/\sqrt2=1/2$,
как прежде.
$\квадрат$ 3$ дает нужную формулу.
3$ дает нужную формулу.

 92} \cdot (x_{k+1} — x_k),k=1∑n1+(xk+1−xkyk+1−yk)2⋅(xk+1−xk ), дает выражение, очень похожее на сумму Римана (еще один способ выражения интеграла). Вспоминая, что yk+1−ykxk+1−xk\frac{y_{k+1} — y_k}{x_{k+1} — x_k}xk+1−xkyk+1−yk аппроксимация производной функции (наклон ее касательной), результат очень похож на приведенную выше формулу. При увеличении nnn значения фактически становятся равными.
92} \cdot (x_{k+1} — x_k),k=1∑n1+(xk+1−xkyk+1−yk)2⋅(xk+1−xk ), дает выражение, очень похожее на сумму Римана (еще один способ выражения интеграла). Вспоминая, что yk+1−ykxk+1−xk\frac{y_{k+1} — y_k}{x_{k+1} — x_k}xk+1−xkyk+1−yk аппроксимация производной функции (наклон ее касательной), результат очень похож на приведенную выше формулу. При увеличении nnn значения фактически становятся равными. Находить
limn→∞(n−f(n)).\lim_{n\to\infty}\big(n-f(n)\big).n→∞lim(n−f(n)).
Если ваш ответ имеет форму ln(a−b)+c−d\ln\left(\sqrt{a}-b\right)+\sqrt{c}-dln(a−b)+c −d, где aaa, bbb, ccc и ddd — целые неотрицательные числа, а aaa и ccc — неполные квадраты, найти a+b+c+da+b+c+da+b+c+d.
Находить
limn→∞(n−f(n)).\lim_{n\to\infty}\big(n-f(n)\big).n→∞lim(n−f(n)).
Если ваш ответ имеет форму ln(a−b)+c−d\ln\left(\sqrt{a}-b\right)+\sqrt{c}-dln(a−b)+c −d, где aaa, bbb, ccc и ddd — целые неотрицательные числа, а aaa и ccc — неполные квадраты, найти a+b+c+da+b+c+da+b+c+d. C.C. 92} \, д\тета.
L=∫abr2+(dθdr)2dθ.
C.C. 92} \, д\тета.
L=∫abr2+(dθdr)2dθ.

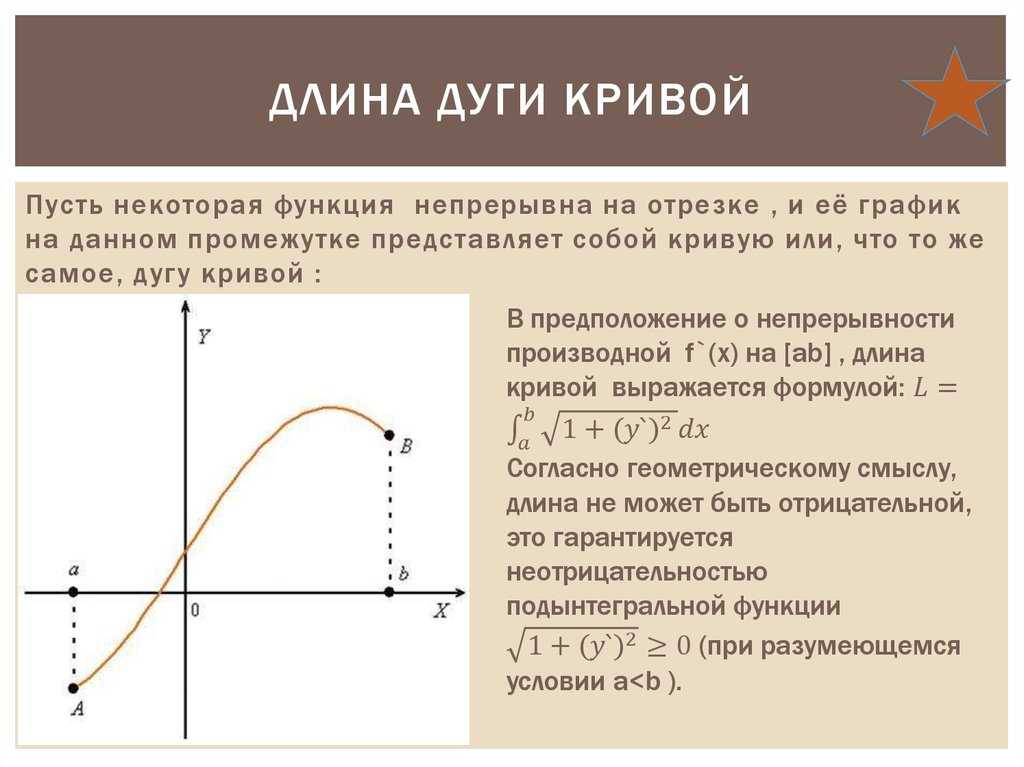


 В некоторых случаях нам, возможно, придется использовать компьютер или калькулятор для аппроксимации значения интеграла.
В некоторых случаях нам, возможно, придется использовать компьютер или калькулятор для аппроксимации значения интеграла. Если мы хотим найти длину дуги графика функции y,
Если мы хотим найти длину дуги графика функции y,

 Пусть r1
Пусть r1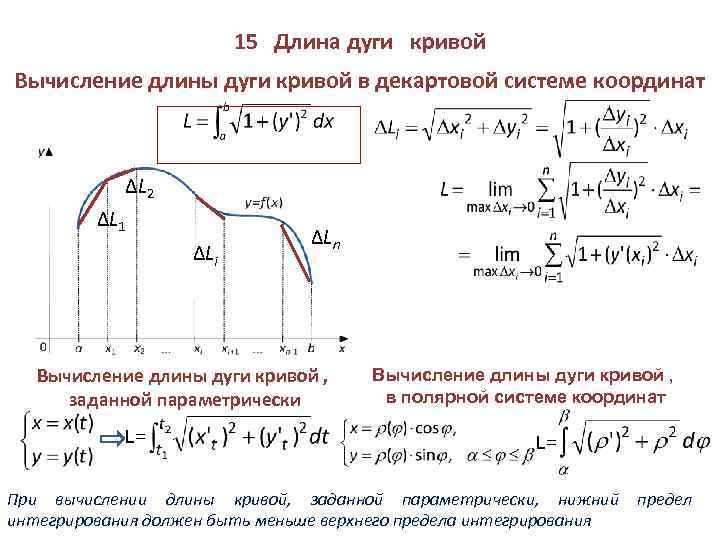
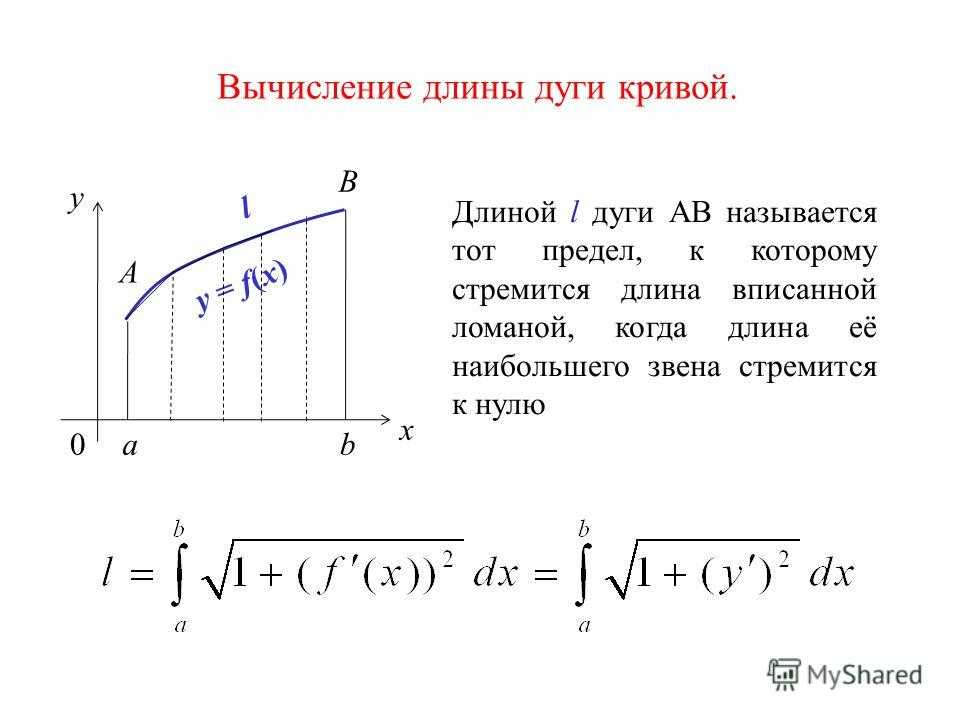


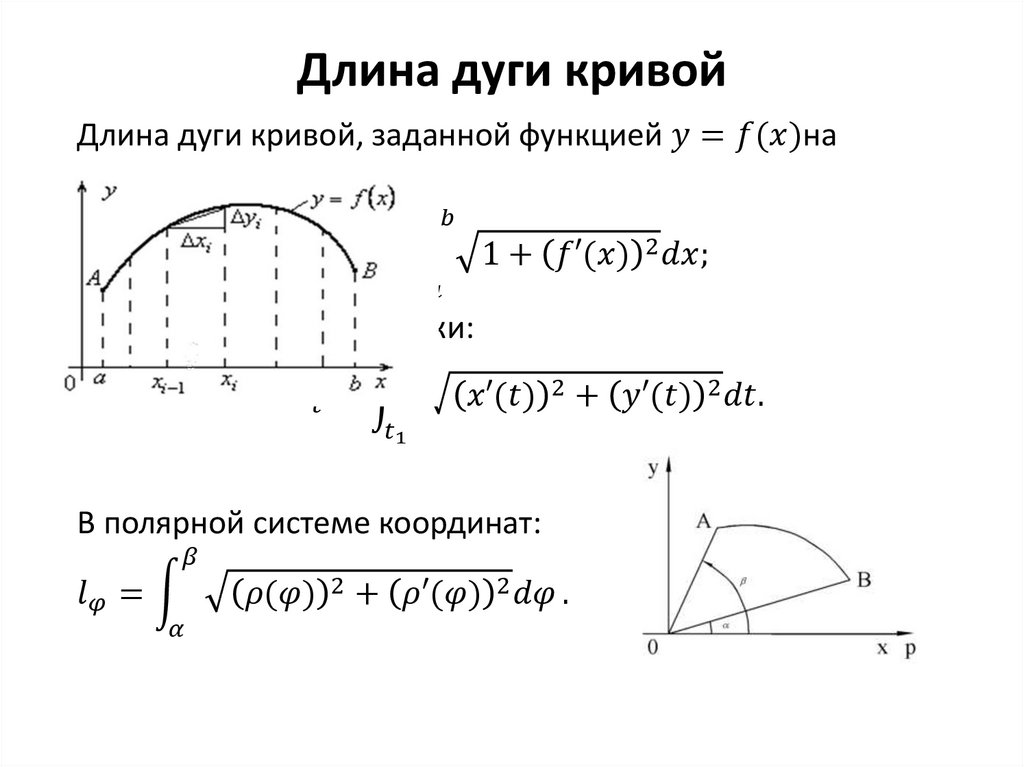


 Если вы не можете точно вычислить интеграл, используйте технологию для его аппроксимации.
Если вы не можете точно вычислить интеграл, используйте технологию для его аппроксимации.
 Создайте интеграл для площади поверхности этой кривой и вычислите его.
Создайте интеграл для площади поверхности этой кривой и вычислите его. Если якорь находится на 23
Если якорь находится на 23