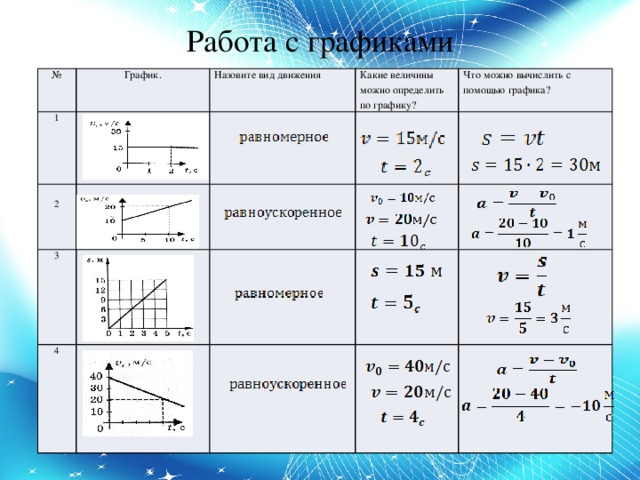
Формула средней скорости при равноускоренном прямолинейном движении
Из первого уравнения системы (1) имеем:
\[a_x=\frac{v_x-v_{0x}}{t}\left(7\right).\]
Величину ускорения из уравнения (7) подставим в формулу (5) получим, что перемещение по оси X равно:
\[\Delta x=\frac{v_x+v_{0x}}{2}t\left(8\right).\]
Найдем проекцию средней скорости на ось X из определения средней скорости движения:
\[{\left\langle v\right\rangle }_x=\frac{\Delta x}{t}\left(9\right).\]
Разделим правую и левую части выражения (8) на время движения тела. Получим, что средняя скорость при рассматриваемом движении равна:
\[\frac{\Delta x}{t}=\frac{v_x+v_{0x}}{2}={\left\langle v\right\rangle }_x\left(10\right).\]
Примеры задач с решением
Пример 1
Задание. 2}$
2}$
Читать дальше: формулы свободного падения.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
9 Класс — Физика
posted Oct 15, 2009, 1:24 AM by Дмитрий Белозёров [ updated Dec 23, 2014, 6:24 AM ]
Из курса физики седьмого класса мы помним, что механическое движение тела – это его перемещение во времени относительно других тел. Исходя из таких сведений, мы можем предположить необходимый набор инструментов для расчета движения тела. Во-первых, нам необходимо нечто, относительно чего мы будем производить наши расчеты. Далее, нам потребуется условиться, каким образом мы будем определять положение тела относительно этого «нечто». Система отсчета в физикеСистемой отсчета в физике называют совокупность тела отсчета, системы координат, связанной с телом отсчета, и часы или иной прибор для отсчета времени. При этом всегда следует помнить, что всякая система отсчета условна и относительна. Всегда можно принять другую систему отсчета, относительно которой любое движение будет иметь совершенно другие характеристики. Относительность – это вообще немаловажный аспект, который следует учитывать практически при любых расчетах в физике. Например, во многих случаях мы далеко не в любой момент времени можем определить точные координаты движущегося тела. В частности, мы не можем расставить наблюдателей с часами на каждых ста метрах вдоль железнодорожного пути от Москвы до Владивостока. В таком случае мы рассчитываем скорость и местоположение тела приближенно в течение какого-то отрезка времени. Нам не важна точность до одного метра при определении местоположения поезда на пути в несколько сотен или тысяч километров. Для этого в физике существуют приближения. Одним из таких приближений является понятие «материальная точка». Материальная точка в физикеМатериальной точкой в физике обозначают тело, в случаях, когда его размерами и формой можно пренебречь. При этом считается, что материальная точка имеет массу исходного тела. Например, при расчете времени, которое понадобится самолету, чтобы долететь из Новосибирска до Новополоцка, нам не важны размеры и форма самолета. Достаточно знать, какую скорость он развивает и расстояние между городами. В случае же, когда нам надо рассчитать сопротивление ветра на определенной высоте и при определенной скорости, то тут уж никак не обойтись без точного знания формы и размеров того же самолета. Практически всякое тело можно считать материальной точкой либо когда расстояние, преодолеваемое телом велико в сравнении с его размерами, либо когда все точки тела двигаются одинаково. А вот в случае, когда нам надо разместить тот же автомобиль в гараже, его уже никак не сочтешь материальной точкой. Придется учитывать его размеры и форму. Это тоже примеры, когда необходимо учитывать относительность, то есть относительно чего мы производим конкретные расчеты.
Для того, чтобы определить положение тела, которое совершило некоторое перемещение, можно графически приставить вектор перемещения к начальному положению тела. Но на практике часто встречаются задачи в которых необходимо вычислить положение тела, то есть записать его координаты в некоторой системе координат. В этом случае вычисления будут производиться не с самим векторами, а с их проекциями на координатные оси и с их модулями. Эти величины которые будут представлять собой некоторые числа, положительные или отрицательные, но не будут иметь направления. Рассмотрим следующую задачу Необходимо определить координату движущегося тела, по известной начальной координате и известному вектору перемещения.
Определить координаты катеров по отношению к пристани и расстояние между ними. Построим координатную ось Ох, параллельно прямой вдоль которой двигаются катера. Начало оси х=0 совместим с пристанью. За положительное направление примем направление на восток. Спроецируем начала и концы векторов перемещений s1 и s2 на ось Ох, получим отрезки sx1 и sx2. Эти отрезки будут являться проекциями данных векторов. Проекция вектора на ось, будет положительной, если вектор сонаправлен с осью, и отрицательной, если вектор направлен в противоположную оси сторону. В нашем случае sx1 положительная проекция, а sx2 отрицательная проекция. Проекция вектора, будет равна разности координат конца и начала вектора. В нашем случае имеем:
Теперь выразим из этих уравнений координаты x1 и x2. Расстояние между двумя катерами будет равно модулю разности их координат,
Мы получили формулы для вычисления координат точек и расстояния между ними. Из условия задачи, катера встретились на расстоянии 100 км от пристани. х0 – точка встречи. Следовательно расстояние от х0 до пристани(начала координат) 100 км. х0=100 км. Так как мы выбрали ось Ох параллельно векторам перемещений катеров. Длины отрезков sx1 и sx2 будут равны длинам векторов s1 и s2. Модуль каждой проекции будет равен модулю соответствующего ей вектора. По условию у нас даны числа 50 км и 60 км, это и есть модули векторов соответствующий перемещений.
В итоге получаем,
Ответ: х1=160 км, х2=50 км, l=110 км.
Довольно часто в физике приходится иметь дело с прямолинейным равномерным движением. Задача нахождения перемещения при равномерном прямолинейном движении довольно проста. По определению скорость равномерного прямолинейного движения – постоянная векторная величина, которая равна отношению перемещения тела за некий промежуток времени к величине этого промежутка: v(->) = s(->) /t, откуда следует,что перемещение s(->) = v(->) * t . где v(->) – скорость (векторная величина), s(->) – перемещение (векторная величина), t – время. При работе с векторными величинами для нахождения числовых значений величин применяют значения проекций конкретных величин на оси. В случае равномерного прямолинейного движения направления векторов скорости и перемещения совпадают, поэтому можно смело использовать в расчетах модульные значения. s = v*t Но такая формула известна уже давно, и в ней под буквой s понимали путь, пройденный телом. Так что же такое s – путь или модуль перемещения? Как характеризуется перемещение тела при прямолинейном равномерном движении?Дело в том, что при равномерном и прямолинейном движении модуль вектора перемещения за некий промежуток времени будет равен пройденному телом пути за тот же промежуток времени. Это утверждение можно подтвердить рисунком. Если изобразить векторно скорость движения тела в зависимости от времени, то модуль такого перемещения при равномерном прямолинейном движении будет в любой момент времени совпадать с путем, пройденным за это время телом. Если же направление тела будет меняться, то пройденный путь будет больше значения модуля перемещения. Поэтому принятое нами равенство справедливо только для случаев, когда тело двигается равномерно и прямолинейно. Можно изобразить данную ситуацию графически. Для этого проведем из точки 0 оси скорости и времени. И если мы проведем перпендикуляры от временной оси в начальный и конечный моменты времени к линии скорости, то получим прямоугольник, площадь которого и будет равна перемещению за данный промежуток времени. Рис. 1 Стороны этого прямоугольника будут равны все тем же значениям v и t. Таким образом, мы видим, что и при построении проекций векторных величин, принятое нами выше равенство сохраняет свою справедливость. В случае же, когда мы имеем в расчетах дело с двумя телами, двигающимися равномерно и прямолинейно, при этом совпадают направления их движения, то расчеты также можно производить, применяя приведенную выше формулу. Если же два тела двигаются равномерно и прямолинейно, а направления их движения противоположны, но расположены вдоль одной оси, то можно по-прежнему использовать в расчетах значения их модулей.
Хотите провести эксперимент? Да запросто. Возьмите длинную линейку, положите ее горизонтально и приподнимите один конец. У вас получится наклонная плоскость. А теперь возьмите монетку и положите на верхний конец линейки. Монетка начнет скользить вниз по линейке, проследите, как будет двигаться монетка с одинаковой скоростью или нет. Вы заметите, что скорость монетки будет постепенно возрастать. И изменение скорости будет напрямую зависеть от угла наклона линейки. Чем угол наклона круче, тем большую скорость будет набирать монетка к концу пути. Изменение скорости монеткиМожно попытаться узнать, как меняется скорость монетки за каждый одинаковый промежуток времени. В случае с линейкой и монеткой в домашних условиях это трудно проделать, но в условиях лаборатории можно зафиксировать, что при постоянном угле наклона скользящая монетка за каждую секунду изменяет свою скорость на одинаковую величину. Такое движение тела, когда его скорость за любые равные промежутки времени меняется одинаково, а тело при этом движется по прямой линии, называется в физике прямолинейным равноускоренным движением. Под скоростью в данном случае понимается скорость в каждый конкретный момент времени. Такая скорость называется мгновенной скоростью. Мгновенная скорость тела может меняться по-разному: быстрее, медленнее, может возрастать, а может уменьшаться. Для того чтобы охарактеризовать это изменение скорости, вводят величину, называемую ускорением. Понятие ускорения: формулаУскорение это физическая величина, показывающая, насколько изменилась скорость тела за каждый равный промежуток времени. Если скорость меняется одинаковым образом, то ускорение будет величиной постоянной. Так происходит в случае прямолинейного равноускоренного движения. Формула для ускорения выглядит следующим образом: a = (v — v_0 )/ t, где a ускорение, v конечная скорость, v_0 начальная скорость, t время. Измеряется ускорение в метрах на секунду в квадрате (1 м/с2). Немного странная на первый взгляд единица очень легко объясняется: ускорение= скорость/время=(м/с)/с , откуда и выводится такая единица. Ускорение величина векторная. Оно может быть направлена либо в ту же сторону, что и скорость, если скорость возрастает, либо в противоположную сторону, если скорость уменьшается. Пример второго варианта это торможение. Если, например, автомобиль тормозит, то скорость его уменьшается. Тогда ускорение будет являться отрицательной величиной, и направлено оно будет не по ходу движения автомобиля, а в обратную сторону. В случаях, когда скорость у нас меняется от нуля до какой-либо величины, например, при старте ракеты, либо в случае, когда скорость наоборот уменьшается до нуля, например, при торможении поезда до полной остановки, можно использовать в расчетах только одно значение скорости. Формула тогда примет вид: a =v /t для первого случая либо же: a = v_0 /t для второго.
Проекцию скорости на ось Ох при прямолинейном равноускоренном движении можно найти по следующей формуле:
Выразим из этой формулы, формулу для проекции скорости которую имело лвижущееся тело к концу некоторого промежутка времени t.
То есть, зная проекцию вектора начальной скорости V0x и проекцию вектора ускорения ax в любой момент времени можно вычислить проекцию вектора мгновенной скорости Vx, которую будет иметь тело в данной точке.
Графиком уравнения Vx=V0x+ax*t будет прямая линия. Расположение этой лини в системе координат будет определяться значениями ax b V0x. График проекции скорости тела при нулевой начальной скоростиНа следующем рисунке представлен график проекции вектора скорости движущегося тела, которое в начальный момент времени имел нулевую скорость, и двигалось равноускоренно и прямолинейно с ускорением ax=1,5 м/(с^2) в течение 40 секунд. Для построения такого графика, также достаточно взять несколько значений переменной t и посчитать в них значение проекции скорости Vx. А потом соединить их прямой линией. Как видите, график имеет начальную точку не в нуле, в значении, которое имеет начальная скорость. График проекции скорости тела при торможенииЕсли бы ускорение было отрицательным, то есть тело постепенно тормозило, то график составлял бы с положительным направлением оси Ох тупой угол. Ниже представлен график такой ситуации. Из графика видно, что тело начинало свое движение со скоростью 20 м/с, и постепенно замедляло её. За 10 секунд, оно полностью остановилось.
Попытаемся вывести формулу для нахождения проекции вектора перемещения тела, которое двигается прямолинейно и равноускоренно, за любой промежуток времени. Для этого обратимся к графику зависимости проекции скорости прямолинейного равноускоренного движения от времени. График зависимости проекции скорости прямолинейного равноускоренного движения от времениНиже на рисунке представлен график, для проекции скорости некоторого тела, которое движется с начальной скорость V0 и постоянным ускорением а. Если бы у нас было равномерное прямолинейное движение, то для вычисления проекции вектора перемещения, необходимо было бы посчитать площадь фигуры под графиком проекции вектора скорости. Теперь докажем, что и в случае равноускоренного прямолинейного движения проекция вектора перемещения Sx будет определяться таким же образом. То есть проекция вектора перемещения будет равняться площади фигуры под графиком проекции вектора скорости. Найдем площадь фигуры ограниченную осью оt, отрезками АО и ВС, а также отрезком АС.
Выделим на оси ot малый промежуток времени db. Проведем через эти точки перпендикуляры к оси времени, до их пересечения с графикос проекции скорости. Отметим точки пересечения a и c. За этот промежуток времени скорость тела поменяется от Vax до Vbx. Если взять этот промежуток достаточно малым, то можно считать что скорость остается практически неизменной, а следовательно мы будем иметь на этом промежутке дело с равномерным прямолинейным движением. За промежуток t3=3*t1, это тело совершит перемещение S3=9*S1 и т.д., для любого натурального n. Это конечно же будет выполняться, при условии, что время должно отсчитываться от одного и того же момента. На следующем рисунке хорошо представлена эта зависимость.
При увеличении промежутка времени, который отсчитывается от начал движения, в целое число раз по сравнению с t1, модули векторов перемещений будут возрастать как ряд квадратов последовательных натуральных чисел. Помимо этой закономерности, из представленного выше рисунка можно установить еще одну, следующую закономерность:
За последовательные равные промежутки времени, модули векторов перемещений, совершаемых телом, будут относиться между собой как ряд последовательных нечетных чисел. Стоит отметить, что такие закономерности будут верными только в равноускоренном движении.
Представьте себе электричку. Она едет тихонько по рельсам, развозя пассажиров по дачам. И вдруг сидящий в последнем вагоне хулиган и тунеядец Сидоров замечает, что на станции «Сады» в вагон входят контролеры. Билет, естественно, Сидоров не купил, а штраф платить ему хочется еще меньше. Относительность движения безбилетника в поездеИ вот, чтобы его не поймали, он быстренько совершает перемещение при прямолинейном равномерном движении в другой вагон. Контролеры, проверив билеты у всех пассажиров, движутся в том же направлении. Сидоров опять переходит в следующий вагон и так далее. И вот, когда он достигает первого вагона и идти дальше уже некуда, оказывается, что поезд как раз доехал до нужной ему станции «Огороды», и счастливый Сидоров выходит, радуясь тому, что проехал зайцем и не попался. Что мы можем извлечь из этой остросюжетной истории? Мы можем, без сомнения, порадоваться за Сидорова, а можем, кроме того, обнаружить еще один небезынтересный факт. В то время, как поезд за пять минут проехал пять километров от станции «Сады» до станции «Огороды», заяц Сидоров за это же время преодолел такое же расстояние плюс расстояние, равное длине поезда, в котором он ехал, то есть около пяти тысяч двухсот метров за те же пять минут. Получается, что Сидоров двигался быстрее электрички. Впрочем, такую же скорость развили и следующие за ним по пятам контролеры. Учитывая, что скорость поезда была около 60 км/ч впору выдать им всем несколько олимпийских медалей. Однако, конечно же, никто такой глупостью заниматься не будет, потому что все понимают, что невероятная скорость Сидорова была развита им только лишь относительно неподвижных станций, рельсов и огородов, и обусловлена эта скорость была передвижением поезда, а вовсе не невероятными способностями Сидорова. Относительно же поезда Сидоров двигался вовсе и не быстро и не дотягивает не то что до олимпийской медали, но даже до ленточки от нее. Вот тут-то мы и сталкиваемся с таким понятием как относительность движения. Понятие относительности движения: примерыОтносительность движения не имеет определения, так как не является физической величиной. Относительность механического движения проявляется в том, что некоторые характеристики движения, такие как скорость, путь, траектория и так далее, относительны, то есть зависят от наблюдателя. В различных системах отсчета эти характеристики будут различны. Кроме приведенного примера с гражданином Сидоровым в поезде, можно взять практически любое движение любого тела и показать, насколько оно относительно. Идя на работу, вы двигаетесь вперед относительно дома и в то же время передвигаетесь назад относительно автобуса, на который опоздали. Вы стоите на месте относительно плеера в кармане и несетесь с огромной скоростью относительно звезды по имени Солнце. В этом и заключается понятие относительности движения.
С древнейших времен движение материальных тел не переставало волновать умы ученых. Так, например, сам Аристотель считал, что если на тело не действуют никакие силы, то такое тело всегда будет находиться в покое. И лишь только спустя 2000 лет итальянский ученый Галилео Галилей смог исключить из формулировки Аристотеля слово «всегда». Галилей понял, что пребывание тела в состоянии покоя не является единственным следствием отсутствия внешних сил. Тогда Галилей заявил: тело, на которое не действуют никакие силы, будет либо находиться в покое, либо двигаться равномерно прямолинейно. То есть, движение с одинаковой скоростью по прямой траектории, с точки зрения физики, равнозначно состоянию покоя. Что есть состояние покоя?В жизни этот факт наблюдать очень сложно, поскольку всегда имеет место сила трения, которая не дает предметам и вещам покидать свои места. И в самом деле, на тело действую только две силы: сила тяжести и сила реакции опоры. Но расположены они на одной прямой и направлены друг против друга. Таким образом, по принципу суперпозиции, мы имеем, что общая сила, действующая на такое тело равна нулю. Однако это идеальный случай. В жизни сила трения проявляет себя почти во всех случаях. Галилей сделал важное открытие, приравняв состояние покоя и движение с постоянной скоростью по прямой линии. Но этого было недостаточно. Оказалось, что условие это выполняется не во всех случаях. Ясность в этот вопрос внес Исаак Ньютон, обобщивший исследования Галилея и, таким образом, сформулировавший Первый Закон Ньютона. Первый закон Ньютона: формулируем самиСуществуют две формулировки первого закона Ньютона современная и формулировка самого Исаака Ньютона. Современная формулировка звучит следующим образом: «Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго». Инерциальные системы отсчетаИнерциальными называют системы отсчета, в которых выполняется закон инерции. Закон же инерции заключается в том, что тела сохраняют свою скорость неизменной, если на них не действуют другие тела. Получается очень неудобоваримо, малопонятно и напоминает комичную ситуацию, когда на вопрос: “Где это «тут»?” отвечают: “Это здесь”, а на следующий логичный вопрос: “А где это «здесь»?” отвечают: “Это тут”. Формулировка самого Ньютона такова: «Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние». Однако на практике этот закон выполняется не всегда. Убедиться в этом можно элементарно. Когда человек стоит, не держась за поручни, в движущемся автобусе, и автобус резко тормозит, то человек начинает двигаться вперед относительно автобуса, хотя его не понуждает к этому ни одна видимая сила. То есть, относительно автобуса первый закон Ньютона в изначальной формулировке не выполняется. Очевидно, что он нуждается в уточнении. Уточнением и является введение инерциальных систем отсчета. То есть, таких систем отсчета, в которых первый закон Ньютона выполняется. Это не совсем понятно, поэтому попробуем перевести все это на человеческий язык. Инерциальные и неинерциальные системы отсчетаСвойство инерции любого тела таково, что до тех пор, пока тело остается изолированным от других тел, оно будет сохранять свое состояние покоя или равномерного прямолинейного движения. На практике это означает, что если в нашем примере за систему отсчета принять не автобус, а какую-то звезду на окраине Галактики, то первый закон Ньютона будет абсолютно точно выполняться для беспечного пассажира, не держащегося за поручни. При торможении автобуса он будет продолжать свое равномерное движение, пока на него не подействуют другие тела. Вот такие системы отсчета, которые никак не связаны с рассматриваемым телом, и которые никак не влияют на инертность тела, называются инерциальными. Для таких систем отсчета первый закон Ньютона в его исходной формулировке абсолютно справедлив. То есть закон можно сформулировать так: в системах отсчета, абсолютно никак не связанных с телом, скорость тела при отсутствии стороннего воздействия остается неизменной. В таком виде первый закон Ньютона легко доступен для понимания. Проблема заключается в том, что на практике очень сложно рассматривать движение конкретного тела относительно таких систем отсчета. Поэтому за такую систему отсчета условно часто принимают Землю, хотя она и связана с находящимися на ней телами и влияет на характеристики их движения. Но для многих расчетов такое приближение оказывается достаточным. Поэтому примерами инерциальных систем отсчета можно считать Землю для расположенных на ней тел, Солнечную систему для ее планет и так далее. Первый закон Ньютона не описывается какой-либо физической формулой, однако с помощью него выводятся другие понятия и определения. По сути, этот закон постулирует инертность тел. И таким образом выходит, что для инерциальных систем отсчета закон инерции и есть первый закон Ньютона. Еще примеры инерциальных систем и первого закона НьютонаТак, например, если тележка с шаром будет ехать сначала по ровной поверхности, с постоянной скоростью, а потом заедет на песчаную поверхность, то шар внутри тележки начнет ускоренное движение, хотя никакие силы на него не действуют (на самом деле, действуют, но их сумма равна нулю). Происходит это от того, что система отсчета (в данном случае, тележка) в момент попадания на песчаную поверхность, становится неинерциальной, то есть перестает двигаться с постоянной скоростью. Первый Закон Ньютона вносит важное разграничение между инерциальными и неинерциальными системами отсчета. Также важным следствием этого закона является тот факт, что ускорение, в некотором смысле, важнее скорости тела. Поскольку движение с постоянной скоростью по прямой линии суть нахождение в состоянии покоя. Тогда как движение с ускорением явно свидетельствуют о том, что либо сумма сил, приложенных к телу, не равно нулю, либо сама система отсчета, в которой находится тело, является неинерциальной, то есть движется с ускорением. Причем ускорение может быть как положительным (тело ускоряется), так и отрицательным (тело замедляется).
Второй закон Ньютона связывает вместе три, на первый взгляд, совершенно не связанные друг с другом величины: ускорение, массу и силу. Элементарный опыт по второму закону НьютонаНачнем с практической части. Нагрузите чем-нибудь две сумки или два пакета. Один чуть-чуть, а второй очень сильно. Только пакеты берите покрепче. А теперь примерно с одинаковой силой по очереди резко поднимите оба пакета вверх. Вы увидите, что легкий пакет практически взлетит, а вот тяжелый перемещаться будет намного медленнее. А теперь другой опыт положите на землю футбольный мячик и пните его пару раз. Один раз легонько, а второй раз со всей силы. Понаблюдайте, как изменится скорость мяча после пинка. В первом случае он потихоньку откатится на небольшое расстояние, во втором улетит далеко и на весьма приличной скорости. Ну вот и все, с практической частью закончили. Теперь немного порассуждаем. Действие равнодействующей силыМы знаем, что скорость тела изменяется под действием приложенной к нему силы. То есть, фактически, все случаи приложения различных сил в конкретный момент времени можно свести к действию одной равнодействующей силы. Таким образом, чтобы найти, как изменилась скорость тела, нам надо знать, какая сила действует на тело. Какое ускорение получает тело?В зависимости от величины и направления силы тело получит то или иное ускорение. Это четко видно в опыте с мячом. Когда мы подействовали на тело небольшой силой, мяч ускорился не очень сильно. Когда же сила воздействия увеличилась, то мяч приобрел гораздо большее ускорение. То есть, ускорение связано с приложенной силой прямо пропорционально. Чем больше сила воздействия, тем большее ускорение приобретает тело. От чего еще зависит ускорение, полученное телом в результате воздействия на него? Вспомним первую часть нашего опыта. То есть, второй вывод это то, что масса тела напрямую связана с ускорением, приобретаемым телом в результате воздействия силы. При этом, масса тела обратно пропорциональна полученному ускорению. Чем больше масса, тем меньше будет величина ускорения. Второй Закон Ньютона: формула и определениеИсходя из всего вышесказанного, приходим к тому, что можно записать второй закон Ньютона в виде следующей формулы: a =F / m , где a ускорение, F сила воздействия, m масса тела. Соответственно, второму закону Ньютона можно дать такое определение: ускорение, приобретаемое телом в результате воздействия на него, прямо пропорционально силе или равнодействующей сил этого воздействия и обратно пропорционально массе тела.
В первом законе Ньютона говорится о поведении тела, изолированного от воздействия других тел. Второй закон говорит о прямо противоположной ситуации. В нем рассматриваются случаи, когда тело или несколько тел воздействуют на данное. Оба эти закона описывают поведение одного конкретного тела. Но во взаимодействии всегда участвуют минимум два тела. Что будет происходить с обоими этими телами? Как описать их взаимодействие? Анализом этой ситуации и занялся Ньютон после формулировки своих первых двух законов. Займемся и мы такими же изысканиями. Взаимодействие двух телМы знаем, что при взаимодействии воздействуют друг на друга оба тела. Не бывает такого, чтобы одно тело толкнуло другое, а второе в ответ никак не отреагировало бы. Такое может происходить среди по-разному воспитанных людей, но никак не в природе. Мы знаем, что если мы пинаем мяч, то мяч в ответ пинает нас. Другое дело, что мяч имеет намного меньшую массу, чем тело человека, и потому его воздействие практически не ощутимо. Однако, если вы попробуете пнуть тяжелый железный мяч, то живо ощутите это ответное воздействие. Фактически, мы каждый день по многу раз пинаем очень и очень тяжелый мяч нашу планету. Мы толкаем ее каждым своим шагом, только при этом отлетает не она, а мы. А все потому, что планета в миллионы раз превосходит нас по массе. Соотношение сил во взаимодействии между теламиТак что из этих рассуждений видно, что при взаимодействии двух тел, не только первое действует на второе с некоторой силой, но и второе в ответ действует на первое также с некоторой силой. Возникает вопрос: а как соотносятся эти силы? Какая из них больше, какая меньше? Для этого необходимо проделать некоторые измерения. Потребуются два динамометра, но в домашних условиях их вполне могу заменить два безмена. Они измеряют вес, а вес это тоже сила, только выраженная в единицах массы в случае безмена. Поэтому, если у вас есть два безмена, то проделайте следующее. Один из них оденьте колечком на что-то неподвижное, например, на гвоздь в стене, а второй соедините с первым крючками. И хотя мы тянем только за один из них, окажется, что показания обоих, как на очной ставке, будут совпадать. Получается, что сила, с которой мы воздействуем вторым безменом на первый, равна силе, с которой первый безмен воздействует на второй. Третий закон Ньютона: определение и формулаСила действия равна силе противодействия. В этом и состоит суть третьего закона Ньютона. Определение его таково: силы, с которыми два тела действуют друг на друга, равны по величине и противоположны по направлению. Третий закон Ньютона можно записать в виде формулы: F_1 = — F_2, Где F_1 и F_2 силы действия друг на друга соответственно первого и второго тела. Справедливость третьего закона Ньютона была подтверждена многочисленными экспериментами. Этот закон справедлив как для случая, когда одно тело тянет другое, так и для случая, когда тела отталкиваются.
Как вы думаете, одновременно ли долетят до земли, сброшенные с крыши перо, пластиковая бутылка и монета? Можно проделать такой опыт и убедиться, что монета приземлится первой, бутылка второй, а перо долго будет болтаться в воздухе и может вообще не долететь до земли, если его подхватит и унесет внезапный ветерок. Так ли свободно свободное падение тел?Соответственно, делаем вывод, что свободное падение тел не подчиняется какому-либо одному правилу, и все предметы падают на землю по-своему. Тут бы как говорится, и сказке конец, но некоторые физики на этом не успокоились и предположили, что на свободное падение тел может оказывать влияние сила сопротивления воздуха и, соответственно, такие результаты эксперимента нельзя считать окончательными. Они взяли длинную стеклянную трубку и поместили в нее перо, дробинку, деревянную пробку и монету. Потом они закупорили трубку, откачали из нее воздух и перевернули. где v конечная скорость, v_0 начальная скорость, s перемещение, t время, g ускорение свободного падения. Вывод, что свободное падение любых тел происходит одинаково, на первый взгляд кажется нелепым с точки зрения повседневного опыта. Но на самом деле все правильно и логично. Просто, незначительная на первый взгляд величина сопротивления воздуха для многих падающих тел оказывается довольно ощутимой, а потому очень сильно замедляет их падение.
Как нам уже известно, сила тяжести действует на все тела, которые находятся на поверхности Земли и вблизи неё. При этом не важно, находятся ли они в состоянии покоя или совершают движение. Если некоторое тело будет свободно падать на Землю, то при этом оно будет совершать равноускоренное движение, причем скорость будет возрастать постоянно, так как вектор скорости и вектор ускорения свободного падения будут сонаправлены между собой. Суть движения вертикально вверхЕсли же подбросить некоторое тело вертикально вверх, и при этом считать что сопротивление воздуха отсутствует, то можно считать что оно тоже совершает равноускоренное движение, с ускорением свободного падения, которое вызвано силой тяжести. Через некоторое время наступит момент, когда скорость станет равняться нулю. В этот момент тело достигнет своей максимальной высоты и на какой-то момент остановится. Очевидно, что, чем большую начальную скорость мы придадим телу, тем на большую высоту оно поднимется к моменту остановки.
Как решать задачиКогда вы столкнетесь с задачами на движение тела вверх, при котором не учитывается сопротивление воздуха и другие силы, а считается, что на тело действует только сила тяжести, то так как движение равноускоренное, то можно применять те же самые формулы, что и при прямолинейном равноускоренном движении с некоторой начальной скорость V0. Необходимо также учитывать, что при движении вверх вектор ускорения свободного падения направлен вниз, а вектор скорости вверх, то есть они разнонаправлены, а следовательно, их проекции будут иметь разные знаки. Например, если Ось Ох направить вверх, то проекция вектора скорости при движении вверх, будет положительна, а проекция ускорения свободного падения отрицательна. Это надо учитывать, подставляя значения в формулы, иначе получится совершенно неверный результат.
Все мы ходим по Земле потому, что она нас притягивает. Если бы Земля не притягивала все находящиеся на ее поверхности тела, то мы, оттолкнувшись от нее, улетели бы в космос. Но этого не происходит, и всем известно о существовании земного притяжения. Притягиваем ли мы Землю? Притягивает Луна!А притягиваем ли мы сами к себе Землю? Смешной вопрос, правда? Но давайте разберемся. Вы знаете, что такое приливы и отливы в морях и океанах? Каждый день вода уходит от берегов, неизвестно где шляется несколько часов, а потом, как ни в чем не бывало, возвращается обратно. Так вот вода в это время находится не неизвестно где, а примерно посредине океана. Там образуется что-то наподобие горы из воды. Невероятно, правда? Вода, которая имеет свойство растекаться, сама не просто стекается, а еще и образует горы. И в этих горах сосредоточена огромная масса воды. Просто прикиньте весь объем воды, который отходит от берегов во время отливов, и вы поймете, что речь идет о гигантских количествах. Но раз такое происходит, должна же быть какая-то причина. И причина есть. Причина кроется в том, что эту воду притягивает к себе Луна. Вращаясь вокруг Земли, Луна проходит над океанами и притягивает к себе океанические воды. Луна вращается вокруг Земли, потому что она притягивается Землей. Но, выходит, что она и сама при этом притягивает к себе Землю. Земля, правда, для нее великовата, но ее влияние оказывается достаточным для перемещения воды в океанах. Сила и закон всемирного тяготения: понятие и формулаА теперь пойдем дальше и подумаем: если два громадных тела, находясь неподалеку, оба притягивают друг друга, не логично ли предположить, что и тела поменьше тоже будут притягивать друг друга? Просто они намного меньше и сила их притяжения будет маленькой? Оказывается, что такое предположение абсолютно верно. Возвращаясь к нашему исходному вопросу: «притягиваем ли мы Землю?», мы можем с уверенностью ответить: «да». Согласно третьему закону Ньютона мы притягиваем Землю ровно с такой же силой, с какой Земля притягивает нас. Силу эту можно рассчитать из закона всемирного тяготения. А согласно второму закону Ньютона воздействие тел друг на друга какой-либо силой выражается в виде придаваемого ими друг другу ускорения. Но придаваемое ускорение зависит от массы тела. Масса Земли велика, и она придает нам ускорение свободного падения. А наша масса ничтожно мала по сравнению с Землей, и поэтому ускорение, которое мы придаем Земле, практически равно нулю. Именно поэтому мы притягиваемся к Земле и ходим по ней, а не наоборот.
Одним из частных случаев всемирного тяготения является тот факт, что все тела притягиваются к Земле. Для нас, жителей планеты Земля, сила тяжести имеет огромное значение. Сила, с которой тело некоторой массы m будет притягиваться к Земле, согласно закону всемирного тяготения будет вычисляться по следующей формуле:
Чем больше мы поднимем тело над Землей, тем будет меньше ускорение свободного падения. Следовательно, будет уменьшатся и сила тяжести которая действует на это тело. Чаще всего этим увеличением пренебрегают, так как расстояние, на которое поднимается тело от поверхности Земли, по сравнению с радиусом Земли пренебрежимо мало. Например, если человек массой 80 кг поднялся на гору высотой 3 км, то действующая на него сила тяжести уменишилась всего на 0.7 Н. Это очень мало, поэтому в таких случаях при расчетах берут вблизи поверхности земли значение ускорения свободного падения g=9,81. Применение формулы для других небесных телФормула, которую мы записали выше, подходит также для вычисления ускорения свободного падения на любых небесных объектах. То есть вместо радиуса и массы Земли необходимо подставить радиус и массу данного небесного объекта.
Мы знаем, что все тела притягиваются друг к другу. В частности, Луна, например, притягивается к Земле. Для того чтобы ответить на этот вопрос, необходимо рассмотреть виды движения тел. Мы уже знаем, что движение может быть равномерным и неравномерным, но существуют и другие характеристики движения. В частности, в зависимости от направления различают прямолинейное и криволинейное движение. Прямолинейное движениеИзвестно, что тело двигается под действием приложенной к нему силы. Можно проделать несложный эксперимент, показывающий, как направление движения тела будет зависеть от направления приложенной к нему силы. Для этого потребуется произвольный предмет небольшого размера, резиновый шнур и горизонтальная или вертикальная опора. Привязывает шнур одним концом к опоре. На другом конце шнура закрепляем наш предмет. Теперь, если мы оттянем наш предмет на некоторое расстояние, а потом отпустим, то увидим, как он начнет двигаться в направлении опоры. Его движение обусловлено силой упругости шнура. Только вместо силы упругости выступает сила притяжения. А теперь возьмем наш предмет на резинке и толкнем его не в направлении к/от опоры, а вдоль нее. Если бы предмет не был закреплен, он бы просто улетел в сторону. Но так как его держит шнур, то шарик, двигаясь в сторону, слегка растягивает шнур, тот тянет его обратно, и шарик чуть меняет свое направление в сторону опоры. Криволинейное движение по окружностиТак происходит в каждый момент времени, в итоге шарик движется не по первоначальной траектории, но и не прямолинейно к опоре. Шарик будет двигаться вокруг опоры по окружности. Траектория его движения будет криволинейной. Именно так вокруг Земли двигается Луна, не падая на нее. Именно так притяжение Земли захватывает метеориты, которые летят близко от Земли, но не прямо на нее. Эти метеориты становятся спутниками Земли. При этом от того, каким был их первоначальный угол движения по отношению к Земле, зависит, как долго они пробудут на орбите. Движение по окружности с постоянной по модулю скоростьюЕще один момент, который следует отметить, это то, что скорость криволинейного движения по окружности меняется по направлению, но одинакова по значению. А это означает, что движение по окружности с постоянной по модулю скоростью происходит равноускорено. Так как направление движения меняется, значит, движение происходит с ускорением. А так как оно меняется одинаково в каждый момент времени, следовательно, движение будет равноускоренным. А сила притяжения является силой, которая обусловливает постоянное ускорение. Луна двигается вокруг Земли именно благодаря этому, но если вдруг когда-либо движение Луны изменится, например, в нее врежется очень крупный метеорит, то она вполне может сойти со своей орбиты и упасть на Землю.
Вы когда-нибудь соревновались, кто дальше кинет камень или снежок? Все мальчишки наверняка проходили через это. И все знают, что чтобы камень пролетел как можно дальше, надо кинуть его как можно сильнее. То есть нужно придать ему как можно большую скорость. Сила человеческой руки ограничена, и камень мы можем кинуть относительно недалеко. Намного большую скорость телам могут придать различные артиллерийские орудия. Снаряды могут преодолевать несколько километров и даже десятков километров. Однако всегда траекторией всех этих летящих тел является дуга, концом упирающаяся в землю. Бексонечно долгое вращение вокруг ЗемлиЕсли же пойти дальше и предположить, что мы можем придать телу намного большую скорость? Такую, что дуга, которую тело опишет, будет уже не упираться в землю, а проходить на некотором расстоянии вокруг всей Земли? Тогда получится, что мы получим тело, способное бесконечно долго вращаться вокруг Земли. Единственное, что будет мешать нам это сопротивление воздуха. Значит надо избавиться от него. Избавиться от сопротивления воздуха мы можем на большой высоте. На высоте свыше трехсот километров воздуха уже практически нет. Именно начиная с такой высоты, и запускают искусственные спутники Земли. Спутники вращаются вокруг Земли по различным орбитам, но все они не падают на Землю. Движение спутника — пример свободного паденияЭто происходит потому, что запущены они были со скоростью, достаточной для того, чтобы преодолеть земное притяжение. Как ни странно звучит, движение спутника вокруг Земли это пример свободного падения тела. Происходит оно с ускорением, как и положено свободно падающему телу, только ускорение это не увеличивает скорость тела по модулю, а изменяет по направлению. Поэтому спутники и движутся по орбите. Первая и вторая космическая скоростьСкорость, необходимая для того, чтобы тело начало вращаться по орбите вокруг Земли не падая, называется первой космической скоростью. На высоте, например, 500 км эта скорость составляет уже 7,6 км/с. Это объясняется тем, что гравитационные силы уменьшаются с увеличением расстояния между телами. Первой космической скоростью обусловлено движение искусственных спутников земли. А есть ли такая скорость, которая позволит совсем вырваться из оков земного притяжения? Такая скорость есть и называется она второй космической скоростью. Она составляет 11,2 км/с. При такой скорости тела описывают вокруг Земли не дугу, а эллипс, и тело удаляется на расстояние, достаточное для полного освобождения от земного притяжения. Такую скорость развивают ракеты, которые уходят в космическое пространство прочь от Земли.
Проделаем несколько несложных преобразований с формулами. По второму закону Ньютона силу можно найти: F=m*a. Ускорение находится следующим образом: a=v⁄t . Таким образом получаем: F=m*v/t. Определение импульса тела: формулаВыходит, что сила характеризуется изменением произведения массы на скорость во времени. Если обозначить это произведение некой величиной, то мы получим изменение этой величины во времени как характеристику силы. Эту величину назвали импульсом тела. Импульс тела выражается формулой: p=m*v , где p импульс тела, m масса, v скорость. Импульс это векторная величина, при этом его направление всегда совпадает с направлением скорости. Единицей импульса является килограмм на метр в секунду (1 кг*м/с). Что же такое импульс тела: как понять?Попробуем по-простому, «на пальцах» разобраться, что такое импульс тела. Если тело покоится, то его импульс равен нулю. Логично. Если скорость тела изменяется, то у тела появляется некий импульс, который характеризует величину приложенной к нему силы. Если воздействие на тело отсутствует, но оно движется с некоторой скоростью, то есть имеет некий импульс, то его импульс означает, какое воздействие способно оказать данное тело при взаимодействии с другим телом. В формулу импульса входит масса тела и его скорость. То есть чем большей массой и/или скоростью обладает тело, тем большее воздействие оно может оказать. Это понятно и из жизненного опыта. Чтобы сдвинуть тело небольшой массы, нужна небольшая сила. Чем больше масса тела, тем большее придется приложить усилие. То же самое касается и скорости, которую сообщают телу. В случае же воздействия самого тела на другое, импульс также показывает величину, с которой тело способно действовать на другие тела. Эта величина напрямую зависит от скорости и массы исходного тела. Импульс при взаимодействии телВозникает еще один вопрос: что произойдет с импульсом тела при его взаимодействии с другим телом? Масса тела измениться не может, если оно остается целым, а вот скорость может измениться запросто. При этом скорость тела изменится в зависимости от его массы. В самом деле, понятно, что при столкновении тел с очень разными массами, скорость их изменится по-разному. Если летящий на большой скорости футбольный мяч врежется в неготового к этому человека, например зрителя, то зритель может упасть, то есть приобретет некоторую небольшую скорость, но точно не полетит как мячик. А все потому, что масса зрителя намного больше массы мяча. Но при этом сохранится неизменным общий импульс этих двух тел. Закон сохранения импульса: формулаВ этом и заключается закон сохранения импульса: при взаимодействии двух тел их общий импульс остается неизменным. Закон сохранения импульса действует только в замкнутой системе, то есть в такой системе, в которой нет воздействия внешних сил или их суммарное действие равно нулю. В реальности практически всегда на систему тел оказывается стороннее воздействие, но общий импульс, как и энергия, не пропадает в никуда и не возникает из ниоткуда, он распределяется между всеми участниками взаимодействия. Закон сохранения импульса для двух тел в виде формулы будет выглядеть следующим образом: (p_1′ ) +(p_2′ ) = (p_1 ) + (p_2 ), где левая часть уравнения это сумма импульсов тел после взаимодействия, а правая часть после взаимодействия. Уравнение говорит нам, что общий импульс (сумма импульсов) остается неизменнным.
Реактивное движение — это все же движение. А мы знаем, что чтобы происходило движение, необходимо воздействие некоторой силы. Тело либо само должно оттолкнуться от чего-нибудь, либо стороннее тело должно толкнуть данное. Это хорошо известно и понятно нам из жизненного опыта. От чего оттолкнуться в космосе?У поверхности Земли можно оттолкнуться от поверхности либо от находящихся на ней предметов. Для передвижения по поверхности используют ноги, колеса, гусеницы и так далее. В воде и воздухе можно отталкиваться от самих воды и воздуха, имеющих определенную плотность, и потому позволяющих взаимодействовать с ними. Природа для этого приспособила плавники и крылья. Человек создал двигатели на основе пропеллеров, которые во много раз увеличивают площадь контакта со средой за счет вращения и позволяют отталкиваться от воды и воздуха. А как быть в случае безвоздушного пространства? От чего отталкиваться в космосе? Там нет воздуха, там ничего нет. Как осуществлять полеты в космосе? Вот тут-то и приходит на помощь закон сохранения импульса и принцип реактивного движения. Импульс и принцип реактивного движенияИмпульс это произведение массы тела на его скорость. Когда тело неподвижно, его скорость равна нулю. Однако тело обладает некоторой массой. При отсутствии сторонних воздействий, если часть массы отделится от тела с некоторой скоростью, то по закону сохранения импульса, остальная часть тела тоже должна приобрести некоторую скорость, чтобы суммарный импульс остался по-прежнему равным нулю. Причем скорость оставшейся основной части тела будет зависеть от того, с какой скоростью отделится меньшая часть. Чем эта скорость будет выше, тем выше будет и скорость основного тела. Это понятно, если вспомнить поведение тел на льду или в воде. Если два человека будут находиться рядом, а потом один из них толкнет другого, то он не только придаст тому ускорение, но и сам отлетит назад. И чем сильнее он толкнет кого-либо, тем с большей скоростью отлетит сам. Наверняка, вам приходилось бывать в подобной ситуации, и вы можете представить себе, как это происходит. Ракеты, в которых реализован этот принцип, выбрасывают некоторую часть своей массы на большой скорости, вследствие чего сами приобретают некоторое ускорение в противоположном направлении. Потоки раскаленных газов, возникающие в результате сгорания топлива, выбрасываются через узкие сопла для придания им максимально большой скорости. При этом, на величину массы этих газов уменьшается масса ракеты, и она приобретает некую скорость. Таким образом реализован принцип реактивного движения в физике. Принцип полета ракетыВ ракетах применяют многоступенчатую систему. Во время полета нижняя ступень, израсходовав весь свой запас топлива, отделяется от ракеты, чтобы уменьшить ее общую массу и облегчить полет. Количество ступеней уменьшается, пока не остается рабочая часть в виде спутника или иного космического аппарата. Топливо рассчитывают таким образом, чтобы его хватило как раз для выхода на орбиту. При посадках на космические тела рассчитывают количество топлива для посадки и на обратный путь, если он запланирован. |
404 Cтраница не найдена
Размер:
AAA
Изображения Вкл. Выкл.
Обычная версия сайта
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Равноускоренное движение — презентация онлайн
1.
 Равноускоренное движениеПри движении тел их скорости обычно меняются либо по
Равноускоренное движениеПри движении тел их скорости обычно меняются либо помодулю, либо по направлению, либо одновременно и по
модулю, и по направлению.
Нам хорошо известны следующие формулы
х = х0 + sx
х = х0 + v x t
y = y0 + sy
y = y0 + vy t
Данные формулы могут принимать разный вид в зависимости от того,
как движется тело.
Сегодня мы узнаем, как будут выглядеть ЭТИ формулы
для простейшего вида неравномерного прямолинейного движения
Для этого достаточно научиться определять скорость тела в любой
момент времени или его перемещение
v
vx
Х
0
Скорость тела в данный момент времени или в данной точке
траектории называется мгновенной скоростью. Она всегда
направлена по касательной к траектории в данной точке.
Рассмотрим неравномерное движение
тела по произвольной траектории.
Попытаемся определить скорость тела ,
например, в точке А:
s4
А
s3
s2
3. Для еще более маленького участка:
vср3 =
s3
t3
4.
 В результате можно достичь настолько
В результате можно достичь настолькомалого промежутка времени, что скорость
за него практически не успеет измениться,
а траектория стянется в точку, и движение
станет как бы равномерным.
s4
s1
v
=
ср4
1.Выделим небольшой участок траектории,
t4
включающий точку А. Для него значение Именно для такого случая средняя скорость
средней скорости равно:
становится мгновенной скоростью в точке А
vср1 =
s1
t1
s
v =
t
формула мгновенной
скорости
2. Выделим участок поменьше, включающий
точку А:
Теперь, говоря о скорости неравномерного
движения, мы будем иметь ввиду
s2
vср2 =
t2
мгновенную скорость
Наша задача сводится к умению определять мгновенную
скорость тела в любой момент времени
Для простоты рассмотрим такое неравномерное движение, при котором
скорость тела изменяется одинаково за любые равные промежутки времени.
Движение тела, при котором скорость тела за любые равные промежутки
времени изменяется одинаково, называется равноускоренным движением
Прямолинейное движение
равномерное
?
равноускоренное
?
Определение координаты тела
в любой момент времени
Вводили величину, характеризующую
быстроту изменения координаты
СКОРОСТЬ
х — х0
t
!
Определение скорости тела в
любой момент времени
Нужна величина, характеризующая
быстроту изменения скорости
УСКОРЕНИЕ
v – v0
t
Ускорением тела при его равноускоренном движении называется
векторная величина, равная отношению изменения скорости к
промежутку времени, в течение которого это изменение произошло.
а– ускорение
v – v0
а=
t
Единица ускорения в СИ:
1[ a ] = 1 м/с2
Итак, ускорение характеризует быстроту изменения скорости :
чем больше ускорение, тем быстрее изменяется скорость
( увеличивается или уменьшается )
?
а = 1 м/с2
а = 2,5 м/с2
Каков смысл данных значений ускорений тел :
Это значит, что скорость тела за каждую секунду изменяется на 1 м/с
Это значит, что скорость тела за каждую секунду изменяется на 2,5 м/с
Работаем с проекциями величин
Связь знаков проекций скорости vx и ускорения
с характером движения тела
а
v1
0
а
х
х
v3x < 0, ax > 0
v2
0
v3
0
v1x > 0, аx > 0
а
аx
v0
х
v2x < 0, аx <0
0
если векторы а и v
сонаправлены, то
0
скорость увеличивается
v4
а
0
х
v0
а
а=0
х
скорость постоянна
если а = 0 или векторы
перпендикулярны
х
v4x > 0, ax < 0
если векторы а и v
противоположно
направлены
скорость уменьшается
Если известна начальная скорость и ускорение, можно
определить скорость тела в любой момент времени
vx — v0x
аx=
t
vx — v0 x = ax t
vx = v0 x + axt
Полученная формула может видоизменяться в зависимости
от знаков проекций ускорения и начальной скорости
а
1
а
v
v
а
2
4
а
v
3
v
v = v0 + at
v = — v0 — at
v = v0 — at
v = — v0 + at
т.
 к. v1x > 0, аx > 0
к. v1x > 0, аx > 0т.к. v2x < 0, аx <0
т.к. v4x > 0, ax < 0
т.к. v3x < 0, ax > 0
В случае, если v0 = 0 , формула примет вид
v = — at
если ax < 0
v = at
если ax > 0
х
Графическое представление движения
а, м/с2
Графики ускорения и проекции ускорения
4
4
а1
3
аx, м/с2
а1x>0
3
2
t,с
1
2
0
а2
1
1
2
3
4
5
6
7
-1
t,с
0
1
2
3
4
5
6
7
-2
а2x< 0
-3
8
Позволяют определить, скорость какого из
тел изменяется быстрее, но увеличивается
она или уменьшается определить не
позволяют
Позволяют определить, скорость
какого из тел изменяется быстрее, но, кроме того,
если известен знак проекции скорости, можно
определить увеличивается она или уменьшается
График зависимости проекции скорости от времени
vx = v0x + aхt
Если сравнить зависимость координаты от времени при равномерном движении
и зависимость проекции скорости от времени при равноускоренном движении, можно
увидеть, что эти зависимости одинаковы:
х= х0 + vx t
vx = v0x + aхt
Это значит, что и графики зависимостей имеют одинаковый вид.

Первое, с чего нужно начинать работу с графиком – посмотреть на вертикальную ось!
х, м
v , м/с
х
3
1
t,с
1
2
3
4
5
3
х= х0 + vx t
?
vx = v 0 x + aх t
6
2
1
t,с
1
2
3
4
5
6
2
vx = v 0 x + aх t
Учимся «читать» графики
vх , м/с
1 тело
2 тело
25
3
20
15
10
1
Тело движется с начальной скоростью
25
10 м/с
м/с вв положительном
отрицательном направлении
направлении
оси
оси Ох
Ох ( т.к.
т.к. vv0х
0) равнозамедленно
равнозамедленно
0х <
> 0)
(т.к. ах vх )
t, с
Через
4 с 5скорость
тела стала равной
Через
с тело остановилоcь
нулю
и иравноускоренно
оно равноускоренно
продолжило
продолжило
движение
движениеввотрицательном
положительномнаправлении
направлении
Зависимость vх(t) имеет вид
Зависимость vх(t) имеет вид
5
0
1
2
3
4
5
6
-5
-10
2
0 м/с t =t 5=с4 с
v0х = 25
— 10м/с
м/с vхv=
х = 0 м/с
vх – v0 х
00м/с
м/с––25
(-10
м/см/с)
==
=
а1х
=
1х
t
54 с
= -2,5
5 м/с
м/с22
vx = 25 — 5t
vx = -10 + 2,5t
Такие графики «хранят» еще некоторую информацию.
 Так что, продолжим.
Так что, продолжим.Перемещение при равноускоренном движении
vх , м/с
v x = v0x + aх t
В
aх t
А
v0х
aх t
t, с
о
t
С
Если тело движется из состояния покоя,
график проходит через начало координат,
фигура под графиком – треугольник ,
формула принимает вид
Нам хорошо известно, что площадь
фигуры под графиком скорости
численно равна пути, а под графиком
проекции скорости — равна проекции
перемещения.
Поэтому, нам достаточно выразить
площадь трапеции ОАВС
S x=
vх + v0 х
2
t =
a х t2
S x = v0 x t +
2
2v0 x + aх t
2
t
a х t2
S x=
2
Тогда формула координаты имеет вид:
a х t2
x = x 0 + v0 x t +
2
a х t2
x = x0 +
2
Некоторые важные зависимости между величинами
a t2
S =
2
Из данной формулы следует, что для равноускоренного
движения без начальной скорости путь, пройденный
телом, пропорционален квадрату времени.

Значит, пути, пройденные телом за одну, две, три,
четыре… секунды будут относиться как квадраты
последовательных натуральных чисел
S1 : S2 : S3 : S4 … = 1 : 22 : 32 : 42 …
a х t2
S x = v0 x t +
2
Для любого равноускоренного движения, пути,
пройденные телом за любые равные промежутки
времени, будут относиться как последовательный
ряд нечетных чисел
S1-ю : S2-ю : S3-ю : S4-ю …= 1 : 3 : 5 : 7 …
S =
v 2 — v0 2
2а
Формула перемещения без учета времени
Вспомним изученное
• Как называется движение, при котором скорость изменяется ?
• Скорость тела в данный момент времени или в данной точке
vх , м/с
траектории называется
• Что можно сказать о направлении мгновенной скорости ?
• Движение, при котором
скорость
тела за равные промежутки
В
С
времени изменяется одинаково называется
0
t, с
• Дайте определение ускоренияД тела. Единицы ускорения в СИ.
1 2 3 4 5 6
• Опишите характер движения тела, если известно, что
v x < 0, ax > 0
v x > 0, аx > 0
• Опишите характер движения тела, пользуясь зависимостью vx = — 20 — 2t
• На каком участке перемещение тела наибольшее?
• Чему равен путь, пройденный любым телом за
первую секунду равноускоренного движения из состояния покоя?
Домашнее задание
• §§ 11, 13, 14
• Упр.
 3, №№ 2, 3
3, №№ 2, 3• График №3 ( в тетради)
Спасибо за работу !!!
Прямолинейное равноускоренное движение | Физика
1. Определение прямолинейного равноускоренного движения
Поставим опыт
Изучим, как скатывается шарик с наклонной плоскости. На рисунке 5.1 показаны последовательные положения шарика через равные промежутки времени.
Видно, что шарик движется неравномерно: пути, проходимые им за последовательные равные промежутки времени, увеличиваются. Следовательно, скорость шарика увеличивается.
Движение шарика, скатывающегося с наклонной плоскости, является примером прямолинейного равноускоренного движения. Такое движение вы уже изучали в курсе физики основной школы. Напомним его определение.
Прямолинейным равноускоренным движением называют прямолинейное движение, при котором скорость тела за любые равные промежутки времени изменяется на одну и ту же величину.
Прямолинейно равноускоренно может двигаться, например, автомобиль во время разгона (рис. 5.2, а). Однако непривычным может показаться то, что при торможении (рис. 5.2, б) автомобиль тоже может двигаться прямолинейно равноускоренно! Ведь в определении прямолинейного равноускоренного движения речь идет не об увеличении скорости, а только об ее изменении.
5.2, а). Однако непривычным может показаться то, что при торможении (рис. 5.2, б) автомобиль тоже может двигаться прямолинейно равноускоренно! Ведь в определении прямолинейного равноускоренного движения речь идет не об увеличении скорости, а только об ее изменении.
Дело в том, что понятие ускорения в физике шире, чем в разговорном языке. В обыденной речи под ускорением понимают обычно только увеличение скорости. Мы же будем говорить, что тело движется с ускорением всегда, когда скорость тела изменяется со временем любым образом (увеличивается или уменьшается по модулю, изменяется по направлению и т. п.).
Может возникнуть вопрос: почему мы уделяем внимание именно прямолинейному равноускоренному движению? Забегая немного вперед, выдадим «секрет»: именно с таким движением мы будем очень часто иметь дело при изучении механики.
Напомним (об этом уже говорилось в курсе физики основной школы), что под действием постоянной силы тело движется прямолинейно равноускоренно. (Если начальная скорость тела равна нулю или направлена вдоль линии действия силы.) А во многих задачах по механике рассматривается именно такая ситуация. Ниже мы рассмотрим подробно ее различные варианты.
(Если начальная скорость тела равна нулю или направлена вдоль линии действия силы.) А во многих задачах по механике рассматривается именно такая ситуация. Ниже мы рассмотрим подробно ее различные варианты.
2. Ускорение
В определении прямолинейного равноускоренного движения речь идет об изменении скорости. Как определяют изменение скорости?
Обозначим 0 скорость тела в начальный момент времени, а – скорость тела через промежуток времени t. Тогда изменение скорости за этот промежуток времени
Эту формулу можно переписать также в виде
На рисунке 5.3 показано, как найти вектор изменения скорости Δ в случае прямолинейного неравномерного движения.
? 1. Какому из рисунков 5.3 (а или б) соответствует увеличение скорости, а какому – уменьшение?
Введем теперь понятие ускорения.
Ускорением называют отношение изменения скорости Δ к промежутку времени Δt, за который произошло это изменение:
(Здесь в общем случае надо говорить о мгновенном ускорении, которое определяется с помощью достаточно малых промежутков времени – подобно тому, как мы определяли выше мгновенную скорость. При прямолинейном равноускоренном движении мгновенное ускорение постоянно.)
При прямолинейном равноускоренном движении мгновенное ускорение постоянно.)
Как следует из этого определения, ускорение – векторная величина. Она характеризует скорость изменения скорости. Единицей ускорения в СИ является 1 м/с2 (читают: «метр в секунду за секунду» или «метр делить на секунду в квадрате»). Если тело движется с таким по модулю ускорением в одном направлении, то его скорость каждую секунду увеличивается (или уменьшается!) на 1 м/с.
Когда тело падает, оно движется с ускорением, равным примерно 10 м/с2 (если можно пренебречь сопротивлением воздуха).
Рассмотрим теперь, при каком условии скорость тела увеличивается, а при каком – уменьшается. Из определения (3) следует, что
На рисунке 5.4 мы заменили (по сравнению с рисунком 5.3) Δ на равное ему выражение Δt.
Мы видим теперь, что скорость тела увеличивается, если ускорение направлено так же, как начальная скорость (рис. 5.4, а). Если же ускорение направлено противоположно скорости (рис. 5.4, б), то скорость тела уменьшается.
5.4, б), то скорость тела уменьшается.
? 2. На каком из рисунков 5.2 (а или б) ускорение автомобиля направлено влево?
Выберем начальный момент времени t0 = 0, тогда Δt = t – t0 = t – 0 = t. Поскольку Δ = – 0, из формулы (4) получаем
Направим ось x вдоль траектории движения тела. Тогда
vx = v0x + axt. (6)
Здесь vx – проекция скорости в момент времени t, v0x – проекция начальной скорости, ax – проекция ускорения.
В формуле (6) проекция начальной скорости v0x и проекция ускорения ax могут быть положительными и отрицательными. В зависимости от соотношения знаков v0x и ax модуль скорости тела будет увеличиваться или уменьшаться со временем.
Рассмотрим примеры.
? 3. Четыре автомобиля движутся вдоль оси x. В течение некоторого времени зависимость vx(t) выражается для них (в единицах СИ) формулами:
1) vx = 8 + 2t; 2) vx = 20 – 4t; 3) vx = –10 + t; 4) vx = –15 – 3t.
а) Чему равны проекции начальной скорости и ускорения каждого автомобиля?
б) Какие автомобили разгоняются, а какие – тормозят?
в) Скорость какого автомобиля наибольшая по модулю в момент времени t = 2 с? наименьшая?
Выполнив это задание, вы заметите, что скорость тела увеличивается по модулю, если проекция начальной скорости и проекция ускорения имеют одинаковые знаки (обе положительные или обе отрицательные).
Если же проекции начальной скорости и ускорения имеют разные знаки, то скорость тела сначала уменьшается по модулю. В некоторый момент скорость тела станет равной нулю, после чего (если ускорение останется прежним) направление скорости изменится на противоположное и модуль скорости тела начнет увеличиваться. Далее мы рассмотрим это на примере тела, брошенного вертикально вверх.
3. График зависимости скорости от времени
Из формулы (6) следует, что при прямолинейном равноускоренном движении проекция скорости vx линейно зависит от времени t. Поэтому график зависимости vx(t) – отрезок прямой.
На рисунке 5.5 изображены графики зависимости проекции скорости от времени для синего и красного автомобилей, движущихся вдоль оси x.
а) Какой из автомобилей тормозит? Чему равен модуль его ускорения?
б) У какого автомобиля модуль ускорения меньше? Чему он равен?
в) Запишите зависимость vx(t) для каждого автомобиля.
г) Используя эту запись, найдите момент времени, когда скорости автомобилей станут равными. Проверьте полученный ответ по приведенным графикам.
? 5. На рисунке 5.6 изображены графики зависимости проекции скорости от времени для тел, движущихся вдоль оси x.
а) Какие графики описывают движение тела, скорость которого все время увеличивается по модулю?
б) На каких графиках v0x и ax имеют разные знаки?
в) Какие графики описывают случаи, когда направление скорости тела изменяется на противоположное?
г) Начертите для всех изображенных случаев графики зависимости модуля скорости от времени.
? 6. Зависимость проекции скорости от времени для первого тела выражается в единицах СИ формулой v12 = 6 – Зt, а для второго – формулой v2x = 2 + t.
а) Изобразите графики vx(t) для каждого тела.
б) В какой момент скорости тел равны (по модулю и по направлению)?
в) В какие моменты скорости тел равны по модулю?
Дополнительные вопросы и задания
7. От платформы отправляется поезд на восток. В это же время у соседней платформы тормозит поезд, идущий на запад. Сделайте схематический рисунок, на котором покажите направления скорости и ускорения каждого поезда.
8. Как направлено ускорение лифта, когда он:
а) начинает двигаться с первого этажа?
б) тормозит на верхнем этаже?
в) тормозит на третьем этаже, двигаясь вниз?
г) начинает движение на третьем этаже, двигаясь вверх?
Движение лифта при разгоне и торможении считайте равноускоренным.
9. Автомобиль трогается с места в направлении на север и набирает скорость 72 км/ч за 40 с. Движение автомобиля считайте прямолинейным равноускоренным.
а) Как направлено ускорение автомобиля?
б) Чему равно ускорение автомобиля по модулю?
в) Начертите график зависимости проекции скорости автомобиля от времени.
г) Какой была скорость автомобиля через 10 с после начала движения?
ФИЗИКОН Ax, эта физика, физика, физика
На моем столе четыре диска. На них три программы: «Физика в картинках», «Открытая физика» (разросшаяся до двух частей — переработанная и дополненная «Физика в картинках») и «Репетитор». Мысленно я уже разбил диски на две группы: в первой — «Физика в картинках» и «Открытая физика», во второй — «Репетитор», не имеющий пока продолжения.
«Физика в картинках«
Весь материал на диске разбит на небольшие темы, которые образуют шесть разделов. Пять из них по разделам курса: «Механика», «Тепловая физика», «Электромагнетизм», «Оптика» и «Квантовая физика». Шестой — описания классических физических экспериментов, представленные в виде мультфильмов. До современных видеофильмов эти мультфильмы, пожалуй, не дотягивают, но в качестве иллюстрации вполне приемлемы, по крайней мере, с картинками в учебнике их просто не сравнить.
По каждой теме имеется возможность провести физический опыт, основанный на вполне реальном физическом процессе, например беге человека, отражении луча света, колебании струны или полете ракеты. Во время опыта на экране изображаются в виде графиков параметры процесса: ускорение тела, угол его поворота, температура и др. Ваше участие в происходящем заключается в том, что сначала вы должны задать условия проведения опыта, а затем наблюдать за течением процесса и изменениями его параметров. Демонстрация опыта сопровождается теоретическим материалом в текстовой форме с основными определениями и формулами. Он написан неплохо, однако иногда в, казалось бы, знакомой теме вы обнаруживаете понятия из курса старших классов или, наоборот, не можете найти привычных определений. К счастью, такие случаи редки.
Во время опыта на экране изображаются в виде графиков параметры процесса: ускорение тела, угол его поворота, температура и др. Ваше участие в происходящем заключается в том, что сначала вы должны задать условия проведения опыта, а затем наблюдать за течением процесса и изменениями его параметров. Демонстрация опыта сопровождается теоретическим материалом в текстовой форме с основными определениями и формулами. Он написан неплохо, однако иногда в, казалось бы, знакомой теме вы обнаруживаете понятия из курса старших классов или, наоборот, не можете найти привычных определений. К счастью, такие случаи редки.
В одном из разделов программы приведены вопросы. Вы можете проверить себя, отвечая на них самостоятельно, или заглянуть в ответы.
Выполнена «Физика в картинках» достаточно красиво, в основу ее положена интересная идея, ее интерфейс логичен и оригинален. Могу сказать: она мне понравилась хотя бы потому, что запускается в среде DOS, не требуя Windows.
«Открытая физика«
«Открытая физика» — расширенный мультимедийный вариант «Физики в картинках». Здесь можно услышать теорию, посмотреть видеофрагменты (некоторые из них действительно стоит посмотреть). По сравнению с предыдущей версией увеличилось количество тем, появились новые опыты, а некоторые из ранее присутствовавших в «Физике в картинках» выполнены более качественно. В каждой теме для самоконтроля есть несложная задача.
Здесь можно услышать теорию, посмотреть видеофрагменты (некоторые из них действительно стоит посмотреть). По сравнению с предыдущей версией увеличилось количество тем, появились новые опыты, а некоторые из ранее присутствовавших в «Физике в картинках» выполнены более качественно. В каждой теме для самоконтроля есть несложная задача.
Можно также установить украинский интерфейс.
В целом это все та же «Физика в картинках», только доработанная. Текст теории даже по сравнению со школьным учебником написан достаточно сухо, а с научно-популярными изданиями его и вовсе сравнивать не стоит. А если пользователю хочется провести какой-нибудь опыт, то, конечно, гораздо интереснее уйти от вражеского истребителя с помощью фигуры высшего пилотажа.
Впрочем, «Открытая физика» потому, наверное, и «открытая», что предусматривает участие учителя или использование какого-нибудь другого справочного пособия.
Достоинство этих программ заключается хотя бы уже в том, что, просмотрев их даже из простого любопытства, вы как бы повторите то, что учили ранее, а возможно и лучше поймете. Конечно же, этот материал поможет вам подготовиться к зачетам или экзамена особенно если дополнить его учебниками и конспектами лекций. А вот начинать учить физику с помощью этих программ, скорее всего, не стоит.
Конечно же, этот материал поможет вам подготовиться к зачетам или экзамена особенно если дополнить его учебниками и конспектами лекций. А вот начинать учить физику с помощью этих программ, скорее всего, не стоит.
«Репетитор«
Сразу же после запуска «Репетитора» вы поймете, как он отличается от рассмотренных ранее программ. Вместе с воображаемой видеокамерой вы как бы облетаете со всех сторон виртуальный замок, а затем влетаете в ворота. Красиво. Каждая башня замка соответствует одному из разделов курса физики. Затем экран чернеет и перед вами предстает раскрытая книга, по-видимому учебник. На правой странице — знакомый по заставке замок, изображение которого сменяется графиками и мультфильмами, а на левой — оглавление и собственно текст. Справа от книги располагается вертикальный ряд значков: оглавление, формулы, таблицы, исторические сведения, временный выход, выход.
Представленный материал разбит на пять основных разделов, а они в свою очередь делятся на темы. В каждой теме есть теоретическая часть — несколько страниц текста с отдельными словами, выделенными синим цветом. Щелкнув на них, можно вызвать график, параметры которого в определенных случаях можно менять, короткий мультфильм или перейти в другую тему программы. Есть в программе и озвученные видеофрагменты, сопровождаемые озвученным текстом, однако для получения доступа к какому-либо из них нужно войти в тему, с которой он связан. Текст теории не озвучен. Если вы интересуетесь жизнью великих ученых или вам просто нужно сделать доклад о ком-нибудь из них, то к вашим услугам библиотека, содержащая подобные сведения.
В каждой теме есть теоретическая часть — несколько страниц текста с отдельными словами, выделенными синим цветом. Щелкнув на них, можно вызвать график, параметры которого в определенных случаях можно менять, короткий мультфильм или перейти в другую тему программы. Есть в программе и озвученные видеофрагменты, сопровождаемые озвученным текстом, однако для получения доступа к какому-либо из них нужно войти в тему, с которой он связан. Текст теории не озвучен. Если вы интересуетесь жизнью великих ученых или вам просто нужно сделать доклад о ком-нибудь из них, то к вашим услугам библиотека, содержащая подобные сведения.
В отдельные пункты меню вынесены основные формулы и большое количество табличных данных. Итак, перед вами неплохо продуманная программа, включающая в себя обширный материал. Однако по мере работы с ней выявляются ее недостатки.
Во-первых, низкое качество видеофрагментов. Поклонникам Doom оно напомнит их любимую игру: те же разномастные переливающиеся квадратики. Уровень видео «Репетитора» выше, чем у Doom, но сходство улавливается легко.
Уровень видео «Репетитора» выше, чем у Doom, но сходство улавливается легко.
Во-вторых, мелкий, трудный для чтения текст, что особенно неприятно, так как текста много и вряд ли при работе с такой программой зрение пользователя будет улучшаться.
В-третьих, практически полное отсутствие задач и вопросов.
Таким образом, все, что отличат данную программу от книги в лучшую сторону, — это подвижные и озвученные иллюстрации к некоторым физическим явлениям и наличие ссылок, по которым можно перемещаться с помощью одного щелчка мыши. В остальном «Репетитор» — самый обычный справочник, даже по внешнему виду. Только читается тяжело.
Физика в картинках
В программе приведен ряд физических опытов, которые вы сможете осуществить на своем компьютере. В процессе эксперимента параметры можно изменять, что помогает лучше уяснить его смысл. Программа охватывает основные темы школьного курса физики. Существует версия на дискетах.
Системные требования: 286ХТ/АТ, 640-Кбайт ОЗУ. 2Х-дисковод CD-ROM (для версии на дискетах не требуется).
2Х-дисковод CD-ROM (для версии на дискетах не требуется).
Программа работает в среде DOS.
Цена: 18 долл.
«Физикон», тел. в Москве: (095) 408-77-72
Открытая физика
Усовершенствованная версия «Физики в картинках». Больше дикторского текста и видеофрагментов. Интерфейс этой версии интересией, изображения опытов лучше проработаны, да и самих опытов стало больше.
Системные требования: 386SX, 4-Мбайт ОЗУ, 5 Мбайт свободного пространства на жестком диске, 2Х-дисковод CD-ROM, SVGA видеоадаптер (800Х600 точек при отображении 32 768 цветов), звуковая плата, мышь. Программа работает в среде Windows З.х, Windows 95 или Windows NT.
Цена: 22 долл.
«Физикон», тел. в Москве: (095) 408-77-72
Репетитор
Справочник по всем разделам школьного курса физики. Теоретический материал дополнен видеофрагментами и компьютерными мультфильмами. Задач практически нет. Текст мелкий, трудночитаемый.
Системные требования: 48бDX-2-66, 8-Мбайт ОЗУ, 2Х-дисковод CD-ROM, SVGA-видеоадаптер с установленной памятью 1 Мбайт, звуковая плата, мышь. Программа работает в среде Windows 95.
Цена: 36 долл.
«1С», тел. в Москве: (095) 737-92-57
Павел Киселев
ОБ АВТОРЕ
Павел Киселев — ученик 10-го класса,
эксперт Детской тестовой лаборатории журнала «Мир ПК».
Детская тестовая лаборатория журнала «Мир ПК»
благодарит фирму «Вист» за техническую поддержку.
Веб-сайт кабинета физики
Задание VP5: Компоненты вектора
Цели:
- Студент должен уметь определять векторные компоненты и описывать их значение и важность.
- Студент должен уметь использовать графические и тригонометрические методы для определения компонентов заданного вектора.
Чтение:
Учебный класс физики, Векторы и движение в двух измерениях Модуль, Урок 1, Часть dУчебный класс физики, раздел «Векторы и движение в двух измерениях», урок 1, часть e
Компоненты вектора лучше всего определить как . | |
Определение Компонент вектора Компонент вектора — это проекция вектора на горизонтальную или вертикальную ось. | |
Что такое компонент вектора? |
Компоненты вектора важны в физике, потому что они описывают … . | |
Определение Векторный компонент Компонент вектора — это проекция вектора на горизонтальную или вертикальную ось. | |
Вектор, направленный на северо-запад, имеет компоненты, направленные на север и запад. | |
Каково значение векторной компоненты? Что такое компонент вектора? |
Вектор А разлагается на две составляющие — А x и A y . | |
Определение Векторный компонент Компонент вектора — это проекция вектора на горизонтальную или вертикальную ось. | |
Компоненты вектора часто представляются на диаграмме путем построения прямоугольного треугольника вокруг вектора таким образом, что вектор является гипотенузой прямоугольного треугольника. Компоненты являются катетами прямоугольного треугольника. (Вероятно, вы уже видели такие диаграммы и попытаетесь сделать набросок сейчас.) Если вектор является северо-западным вектором, то его компоненты простираются на запад и север. Когда эти два компонента складываются вместе как векторы с использованием метода «голова к хвосту», тогда результатом будет гипотенуза прямоугольного треугольника — та же самая гипотенуза, из которой были найдены компоненты. | |
Что такое компонент вектора? Каково значение векторной компоненты? |
Рассмотрим вектор ниже. Его x- и y-компоненты лучше всего представлены … . | |
Нажмите кнопку ниже, чтобы воспроизвести аудиофайл в отдельном окне. Ваш браузер не поддерживает аудио элементы. Пожалуйста, скачайте и посмотрите здесь. | |
Определение Компонент вектора Компонент вектора — это проекция вектора на горизонтальную или вертикальную ось. | |
Математически компонент — это просто проекция вектора на ось. Чтобы определить компоненты с помощью диаграммы, сначала нарисуйте вектор. Затем нарисуйте оси координат x-y в конце вектора. От стрелки вектора нарисуйте контрольные линии поперек каждой из осей координат так, чтобы линии пересекались с осями перпендикулярно к ней. Компонент x растягивается вдоль оси x от конца вектора до места, где опорная линия пересекается с осью x. Y-компонента простирается вдоль оси y от хвоста вектора до места, где опорная линия пересекается с осью y. | |
Как можно определить направление x- и y-компонент данного вектора? Что такое компонент вектора? |
Рассмотрим вектор ниже. | |
Нажмите кнопку ниже, чтобы воспроизвести аудиофайл в отдельном окне. Ваш браузер не поддерживает аудио элементы. Пожалуйста, скачайте и посмотрите здесь. | |
Определение Векторный компонент Компонент вектора — это проекция вектора на горизонтальную или вертикальную ось. | |
Математически компонент — это просто проекция вектора на ось. Чтобы определить компоненты с помощью диаграммы, сначала нарисуйте вектор. Затем нарисуйте оси координат x-y в конце вектора. От стрелки вектора нарисуйте контрольные линии через каждую из осей координат так, чтобы линии пересекались с осями перпендикулярно к ней. | |
Как можно определить направление x- и y-компонент данного вектора? Что такое компонент вектора? |
Рассмотрим вектор ниже. Его x- и y-компоненты лучше всего представлены … . | |
Нажмите кнопку ниже, чтобы воспроизвести аудиофайл в отдельном окне. Ваш браузер не поддерживает аудио элементы. Пожалуйста, скачайте и посмотрите здесь. | |
Определение Векторный компонент Компонент вектора — это проекция вектора на горизонтальную или вертикальную ось. | |
Математически компонент — это просто проекция вектора на ось. Чтобы определить компоненты с помощью диаграммы, сначала нарисуйте вектор. Затем нарисуйте оси координат x-y в конце вектора. От стрелки вектора нарисуйте контрольные линии через каждую из осей координат так, чтобы линии пересекались с осями перпендикулярно к ней. Компонент x растягивается вдоль оси x от конца вектора до места, где опорная линия пересекается с осью x. Y-компонента простирается вдоль оси y от хвоста вектора до места, где опорная линия пересекается с осью y. | |
Как можно определить направление x- и y-компонент данного вектора? Что такое компонент вектора? |
Рассмотрим вектор ниже. | |
Нажмите кнопку ниже, чтобы воспроизвести аудиофайл в отдельном окне. Ваш браузер не поддерживает аудио элементы. Пожалуйста, скачайте и посмотрите здесь. | |
Определение Векторный компонент Компонент вектора — это проекция вектора на горизонтальную или вертикальную ось. | |
Математически компонент — это просто проекция вектора на ось. Чтобы определить компоненты с помощью диаграммы, сначала нарисуйте вектор. Затем нарисуйте оси координат x-y в конце вектора. От стрелки вектора нарисуйте контрольные линии через каждую из осей координат так, чтобы линии пересекались с осями перпендикулярно к ней. | |
Как можно определить направление x- и y-компонент данного вектора? Что такое компонент вектора? |
Рассмотрим вектор, показанный ниже. Величина и направление вектора известны. Для тригонометрического определения x-компоненты будет использоваться функция ____; а для тригонометрического определения компонента y будет использоваться функция ____. | |
Определение Векторный компонент А 9Компонент вектора 0045 — это проекция вектора на горизонтальную или вертикальную ось. | |
Компоненты вектора часто представляются на диаграмме путем построения прямоугольного треугольника вокруг вектора таким образом, что вектор является гипотенузой прямоугольного треугольника. Компоненты являются катетами прямоугольного треугольника. (Вероятно, вы видели такие диаграммы и теперь можете попытаться нарисовать одну из них.) Если вектор является северо-восточным вектором, то его компоненты простираются на восток и север. Восточная и северная составляющие — это просто восточная и северная стороны треугольника, который был создан из северо-восточного вектора. Тригонометрические функции можно использовать для определения точной величины катетов этих треугольников. Если угол — это угол между восточной осью и вектором, то катет, примыкающий к углу, является x-компонентой, а катет, противоположный углу, является y-компонентой. Таким образом, функция косинуса используется для вычисления x-компоненты, а функция синуса используется для вычисления y-компоненты. | |
СОХ КАХ ТОА Тригонометрические функции синуса, косинуса и тангенса можно использовать для выражения отношения между углом прямоугольного треугольника и длинами прилежащей стороны, противолежащей стороны и гипотенузы. Смысл трех функций: | |
Как можно использовать тригонометрические функции для определения величины x- и y-компонент данного вектора? Что такое компонент вектора? |
Сила 50 Н приложена под углом 30 градусов (иногда это называют 30 градусами к северу от востока). | |
Математически компонент вектора — это проекция вектора на оси x и y. С точки зрения физики, компонент вектора описывает действие вектора в заданном направлении. Северо-восточный вектор силы толкает или тянет объект как на север, так и на восток. Вместе эти два компонента вектора являются равноценной заменой самого вектора. Фактический вектор можно заменить двумя его компонентами, и результат будет таким же. Чтобы правильно ответить на этот вопрос, просто определите компоненты заданного вектора (см. Подумай об этом раздел ниже). | |
Компоненты вектора часто представляются на диаграмме путем построения прямоугольного треугольника вокруг вектора таким образом, что вектор является гипотенузой прямоугольного треугольника. Компоненты являются катетами прямоугольного треугольника. Тригонометрические функции можно использовать для определения точной величины катетов этих треугольников. Если угол — это угол между восточной осью и вектором, то катет, примыкающий к углу, является x-компонентой, а катет, противоположный углу, является y-компонентой. Таким образом, функция косинуса используется для вычисления x-компоненты, а функция синуса используется для вычисления y-компоненты. См. раздел Math Magic ниже. | |
СОХ КАХ ТОА Тригонометрические функции синуса, косинуса и тангенса можно использовать для выражения отношения между углом прямоугольного треугольника и длинами прилежащей стороны, противолежащей стороны и гипотенузы. | |
Как можно использовать тригонометрические функции для определения величины x- и y-компонент данного вектора? Каково значение векторной компоненты? |
Самолет летит на северо-запад из аэропорта О’Хара в Чикаго со скоростью 400 км/ч в направлении 150 градусов (т. е. 30 градусов к северу от запада). Канадская граница находится на расстоянии . | |
Нажмите кнопку ниже, чтобы воспроизвести аудиофайл в отдельном окне. Ваш браузер не поддерживает аудио элементы. Пожалуйста, скачайте и посмотрите здесь. | |
Компонент вектора описывает действие вектора в заданном направлении. Северо-западный вектор, такой как этот вектор скорости, имеет как северную, так и западную составляющую. Северная составляющая здесь очень полезна, потому что она описывает влияние скорости самолета в северном направлении. Если бы величина северной составляющей была 100 км/ч, северной (это не так!), то мы знали бы, что самолет проходит 100 км на север за один час. Ценность знания этой северной составляющей скорости состоит в том, что ее можно использовать, чтобы связать расстояние, пройденное на север, со временем путешествия на север. Наилучшая стратегия для ответа на этот вопрос включает использование SOH CAH TOA (см. раздел Math Magic ниже) для определения северной составляющей скорости, а затем использование отношения d-v-t для определения времени пересечения границы. | |
Компоненты вектора часто представляются на диаграмме путем построения прямоугольного треугольника вокруг вектора таким образом, что вектор является гипотенузой прямоугольного треугольника. Компоненты являются катетами прямоугольного треугольника. (Вероятно, вы уже видели такие диаграммы и попытаетесь сделать набросок сейчас.) Если вектор является северо-западным вектором, то его компоненты простираются на запад и север. Восточная и северная составляющие — это просто восточная и северная стороны треугольника, который был создан из северо-западного вектора. Тригонометрические функции можно использовать для определения точной величины катетов этих треугольников. Если угол представляет собой угол поворота против часовой стрелки от восточной оси и вектора, то компонент x можно рассчитать с помощью функции косинуса; Y-компонента может быть вычислена с помощью функции синуса. где = угол поворота против часовой стрелки вектора А с востока | |
Связь между скоростью ( v ), расстоянием ( d ) и временем ( t ) выражается уравнением | |
Определение числа Векторный компонент Компонент вектора — это проекция вектора на горизонтальную или вертикальную ось. | |
Как можно использовать компонент вектора скорости для определения влияния скорости в направлении компонента? Как можно использовать тригонометрические функции для определения величины x- и y-компонент данного вектора? Каково значение векторной компоненты? |
Подписывайтесь на нас
Векторы Практические решения — physics-prep.comПрактические задачи: векторные решения 1. (простой) Вектор A представляет 5,0 м смещения на восток. Если вектор B представляет 10,0 м смещения на север, найдите сумму двух перемещений ( Р ). 3. (умеренная) Автомобиль движется на 150,0 м под углом 63° к «северо-востоку» (это просто означает 63° от оси x). ). Некоторое время он остается в покое, а затем перемещается на 300 м под углом 34° к юго-западу (это означает, что он находится на расстоянии 214° от оси X). Найдите полное перемещение автомобиля.
а) Первая сила имеет величину 10 Н и действует на восток. Вторая сила имеет величину 4 Н и действует на запад. 5. (умеренная сила) Найдите описанную здесь систему уравновешивающих сил для:
| A x -3 J ) A x -3 J ) 0 A x -3 J ) 0 A x -3 J ) B = -6 K + 4 J — 30 K — 12 I + 15 J + I ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
8. (умеренная) направление и вектор силы F 2 имеет величину 60 Н, направленную в направлении +x, определите скалярное произведение ( F 1 • F 2 ) и векторное произведение ( F ) 1 x F 2 ). Как изменились бы ответы, если бы векторы поменялись местами в уравнениях?
Как изменились бы ответы, если бы векторы поменялись местами в уравнениях?
F 1 • F 2 = (F 1 )(F 2 )cos90 = (30)(60)(0) = 0, поскольку произведение точек
не имеет значения векторы находятся под углом 90° друг к другу)
| F 1 x F 2 | = (30)(60)sin 90 = 1800 N 2
(величина векторного произведения)
Чтобы определить направление, используйте RHR:
Пальцы в направлении -z
Изгиб в направлении +x
-у.
(Перекрестное произведение указывает на экран вниз)
Ответ скалярного произведения не изменится, если векторы поменяются местами, но векторное произведение будет иметь противоположное направление (+y) при сохранении той же величины (1800 м 2 ).
9. (умеренное) Два смещения с величинами 10 м и 12 м могут быть объединены для формирования результирующих векторов с множеством различных величин. Какая из следующих величин может быть результатом этих двух смещений? 22 м, 2 м, 30,9 м, 15,6 м. Какой угол существует для возможных равнодействующих между первоначальными смещениями?
Какая из следующих величин может быть результатом этих двух смещений? 22 м, 2 м, 30,9 м, 15,6 м. Какой угол существует для возможных равнодействующих между первоначальными смещениями?
Если смещения параллельны (угол между ними 0°): R = 22 м
Если смещения антипараллельны (угол между ними 180°): R = 2 м
Если смещения перпендикулярны (угол 90° между ними) : R = 15,6 м
Результат больше 22 м невозможен.
10. (умеренная) Велосипедная шина (Радиус = R = 0,4 м) катится по земле (без проскальзывания) на три четверти оборота. Рассмотрим точку на шине, которая изначально касалась земли. На какое расстояние он сместился от своего исходного положения?
Точка перемещается на три четверти окружности (это расстояние, пройденное центром системы) плюс 1 радиус вдоль земли (за пределами места, где движется центральная точка) в направлении x и 1 радиус вверх в направлении y .
РЕЗУЛЬТАТ = [(0,75) π (2R)+ R] I + R J
. ) ½ = 2,31 м
) ½ = 2,31 м
11. (умеренная) Учащийся несет кусок глины от двери первого этажа (на первом этаже) небоскреба (на Грант-стрит) к лифту, находящемуся на расстоянии 24 м. Затем она поднимается на лифте на 11-й этаж. Наконец, она выходит из лифта и несет глину 12 м обратно в сторону Грант-стрит. Определить полное перемещение глины, если каждый этаж находится на 4,2 м выше нижнего этажа.
| Рабочий объем | Величина (м) | Угол (°) | х-комп (м) | у-комп (м) |
| 1 | 24 | 0 | 24 | 0 |
| 2 | 42 | 90 | 0 | 42 |
| 3 | 12 | 180 | -12 | 0 |
| Р | 44 | 74 | 12 | 42 |
Лаборатория 1 — Таблица сил
Введение
Все измеримые величины могут быть классифицированы либо как скаляр, либо как вектор. У скаляра есть только величина, а у вектора есть и величина, и направление. Примерами скалярных величин являются количество учеников в классе, масса объекта или скорость объекта, и это лишь некоторые из них. Скорость, сила и ускорение являются примерами векторных величин. Утверждение «автомобиль движется со скоростью 60 миль в час» говорит нам о том, как быстро движется автомобиль, но не о том, в каком направлении он движется. В этом случае мы знаем, что скорость автомобиля равна 60 км/ч. С другой стороны, утверждение «автомобиль, движущийся со скоростью 60 миль в час строго на восток» дает нам не только скорость автомобиля, но и направление. В этом случае скорость автомобиля составляет 60 миль в час строго на восток, и это векторная величина. В отличие от скалярных величин, которые складываются арифметически, сложение векторных величин включает в себя как величину, так и направление. В этой лабораторной работе мы будем использовать таблицу сил для определения равнодействующей двух или более векторов сил и научимся складывать векторы, используя как графические, так и аналитические методы.
У скаляра есть только величина, а у вектора есть и величина, и направление. Примерами скалярных величин являются количество учеников в классе, масса объекта или скорость объекта, и это лишь некоторые из них. Скорость, сила и ускорение являются примерами векторных величин. Утверждение «автомобиль движется со скоростью 60 миль в час» говорит нам о том, как быстро движется автомобиль, но не о том, в каком направлении он движется. В этом случае мы знаем, что скорость автомобиля равна 60 км/ч. С другой стороны, утверждение «автомобиль, движущийся со скоростью 60 миль в час строго на восток» дает нам не только скорость автомобиля, но и направление. В этом случае скорость автомобиля составляет 60 миль в час строго на восток, и это векторная величина. В отличие от скалярных величин, которые складываются арифметически, сложение векторных величин включает в себя как величину, так и направление. В этой лабораторной работе мы будем использовать таблицу сил для определения равнодействующей двух или более векторов сил и научимся складывать векторы, используя как графические, так и аналитические методы.
Обсуждение принципов
Векторное представление
Как упоминалось выше, векторная величина имеет как величину, так и направление. Вектор обычно представляется стрелкой, где направление стрелки представляет собой направление вектора, а длина стрелки представляет величину вектора. В трехмерном пространстве вектор, направленный за пределы страницы (или вдоль положительной оси z ), представлен (кругом с точкой внутри него), а вектор, направленный внутрь страницы (или вдоль отрицательной оси z -ось) обозначается (кругом со знаком × внутри). В математических уравнениях вектор представляется как
A
. В некоторых учебниках вектор представлен жирной буквой A . Отрицательным вектором
A
является вектор той же длины, но с направлением, противоположным направлению
A
. См. рис. 1 ниже.
См. рис. 1 ниже.
Рисунок 1 : Векторы в виде стрелок
Декартова система координат используется для графического представления векторов. Хвост вектора помещается в начало координат, а направление вектора определяется углом θ (тета) между положительной осью x и вектором, как показано на рис. 2.
Рисунок 2 : Графическое представление вектора
Компоненты векторов
Важным приемом математической работы с векторами является их разбиение на 9 частей.Компоненты 1967 x и и . В этом примере мы рассмотрим вектор положения
A
, направленный под углом 30° к оси + x и имеющий величину 8,0 миль. Из головы вектора проведите линию, перпендикулярную оси x , и вторую линию, перпендикулярную оси y . Мы называем эти линии проекциями вектора на оси x и y . Проекция вектора на 9Ось 1967 y дает величину компонента вектора x (зеленая линия на рис. 3 ниже), а проекция вектора на ось x дает величину компонента y . (красная линия на рис. 3).
Мы называем эти линии проекциями вектора на оси x и y . Проекция вектора на 9Ось 1967 y дает величину компонента вектора x (зеленая линия на рис. 3 ниже), а проекция вектора на ось x дает величину компонента y . (красная линия на рис. 3).
Рисунок 3 : Разбиение вектора на компоненты x и y
Обратите внимание, что зеленые и красные линии на диаграмме выше образуют две стороны прямоугольника с вектором в качестве диагонали прямоугольника. Мы также можем посмотреть на описанную выше ситуацию двумя другими способами, как показано на рис. 4.
Рисунок 4 : Представление компонентов вектора
На рис. 4а у нас есть прямоугольный треугольник, в котором вектор является гипотенузой, сторона, параллельная оси x (зеленая стрелка), является x -компонентой вектора, а сторона параллельна y -ось (красная стрелка) — это y -компонент вектора. Рисунок 4b математически эквивалентен рис. 4a, но теперь
Рисунок 4b математически эквивалентен рис. 4a, но теперь
A y
рисуется вдоль оси y .
Нахождение компонентов по величине и направлению вектора
Мы знаем направления векторов
A x
и
A y
, но чтобы найти их величины, нам нужно использовать некоторые тригонометрические тождества. На рис. 5 гипотенуза представляет модуль вектора
A
, а две другие стороны прямоугольного треугольника представляют x и y компоненты вектора
A
.
Рисунок 5 : Нахождение компонентов вектора
Для любого прямоугольного треугольника справедливы следующие тригонометрические тождества.
(1)
COS θ =
| Прилегающая сторона |
| Гипотенуза |
(2)
SIN
(2)
SIN
(2)
SIN .
1111118.0032
Здесь смежная сторона относится к стороне, примыкающей к углу θ , а противоположная сторона относится к стороне, противоположной углу θ . Рассмотрим установку на рис. 5а. Используя определения в уравнениях.
(1)cos θ =
| смежная сторона |
| гипотенуза |
и
(2) sin01042 =| противоположная сторона |
| гипотенуза |
, имеем
(3)
COS θ = или A x = A COS θ
(4)
SIN θ = или A Y = A SIN θ = или A Y = A SIN θ = или A Y = A SIN θ = Y = A SIN θ 9042
 Однако на фиг. 5b угол θ определен иначе. В таком случае
Однако на фиг. 5b угол θ определен иначе. В таком случае( 5 )
sin θ = или A x = A sin θ
( 6 )
cos θ = или A y = A cos θ
Распространенной ошибкой является предположение, что
A x
всегда является компонентом косинуса, а
A y
всегда является компонентом синуса. Однако это будет зависеть от того, какой из двух углов прямоугольного треугольника определяется как θ . Обратите внимание, что
A x
примыкает к углу θ на рис. 5а, а на рис. 5б
A y
примыкает к углу θ . На рис. 3 звездная величина
A
составляет 8,0 миль, а ее направление на 30° выше оси + x . Таким образом, вы находите величины
Таким образом, вы находите величины
A x
и
A y
следующим образом:
( 7 )
A x = A cos θ = 8,0 миль * cos(30°) = 6,9 миль
( 8 )
A y = A sin θ = 8,0 миль * sin(30°) = 4 мили
Другими словами, если бы вы шли пешком, вы могли бы пройти 6,9 мили строго на восток (вдоль оси + x ), а затем 4 мили на север (вдоль оси + y ). Это привело бы вас к тому же месту назначения, если бы вы прошли 8 миль в направлении, которое составляет 30° от оси + x -.
Нахождение модуля и направления вектора по компонентам
Если вы не знаете величину или направление вектора, но знаете расстояния, пройденные в направлениях x и y , вы можете использовать теорему Пифагора, чтобы найти гипотенузу, то есть общее пройденное расстояние.
( 9 )
A 2 = A x 2 + A y 2 или A =
| А x 2 + А у 2 |
Направление вектора можно найти с помощью одного из следующих уравнений.
( 10 )
θ = sin −1
( 11 )
θ = cos −1
( 12 )
θ = tan −1
Some Basic Properties of Vectors
Два вектора равны, если они имеют одинаковую величину и направление. Итак, на бумаге вы можете переместить вектор в другое место, но пока вы сохраняете ту же длину и ориентацию стрелки, два вектора будут равны. На рис. 6а два вектора
Итак, на бумаге вы можете переместить вектор в другое место, но пока вы сохраняете ту же длину и ориентацию стрелки, два вектора будут равны. На рис. 6а два вектора
A
и
B
имеют одинаковую длину и ориентацию. Негатив вектора имеет ту же длину, но с обратным направлением, как показано на рис. 6b. Вектор, умноженный на скаляр, будет вектором того же направления, что и исходный вектор, но с другой величиной. На рис. 6с p — это скаляр. Вектор
B
имеет то же направление, что и
A
, но длиннее в 9 раз.1967 p с p больше 1. Если бы p было меньше 1, то
B
было бы короче, чем
A
.
Рисунок 6 : Свойства вектора
Графический метод сложения векторов
Рассмотрим два вектора
A
и
B
, ориентированные, как показано на рис. 7. Нам нужно найти сумму и разность двух векторов. В отличие от добавления скалярных величин, в этом случае нам нужно учитывать как величину, так и направление.
Рисунок 7 : Два вектора
Чтобы добавить два вектора, сдвиньте второй вектор так, чтобы его хвост оказался в начале первого вектора. Сумма двух векторов представляет собой вектор, проведенный из хвоста первого вектора в начало второго вектора. На рис. 8а
B
перемещается так, что его хвост находится в голове
A
. Обратите внимание, что направление
Обратите внимание, что направление
B
не меняется. Красная стрелка дает сумму
Р = А + В
. Сложение является коммутативным, поэтому вы получите тот же результат, переместив
A
в начало числа
B
. Чтобы найти разность двух векторов, мы можем взять отрицательное значение второго вектора и добавить его к первому вектору, выполнив шаги, описанные выше для сложения. Другими словами,
А — В = А + (-В)
. Это показано на рис. 8b.
Рисунок 8 : Сумма и разность двух векторов
Аналитический метод сложения векторов
Сложение или вычитание векторов включает в себя разбиение векторов на компоненты, а затем выполнение сложения или вычитания компонентов x и y по отдельности.
(13)
R x = A x + B x
(14)
R Y = A Y + B = Y + B Y = A Y + B Y = A Y + B = Y + B = Y + B = Y + B = Y + B = Y0012 Теперь, используя уравнения. A 2 = A x 2 + A y 2 or A = и θ = TAN -1 Р . Этот процесс будет таким же, если вы добавляете более двух векторов или вычитаете векторы. In Fig. 5a, A x = 1 and B x = 3 giving A x + B x = 4; A y = −3 и B y = 2 дает A y + B 4 y = 1901. Эти значения согласуются с компонентами x и y красной стрелки на рис. 5а. В случае вычитания А х — В х = -2; А г — В г = -5 . Эти значения согласуются с компонентами x и y красной стрелки на рис. В этой лабораторной работе вы будете иметь дело с векторами силы. В дополнение к общим свойствам векторов, обсуждавшимся до сих пор в этой лабораторной работе, следующие определения будут полезны при работе с этой лабораторной работой. Векторная сумма двух или более сил равна результат . Результирующий может, по сути, заменить отдельные векторы. уравновешенных набора сил — это сила, необходимая для удержания системы в равновесии. Она равна и противоположна равнодействующей совокупности сил. Цель этого эксперимента состоит в том, чтобы найти равновесие одной или нескольких известных сил с помощью таблицы сил и сравнить результаты с результатами, полученными аналитическим методом. Имея два вектора силы, вы определите третью силу, которая установит равновесие в системе. Рисунок 9 : Таблица сил Висячие массы будут создавать силу натяжения в каждой струне. Массы прямо пропорциональны гравитационной силе (о которой вы узнаете позже в курсе). Сила натяжения каждой струны равна силе тяжести. Рисунок 10 : Таблица сил с осями 1 Воспользуйтесь пузырьковым уровнем, чтобы проверить горизонтальность круглой платформы. При необходимости используйте регулировочные винты для выполнения необходимых регулировок. 2 Вам даны два груза массой 150 г, которые нужно расположить под углами 60° и 300°. Помните, что подвески для гирь имеют массу 50 г каждая, и это должно быть включено как часть массы для подвешивания. Вы определите величину (в ньютонах) и угол третьей силы, необходимые для уравновешивания сил этих двух масс. 3 Представьте эти силы в виде векторов на диаграмме в рабочем листе. Обязательно включите оси. Каждый вектор на диаграмме должен быть нарисован так, чтобы чем больше вектор, тем большую силу он представлял. 4 Вычислите компоненты x и y (с точностью до тысячной ньютона) и введите эти значения в Таблицу данных 1 на рабочем листе. 5 г. Найдите компоненты x и y равнодействующей двух векторов и введите эти значения в Таблицу данных 1 на рабочем листе. 6 Теперь вычислите компоненты равновесия этих двух векторов x и y и введите эти значения в рабочий лист. 7 Используя уравнения А 2 = А х 2 + А у 2 or A = and θ = tan −1 вычислить величину и угол равновесия. Введите эти значения в рабочий лист. Это расчетное значение третьей силы. 8 г. Добавьте этот вектор на диаграмму, чтобы представить третью силу. 9 Расположите третью струну под углом, который вы определили в шаге 6, и повесьте груз (включая подвесной груз), соответствующий расчетной третьей силе, представляющей третью силу. Отрегулируйте (при необходимости) массу и угол, пока кольцо не окажется в центре. Запишите это значение в рабочий лист. 10 Сравните рассчитанные и экспериментальные значения для третьей силы, вычислив разницу в процентах между двумя значениями. См. Приложение Б. 11 Сравните расчетные и экспериментальные значения угла для третьей силы, вычислив процентную разницу между двумя значениями угла. КПП 1: 12 Подвесьте груз массой 300 г (включая подвеску) на отметке угла 150°. 13 Выберите значения для величины и угла второй массы и введите это значение в Таблицу данных 2 на рабочем листе. Используйте грузы только с шагом 10 г. Значения для F 2 должны отличаться от значений, используемых в процедуре A. Подумайте о симметрии при выборе угла для F 2 . 15 Начертите силовую диаграмму для этой установки в отведенном для этого месте рабочего листа. 16 Заполните Таблицу данных 2 и определите величину и угол для F 3 , необходимые для достижения равновесия; т. е. привести кольцо к центру силового стола. 17 Теперь подвесьте два выбранных груза под выбранными углами. Отрегулируйте одну или обе эти массы, а также их углы, если необходимо, так, чтобы кольцо располагалось по центру силового стола. 18 Вычислите процентную разницу между выбранными значениями и экспериментальными значениями для величины двух сил и запишите их в рабочий лист. 19 Вычислите процентную разницу между выбранными значениями и экспериментальными значениями углов двух сил и запишите их в рабочий лист. КПП 2: Эта статья научит вас находить компоненты x и y вектора. Мы уже знаем, что такое векторы и скаляры и насколько они важны, когда изучаем физику. Нахождение векторных компонентов противоположно векторному сложению, когда мы находим векторное сложение двух или более векторов. Здесь вектор разбивается на две составляющие. В задачах по физике вам иногда дают угол и величину для описания вектора. Нахождение горизонтальной составляющей силы F величиной 12 Н, действующей на брусок под углом 30 градусов к горизонтальной оси, является одним из таких примеров. Если вы хотите вычислить работу, совершаемую этой силой при горизонтальном перемещении блока, вы должны сначала вычислить горизонтальную составляющую силы F. Векторы могут существовать в одном, двух или трех измерениях пространства. Компоненты вектора определяются количеством измерений в нашем пространстве. Если рассматриваемый объект говорит, что автомобиль движется прямолинейно, то говорят, что он движется прямолинейно. При таком типе движения мы работаем в одномерном пространстве. Учтите, что наша машина движется слева направо. Этот $\vec A$ , как показано ниже на рисунке, представляет вектор движущегося автомобиля между точками O и A. Поскольку наш автомобиль движется только в одном направлении, этот вектор $\vec A$ имеет только одну компоненту. Итак, в одном измерении этот вектор можно разбить только на x-компоненту. $\vec A = \vec{A_x}$ где $\vec{A_x}$ — x-компонента вектора $\vec A$ Этот $\vec{A_x}$ указывает, как далеко вектор движется в горизонтальном направлении. Его движение может быть влево или вправо. Векторы в двух измерениях означают, что они имеют два направления влияния. Это означает, что он состоит из двух отдельных частей или компонентов. Во всех двумерных векторах есть компоненты x и y. Компонент x вектора говорит нам, как далеко вектор идет в горизонтальном направлении. Y-компонента говорит нам, как далеко вектор перемещается в вертикальном направлении. Мы называем их компонентами x и y. Давайте разберемся в этом с помощью примера вектора, показанного ниже на рисунке. На этом рисунке вектор $\vec A$ разбит на две составляющие: Компонента x вектора – $A_x$ и Компонента y вектора – $A_y$. Здесь $\theta$ — угол между x и y компонентами вектора. Как видно из рисунка, x-компонента и y-компонента вектора идут вдоль положительной оси x и положительной оси y системы координат. Вектор и его компоненты образуют прямоугольный треугольник, как показано ниже на рисунке Как показано на рисунке, вы должны использовать тригонометрию, чтобы разделить этот вектор на его компоненты. Тригонометр прост, если вы знаете об углах и тригонометрических соотношениях. Тригонометрические отношения или тригонометрические функции выражают взаимосвязь между величиной вектора и его компонентами. Тригонометрические отношения применимы только к прямоугольным треугольникам. Каждая сторона прямоугольного треугольника названа. Чтобы найти горизонтальную и вертикальную компоненты нашего исходного вектора $vec A$, используйте формулы тригонометрического отношения. Итак, у нас есть Функция косинуса, $cos\theta = \frac{Adjacent}{Hypotenuse}=\frac{A_x}{|\vec A|}$ или, $A_x=|\vec A|\cos\theta \tag{1} $ Синусоидальная функция, $sin\theta = \frac{Противоположность}{Гипотенуза}=\frac{A_y}{|\vec A|}$ или, $A_y=|\vec A|\sin\ theta \tag{2}$ Итак, чтобы определить компоненты вектора по его величине и направлению, мы используем уравнения 1 и 2. Чтобы найти направление вектора, когда известны его компоненты $A_x$ и $A_y$, мы используем 92}$ Итак, модуль вектора в прямоугольной системе равен квадратному корню из суммы квадратов его компонентов. Гипотенуза прямоугольного треугольника всегда образует результирующий вектор. Из рисунка видно, что прямоугольный треугольник имеет угол 60°, а это означает, что вы можете написать следующее как триггерное отношение для этого угла, используя синус и косинус. : $cos\theta = \frac{Adjacent}{Hypotenuse}=\frac{\text{x-component}}{10}$ Синусоидальная функция, $sin\theta = \frac{Opposite}{ Гипотенуза}=\frac{\text{y-component}}{10}$ Перестановка их путем решения для y- и x-компонент дает: 90 = 8.6$ Многие предметы, с которыми мы сталкиваемся в повседневной жизни, находятся в движении или состоят из частей.
которые находятся в движении. Движение – это правило, а не исключение. Физические законы, управляющие движением
этих объектов
универсальны, т.е. все объекты движутся по одним и тем же правилам,
и одна из целей этого класса состоит в том, чтобы понять эти правила. Когда объект движется, его позиция изменяется как функция времени. Положение объекта
дано относительно некоторой согласованной точки отсчета. Недостаточно просто
укажите расстояние от
ориентир. Мы также должны указать направление . Расстояние скаляр количество, это число, указанное в каких-то единицах . Позиция — это вектор количество. Он также имеет величину
как направление. Величина векторной величины представляет собой число (с единицами)
сообщая вам, сколько есть количества, и направление говорит вам, какое
как он указывает. Единичный вектор — это направление
индикатор. Это безразмерный вектор с величиной 1, используемый для указания
направление. В тексте векторные величины обычно выделяются жирным шрифтом. Ссылки: Удобный способ указать позицию
объекта
с помощью системы координат .
Мы выбираем фиксированную точку, называемую началом координат .
и три направленные линии, которые проходят через начало координат и
перпендикулярны друг другу. Эти линии называются осей координат трехмерной прямоугольной (декартовой) системы координат и помечены
оси x, y и z. Три числа с единицами определяют положение
точка P. Эти числа представляют собой координаты x, y и z точки P.
Координаты точки P на
на диаграмме справа (а, б, в). Координаты точки P
являются компонентами вектора положения. Компоненты любого вектора в сумме образуют
сам вектор. Ниже приведено трехмерное представление вектора положения. r = a i + b j + c k . Пожалуйста, нажмите
на рисунке! Вектор положения Nielsen Physics Building на небольшой карте с левым нижним углом в качестве начала координат. Изменение положения называется смещением . На приведенной ниже диаграмме показано
позиции P 1 и P 2 игрока в два разных момента времени. Стрелка, указывающая от P 1 к P 2 , является вектор смещения . Расстояние между двумя точками P 1 с координатами (х 1 ,
у 1 ,
z 1 ) и P 2 с координатами (x 2 , y 2 , z 2 ) равно Тройка действительных чисел d x = (x 2 — x 1 ), d y = (y 2 — y 1 ), d z = (z 2 — z 1 )
называются декартовыми компонентами d . Ссылка:
Расстояние и смещение (Пожалуйста, изучите!) Футбольный защитник пробегает 15,0 м. Решение: Во время движения по прямому межгосударственному шоссе вы
обратите внимание, что на отметке 260 миль.
отметку, а затем вернитесь к отметке 175 миль. Что это
величина вашего результирующего смещения от 260-мильной отметки? Решение: Кончик лопасти вертолета
5,00 м от центра вращения.
За один оборот лезвия
вычислить вектор смещения и
общее расстояние, пройденное наконечником
лезвия. Решение: Вектор смещения имеет одинаковую величину и направление независимо от выбор начала координат системы координат. Величина и направление
вектор смещения, однако, зависят от система отсчета , в которой
система координат закреплена и находится в состоянии покоя. A x 2 + A y 2 .
 0012
0012 5b.
5b. Векторы силы
Объектив
Оборудование
Процедура
 Эта третья сила известна как уравновешивающая, и она будет равна и противоположна равнодействующей двух известных сил. Вы будете использовать таблицу сил, как показано на рис. 9., и работать с векторами силы. Силовой стол представляет собой круглую платформу, установленную на треноге. Три ножки штатива имеют регулируемые винты, которые можно использовать для выравнивания круглой платформы. Круглая платформа имеет маркировку угла в градусах на своей поверхности. Два или более шкива могут быть зажаты в любом месте вдоль края платформы. В этой лабораторной работе мы будем использовать три шкива. Три струны прикреплены к центральному кольцу, а затем каждая струна пропущена через шкив. К другому концу струн добавляются массы.
Эта третья сила известна как уравновешивающая, и она будет равна и противоположна равнодействующей двух известных сил. Вы будете использовать таблицу сил, как показано на рис. 9., и работать с векторами силы. Силовой стол представляет собой круглую платформу, установленную на треноге. Три ножки штатива имеют регулируемые винты, которые можно использовать для выравнивания круглой платформы. Круглая платформа имеет маркировку угла в градусах на своей поверхности. Два или более шкива могут быть зажаты в любом месте вдоль края платформы. В этой лабораторной работе мы будем использовать три шкива. Три струны прикреплены к центральному кольцу, а затем каждая струна пропущена через шкив. К другому концу струн добавляются массы. Например, удвоение массы удваивает силу и т. д. Когда силы уравновешены, кольцо будет расположено точно в центре стола. Когда силы не уравновешены, кольцо будет упираться в одну сторону центральной стойки. Примечание : Сила каждой подвешенной массы будет равна мг , где г — ускорение свободного падения. Чтобы упростить чтение углов, предположим, что ось x проходит от отметки 180° до отметки 0°, где 0° является положительным направлением x , а ось y начинается от отметку 270° к отметке 90°, где 90° является положительным направлением и . См. рис. 10.
Например, удвоение массы удваивает силу и т. д. Когда силы уравновешены, кольцо будет расположено точно в центре стола. Когда силы не уравновешены, кольцо будет упираться в одну сторону центральной стойки. Примечание : Сила каждой подвешенной массы будет равна мг , где г — ускорение свободного падения. Чтобы упростить чтение углов, предположим, что ось x проходит от отметки 180° до отметки 0°, где 0° является положительным направлением x , а ось y начинается от отметку 270° к отметке 90°, где 90° является положительным направлением и . См. рис. 10. Процедура A: Нахождение равновесия двух известных сил


A x 2 + A y 2 
Попросите вашего ассистента проверить вашу диаграмму, расчеты и настройку таблицы сил. Процедура B: Определение размещения двух неизвестных сил

 Введите эти значения в рабочий лист.
Введите эти значения в рабочий лист.
Попросите вашего ассистента проверить вашу диаграмму, расчеты и настройки таблицы Force Table. Компоненты вектора — нахождение компонентов x и y вектора
 Затем вам нужно использовать тригонометрию, чтобы найти компоненты.
Затем вам нужно использовать тригонометрию, чтобы найти компоненты. Компоненты вектора
Компоненты векторов в одном измерении

Компоненты векторов в двух измерениях


Как найти компоненты вектора по модулю и углу
Как найти направление вектора по данным компонентам?
 0$ 90 по горизонтали. Если мы нарисуем фигуру для этого вектора, она будет выглядеть так:
0$ 90 по горизонтали. Если мы нарисуем фигуру для этого вектора, она будет выглядеть так: Положение и смещение
Положение и смещение
 введите или со стрелкой над символом. Таким образом, хотя d = расстояние, д = смещение.
введите или со стрелкой над символом. Таким образом, хотя d = расстояние, д = смещение.
Скаляры и векторы
(Пожалуйста, изучите!)
Направление вектора Позиция
 Единичный вектор
указание в направлении x имеет x-компоненту 1 и y- и z-компоненты
нуль. Обозначается цифрой и . Точно так же единичный вектор
, указывающий в направлении y, обозначается j , а единичный вектор
направление в направлении z обозначается k . Единичные векторы
являются указателями поворота.
Единичный вектор
указание в направлении x имеет x-компоненту 1 и y- и z-компоненты
нуль. Обозначается цифрой и . Точно так же единичный вектор
, указывающий в направлении y, обозначается j , а единичный вектор
направление в направлении z обозначается k . Единичные векторы
являются указателями поворота.
Вектор положения точки P с координатами (a, b, c)
может быть записано с точки зрения его компонентов как
р = а и + б к +
с к .
Величина вектора положения равна его длине r. Это
зависит от выбора начала системы координат. Это
— прямолинейное расстояние P от начала координат.
(Используйте современный браузер. 3D-приложения не работают в Internet Explorer.
или более старые браузеры.)
3D-приложения не работают в Internet Explorer.
или более старые браузеры.)
Чтобы получить наилучший вид, измените окно просмотра, перетащив мышь и
увеличить или уменьшить масштаб по мере необходимости.
Нажмите кнопки, чтобы выбрать другой вектор
или другая схема добавления векторов компонентов. Пример:
Рабочий объем
Его величина является прямой расстояние между P 1 и P 2 .
Компоненты смещения
вектор из P 1 по
P 2 (x 2 — x 1 ) вдоль оси x, (y 2 —
y 1 ) по оси Y.
Вектор смещения d от P 1 до P 2 может
можно записать как d = (x 2 — x 1 ) i + (y 2 -у 1 ) у .
Водоизмещение d составляет (x 2 — x 1 ) единиц в
направление x плюс (y 2 — y 1 ) единицы измерения в направлении y.
Величина смещения
d = ((x 2 — х 1 ) 2 + (у 2 — у 1 ) 2 ) ½ . Этот
следует из
пифагорейский
теорема.
d =
((х 2 — х 1 ) 2 + (у 2 — у 1 ) 2 + (z 2 — z1) 2 )½ .
Проблема:
 прямо на игровом поле (в
положительное направление x) за 2,50 с.
Затем его ударили и толкнули на 3,00 м.
прямо назад за 1,75 с. Он
ломает снасть и бежит прямо
вперед еще 21,0 м за 5,20 с.
Вычислите его вектор смещения и
общее пройденное расстояние.
прямо на игровом поле (в
положительное направление x) за 2,50 с.
Затем его ударили и толкнули на 3,00 м.
прямо назад за 1,75 с. Он
ломает снасть и бежит прямо
вперед еще 21,0 м за 5,20 с.
Вычислите его вектор смещения и
общее пройденное расстояние. Проблема:
Результирующее смещение представляет собой вектор d , сумму двух векторов д 1 и d 2 , которые указывают в противоположных направлениях.
Результирующее смещение представляет собой вектор d , сумму двух векторов д 1 и d 2 , которые указывают в противоположных направлениях.
Проблема:
После одного оборота наконечник
возвращается в исходное положение.
Вектор его смещения д =
0.
Общее пройденное расстояние
кончик равен окружности
окружности радиусом r = 5 м.
Окружность = 2πr = 31,42 м.
Общее расстояние, пройденное
вершина 31,42 м.



 Например, автомобиль, проехавший несколько метров от магазина до перекрестка, вполне сравним с этим расстоянием. Но даже в такой ситуации его можно считать материальной точкой, потому что все части автомобиля перемещались одинаково и на равное расстояние.
Например, автомобиль, проехавший несколько метров от магазина до перекрестка, вполне сравним с этим расстоянием. Но даже в такой ситуации его можно считать материальной точкой, потому что все части автомобиля перемещались одинаково и на равное расстояние.


 Тогда формула принимает вид:
Тогда формула принимает вид: (Рис. 1)Если применить проекции значений скорости и времени на оси, то тогда мы увидим, что скорость, как величина постоянная является прямой, проходящей параллельно оси времени.
(Рис. 1)Если применить проекции значений скорости и времени на оси, то тогда мы увидим, что скорость, как величина постоянная является прямой, проходящей параллельно оси времени. Но необходимо будет брать значение величин для одного тела со знаком минус в зависимости от того, направление какого из тел мы примем за положительное.
Но необходимо будет брать значение величин для одного тела со знаком минус в зависимости от того, направление какого из тел мы примем за положительное.

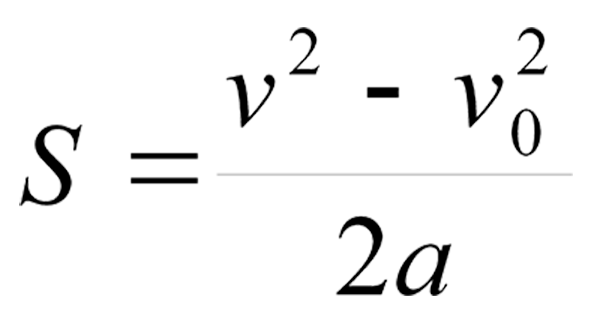
 2) в течение 4 секунд.
2) в течение 4 секунд.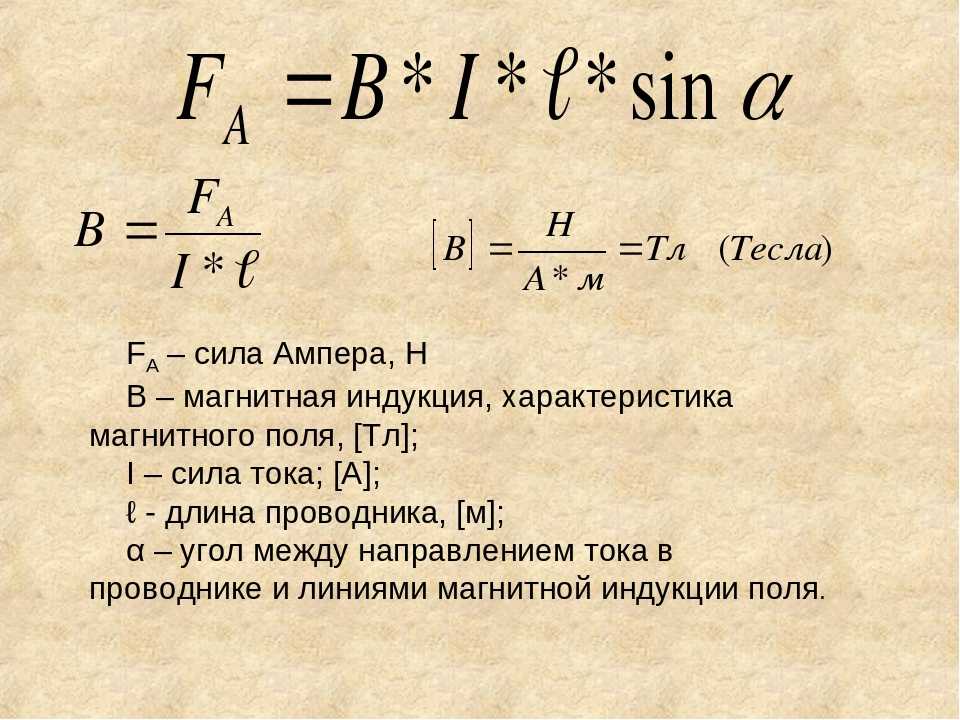
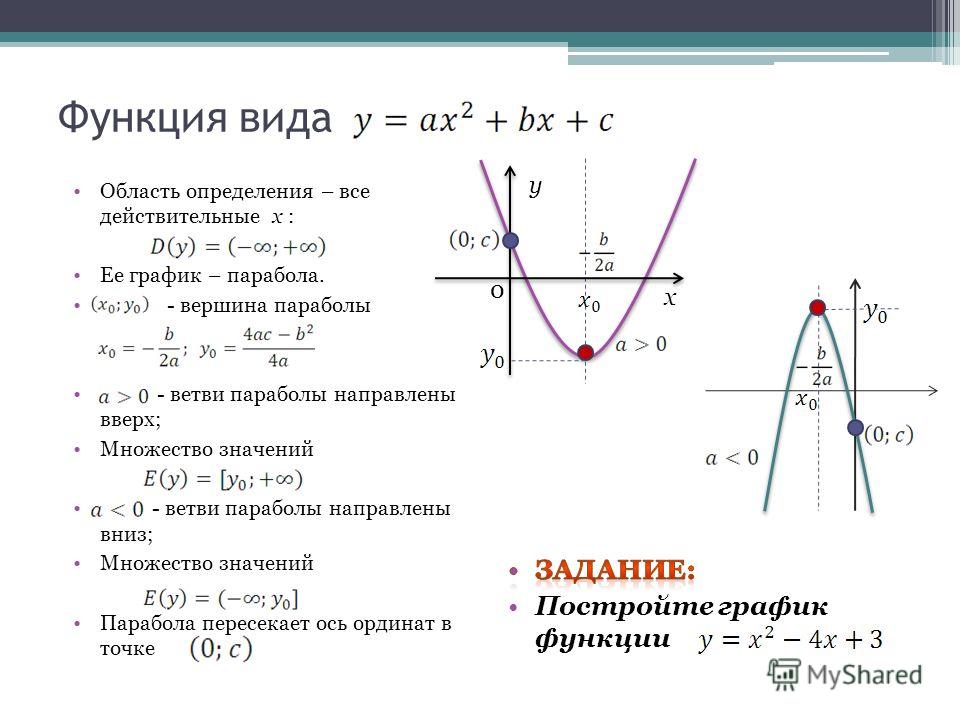 2=4*S1.
2=4*S1.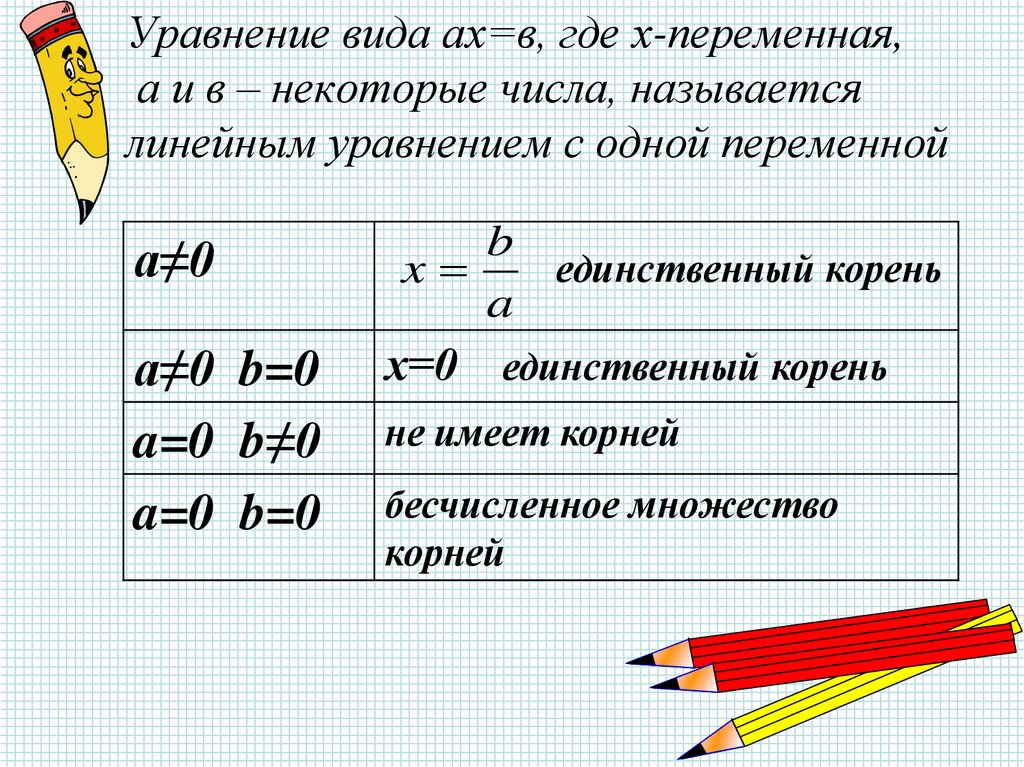 То есть они являются как бы неким своеобразным признаком равноускоренного движения. Если необходимо проверить, является ли движение равноускоренным, то можно проверить эти закономерности, и если они будут выполняться, то движение будет равноускоренным.
То есть они являются как бы неким своеобразным признаком равноускоренного движения. Если необходимо проверить, является ли движение равноускоренным, то можно проверить эти закономерности, и если они будут выполняться, то движение будет равноускоренным.
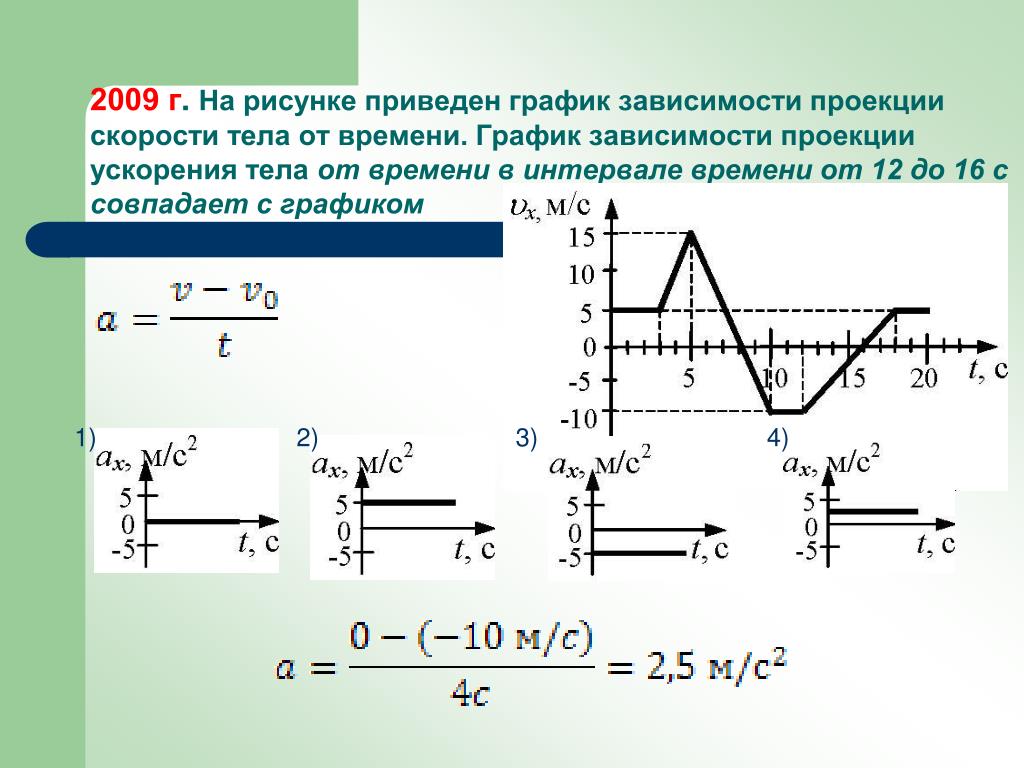
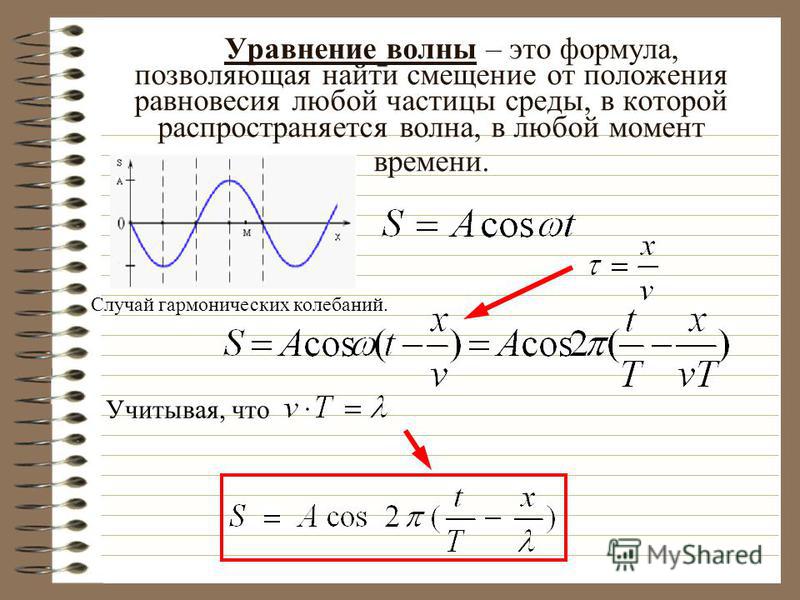 Каждый ваш шаг будет гигантским расстоянием для молекулы асфальта и ничтожным для планеты Земля. Любое движение, как и все его характеристики всегда имеют смысл только относительно чего-либо еще.
Каждый ваш шаг будет гигантским расстоянием для молекулы асфальта и ничтожным для планеты Земля. Любое движение, как и все его характеристики всегда имеют смысл только относительно чего-либо еще. Но если представить себе бесконечно длинный, абсолютно скользкий и гладкий каток, на котором стоит тело, то станет очевидно, что если придать телу импульс, то тело будет двигаться бесконечно долго и по одной прямой.
Но если представить себе бесконечно длинный, абсолютно скользкий и гладкий каток, на котором стоит тело, то станет очевидно, что если придать телу импульс, то тело будет двигаться бесконечно долго и по одной прямой. В исходном варианте первый закон Ньютона несколько неточен, а современный вариант в попытках исправить эту неточность оказался очень запутанным и потому неудачным. Ну а так как истина всегда где-то рядом, то попытаемся найти это «рядом» и разобраться, что же представляет собой данный закон.
В исходном варианте первый закон Ньютона несколько неточен, а современный вариант в попытках исправить эту неточность оказался очень запутанным и потому неудачным. Ну а так как истина всегда где-то рядом, то попытаемся найти это «рядом» и разобраться, что же представляет собой данный закон.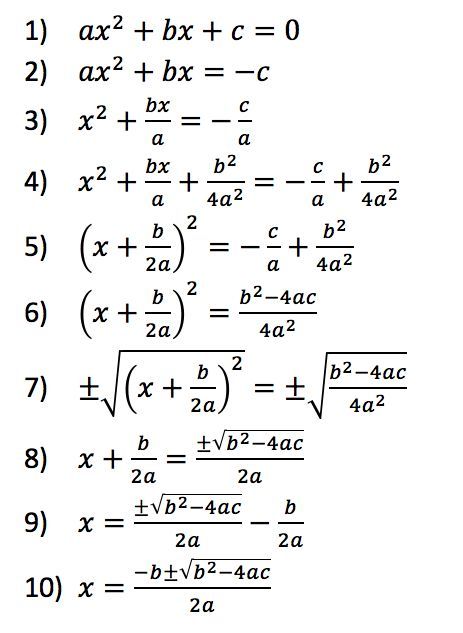 Масло масляное. Замкнутый круг.
Масло масляное. Замкнутый круг. «Изолированным» — это значит никак не связанным, бесконечно удаленным от других тел.
«Изолированным» — это значит никак не связанным, бесконечно удаленным от других тел. Мы не можем переместиться на бесконечно далекую звезду и оттуда осуществлять какие-либо опыты на Земле.
Мы не можем переместиться на бесконечно далекую звезду и оттуда осуществлять какие-либо опыты на Земле.
 Хотите легко и быстро, на примерах понять, как это происходит? Запросто. Надо будет проделать пару элементарных опытов и немного порассуждать.
Хотите легко и быстро, на примерах понять, как это происходит? Запросто. Надо будет проделать пару элементарных опытов и немного порассуждать. Если на тело действуют несколько сил, то находят равнодействующую этих сил, то есть некую общую суммарную силу, обладающую определенным направлением и числовым значением.
Если на тело действуют несколько сил, то находят равнодействующую этих сил, то есть некую общую суммарную силу, обладающую определенным направлением и числовым значением. Ускорение двух грузов у нас было ощутимо разным, хотя силу мы старались прикладывать одинаковую. А вот масса грузов у нас отличалась. И в случае с большей массой ускорение тела было небольшим, а в случае меньшей массы намного большим.
Ускорение двух грузов у нас было ощутимо разным, хотя силу мы старались прикладывать одинаковую. А вот масса грузов у нас отличалась. И в случае с большей массой ускорение тела было небольшим, а в случае меньшей массы намного большим. Это и есть второй закон Ньютона.
Это и есть второй закон Ньютона.
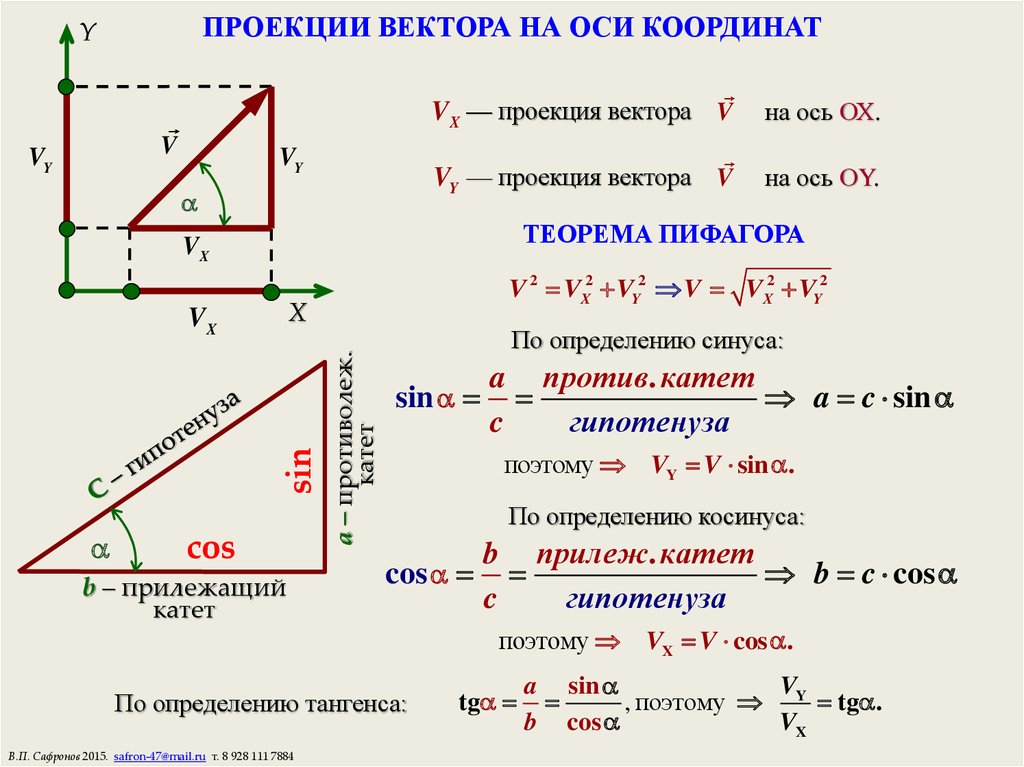 И потяните за колечко второго безмена. Проследите за показаниями обоих приборов. Каждый из них покажет силу, с которой на него воздействует другой безмен.
И потяните за колечко второго безмена. Проследите за показаниями обоих приборов. Каждый из них покажет силу, с которой на него воздействует другой безмен. Все тела во Вселенной взаимодействуют друг с другом, подчиняясь этому закону.
Все тела во Вселенной взаимодействуют друг с другом, подчиняясь этому закону.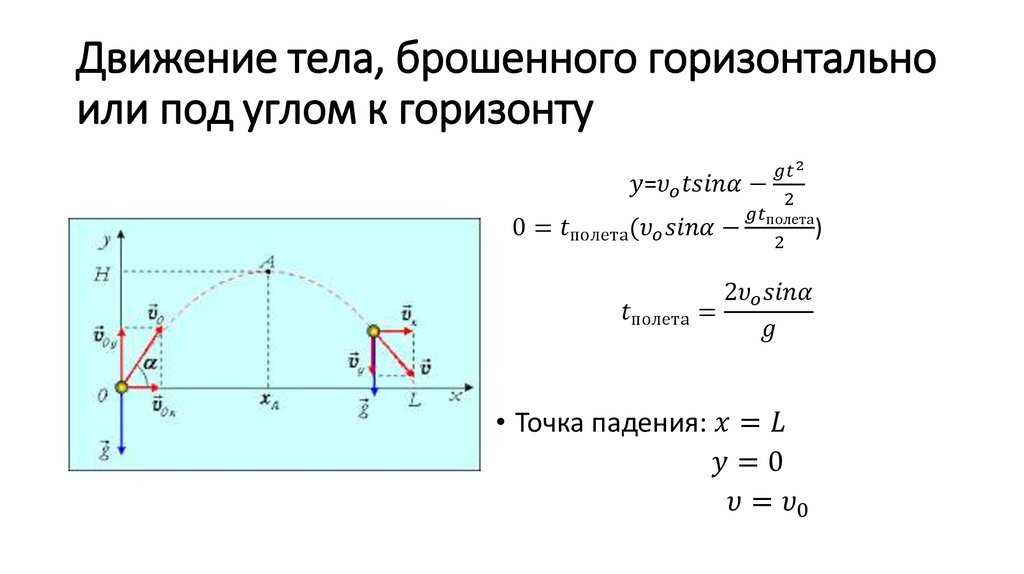 2)/2 (если v_0 = 0), соответственно,
2)/2 (если v_0 = 0), соответственно, Только в этом случае, скорость, которую мы придали телу при броске, будет направлена вверх, а ускорение свободного падения направлено вниз, то есть они будут противоположно направлены друг к другу. Поэтому скорость будет постепенно уменьшаться.
Только в этом случае, скорость, которую мы придали телу при броске, будет направлена вверх, а ускорение свободного падения направлено вниз, то есть они будут противоположно направлены друг к другу. Поэтому скорость будет постепенно уменьшаться. 2)/2.
2)/2.
 2 .
2 . 2).
2). Но возникает вопрос: если Луна притягивается к Земле, почему она вращается вокруг нее, а не падает на Землю?
Но возникает вопрос: если Луна притягивается к Земле, почему она вращается вокруг нее, а не падает на Землю? Именно так Земля притягивает все тела на ее поверхности, а также летящие из космоса метеориты.
Именно так Земля притягивает все тела на ее поверхности, а также летящие из космоса метеориты. Если их движение было перпендикулярно Земле, то они могут находиться на орбите бесконечно долго. Если же угол был меньше 90˚, то они будут двигаться по снижающейся спирали, и постепенно все-таки упадут на землю.
Если их движение было перпендикулярно Земле, то они могут находиться на орбите бесконечно долго. Если же угол был меньше 90˚, то они будут двигаться по снижающейся спирали, и постепенно все-таки упадут на землю..jpg) Нам остается лишь надеяться, что этот момент не наступит никогда.
Нам остается лишь надеяться, что этот момент не наступит никогда.
 Она составляет от 7,9 км/с. Чем больше высота тела над землей, тем величина этой скорости меньше.
Она составляет от 7,9 км/с. Чем больше высота тела над землей, тем величина этой скорости меньше.

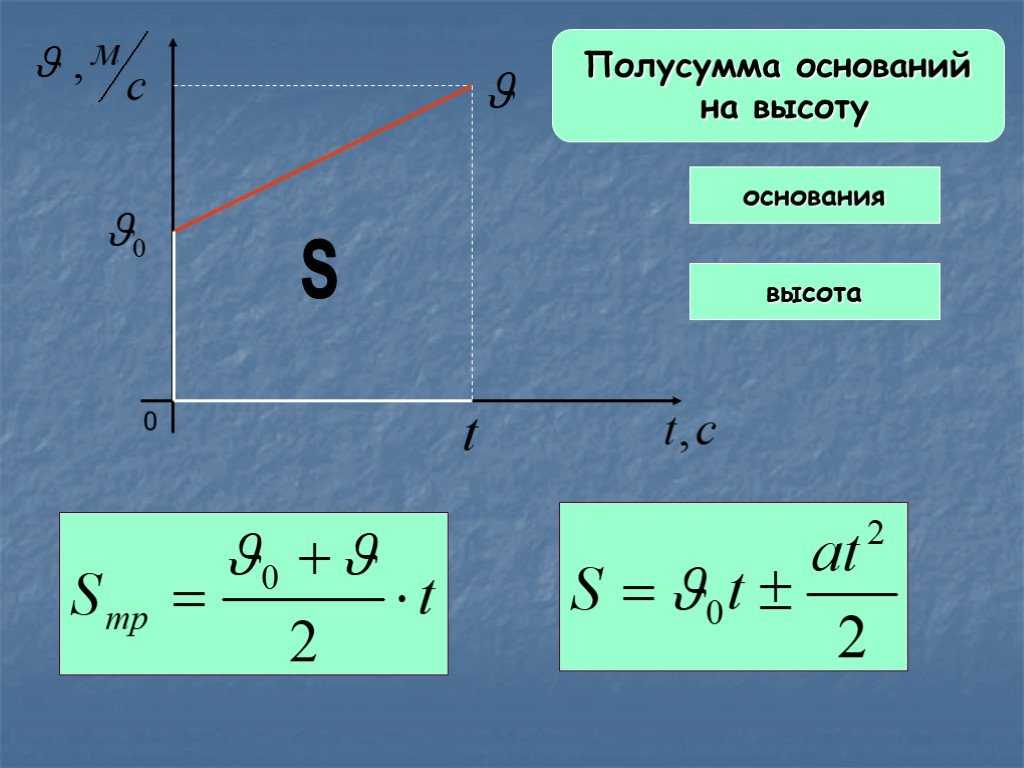

 Разберем подробнее.
Разберем подробнее. Так вот, именно на этом и основано реактивное движение.
Так вот, именно на этом и основано реактивное движение.

 .. .
.. . Северная составляющая — это проекция вектора на ось север-юг. Западная составляющая является проекцией вектора на ось восток-запад. Если самолет летит на северо-запад со скоростью, скажем, 200 км/ч под углом 120 градусов, то самолет имеет северную и западную составляющие скорости. Северная составляющая скорости описывает влияние скорости самолета в северном направлении. Западная составляющая скорости описывает влияние скорости самолета в западном направлении. В физике компоненты просто описывают действие вектора в заданном направлении.
Северная составляющая — это проекция вектора на ось север-юг. Западная составляющая является проекцией вектора на ось восток-запад. Если самолет летит на северо-запад со скоростью, скажем, 200 км/ч под углом 120 градусов, то самолет имеет северную и западную составляющие скорости. Северная составляющая скорости описывает влияние скорости самолета в северном направлении. Западная составляющая скорости описывает влияние скорости самолета в западном направлении. В физике компоненты просто описывают действие вектора в заданном направлении. Если два компонента сложить вместе по принципу «голова к хвосту», то в результате получится… .
Если два компонента сложить вместе по принципу «голова к хвосту», то в результате получится… . Таким образом, разрешение вектора по перпендикулярным осям создает компоненты. И добавление двух компонентов дает результирующий исходный вектор.
Таким образом, разрешение вектора по перпендикулярным осям создает компоненты. И добавление двух компонентов дает результирующий исходный вектор.
 Его x- и y-компоненты лучше всего представлены … .
Его x- и y-компоненты лучше всего представлены … .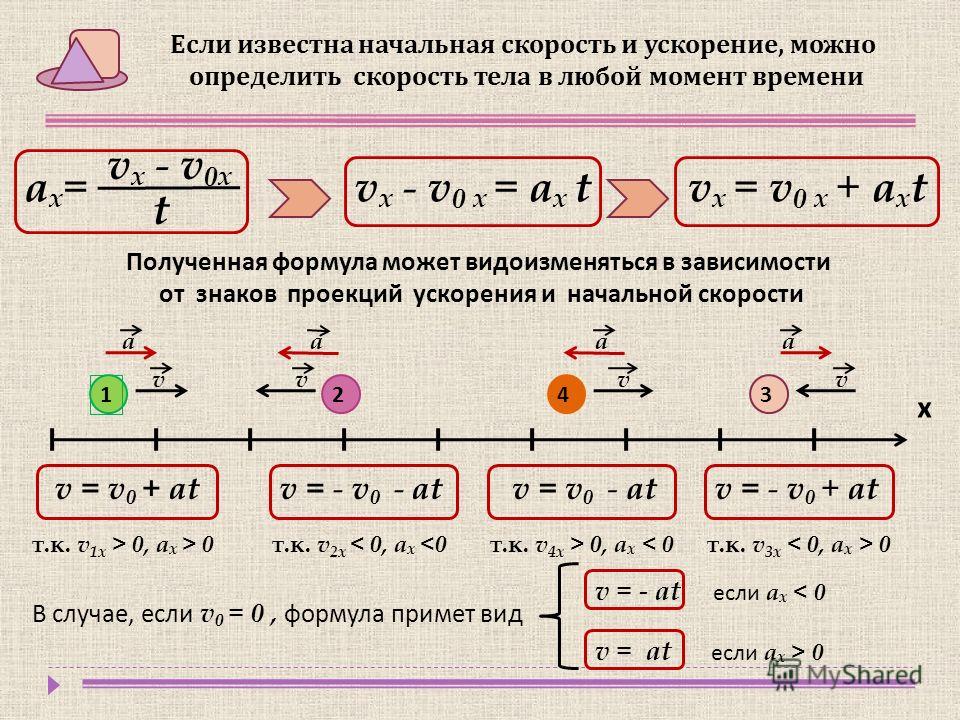 Компонент x растягивается вдоль оси x от конца вектора до места, где опорная линия пересекается с осью x. Y-компонента простирается вдоль оси y от хвоста вектора до места, где опорная линия пересекается с осью y.
Компонент x растягивается вдоль оси x от конца вектора до места, где опорная линия пересекается с осью x. Y-компонента простирается вдоль оси y от хвоста вектора до места, где опорная линия пересекается с осью y.
 Его x- и y-компоненты лучше всего представлены … .
Его x- и y-компоненты лучше всего представлены … . Компонент x растягивается вдоль оси x от конца вектора до места, где опорная линия пересекается с осью x. Y-компонента простирается вдоль оси y от хвоста вектора до места, где опорная линия пересекается с осью y.
Компонент x растягивается вдоль оси x от конца вектора до места, где опорная линия пересекается с осью x. Y-компонента простирается вдоль оси y от хвоста вектора до места, где опорная линия пересекается с осью y.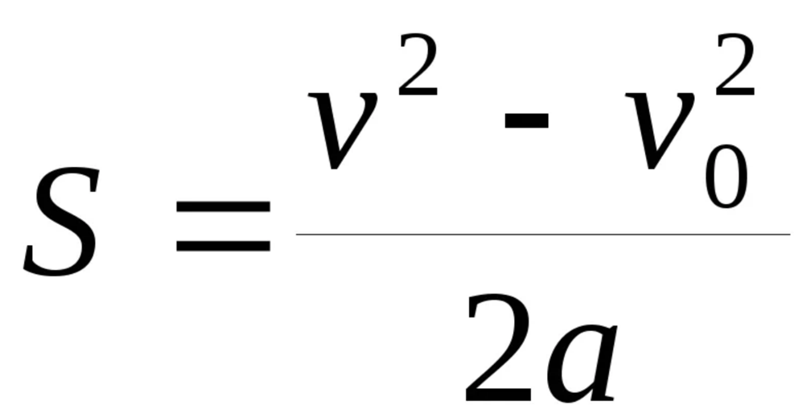

 Это было бы то же самое, что приложить две силы в … .
Это было бы то же самое, что приложить две силы в … . (Вероятно, вы видели такие диаграммы и теперь можете попытаться нарисовать одну из них.) Если вектор является северо-восточным вектором, то его компоненты простираются на восток и север. Восточная и северная составляющие — это просто восточная и северная стороны треугольника, который был создан из северо-восточного вектора.
(Вероятно, вы видели такие диаграммы и теперь можете попытаться нарисовать одну из них.) Если вектор является северо-восточным вектором, то его компоненты простираются на восток и север. Восточная и северная составляющие — это просто восточная и северная стороны треугольника, который был создан из северо-восточного вектора. Смысл трех функций:
Смысл трех функций: