Длина дуги интеграл: Как найти длину дуги кривой с помощью интеграла

Длина дуги пространственной кривой

Длину дуги получают интегрированием дифференциала дуги от первой точки к конечной. Сложность вычислений заключается в том, что кривая, как правило, заданная двумя или и тремя уравнениями изменения координат по осям, а интегрирование нужно свести к одной координате. Для этого нужно найти дифференциал дуги.
Формулы дифференциалу дуги для пространственных и плоских кривых, заданных явно и параметрически хорошо расписаны.
Их здесь повторять не будем, а лишь выделим цветом в формулах.
Когда известен дифференциал дуги, интеграл вычисляют всеми возможными способами:
непосредственное интегрирование, замена переменных, интегрирования частями.
Часть методов дальше применим для решения заданий.

Пример 1 Найти длину дуги пространственной кривой:
x=3t, y=3t², z=2t³, от точки O(0,0,0) к точке A(3,3,2).
Решение: Найдем производные по переменной t от заданных функций x=x(t), y=y(t) и z=z(t):
x’=3, y’=6t, z’=6t².
Производные нам нужны для нахождения дифференциала дуги ds заданной кривой:

Эта формула справедлива для всех пространственных кривых, заданных параметрически.
Следующим шагом определим пределы интегрирования.
Чтобы их найти нужно в уравнение пространственной кривой

подставить две точки О, А.
Складываем уравнение на определение пределов изменения параметра t:


При решении установили, что параметр должен принадлежать интервалу 0≤t≤1.

Вычислим длину дуги заданной кривой, при 0≤t≤1:

Интеграл найти не трудно, поскольку под корнем легко выделить квадрат, а дальше уже имеем дело с квадратичной функцией, которую легко интегрировать.
Дальше рассмотрим более сложные задания в которых вычисление производных и дифференциала дуги усложняется.

 

Пример 2 Найти длину дуги пространственной кривой (a>0) :
(x-y)²=a(x+y), x²-y²=9/8-z², от точки O(0,0,0) к точке A(x₀,y₀,z₀).
Решение: В подобных примерах целесообразно сделать замену переменных:

Тогда заданное уравнение (x-y)²=a(x+y) приобретет вид:

Отсюда

Подобные превращения выполняем для второго уравнения кривой
x²-y²=9/8-z², или (x-y)(x+y)=9/8-z²:

отсюда
(1).
Имеем , получим:
(2).
Найдем производные по переменной z от функций u=u(z) и v=v(z):
после упрощений получим такие конечные значения

Запишем как изменяется z от точки O(0,0,0) к точке A(x₀, y₀, z₀):
0≤z≤z₀.
Следующим шагом найдем дифференциал дуги ds по формуле:

Под корнем выделили полный квадрат, поэтому дифференциал упростился.

Через интеграл вычисляем длину дуги кривой:

Найти интеграл в этом случае тоже не складывает больших трудностей.

 

Пример 3 Найти длину дуги пространственной кривой (a>0) :

от точки O(0,0,0) к точке A(x₀, y₀, z₀).
Решение: Превратим заданные функции так, чтобы они выражались через переменную y:

отсюда получим

Для вычисления обратной функции к двум сторонам зависимости применили синус преобразование.
Дальше найденное значение обратной функции x(y) и подставляем во второе уравнение пространственной кривой

то есть

Окончательно получим

Значение функций в точке A(x₀, y₀, z₀):

Найдем производные по переменной y функций x=x(y), z=z(y):

За свойством логарифма превратим логарифм дроби в разницу логарифмов

Такой прием поможет при вычислении производной составленной функции

Запишем пределы интегрирования y, когда точка проходит значение от O(0,0,0) к A(x₀, y₀, z₀):
0≤y≤y₀.
Дифференциал дуги ds кривой вычислим по формуле:

Длину дуги пространственной кривой найдем по формуле:

В интеграле сделали замену переменных и интегрировали частями.

 

Пример 4 Вычислить длину дуги пространственной кривой (a>0, c>0) :
x²+y²=cz, y/x=tg (z/c), от точки O(0,0,0) к точке A(x₀, y₀, z₀).
Решение: Перейдем к полярной системе координат с помощью формул перехода:

Превращаем первое уравнение кривой

дальше второе

Из формул видим насколько проще стали уравнения кривой.
Запишем все три пространственные координаты через параметр угла φ:

здесь переменная пробегает значение 0≤φ≤z₀/c, поскольку φ=z/c.
Запишем производные по переменной φ для функций x=x(φ), y=y(φ) но z=z(φ):

Вычислим дифференциал дуги ds кривой по формуле:

Не забывайте в подобных заданиях выделять полный квадрат под корнем.
Без этого Вы не сможете найти интеграла.
Через интеграл найдем длину дуги пространственной кривой:

Из приведенных примеров можно сделать вывод, что сложность вычисления криволинейных интегралов имеет место лишь в выборе системы координат, нахождении производных и дифференциалов дуг.
Найти интеграл в большинстве случаев достаточно легко, сложные задания, как правило, преподаватели Вам не дадут вычислять.

Краткий курс высшей математики

Краткий курс высшей математики

Шнейдер В. Е. и др. Краткий курс высшей математики. Учеб. пособие для втузов. М., «Высш. школа», 1972. 640 с. Данное учебное пособие предназначено для студентов вечерних факультетов втузов и заводов-втузов. Оно в основном охватывает весь материал, предусмотренный обязательной программой. Достаточное количество решенных примеров и задач способствует лучшему усвоению теоретического материала. Оглавление ПРЕДИСЛОВИЕ ГЛАВА I. МЕТОД КООРДИНАТ. ПОНЯТИЕ ФУНКЦИИ § 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КООРДИНАТЫ ТОЧКИ НА ПРЯМОЙ 2. Геометрическое изображение действительных чисел. Координаты точки на прямой 3. Абсолютная величина действительного числа 4. Расстояние между двумя точками на прямой § 2. КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ 2. Расстояние между двумя точками на плоскости 3. Деление отрезка в данном отношении 4. Координаты точки в пространстве 5. Расстояние между двумя точками в пространстве § 3. УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ 2. Полярные координаты 3. Зависимость между декартовыми и полярными координатами § 4. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ 2. Понятие функции 3. График функции 4. Способы задания функций 5. Основные элементарные функции и их графики 6. Сложные функции. Элементарные функции 7. Целые и дробно-рациональные функции 8. Функции четные и нечетные. Периодические функции § 5. УРАВНЕНИЕ ЛИНИИ 2. Нахождение уравнения линии по ее геометрическим свойствам § 6 ПРЕОБРАЗОВАНИЕ КООРДИНАТ 2. Поворот осей координат ГЛАВА II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ § 1. ПРЯМАЯ 2. Уравнение прямой с угловым коэффициентом 3. Уравнение прямой, параллельной оси ординат 4. Общее уравнение прямой и его частные случаи 5. Точка пересечения прямых. Построение прямой по ее уравнению 6. Вычисление угла между двумя прямыми. Условия параллельности и перпендикулярности двух прямых 7. Уравнение прямой, проходящей через данную точку в заданном направлении 8. Пучок прямых 9. Уравнение прямой, проходящей через две данные точки 10. Расстояние от точки до прямой § 2. КРИВЫЕ ВТОРОГО ПОРЯДКА 2. Окружность 3. Эллипс 4. Гипербола 5. Парабола 6. Окружность, эллипс, гипербола и парабола как конические сечения 7. Упрощение уравнения кривой второго порядка. График квадратного трехчлена 8. Уравнение равносторонней гиперболы, асимптоты которой приняты за оси координат 9. График дробно-линейной функции 10. Преобразование уравнения кривой второго порядка, не содержащего члена с произведением координат ГЛАВА III. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ § 1. ЭЛЕМЕНТЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ 2. Определитель третьего порядка 3. Понятие об определителях высших порядков § 2. СИСТЕМЫ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ 2. Однородная система двух уравнений первой степени с тремя неизвестными 3. Система трех уравнений первой степени с тремя неизвестными 4. Однородная система трех уравнений первой степени с тремя неизвестными § 3. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ 2. Линейные операции над векторами 4. Проекция вектора на ось и составляются вектора по оси 5. Разложение вектора на составляющие по осям координат 6. Направляющие косинусы вектора 7. Условие коллинеарности двух векторов 8. Скалярное произведение 9. Выражение скалярного произведения через проекции перемножаемых векторов 10. Косинус угла между двумя векторами 11. Векторное произведение 12. Выражение векторного произведения через проекции перемножаемых векторов 13. Смешанное произведение трех векторов 14. Геометрический смысл смешанного произведения 15. Условие компланарности трех векторов § 4. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ 2. Равенство матриц. Действия над матрицами 3. Обратная матрица 4. Матричная запись и матричное решение системы уравнений первой степени § 5. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ 2. Преобразование координат 3. Приведение квадратичной формы к каноническому виду 4. Упрощение общего уравнения кривой второго порядка ГЛАВА IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ § 1. ПЛОСКОСТЬ 2. Нормальный вектор плоскости. Уравнение плоскости, проходящей через данную точку 3. Общее уравнение плоскости и его частные случаи 4. Построение плоскости по ее уравнению 5. Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей 6. Точка пересечения трех плоскостей § 2. ПРЯМАЯ В ПРОСТРАНСТВЕ 2. Общие уравнения прямой 3. Векторное уравнение прямой. Параметрические уравнения прямой 4. Канонические уравнения прямой 5. Уравнения прямой, проходящей через две точки 6. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых § 3. Прямая и плоскость в пространстве 2. Точка пересечения прямой с плоскостью 3. Расстояние от точки до плоскости 4. Пучок плоскостей § 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА 2. Цилиндрические поверхности 3. Конические поверхности 4. Поверхность вращения 6. Гиперболоиды 7. Параболоиды ГЛАВА V. ТЕОРИЯ ПРЕДЕЛОВ § 1. ПРЕДЕЛ ФУНКЦИИ 2. Предел функции при х -> -оо 3. Предел функции при х->х0 4. Бесконечно малые функции. Ограниченные функции 5. Бесконечно большие функции и их связь с бесконечно малыми функциями 6. Основные теоремы о пределах 7. Предел функции при x -> 0 8. Последовательность. Число e 9. Натуральные логарифмы 10. Сравнение бесконечно малых функций § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 2. Операции над непрерывными функциями. Непрерывность элементарных функций 3. Свойства функций, непрерывных на сегменте 4. Понятие об обратной функции 5. Обратные тригонометрические функции 6. Показательная и логарифмическая функции 7. Понятие о гиперболических функциях ГЛАВА VI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ 1. Приращение аргумента и приращение функции 2. Определение непрерывности функции с помощью понятии приращения аргумента и приращения функции 3. Задачи, приводящие к понятию производной 4. Определение производной и ее механический смысл 5. Дифференцируемость функции 6. Геометрический смысл производной 7. Производные некоторых основных элементарных функций 8. Основные правила дифференцирования 9. Производная обратной функции 10. Производные обратных тригонометрических функций 11. Производная сложной функции § 12. Производные гиперболических функций 13. Производная степенной функции с любым показателем 14. Сводная таблица формул дифференцирования 15. Неявные функции и их дифференцирование 16. Уравнения касательной а нормали к кривой 17. Графическое дифференцирование § 2. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ 1. Нахождение производных высших порядков 2. Механический смысл второй производной § 3. ДИФФЕРЕНЦИАЛ ФУНКЦИИ 2. Производная как отношение дифференциалов 3. Дифференциал суммы, произведения и частного функций 4. Дифференциал сложной функции. Инвариантность формы дифференциала 5. Применение дифференциала к приближенным вычислениям 6. Дифференциалы высших порядков § 4. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ, И ИХ ДИФФЕРЕНЦИРОВАНИЕ 2. Дифференцирование функций, заданных параметрически § 5. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА 2. Векторная функция скалярного аргумента и ее производная 3. Уравнения касательной прямой и нормальной плоскости к пространственной кривой 4. Механический смысл первой и второй производных векторной функции скалярного аргумента § 6. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ 2. Теорема Ролля 3. Теорема Лагранжа 4. Правило Лопиталя § 7. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ 2. Максимум и минимум функции 3. Достаточный признак существования экстремума, основанный на знаке второй производной 4. Отыскание наибольшего и наименьшего значений функции 5. Применение теории максимума и минимума к решению задач 6. Выпуклость и вогнутость графика функции. Точки перегиба 7. Асимптоты графика функции 8. Общая схема исследования функции и построение ее графика § 8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 2. Уточнение найденных значений корней методом хорд и касательных § 9. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА ГЛАВА VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА 2. Геометрический смысл неопределенного интеграла 3. Таблица основных интегралов 4. Основные свойства неопределенного интеграла § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 2. Интегрирование методом замены переменной 3. Интегрирование по частям § 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Рациональные дроби. Выделение правильной рациональной дроби 3. Интегрирование простейших рациональных дробей 4. Разложение правильной рациональной дроби на простейшие дроби 5. Метод неопределенных коэффициентов 6. Интегрирование рациональных дробей § 4. Интегрирование тригонометрических функций 2. Рациональные функции двух переменных 3. Интегралы вида § 5. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Интеграл вида 3. Интегралы видов 4. Интегралы вида § 6. ОБЩИЕ ЗАМЕЧАНИЯ О МЕТОДАХ ИНТЕГРИРОВАНИЯ. ИНТЕГРАЛЫ, НЕ БЕРУЩИЕСЯ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ 2. Понятие об интегралах, не берущихся в элементарных функциях ГЛАВА VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ОПРЕДЕЛЕННОМУ ИНТЕГРАЛУ 2. Задача о работе переменной силы § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 2. Свойства определенного интеграла 3. Производная интеграла по переменной верхней границе 4. Формула Ньютона—Лейбница 5. Замена переменной в определенном интеграле 6. Интегрирование по частям в определенном интеграле § 3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 2. Вычисление площади в полярных координатах 3. Вычисление объема тела по известным поперечным сечениям 4. Объем тела вращения 5. Длина дуги кривой 6. Дифференциал дуги 7. Площадь поверхности вращения 8. Общие замечания о решении задач методом интегральных сумм § 4. КРИВИЗНА ПЛОСКОЙ КРИВОЙ 2. Вычисление кривизны 3. Радиус кривизны. Круг кривизны. Центр кривизны 4. Эволюта и эвольвента § 5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2. Интегралы от разрывных функций 3. Признаки сходимости несобственных интегралов § 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 2. Метод трапеций 3. Метод параболических трапеций (метод Симпсона) ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. График функции двух переменных 3. Функции трех и большего числа переменных § 2. Предел функции нескольких переменных. Непрерывность функции. Точки разрыва 2. Непрерывность функции нескольких переменных 3. Понятие области 4. Точки разрыва 5. Свойства функций, непрерывных в ограниченной замкнутой области § 3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ 2. Геометрический смысл частных производных функции двух переменных 3. Частные производные высших порядков § 4. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. Полный дифференциал функции 3. Приложение полного дифференциала к приближенным вычислениям § 5. Дифференцирование сложных и неявных функций 2. Инвариантность формы полного дифференциала 3. Дифференцирование неявных функций § 6. СКАЛЯРНОЕ ПОЛЕ 2. Производная по направлению 3. Градиент 4. Касательная плоскость а нормаль к поверхности 5. Геометрический смысл полного дифференциала функции двух переменных § 7. ЭКСТРЕМУМ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ 2. Наибольшее и наименьшее значения функции двух переменных ГЛАВА X. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ § 1. ДВОЙНОЙ ИНТЕГРАЛ 2. Двойной интеграл. Теорема существования 3. Свойства двойного интеграла 4. Вычисление двойного интеграла в декартовых координатах 5. Вычисление двойного интеграла в полярных координатах 6. Приложения двойного интеграла § 2. ТРОЙНОЙ ИНТЕГРАЛ 2. Тройной интеграл и его свойства 3. Вычисление тройного интеграла в декартовых координатах 4. Вычисление тройного интеграла в цилиндрических координатах 5. Приложения тройного интеграла § 3. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 2. Задача о работе. Криволинейный интеграл 3. Вычисление криволинейного интеграла 4. Формула Остроградского — Грина 5. Независимость криволинейного интеграла от пути интегрирования 6. Отыскание первообразной по полному дифференциалу 7. Криволинейный интеграл по длине дуги ГЛАВА XI. РЯДЫ § 1. ЧИСЛОВЫЕ РЯДЫ 2. Геометрическая прогрессия 3. Простейшие свойства числовых рядов 4. Необходимый признак сходимости ряда 5. Достаточные признаки сходимости знакоположительных рядов 6. Знакопеременные ряды 7. Остаток ряда и его оценка § 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ 2. Правильно сходящиеся функциональные ряды и их свойства § 3. СТЕПЕННЫЕ РЯДЫ 2. Свойства степенных рядов 3. Ряды по степеням разности х-а 4. Разложение функций в степенные ряды. Ряд Тейлора 5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена § 4. ПРИЛОЖЕНИЕ РЯДОВ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ 2. Приближенное вычисление интегралов § 5. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. СТЕПЕННЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ 2. Числовые ряды с комплексными членами 3. Степенные ряды в комплексной области § 6. РЯДЫ ФУРЬЕ 2. Ряд Фурье 3. Сходимость ряда Фурье 4. Ряды Фурье для четных и нечетных функций 5. Разложение в ряд Фурье функций с периодом 2l ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 2. Дифференциальные уравнения первого порядка 3. Уравнения с разделяющимися переменными 4. Однородные уравнения 5. Линейные уравнения 6. Уравнение в полных дифференциалах 7. Особые решения 8. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2. Простейшие уравнения второго порядка, допускающие понижение порядка 3. Понятие о дифференциальных уравнениях высших порядков § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2. Линейные однородные дифференциальные уравнения второго порядка 3. Линейные неоднородные дифференциальные уравнения второго порядка 4. Метод вариации произвольных постоянных § 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 2. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 3. Приложение линейных дифференциальных уравнений второго порядка к изучению механических и электрических колебаний § 5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ 2. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами § 6. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ § 7. ПОНЯТИЕ О СИСТЕМАХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 2. Системы линейных дифференциальных уравнений с постоянными коэффициентами ПРИЛОЖЕНИЕ 1. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА ПРИЛОЖЕНИЕ 2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

Исчисление II — длина дуги с параметрическими уравнениями

Онлайн-заметки Пола
Главная / Исчисление II / Параметрические уравнения и полярные координаты / Длина дуги с параметрическими уравнениями

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 9.4: Длина дуги с параметрическими уравнениями

В предыдущих двух разделах мы рассмотрели пару тем исчисления I с точки зрения параметрических уравнений. Теперь нам нужно рассмотреть пару тем Calculus II с точки зрения параметрических уравнений.

В этом разделе мы рассмотрим длину дуги параметрической кривой, заданную выражением

. \[x = f\left( t \right)\hspace{0.5in}y = g\left( t \right)\hspace{0.5in}\alpha \le t \le \beta\]

Мы также будем предполагать, что кривая вычерчивается ровно один раз при увеличении \(t\) от \(\alpha\) до \(\beta\).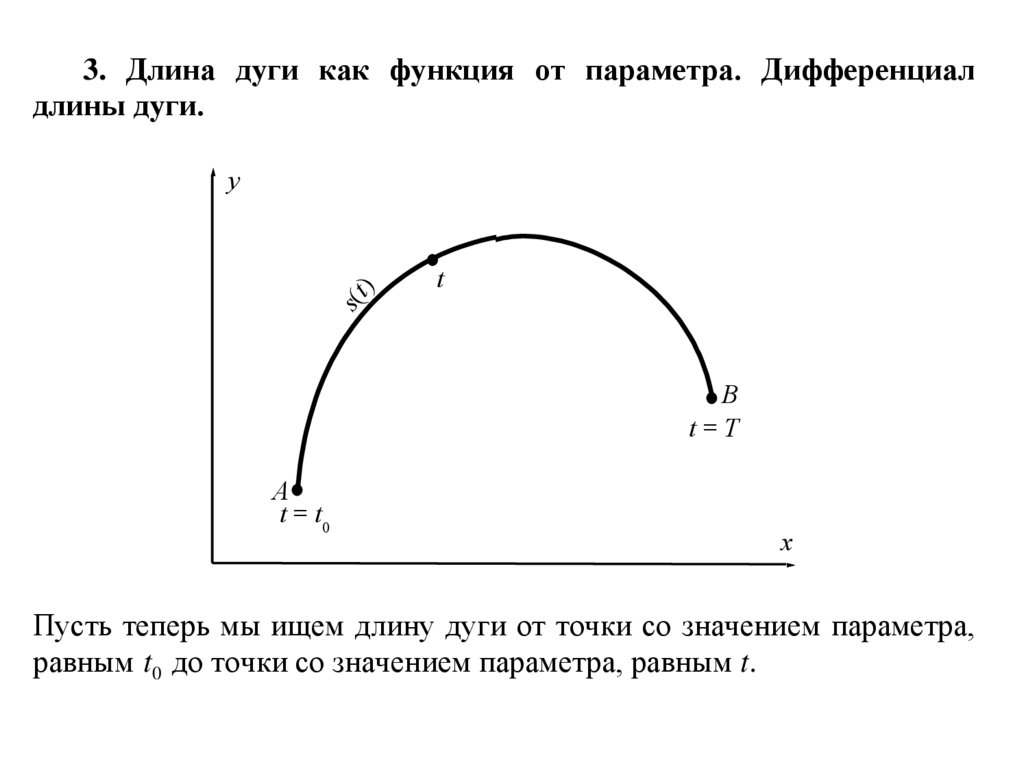 2}} \,dy\,\hspace{0,25 дюйма}{\mbox{if }}x = h\left( y \right),\ ,\,c \le y \le d\end{align*}\] 92}} \,\,дт\,}}\]

Обратите внимание, что мы могли бы использовать вторую формулу для \(ds\) выше, если бы предположили, что

\[\frac{{dy}}{{dt}} \ge 0\hspace{0.5in}{\mbox{for}}\alpha \le t \le \beta \]

Если бы мы пошли по этому пути при выводе, то получили бы ту же самую формулу.

Давайте рассмотрим пример.

Пример 1. Определите длину параметрической кривой, заданной следующими параметрическими уравнениями. \[x = 3\sin \left( t \right)\hspace{0.5in}y = 3\cos \left( t \right)\hspace{0.5in}0 \le t \le 2\pi \]

Показать решение

Мы знаем, что это окружность радиуса 3 с центром в начале координат из нашего предыдущего обсуждения графических параметрических кривых. Мы также знаем из этого обсуждения, что он будет трассирован ровно один раз в этом диапазоне.

Итак, мы можем использовать формулу, которую мы вывели выше. Сначала нам понадобится следующее:

. \[\frac{{dx}}{{dt}} = 3\cos \left( t \right)\hspace{0,5 дюйма}\hspace{0,25 дюйма}\frac{{dy}}{{dt}} = — 3\sin\left( t \right)\] 9{{\,2\pi}}{{\,dt\,}}\\ & = 6\pi \end{align*}\]

Поскольку это круг, мы могли бы просто использовать тот факт, что длина круга — это длина его окружности. В данном случае это хороший способ проверить наш результат.

Давайте рассмотрим одно возможное последствие, если кривая трассируется более одного раза, и мы пытаемся найти длину кривой, не принимая этого во внимание.

Пример 2 Используйте формулу длины дуги для следующих параметрических уравнений. \[x = 3\sin \left( {3t} \right)\hspace{0.5in}y = 3\cos \left( {3t} \right)\hspace{0.5in}0 \le t \le 2\ Пи \]

Показать решение

Обратите внимание, что это тот же круг, что и в предыдущем примере, поэтому его длина по-прежнему равна 6\(p\). Однако для заданного диапазона, который мы знаем, он будет трассировать кривую три раза, а не один раз, как требуется для формулы. Несмотря на это ограничение, давайте все же воспользуемся формулой и посмотрим, что произойдет.

В этом случае производные

\[\frac{{dx}}{{dt}} = 9\cos \left( {3t} \right)\hspace{0,5 дюйма}\hspace{0,25 дюйма}\frac{{dy}}{{dt} } = — 9{{\,2\pi}}{{9\,\,dt\,}}\\ & = 18\pi \end{align*}\]

Ответ, который мы получили из формулы длины дуги в этом примере, был в 3 раза больше фактической длины. Вспоминая, что мы также определили, что этот круг будет повторяться три раза в заданном диапазоне, ответ должен иметь некоторый смысл.

Если бы мы хотели определить длину окружности для этого набора параметрических уравнений, нам нужно было бы определить диапазон \(t\), для которого эта окружность очерчивается ровно один раз. Это \(0 \le t \le \frac{{2\pi}}{3}\). Используя этот диапазон \(t\), мы получаем следующее для длины. 9{{\,\frac{{2\pi}}{3}}}{{9\,\,dt\,}}\\ & = 6\pi \end{align*}\]

это правильный ответ.

Будьте осторожны и не делайте предположения, что это всегда произойдет, если кривая трассируется более одного раза. Тот факт, что кривая повторяет \(n\) раз, не означает, что формула длины дуги даст нам \(n\) раз фактическую длину кривой!

Прежде чем перейти к следующему разделу, давайте заметим, что мы можем привести формулу длины дуги, полученную в этом разделе, в ту же форму, что и при первом рассмотрении длины дуги. Единственное отличие состоит в том, что мы добавим определение для \(ds\), когда у нас есть параметрические уравнения. 92}} \,\,dt\hspace{0.25in}{\mbox{if }}x = f\left( t \right),y = g\left( t \right),\,\,\alpha \ le t \le \beta \end{align*}\]

Формула длины дуги в исчислении: полное и подробное руководство

Вычисление длины дуги на графике работает иначе, чем если бы вы пытались найти длину сегмента окружности. Если длину сегмента окружности можно вычислить с помощью некоторых простых знаний геометрии (или тригонометрии), то найти длину дуги функции немного сложнее. Для этого нужно использовать вычисления.

Определение длины дуги работает почти так же, как определение длины между отрезками прямой. В каком-то смысле вы могли бы возразить, что именно это вы и делаете, если не считать бесконечно точного масштаба, потому что разрешение кривой, насколько вы можете судить, бесконечно. Нет зазубренных краев или линейных сегментов.

Быстрая навигация

 

Использование сегментов линии для аппроксимации длины дуги

Что такое производная?

Интегралы

Общие правила интегрирования

Формула длины дуги

Более сложные функции

Существуют ли исключения в формуле длины дуги?

Что нужно иметь в виду

Заключительные мысли

Использование сегментов линии для аппроксимации длины дуги

Для начала предположим, что у вас есть заданная функция без прерываний и с равномерной гладкостью. Чтобы получить общее представление о том, какой длины была дуга, вы должны начать с разделения функции на отрезки, расположенные с одинаковыми значениями x. Например, вы можете нанести сегменты дуги на координаты x = 2, x = 4, x = 6 и т. д.

Затем вы используете теорему Пифагора для вычисления расстояний между двумя точками. Однако вы соединяете две точки напрямую, а не по кривой. Это означает, что вам может не хватать длины или добавлена ​​дополнительная длина, если участок графика представляет собой вогнутую кривую. Что вы делаете?

Вы можете взять больше секций, поместив точки сегмента линии в точки x = 1, x = 2, x = 4 и т. д. Это будет более точно аппроксимировать кривую графика. Тем не менее, это все равно не будет полностью соответствовать. Неважно, насколько маленькими вы сделаете секции: вы не сможете точно сопоставить длину секции с помощью обычной математики.

Здесь в игру вступает исчисление. Вы должны взять производные и использовать интегральные функции, чтобы использовать формулу длины дуги в исчислении. Мы познакомим вас с определениями производных и интегралов.

Что такое производная?

Производная любой функции есть не что иное, как наклон. Существует несколько правил и общих производных функций, которым вы можете следовать на основе функции. Например, если у вас есть константа, такая как x = 6, производная равна 0, потому что наклона нет. Для функции f(x) – ax, где a – наклон, производная – это переменная a.

Если у вас есть x ² , производная по x равна 2x. Другими словами, в любой заданной точке x на функции, когда предел приближается к нулю для данного значения delta-x, ее производная будет равна 2x.

Это всего лишь несколько примеров использования производной, и вам необходимо знать или иметь к ним доступ при определении длины дуги.

Интегралы

 

Изображение pixabay

Интеграл — это одна из двух фундаментальных операций в исчислении, вторая — дифференцирование. Когда мы говорили об отрезках прямой как о части длины дуги, это была грубая форма дифференциации. Интеграл — это действие по взятию дискретных сегментов и объединению их в один. Как и в случае с производными, интегралы имеют свои правила и основные функции.

Общие правила интегрирования

Интеграл от ax dx, где dx — это просто еще один способ сказать «по мере приближения дельта-x к нулю», равен ax + C, где C — постоянная интегрирования. Вам не обязательно знать постоянную интегрирования, потому что это может быть любое число, когда вы имеете дело с неопределенным интегралом.

Неопределенный интеграл не устанавливает верхнюю или нижнюю границу для x. На практике вы не встретите много функций с отрицательными значениями x или y, поэтому вы будете просто брать площадь под кривой в положительном квадранте x-y.

Когда вы пытаетесь найти формулу длины дуги, вам нужно использовать определенные интегралы. Определенный интеграл устанавливает границы на x. Чтобы найти определенный интеграл, то есть площадь под кривой, вы находите интеграл, используя большее значение x, затем меньшее значение x, и берете разницу двух чисел.

Формула длины дуги

Формула для длины дуги: ∫ _a ^b √1+(f’(x)) ² dx. Когда вы видите утверждение f’(x), это просто означает производную от f(x). В интеграле a и b являются двумя границами сегмента дуги. Следовательно, все, что вам нужно сделать, это взять производную функции, вставить ее в соответствующий слот и подставить два значения x.

Например, предположим, что у вас есть ∫ ₁ ⁴ √1+(f’(x)) ² dx. Предположим также, что f(x) равно 2×2 + 2. В этом случае не имеет значения, что в конце есть + 2. Все, что нужно было найти, это производная, которая остается неизменной независимо от того, где на самом деле находится функция на графике. В этом случае производная 2×2 равна 4x. В любой точке графика это будет производная.

Теперь вы можете подставить 4x в формулу: ∫ ₁ ⁴ √1+(4x) ² dx.

После этого вам нужно подставить вместо x первое значение, равное 1. ∫ ₁ ⁴ √1+(4(1)) ² dx. Помните порядок операций при работе с этими числами: сначала вы должны умножить 1 на 4, чтобы получить 4, а затем возвести в квадрат, чтобы получить 16. 16 + 1 равно 17, поэтому интеграл этой функции равен квадратному корню из 17.

Затем используйте ту же формулу и подставьте 4 в x. ∫ ₁ ⁴ √1+4(4)) ² дх. В этом случае вы получите квадратный корень из 257. Так как преобразование квадратных корней в дальнейшее не упрощает, вы должны выразить длину дуги для этой функции и этих границ как √257 – √17. Помещение двух чисел под одним радикалом будет неправильным; √9-4 не то же самое, что √9 – √4.

Более сложные функции

Если у вас есть более сложная функция, например, кубическая функция или многочлен более высокой степени, вычисление производных и интегралов будет не таким простым делом. Здесь может помочь метод замещения. Заменив всю функцию переменной u и взяв соответствующую производную, работать с функцией будет проще, чем это было бы в противном случае.

Просто помните, что если вы используете метод подстановки, вы должны обратить подстановку, поместив исходные функции обратно в интеграл, где они должны быть. В противном случае вы, скорее всего, получите неправильный ответ.

Существуют ли исключения из формулы длины дуги?

 

Изображение Pixab​ay

Формула длины дуги работает только для функций, которые не имеют изломов или асимптот. Например, если у вас есть функция с асимптотой при x = 4 с каждой стороны, вы не можете использовать формулу длины дуги для двух секций. Точно так же, если есть предел, вы не можете вычислить длину за этим пределом.

Нахождение длины дуги функционально ничем не отличается от нахождения длины диагонального отрезка на графике, хотя для получения правильного результата приходится использовать более сложную математику. Всегда проверяйте свою функцию перед запуском проблемы.

О чем следует помнить

 

Изображение от Pixabay

Если у вас есть учебник по математическому анализу или шпаргалка со списками правил для производных и интегрирования, держите их под рукой или запомните. Если вы достаточно поработаете над этими задачами, то правила начнут запоминаться естественным образом, но поначалу неплохо держать записи поблизости. Это снижает вероятность того, что вы будете использовать неправильную производную при решении задач.

Не забудьте изучить следующее:

• Интегралы

• Производные

• Правило замены

Практическое применение определения длины дуги

Если вам дана функция и вам нужно найти длину дуги, она может пригодиться в различных ситуациях. Одним из самых известных является машиностроение. Если у вас есть линии электропередач, отстоящие друг от друга на определенную длину, и вы знаете, что их изгиб под действием силы тяжести может быть выражен заданной функцией, вы можете вычислить, сколько проводов нужно пройти от одного полюса к другому.