Длина дуги кривой: Как найти длину дуги кривой с помощью интеграла

Как найти длину дуги в прямоугольных координатах?

Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича).

Для запоминания основных моментов схема интегрирования и вычисление дуги кривой из примера в пример будет повторяться. По возможности сами решения будут проиллюстрированы графиками кривых.

Пример 2.117 (2431) Вычислить длину дуги кривой y=x^3/2 (полукубическая парабола Нейля) xє[0;4] .
Вычисление: Найдем производную заданной функции по переменной x:

График полукубической параболы Нейля имеет вид

Выписываем пределы интегрирования:
a=0, b=4 (известны из начального условия).
По формуле находим длину дуги на заданном отрезке:

Во время интегрирования для приведения подынтегральной функции к табличному виду выполнили замену переменных.
При этом нужно перечислять пределы интегрирования.
В результате пришлось интегрировать корневую функцию, а длина дуги после вычислений приблизительно равна l=9,07.
Помните, что все длины измеряются в единицах (од.) !!!

Пример 2.118 (2432) Найти длину дуги кривой y²=2px (парабола) xє[0;x₀].
Вычисление: Поскольку отрезок дуги параболы задан в пределах [0;x₀], то заданная функция будет иметь вид положительной ветки корневой функции
Вычислим производную функции по переменной x:

Запишем пределы интегрирования:
a=0, b=x₀ .

График параболы приведен ниже

Вычислим длину дуги через определенный интеграл:
для сведения к простым формулам интегрирования применяем замену переменных, при этом не забываем перечислить изменение пределов интегрирования:

В конце вычислений применено интегрирование частями.

Пример 2.119 (2434) Найти длину дуги кривой y=e^x, [0;x₀].
Вычисление: Для интегрирования находим производную (по переменной x) экспоненты :
y’=(e^x)’=e^x.
Поскольку показатель не содержит никаких коэффициентов при переменной, то производная равна самой экспоненте.
Из начального условия выписываем пределы интегрирования:
a=0, b=x₀.
График экспоненты имеет вид

Чтобы вычислить длину дуги экспоненты переходим к новой переменной.
Это ведет к изменению и пределов интегрирования и самого дифференциала:

Напоследок расчетов приходим к формуле дуги, которая содержит корневую и логарифмическую зависимости от бегущей координаты.

Пример 2.120 ( 2435) Найти длину дуги кривой x=1/4y²-ln(y)/2, yє[1;e].
Вычисление: Вычислим производную (по переменной y ) заданной функции:

Приведенная формула работает и для обратных функций x=x(y), особенно если функция изменяется как показано на графике

Пределы интегрирования: a=1, b=e .
Находим длину дуги кривой на заданном отрезке:

При возведении к квадрату производной получим простую для интегрирования функцию, которая в результате дает l=(e²+1)/4.

Пример 2.121 (2436) Вычислить длину дуги кривой

Вычисление: Найдем производную по переменной x функции:

Пределы интегрирования для этой дуги равны [0;b].
График исследуемого логарифма имеет вид

Интегрированием находим длину дуги кривой:

Со всеми превращениями подинтегральной функции попробуйте разобраться самостоятельно.

Пример 2.122 (2437) Вычислить длину дуги кривой y=ln(cos(x)), 0<x<a<Pi/2.
Вычисление: Найдем производную (по переменной x) заданной функции :

Запишем пределы интегрирования: (известны за условием).

Вычислим длину дуги кривой на заданном отрезке:

Если воспользоваться тригонометрическими формулами то перейдем к тангенсу, а сама длина дуги равна
l=ln(tg (Pi/4+a/2)).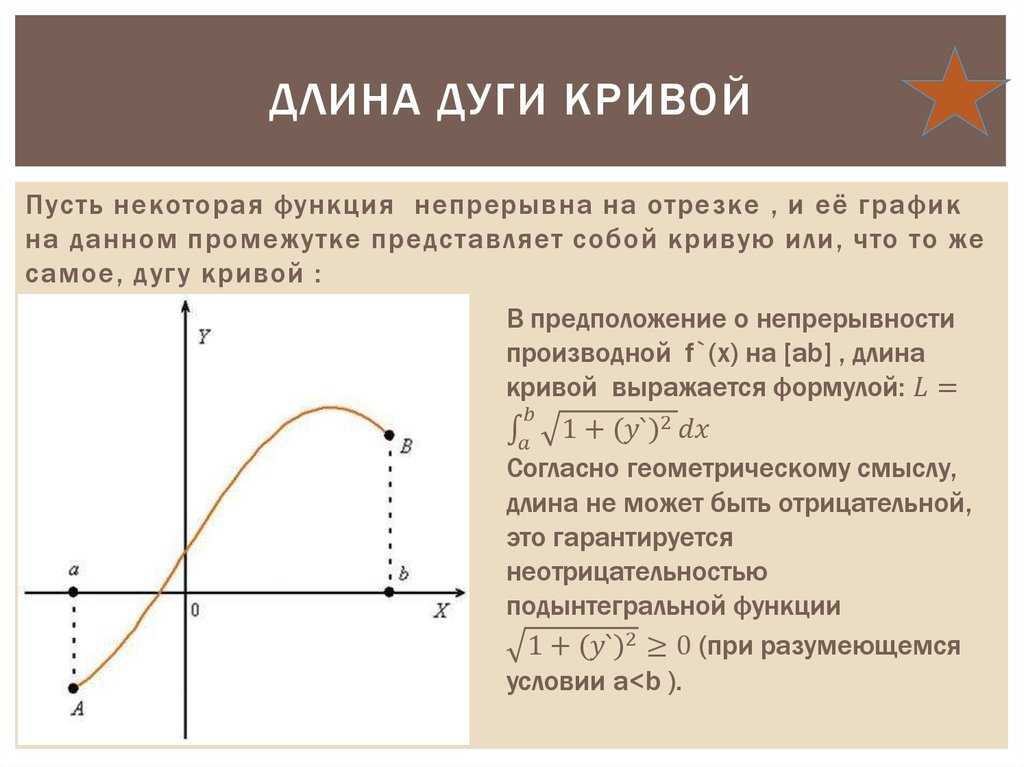

Пример 2.123 Найти длину дуги кривой y=ln(x),
Вычисление: Вычисляем производную от логарифма:
y’=1/x.
Пределы интегрирования переписываем из условия:

График логарифма имеет вид

Интегрирование по длине дуги достаточно непростое, требует добрых умений.
Расписав подынтегральную функцию, и применив замену переменных к одному из интегралов, приходим к логарифмам, которые при указанных пределах интегрирования несколько упрощаются.

Невзирая на трехэтажные выражения конечное значение длины дуги выраженно простой зависимостью.

Пример 2.124 Найти длину дуги кривой y=ln(1-x₂), x[0;0,5].
Вычисление: Найдем производную (по переменной x) заданной функции :

Из начального условия имеем такие пределы интегрирования: [0;0,5].
График исследуемого логарифма имеет вид

Вычисляем длину дуги логарифма:

Если округлить конечное значение, то будем иметь l=0,5986.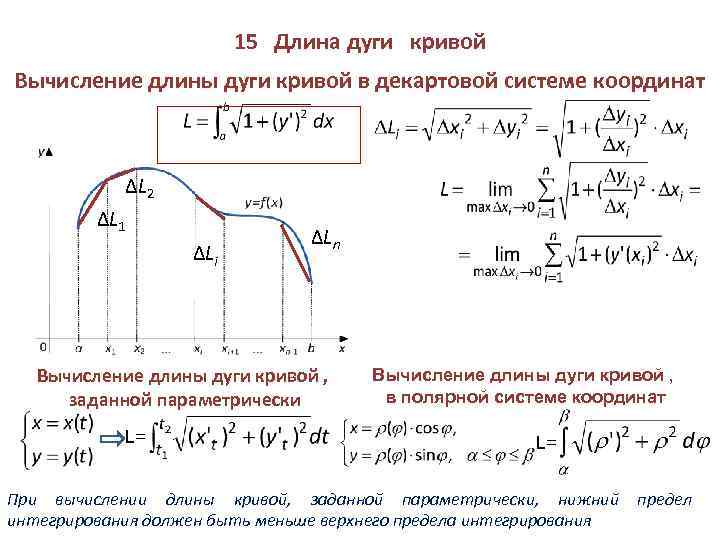

Пример 2.125 (2439) Вычислить длину дуги кривой
Вычисление: Поскольку график заданной функции симметричен относительно оси Ox, то вычислим длину дуги для положительной части функции

и результат умножим на 2.
Найдем производную функции и саму подинтегральную функцию:

Пределы интегрирования известны:

График веток в декартовой плоскости имеет вид.

При нахождении длины дуги дважды выполняем замену переменных.
Как и в предыдущих примерах ответ получаем через логарифмы

Кому в учебе придется вычислять подобное задание, просьба разобраться с превращениями.
А еще лучше — придумать и решить подобный пример.

Пример 2.126 (2438) Найти длину дуги кривой (трактриса).
Вычисление: Запишем производную по переменной y трактрисы (см. 2408):

Пределы интегрирования:

График трактрисы имеет вид

По формуле дуги кривой интегрируем и находим длину трактрисы:

Конечная формула достаточно простая для расчетов.
От края следует несколько отойти, в ином случае длина трактрисы направляется к безконечности.

Пример 2433 Найти длину дуги кривой (цепная линия) от точки A(0;a) к точке B(b;h) .
Вычисление: Цепная линия — это кривая, форму которой принимает цепь (нить) под действием силы притяжения, которая подвешена за оба конца.
Поскольку и , то

Найдем производную трактрисы:

Пределы интегрирования по аргументу следующие:

Рисунок цепной линии приведен ниже

Вычислим длину дуги кривой на заданном отрезке:

Пример 2440 Найти длину дуги астроиды
Вычисление: Для астроиды оси прямоугольной системы координат делят линию на 4 части (смотри 2429), поэтому длину будем искать для чверти и результат умножим на 4.
Выражаем функцию для чверти астроиды

Найдем производную от полученной зависимости и подинтегральную функцию:

Пределы интегрирования: [0;a] (для чверти астроиды).
Вычислить длину дуги астроиды на практике достаточно легко:

Дело в том, что единицы сокращаются и получаем простой табличный интеграл.
В результате длина астроиды равна l=6a.

4.2. Длина дуги плоской кривой

Предварительно изучите по учебнику Г. М. Фихтен-гольца главу XII, п° п° 199,201, 202. Разберите подробно примеры, решенные в п° 201.

I. Уравнение кривой задано в декартовой системе координат. В теоретическом курсе доказывается, что длина дуги плоской кривой у = f (х) может быть вычислена при помощи определенного интеграла:

I= J у I + у’Ых

ИЛИ

I= j V I — f — х’2 dy,

где а и b — абсциссы, а с и d — ординаты точек концов данной дуги.

483. Вычислить длину дуги параболы у2 = 4х от точки х = 0 до х = I.

Решение. Для вычисления длины данной дуги воспользуемся второй из данных формул. Заметим, что при х = 0 будет у = 0, а при х = I будет у = + 2.

Из уравнения параболы находим, следователь

но,, отсюда

484. Вычислить длину дуги кривей у=\—In cosх от точки M (О, I) до точки N \ 2 J.

Решение. Для вычисления длины дуги воспользуемся первой из данных формул, тогда у = I — Incosx, , следовательно,

до точки В

485. Вычислить длину дуги цепной линии

от точки А

488. Найти длину дуги OA параболы, где

0(0; 0), А (2; 4). Вычисление провести двумя способами.

487. Спрямить кривую

488. Вычислить длину дуги кривой заключенной внутри параболы

489. Найти длину дуги астроиды

490. Найти длину дуги полукубической параболы

Между точками х = 0 и х = 2а.

491. Найти длину дуги кривойIn у от точки у = I до точки у = 2.

492. Найти длину дуги кривойОт х = а

До х = 6.

2. Кривые заданы параметрическими уравнениями или в полярной системе координат. Как известно из теоретического курса, длина дуги кривой, заданной параметрическими уравнениямиГде функции иНепрерывны вместесо своими производными

ИНаВычисляется по формуле:

493.

следовательно,

Решение. Найдем точки пересечения кривой с осью Ох:

;___L/3 = 0; ti = Qi t2 = VT.

Так как данная кривая расположена симметрично относительно оси Ox1 что видно из уравнений кривой, то

VT VH

I = 2 j V(It)2 — j— (I — t2)2 dt = 2 j (I — f t2) dt =

о о

0 < ф < Зя. Найдем р’=а sin2 — • cos —. Вычислим

3 3

Рекомендуется подробнее исследовать данную функцию и построить ее график.

Из теоретического курса известно, что длина дуги кривой р=/(ф), заданной в полярной системе координат, где функции р=/ (ф) и р’ = [/(ф)]’ непрерывны на ф2 < ф <ф2, вычисляется по формуле:

Р _

1 = J ]/У2 + P2 dtp.

<Р I

496. Найти длину кривой: р = a sin3 —.

Решение. Найдем пределы интегрирования. Когда п 3

угол ф изменяется от 0 до —я, полярный радиус р воз-

растает от 0 до а. Затем при изменении угла ф от — 7г

до Зл величина р убывает от а до 0. Таким образом, 0 < ф <

сумму:

Длина дуги данной кривой равна:

497. Вычислить длину кардиоиды:

Решение. Так как данная функция—четная, то, следовательно, кривая расположена симметрично относительно Полярной оси. Поэтому достаточно найти половину длины д<уги кардиоиды, для которой полярный угол ф изменяется от 0 до я, и удвоить полученный результат:

498. Вычислить длину дуги астроиды:

499. Вычислить длину дуги эволюты круга: отДо

500. Вычислить длину одного витка спирали Архимеда:

501. Вычислить длину окружности:

502. Найти длину дуги гиперболической спирали от точкиДо точки

< Предыдущая		Следующая >

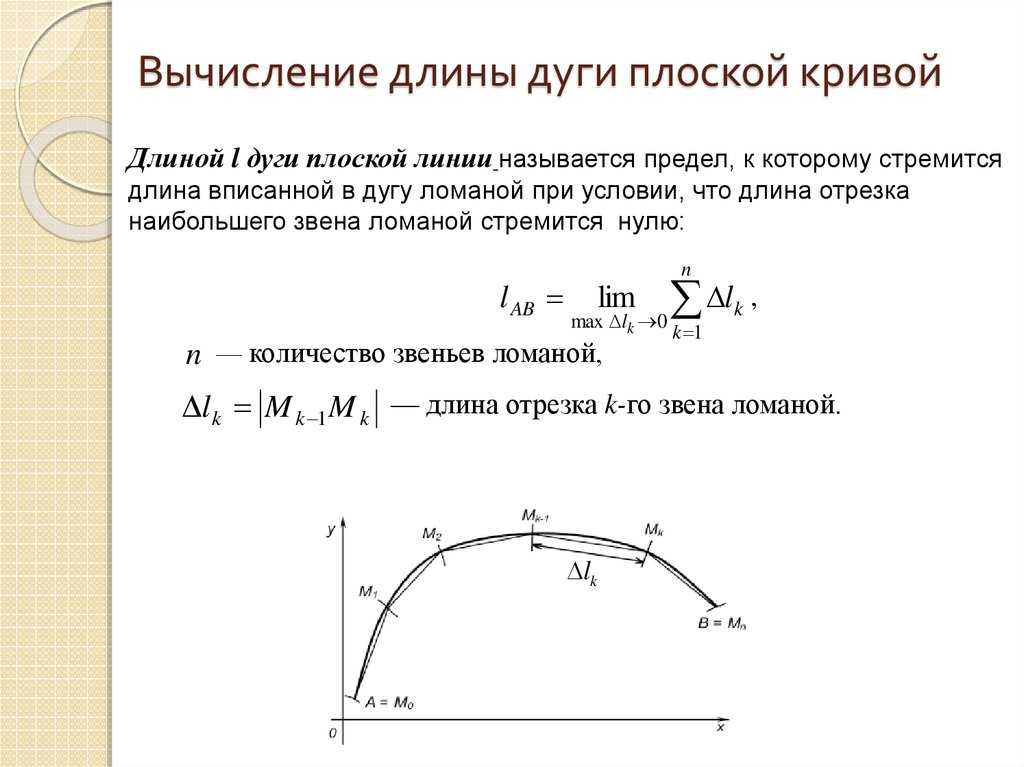
Длина дуги кривой

Математические слова: Длина дуги кривой

индекс: нажмите на букву






индекс: предметные области

Дуга Длина кривой

Длина кривой или линии.

Длина дуги может быть найдена по одной из формул ниже для любой дифференцируемой кривой, определяемой прямоугольными, полярными, или параметрические уравнения.

Чтобы узнать длину дуги окружности, см. дуга круга.

Формула:
	, где a и b представляют x , y , t или значения θ в зависимости от ситуации и ds можно найти следующим образом. 1. В прямоугольной форме используйте любой из следующих вариантов: 2. В параметрической форме используйте . 3. В полярной форме используйте .
Пример 1: прямоугольный	Найдите длину дуги кривой y = (1/6) x ³ + (1/2) x ^–1 из
	х = 1 до х = 2.
Пример 2: параметрический	Найти длину дуги за один период циклоиды х = t – sin t , y = 1 – cos t . Значения t варьируются от 0 до 2π.
Пример 3: Polar	Найти длину первого витка логарифмической спирали r = e ^θ . Значения θ варьируются от 0 до 2π.

См. также

Площадь поверхности революции

эта страница обновлена 19 июля 17
Математические слова: термины и формулы от алгебры I до исчисления
написано, проиллюстрировано и создано веб-мастером Брюсом Симмонсом
Авторское право © Брюс Симмонс, 2000 г.

Как найти длину дуги в прямоугольных координатах?

4.2. Длина дуги плоской кривой

Длина дуги кривой

Добавить комментарий Отменить ответ