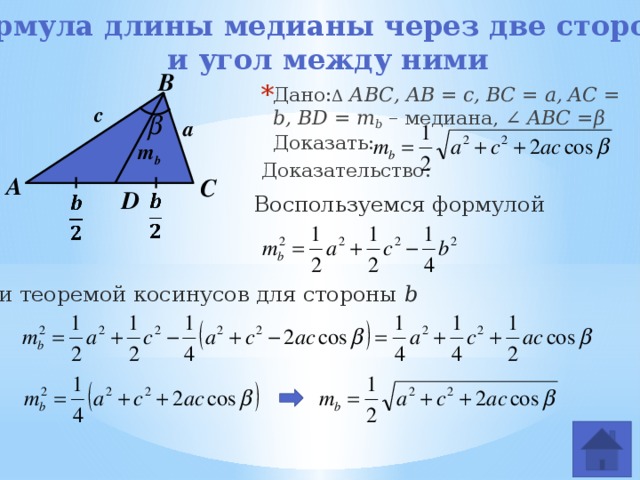
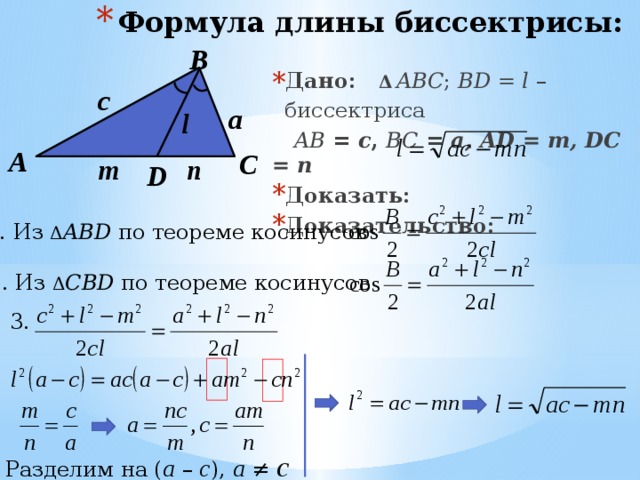
№№ | Название тематических разделов | Произвольный треугольник | Прямоугольный треугольник | Равнобедренный треугольник | Равносторонний треугольник |
1. | Элементы треугольника | Три угла и три стороны | Гипотенуза и два катета. Прямой угол и два острых угла | а Две равные боковые стороны и основание. Два равных острых угла и третий угол может быть острым, тупым и прямым | Стороны равны и углы по 600 |
2. | Признаки равенства треугольников Вывод: Из равенства треугольников следует равенство всех соответствующих элементов: высот, биссектрис, медиан, радиусов вписанных и описанных окружностей и т. | 1 признак: Если две стороны одного треугольника и угол между ними равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. 2 признак: Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. 3 признак: Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. | 1 признак: Если катеты одного прямоугольного треугольника равны катетам другого прямоугольного треугольника, то треугольники равны. 2 признак: Если катет и острый угол одного прямоугольного треугольника равны соответственно катету и острому углу другого прямоугольного треугольника, то такие треугольники равны. 3 признак: Если гипотенуза и острый угол одного прямоугольного треугольника равны соответственно гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны. 4 признак: Если гипотенуза и катет одного прямоугольного треугольника равны соответственно гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны. | 1 признак: Если угол и боковая сторона одного равнобедренного треугольника равны углу боковой стороне другого равнобедренного треугольника, то треугольники равны 2 признак: Если угол и основание одного равнобедренного треугольника равны углу основанию другого равнобедренного треугольника, то треугольники равны 3 признак: Если боковая сторона и основание одного равнобедренного треугольника равны боковой стороне и основанию другого равнобедренного треугольника, то треугольники равны | Признак: Если одна из сторон одного равностороннего треугольника, равна стороне другого треугольника, то треугольники равны. |
3. | Признаки подобия треугольников | 1 признак:. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2 признак: Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны. 3 признак: Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны. | 1 признак: Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны 2 признак:. Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны 3 признак: Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны. | 1 признак: Если равнобедренные треугольник имеют равные углы между боковыми сторонами, то такие треугольники подобны. 2 признак: Если равнобедренные треугольники имеют равные углы между основанием и боковой стороной, то такие треугольники подобны. 3 признак: Если основание и боковая сторона одного равнобедренного треугольника пропорциональны основанию и боковой стороне другого равнобедренного треугольника, то такие треугольники подобны. | Любые равносторонние треугольники подобны. |
4. | Свойства треугольников | 1. Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1 2. Биссектриса треугольника разделяет противополжную сторону на отрезки пропорциональные сторонам угла. y:b=x:a 3. 4.Против большей стороны лежит больший угол, и наоборот. 5.Сумма углов треугольника равна 180 º . 6. Любая сторона треугольника меньше суммы двух других сторон и больше их разности | 1.Сумма острых углов в прямоугольном треугольнике равна 90 градусов 2. В прямоугольном треугольнике катет лежащий против угла в 30 градусов равен половине гипотенузы. 3. Если в прямоугольном треугольнике катет равен половине гипотенузы, то он лежит против угла в 30 градусов. 4. В прямоугольном треугольнике, медиана, проведенная из вершины прямого угла, равна половине гипотенузы и равна радиусу описанной окружности 5. Если в прямоугольном треугольнике угол равен 450, то треугольник равнобедренный 6. пропорциональные отрезки а= h = | 1.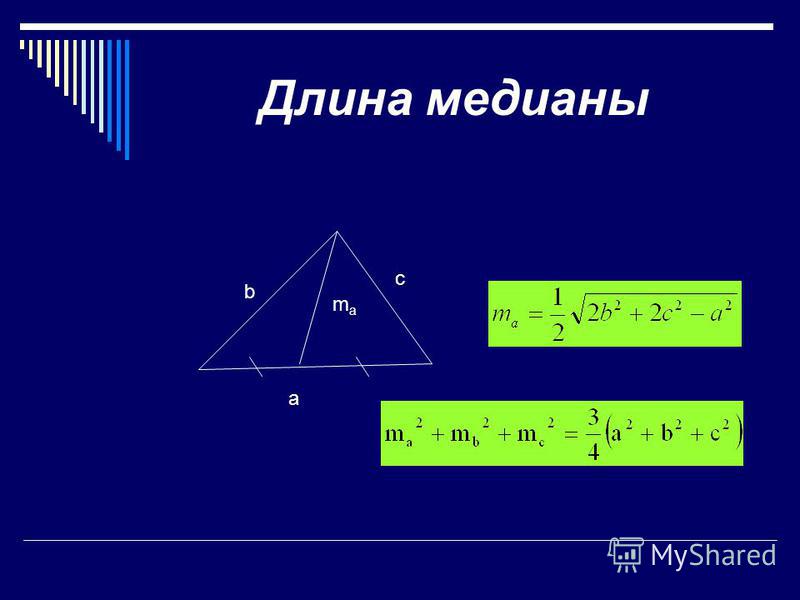 В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике углы при основании равны.2.В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой. 3 В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой. 4. В равнобедренном треугольнике медиана, проведенная к основанию, является высотой и биссектрисой. 5. Средние линии проведённые параллельно к боковым сторонам образуют ромб. 6. Все замечательные точки лежат на биссектрисе (медиане, высоте) проведённой к основанию. 7. В равнобедренном треугольнике — биссектрисы, высоты, медианы, проведенные из вершин при основании, равны; | 1.Все углы равностороннего треугольника равны по 60º. 2. Высота, медиана и биссектриса, проведённые к каждой из сторон равностороннего треугольника, совпадают: 3.Точка пересечения высот, биссектрис и медиан называется центром правильного треугольника и является центром вписанной и описанной окружностей 4. |
5. | Окружность вписанная в треугольник | В любой треугольник можно вписать окружность . Её центром является точка пересечения биссектрис треугольника Формула нахождения радиуса: p= | Формула нахождения радиуса: r=1/2 (a + b –c) | Формула нахождения радиуса: r = | 1.Расстояние от точки пересечения высот, биссектрис и медиан до любой стороны треугольника равно радиусу вписанной окружности. 2. Сумма радиусов вписанной и описанной окружностей правильного треугольника равна его высоте, медиане и биссектрисе: R+ r= h. 3.Радиус вписанной в правильный треугольник окружности в два раза меньше радиуса описанной окружности: Формула нахождения радиуса : r = 1/2R = |
6. | Окружность описанная около треугольника | Около треугольника можно описать окружность, притом только одну. Её центром будет являться точка пересечения серединных перпендикуляров . Формулы нахождения радиуса: R = R= | Центр описанной окружности совпадает с серединой гипотенузы, а радиус равен: 1. Половине гипотенузы. 2. Медиане, проведенной к гипотенузе. Формула нахождения радиуса: R = ½ c | Центр окружности лежит высоте, проведенной к основанию равнобедренного треугольника Формула нахождения радиуса: | 1. Формула нахождения радиуса: R = |
7. | Формулы площадей треугольников | 1. Площадь треугольника равна половине произведения основания на высоту S = ½ aha 2. Площадь треугольника равна половине произведения двух сторон на синус угла между ними. S =1/2ab sin 3. Нахождение площади произвольного треугольника по формуле Герона. S= P = ½( a + b +c) 4. S = 5. S= 1/2Pr | 1.Площадь прямоугольного треугольника равна половине произведения катетов S= 1/2ab | S =1/2a2 sin 2. P = ½( 2а +c)
| S = |
8. | Основные формулы | 1.Теорема косинусов: a² = b²+c² — 2bc cosα b² = a²+c² — 2ac cosβ c² = b²+a² — 2ab cosγ 2.Теорема синусов: a/sinα = b/sinβ = c/sinγ = 2R 3.Длина медианы: mb = 4.Длина бессектрисы: la | 1. Теорема Пифагора: Квадрат гипотенузы равен сумме квадратов катетов АС2 + ВС2 = АВ2 2. sinA=a/c cosA=b/c tgA=a/b ctgA=b/a 3.Длина медианы: ma2 + mb2 = 5 mc2 = 5/4c2 4.Пропорциональные отрезки прямоугольного треугольника: h2 = ac bc a2=ac c b2= bc c | ||
9. | Задачи, с практическим содержанием | Задача: Стороны треугольника равны 5 и 6. Угол между ними составляет 60 градусов. Найдите площадь треугольника. Решение: S=1/2*ab*sin a. Подставим значения: S=1/2*5*6*sin 60=15√3/2 Ответ: S=15√3/2 | Задача: в треугольнике ABC , a=6, b=8, c=10. Найти площадь треугольника. Решение: для вычисления площади, сначала нам нужно найти полупериметр данного треугольника: p=a+b+c/2. Подставляем: p=6+8+10/2=12 Теперь найдём площадь: S=√p(p-a)(p-b)(p-c)=√12(12-6)(12-8)(12-10)=√576=24 Ответ: S=24 | Задачи : №1 .Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 300. Боковая сторона треугольника равна 5. Найдите площадь этого треугольника. Решение: Известно, что в равнобедренном треугольнике боковые стороны равны. Используем формулу для нахождения площади: *Площадь треугольника равна половине произведения двух соседних сторон на синус угла между ними. В данном случае: S=1/2AC*BC*sin c =1/2*5*5*sin 30=1/2*25*1/2=6,25 Ответ: S = 6,25 №3 Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника . Решение :Если опустить высоту на основание то она делит основание на две равные части по теореме Пифагора: CD=4 S=1/2*АB*CD=1/2*6*4=6/2*4=3*4=12 Ответ: S=12 | |
10. | Задачи | Задача 1. Через вершину С треугольника АВС проведена прямая параллельная его биссектрисе АА1, и пересекающая прямую АВ в точке D. Докажите,что AC=AD. Решение: 1 Способ: 1.)угол 3=углу 1(т.к.накрест лежащие, при DC||AA1) 2)угол4=углу 2(т.к они соответственные при DC||AA1) 3) угол 3=углу 1=углу2=углу 4 Тогда треугольник DCA – равнобедренный т. 2Способ: DC||AA1,тогда угол 3 = углу 1(накрест лежащие) Угол САВ — внешний для треугольника DCA. Угол САВ=угол 4+угол 3, но угол САВ=угол1+ угол2 Угол 1+угол 2=угол 4+угол 3, с учетом п.1 заключаем, что угол 4= углу 2 3)тогда угол 3=углу 1=углу 2=углу 4, угол 4 = углу 3 , треугольник DCA равнобедренный т.е. АС=AD ч.т.д. | Задача 2. Медиана и высота треугольника, проведенные из одной вершины треугольника, делят этот угол на три равные части. Доказать, что треугольник прямоугольный. Решение: Треугольник АСВ, СМ – высота ,CN- медиана ,т.е.AN=NB. 1 Способ: 1.)треугольник АСМ=NCM- прямоугольные , т.к. СМ — общая, угол 1 = углу 2. 2) Из равенства треугольников следует: AM=MN и AC=CN. 3) Т.к. CN — медиана ,т.е. AN = NB. То MC=0.5AN=0. 4) Проведем NK, NK перпендикулярно ВС. 5) треугольник CMN= треугольнику CNK – прямоугольные, CN – общая, угол2 = углу 3, MN=NK=0.5NB. 6) треугольник NKB : угол NKB – 90° . NK=0.5NB,тогда угол NBC=30°. 7) треугольник СМВ : угол MCB= 90°- 30°=60°. то угол 2=30° н угол 1=30°. Следовательно угол ACB = 90° . 2 способ: 1) Очевидно треугольник AСМ подобен треугольнику АВС. Из подобия треугольников следует угол 1= углу ACM = углу B 2) треуг.САМ = треуг.CNM — прямоугольные (общая сторона СМ, угол l = углу 2). Тогда AC=CN. Отсюда, треугольник ACN — равнобедренный. 3) треуг.ACN : СМ — биссектриса, высота, медиана. Следовательно, В прямоугольном треугольнике СМВ :CN — биссектриса угла MCB. По свойству биссектрисы треугольника Т.е. СМ =0.5СВ . Что означает: угол В = 30 градусам. 5) но угол B= углу 1 = углу 2 = углу 3 = 30 градусам, угол C =3* угол1=90°. | Задача 3. На высоте равнобедренного треугольника АВС (АВ = ВС) ВВ1,, взята точка D. Докажите,, что : I) треугольник АВD = треугольнику BDC 2) треугольник ADB1=треугольнику DB1C. Решение: Первая часть — равенство треугольников ABD и BDC докатывается Легко. Рассмотрим способы доказательства второго равенства. 1 Способ: Треугольник ADB1= треугольнику DB1C т.к. а) AD=DC из равенства треугольников ABD и В DC, б) B1D-общая. в) угол ADB1 = углу В1DC (т.к. смежные с ними углы ADB и BDC равны из равенства треугольников ABD и BDC). 2 способ. Треугольник ADC — равнобедренный (из равенства треугольников ABD и BDC). DB1- высота этого треугольника, а значит и биссектриса угла ADC. Тогда треугольник ADB1= треугольнику DB1C по двум сторонам и углу между ними. | Задача 4. Стороны треугольника a,b,c. Найдите радиус окружности, имеющей свой центр на стороне с и касающейся 2-х других сторон a и b. (a,b,c— заданные числа.) Решение: 1 способ: 1.) углы А и В находим по теореме косинусов. 2.) из треугольника ADO 3.) из треугольника OEB 4.)из уравнения 2 способ: 1.) обозначим AD через х 2.)из треугольника AOD 3.) из треугольника COD 4.) CE=CD=b-x( по свойству касательны, проведенных из одной точки) 5.) BE=a-b+x 6.)из треугольника OBE 7.) решим уравнение |
Формулы для нахождения медианы. Площадь треугольника онлайн расчет
Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.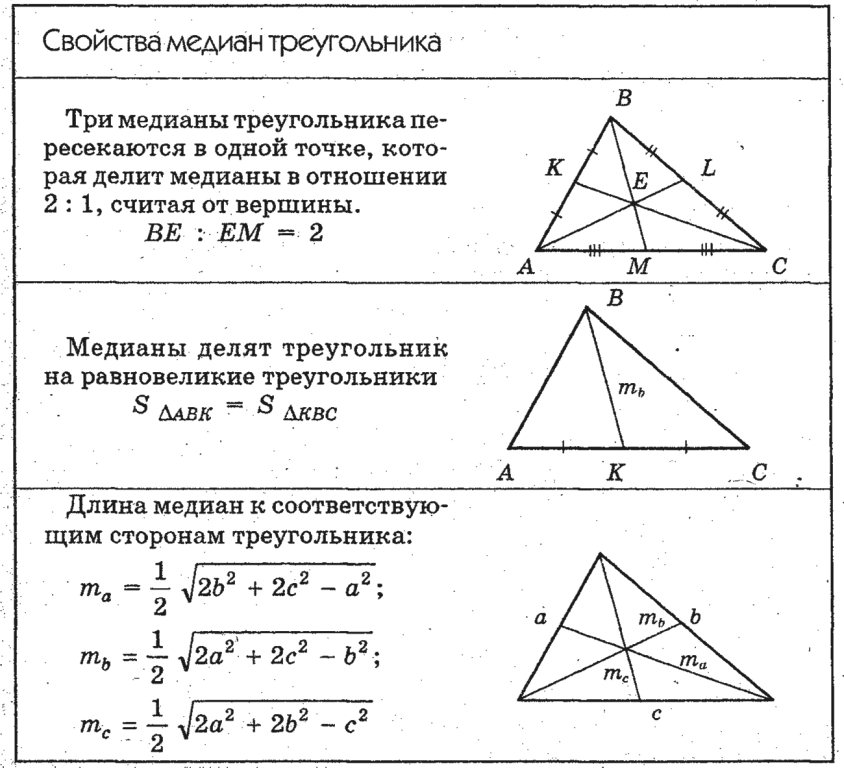
Свойства медиан треугольника
1. Медиана разбивает треугольник на два треугольника одинаковой площади.
2. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника (центроидом).
3. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
Длина медианы проведенной к стороне: (док-во достроением до параллелограмма и использованием равенства в параллелограмме удвоенной суммы квадратов сторон и суммы квадратов диагоналей )
Т1. Три медианы треугольника пересекаются в одной точке М, которая делит каждую из них в отношении 2:1, считая от вершин треугольника. Дано: ∆
∆ABC . Доказать: и
Д-во: Пусть М — точка пересечения медиан СС 1 , АА 1 треугольника ABC. Отметим A 2 — середину отрезка AM и С 2 — середину отрезка СМ. Тогда A 2 C 2 — средняя линия треугольника АМС. Значит,А 2 С 2 || АС
Значит,А 2 С 2 || АС
и A 2 C 2 = 0,5*АС. С 1 А 1 — средняя линия треугольника ABC. Значит, А 1 С 1 || АС и А 1 С 1 = 0,5*АС.
Четырехугольник А 2 С 1 А 1 С 2 — параллелограмм, так как его противоположные стороны А 1 С 1 и А 2 С 2 равны и параллельны. Следовательно, А 2 М = МА 1 и С 2 М = МC 1 . Это означает, что точки А 2 и M делят медиану АА 2
на три равные части, т. е. AM = 2МА 2 . Аналогично СМ = 2MC 1 . Итак, точка М пересечения двух медиан АА 2 и CC 2 треугольника ABC делит каждую из них в отношении 2:1, считая от вершин треугольника. Совершенно аналогично доказывается, что точка пересечения медиан АА 1 и BB 1 делит каждую из них в отношении 2:1, считая от вершин треугольника.На медиане АА 1 такой точкой является точка М, следовательно, точка М и есть точка пересечения медиан АА 1 иBB 1.
Таким образом, n
T2.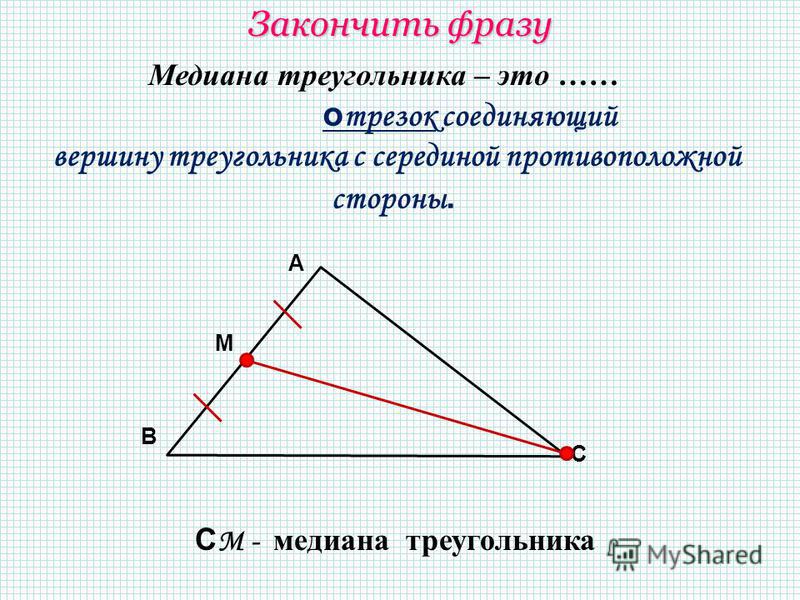 Докажите, что отрезки, которые соединяют центроид с вершинами треугольника, делят его на три равновеликие части. Дано: ∆ABC , — его медианы.
Докажите, что отрезки, которые соединяют центроид с вершинами треугольника, делят его на три равновеликие части. Дано: ∆ABC , — его медианы.
Доказать:S AMB =S BMC =S AMC . Доказательство. В, у них общая. т.к. равны их основания и высота, проведенная из вершины М, у них общая. Тогда
Аналогичным образом доказывается, что
Биссектриса треугольника.Теоремы связанные с биссектрисами треугольника. Формулы для нахождения биссектрис
Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Биссектриса угла есть геометрическое место точек внутри угла, равноудалённых от сторон угла.
Свойства
1. Теорема о биссектрисе: Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон
2. Биссектрисы внутренних углов треугольника пересекаются в одной точке — инцентре — центре вписанной в этот треугольник окружности.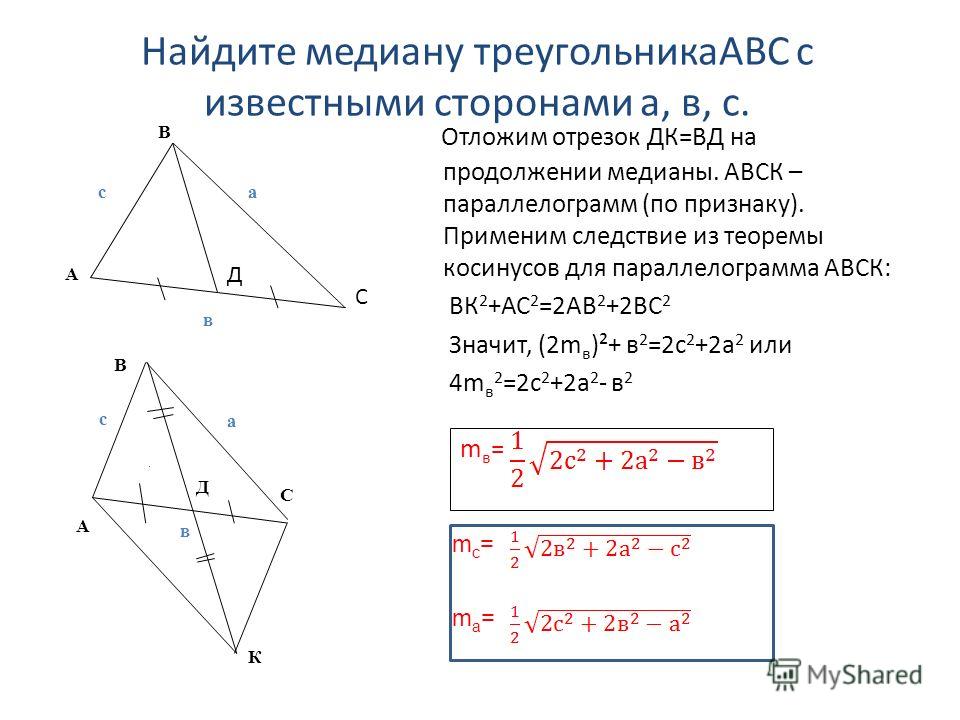
3. Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса).
Вычисление длины биссектрисы
l c — длина биссектрисы, проведённой к стороне c,
a,b,c — стороны треугольника против вершин A,B,C соответственно,
p — полупериметр треугольника,
a l ,b l — длины отрезков, на которые биссектриса l c делит сторону c,
α,β,γ — внутренние углы треугольника при вершинах A,B,C соответственно,
h c — высота треугольника, опущенная на сторону c.
Метод площадей.
Характеристика метода. Из названия следует, что главным объектом данного метода является площадь. Для ряда фигур, например для треугольника, площадь довольно просто выражается через разнообразные комбинации элементов фигуры (треугольника). Поэтому весьма эффективным оказывается прием, когда сравниваются различные выражения для площади данной фигуры. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, разрешая которое мы определяем неизвестное.
1) Метод сравнения: связан с большим кол-вом формул S одних и тех же фигур
2) Метод отношения S: основан на след опорных задачах:
Теорема Чевы
Пусть точки A»,B»,C» лежат на прямых BC,CA,AB треугольника. Прямые AA»,BB»,CC» пересекаются в одной точке тогда и только тогда, когда
Доказательство.
Обозначим через точку пересечения отрезков и . Опустим из точек С и А перпендикуляры на прямую ВВ 1 до пересечения с ней в точках Kи L соответственно (см. рисунок).
Поскольку треугольники и имеют общую сторону , то их площади относятся как высоты, проведенные на эту сторону, т.е. AL иCK:
Последнее равенство справедливо, так как прямоугольные треугольники и подобны по острому углу.
Аналогично получаем и
Перемножим эти три равенства:
что и требовалось доказать.
Замечание. Отрезок (или продолжение отрезка), соединяющий вершину треугольника с точкой, лежащей на противоположной стороне или ее продолжении, называется чевианой.
Теорема (обратная теорема Чевы) . Пусть точки A»,B»,C» лежат на сторонах BC,CA и AB треугольника ABC соответственно. Пусть выполняется соотношение
Тогда отрезки AA»,BB»,CC» и пересекаются в одной точке.
Теорема Менелая
Теорема Менелая. Пусть прямая пересекает треугольник ABC, причем C 1 – точка ее пересечения со стороной AB, A 1 – точка ее пересечения со стороной BC, и B 1 – точка ее пересечения с продолжением стороны AC. Тогда
Доказательство . Проведем через точку C прямую, параллельную AB. Обозначим через K ее точку пересечения с прямой B 1 C 1 .
ТреугольникиAC 1 B 1 иCKB 1 подобны (∟C 1 AB 1 = ∟KCB 1 , ∟AC 1 B 1 = ∟CKB 1). Следовательно,
ТреугольникиBC 1 A 1 иCKA 1 такжеподобны (∟BA 1 C 1 =∟KA 1 C, ∟BC 1 A 1 =∟CKA 1). Значит,
Из каждого равенства выразим CK:
Откуда что и требовалось доказать.
Теорема (обратная теорема Менелая). Пусть дан треугольник ABC. Пусть точка C 1 лежит на стороне AB, точка A 1 – на стороне BC, а точка B 1 – на продолжении стороны AC, причем выполняется соотношение
Тогда точки A 1 ,B 1 и C 1 лежат на одной прямой.
Чтобы по сторонам треугольника найти медиану, не обязательно запоминать дополнительную формулу. Достаточно знать алгоритм решения.
Для начала рассмотрим задачу в общем виде.
Дан треугольник со сторонами a, b, c. Найти длину медианы, проведенной к стороне b.
AB=a, AC=b, BC=c.
На луче BF отложим отрезок FD, FD=BF.
Соединим точку D с точками A и C.
Четырехугольник ABCD — параллелограмм (по признаку), так как у него диагонали в точке пересечения делятся пополам.
Свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Отсюда: AC²+BD²=2(AB²+BC²), значит, b²+BD²=2(a²+c²),
BD²=2(a²+c²)-b².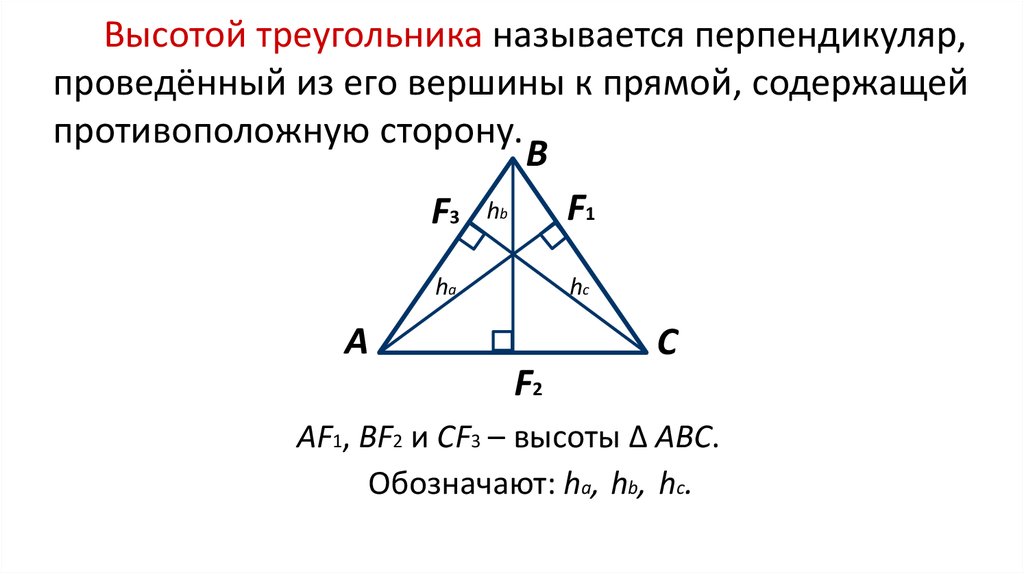 По построению, BF — половина BD, следовательно,
По построению, BF — половина BD, следовательно,
Это — формула нахождения медианы треугольника по его сторонам. Обычно ее записывают так:
Переходим к рассмотрению конкретной задачи.
Стороны треугольника равны 13 см, 14 см и 15 см. Найти медиану треугольника, проведенную к его средней по длине стороне.
Применяя аналогичные рассуждения, получаем:
AC²+BD²=2(AB²+BC²).
14²+BD²=2(13²+15²)
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Медианой именуется отрезок, проведенный из вершины треугольника на середину противоположной стороны, то есть делит ее точкой пересечения пополам. Точка, в которой медиана пересекает противоположную вершине, из которой она выходит, сторону, именуется основанием. Через одну точку, называемую точкой пересечения, проходит каждая медиана треугольника. Формула длины ее может выражаться несколькими способами.
Формулы для выражения длины медианы
- Зачастую в задачах по геометрии ученикам приходится иметь дело с таким отрезком, как медиана треугольника. Формула ее длины выражается через стороны:
где a, b и c — стороны. Причем с является стороной, на которую медиана опускается.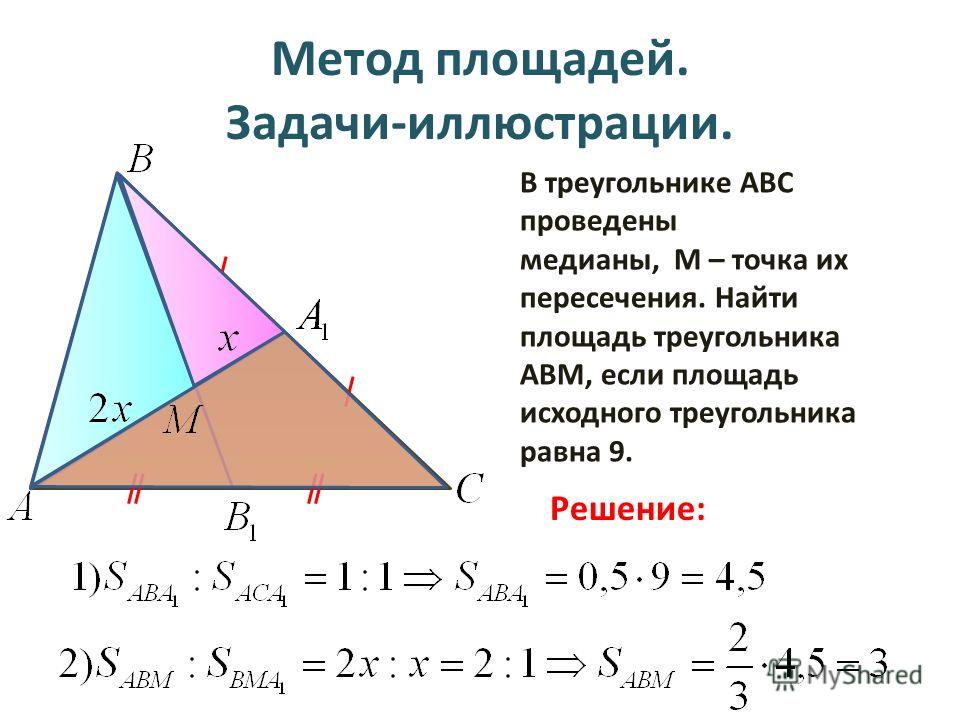 Таким образом выглядит самая простая формула. Медианы треугольника иногда требуется проводить для вспомогательных расчетов. Есть и другие формулы.
Таким образом выглядит самая простая формула. Медианы треугольника иногда требуется проводить для вспомогательных расчетов. Есть и другие формулы.
- Если при расчете известны две стороны треугольника и определенный угол α, находящийся между ними, то длина медианы треугольника, опущенной к третьей стороне, будет выражаться так.
Основные свойства
- Все медианы имеют одну общую точку пересечения O и ею же делятся в отношении два к одному, если вести отсчет от вершины. Такая точка носит название центра тяжести треугольника.
- Медиана разделяет треугольник на два других, площади которых равны. Такие треугольники называются равновеликими.
- Если провести все медианы, то треугольник будет разделен на 6 равновеликих фигур, которые также будут треугольниками.
- Если в треугольнике все три стороны равны, то в нем каждая из медиан будет также высотой и биссектрисой, то есть перпендикулярна той стороне, к которой она проведена, и делит надвое угол, из которого она выходит.

- В равнобедренном треугольнике медиана, опущенная из вершины, которая находится напротив стороны, не равной никакой другой, будет также высотой и биссектрисой. Медианы, опущенные из других вершин, равны. Это также является необходимым и достаточным условием равнобедренности.
- Если треугольник является основанием правильной пирамиды, то высота, опущенная на данное основание, проецируется в точку пересечения всех медиан.
- В прямоугольном треугольнике медиана, проведенная к наибольшей стороне, равняется половине ее длины.
- Пусть O — точка пересечения медиан треугольника. Формула, приведенная ниже, будет верная для любой точки M.
- Еще одним свойством обладает медиана треугольника. Формула квадрата ее длины через квадраты сторон представлена ниже.
Свойства сторон, к которым проведена медиана
- Если соединить любые две точки пересечения медиан со сторонами, на которые они опущены, то полученный отрезок будет являться средней линией треугольника и составлять одну вторую от стороны треугольника, с которой она не имеет общих точек.

- Основания высот и медиан в треугольнике, а также середины отрезков, соединяющих вершины треугольника с точкой пересечения высот, лежат на одной окружности.
В заключение логично сказать, что одним из самых важных отрезков является именно медиана треугольника. Формула ее может использоваться при нахождении длин других его сторон.
Свойства
- Медианы треугольника пересекаются в одной точке , которая называется центроидом , и делятся этой точкой на две части в отношении 2:1, считая от вершины.
- Треугольник делится тремя медианами на шесть равновеликих треугольников.
- Большей стороне треугольника соответствует меньшая медиана.
- Из векторов, образующих медианы, можно составить треугольник.
- При аффинных преобразованиях медиана переходит в медиану.
- Медиана треугольника делит его на две равновеликие части.
Формулы
- Формула медианы через стороны (выводится через теорему Стюарта или достроением до параллелограмма и использованием равенства в параллелограмме суммы квадратов сторон и суммы квадратов диагоналей):
, где m c — медиана к стороне c; a, b, c — стороны треугольника,
поэтому сумма квадратов медиан произвольного треугольника всегда в 4/3 раза меньше суммы квадратов его сторон.
- Формула стороны через медианы:
, где медианы к соответствующим сторонам треугольника, — стороны треугольника.
Если две медианы перпендикулярны, то сумма квадратов сторон, на которые они опущены, в 5 раз больше квадрата третьей стороны.
Мнемоническое правило
Медиана-обезьяна,
у которой зоркий глаз,
прыгнет точно в середину
стороны против вершины,
где находится сейчас.
Примечания
См. также
Ссылки
Wikimedia Foundation . 2010 .
Смотреть что такое «Медиана треугольника» в других словарях:
Медиана: Медиана треугольника в планиметрии, отрезок соединяющий вершину треугольника с серединой противоположной стороны в статистике медианой называется значение совокупности, делящее ранжированный ряд данных пополам Медиана (статистика) … … Википедия
Медиана: Медиана треугольника в планиметрии, отрезок, соединяющий вершину треугольника с серединой противоположной стороны Медиана (статистика) квантиль 0.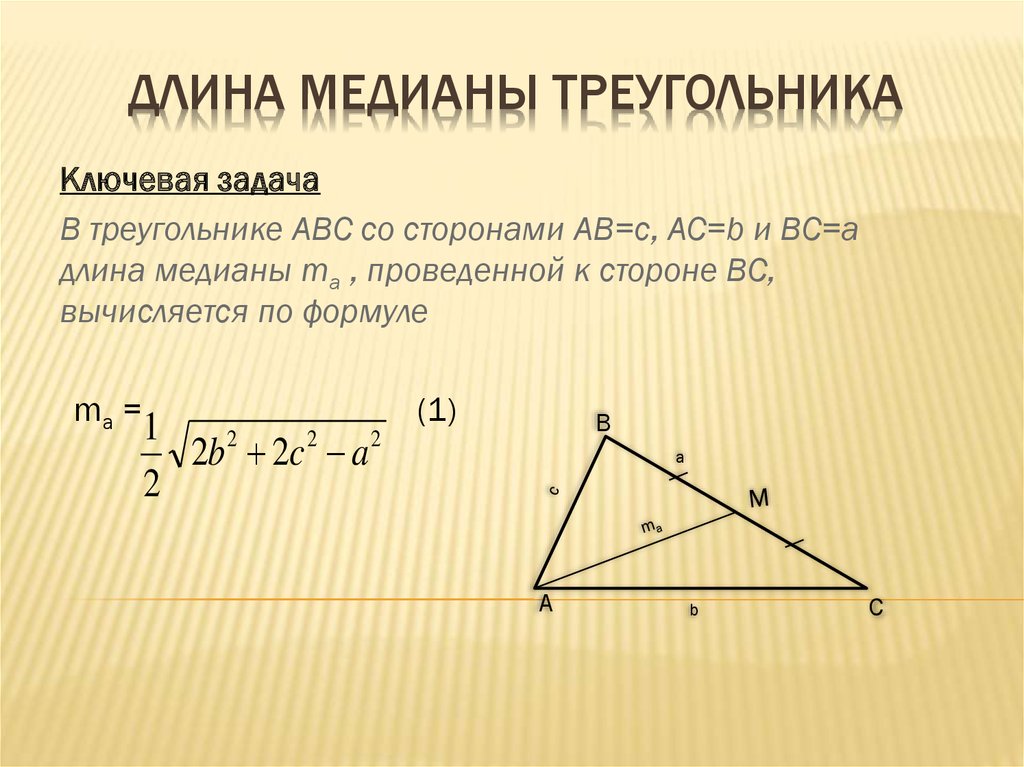 5 Медиана (трасса) средняя линия трассы, проведённая между правым и левым … Википедия
5 Медиана (трасса) средняя линия трассы, проведённая между правым и левым … Википедия
Треугольник и его медианы. Медиана треугольника ― отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок. Содержание 1 Свойства 2 Формулы … Википедия
Линия, соединяющая вершину треугольника с серединой его основания. Полный словарь иностранных слов, вошедших в употребление в русском языке. Попов М., 1907. медиана (лат. mediana средняя) 1) геол. отрезок, соединяющий вершину треугольника с… … Словарь иностранных слов русского языка
Медиана (от латинского mediana средняя) в геометрии, отрезок, соединяющий одну из вершин треугольника с серединой противоположной стороны. Три М. треугольника пересекаются в одной точке, которую иногда называют «центром тяжести» треугольника, так … Большая советская энциклопедия
Треугольника прямая (или ее отрезок внутри треугольника), соединяющая вершину треугольника с серединой противоположной стороны. Три М. треугольника пересекаются в одной точке, к рая называется центром тяжести треугольника, центроидом, или… … Математическая энциклопедия
Три М. треугольника пересекаются в одной точке, к рая называется центром тяжести треугольника, центроидом, или… … Математическая энциклопедия
— (от лат. mediana средняя) отрезок, соединяющий вершину треугольника с серединой противоположной стороны … Большой Энциклопедический словарь
МЕДИАНА, медианы, жен. (лат. mediana, букв. средняя). 1. Прямая линия, проведенная от вершины треугольника к середине противолежащей стороны (мат.). 2. В статистике для ряда многих данных величина, обладающая тем свойством, что число данных,… … Толковый словарь Ушакова
МЕДИАНА, ы, жен. В математике: отрезок прямой линии, соединяющий вершину треугольника с серединой противоположной стороны. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
МЕДИАНА (от лат. mediana средняя), отрезок, соединяющий вершину треугольника с серединой противоположной стороны … Энциклопедический словарь
геометрия — Нахождение длины медианы треугольника с длинами сторон 8, 5 и 6
спросил
Изменено 5 лет, 1 месяц назад
Просмотрено 2к раз
$\begingroup$
У меня такая проблема:
Треугольник ABC имеет длины сторон AB = 6, AC = 5 и BC = 8. 2$$
где $$a=8$$ тогда неизвестные $x,h_a,m_a$ можете закончить?
2$$
где $$a=8$$ тогда неизвестные $x,h_a,m_a$ можете закончить?
$\endgroup$
1
$\begingroup$
Вы можете использовать обобщение теоремы Пифагора, закон косинусов. Это дает вам отношение между 3 сторонами и одним углом ЛЮБОГО треугольника.
Учитывая треугольник ABC, вы можете использовать закон косинусов, чтобы получить угол в углу B. Затем снова используйте закон косинусов с треугольником ABD, чтобы получить длину AD.
$\endgroup$
$\begingroup$
Спасибо Джеку Д’Аурицио за то, что он объяснил мне, что означает эта формула.
В параллелограмме сумма квадратов длин диагоналей равна сумме квадратов длин сторон (поляризационное тождество). Таким образом, в основном, если я вырезаю и вставляю параллелограмм в прямоугольник, диагонали являются гипотенузой прямоугольника, которая является суммой новых четырех сторон (которые равны исходным четырем сторонам) в квадрате. 92$
92$
что решает $x = \pm\sqrt19$,
$x = \sqrt19$
$\endgroup$
$\begingroup$
Вам просто нужна формула Герона и теорема Пифгора.
Пусть $AE$ будет высотой. Используйте формулу Герона, чтобы найти площадь треугольника. Пусть это будет $S$. Тогда $\frac 12*8*AE=S$. Вы получите $AE$. Затем используйте теорему Пифгора в $\Delta AEC$, чтобы найти $EC$. Тогда вы можете получить $DE$. Затем снова используйте теорему Пифгора в $\Delta AED$, чтобы найти $AD$.
$\endgroup$
геометрия — Длина медианы треугольника
спросил
Изменено 2 года, 9 месяцев назад
Просмотрено 71 раз
$\begingroup$
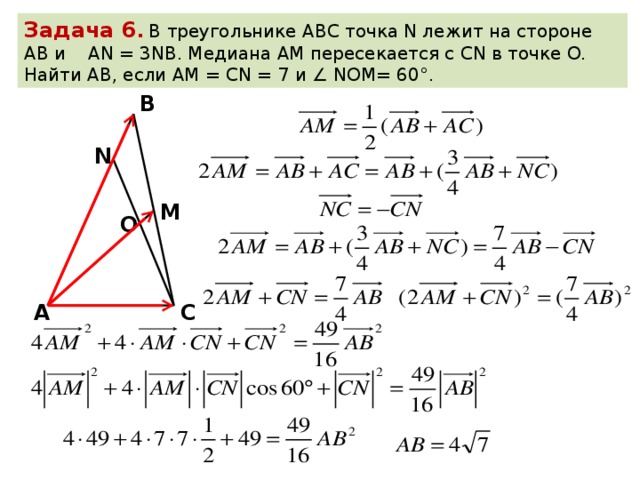
Дан треугольник со сторонами 11,60 и 61 единицами. Какова длина медианы до стороны длиной 61 единица от противоположной ей вершины? Я решил это с помощью теоремы Стюарда и получил значение 61/2. Мой вопрос в том, можно ли его рассчитать каким-то другим способом.
Какова длина медианы до стороны длиной 61 единица от противоположной ей вершины? Я решил это с помощью теоремы Стюарда и получил значение 61/2. Мой вопрос в том, можно ли его рассчитать каким-то другим способом.
- геометрия
$\endgroup$
1
$\begingroup$
Отказ от ответственности: когда я набирал это, @DreiCleaner написал свой комментарий.
У вас есть прямоугольный треугольник. Теперь, зная это, поскольку вы получаете медиану для стороны гипотенузы, заметно, что вы разделили гипотенузу на 2, и в результате, проведя линии, параллельные одной из других сторон, из середины гипотенузы, вы будете получить прямоугольный треугольник, аналогичный треугольнику 11, 60, 61 (с длинами сторон, равными половине длин сторон исходного треугольника). Это видно по этой картинке:
Таким образом, перевернув подобный треугольник на сторону, которая не является общей с большим треугольником, мы увидим, что медиана равна половине длины гипотенузы большего треугольника, которая равна $\frac{61}{2}$
$\endgroup$
$\begingroup$
Я думал не так, как @justaguy.

 д.
д.
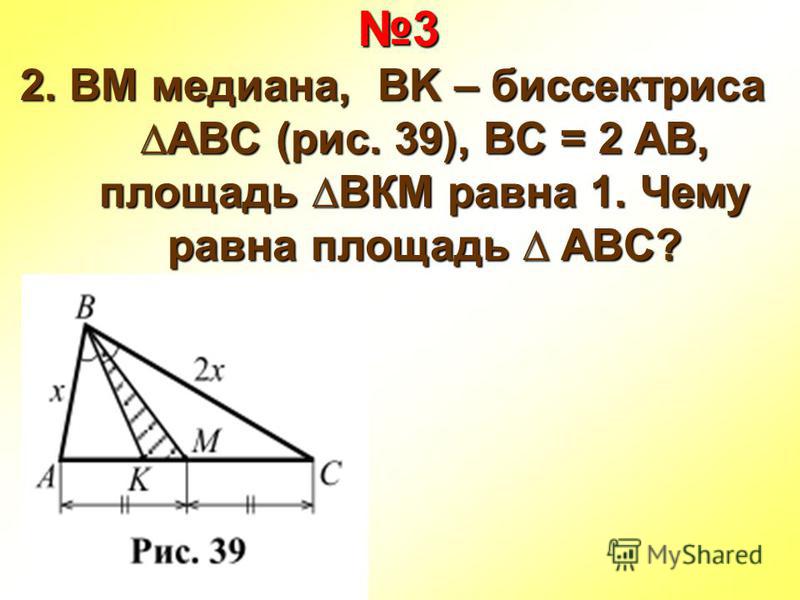
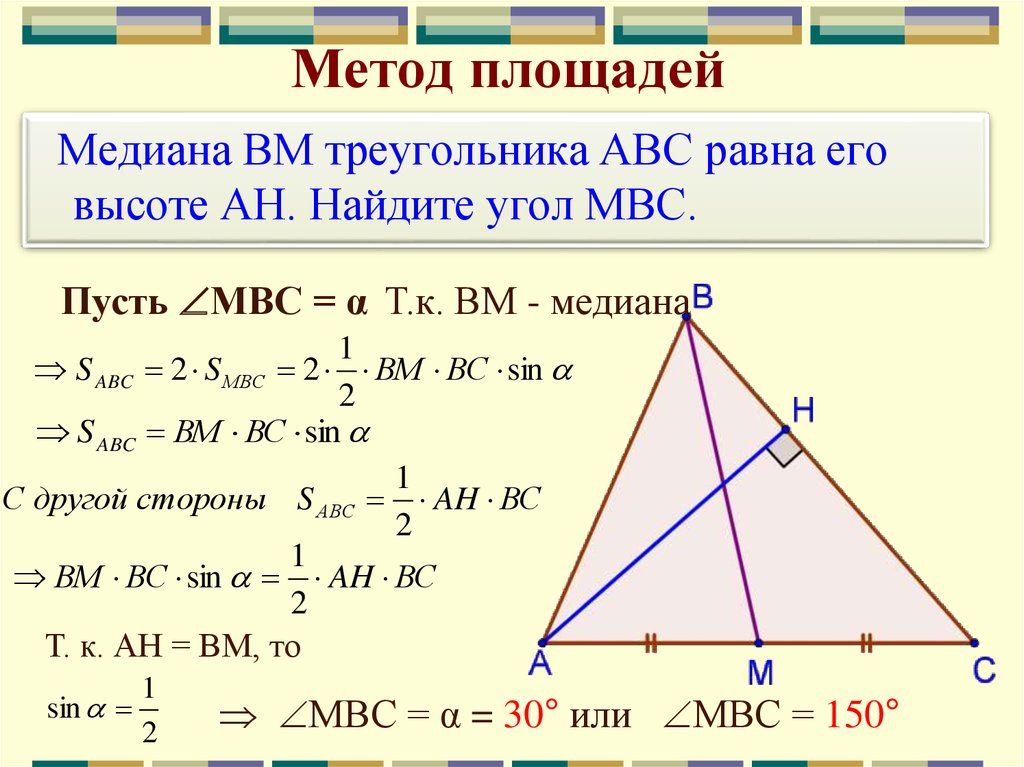 Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.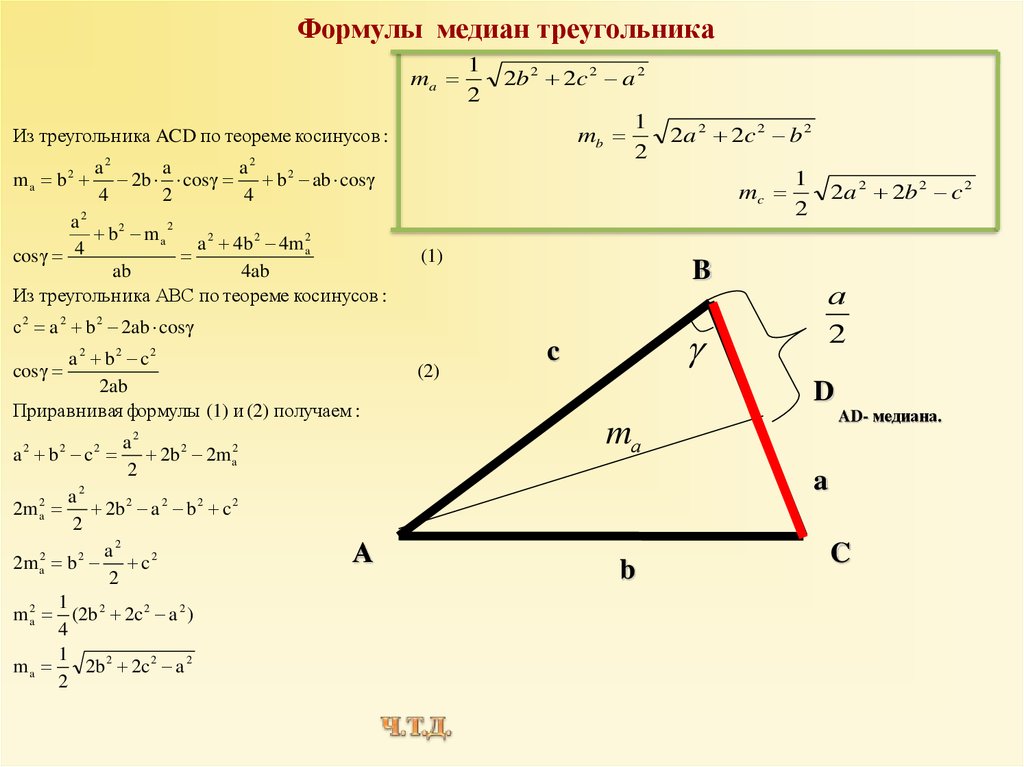 Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, считая от вершин
Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, считая от вершин
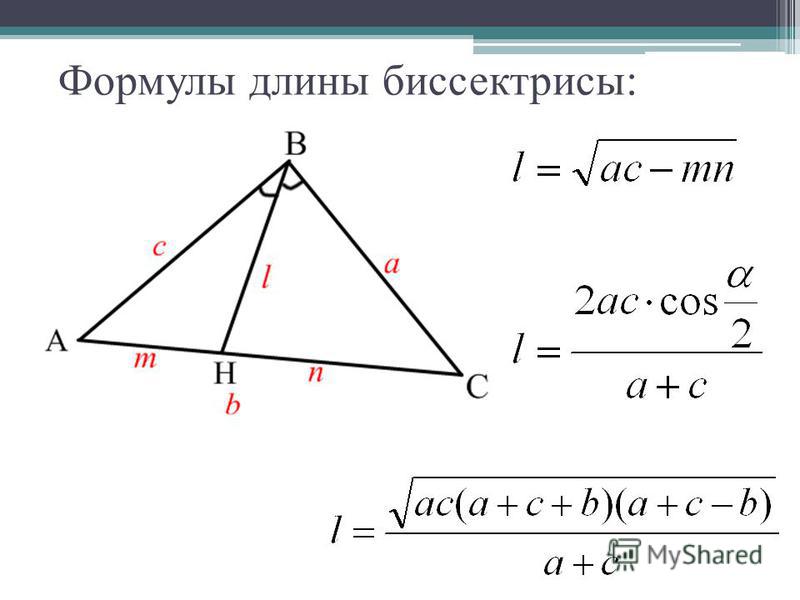 Расстояние от точки пересечения высот, биссектрис и медиан до любой вершины треугольника равно радиусу описанной окружности:
Расстояние от точки пересечения высот, биссектрис и медиан до любой вершины треугольника равно радиусу описанной окружности: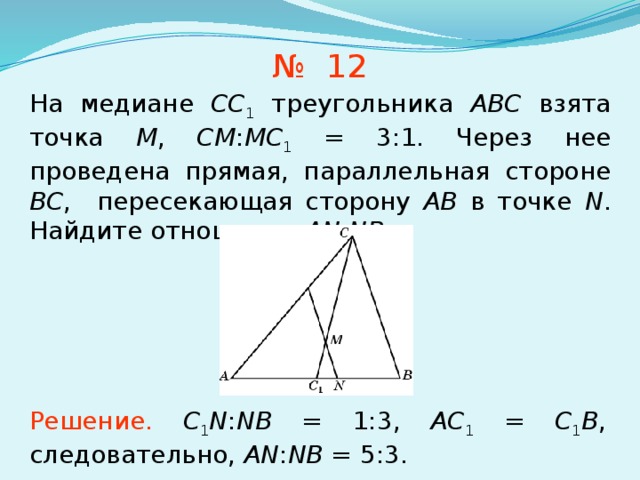 S=
S=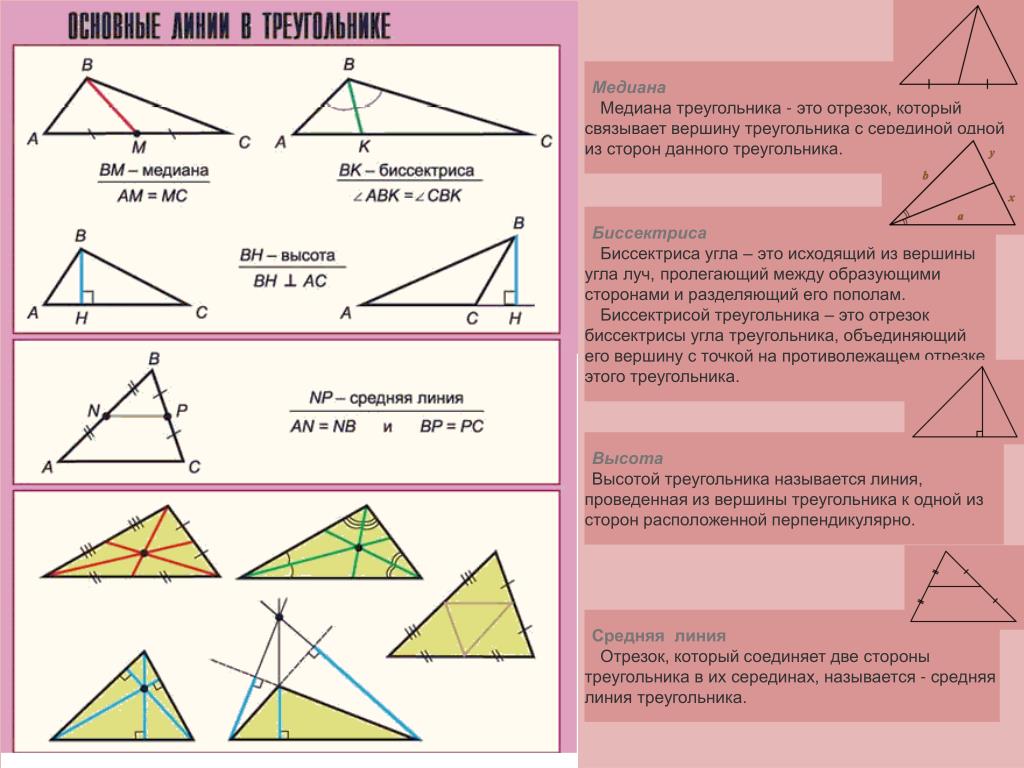

 е. AC=AD ч.т.д
е. AC=AD ч.т.д 5NB.
5NB.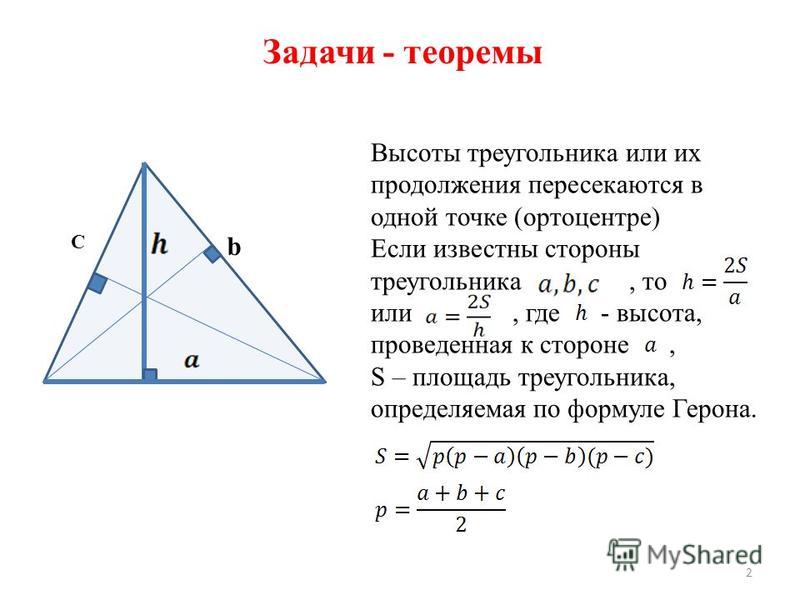
 )
)