Формула длины отрезка в координатах. Нахождение координат середины отрезка, примеры, решения
Приведу подробный пример, как можно определить длину отрезка по заданным координатам, воспользовавшись сервисом онлайн на сайте Контрольная работа Ру.
Допустим, вам надо найти длину отрезка на плоскости
(в пространстве вы можете по-аналогии расчитывать, только надо изменить точку на размерность трёх)
Отрезок AB имеет концы с координатами A (1, 2) и B (3, 4).
Для того, чтобы вычислить длину отрезка AB воспользуйтесь следующими шагами:
1. Перейдите на страницу сервиса по нахождению расстояния между двумя точками онлайн:
Мы можем этим пользоваться, т.к. длина отрезка по коорд. как раз и равна расстоянию между точками A и B.
Чтобы задать правильную размерность точки A, то потяните за нижний правый край влево, как показано на рис.
После того, как ввели координаты первой точки A(1, 2), то нажмите на кнопку
3. На втором шаге вы увидите форму для ввода второй точки B, введите её координаты, как рис.
Точки a и b введены! Решение:
| Даны точки a = | и b = |
Найдем расстояние между точками (s)
Отрезком называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1 , а на ось Х длина проекции равна x2-x1 . Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)² . В данном случае |AB| является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5) . Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5 . А это значит, что длина нашего отрезка равна 5:1/2 .
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1 .
Рассчитаем длину отрезка А , для этого найдем квадратный корень:
A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²) .
Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1 , то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61 .
Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат каждая точка имеет три координаты. 2))
2))
Пусть отрезок задан двумя точками в плоскости координат, тогда можно найти его длину с помощью теоремы Пифагора.
Инструкция
Пусть заданы координаты концов отрезка (x1- y1) и (x2- y2). Начертите отрезок в системе координат.
Опустите перпендикуляры из концов отрезка на оси X и Y. Отрезки, отмеченные на рисунке красным, являются проекциями исходного отрезка на оси координат.
Если выполнить параллельный перенос, отрезков-проекций к концам отрезков, то получится прямоугольный треугольник. Катетами этого треугольника будут являться перенесенные проекции, а гипотенузой — сам отрезок AB.
Длины проекций легко вычисляются. Длина проекции на ось Y будет равна y2-y1, а длина проекции на ось X — x2-x1. Тогда по теореме Пифагора |AB|²- = (y2 — y1)²- + (x2 — x1)²-, где |AB| — длина отрезка.
Представив эту схему нахождения длины отрезка в общем случае, легко вычислять длину отрезка, не строя отрезок. Посчитаем длину отрезка, координаты концов которого (1-3) и (2-5).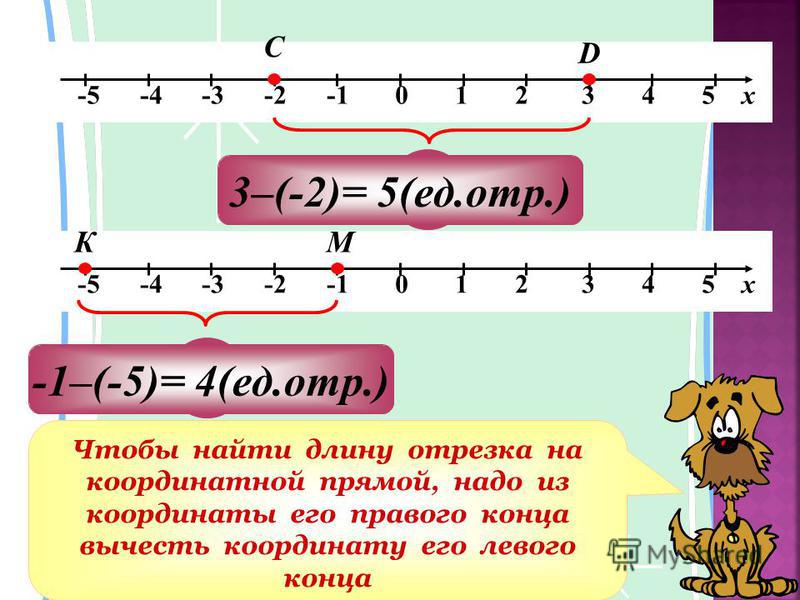 1/2.
1/2.
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант
Пример 3
Решение: по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж
Отрезок – это не вектор , и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём – вынесение множителя из-под корня . В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся.
Готово.
Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
Измерить отрезок — значит найти его длину. Длина отрезка — это расстояние между его концами.
Измерение отрезков производится путём сравнения данного отрезка с другим отрезком, принятым за единицу измерения. Отрезок, принятый за единицу измерения, называется единичным отрезком .
Отрезок, принятый за единицу измерения, называется единичным отрезком .
Если за единичный отрезок принят сантиметр, то для определения длины данного отрезка надо узнать, сколько раз в данном отрезке помещается сантиметр. В этом случае измерение удобно производить с помощью сантиметровой линейки.
Начертим отрезок AB и измерим его длину. Приложим шкалу сантиметровой линейки к отрезку AB так, чтобы её нулевая точка (0) совпала с точкой A :
Если при этом окажется, что точка B совпадает с некоторым делением шкалы — например, 5, то говорят: длина отрезка AB равна 5 см, и пишут: AB = 5 см.
Свойства измерения отрезков
Когда точка делит отрезок на две части (на два отрезка), длина всего отрезка равна сумме длин этих двух отрезков.
Рассмотрим отрезок AB :
Точка C делит его на два отрезка: AC и CB . Мы видим, что AC = 3 см, CB = 4 см и AB = 7 см. Таким образом, AC + CB = AB .
Таким образом, AC + CB = AB .
Любой отрезок имеет определённую длину, большую нуля.
Формула длины отрезка по двум точкам. Нахождение координат середины отрезка: примеры, решения
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант
Пример 3
Решение: по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж
Отрезок –

Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём – вынесение множителя из-под корня . В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: .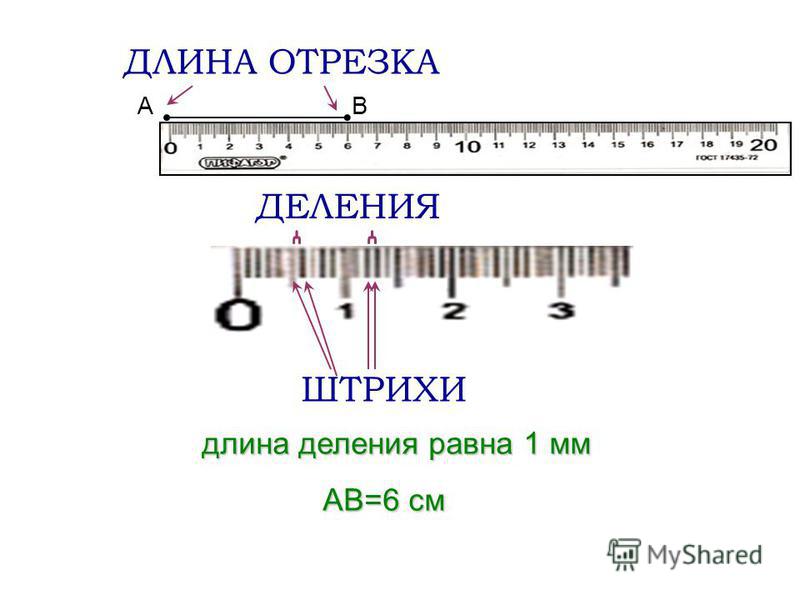 Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.
Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Найти длину отрезка .
Решение и ответ в конце урока.
Отрезком называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1 , а на ось Х длина проекции равна x2-x1 . Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)² . В данном случае |AB| является длиной отрезка.
Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)² . В данном случае |AB| является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5) . Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5 . А это значит, что длина нашего отрезка равна 5:1/2 .
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1 .
Рассчитаем длину отрезка А , для этого найдем квадратный корень:
A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²) .
Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1 , то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61 .
Если вы хорошо заточенным карандашом прикоснетесь к тетрадному листу, то останется след, который дает представление о точке. (рис. 3 ).
Отметим на листе бумаги две точки A
и B.
Эти точки можно соединить различными линиями (рис. 4
). А как соединить точки A
и B
самой короткой линией? Это можно сделать с помощь линейки (рис. 5
). Полученную линию называют отрезком .
5
). Полученную линию называют отрезком .
Точка и отрезок − примеры геометрических фигур .
Точки A и B называют концами отрезка .
Существует единственный отрезок, концами которого являются точки A и B. Поэтому отрезок обозначают, записывая точки, которые являются его концами. Например, отрезок на рисунке 5 обозначают одним из двух способов: AB или BA. Читают: «отрезок AB» или «отрезок BA».
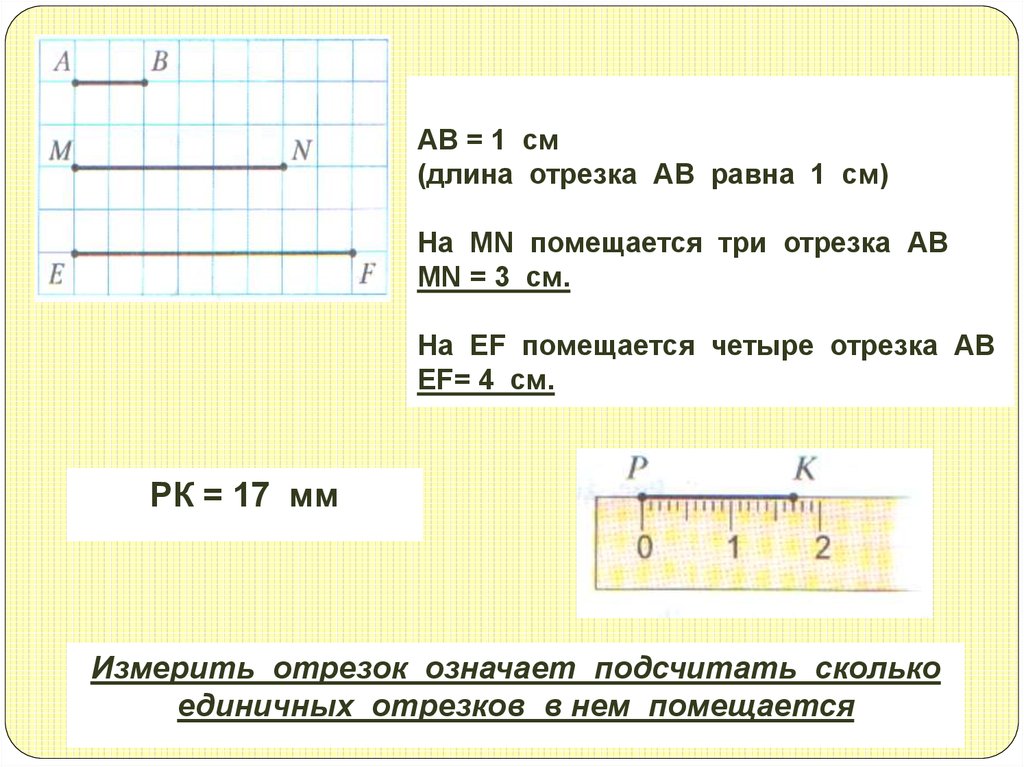
На рисунке 6 изображены три отрезка. Длина отрезка AB равна 1 см. Он помещается в отрезке MN ровно три раза, а в отрезке EF − ровно 4 раза. Будем говорить, что длина отрезка MN равна 3 см, а длина отрезка EF − 4 см.
Также принято говорить: «отрезок MN равен 3 см», «отрезок EF равен 4 см». Пишут: MN = 3 см, EF = 4 см.
Длины отрезков MN
и EF
мы измерили единичным отрезком , длина которого равна 1
см. Для измерения отрезков можно выбрать и другие единицы длины , например: 1
мм, 1
дм, 1
км. На рисунке 7
длина отрезка равна 17
мм. Он измерен единичным отрезком, длина которого равна 1
мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7
).
Он измерен единичным отрезком, длина которого равна 1
мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7
).
Вообще, измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается .
Длина отрезка обладает следующим свойством.
Если на отрезке AB отметить точку C, то длина отрезка AB равна сумме длин отрезков AC и CB (рис. 8 ).
Пишут: AB = AC + CB.
На рисунке 9 изображены два отрезка AB и CD. Эти отрезки при наложении совпадут.
Два отрезка называют равными, если они совпадут при наложении.
Следовательно отрезки AB и CD равны. Пишут: AB = CD.
Равные отрезки имеют равные длины.
Из двух неравных отрезков бОльшим будем считать тот, у уоторого длина больше. Например, на рисунке 6 отрезок EF больше отрезка MN.
Длину отрезка AB называют расстоянием между точками A и B.
Если несколько отрезков расположить так, как показано на рисунке 10,
то получится геометрическая фигура, которую называют ломаная . Заметим, что все отрезки на рисунке 11
ломаную не образуют. Считают, что отрезки, образуют ломаную, если конец первого отрезка совпадает с концом второго, а другой конец второго отрезка − с концом третьего и т. д.
Заметим, что все отрезки на рисунке 11
ломаную не образуют. Считают, что отрезки, образуют ломаную, если конец первого отрезка совпадает с концом второго, а другой конец второго отрезка − с концом третьего и т. д.
Точки A, B, C, D, E − вершины ломаной ABCDE, точки A и E − концы ломаной , а отрезки AB, BC, CD, DE − ее звенья (см. рис. 10 ).
Длиной ломаной называют сумму длин всех ее звеньев.
На рисунке 12 изображены две ломаные, концы которых совпадают. Такие ломаные называют замкнутыми .
Пример 1 . Отрезок BC на 3 см меньше отрезка AB, длина которого равна 8 см (рис. 13 ). Найдите длину отрезка AC.
Решение. Имеем: BC = 8 − 3 = 5 (см).
Воспользовавшись свойством длины отрезка, можно записать AC = AB + BC. Отсюда AC = 8 + 5 = 13 (см).
Ответ: 13 см.
Пример 2 . Известно, что MK = 24 см, NP = 32 см, MP = 50 см (рис. 14 ). Найдите длину отрезка NK.
Решение. Имеем: MN = MP − NP.
Имеем: MN = MP − NP.
Отсюда MN = 50 − 32 = 18 (см).
Имеем: NK = MK − MN.
Отсюда NK = 24 − 18 = 6 (см).
Ответ: 6 см.
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Yandex.RTB R-A-339285-1 Определение 1
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Определение 2
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины).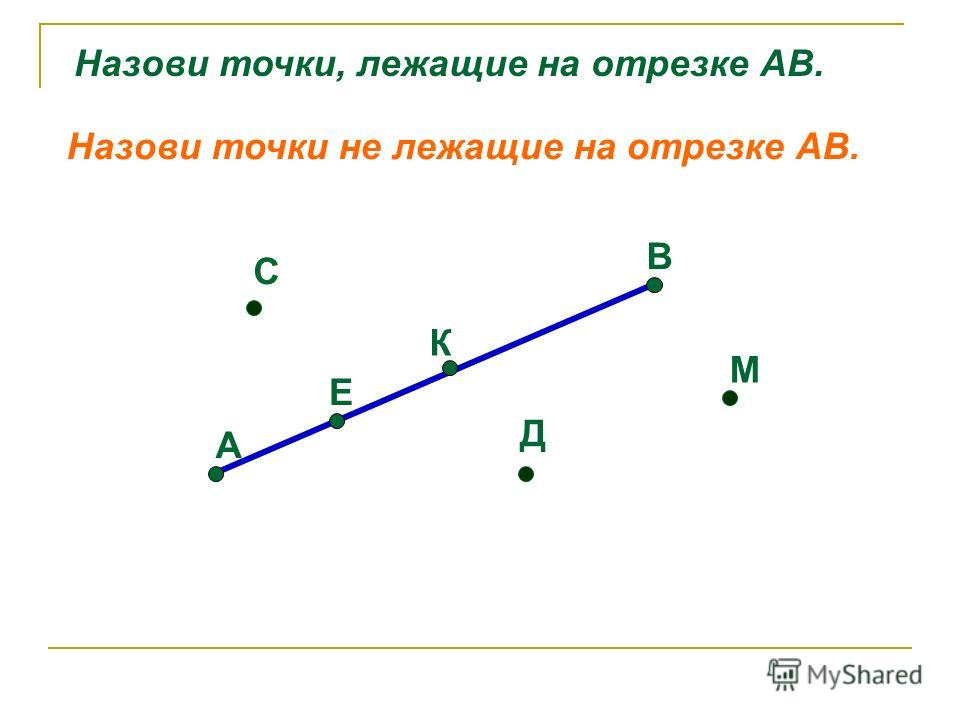 Длину отрезка A B обозначим следующим образом: A B .
Длину отрезка A B обозначим следующим образом: A B .
Определение 3
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):
Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно.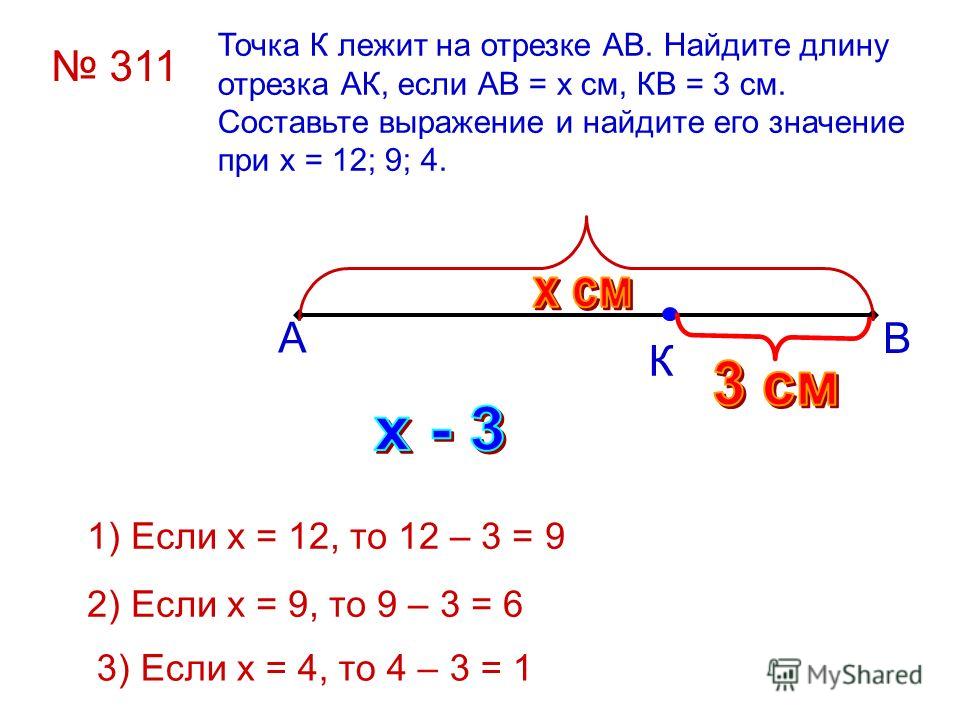 Тогда, для определения координат середины отрезка в пространстве верны формулы:
Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.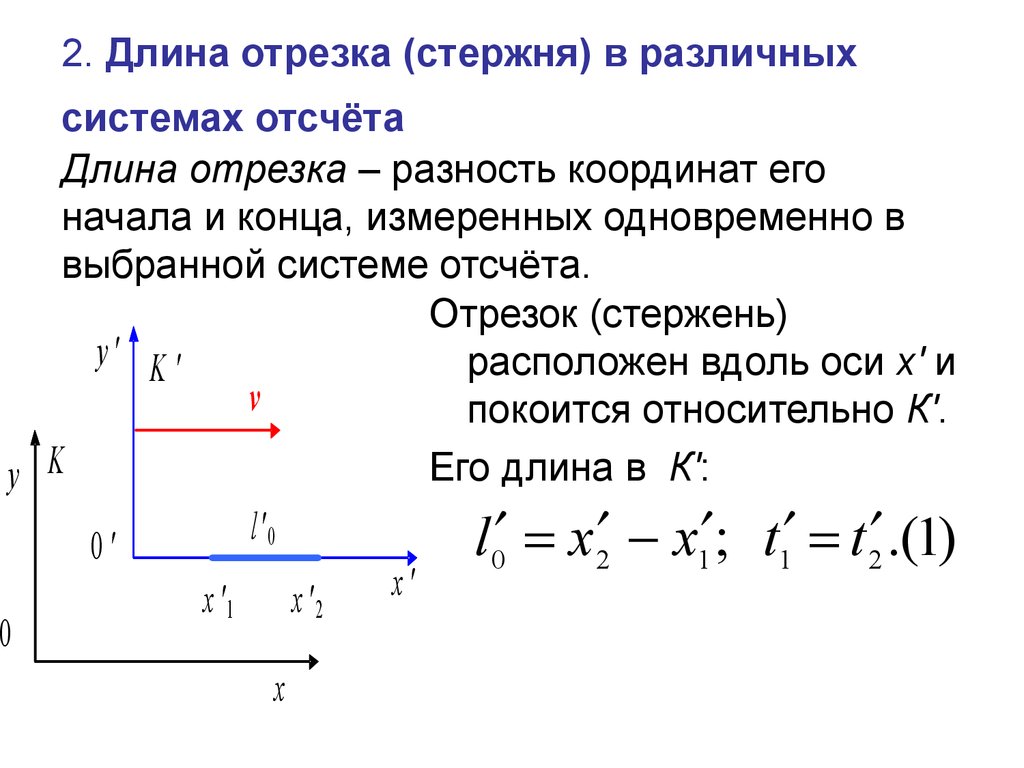 е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Рассмотрим характерные примеры.
Пример 1
Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ : координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ: 58
Пример 3
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ: координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Урок 75. длина отрезка — Математика — 6 класс
Математика
6 класс
Урок № 75
Длина отрезка
Перечень рассматриваемых вопросов:
- длина отрезка;
- единицы измерения длины;
- способы измерения длины отрезка;
- решение задач на вычисление длины отрезка.

Тезаурус
Отрезок – это часть прямой, ограниченная двумя точками.
Длина отрезка – это расстояние между его концами.
Измерение длины отрезка – это сравнение длины отрезка с выбранной единицей измерения.
Длиной отрезка называется положительная величина, определённая для каждого отрезка.
Любой отрезок имеет определённую длину, большую нуля.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Что такое отрезок?
Отрезок – это часть прямой, ограниченная двумя точками.
Как отрезки обозначаются на чертежах?
Отрезок можно обозначить двумя заглавными буквами – отрезок АВ. Или можно обозначить отрезок одной строчной буквой – отрезок с.
Любой отрезок имеет определённую длину, большую нуля.
Длина может быть выражена натуральным или дробным числом.
Измерить отрезок – значит найти его длину.
Длина отрезка – это расстояние между его концами.
Свойства длин отрезков:
– равные отрезки имеют равные длины;
– если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.
Эти свойства длины отрезка используются при её измерении. Чтобы измерить длину отрезка, нужно выбрать единицу длины.
Такой единицей может быть длина произвольного отрезка. В мультфильме «38 попугаев» герои измеряли длину удава в попугаях.
Для определения длины отрезка надо узнать, сколько раз в данном отрезке помещается выбранная единица измерения.
Можно сравнивать длины отрезков, не имея под рукой линейки.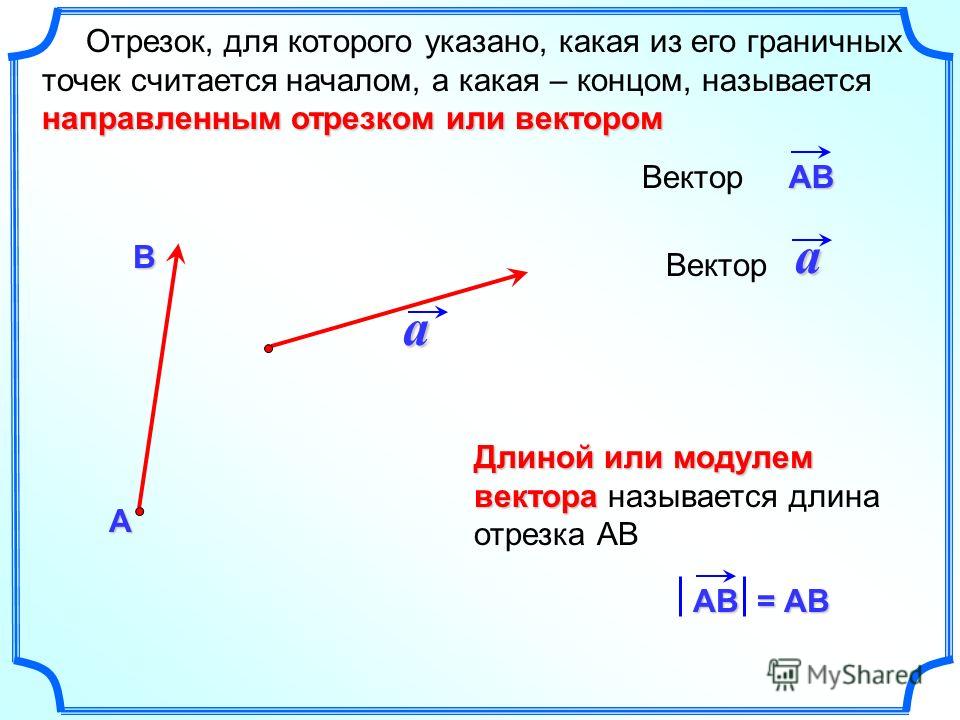 Например, прикладывать к отрезкам один и тот же карандаш, ластик или использовать циркуль. Для этого нужно установить иглу в начало отрезка, провести дугу, пересекающую отрезок, затем, не меняя расстояния между иглой и карандашом циркуля, переставить иглу в точку пересечения и повторить действия.
Например, прикладывать к отрезкам один и тот же карандаш, ластик или использовать циркуль. Для этого нужно установить иглу в начало отрезка, провести дугу, пересекающую отрезок, затем, не меняя расстояния между иглой и карандашом циркуля, переставить иглу в точку пересечения и повторить действия.
В десятичной системе мер единицами измерения длины являются 1 мм, 1 см, 1 дм, 1 м и т. д.
Рассмотрим несколько примеров измерения длины отрезка. Измерения небольших отрезков удобно производить с помощью линейки.
Прикладываем линейку так, чтобы один конец отрезка совместился с нулём. Единичный отрезок 1 см отложился 7 раз, значит, длина отрезка АВ = 7 см.
Если единичный отрезок 1 см отложился n раз, и осталась часть меньшая 1 см, то откладываем отрезки равные 1/10 см. Длина отрезка СD = 8,7 см.
При необходимости можно продолжить откладывать по 1/100 части единичного отрезка и т. д.
Алгоритм измерения длины отрезков:
– выбрать какой-либо отрезок и принять его за единицу длины;
– от одного из концов отрезка отложить последовательно отрезки, равные единичному;
– если единичные отрезки отложились n раз и конец последнего совпал с концом измеряемого отрезка, то значение его длины равно n единиц длины;
– если отрезок или его часть меньше единичного отрезка, то нужно отложить отрезки, равные 1/10 части единичного отрезка;
– если десятые части единичного отрезка отложились ровно n раз, то длина измеряемого отрезка есть конечная десятичная дробь, в которой целая часть равна количеству целых единичных отрезков, а после запятой в разряде десятых стоит количество десятых частей единичного отрезка;
– при необходимости можно откладывать 1/100 часть единичного отрезка и т. д.
д.
Таким образом, для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.
И для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.
На практике используют приближённое значение длин отрезков, например, с точностью 1/10 или 1/100 части единичного отрезка, но точность приближения зависит от поставленной задачи.
Рассмотрим фигуры, составленные из отрезков.
Возьмем на плоскости несколько точек и соединим их отрезками. Если никакие два из этих отрезков, имеющих общие точки, не лежат на одной прямой, то линию называют ломаной.
Отрезки, из которых состоит ломаная, называются звеньями, а концы этих отрезков – вершинами ломаной.
Длина ломаной – это сумма длин всех её звеньев.
Если концы ломаной совпадают, то такая ломаная называется замкнутой.
Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником.
Периметр многоугольника равен сумме длин всех его сторон.
Разбор заданий тренировочного модуля
Тип 1. Ввод с клавиатуры пропущенных элементов в тексте.
Впишите верный ответ.
Точка P лежит на отрезке AB. Известно, что отрезок AP больше отрезка PB на 3,6 см, а отрезок AB = 10,4 см. Найдите длину отрезка PB.
Решение:
Пусть PB = x, тогда AP = x + 3,6 см.
По условию AB = 10,4 см.
Если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.
PB + AP = AB.
Составим и решим уравнение:
x + x + 3,6 = 10,4,
2x + 3,6 = 10,4,
2x = 10,4 – 3,6,
2x = 6,8,
x = 3,4.
Значит, длина отрезка PB = 3,4 см.
Ответ: 3,4 см.
Тип 2. Множественный выбор
Выберите верные ответы.
Задача 2
Известно, что отрезок AС = 3,6 см, а отрезок BС = 7,5 см. Найдите длину отрезка АB, если все три точки лежат на одной прямой.
Варианты ответов: 3,9; 11,1; 4,8; 13,2; 16,5; 2,9.
Первый вариант решения
В этом случае АВ = АС + ВС = 3,6 + 7,5 = 11,1 (см).
Второй вариант
BC = AB + AC,
АВ = ВС – АС = 7,5 – 3,6 = 3,9 (см).
Значит, длина отрезка АВ может быть равна 11,1 см или 3,9 см. Выбираем эти варианты.
Ответ: 11,1; 3,9.
Длина отрезка и ее измерение. Длина отрезка и ее измерение Чему равна длина отрезка прямой
ПОВТОРЯЕМ ТЕОРИЮ
16. Заполните пропуски.
1) Точка и отрезок являются примерами геометрических
фигур.
2) Измерить отрезок означает подсчитать, сколько единых отрезков
в нем помещается.
3) Если на отрезке АВ ометить точку С, то длинна отрезка АВ равна сумме длин
отрезков АС +СВ
4) Два отрезка называют равными, если они совпадают при наложении
.
5) Равные отрезки имеют равные
длины.
6) Расстоянием между точками А и В называют длину отрезка
АВ.
РЕШАЕМ ЗАДАЧИ
17. Обозначьте отрезки, изображенные на рисунке, и измерьте их длины.
18. Проведите все возможные отрезки с концами в точках A, B, C и D. Запишите обозначения всех проведенных отрезков.
AB, ВC, СD, АD, АС, ВD
19. Запишите все отрезки, изображенные на рисунке.
20. Начертите отрезки СК и АD так, чтобы СК=4 см 6 мм, АD=2 см 5 мм.
21. Начертите отрезок ВЕ, длина которого равна 5 см 3 мм. Отметьте на нем точку А так, чтобы ВА = 3 см 8 мм. Какова длина отрезка АЕ?
АЕ=ВЕ-ВА= 5 см 3 мм — 3см 8мм = 1 см 5мм
22. Выразите данную величину в указанных единицах измерения.
23. Запишите звенья ломаной и измерьте их длины (в миллиметрах). Вычислите длину ломаной.
24. Отметьте точку В, расположенную на 6 клеток левее и на 1 клетку ниже точки А; точку С, расположенную на 3 клетки правее и на 3 клетки ниже точки В; точку D, расположенную на 7 клеток правее и на 2 клетки выше точки С. Соедините последовательно отрезками точки А, В, С и D.
Образовалась ломаная АВСD, состоящая из 3 звеньев.
25. Вычислите длину ломаной, изображенной на рисунке.
а) 5*36 = 180 мм
б) 3*28 = 84 мм
в) 10*10+15*4 = 160 мм
26. Постройте ломаную DСЕК так, чтобы DС=18 мм, СЕ=37 мм, ЕК=26 мм. Вычислите длину ломаной.
27. Известно, что АС=17 см, ВD=9см, ВС=3 см. Вычислите длину отрезка АD.
28. Известно, что МК=KN=NP=PR=RT=3 см. Какие еще равные отрезки есть на этом рисунке? Найдите их длины.
29. На прямой отметили точки так, что расстояние между двумя любыми соседними точками равно 4 см, а между крайними точками — 36 см. Сколько точек отмечено?
30. Начертите, не отрывая карандаша от бумаги, фигуры, изображенные на рисунке. По каждой линии можно проводить карандашом только один раз.
Если вы хорошо заточенным карандашом прикоснетесь к тетрадному листу, то останется след, который дает представление о точке. (рис. 3 ).
Отметим на листе бумаги две точки A
и B. Эти точки можно соединить различными линиями (рис. 4
). А как соединить точки A
и B
самой короткой линией? Это можно сделать с помощь линейки (рис. 5
). Полученную линию называют отрезком .
Эти точки можно соединить различными линиями (рис. 4
). А как соединить точки A
и B
самой короткой линией? Это можно сделать с помощь линейки (рис. 5
). Полученную линию называют отрезком .
Точка и отрезок − примеры геометрических фигур .
Точки A и B называют концами отрезка .
Существует единственный отрезок, концами которого являются точки A и B. Поэтому отрезок обозначают, записывая точки, которые являются его концами. Например, отрезок на рисунке 5 обозначают одним из двух способов: AB или BA. Читают: «отрезок AB» или «отрезок BA».
На рисунке 6 изображены три отрезка. Длина отрезка AB равна 1 см. Он помещается в отрезке MN ровно три раза, а в отрезке EF − ровно 4 раза. Будем говорить, что длина отрезка MN равна 3 см, а длина отрезка EF − 4 см.
Также принято говорить: «отрезок MN равен 3 см», «отрезок EF равен 4 см». Пишут: MN = 3 см, EF = 4 см.
Длины отрезков MN
и EF
мы измерили единичным отрезком , длина которого равна 1
см. Для измерения отрезков можно выбрать и другие единицы длины , например: 1
мм, 1
дм, 1
км. На рисунке 7
длина отрезка равна 17
мм. Он измерен единичным отрезком, длина которого равна 1
мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7
).
Для измерения отрезков можно выбрать и другие единицы длины , например: 1
мм, 1
дм, 1
км. На рисунке 7
длина отрезка равна 17
мм. Он измерен единичным отрезком, длина которого равна 1
мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7
).
Вообще, измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается .
Длина отрезка обладает следующим свойством.
Если на отрезке AB отметить точку C, то длина отрезка AB равна сумме длин отрезков AC и CB (рис. 8 ).
Пишут: AB = AC + CB.
На рисунке 9 изображены два отрезка AB и CD. Эти отрезки при наложении совпадут.
Два отрезка называют равными, если они совпадут при наложении.
Следовательно отрезки AB и CD равны. Пишут: AB = CD.
Равные отрезки имеют равные длины.
Из двух неравных отрезков бОльшим будем считать тот, у уоторого длина больше. Например, на рисунке 6
отрезок EF
больше отрезка MN.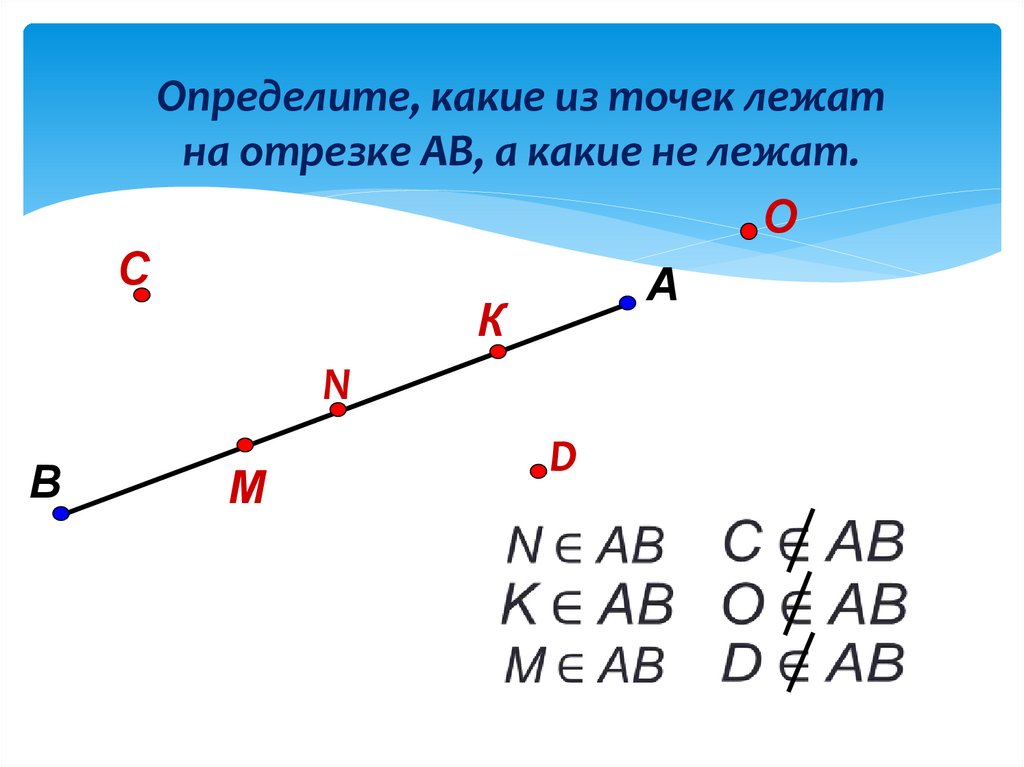
Длину отрезка AB называют расстоянием между точками A и B.
Если несколько отрезков расположить так, как показано на рисунке 10, то получится геометрическая фигура, которую называют ломаная . Заметим, что все отрезки на рисунке 11 ломаную не образуют. Считают, что отрезки, образуют ломаную, если конец первого отрезка совпадает с концом второго, а другой конец второго отрезка − с концом третьего и т. д.
Точки A, B, C, D, E − вершины ломаной ABCDE, точки A и E − концы ломаной , а отрезки AB, BC, CD, DE − ее звенья (см. рис. 10 ).
Длиной ломаной называют сумму длин всех ее звеньев.
На рисунке 12 изображены две ломаные, концы которых совпадают. Такие ломаные называют замкнутыми .
Пример 1 . Отрезок BC на 3 см меньше отрезка AB, длина которого равна 8 см (рис. 13 ). Найдите длину отрезка AC.
Решение. Имеем: BC = 8 − 3 = 5 (см).
Воспользовавшись свойством длины отрезка, можно записать AC = AB + BC. Отсюда AC =
8
+ 5
= 13
(см).
Отсюда AC =
8
+ 5
= 13
(см).
Ответ: 13 см.
Пример 2 . Известно, что MK = 24 см, NP = 32 см, MP = 50 см (рис. 14 ). Найдите длину отрезка NK.
Решение. Имеем: MN = MP − NP.
Отсюда MN = 50 − 32 = 18 (см).
Имеем: NK = MK − MN.
Отсюда NK = 24 − 18 = 6 (см).
Ответ: 6 см.
Понятие длины отрезка и ее измерения были уже использованы неоднократно, в частности, когда рассматривали натуральное число как меру величины. В этом пункте мы только обобщим представления о длине отрезка как геометрической величине.
В геометрии длина — это величина, характеризующая протяженность отрезка, а также других линий (ломаной, кривой). В нашем курсе будет рассмотрено только понятие длины отрезка. При его определении будем использовать введенное в теме 18 понятие «отрезок состоит из отрезков».
Определение. Длиной отрезка называется положительная величина, обладающая следующими свойствами: 1) равные отрезки имеют равные длины; 2) если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.
Эти свойства длины отрезка используются при ее измерении. Чтобы измерить длину отрезка, нужно иметь единицу длины. В геометрии такой единицей является длина произвольного отрезка.
Как показано в теме 18, результатом измерения длины отрезка является положительное действительное число — его называют численным значением длины отрезка при выбранной единице длины или мерой длины данного отрезка. Если обозначить длину отрезка буквой X, единицу длины — Е, а получаемое при измерении действительное число — буквой а, то можно записать: а=m Е (Х) или Х = а∙Е.
Получаемое при измерении длины отрезка положительное действительное число должно удовлетворять ряду требований:
1. Если два отрезка равны, то численные значения их длин тоже равны.
2. Если отрезок х состоит из отрезков х 1 и х 2 , то численное значение его длины равно сумме численных значений длин отрезков х 1 и х 2 .
3. При замене единицы длины численное значение длины данного отрезка увеличивается (уменьшается) во столько раз, во сколько новая единица меньше (больше) старой.
4. Численное значение длины единичного отрезка равно единице.
Доказано, что положительное действительное число, являющееся мерой длины заданного отрезка, всегда существует и единственно. Доказано также, что для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.
Заметим, что часто, ради краткости речи, численное значение длины отрезка называют просто длиной. Например, в задании «Найдите длину данного отрезка» под словом «длина» подразумевается численное значение длины отрезка. Не менее часто допускают и другую вольность — говорят: «Измерь отрезок» вместо «Измерь длину отрезка».
Задача. Построить отрезок, длина которого 3,2Е. Каким будет численное значение длины этого отрезка, если единицу длины Е увеличить в 3 раза?
Решение. Построим произвольный отрезок и будем считать его единичным. Затем построим прямую, отметим на ней точку А и отложим от нее 3 отрезка, длины которых равны Е. Получим отрезок АВ, длина которого 3Е (рис. 1).
1).
Чтобы получить отрезок длиной 3,2Е, надо ввести новую единицу длины. Для этого единичный отрезок надо разбить либо на 10 равных частей, либо на 5, поскольку 0,2 = . Если от точки В отложить отрезок, равный единичного, то длина отрезка АС будет равна 3,2Е.
Чтобы выполнить второе требование задачи, воспользуемся свойством 3, согласно которому при увеличении единицы длины в 3 раза численное значение длины данного отрезка уменьшается в 3 раза. Разделим 3,2 на 3, получим:
3,2: 3 == 3 : 3 = = 1 . Таким образом, при единице длины 3Е численное значение длины построенного отрезка АС будет равно 1 .
Отрезком называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1 , а на ось Х длина проекции равна x2-x1 . Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)² . В данном случае |AB| является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5) . Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5 . А это значит, что длина нашего отрезка равна 5:1/2 .
А это значит, что длина нашего отрезка равна 5:1/2 .
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1 .
Рассчитаем длину отрезка А , для этого найдем квадратный корень:
A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²) .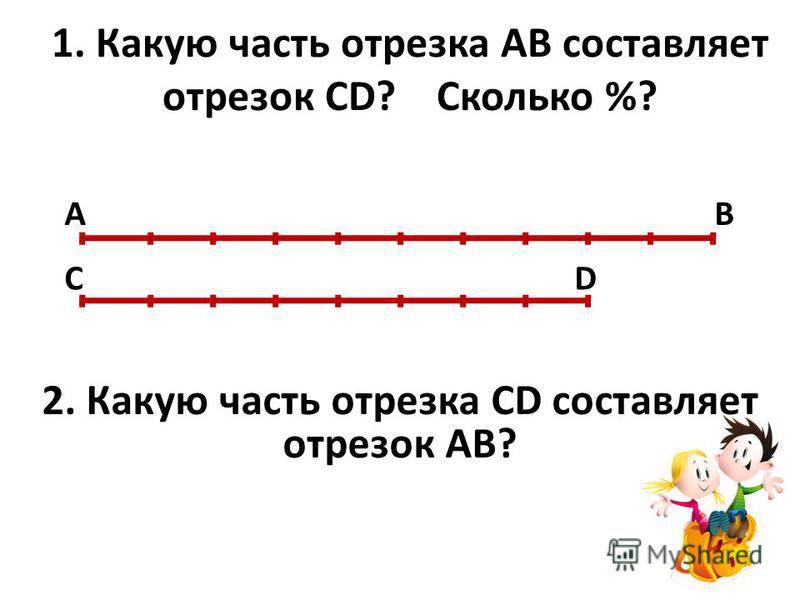
Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1 , то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61 .
Как найти длину отрезка если известны координаты. Метод координат в пространстве
Существует целая группа заданий (входящих в экзаменационные типы задач), связанная с координатной плоскостью. Это задачи начиная с самых элементарных, которые решаются устно (определение ординаты или абсциссы заданной точки, либо точки симметричной заданной и другие), заканчивая задачами в которых требуется качественное знание, понимание и хорошие навыки (задачи связанные с угловым коэффициентом прямой).
Постепенно мы с вами рассмотрим все их. В этой статье начнём с элементарных. Это простые задачи на определение: абсциссы и ординаты точки, длинны отрезка, середины отрезка, синуса или косинуса угла наклона прямой. Большинству эти задания будут не интересны. Но изложить их считаю необходимым.
Дело в том, что не все учатся в школе. Очень многие сдают ЕГЭ спустя 3-4 и более лет после её окончания и что такое абсцисса и ордината помнят смутно. Будем разбирать и другие задачи, связанные с координатной плоскостью, не пропустите, подпишитесь, на обновление блога. Теперь н
емного теории.
Очень многие сдают ЕГЭ спустя 3-4 и более лет после её окончания и что такое абсцисса и ордината помнят смутно. Будем разбирать и другие задачи, связанные с координатной плоскостью, не пропустите, подпишитесь, на обновление блога. Теперь н
емного теории.
Построим на координатной плоскости точку А с координатами х= 6, y=3.
Говорят, что абсцисса точки А равна шести, ордината точки А равна трём.
Если выразиться просто, то ось ох это ось абсцисс, ось оу это ость ординат.
То есть, абсцисса это точка на оси ох в которую проецируется точка заданная на координатной плоскости; ордината это точка на оси оу в которую проецируется оговоренная точка.
Длина отрезка на координатной плоскости
Формула для определения длины отрезка, если известны координаты его концов:
Как вы видите, длина отрезка — это длина гипотенузы в прямоугольными треугольнике с катетами равными
Х В – Х А и У В – У А
* * *
Середина отрезка. Её Координаты.
Её Координаты.
Формула для нахождения координат середины отрезка:
Уравнение прямой проходящей через две данные точки
Формула уравнения прямой походящей через две данные точки имеет вид:
где (х 1 ;у 1 ) и (х 2 ;у 2 ) координаты заданных точек.
Подставив значения координат в формулу, она приводится к виду:
y = kx + b , где k — это угловой коэффициент прямой
Эта информация нам понадобиться при решении другой группы задач связанных с координатной плоскостью. Статья об этом будет, не пропустите!
Что ещё можно добавить?
Угол наклона прямой (или отрезка) это угол между осью оХ и этой прямой, лежит в пределах от 0 до 180 градусов.
Рассмотрим задачи.
Из точки (6;8) опущен перпендикуляр на ось ординат. Найдите ординату основания перпендикуляра.
Основание перпендикуляра опущенного на ось ординат будет иметь координаты (0;8). Ордината равна восьми.
Ответ: 8
Найдите расстояние от точки A с координатами (6;8) до оси ординат.
Расстояние от точки А до оси ординат равно абсциссе точки А.
Ответ: 6.
A (6;8) относительно оси Ox .
Точка симметричная точке А относительно оси оХ имеет координаты (6;– 8).
Ордината равна минус восьми.
Ответ: – 8
Найдите ординату точки, симметричной точке A (6;8) относительно начала координат.
Точка симметричная точке А относительно начала координат имеет координаты (– 6;– 8).
Её ордината равна – 8.
Ответ: –8
Найдите абсциссу середины отрезка, соединяющего точки O (0;0) и A (6;8).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (0;0) и (6;8).
Вычисляем по формуле:
Получили (3;4). Абсцисса равна трём.
Ответ: 3
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку. Середину отрезка несложно будет определить по клеткам.
Середину отрезка несложно будет определить по клеткам.
Найдите абсциссу середины отрезка, соединяющего точки A (6;8) и B (–2;2).
Для того, решить поставленную задачу необходимо найти координаты середины отрезка. Координаты концов нашего отрезка (–2;2) и (6;8).
Вычисляем по формуле:
Получили (2;5). Абсцисса равна двум.
Ответ: 2
*Абсциссу середины отрезка можно определить без вычисления по формуле, построив данный отрезок на координатной плоскости на листе в клетку.
Найдите длину отрезка, соединяющего точки (0;0) и (6;8).
Длина отрезка при данных координатах его концов вычисляется по формуле:
в нашем случае имеем О(0;0) и А(6;8). Значит,
*Порядок координат при вычитании не имеет значения. Можно из абсциссы и ординаты точки О вычесть абсциссу и ординату точки А:
Ответ:10
Найдите косинус угла наклона отрезка, соединяющего точки O (0;0) и A (6;8), с осью абсцисс.
Угол наклона отрезка – это угол между этим отрезком и осью оХ.
Из точки А опустим перпендикуляр на ось оХ:
То есть, угол наклона отрезка это угол ВОА в прямоугольном треугольнике АВО.
Косинусом острого угла в прямоугольном треугольнике является
отношение прилежащего катета к гипотенузе
Необходимо найти гипотенузу ОА.
По теореме Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Таким образом, косинус угла наклона равен 0,6
Ответ: 0,6
Из точки (6;8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.
Через точку (6;8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью оУ .
Найдите расстояние от точки A с координатами (6;8) до оси абсцисс.
Найдите расстояние от точки A с координатами (6;8) до начала координат.
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание: Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант
Пример 3
Решение: по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж
Отрезок – это не вектор , и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Обратите внимание на важный технический приём – вынесение множителя из-под корня . В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Пробуем поделить на девять: . В результате:
Готово.
Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
Если вы хорошо заточенным карандашом прикоснетесь к тетрадному листу, то останется след, который дает представление о точке. (рис. 3
).
(рис. 3
).
Отметим на листе бумаги две точки A и B. Эти точки можно соединить различными линиями (рис. 4 ). А как соединить точки A и B самой короткой линией? Это можно сделать с помощь линейки (рис. 5 ). Полученную линию называют отрезком .
Точка и отрезок − примеры геометрических фигур .
Точки A и B называют концами отрезка .
Существует единственный отрезок, концами которого являются точки A и B. Поэтому отрезок обозначают, записывая точки, которые являются его концами. Например, отрезок на рисунке 5 обозначают одним из двух способов: AB или BA. Читают: «отрезок AB» или «отрезок BA».
На рисунке 6 изображены три отрезка. Длина отрезка AB равна 1 см. Он помещается в отрезке MN ровно три раза, а в отрезке EF − ровно 4 раза. Будем говорить, что длина отрезка MN равна 3 см, а длина отрезка EF − 4 см.
Также принято говорить: «отрезок MN равен 3 см», «отрезок EF равен 4 см». Пишут: MN = 3 см, EF = 4 см.
Длины отрезков MN
и EF
мы измерили единичным отрезком , длина которого равна 1
см. Для измерения отрезков можно выбрать и другие единицы длины , например: 1
мм, 1
дм, 1
км. На рисунке 7
длина отрезка равна 17
мм. Он измерен единичным отрезком, длина которого равна 1
мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7
).
Для измерения отрезков можно выбрать и другие единицы длины , например: 1
мм, 1
дм, 1
км. На рисунке 7
длина отрезка равна 17
мм. Он измерен единичным отрезком, длина которого равна 1
мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7
).
Вообще, измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается .
Длина отрезка обладает следующим свойством.
Если на отрезке AB отметить точку C, то длина отрезка AB равна сумме длин отрезков AC и CB (рис. 8 ).
Пишут: AB = AC + CB.
На рисунке 9 изображены два отрезка AB и CD. Эти отрезки при наложении совпадут.
Два отрезка называют равными, если они совпадут при наложении.
Следовательно отрезки AB и CD равны. Пишут: AB = CD.
Равные отрезки имеют равные длины.
Из двух неравных отрезков бОльшим будем считать тот, у уоторого длина больше. Например, на рисунке 6
отрезок EF
больше отрезка MN.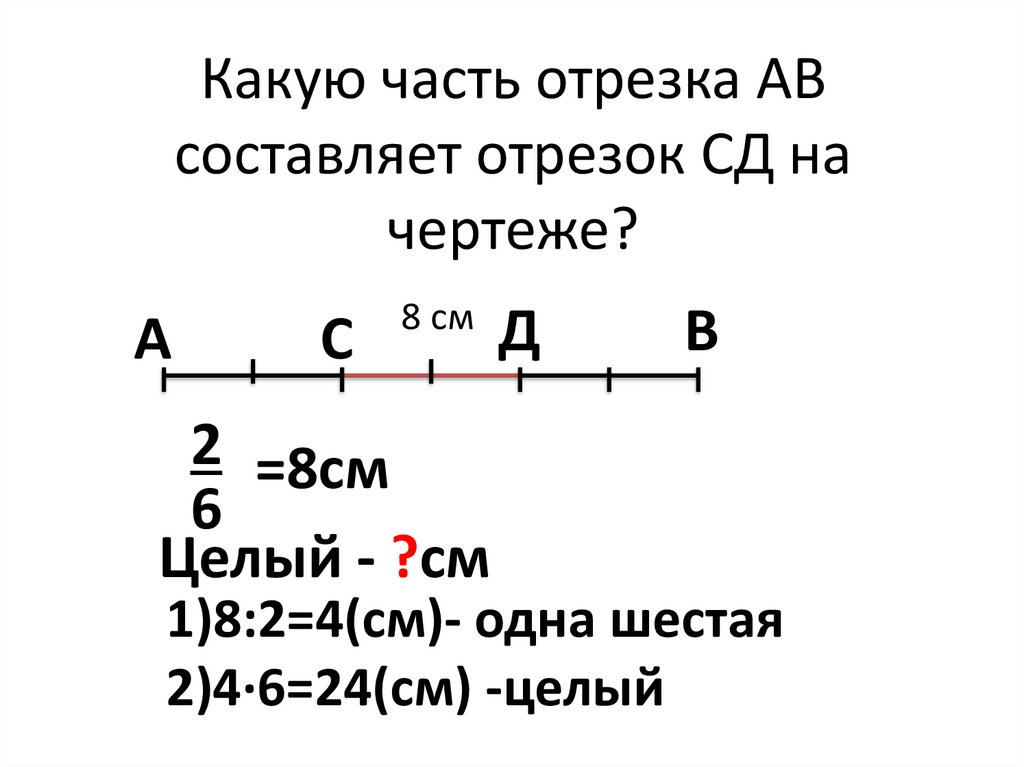
Длину отрезка AB называют расстоянием между точками A и B.
Если несколько отрезков расположить так, как показано на рисунке 10, то получится геометрическая фигура, которую называют ломаная . Заметим, что все отрезки на рисунке 11 ломаную не образуют. Считают, что отрезки, образуют ломаную, если конец первого отрезка совпадает с концом второго, а другой конец второго отрезка − с концом третьего и т. д.
Точки A, B, C, D, E − вершины ломаной ABCDE, точки A и E − концы ломаной , а отрезки AB, BC, CD, DE − ее звенья (см. рис. 10 ).
Длиной ломаной называют сумму длин всех ее звеньев.
На рисунке 12 изображены две ломаные, концы которых совпадают. Такие ломаные называют замкнутыми .
Пример 1 . Отрезок BC на 3 см меньше отрезка AB, длина которого равна 8 см (рис. 13 ). Найдите длину отрезка AC.
Решение. Имеем: BC = 8 − 3 = 5 (см).
Воспользовавшись свойством длины отрезка, можно записать AC = AB + BC. Отсюда AC =
8
+ 5
= 13
(см).
Отсюда AC =
8
+ 5
= 13
(см).
Ответ: 13 см.
Пример 2 . Известно, что MK = 24 см, NP = 32 см, MP = 50 см (рис. 14 ). Найдите длину отрезка NK.
Решение. Имеем: MN = MP − NP.
Отсюда MN = 50 − 32 = 18 (см).
Имеем: NK = MK − MN.
Отсюда NK = 24 − 18 = 6 (см).
Ответ: 6 см.
Инструкция
Если координаты крайних точек отрезка даны в двухмерной координат, то проведя через эти точки линии, перпендикулярные осям координат, вы получите прямоугольный треугольник. Его гипотенузой будет исходный отрезок, а катеты образуют отрезки, длина которых равна гипотенузы на каждую из координатных осей. Из теоремы Пифагора, определяющей длины гипотенузы как сумму квадратов длин катетов, можно сделать , что для нахождения длины исходного отрезка достаточно найти длины двух его проекций на координатные оси.
Найдите длины (X и Y) проекций исходного отрезка на каждую ось системы координат. В двухмерной системе из крайних точек представлена парой числовых значений (X1;Y1 и X2;Y2).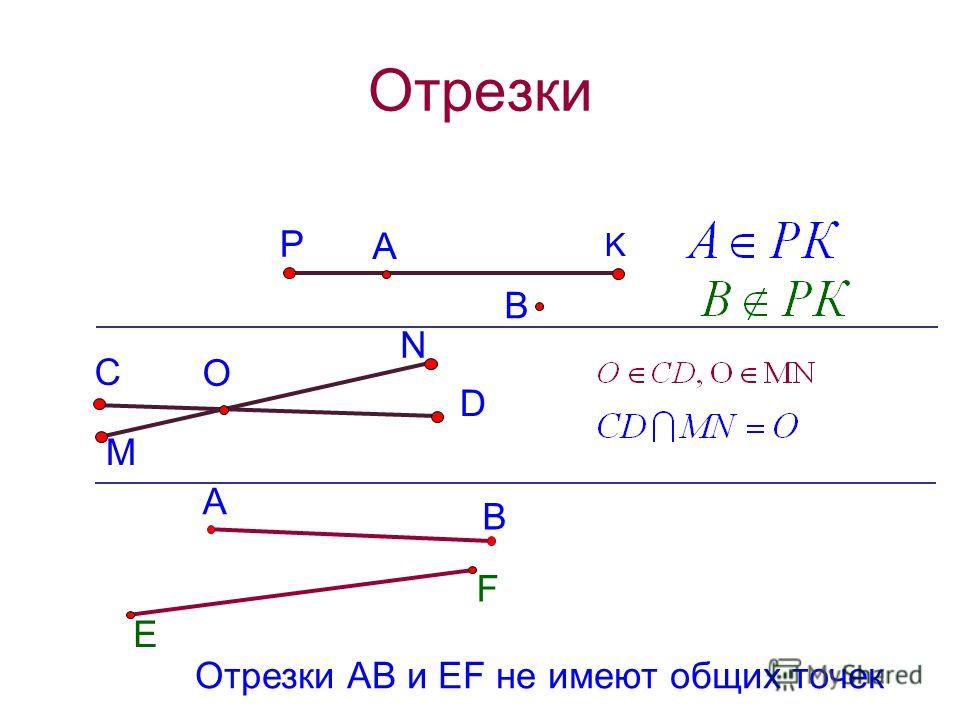 Длины проекций вычисляются нахождением разницы координат этих точек по каждой оси: X = X2-X1, Y = Y2-Y1. Возможно, что одно или оба полученных значения будут , но в данном случае это не никакой роли.
Длины проекций вычисляются нахождением разницы координат этих точек по каждой оси: X = X2-X1, Y = Y2-Y1. Возможно, что одно или оба полученных значения будут , но в данном случае это не никакой роли.
Рассчитайте длину исходного отрезка (A), найдя квадратный корень из квадратов рассчитанных на предыдущем шаге длин проекций на оси координат: A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²). Например, если отрезок проведен между точками с координатами 2;4 и 4;1, то длина его будет равна √((4-2)²+(1-4)²) = √13 ≈ 3,61.
Если координаты точек, ограничивающих отрезок, даны в трехмерной системе координат (X1;Y1;Z1 и X2;Y2;Z2), то длины (A) этого отрезка будет аналогична полученной на предыдущем шаге. В этом случае надо найти квадратный корень из суммы квадратов проекций на три координатные оси: A = √((X2-X1)²+(Y2-Y1)²+(Z2-Z1)²). Например, если отрезок проведен между точками , с координатами 2;4;1 и 4;1;3, то длина его будет равна √((4-2)²+(1-4)²+(3-1)²) = √17 ≈ 4,12.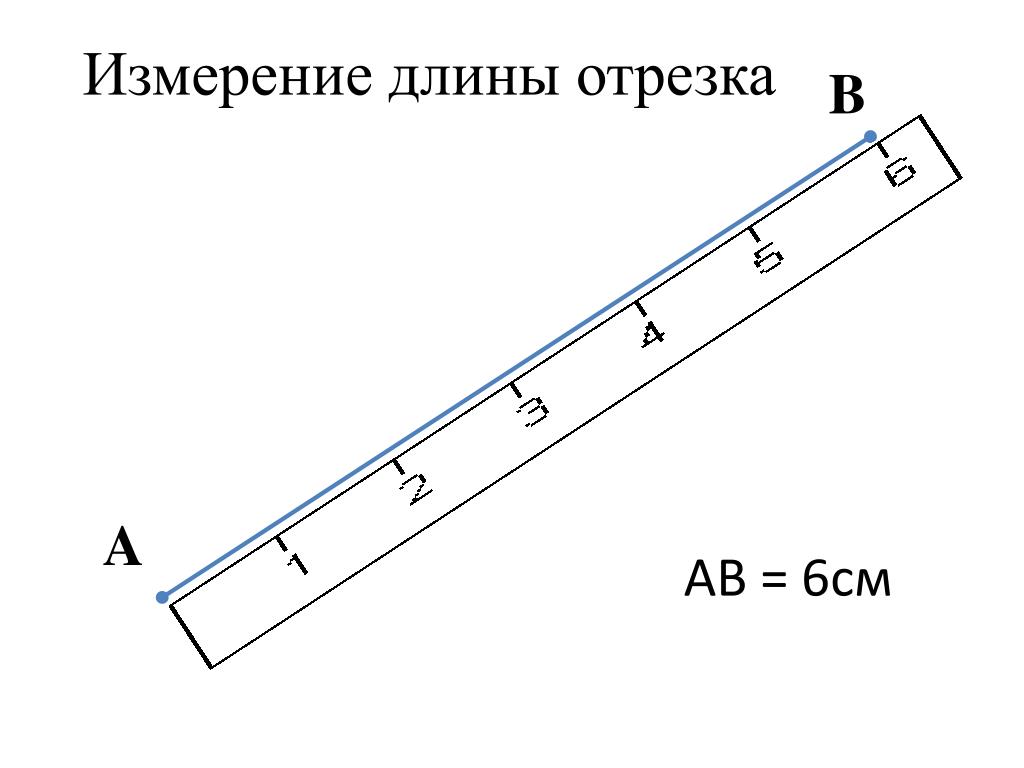 1/2.
1/2.
Видео по теме
Источники:
- Длина отрезка
- что такое длина отрезка
Иногда в повседневной деятельности может возникнуть необходимость найти середину отрезка прямой линии. Скажем, если предстоит сделать выкройку, эскиз изделия или просто распилить на две равные части деревянный брусок. На помощь приходит геометрия и немного житейской смекалки.
Вам понадобится
- Циркуль, линейка; булавка, карандаш, нить
Инструкция
Воспользуйтесь обычными инструментами, предназначенными для длины. Это самый простой способ отыскать середину отрезка. Измерьте линейкой или длину отрезка, разделите полученное пополам и отмерьте от одного из концов отрезка полученный результат. Вы получите точку, соответствующую середине отрезка.
Установите расстояние между ножками циркуля так, чтобы оно было равным длине отрезка или же большим, чем половина отрезка. Затем поставьте иглу циркуля в один из концов отрезка и проведите так, чтобы она пересекала отрезок.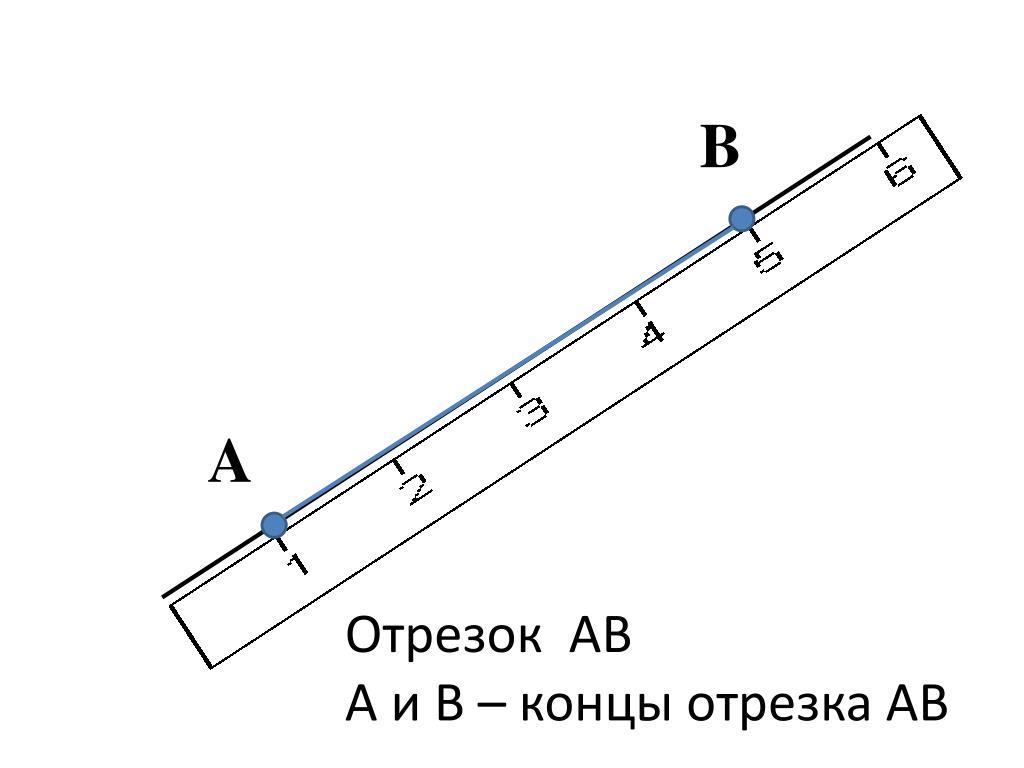 Переставьте иглу в другой конец отрезка и, не меняя размах ножек циркуля, проведите вторую полуокружность точно таким же образом.
Переставьте иглу в другой конец отрезка и, не меняя размах ножек циркуля, проведите вторую полуокружность точно таким же образом.
Если под рукой не оказалось циркуля или длина отрезка существенно превышает допустимый размах его ножек, можно воспользоваться простым приспособлением из подручных . Изготовить его можно из обычной булавки, нитки и карандаша. Привяжите концы нитки к булавке и карандашу, при этом длина нитки должна немного превышать длину отрезка. Таким импровизированным заменителем циркуля остается проделать шаги, описанные выше.
Видео по теме
Полезный совет
Достаточно точно найти середину доски или бруска вы можете, использовав обычную нитку или шнур. Для этого отрежьте нить так, чтобы она соответствовала длине доски или бруска. Остается сложить нить точно пополам и разрезать на две равные части. Приложите один конец полученной мерки к концу измеряемого предмета, а второй конец будет соответствовать его середине.
Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат каждая точка имеет три координаты. Зная координаты двух точек, можно определить расстояние между этими двумя точками.
В этих системах координат каждая точка имеет три координаты. Зная координаты двух точек, можно определить расстояние между этими двумя точками.
Вам понадобится
- Декартовы, полярные и сферические координаты концов отрезка
Инструкция
Рассмотрите для начала прямоугольную декартову координат. Положение точки в пространстве в этой координат определяется координатами x,y и z. Из начала координат к точке проводится радиус- . Проекции этого радиус-вектора на координатные оси и будут координатами этой точки.
Пусть у вас теперь есть две точки с координатами x1,y1,z1 и x2,y2 и z2 соответственно. Обозначьте за r1 и r2, соответственно, радиус-векторы первой и точки. Очевидно, что расстояние между этими точками будет модулю вектора r = r1-r2, где (r1-r2) — векторная разность.
Координаты вектора r, очевидно, будут следующими: x1-x2, y1-y2, z1-z2. Тогда вектора r или расстояние между двумя точками будет равно: r = sqrt(((x1-x2)^2)+((y1-y2)^2)+((z1-z2)^2)).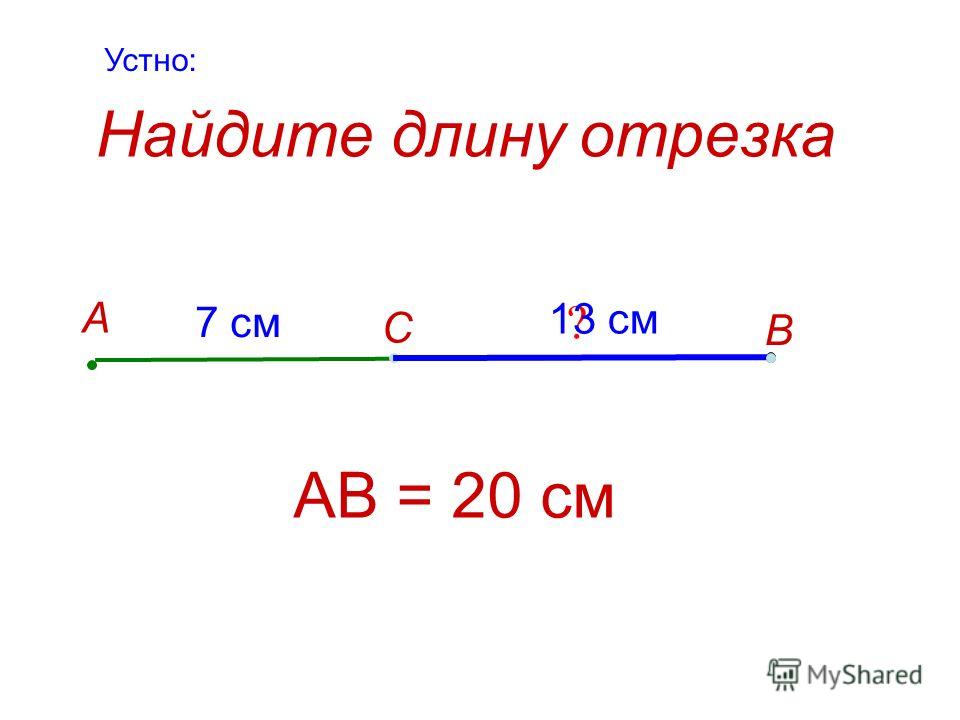 2))
2))
Видео по теме
Отрезок прямой определяется двумя крайними точками и состоит из множества точек, лежащих на проходящей через крайние точки прямой линии. Если отрезок помещен в какую-либо систему координат, то, найдя средние точки его проекций на каждую из осей, можно узнать координаты середины отрезка . По сути, операция сводится к нахождению среднего арифметического значения пар чисел для каждой из координатных осей.
Инструкция
Делите пополам сумму начальной и конечной координат крайних точек отрезка вдоль каждой оси, чтобы средней точки вдоль этой оси. Например, пусть отрезок помещен в трехмерную систему координат XYZ и известны координаты его крайних точек A(Xa,Ya,Za) и C(Xc,Yc,Zc). Тогда координаты его средней точки E(Xe,Ye,Ze) можно по формулам Xe=(Xa+Xc)/2, Ye=(Ya+Yc)/2, Ze=(Za+Zc)/2.
Используйте любой из калькуляторов, если вычислить средние значения координат крайних точек отрезка в уме не представляется возможным. Если под рукой нет такого гаджета, то используйте программный из состава ОС Windows. Его можно запустить, если, щелкнув кнопку «Пуск» раскрыть меню системы. В меню надо перейти в раздел «Стандартные», затем в подраздел «Служебные», а потом в секции «Все » выбрать пункт «Калькулятор». Можно обойтись без главного меню, если нажать сочетание клавиш WIN + R, ввести команду calc, а затем нажать клавишу Enter.
Если под рукой нет такого гаджета, то используйте программный из состава ОС Windows. Его можно запустить, если, щелкнув кнопку «Пуск» раскрыть меню системы. В меню надо перейти в раздел «Стандартные», затем в подраздел «Служебные», а потом в секции «Все » выбрать пункт «Калькулятор». Можно обойтись без главного меню, если нажать сочетание клавиш WIN + R, ввести команду calc, а затем нажать клавишу Enter.
Суммируйте попарно начальные и конечные координаты крайних точек отрезка вдоль каждой оси и делите результат на два. Интерфейс программного калькулятора имитирует обычный калькулятор, а вводить числовые значения и символы математических операций можно как щелкая кнопки курсором мыши на экране, так и нажимая клавиши на клавиатуре. Никаких сложностей с этими вычислениями возникнуть не .
Записывайте математические операции в текстовом виде и вводите их в поле поискового запроса на главной странице сайта Google, если -либо не можете использовать калькулятор, но имеете доступ в интернет. Этот поисковик имеет встроенный многофункциональный калькулятор, пользоваться которым намного проще, чем любым другим. Здесь нет интерфейса с кнопками — вводить все данные надо в текстовом виде в единственное поле. Например, если известны координаты крайних точек отрезка в трехмерной системе координат A(51,34 17,2 13,02) и A(-11,82 7,46 33,5), то координаты средней точки отрезка C((51,34-11,82)/2 (17,2+7,46)/2 (13,02+33,5)/2). Вводя в поле поискового запроса (51,34-11,82)/2, затем (17,2+7,46)/2 и (13,02+33,5)/2, можно с помощью Google получить координаты С(19,76 12,33 23,26).
Этот поисковик имеет встроенный многофункциональный калькулятор, пользоваться которым намного проще, чем любым другим. Здесь нет интерфейса с кнопками — вводить все данные надо в текстовом виде в единственное поле. Например, если известны координаты крайних точек отрезка в трехмерной системе координат A(51,34 17,2 13,02) и A(-11,82 7,46 33,5), то координаты средней точки отрезка C((51,34-11,82)/2 (17,2+7,46)/2 (13,02+33,5)/2). Вводя в поле поискового запроса (51,34-11,82)/2, затем (17,2+7,46)/2 и (13,02+33,5)/2, можно с помощью Google получить координаты С(19,76 12,33 23,26).
Как найти длину отрезка зная координаты точек. Нахождение координат середины отрезка, примеры, решения
Отрезком называют часть прямой линии, состоящей из всех точек этой линии, которые расположены между данными двумя точками — их называют концами отрезка.
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1 , а на ось Х длина проекции равна x2-x1 . Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)² . В данном случае |AB| является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5) . Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5 . А это значит, что длина нашего отрезка равна 5:1/2 .
Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5) . Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5 . А это значит, что длина нашего отрезка равна 5:1/2 .
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.
Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1 .
Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1 .
Рассчитаем длину отрезка А , для этого найдем квадратный корень:
A = √(X²+Y²) = √ ((X2-X1)²+(Y2-Y1)²) .
Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1 , то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61 .
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Yandex.RTB R-A-339285-1 Определение 1
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Определение 2
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Определение 3
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B: необходимо определить координату x C .
Поскольку точка C является серединой отрезка А В, верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т. е.
е.
| А С | = | С В | ⇔ x C — x A = x B — x C
Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — (x B — x C)
Из первого равенства выведем формулу для координаты точки C: x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A (x A) и B (x B):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A (x A , y A) и B (x B , y B) определяются как :
(x A + x B 2 , y A + y B 2)
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A (x A , y A , z A) и B (x B , y B , z B) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A (x A , y A) и B (x B , x B) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = (x A , y A) , O B → = (x B , y B) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C (x A + x B 2 , y A + y B 2 , z A + z B 2)
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Рассмотрим характерные примеры.
Пример 1
Исходные данные: на плоскости – точки с заданными координатами А (- 7 , 3) и В (2 , 4) . Необходимо найти координаты середины отрезка А В.
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ : координаты середины отрезка А В — 5 2 , 7 2 .
Пример 2
Исходные данные: известны координаты треугольника А В С: А (- 1 , 0) , В (3 , 2) , С (9 , — 8) . Необходимо найти длину медианы А М.
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = — 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М:
A M = (6 — (- 1)) 2 + (- 3 — 0) 2 = 58
Ответ: 58
Пример 3
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Заданы координаты точки C 1 (1 , 1 , 0) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M (4 , 2 , — 4) . Необходимо рассчитать координаты точки А.
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А: x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · (- 4) — 0 = — 8
Ответ: координаты точки А (7 , 3 , — 8) .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Определить длину отрезка возможно разными способами. Для того чтобы узнать, как найти длину отрезка, достаточно иметь в наличии линейку или знать специальные формулы для расчета.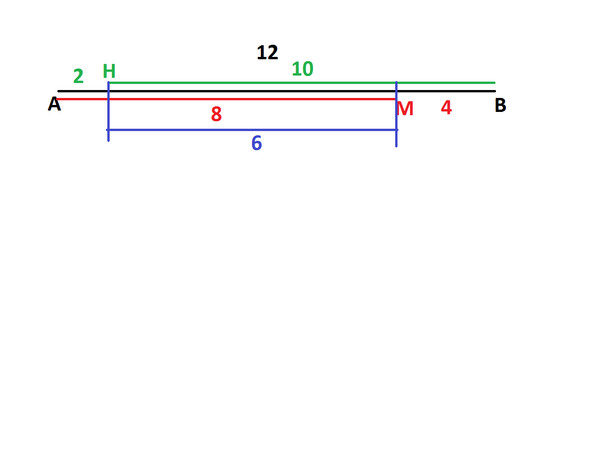
Длина отрезка с помощью линейки
Для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.
Метод координат на плоскости
Если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.
Рассмотрим пример, как найти длину отрезка по координатам.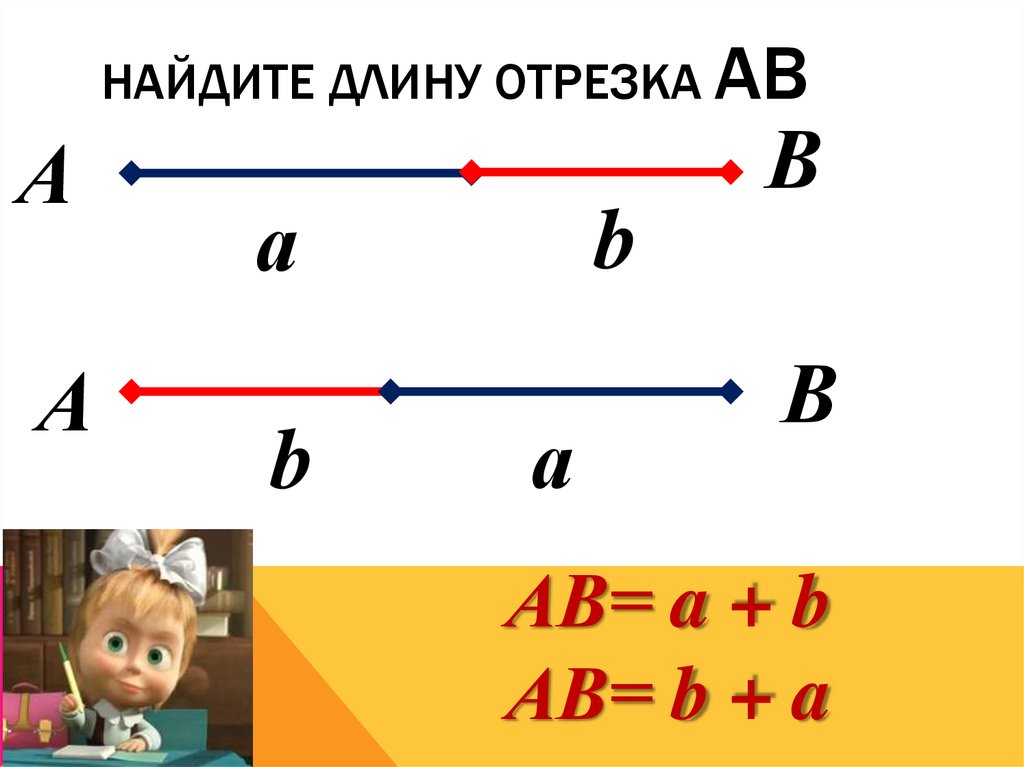 Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Есть координаты двух точек (-1;2) и (4;7). При нахождении разности координат точек получаем следующие значения: х = 5, у =5. Полученные числа и будут являться координатами отрезка. Затем каждое число возводим в квадрат и находим сумму результатов, она равна 50. Из этого числа извлекаем квадратный корень. Результат таков: 5 корней из 2. Это длина отрезка.
Метод координат в пространстве
Для этого необходимо рассмотреть, как найти длину вектора. Именно он и будет являться отрезком в евклидовом пространстве. Находится он почти таким же образом, как длина отрезка на плоскости. Построение вектора происходит в разных плоскостях . Как найти длину вектора?
- Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.
- После этого нужно возвести каждую координату вектора в квадрат.
- Затем складываем квадраты координат.
- Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат.

Рассмотрим алгоритм вычисления на примере. Необходимо найти координаты вектора АВ. Точки А и В имеют следующие координаты: А (1;6;3) и В (3;-1;7). Начало вектора лежит в точке А, конец расположен в точке В. Таким образом, чтобы найти его координаты, необходимо вычесть координаты точки А из координат точки В: (3 — 1; -1 — 6;7 — 3) = (2;-7;4).
Теперь возводим каждую координату в квадрат и складываем их: 4+49+16=69. И наконец, извлекает квадратный корень из данного числа. Его трудно извлечь, поэтому результат записываем таким образом: длина вектора равна корню из 69.
Если же вам не важно самому высчитывать длину отрезков и векторов, а нужен просто результат, то вы можете воспользоваться онлайн-калькулятором, например, этим .
Теперь, изучив данные способы и рассмотрев представленные примеры, вы без проблем сможете найти длину отрезка в любой задаче.
Если вы хорошо заточенным карандашом прикоснетесь к тетрадному листу, то останется след, который дает представление о точке. (рис. 3
).
(рис. 3
).
Отметим на листе бумаги две точки A и B. Эти точки можно соединить различными линиями (рис. 4 ). А как соединить точки A и B самой короткой линией? Это можно сделать с помощь линейки (рис. 5 ). Полученную линию называют отрезком .
Точка и отрезок − примеры геометрических фигур .
Точки A и B называют концами отрезка .
Существует единственный отрезок, концами которого являются точки A и B. Поэтому отрезок обозначают, записывая точки, которые являются его концами. Например, отрезок на рисунке 5 обозначают одним из двух способов: AB или BA. Читают: «отрезок AB» или «отрезок BA».
На рисунке 6 изображены три отрезка. Длина отрезка AB равна 1 см. Он помещается в отрезке MN ровно три раза, а в отрезке EF − ровно 4 раза. Будем говорить, что длина отрезка MN равна 3 см, а длина отрезка EF − 4 см.
Также принято говорить: «отрезок MN равен 3 см», «отрезок EF равен 4 см». Пишут: MN = 3 см, EF = 4 см.
Длины отрезков MN
и EF
мы измерили единичным отрезком , длина которого равна 1
см. Для измерения отрезков можно выбрать и другие единицы длины , например: 1
мм, 1
дм, 1
км. На рисунке 7
длина отрезка равна 17
мм. Он измерен единичным отрезком, длина которого равна 1
мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7
).
Для измерения отрезков можно выбрать и другие единицы длины , например: 1
мм, 1
дм, 1
км. На рисунке 7
длина отрезка равна 17
мм. Он измерен единичным отрезком, длина которого равна 1
мм, с помощью линейки с делениями. Также с помощью линейки можно построить (начертить) отрезок заданной длины (см. рис. 7
).
Вообще, измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается .
Длина отрезка обладает следующим свойством.
Если на отрезке AB отметить точку C, то длина отрезка AB равна сумме длин отрезков AC и CB (рис. 8 ).
Пишут: AB = AC + CB.
На рисунке 9 изображены два отрезка AB и CD. Эти отрезки при наложении совпадут.
Два отрезка называют равными, если они совпадут при наложении.
Следовательно отрезки AB и CD равны. Пишут: AB = CD.
Равные отрезки имеют равные длины.
Из двух неравных отрезков бОльшим будем считать тот, у уоторого длина больше. Например, на рисунке 6
отрезок EF
больше отрезка MN.
Длину отрезка AB называют расстоянием между точками A и B.
Если несколько отрезков расположить так, как показано на рисунке 10, то получится геометрическая фигура, которую называют ломаная . Заметим, что все отрезки на рисунке 11 ломаную не образуют. Считают, что отрезки, образуют ломаную, если конец первого отрезка совпадает с концом второго, а другой конец второго отрезка − с концом третьего и т. д.
Точки A, B, C, D, E − вершины ломаной ABCDE, точки A и E − концы ломаной , а отрезки AB, BC, CD, DE − ее звенья (см. рис. 10 ).
Длиной ломаной называют сумму длин всех ее звеньев.
На рисунке 12 изображены две ломаные, концы которых совпадают. Такие ломаные называют замкнутыми .
Пример 1 . Отрезок BC на 3 см меньше отрезка AB, длина которого равна 8 см (рис. 13 ). Найдите длину отрезка AC.
Решение. Имеем: BC = 8 − 3 = 5 (см).
Воспользовавшись свойством длины отрезка, можно записать AC = AB + BC.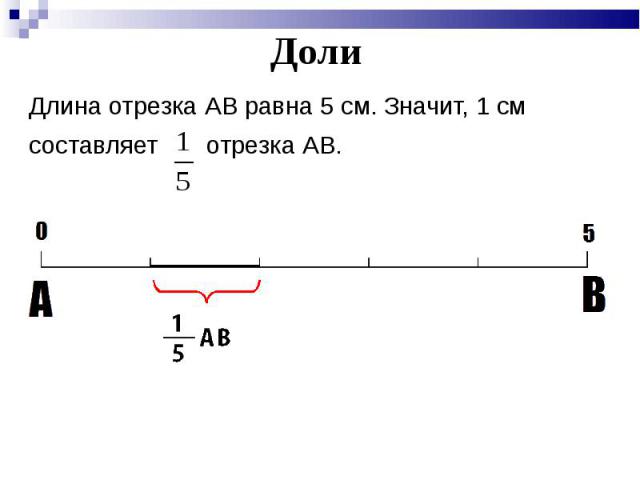 Отсюда AC =
8
+ 5
= 13
(см).
Отсюда AC =
8
+ 5
= 13
(см).
Ответ: 13 см.
Пример 2 . Известно, что MK = 24 см, NP = 32 см, MP = 50 см (рис. 14 ). Найдите длину отрезка NK.
Решение. Имеем: MN = MP − NP.
Отсюда MN = 50 − 32 = 18 (см).
Имеем: NK = MK − MN.
Отсюда NK = 24 − 18 = 6 (см).
Ответ: 6 см.
Существуют три основных системы координат, используемых в геометрии, теоретической механике, других разделах физики: декартова, полярная и сферическая. В этих системах координат вся точка имеет три координаты. Зная координаты 2-х точек, дозволено определить расстояние между этими двумя точками.
Вам понадобится
- Декартовы, полярные и сферические координаты концов отрезка
Инструкция
1. Разглядите для начала прямоугольную декартову систему координат. Расположение точки в пространстве в этой системе координат определяется координатами x,y и z. Из начала координат к точке проводится радиус-вектор.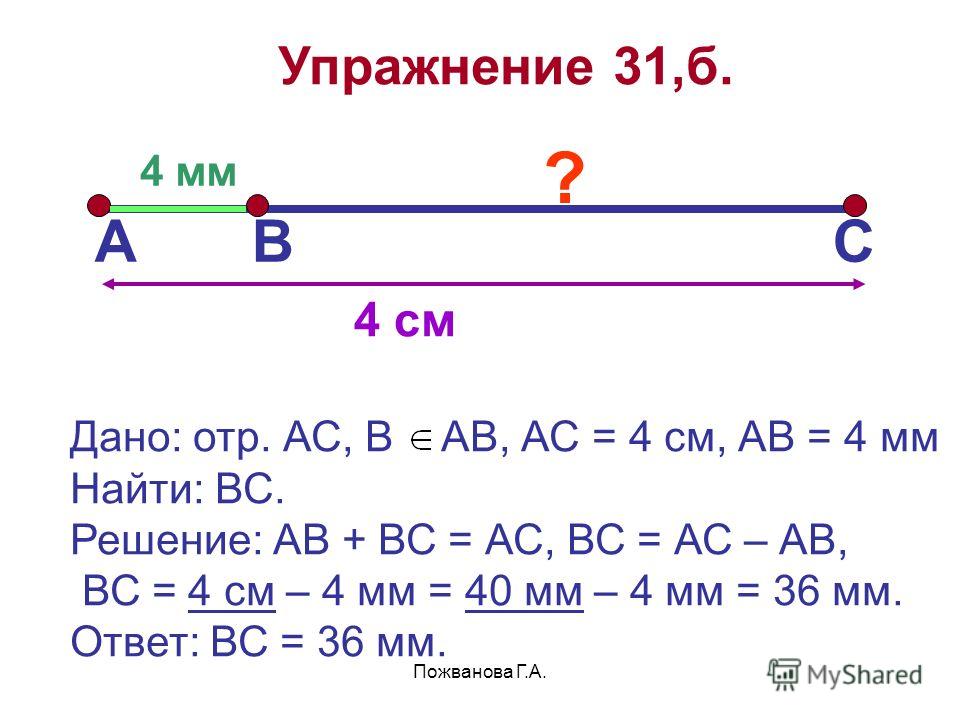 2))
2))
Видео по теме
Отрезок линии – определение, формула, примеры
Отрезок линии – это часть линии, имеющая две конечные точки и фиксированную длину. Она отличается от линии, у которой нет ни начала, ни конца и которая может быть продолжена в обоих направлениях. В этом уроке мы узнаем больше о отрезке прямой, его символе и способе измерения отрезка прямой.
| 1. | Что такое линейный сегмент? |
| 2. | Как измерить отрезки линии? |
| 3. | Формула сегмента линии |
| 4. | Разница между линией, сегментом линии и лучом |
| 5. | Часто задаваемые вопросы по сегменту линии |
Что такое линейный сегмент?
Отрезок линии — это путь между двумя точками, который можно измерить. Поскольку отрезки имеют определенную длину, они могут образовывать стороны любого многоугольника. На приведенном ниже рисунке показан отрезок AB, где длина отрезка AB относится к расстоянию между его конечными точками A и B.
На приведенном ниже рисунке показан отрезок AB, где длина отрезка AB относится к расстоянию между его конечными точками A и B.
Символ сегмента линии
Сегмент линии представлен полосой сверху, которая является символом сегмента линии. Записывается как \(\overline{AB}\).
Как измерить отрезки линии?
Отрезки можно измерять с помощью линейки (шкалы). Давайте посмотрим, как измерить данный отрезок линии и назвать его PQ.
- Шаг 1: Аккуратно разместите кончик линейки так, чтобы ноль оказался в начальной точке P данного отрезка.
- Шаг 2: Теперь начните читать значения, указанные на линейке, и найдите число, которое находится на другой конечной точке Q.
- Шаг 3: Таким образом, длина отрезка равна 4 дюймам, что можно записать как \(\overline{PQ}\) = 4 дюйма.
Формула сегмента линии
В приведенном выше примере мы измерили длину отрезка линии PQ как 4 дюйма.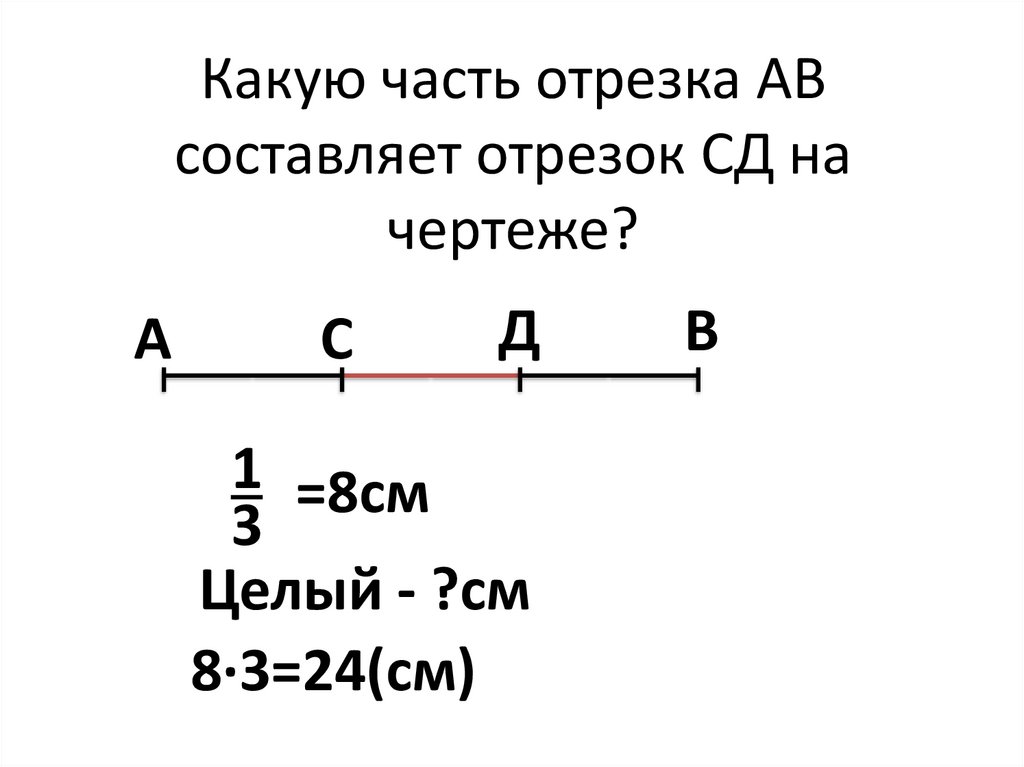 Это записывается как \(\overline{PQ}\) = 4 дюйма. Теперь давайте посмотрим, как найти длину отрезка, когда заданы координаты двух конечных точек. В этом случае мы используем формулу расстояния, то есть D = √[(\(x_{2}-x_{1}\)) 2 + (\(y_{2}-y_{1}\)) 2 ]. Здесь (\(x_{1}\), \(y_{1}\)) и (\(x_{2}\), \(y_{2}\)) — координаты заданных точек.
Это записывается как \(\overline{PQ}\) = 4 дюйма. Теперь давайте посмотрим, как найти длину отрезка, когда заданы координаты двух конечных точек. В этом случае мы используем формулу расстояния, то есть D = √[(\(x_{2}-x_{1}\)) 2 + (\(y_{2}-y_{1}\)) 2 ]. Здесь (\(x_{1}\), \(y_{1}\)) и (\(x_{2}\), \(y_{2}\)) — координаты заданных точек.
Например, отрезок имеет следующие координаты: (-2, 1) и (4, –3). Применим формулу расстояния, чтобы найти длину отрезка. Здесь \(x_{1}\) = -2; \(х_{2}\) = 4; \(у_{1}\) = 1; \(у_{2}\) = -3. После подстановки этих значений в формулу расстояния получаем: D =√[(4-(-2)) 2 + (-3-1) 2 ) = √((4+2) 2 + (-3-1) 2 ] = √(6 2 + (-4) 2 ) = √(36 + 16) = √52 = 7,21 единиц. Следовательно, используя формулу расстояния, мы нашли, что длина отрезка с координатами (-2, 1) и (4, -3) составляет 7,21 единицы.
Разница между линией, сегментом линии и лучом
Обратите внимание на приведенные ниже рисунки, чтобы понять разницу между линией, сегментом линии и лучом.
| Строка | Линейный сегмент | Рэй |
|---|---|---|
Линия — это набор точек, бесконечно простирающихся в двух противоположных направлениях. | Отрезок линии — это часть линии, имеющая начальную и конечную точки. | Луч — это часть линии, которая имеет начальную точку, но не имеет определенной конечной точки. |
| Обозначается стрелками на обоих концах, чтобы показать, что это продолжается вечно. | Имеет определенную длину и обозначается двумя концами. | Он показывает одну начальную точку и стрелку на другом конце, что означает, что он будет продолжаться вечно в одном направлении. |
Он не имеет конечных точек и записывается как \(\overleftrightarrow{AB}\). | Обозначается полосой сверху, которая является символом сегмента линии. Записывается как \(\overline{CD}\). Записывается как \(\overline{CD}\). | Записывается как \(\overrightarrow{\mathrm{EF}}\). |
Важные примечания
- Линия имеет бесконечные концы и не может быть измерена.
- Отрезок имеет начальную и конечную точки, поэтому его можно измерить.
- Отрезки имеют определенную длину, следовательно, они образуют стороны любого многоугольника.
- Луч имеет только одну начальную точку и не имеет конечной точки, поэтому его нельзя измерить.
- Понятие лучей можно понять на примере солнечных лучей, у которых есть начальная точка, но нет конечной.
☛Связанные темы
Ознакомьтесь со следующими страницами, посвященными линейному сегменту.
- Разница между линией и линейным сегментом
- Рабочие листы «Линии, лучи и сегменты линий»
- Как узнать, перпендикулярны ли два отрезка прямой?
Примеры линейных сегментов
Пример 1: Определите, является ли данная фигура отрезком, линией или лучом.

Решение:
Рисунок имеет одну начальную точку, но стрелку на другом конце. Это показывает, что это не отрезок или линия, это луч. Следовательно, LM — луч.
Пример 2: Назовите отрезки в данном треугольнике.
Решение:
Треугольник образуют отрезки \(\overline{PQ}\), \(\overline{QR}\) и \(\overline{PR}\).
Следовательно, отрезки в данном треугольнике равны \(\overline{PQ}\), \(\overline{QR}\) и \(\overline{PR}\).Пример 3: Найдите длину отрезка PQ, если координаты P и Q равны (3, 4) и (2, 0) соответственно.
Решение:
Координаты точек P и Q: (3, 4) и (2, 0). Применим формулу расстояния: D = √[(\(x_{2}-x_{1}\)) 2 + (\(y_{2}-y_{1}\)) 2 ]. Здесь \(x_{1}\) = 3; \(х_{2}\) = 2; \(у_{1}\) = 4; \(y_{2}\) = 0. Следовательно, длина отрезка D = √[(2-3) 2 +(0-4) 2 ] = √((-1) 2 +(-4) 2 ) = √(1 + 16) = √17 = 4,123 единицы.

Следовательно, \(\overline{PQ}\) = 4,123 единицы.
перейти к слайду перейти к слайду перейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатное пробное занятие
Практические вопросы в онлайн-сегменте
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по линейному сегменту
Что такое отрезок в математике?
Отрезок — это часть линии, соединяющая две точки, которые считаются ее конечными точками. Это расстояние между двумя точками, которое можно измерить. Поскольку отрезки имеют определенную длину, они могут образовывать стороны любого многоугольника.
В чем разница между линией и сегментом линии?
Линия не имеет конечных точек и может быть продолжена в оба конца, в то время как отрезок прямой имеет две фиксированные конечные точки, а луч имеет только одну начальную точку, но не имеет конечной точки.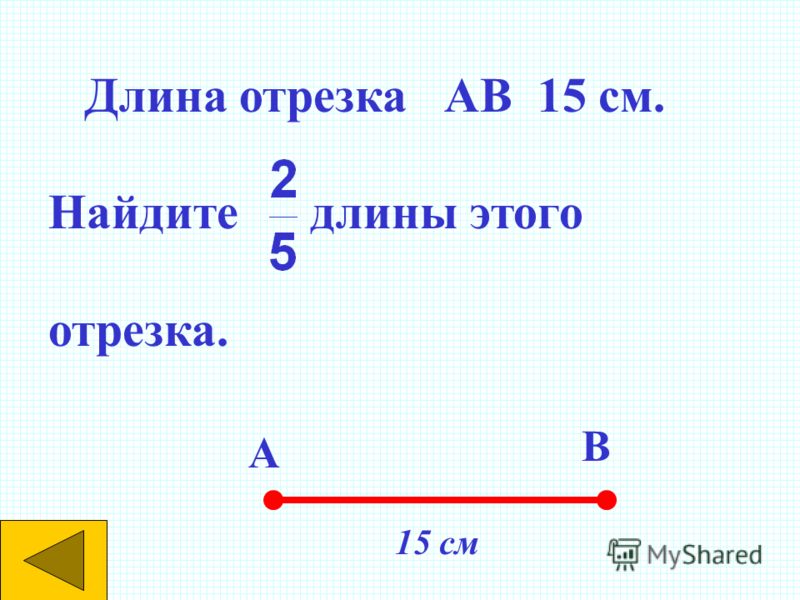
Как нарисовать отрезок?
Чтобы построить отрезок любой длины, в основном есть два метода. Один использует линейку, а другой использует линейку и циркуль. Первый метод построения отрезка прост, в котором мы берем линейку (шкалу) и отмечаем начальную точку как P, затем нам нужно отметить конечную точку как Q с необходимой длиной отрезка. Например, если требуемая длина составляет 4 дюйма, мы отмечаем Q равным 4 дюймам с помощью линейки. После этого шага две точки соединяются вместе, что показывает отрезок линии желаемой длины. Посетите страницу «Методы рисования сегмента линии» для подробного объяснения.
Что такое середина отрезка?
Под серединой отрезка понимается точка, которая делит его на две равные части и находится посередине отрезка.
Как найти середину отрезка?
Середину отрезка можно вычислить, если известны координаты конечных точек. Например, если (x 1 , y 1 ) и (y 1, y 2 ) являются двумя конечными точками, то середина отрезка может быть вычислена по формуле Midpoint = [( х 1 + x 2 )/2, (y 1 + y 2 )/2]
Каковы примеры отрезков в реальной жизни?
Мы знаем, что отрезки имеют фиксированную длину или меру.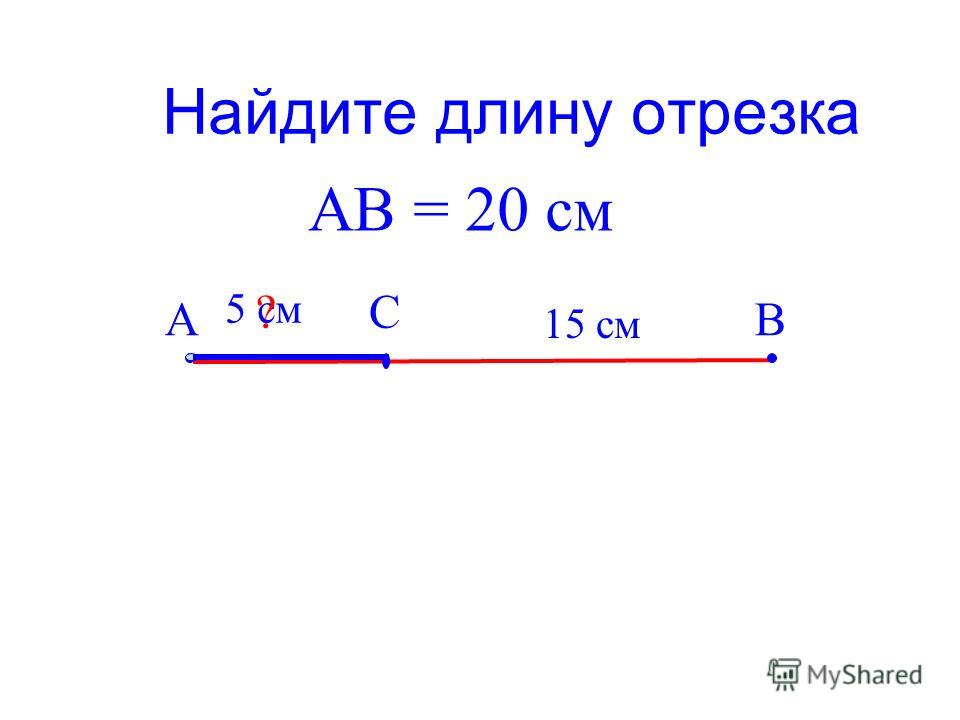 Таким образом, примерами отрезков в реальной жизни являются стороны многоугольника, края линейки, края бумаги и т. д.
Таким образом, примерами отрезков в реальной жизни являются стороны многоугольника, края линейки, края бумаги и т. д.
Что такое символ отрезка?
Отрезок линии обозначается чертой сверху (—), например \(\overline{AB}\). Эта полоса считается символом сегмента линии.
Как найти длину отрезка?
Чтобы найти длину отрезка, мы используем шкалу (линейку) для измерения его размеров. В некоторых случаях, если координаты концов отрезка заданы, то мы применяем формулу расстояния, D = √[(\(x_{2}-x_{1}\)) 2 + (\( y_{2}-y_{1}\)) 2 ], где «D» — расстояние между концами отрезка и (\(x_{1}\), \(y_{1}\) ) и (\(x_{2}\), \(y_{2}\)) — координаты двух точек.
Когда отрезки конгруэнтны?
Две фигуры называются конгруэнтными, если они имеют одинаковый размер и форму. Таким образом, любые два отрезка можно считать конгруэнтными, если они имеют одинаковую длину.
Можно ли расширить сегмент линии?
Нет, отрезок нельзя удлинить, потому что он имеет фиксированную и определенную длину. Хотя линию можно бесконечно продолжать в двух противоположных направлениях, а луч можно продолжать и с одного конца.
Хотя линию можно бесконечно продолжать в двух противоположных направлениях, а луч можно продолжать и с одного конца.
Что такое линейный сегмент? — [Факты и пример определения]
Что такое линейный сегмент?
Отрезок линии — это участок линии, который может соединить две точки.
Давайте поймем, что такое отрезок с помощью следующих диаграмм:
Это линия! Он не имеет концов и бесконечно простирается в обоих направлениях.
Если отметить на нем две точки A и B и выбрать этот отрезок отдельно, он станет отрезком прямой.
Этот отрезок имеет две конечные точки A и B, длина которых фиксирована. Длина этого отрезка равна расстоянию между его конечными точками A и B.
Итак, отрезок — это часть или часть линии, имеющая две конечные точки. В отличие от прямой, отрезок прямой имеет определенную длину.
Длина отрезка может быть измерена либо в метрических единицах, таких как миллиметры, сантиметры, либо в обычных единицах, таких как футы или дюймы.
Символ
Отрезок линии обычно обозначается символом полосы (—) над конечными точками. Скажем, отрезок имеет концы P и Q, его можно обозначить $\overline{PQ}$.
Реальные примеры сегментов линии
- Края таблицы.
- Сторона квадрата или треугольника
- Спичка.
- Карандаш
- Край линейки.
Как измерить отрезок линии?
Когда у вас есть два отрезка, вы можете сказать, длиннее или короче другой отрезок, просто взглянув на них. Мы видим, что отрезок CD длиннее, чем AB. Однако мы не всегда можем полагаться на наблюдение, чтобы найти длину отрезка.
Чтобы измерить длину отрезка, выполните следующие шаги:
Шаг 1: Возьмите весы для измерения длины отрезка. Обычно меньшие сегменты линий измеряются с использованием сантиметровой шкалы.
Шаг 2: Определите сегмент линии, который вы хотите измерить.
Шаг 3: Поместите нулевую отметку линейки в начальную точку отрезка.
Шаг 4: Прочтите число на шкале, где заканчивается сегмент линии. В данном случае это 5. Значит, длина данного отрезка равна 5 см.
Рисование отрезка с помощью линейки и циркуля
Предположим, нам нужно нарисовать отрезок длиной 5 см. Мы будем следовать данным шагам:
- Шаг 1: Нарисуйте линию любой длины. Отметьте на прямой точку А, которая является начальной точкой отрезка прямой.
- Шаг 2: С помощью линейки поместите стрелку циркуля на расстоянии 5 см от грифеля карандаша.
- Шаг 3: Поместите стрелку компаса в точку A и отметьте дугу на линии кончиком карандаша.
- Шаг 4: Отметьте точку пересечения дуги и прямой как B.
- Шаг 5: AB — необходимый отрезок линии длиной 5 см.
Интересные факты об сегментах линии
Два слова, линия и сегмент, объединяются, чтобы сформировать сегмент линии. Слово «линия» происходит от латинского Segmentum, что означает полосу, отрезанный кусок или сегмент земли, а сегмент происходит от латинского Segmentum, что означает полосу, отрезанный кусок или сегмент земли.
Слово «линия» происходит от латинского Segmentum, что означает полосу, отрезанный кусок или сегмент земли, а сегмент происходит от латинского Segmentum, что означает полосу, отрезанный кусок или сегмент земли.
Решенные примеры
Пример 1: Запишите названия заданных отрезков.
Решение:
$\overline{PQ}$ , $\overline{XY}$
Пример 2. Запишите все возможные отрезки на данном рисунке.
Решение:
$\overline{UV}$, $\overline{VW}$ , $\overline{UW}$
Пример 3. Подсчитайте количество отрезков на заданном рисунке. .
Решение:
Данная фигура состоит из 7 отрезков.
Практические задачи
Луч
Отрезок
Отрезок
Правильный ответ: Отрезок
Отрезок имеет 2 конца $
$\overleftarrow{LM}$
$\overline{LM}$
Правильный ответ: $\overline{LM}$
Отрезок обычно обозначается символом полосы (—) в верхней части конечные точки.
2
3
4
5
Правильный ответ: 3
Прямоугольник имеет четыре стороны. Итак, 4 отрезка.
Литр
Миллиметр
Килограмм
Кубический метр
Правильный ответ: Миллиметр
Миллиметр — метрическая единица измерения отрезка прямой.
Заключение
Если вы хотите узнать больше об сегментах линий в увлекательной игровой форме и по-новому или хотите легко изучить похожие математические понятия, такие как отношения, дроби и т. д., посетите SplashLearn, где вы найдете несколько интересных вопросов и ответов и решенные примеры. Более того, SplashLearn предлагает вам зарегистрироваться бесплатно прямо сейчас!
Часто задаваемые вопросы
В чем разница между линией и сегментом линии?
Отрезок прямой имеет конечные точки, в то время как отрезок можно бесконечно удлинять с обоих концов.
Есть ли разница между отрезком и лучом?
Да. Луч и отрезок разные. У луча одна конечная точка, а у отрезка две. Один конец луча простирается бесконечно, тогда как в отрезке линии конечные точки всегда определены и фиксированы.
Луч и отрезок разные. У луча одна конечная точка, а у отрезка две. Один конец луча простирается бесконечно, тогда как в отрезке линии конечные точки всегда определены и фиксированы.
Как определить середину отрезка?
Середина отрезка — это точка в середине отрезка, которая делит его на две равные части.
Что такое конгруэнтность отрезков?
Если две фигуры одинакового размера и формы, они конгруэнтны. В результате любые два отрезка прямой одинаковой длины могут считаться конгруэнтными.
Как найти концы отрезка
Как найти концы отрезка — СБ Математика—>
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский диалект
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все математические ресурсы SAT
16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept
SAT Math Help » Геометрия » Координатная геометрия » Линии » Формула середины » Как найти концы отрезка
Середина отрезка AB равна (2, -5).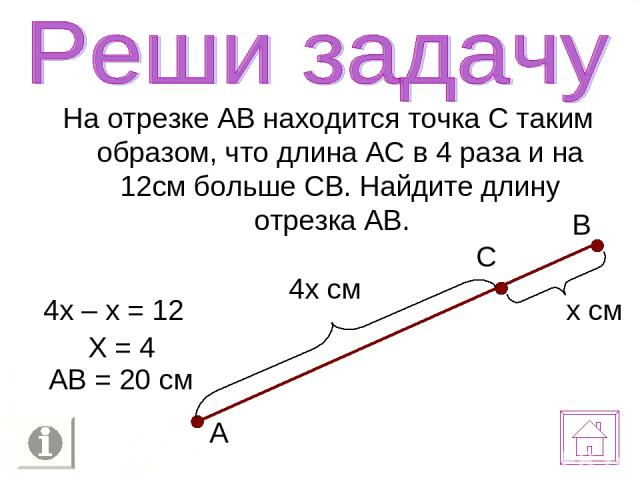 Если координаты точки А равны (4, 4), то каковы координаты точки В?
Если координаты точки А равны (4, 4), то каковы координаты точки В?
Возможные ответы:
(0, -14)
(6, 13)
(0, -13)
(6, 14)
(3, -0.8) Правильный ответ 905 :
(0, -14)
Объяснение:
Самый быстрый способ найти отсутствующую конечную точку — определить расстояние от известной конечной точки до средней точки, а затем выполнить такое же преобразование для средней точки. В этом случае координата x перемещается с 4 на 2 или вниз на 2, поэтому новая координата x должна быть 2-2 = 0. Координата y перемещается с 4 на -5 или вниз на 9., поэтому новая координата y должна быть -5-9 = -14.
Альтернативным решением может быть замена (4,4) вместо (x 1 ,y 1 ) и (2,-5) вместо (x,y) в формуле средней точки:
x= (x 1 +x 2 )/2
y=(y 1 +y 2 )/2
Решение каждого уравнения для (x 2 ,1y 2902 дает решение) 22 ,1y 2902 (0,-14).
Сообщить об ошибке
Точка A (5, 7). Точка B равна (x, y). Середина AB равна (17, –4). Какова ценность Б?
Возможные ответы:
Ни один из других ответов
(22, –9)
(8,5, –2)
(12, –11)
(29, –15)
Правильный ответ:
(29, –15)
Пояснение:
Точка А (5, 7). Точка B равна (x, y). Середина AB равна (17, –4). Какова ценность Б?
Нам нужно использовать нашу обобщенную формулу средней точки:
MP = ((5 + x)/2, (7 + y)/2)
Решить каждое по отдельности:
(5 + x)/2 = 17 → 5 + x = 34 → x = 29
(7 + y)/2 = –4 → 7 + y = –8 → y = – 15
Следовательно, B равно (29, –15).
Сообщить об ошибке
Отрезок AB имеет конечную точку A, расположенную в точке , и среднюю точку в точке . Каковы координаты точки B отрезка AB?
Возможные ответы:
Вторая конечная точка не может существовать
Правильный ответ:
Объяснение:
С конечной точкой A, расположенной в (10,-1), и средней точкой в (10,0), мы хотим добавить длину от A до середины на другой стороне сегмента, чтобы найти точку B. Общая длина отрезка должна быть в два раза больше расстояния от точки А до середины.
Общая длина отрезка должна быть в два раза больше расстояния от точки А до середины.
A расположен ровно на одну единицу ниже средней точки по оси Y, что соответствует общему смещению (0,1). Чтобы найти точку B, мы добавляем (10+0, 0+1) и получаем координаты для B: (10,1).
Сообщить об ошибке
Решите каждую проблему и выберите лучший из предложенных вариантов.
Какое расстояние между точками и на стандартной координатной плоскости?
Возможные ответы:
Правильный ответ:
Пояснение:
Сделай треугольник. Точки отстоят друг от друга на 8 единиц по -оси и на единиц друг от друга по -оси. Затем используйте теорему Пифагора, чтобы найти расстояние до гипотенузы, которое в конечном итоге равно .
Еще один способ решить эту проблему — использовать формулу расстояния,
Подключение двух точек, которые мы получаем,
Отчет о ошибке
Уведомление о авторском правом
View Sat Mathematics
Уильям
Сертифицированный преподаватель
Джорджтаунский университет, бакалавр искусств, история. Йельский университет, доктор философии, истории.
Йельский университет, доктор философии, истории.
View SAT Репетиторы по математике
Joscelyn
Сертифицированный преподаватель
Университет Рутгерса, Нью-Брансуик, бакалавр наук, промышленная инженерия.
View SAT Репетиторы по математике
Алонсо
Сертифицированный репетитор
Государственный университет Трумэна, бакалавр наук, специальность математика, дополнительная статистика.
Все математические ресурсы SAT
16 диагностических тестов 660 практических тестов Вопрос дня Карточки Учитесь по концепции
Длина сегмента: определение, формула и примеры
Кто любит альпинизм? Я помню, как часть нашего поступления в колледж, мы, новички, должны были преодолевать большие расстояния, включая альпинизм. Чтобы мы не упали в обморок в пути, это долгое путешествие было разделено на несколько остановок, которые назывались «альпинистскими сегментами». В этой статье будет рассмотрено все, что вам следует знать о длине сегмента .
В этой статье будет рассмотрено все, что вам следует знать о длине сегмента .
Что означает длина сегмента?
Расстояние между двумя точками на отрезке прямой равно длине отрезка.
Это очень краткое определение. Короче говоря, длина сегмента — это «от одной точки до другой». Вспомните альпинистские отрезки, это были лишь части общей дистанции, которую нам предстояло преодолеть.
Иллюстрация сегментов линии с дорогой, StudySmarter Originals
Между тем, невозможно понять длину сегмента, не принимая во внимание точки перспективы, потому что вы сосредоточены на определении того, где сегмент начинается, а также где он заканчивается.
Какова длина отрезка между двумя точками?
Длина отрезка между двумя точками — это расстояние между двумя точками. Одна точка служит отправной точкой, с которой начинается измерение. Между тем, другой — это конечная точка, в которой останавливается измерение. Иногда это имя с маленькой буквы или с буквами в верхнем регистре. Например, если есть две точки А и В, мы можем назвать отрезок длины, существующий между А и В, или с, или мы можем просто назвать отрезок прямой АВ.
Например, если есть две точки А и В, мы можем назвать отрезок длины, существующий между А и В, или с, или мы можем просто назвать отрезок прямой АВ.
Изображение длины отрезка, StudySmarter Originals
Какие координаты существуют на длине отрезка между двумя точками?
Поскольку мы имеем дело с точками, нам нужно знать их положение на декартовой плоскости. Другими словами, мы должны знать положение начальной и конечной точки по осям x и y. Это положение называется координатами точек отрезка длины и записывается в виде (x 1 , y 1 ) и (х 2 , у 2 ).
Здесь
x 1 означает положение начальной точки по оси X,
y 1 означает положение начальной точки по оси Y,
x 2 означает положение начальной точки по оси Y. положение конечной точки по оси x
и
y 2 означает положение конечной точки по оси y.
На изображении ниже это ясно показано.
Графическое изображение двух точек длины отрезка с указанием их координат, StudySmarter Originals
Теперь мы можем видеть отрезок длины не только как расстояние, но теперь мы рассматриваем точки, определяющие это расстояние.
Теперь вы должны подумать о том, как определить длину отрезков, когда вы знаете их начальную и конечную точки.
Какая формула для длины отрезка между двумя координатами?
Чтобы найти длину отрезка, мы можем создать прямоугольный треугольник и, следовательно, использовать теорему Пифагора для определения расстояния:
На изображении показано использование теоремы Пифагора для вычисления длины отрезка по двум точкам, StudySmarter Оригиналы
Мы можем видеть, что это расстояние по вертикали между точками A и B. это расстояние по горизонтали между точками A и B. Следовательно, мы можем составить пифагорейский треугольник, подставив расстояние между точками A и B как .
Используя теорему Пифагора, мы знаем:
Поскольку расстояние между двумя точками не может быть отрицательным, мы знаем:
Для точек A=() и B=():
и
Следовательно:
Обратите внимание, что поскольку ∆y и ∆x возводятся в квадрат, нет необходимости брать абсолютное значение этих чисел, так как их возведение в квадрат делает их положительными. Также обратите внимание, что квадратный корень не отменяет того факта, что ∆y и ∆x возводятся в квадрат, поскольку уравнение добавляет эти члены, а не умножает их.
Также обратите внимание, что квадратный корень не отменяет того факта, что ∆y и ∆x возводятся в квадрат, поскольку уравнение добавляет эти члены, а не умножает их.
Найти расстояние между точками A=(5, 0) и B=(3,7)
Решение:
Подставив координаты в уравнение для длины отрезка:
2
3
Если не указано иное, вы можете оставить свой ответ в точной или числовой форме.
Длина сегмента с конечными точками
В некоторых случаях вам могут быть заданы только конечные и средние точки, и вам потребуется определить длину всего сегмента.
Середина — это точка на полпути между начальной и конечной точками.
Когда это происходит, первым шагом является поиск начальной точки, которая не была задана изначально. Итак, для начальной точки A(x 1 , y 2 ), середины M (x m , y m ) и конечной точки B (x 2 , y 2 ) средняя точка для ось x рассчитывается как:
, а средняя точка оси y рассчитывается как:
Однако нас интересует нахождение начальной точки, когда заданы только конечная и средняя точки. В этом случае вам просто нужно сделать в соответствующих падежах x 1 или y 1 субъекта формулы. Это означает, что координата начальной точки по оси x, x 1 равна:
В этом случае вам просто нужно сделать в соответствующих падежах x 1 или y 1 субъекта формулы. Это означает, что координата начальной точки по оси x, x 1 равна:
Решается как
, а координата начальной точки по оси y, y 1 равна:
Решается как
Если Нонсо находится в путешествии, в котором его путь является линейным, и на данный момент он преодолел половину расстояния. Если его текущая координата равна (4, -2), а его путь заканчивается в точке K (9, 5), найдите длину отрезка всего пути.
Решение:
Судя по предоставленной информации, Нонсо в настоящее время находится в середине всего пути, который является длиной отрезка пути. Поскольку K — это место, где заканчивается путешествие, это означает, что у нас есть конечная точка. С их помощью мы теперь можем найти координаты нашей отправной точки как
и
Это означает, что Нонсо начал свое путешествие в точке (-1,-9).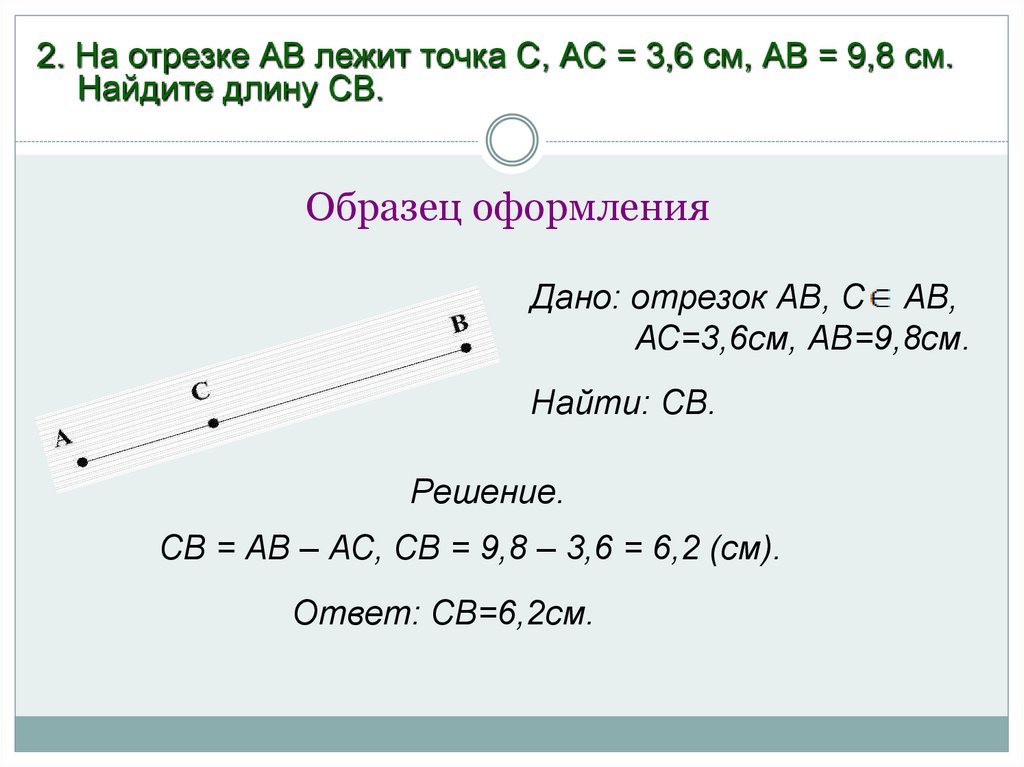
Теперь, когда мы знаем его начальную точку, мы можем рассчитать длину отрезка пути как:
Какова длина отрезка окружности?
Отрезок окружности ограничен дугой и хордой. Линейный сегмент круга может быть либо диаметром круга, когда линия проходит через центр круга, либо хордой, если линия проходит в любом другом месте, кроме центра круга.
Чтобы вычислить длину сегмента окружности, когда он проходит через центр, умножьте заданный радиус на 2. Однако, когда он проходит вне центра, тогда длина сегмента окружности равна длине хорды, вычисляемой как
Где r — радиус, а θ — угол, образуемый сектором, образующим сегмент.
Эта формула была получена из описания изображения ниже;
Изображение, иллюстрирующее получение длины сегмента окружности, StudySmarter Originals
из изображения с помощью SOHCATOA мы получаем
Найдите длину отрезка окружности радиусом 10 см, который стягивается на 120° в центре.
Решение:
Пример сегмента линии в круге, StudySmarter Originals
Длина сегмента линии равна
Длина сегмента — основные выводы
- Расстояние между двумя сегментами — это координаты.
- Рассчитывается по теореме Пифагора.
- Длину сегмента можно рассчитать, если заданы конечная и средняя точки.
- Отрезок окружности представляет собой либо диаметр, либо хорду, в зависимости от того, проходит ли линия через центр окружности.
Нарисуйте отрезок AB длиной 4 см Нарисуйте прямую, перпендикулярную AB, через A и B соответственно…
Перейти к
- Конструкции — упражнение 11.1
- Построения — упражнение 11.2
- Конструкции — упражнение 11.
 3
3 - Построения — упражнение 11.4
- Системы счисления
- Полиномы
- Координатная геометрия
- Линейные уравнения с двумя переменными
- Введение в геометрию Евклида
- Линии и углы
- Треугольники
- Четырехугольники
- Площади параллелограммов и треугольников
- Круги
- Конструкции
- Формула Герона
- Площади поверхности и объемы
- Статистика и вероятность
Главная >
Образцовые решения NCERT
Класс 9
Математика
>
Глава 11 — Конструкции
>
Конструкции — упражнение 11. 3
>
Вопрос 2
3
>
Вопрос 2
Вопрос 2 Конструкции – Упражнение 11.3
Нарисуйте отрезок АВ длиной 4 см. Проведите прямую, перпендикулярную AB, через точки A и B соответственно. Эти прямые параллельны?
Ответ:
Согласно вопросу,
Отрезок AB длиной 4см.
Чтобы провести перпендикуляр к АВ через точки А и В соответственно.
Этапы строительства:
Начертить АВ = 4 см.
С центром А нарисуйте дугу, пересекающую АВ в точке Р.
Используя P в качестве центра и того же радиуса, нарисуйте дугу, пересекающую дугу, нарисованную на шаге 2, в точке Q.
Используя Q в качестве центра и того же радиуса, нарисуйте дугу, пересекающую дугу, нарисованную в шаге 3, на R.
Используя R в качестве центра и того же радиуса, нарисуйте дугу, пересекающую дугу, нарисованную в шаге 5, в точке X.
Нарисуйте OX и произведите его для C и D.

Теперь повторите шаги со 2 по 7, чтобы провести линию EF перпендикулярно точке B.
Да, эти прямые параллельны, поскольку сумма внутренних углов по одну сторону от поперечной
равна 180°
Расшифровка видео
сеанс решения сомнений и на сегодняшней сессии мы собираемся решить еще одну проблему, связанную с геометрия в порядке так что сначала я собираюсь прочитать вопрос нарисуйте отрезок a b длиной 4 сантиметра в длину провести линию, перпендикулярную a b через а и б соответственно и мы собираемся проверить, хорошо ли эти строки параллельно или не все в порядке так что давайте быстро сделать это строительство Итак, сначала то, что мы собираемся делать нам надо нарисуйте отрезок a b из четырех сантиметр но вот что я буду делать я буду рисовать отрезок линии a b более четырех сантиметр точно хорошо ради объяснения ты можешь сделать во время рисования вы можете нарисовать точно четыре сантиметра хорошо так сначала хорошо я нарисую сегмент линии поэтому я нарисую прямую линию, я буду рисовать со случайным расстоянием хорошо, так что это отрезок линии хорошо a b так я нарисовал здесь случайным образом расстояние хорошо, пока рисуешь, что ты можешь сделать может рисовать ровно на четыре сантиметра Правильно Хорошо, я упомяну здесь два пункта ладно это первое точка, которая является точкой a и вот в чем дело b хорошо, так что это отрезок линии теперь то, что мы собираемся сделать через точка а и пункт б мы правы хорошо мы собираюсь рисовать хорошо линия хорошо, которая перпендикулярна нормально перпендикулярно а б верно и мы проверим являются ли эти строки параллельно или не так, чтобы нарисовать это нам нужен компост, так что это наш компас я возьму некоторое случайное расстояние в компас хорошо, я поставлю указатель на первом месте и от того, что я собираюсь сделать, я собираюсь нарисовать один р хорошо хорошо эту дугу я нарисовал ладно вот у меня новый точка пересечения что хорошо, это это новая точка пересечения и эта точка есть точка p хорошо, так что это точка п хорошо сейчас без изменения расстояния хорошо что я собираюсь сделать я собираюсь положить указатель в точку p хорошо, и я собираюсь отметка хорошо, еще один момент здесь хорошо, это мой указатель на точку b и через это я собираюсь хорошо, отметьте еще один пункт здесь хорошо, предположим, что этот момент перекресток является вот точка пересечения давайте предположим, что это точка о все прямо сейчас, не меняя расстояние еще раз, что я собираюсь сделать, я собираюсь я поставлю указатель на точка о хорошо и снова я отмечу еще один указать на тот же, все в порядке хорошо, у нас есть еще один новый пункт предположим, что эта точка является точкой р хорошо, это точка r хорошо, что я буду делать, я подумаю оба пункта o и точку r и через эти точки что я собираюсь делать я собираюсь без изменения расстояния я собираюсь отметить дугу, чтобы я получить точку пересечения здесь ладно так от точку я отмечу дугу здесь от точка o сначала хорошо, сейчас я поставлю указатель на точку r и я отмечу я нарисую дугу хорошо, так что я получить точка пересечения вот так вот у меня есть еще один точка пересечения предположим, что эта точка является точкой x хорошо сейчас у меня есть два пункта, которые точка х и укажите, что я собираюсь делать, я буду рисовать ладно одна линия другой один луч линии Хорошо, мы присоединяемся к обоим пунктам правильно, это точка х и точка хорошо так это новый сегмент линии хорошо, что параллельно которая перпендикулярна прямой a b Правильно так что предположим, что эта линия в порядке линия да ладно, так что в основном линия a y перпендикулярен прямой a b прямо сейчас, что я собираюсь сделать, я собираюсь сделать те же конструкции хорошо в точке б а так я возьму компас здесь хорошо, и что я собираюсь сделать, я сделаю отойдите на некоторое расстояние, хорошо поэтому я возьму здесь случайное расстояние Хорошо, я поставлю эту композицию на точку б и что я собираюсь делать я собираюсь нарисовать один дуга здесь все в порядке так что здесь я нарисую одну дугу хорошо, так что я понял еще один момент пересечения будем рассматривать эту точку как точку c ладно теперь через точку c хорошо, я поставлю свой хорошо, я поставлю указатель компост в точке c хорошо, и что я собираюсь делать, я собираюсь сделать еще одну точку здесь хорошо Хорошо, здесь я получил еще один новый момент хорошо, предположим, что это точка д хорошо, это точка d хорошо и снова через точку d без изменение расстояния, которое я собираюсь отметить еще один момент здесь поэтому я поставлю указатель на точку d и я отмечу здесь еще один момент хорошо, предположим, я получил эту новую точку как точка е [Музыка] все прямо сейчас с точки e у нас все в порядке еще два очка здесь остроконечный и острый так что теперь, что я собираюсь сделать, я собираюсь хорошо отметить точку пересечения от точка е и точка Хорошо, так что первое, что я собираюсь сделать я отмечу ладно от отметки 1 r от точки b здесь все в порядке теперь я буду поставить указатель сочинения на точку е и без изменения дистанции нормально я собираюсь отметить точку перекресток здесь ну вот мы и поняли перекресток ладно предположим этот момент пересечение я в порядке хорошо сейчас мы получили два пункта, который является пунктом один точка это точка б и точка z и что я собираюсь делать ладно я нарисую луч хорошо, что соединяет две точки так ладно ладно так здесь у нас все в порядке линия ладно это сегмент линии Правильно а если внимательно понаблюдать то ладно обе линии, которые ладно линия да ладно это линия y и линия z параллельно друг другу все правильно так что это все о сегодняшней сессии, если у тебя есть сомнения пожалуйста, оставьте свой комментарий ниже и пожалуйста, подпишитесь на этот канал спасибо за просмотр видео до свидания
Связанные вопросы
С помощью транспортира начертите угол 110° и разделите его пополам. Измерьте каждый угол.
Измерьте каждый угол.
С помощью транспортира начертите угол 80°. Затем постройте углы (i) 40° (ii) 160° (iii) 120…
Постройте треугольник, стороны которого равны 3,6 см, 3,0 см и 4,8 см. Разделите наименьший угол пополам и измерьте…
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Построения — Упражнение 11.1
Построения — Упражнение 11.2
Построения — Упражнение 11.3
Построения — Упражнение 11.4
ГЛАВ
Числовые системы
Полиномиалы
Координатная геометрия
Линейные уравнения в двух переменных
Введение в геометрию Euclid
. Построения
Построения
Формула Герона
Площади поверхностей и объемы
Статистика и вероятность
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
Геометрия: сегменты
Сегменты и линии находятся в подмножестве лучей. Сегмент — это часть линии, имеющая две конечные точки и имеющая определенную длину. С другой стороны, луч также является частью линии, имеющей одну конечную точку, а другое направление простирается до бесконечности. На рис. 1 показаны отрезок и луч.
Термины, которые необходимо запомнить
- конгруэнтный
— одинаковые по размеру и форме.
- Расстояние
— числовое значение, описывающее, насколько далеко находятся два объекта.

- Конечная точка
— точка, расположенная в конечной части отрезка, определяющая его границу.
- Противоположный
— реверс по положению или направлению.
- Подмножество
— часть набора.
- Вертикальный
— положение вверх-вниз.
Определение сегмента
Сегмент представляет собой набор точек, состоящий из двух точек линии, называемых конечными точками, и всех точек линии между конечных точек . Он обычно используется для представления длины, высоты или ширины определенного объекта и расстояния между двумя объектами. Он назван с использованием метки его конечных точек и вставки строки (( ) ̅) над буквами. На рис. 2 показан отрезок AB, который также можно записать как (AB) ̅.
Он обычно используется для представления длины, высоты или ширины определенного объекта и расстояния между двумя объектами. Он назван с использованием метки его конечных точек и вставки строки (( ) ̅) над буквами. На рис. 2 показан отрезок AB, который также можно записать как (AB) ̅.
Пример 1
Розыгрыш (CD) .
Объяснение:
Нарисуйте две точки и обозначьте их как C и D.
Соедините две точки прямо друг с другом.
Пример 2
Сколько сегментов в строке ниже?
Объяснение:
Используйте точки на линии как конечные точки сегментов.
Сегменты: (QR) , (RS) , (ST) , (QS) , (RT) и (QT) .
Середина отрезка
Середина отрезка — это точка, которая делит отрезок прямой на две конгруэнтные части. Он расположен в центре сегмента. На рис. 3 показана середина сегмента.
Примечание. Две вертикальные линии указывают на то, что расстояния от средней точки до обеих конечных точек равны.
Пример 3
Длина (XY) равна 12, а Z является серединой (XY) . Найдите длину (XZ) .
Объяснение:
Середина Z делит (XY) на две конгруэнтные части: (XZ) и (YZ) .
Длина (XZ) составляет ½ длины (XY), что составляет ½ 12 = 6.
Пример 4
O — середина (NP). Если (НЕТ) = 9, какова длина (NP) ?
Ответ: 18
Объяснение:
Середина O делит (NP) ̅ на две конгруэнтные части: (NO) ̅ и (PO) ̅.
sДлина (NP) ̅ в два раза больше длины (NO) ̅, что равно 2 9 = 18.
Сложение и вычитание отрезков
На рис. 4 показаны три коллинеарные точки E, F и G, образующие отрезок .
Точки E и G являются конечными точками отрезка (EG), а точка F между ними делит (EG) на два отрезка: (EF) и (FG) . Сумма длин (EF) и (FG) равна длине (EG) . Следовательно, (EF) + (FG) = (EG) . Выражение представляет собой отрезок, если точка F находится между точками E и G.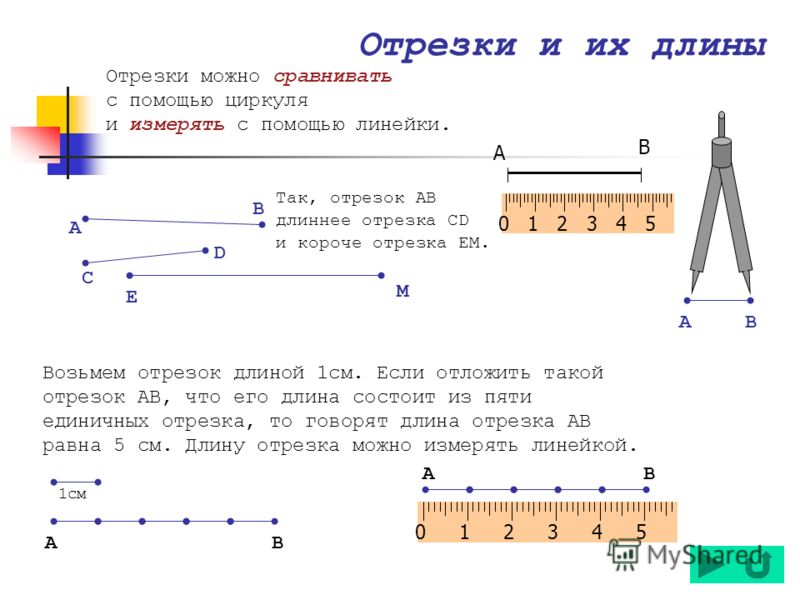
Следующие выражения также верны для длин отрезков: ) = (EG) – (EF)
Пример 5
Найдите длину (JL) на рисунке.
Объяснение:
Точки J и L являются конечными точками (JL), а точка K находится между точками J и L.
Следовательно, (JK) + (KL) = (JL) .
(JL) = 6 + 4 = 10.
Пример 6
Длина (UV) равна 13, а W находится между точками U и V. Если (WU) = 5, какова длина (VW ) ?
Точки U и V являются конечными точками (UV), а точка W находится между точками U и V.
Следовательно, (UW) + (VW) = (UV) .
(UW) = (WU) = 5
Итак, (VW) = (UV) — (UW) = 13 – 5 = 8.
Определение луча
A луч состоит из точки на линии и всех точек по одну сторону от точки. Он имеет только одну конечную точку. Лучи обычно используются в физике для обозначения направления, а также силы. При именовании луча учитывайте две точки луча: одна — конечная точка, а другая — любая точка луча.


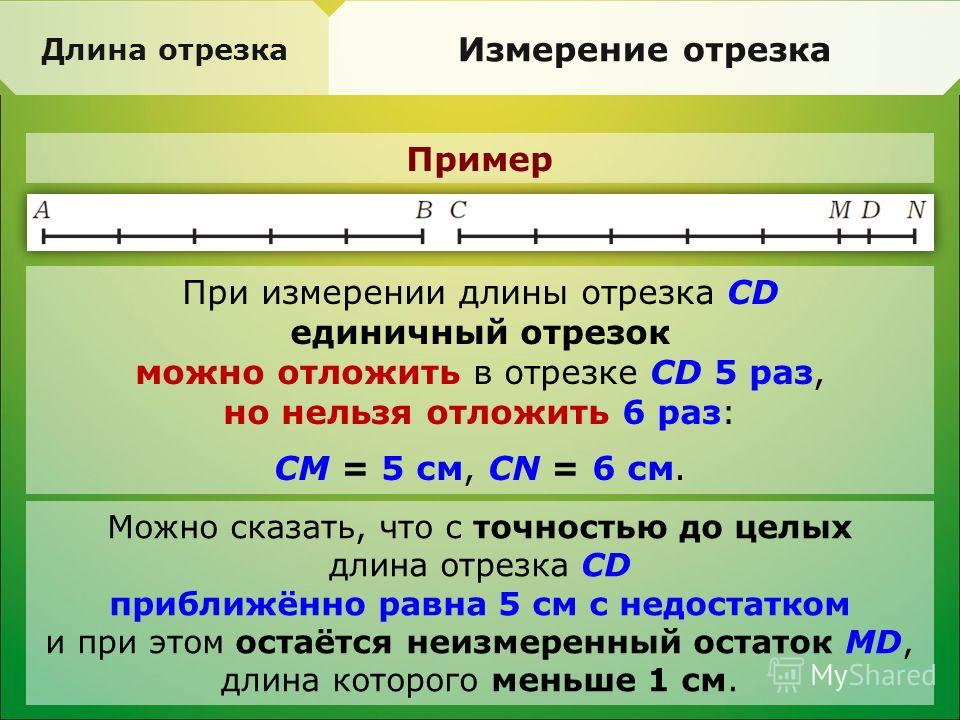


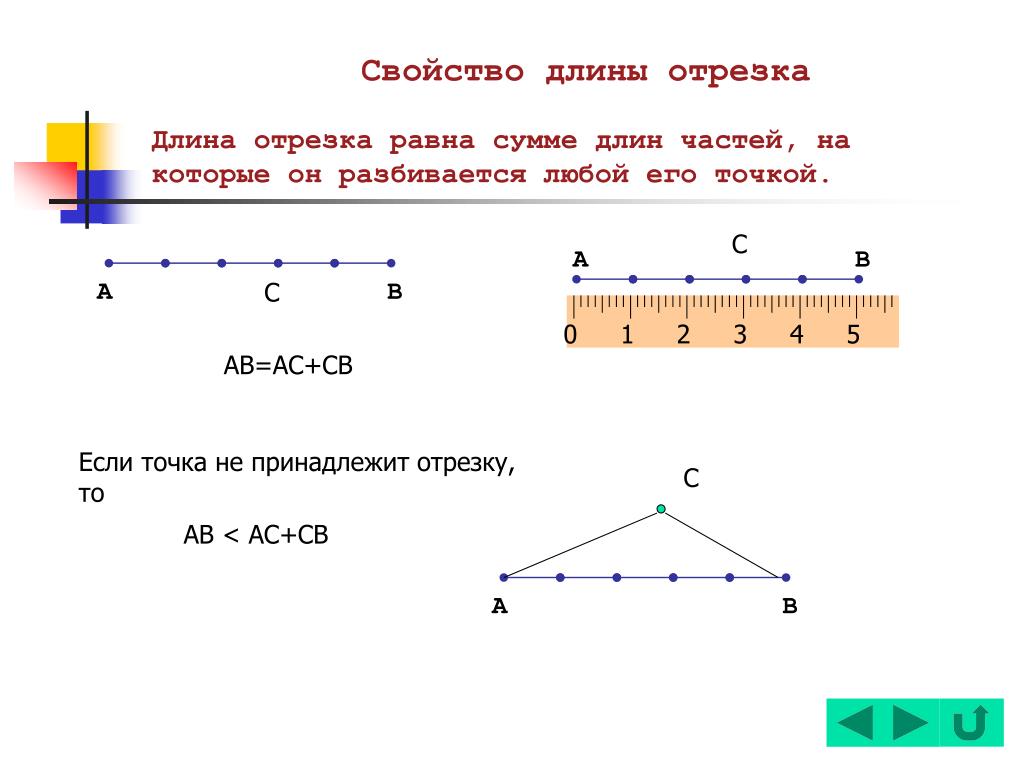 3
3