Как найти длину окружности: формула через радиус, диаметр
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение длины окружности: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать длину/периметр окружности (круга) и разберем примеры решения задач.
- Формула вычисления длины/периметра
- Примеры задач
Формула вычисления длины/периметра
1. Через радиус
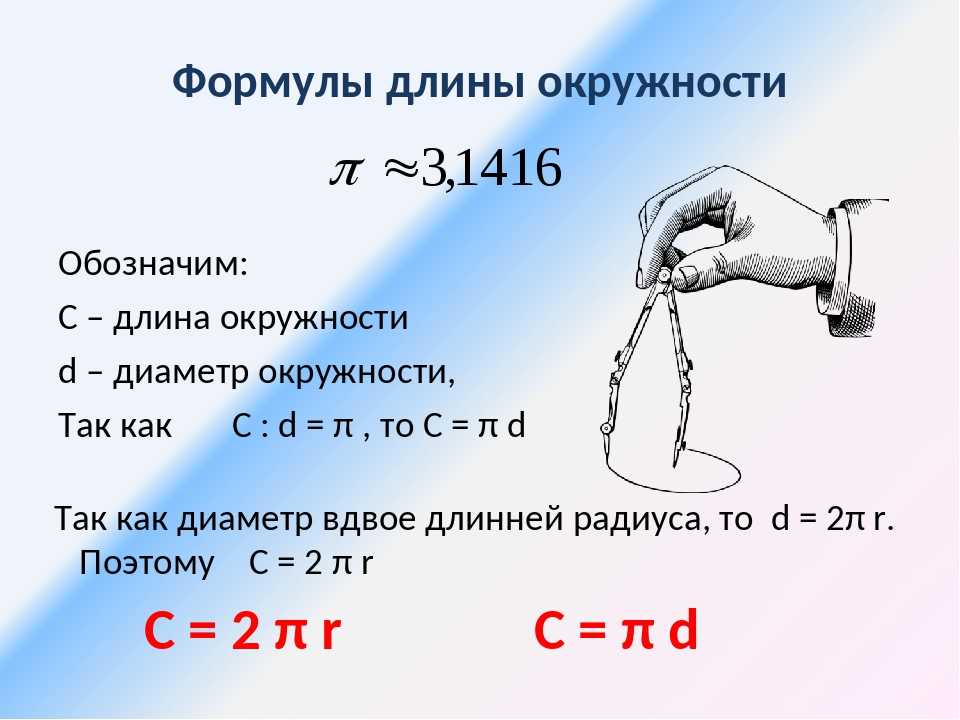
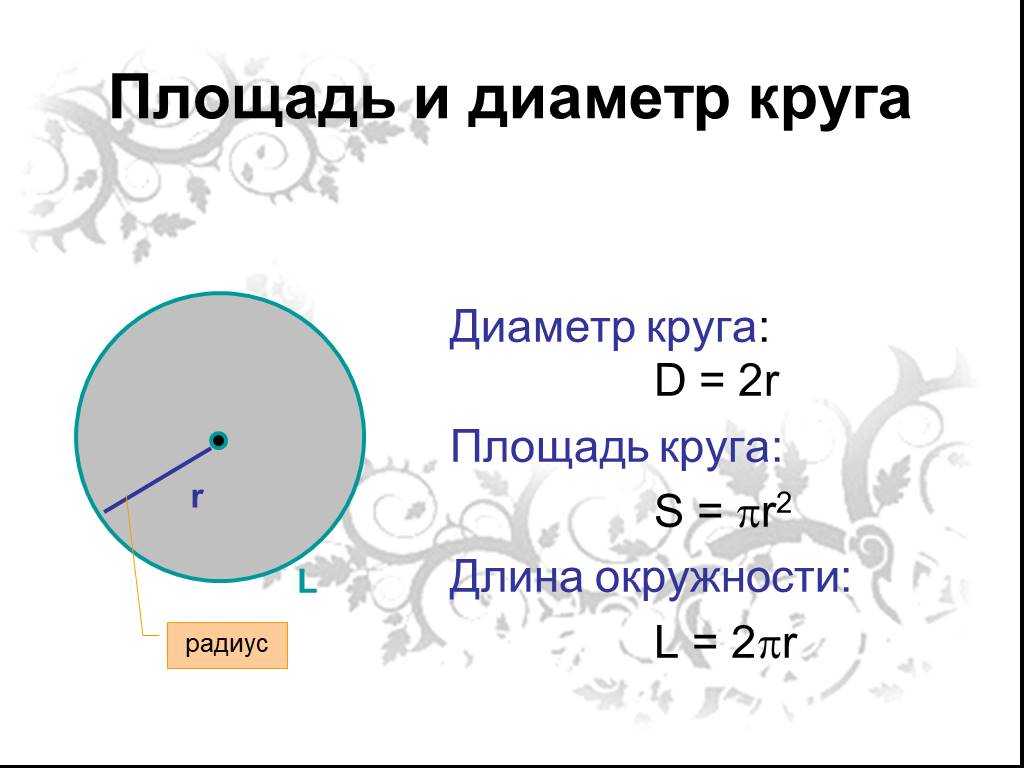
Периметр круга или длина окружности (C) равняется удвоенному произведению ее радиуса на число π:
C = 2 * π * r
Радиус (r) – это отрезок, который соединяет центр окружности и любую точку на ней.
2. Через диаметр
Периметр/длина окружности считается как произведение ее диаметра на число π:
C = π * d
Диаметр (d) равен двум радиусам (d=2r). Это отрезок, соединяющий две противоположные точки на окружности.
Это отрезок, соединяющий две противоположные точки на окружности.
Примечание: в расчетах значение числа π округляется до 3,14.
Примеры задач
Задание 1
Найдите длину окружности, если ее радиус равен 12 см.
Решение:
Воспользуемся первой формулой, в которой участвует значение радиуса: C = 2 * 3,14 * 12 см = 75,36 см.
Задание 2
Найдите периметр круга, если ее диаметр составляет 15 см.
Решение:
Применим формулу, в которой используется диаметр: C = 3,14 * 15 см = 47,1 см.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
Пользуйтесь нашим приложением
Калькулятор длины окружности в диаметр — MathCracker.com
Инструкции: Используйте этот калькулятор, чтобы вычислить диаметр круга по его окружности, показывая все шаги. Пожалуйста, введите
значение окружности в форме ниже.
Об этом калькуляторе отношения окружности к диаметру
Часто требуется переход от длины окружности к диаметру, и этот калькулятор позволит вам сделать это. Все, что вам нужно указать, — это действительное числовое выражение, такое как «1/3» или «4» и т. д. Единственное ограничение состоит в том, что предоставленное выражение должно быть положительным.
После того, как вы укажете действительный диаметр (это должно быть положительное числовое выражение), вам нужно нажать кнопку «Рассчитать», и вам будет предоставлен расчеты и все шаги.
Этот калькулятор тесно связан с калькулятором, который переводит диаметр в длину окружности, только он обратный процесс.
Как перейти от длины окружности к диаметру?
Ключевым моментом процесса является использование базовой формулы, которая связывает длину окружности и диаметр.
\[С = \пи д \]
То есть длина окружности соответствует умножению π на d. Теперь, находя d, мы непосредственно находим, что:
\[d = \displaystyle \frac{C}{\pi} \]
Затем, чтобы перейти от длины окружности к диаметру, вы просто делите длину окружности на π.
Какие шаги нужно пройти, чтобы перейти от длины окружности к диаметру?
- Шаг 1: Определите длину окружности и ее потенциальную единицу длины. Он должен быть положительным, иначе вы не сможете продолжить
- Шаг 2: Получив действительную длину окружности C, вы делите ее на π, чтобы получить диаметр
- Шаг 3: Диаметр сохраняет ту же единицу длины, что и длина окружности, если она указана.
- Шаг 4: Диаметр может быть выражен через π. Вы можете оставить его как есть или получить его приблизительное численное значение, используя
калькулятор выражений.

Принято оставлять результаты в единицах π, максимально упрощая. Иногда вам захочется иметь представление о числовом значении, в этом случае для этого можно использовать калькулятор.
Сколько диаметров в окружности?
Длина окружности равна ровно π диаметрам. Это магия константы π, которая обеспечивает связь между окружностью и диаметром.
В определенном смысле число π отражает нерациональное отношение между длинами прямых и длин окружностей.
Зачем вычислять диаметр по окружности?
Можно указать либо площадь, либо длину окружности, и в этом случае было бы полезно иметь возможность получить диаметр из его, или ради той же цели, чтобы знать радиус.
Пример: Расчет диаметра по окружности
Вычислить диаметр, если известно, что длина окружности равна \\(3\\pi\\)
Решение: Нам нужно найти диаметр \(d\) круг, и из предоставленной информации мы знаем, что длина окружности
окружность \(C = 3\pi\).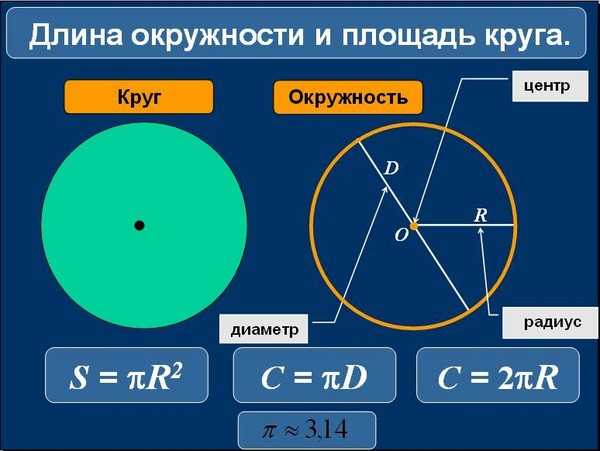
\[С = д \пи \]
Приведенная выше формула показывает, как выразить длину окружности через диаметр, и мы также можем решить формулу для \(d\):
\[d = \displaystyle\frac{C}{\pi}\]
Следовательно, все, что нам нужно сделать, это подставить в приведенную выше формулу известное значение длины окружности \(C = 3\pi\). Получается следующее:
\[ \begin{array}{ccl}\displaystyle d & = & \displaystyle\frac{C}{\pi} \\\\ \\\\ & = & \displaystyle\frac{3\pi}{\pi } \\\\ \\\\ & = & \displaystyle 3 \end{массив} \]
На этом расчет завершен. Мы нашли, что диаметр круга равен \(\displaystyle d = 3\).
Пример: отношение длины окружности к диаметру
Если известно, что длина окружности равна \(4\pi\), то каков ее диаметр?
Решение: Нам нужно найти диаметр \(d\) круга, и в этом случае мы знаем, что длина окружности
окружность \(C = 4\pi\).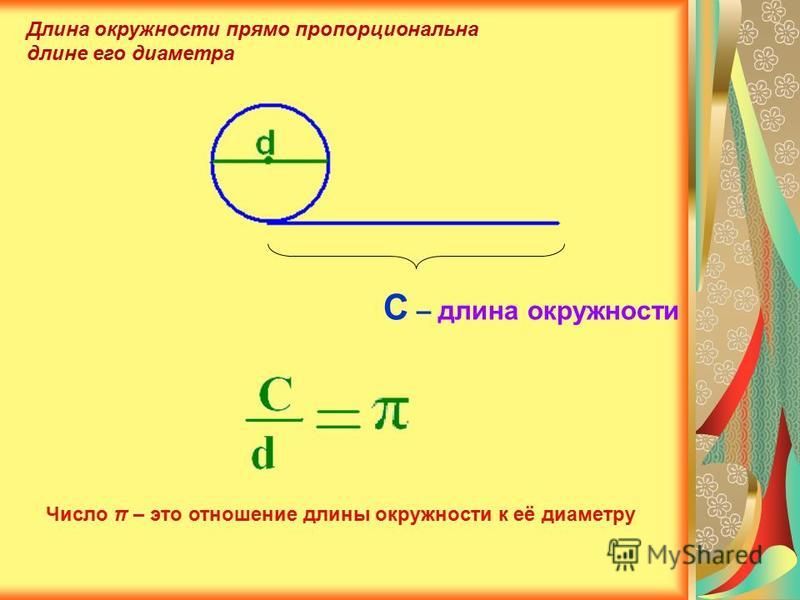
Нам нужно использовать формулу:
\[d = \displaystyle\frac{C}{\pi} = \displaystyle\frac{4\pi}{\pi} = 4\]
Следовательно, диаметр равен \(\displaystyle d = 4\).
Пример: Другая окружность равна диаметру
Предположим, что половина окружности равна \(\frac{3\pi}{2}\). Найдите диаметр круга.
Решение: В этом случае нам предоставлена не окружность, а половина окружности, которая равна \(\frac{3\pi}{2}\) .
Следовательно, длина окружности равна \(C = 2 \cdot \frac{3\pi}{2} = 3\pi \). Итак, теперь мы можем использовать формулу:
\[d = \displaystyle\frac{C}{\pi} = \displaystyle\frac{3\pi}{\pi} = 3\]
Следовательно, диаметр равен \(\displaystyle d = 3\).
Больше круговых калькуляторов
Кроме того, при работе с окружностями вам может потребоваться преобразование углов, например, радиан в градусы или
градусов в радианы.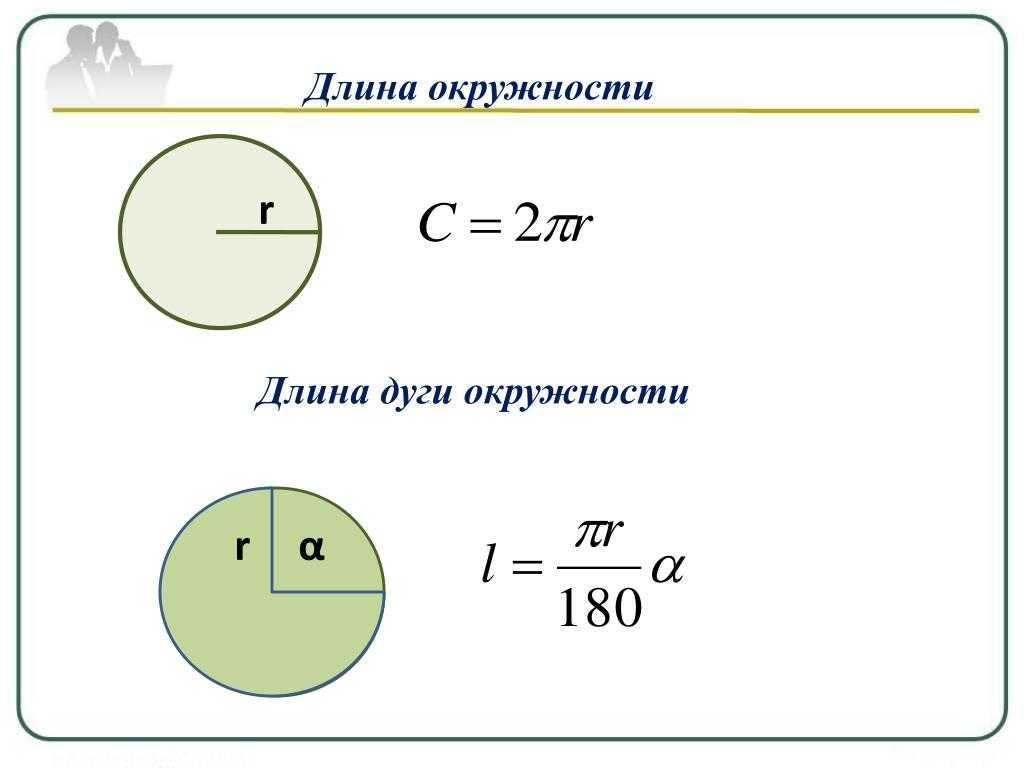

 14 * 200 = 628 мм.
14 * 200 = 628 мм.