Как найти обратную функцию — MathCracker.com
Алгебра Учебники
Многие приложения в алгебре и исчислении зависят от знания того, как найти обратную функцию, и это тема данного руководства.
Прежде всего, вам нужно понять, что перед тем, как найти инверсию функции, вы должны убедиться, что такая инверсия существует.
Преимущество метода поиска обратного, который мы будем использовать, заключается в том, что мы найдем обратное и выясним, существует ли оно одновременно.
Готовый?? Тогда пристегнитесь.
Как узнать, есть ли у функции инверсия?
Технически функция имеет инверсию, когда она взаимно однозначна (инъективна) и сюръективна.
Однако решающим условием является то, что она должна быть взаимно однозначной, потому что функцию можно сделать сюръективной, ограничив ее диапазон своим собственным изображением.
Как узнать, что функция взаимно однозначна?
Что ж, есть как минимум пара способов. Один из них — алгебраический, а другой — графический (держу пари, я знаю, какой из них вы предпочитаете, да?)
Один из них — алгебраический, а другой — графический (держу пари, я знаю, какой из них вы предпочитаете, да?)
Алгебраический путь
Для алгебраического подхода, чтобы функция \(f\) была взаимно однозначной, нам нужно доказать, что каждый раз, когда это \(f(x) = f(y)\), нам нужно иметь это \(x = y\).
Другими словами, нам нужно доказать, что
\[f(x) = f(y) \,\,\Rightarrow \,\, x = y\]Графический способ
Для графического способа нам нужно использовать проверка горизонтальной линии
: Для любой горизонтальной линии, которую мы рисуем, график функции не более одного раза пересекает эту горизонтальную линию.
Графически:
Проходит тест горизонтальной линии
Не проходит тест горизонтальной линии
В поисках обратного
Чтобы найти обратную функцию для заданной функции \(f(x)\), необходимо решить уравнение.
Действительно, у вас есть уравнение \(f(x) = y\), вы берете \(y\) как заданное число, и вам нужно решить его для \(x\), и вам нужно убедиться, что решение УНИКАЛЬНО.
Это все. Легко, правда ??
Теперь о практических шагах:Шаг 1: Для заданного \(y\) задайте уравнение:
\[f(x) = y\]
и решите его для \(x\). {-1}(x)\).
{-1}(x)\).
ПРИМЕР 1
Найдите обратную функцию \(f(x) = \sqrt x\)
ОТВЕЧАТЬ:
Итак, мы берем \(y\) как данное, и нам нужно решить \(f(x) = y\), что в данном случае соответствует решению
\[\sqrt x = y\]
Обратите внимание, что квадратный корень всегда неотрицателен, поэтому для решения нам понадобится \(y\ge 0\). 2\]
2\]
для \(x\ge 0\).
ПРИМЕР 2
Найдите обратную функцию \(f(x) = \displaystyle \frac{x}{x+1}\) для \(x > -1\)
ОТВЕЧАТЬ:
Опять же, мы берем \(y\) как дано, и теперь нам нужно решить для \(x\) уравнение \(f(x) = y\). Итак, у нас есть
\[\displaystyle \frac{x}{x+1} = y\] \[\Rightarrow \,\, x = y(x+1)\] \[\Rightarrow \,\, x = yx + y\] \[\Rightarrow \,\, x — yx = y\] \[\Rightarrow \,\, x(1 — y) = y\] \[\Rightarrow \displaystyle \,\, x = \frac{y}{1-y}\]Подробнее о поиске обратной функции
Одним из важнейших свойств обратной функции \(f^{-1}(x)\) является то, что \(f(f^{-1}(x)) = x\).
Подумайте, о чем это говорит. Что-то вроде: «Функция, вычисленная в обратном порядке, дает вам идентичность».
Или, другими словами, вычисление инверсии через функцию похоже на бездействие с аргументом.
Или, как некоторые любят говорить: функция может каким-то образом отменить обратное.
Вы выбираете свою версию.
Как найти обратную квадратичную функцию? Ты можешь?
Собственно, ответ таков: это зависит от обстоятельств. Это потому, что если мы рассмотрим квадратичную функцию по всей реальной линии , то это не один к одному, поскольку он не проходит тест горизонтальной линии, как вы можете видеть на диаграмме ниже:
Не пройдя тест горизонтальной линии, мы можем увидеть, что для данного \(y\) существует более одного значения \(x\), так что \(f(x) = y\), поэтому мы не можем «решить» для \(x\), поскольку существует более одного \(x\).
НО, если вы ограничите домен и рассмотрите, скажем, только положительные числа, мы получим следующее:
который проходит проверку горизонтальной линии, и, следовательно, квадратичная функция обратима.
НРАВСТВЕННОСТЬ ИСТОРИИ: Чтобы проверить, является ли что-то обратимым, речь идет НЕ только о функции. Речь идет о функции И ее домен и диапазон .
Как быстро построить график обратных функций
Всегда существует требование оценки, является ли функция \(f(x)\) обратимой или нет (проверяя, является ли она взаимно однозначной). {-1}(x) = \arcsin x\).
{-1}(x) = \arcsin x\).
Другой способ увидеть это — использовать оригинал график и измените значение \(x\) на значение \(y\).
Есть ли способ сделать функцию обратной?
Да, это действительно возможно, но это происходит только для функции идентификации, то есть с \(f(x) = x\).
Учебник по алгебре Построение обратного Как найти обратную функцию Индивидуальные функции
Обратные функции и их производные
18.
 1Обратные функции
1Обратные функции18.1.1Определение обратного отображения
Пусть отображение f:X→Y инъективно, то есть не склеивает точки. Если представить себе его в виде картинки со стрелочками (см. рис. 18.1 слева), это будет означать, что нет двух стрелочек, приходящих в один и тот же элемент множества Y. Обратим направления всех стрелочек (тот же рис. справа).
Рис. 18.1: Отображения f и f−1.
Теперь из некоторых (но может быть не всех) точек множества Y выходит по одной стрелочке, ведущей в X. Так мы получили новое отображение. Оно называется обратным к отображению f и обозначается f−1.
Какова область определения f−1? Это множество всех точек X, в которые
входит стрелочка, соответствующая отображению f. Иными словами, это множество
тех точек, в которые переходят какие-то точки из X, то есть полный образ
X под действием f. Он обозначается f(X):
f(X):={f(x)∣x∈X}⊂Y;f−1:f(X)→X. Если отображение f биективно, то f(X)=Y и обратное
действует из Y в X.
Если отображение f биективно, то f(X)=Y и обратное
действует из Y в X.
Как записать формально, что значит, что мы «обратили стрелочки»? Возьмём любую точку x∈X. Подействуем на неё отображеним f, получим точку f(x)∈Y. Теперь подействуем на f(x) отображением f−1. Мы обязаны вернуться в x. Итак, можно дать формальное определение.
Определение 1. Пусть f:X→Y — некоторое инъективное отображение. Отображение g:f(X)→X называется обратным к отображению f, если для всякого x∈X
g(f(x))=x.
В этом случае g обозначается через f−1.
18.1.2Обратимость и графики функций
Рассмотрим функцию f, заданную графиком. Как понять, является ли она обратимой
(то есть инъективной)? Для этого надо провести всевозможные горизонтальные
прямые и посмотреть на их точки пересечения с графиком y=f(x), см.
18.2. Если есть горизонтальные прямые, пересекающие график
в двух и более точках, функция необратима. Действительно, пусть прямая y=c
пересекает график y=f(x) в двух точках: (x1,c) и (x2,c), x1≠x2. Тогда, по определению графика, это означает, что f(x1)=c и f(x2)=c, и
значит функция необратима.
Действительно, пусть прямая y=c
пересекает график y=f(x) в двух точках: (x1,c) и (x2,c), x1≠x2. Тогда, по определению графика, это означает, что f(x1)=c и f(x2)=c, и
значит функция необратима.
Рис. 18.2: График необратимой функции
Если же все горизонтальные прямые пересекают график не более, чем в одной точке, обратная функция существует, см. рис. 18.3. Если прямая y=c не пересекает график функции f вообще, это означает, что точка c не лежит в области значений f и обратная функция в ней не определена. Если прямая y=c пересекает график ровно в одной точке, обозначим эту точку через (x1,c). Тогда f(x1)=c и стало быть f−1(c)=x1. Таким образом, мы однозначно определили f−1 во всех точках, в которых эта функция определена.
Рис. 18.3: График обратимой функции
Пример 1. Рассмотрим функцию f:R→R, f(x)=x2. Является
ли эта функция обратимой? Нет, не является: например, прямая y=1
пересекает график в двух точках: (−1,1) и (1,1), см. рис. 18.4 слева.
рис. 18.4 слева.
Рис. 18.4: Функция f(x)=x2 не является обратимой всюду, но становится обратимой, если её ограничить на неотрицательные числа
Однако, можно рассмотреть ограничение функции f на подмножество [0,+∞), то есть рассмотреть новую функцию ~f, заданную следующим образом: ~f:[0,+∞)→R,∀x∈[0,+∞):~f(x)=f(x). Обозначают ~f=f|[0,+∞). Графиком ~f будет правая ветвь параболы (см. тот же рисунок, справа), и, в отличие от исходной функции f, функция ~f является обратимой. Её обратной является квадратный корень (вернее, арифметический квадратный корень): ~f−1(y)=√y. Областью определения обратной является множество [0,+∞), поскольку квадраты вещественных чисел неотрицательны.
Вопрос 1. Найдите обратную к функции f|(−∞,0], то есть ограничению f на множество неположительных чисел.
g(y)=√y
Неверный ответ.
Нет, потому что если x=−2, √x2=√4=2≠−2, то
есть мы не вернулись в ту точку, из которой вышли.
g(y)=√−y
Неверный ответ. Нет. Подсказка: область определения обратной должна совпадать с областью значения исходной функции, а область значений исходной функции — все неотрицательные числа.
g(y)=−√y
Верный ответ. Верно, да. Для всех x≤0, g(f(x))=−√x2=x.
g(y)=−√−y
Неверный ответ. Нет. Подсказка: область определения обратной должна совпадать с областью значения исходной функции, а область значений исходной функции — все неотрицательные числа.
Вопрос 2. Рассмотрим функцию f:R→R:
f(x)=√x2
Верно ли, что f(x)=x для всех вещественных x?
Верно, посколько корень и возведение в квадрат — взаимно обратные функции, см. замечание 1.
Неверный ответ. Нет. Найдите f(−1).
Нет, поскольку функция в левой части определена только для
неотрицательных x.
Неверный ответ. Да нет, вообще нет никаких проблем найти f(−1). Попробуйте!
Неверно, получатся разные функции.
Верный ответ. Так и есть! При неотрицательных x равенство верно, а при x<0, x2=(−x)2 и √x2=√(−x)2=−x (поскольку корень обязан принимать неотрицательные значения). Значит, √x2=|x|.
Пример 2. Функция f(x)=sinx также не является обратимой на всей области определения, но её ограничение на отрезок [−π/2,π/2] обратимо. Обратная к этому ограничению называется арксинусом:
arcsin:[−1,1]→[−π/2,π/2].
Рис. 18.5: Синус не является обратимой функцией, но его ограничение на [−π/2,π/2] обратимо
Вопрос 3. Найдите обратную к функции sin|[−3π/2,−π/2].
arcsin(y+π)
Неверный ответ.
Не-не-не, и у арксинуса, и у нашей обратной функции область
определения [−1,1], никакого π добавлять к аргументу не
нужно.
arcsin(y)+π
Неверный ответ. Множеством значений обратной функции является область определения исходной. Например, если подставить y=0, получится π, что лежит вне области определения нашей функции.
−arcsin(y)−π
Верный ответ. Верно! Наверное, самый разумный способ понять, какой ответ правильный, такой: построить график, провести горизонтальную прямую y=c и отметить две точки на графике: одна соответствует arcsin(c), а другая — искомой обратной функции. И понять, как связаны их x-координаты.
arcsin(y)−π
Неверный ответ. Возьмём, например, y=1. Чему равняется sin(arcsin(1)−π)?
18.1.3Графики прямой и обратной функции
Если выбрать одинаковые масштабы горизонтальной и вертикальной оси и нарисовать
на одной и той же картинке графики функций y=x2, x≥0 и y=√x, мы
увидим, что они получаются друг из друга отражением относительно прямой y=x,
см. рис. 18.6 слева.
Это неудивительно: чтобы превратить график x2 в √x, нужно поменять
ролями вертикальную и горизонтальную оси, и отражение относительно y=x делает
именно это. Можно представить себе, что наша картинка нарисована на прозрачной
плёнке. Мы подняли её и повернули вокруг оси вращения, проходящей через прямую
y=x, а затем снова положили на стол. При этом координатная ось Ox легла на
место координатной оси Oy и наоборот, а кусочек параболы лёг на место графика
квадратного корня. То же самое происходит и с арксинусом (см. тот же рисунок,
справа).
рис. 18.6 слева.
Это неудивительно: чтобы превратить график x2 в √x, нужно поменять
ролями вертикальную и горизонтальную оси, и отражение относительно y=x делает
именно это. Можно представить себе, что наша картинка нарисована на прозрачной
плёнке. Мы подняли её и повернули вокруг оси вращения, проходящей через прямую
y=x, а затем снова положили на стол. При этом координатная ось Ox легла на
место координатной оси Oy и наоборот, а кусочек параболы лёг на место графика
квадратного корня. То же самое происходит и с арксинусом (см. тот же рисунок,
справа).
Рис. 18.6: Примеры графиков функций и их обратных
Утверждение 1. Аналогичное утверждение будет верным и для любых других пар взаимно обратных функций f и f−1.
Доказательство. Для формального доказательства нам понадобится немножко школьной планиметрии, см. рис. 18.7.
Рис. 18.7: Иллюстрация к доказательству утверждения о симметрии графиков
Возьмём любую точку P=(x0,f(x0)) на графике y=f(x). Точка P′=(f(x0),x0)
будет принадлежать графику обратной функции, поскольку f−1(f(x))=x.
Пусть A=(0,f(x0)) и A′=(f(x0),0). Рассмотрим треугольники OPA и
OP′A′. Это прямоугольные треугольники, они равны по двум сторонам
(|OA|=|OA′|, |AP|=|A′P′|). Значит, |OP|=|OP′| и треугольник OPP′
равнобедренный. Прямая y=x является биссектрисой угла POP′, поскольку
она является биссектрисой прямого угла AOA′ и углы AOP и A′OP′ равны.
Значит, она является медианой и высотой треугольника OPP′. Значит отрезок
PP′ перпендикулярен бисектрисе и разбивается ей на равные отрезки. Это и
означает, что точки P и P′ симметричны относительно прямой y=x.∎
Точка P′=(f(x0),x0)
будет принадлежать графику обратной функции, поскольку f−1(f(x))=x.
Пусть A=(0,f(x0)) и A′=(f(x0),0). Рассмотрим треугольники OPA и
OP′A′. Это прямоугольные треугольники, они равны по двум сторонам
(|OA|=|OA′|, |AP|=|A′P′|). Значит, |OP|=|OP′| и треугольник OPP′
равнобедренный. Прямая y=x является биссектрисой угла POP′, поскольку
она является биссектрисой прямого угла AOA′ и углы AOP и A′OP′ равны.
Значит, она является медианой и высотой треугольника OPP′. Значит отрезок
PP′ перпендикулярен бисектрисе и разбивается ей на равные отрезки. Это и
означает, что точки P и P′ симметричны относительно прямой y=x.∎
18.1.4Обратные функции и непрерывность
Утверждение 2. Пусть функция f строго возрастает (убывает) и обратима. Тогда обратная функция строго возрастает (убывает).
Доказательство. Рассмотрим случай когда f строго возрастает (обратный случай
рассматривается аналогично). Пусть f−1 не является строго возрастающей
функцией. Тогда найдутся точки y1 и y2, y2>y1, для которых
f−1(y2)<f−1(y1) (равенства быть не может в силу обратимости).
Но в силу возрастания f тогда
Тогда найдутся точки y1 и y2, y2>y1, для которых
f−1(y2)<f−1(y1) (равенства быть не может в силу обратимости).
Но в силу возрастания f тогда
f((f−1(y2))<f(f−1(y1)).
По определению обратной функции (см. замечание 1), f(f−1)(y2)=y2 и f(f−1)(y1)=y1. Значит y2<y1 вопреки предположению.∎
Утверждение 3. Пусть функция непрерывна на [a,b] и обратима. Тогда f строго монотонна на [a,b].
Доказательство. От противного. Пусть f(b)>f(a), обратный случай рассматривается аналогично. Поскольку функция по предположению не является монотонной, она в частности не является строго возрастающей. Значит, найдутся такие точки x1,x2∈[a,b], что x2>x1 и f(x2)≤f(x1). Равенства на самом деле быть не может в силу инъективности f. Таким образом, f(x2)<f(x1). Возможно два варианта.
Рис. 18.8: Иллюстрация к доказательству утверждения о монотонности обратимых непрерывных функций
- Пусть f(x1)>f(a), см.
 рис. 18.8 слева.
Пусть y∗∈(max(f(a),f(x2)),f(x1)). По теореме о
промежуточном значении на [a,x1]
найдётся такая точка c1, что f(c1)=y∗. По той же теореме на
[x1,x2] найдётся такая точка c2, что f(c2)=y∗.
Противоречие с обратимостью.
рис. 18.8 слева.
Пусть y∗∈(max(f(a),f(x2)),f(x1)). По теореме о
промежуточном значении на [a,x1]
найдётся такая точка c1, что f(c1)=y∗. По той же теореме на
[x1,x2] найдётся такая точка c2, что f(c2)=y∗.
Противоречие с обратимостью. - Пусть f(x1)<f(a) (см. тот же рисунок, справа). Тогда аналогичное рассуждение можно применить к точкам x1, x2, b. (Примените!)
Вопрос 4. На каком интервале нужно выбирать y∗ при рассмотрении второго случая?
y∗∈(f(x2),max(f(x1),f(b)))
Неверный ответ. А вот и не максимум.
y∗∈(f(x2),min(f(x1),f(b)))
Верный ответ. Это в принципе верно, но нужен ли минимум?
y∗∈(f(x2),f(x1))
Верный ответ.
Да! Заметим, что тут не нужен аналог взятия максимума
max(f(a),f(x2)). По предположению, f(x2)<f(x1).
При этом f(x1)<f(a) (в нашем случае) и f(a)<f(b)
(снова по предположению). Значит, f(x1)<f(b).
Следовательно, любая y∗ точка из интервала (f(x2),f(x1)) нам подходит: график обязательно пересечёт прямую
y=y∗ на интервале (x1,x2) и потом снова пересечёт на
интервале (x2,b), поскольку должен подняться выше уровня
y=f(x1) и значит выше y=y∗.
Значит, f(x1)<f(b).
Следовательно, любая y∗ точка из интервала (f(x2),f(x1)) нам подходит: график обязательно пересечёт прямую
y=y∗ на интервале (x1,x2) и потом снова пересечёт на
интервале (x2,b), поскольку должен подняться выше уровня
y=f(x1) и значит выше y=y∗.
∎
Следствие 1. Пусть областью определения функции f является отрезок [a,b], функция непрерывна и обратима и [x1,x2]⊂[a,b]. Тогда образом отрезка [x1,x2] под действием f является отрезок с концами в точках f(x1) и f(x2) (то есть [f(x1),f(x2)] или [f(x2),f(x1)], в зависимости взаимного расположения f(x1) и f(x2)).
Доказательство. Нам нужно доказать два утверждения:
- Все точки y между f(x1) и f(x2) являются образами каких-то точек x∈[x1,x2].
- Никакие другие точки не являются образами точек x∈[x1,x2].
Докажем первое утверждение. Все значения y между f(x1) и f(x2) принимаются по
теореме о промеужточном значении. Доказали.
Доказали.
Докажем второе. Если x1≤x≤x2 и функция строго возрастает, то f(x1)≤f(x)≤f(x2), а если строго убывает,то f(x1)≥f(x)≥f(x2). В обоих случаях f(x) принадлежит отрезку с концами в точках f(x1) и f(x2), и это верно для всякого x∈[x1,x2]. Тоже доказали.∎
Следствие 2. Пусть областью определения функции f являтеся отрезок [a,b], функция непрерывна и обратима. Пусть также [y1,y2] лежит в области значений f. Тогда прообразом этого отрезка под действием f, то есть множеством
f−1([y1,y2]):={x∈[a,b]:f(x)∈[y1,y2]}
будет отрезок I с концами в точках f−1(y1) и f−1(y2).
Упражнение. Докажите это следствие.
Узнать ответ
Верный ответ.
По утверждению 3, f строго монотонна, а следовательно
(по утверждению 2) обратная функция тоже строго монотонна. Значит
для всех y∈[y1,y2], f−1(y) лежит между точкам f−1(y1) и
f−1(y2). То есть у любой точки y есть единственный прообраз (это
следует из обратимости), и он лежит на отрезке I (это следует из
монотонности). Значит, никакая точка вне этого отрезка не лежит в
f−1([y1,y2]). Наоборот, любая точка x∈I под действием f
переходит в точку отрезка [y1,y2] (в силу монотонности f), и значит
все такие точки x лежат в f−1([y1,y2]).
Значит, никакая точка вне этого отрезка не лежит в
f−1([y1,y2]). Наоборот, любая точка x∈I под действием f
переходит в точку отрезка [y1,y2] (в силу монотонности f), и значит
все такие точки x лежат в f−1([y1,y2]).
Упражнение 1. Приведите контрпримеры, демонстрирующие, что требования непрерывности и обратимости являются существенными для двух доказанных выше следствий, то есть что если хотя бы одно из них нарушается, утверждения перестают быть верными. Пока вы этого не сделали, вы не можете считать, что понимаете доказательства.
Утверждение 4. Пусть f непрерывна на [a,b] и обратима. Тогда f−1 также непрерывна.
Доказательство. Пусть для определённости f(b)>f(a) (обратный случай рассматривается
аналогично). Тогда функция обязана возрастать: она будет монотонной в силу
обратимости, но убывать не может. Рассмотрим точку y0∈(f(a),f(b)) и
докажем, что f−1 непрерывна в y0 (односторонняя непрерывность в
концах отрезка доказывается аналогично). Пусть y0=f(x0). Мы хотим
доказать, что
Пусть y0=f(x0). Мы хотим
доказать, что
limy→y0f−1(y)=f−1(y0)=x0.
Рис. 18.9: Иллюстрация к доказательству утверждения о непрерывности обратной к непрерывной функции
Для всякого ε>0 рассмотрим интервал Uε(x0)=(x0−ε,x0+ε), см. рис. 18.9. Нам нужно доказать, что
найдётся такая окрестность ˚Uδ(y0), что все точки из этой
окрестности перейдут в Uε(x0) под действием обратного отображения
f−1. (Поскольку мы рассматриваем обратное отображение, мы, вопреки
обыкновению, ε-окрестности рисуем на горизонтальной оси, а
δ-окрестности — на вертикальной.) Будем считать, что ε
достаточно мало, чтобы Uε целиком лежал в интервале (a,b). По
следствию 1 и замечанию 2, образом
Uε под действием f является интервал V:=(f(x0−ε),f(x0+ε))
(он непуст, поскольку мы рассматриваем случай, когда f возрастает, и
значит правый конец будет правее левого). Поскольку y0=f(x0), y0∈V (в силу монотонности функции f), то есть V является окрестностью
точки y0. Поскольку под действием f окрестность Uε(x0) переходит
в окрестность V, то под действием обратного отображения f−1
окрестность (f(x0−ε),f(x0+ε)) перейдёт назад в Uε(x0).
Итак, мы получили окрестность точки f(x0), все точки из которой переходят в ε-окрестность точки x0 под действием f−1. Это почти то, что нам нужно. Давайте впишем в неё какую-то симметричную окрестность — она и будет искомой δ-окрестностью (это немножко технический шаг, но в определении предела мы используем симметричные окрестности, и нам формально нужно получить именно такую).
Пусть δ=min(|y0−f(x0−ε)|,|y0−f(x0+ε)|)>0. Тогда Uδ(y0)⊂(f(x0−ε),f(x0+ε)) и f−1(Uδ(y0))⊂(x0−ε,x0+ε)=Uε(x0). (Если всё множество V отображалось под действием f−1 в Uε(x0), то подмножество V отображается в некоторое подмножество Uε(x0). Таким образом, для любого y∈Uδ(y0), f−1(y)∈Uε(x0). Тем самым, построенная нами δ удовлетворяет условию в определении искомого предела.∎
Пример 3. Мы знаем, что функция f(x)=expx=ex непрерывна и строго монотонна, её
областью определения является вся прямая и она принимает все положительные
значения. Значит, у неё существует непрерывная обратная. Она называется натуральным логарифмом:
Она называется натуральным логарифмом:
ln:(0,+∞)→R.
Для всех x∈R, lnex=x. Наоборот, для всех y>0, elny=y. Натуральный логарифм, так же, как и экспонента, монотонно возрастает.
Рис. 18.10: Графики экспоненты и натурального логарифма
18.2Производная обратной функции
18.2.1Мотивировка и формула
Будем использовать ту же интерпретацию производных, как в доказательстве теоремы о производной сложной функции.
Рассмотрим две оси, x и y. Пусть f(x0)=y0. Рассмотрим небольшой отрезок I=[x0,x0+Δx] на оси x и его образ под действием f: отрезок f(I)=[f(x0),f(x0+Δx)] на оси y. (Для иллюстрации будем считать, что f возрастает и Δx>0.) Тогда производная f′(x0) показывает, во сколько (примерно) раз f(I) длиннее I, то есть во сколько раз отрезок I растягивается отображением f, то есть f′(x0)≈|f(I)|/|I|.
Рис. 18.11: Производная функции f показывает, во сколько раз растягивается
маленький отрезок. Если f растягивает, то f−1 будет сжимать, то
есть производная обратной функции обратна к производной прямой функции.
Главное — разобраться, в каких точках эти производные нужно считать.
Если f растягивает, то f−1 будет сжимать, то
есть производная обратной функции обратна к производной прямой функции.
Главное — разобраться, в каких точках эти производные нужно считать.
Посмотрим теперь на обратное отображение f−1. Оно переводит отрезок f(I) назад в отрезок I. Когда I маленький, f(I) тоже маленький. Поэтому (f−1)′(y0)≈|I|/|f(I)|. Обратите внимание: нам нужно брать производную в точке, которая является концом отрезка f(I), то есть в точке y0. Но y0=f(x0). Таким образом, можно ожидать, что
(f−1)′(f(x0))=1f′(x0).
Эту формулу мы и будем доказывать.
18.2.2Аккуратная формулировка и доказательство
Теорема 1. Пусть функция f непрерывна в окрестности точки x0 и дифференцируема в x0. Пусть также f′(x0)≠0 и f обратима. Тогда f−1 дифференцируема в точке y0=f(x0) и
(f−1)′(f(x0))=1f′(x0).
Поскольку x0=f−1(y0), это равенство можно записать так:
(f−1)′(y0)=1f′(f−1(y0)).
Доказательство. Для упрощения формул будем обозначать f−1 через g. Рассмотрим предел, используемый в определении производной функции g в точке y0:
limΔy→0g(y0+Δy)−g(y0)Δy.(18.2)
Рассмотрим функцию
Δg(Δy)=g(y0+Δy)−g(y0).
В силу непрерывности g, Δg(Δy)→0 при Δy→0. Также Δg(Δy)≠0 при Δy≠0, иначе у одной точки x0 было бы два образа под действием f. Заметим, что справедливо тождество (см. рис. 18.12):
Δy=f(x0+Δg(Δy))−f(x0).
Рис. 18.12: Иллюстрация к доказательству теоремы о производной обратной функции
Запишем теперь предел (18.2) в следующем виде:
limΔy→0g(y+Δy)−g(y)Δy=limΔy→0Δg(Δy)Δy=limΔy→01ΔyΔg(Δy)=limΔy→01f(x0+Δg(Δy))−f(x0)Δg(Δy)=…(18.3)
limΔy→0g(y+Δy)−g(y)Δy==limΔy→0Δg(Δy)Δy==limΔy→01ΔyΔg(Δy)==limΔy→01f(x0+Δg(Δy))−f(x0)Δg(Δy)=…(18.3)
Рассмотрим функцию
F(Δx)=f(x0+Δx)−f(x0)Δx.
Тогда можно продолжить равенство (18.3):
…=limΔy→01F(Δg(Δy))=…(18.4)
Поскольку Δg(Δy)→0 при Δy→0 и Δg(Δy)≠0 при Δy≠0, можно воспользоваться теоремой о пределе сложной функции (см. упражнение 2 из лекции 13):
limΔy→0F(Δg(Δy))=limΔx→0F(Δx)=f′(x0).
Теперь можно применить теорему о пределе частного к (18.4) (мы потребовали, чтобы f′(x0)≠0, так что делить можно) и получить:
…=1limΔy→0F(Δg(Δy))=1f′(x0).
Теорема о пределе обратной функции доказана.∎
Пример 4. Найдём производную натурального логарифма. Известно, что (ex)′=ex. Рассмотрим обратную функцию x=lny. Имеем:
(lny)′=1(ex)′|x=lny=1elny=1y,
где (ex)′|x=lny означает, что нужно вычислить производную функции ex и в неё подставить значение x=lny.
18.3Заключение
Обратные функции часто встречаются на практике — всегда, когда нам нужно найти
решение уравнения f(x)=c, нам нужно использовать обратную функцию. Однако,
далеко не всегда это можно сделать явно — даже алгебраические уравнения (где f
— многочлен) степени выше четвертой не имеют явных формул (использующих
элементарные функции) для своего решения (мы не просто не знаем этих формул
— можно доказать, что их не существует). Тем не менее, очень часто они и не
нужны, потому что нас интересуют не формулы, а то, как ведут себя
функции, и это часто можно понять и без формулы. Именно это демонстрирует
теорема, которую мы доказали — она позволяет находить производную обратной
функции, не имея явного вида самой этой обратной функции.
Однако,
далеко не всегда это можно сделать явно — даже алгебраические уравнения (где f
— многочлен) степени выше четвертой не имеют явных формул (использующих
элементарные функции) для своего решения (мы не просто не знаем этих формул
— можно доказать, что их не существует). Тем не менее, очень часто они и не
нужны, потому что нас интересуют не формулы, а то, как ведут себя
функции, и это часто можно понять и без формулы. Именно это демонстрирует
теорема, которую мы доказали — она позволяет находить производную обратной
функции, не имея явного вида самой этой обратной функции.
← Предыдущая глава Следующая глава →
Определение обратной функции ее свойства и график. Взаимно обратные функции
Пусть множества $X$ и $Y$ включены в множество действительных чисел. Введем понятие обратимой функции .
Определение 1
Функция $f:X\to Y$ отображающая множество $X$ в множество $Y$ называется обратимой, если для любых элементов $x_1,x_2\in X$ из того что $x_1\ne x_2$ следует, что $f(x_1)\ne f(x_2)$. 3$:
3$:
Находим подходящие значения $x$
Значение в нашем случае подходит (так как область определения — все числа)
Переопределим переменные, получим, что обратная функция имеет вид
Пример 4
Найти обратную функцию для функции $y=cosx$ на промежутке $$
Решение.
Рассмотрим на множестве $X=\left$ функцию $y=cosx$. Она непрерывна и убывает на множестве $X$ и отображает множество $X=\left$ на множество $Y=[-1,1]$, поэтому по теореме о существовании обратной непрерывной монотонной функции у функции $y=cosx$ в множестве $Y$ существует обратная функция, которая также непрерывна и возрастает в множестве $Y=[-1,1]$ и отображает множество $[-1,1]$ на множество $\left$.
Найдем $x$ из уравнения $y=cosx$:
Находим подходящие значения $x$
Переопределим переменные, получим, что обратная функция имеет вид
Пример 5
Найти обратную функцию для функции $y=tgx$ на промежутке $\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$.
Решение.
Рассмотрим на множестве $X=\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$ функцию $y=tgx$. Она непрерывна и возрастает на множестве $X$ и отображает множество $X=\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$ на множество $Y=R$, поэтому по теореме о существовании обратной непрерывной монотонной функции у функции $y=tgx$ в множестве $Y$ существует обратная функция, которая также непрерывна и возрастает в множестве $Y=R$ и отображает множество $R$ на множество $\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$
Найдем $x$ из уравнения $y=tgx$:
Находим подходящие значения $x$
Переопределим переменные, получим, что обратная функция имеет вид
Что такое обратная функция? Как найти функцию, обратную данной?
Определение .
Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.
Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.
Чтобы найти функцию, обратную данной функции y=f(x), надо :
1) В формулу функции вместо y подставить x, вместо x — y:
2) Из полученного равенства выразить y через x:
Найти функцию, обратную функции y=2x-6.
Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.
Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).
y=2x-6 и y=0,5x+3 — . Графиком линейной функции является . Для построения прямой берём две точки.
Однозначно выразить y через x можно в том случае, когда уравнение x=f(y) имеет единственное решение. Это можно сделать в том случае, если каждое своё значение функция y=f(x) принимает в единственной точке её области определения (такая функция называется обратимой ).
Теорема (необходимое и достаточное условие обратимости функции)
Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.
Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.
Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.
Классический пример — . На промежутке
Е(у) = [-π/2;π/2]
у (-х) = arcsin(-х) = — arcsin х – функция нечетная, график симметричен относительно точки О(0;0).
arcsin х = 0 при х = 0.
arcsin х > 0 при х є (0;1]
arcsin х
у = arcsin х возрастает при любом х є [-1;1]
1 ≤ х 1 arcsin х 1
Арккосинус
Функция
косинус убывает на отрезке
и принимает все значения от -1 до 1. Поэтому
для любого числа а, такого, что |а|1,
на отрезке
существует единственный корень в
уравнении cosx=a.
Это число в называют арккосинусом числа
а и обозначают arcos
а.
Поэтому
для любого числа а, такого, что |а|1,
на отрезке
существует единственный корень в
уравнении cosx=a.
Это число в называют арккосинусом числа
а и обозначают arcos
а.
Определение . Арккосинусом числа а, где -1 а 1, называется такое число из отрезка , косинус которого равен а.
Свойства.
Е(у) =
у(-х) = arccos(-х) = π — arccos х – функция не является ни четной, ни нечетной.
arccos х = 0 при х = 1
arccos х > 0 при х є [-1;1)
arccos х
у = arccos х убывает при любом х є [-1;1]
1 ≤ х 1 arcsin х 1 ≥ arcsin х 2 – убывающая.
Арктангенс
Функция
тангенс возрастает на отрезке
—
,
следовательно, по теореме о корне
уравнение tgx=a,
где а — любое действительное число, имеет
единственный корень х на интервале
-.
Этот
корень называют арктангенсом числа а
и обозначают arctga.
Определение. Арктангенсом
числа a R называется
такое число х , тангенс
которого равен а.
Свойства.
Е(у) = (-π/2;π/2)
у(-х) = у = arctg(-х) = — arctg х – функция является нечетной, график симметричен относительно точки О(0;0).
arctg х = 0 при х = 0
Функция возрастает при любом х є R
-∞ arctg х 1
Арккотангенс
Функция котангенс на интервале (0;) убывает и принимает все значения из R. Поэтому для любого числа а в интервале (0;) существует единственный корень уравнения ctg х = а. Это число а называют арккотангенсом числа а и обозначают arcctg а.
Определение. Арккотангенсом числа а, где а R, называется такое число из интервала (0;), котангенс которого равен а.
Свойства.
Е(у) = (0;π)
у(-х) = arcctg(-х) = π — arcctg х – функция не является ни четной, ни нечетной.
arcctg х = 0 – не существует.
Функция у = arcctg х убывает при любом х є R
-∞ 1 2 arcctg х 1 > arcctg х 2
Функция
непрерывна при любом х є R.
2.3 Тождественные преобразования выражений, содержащих обратные тригонометрические функции
Пример 1 . Упростить выражение:
а)
где
Решение.
Положим
.
Тогда
и
Чтобы найти
,
воспользуемся соотношением
Получаем
Но
.
На этом отрезке косинус принимает только
положительные значения. Таким образом,
,
то есть
где
.
б)
Решение.
в)
Решение.
Положим
.
Тогда
и
Найдем сначала
,
для чего воспользуемся формулой
,
откуда
Так как
и на этом интервале косинус принимает
только положительные значения, то
.
Цели урока:
Образовательная:
- формировать знания по новой теме в соответствии с программным материалом;
- изучить свойство обратимости функции и научить находить функцию, обратную данной;
Развивающая:
- развивать навыки самоконтроля, предметную речь;
- овладеть понятием обратная функция и усвоить методы нахождения обратной функции;
Воспитательная: формировать
коммуникативную компетентность.
Оборудование: компьютер, проектор, экран, интерактивная доска SMART Board, раздаточный материал (самостоятельная работа) для работы в группе.
Ход урока.
1. Организационный момент.
Цель – подготовка учащихся к работе на уроке:
Определение отсутствующих,
Настрой учащихся на работу, организация внимания;
Сообщение темы и цели урока.
2. Актуализация опорных знаний учащихся. Фронтальный опрос.
Цель — установить правильность и осознанность изученного теоретического материала, повторение пройденного материала.
Для учащихся на интерактивной доске демонстрируется график функции. Учителем формулируется задание – рассмотреть график функции и перечислить изученные свойства функции. Учащиеся перечисляют свойства функции в соответствии со схемой исследования. Учитель справа от графика функции маркером на интерактивной доске записывает названные свойства.
Свойства функции:
По окончании исследования учитель
сообщает, что сегодня на уроке они
познакомятся еще с одним свойством функции
– обратимостью. Для осмысленного изучения
нового материала учитель предлагает
ребятам познакомиться с основными
вопросами, на которые учащиеся должны дать
ответ по окончании урока. Вопросы записаны
на обыкновенной доске и в виде раздаточного
материала есть у каждого ученика (раздается
до урока)
Для осмысленного изучения
нового материала учитель предлагает
ребятам познакомиться с основными
вопросами, на которые учащиеся должны дать
ответ по окончании урока. Вопросы записаны
на обыкновенной доске и в виде раздаточного
материала есть у каждого ученика (раздается
до урока)
- Какая функция называется обратимой?
- Любая ли функция обратима?
- Какая функция называется обратной данной?
- Как связаны область определения и множество значений функции и обратной ей функции?
- Если функция задана аналитически, как задать формулой обратную функцию?
- Если функция задана графически, как построить график обратной ей функции?
3. Объяснение нового материала.
Цель — формировать знания по новой теме в соответствии с программным материалом; изучить свойство обратимости функции и научить находить функцию, обратную данной; развивать предметную речь.
Учитель проводит изложение материала в
соответствии с материалом параграфа. На
интерактивной доске учитель проводит
сравнение графиков двух функций, у которых
области определения и множества значений
одинаковы, но одна из функций монотонна, а
другая нет, тем самым подводит учащихся под
понятия обратимой функции.
На
интерактивной доске учитель проводит
сравнение графиков двух функций, у которых
области определения и множества значений
одинаковы, но одна из функций монотонна, а
другая нет, тем самым подводит учащихся под
понятия обратимой функции.
Затем учитель формулирует определение обратимой функции и проводит доказательство теоремы об обратимой функции, используя график монотонной функции на интерактивной доске.
Определение 1: Функцию y=f(x), x X называют обратимой , если любое свое значение она принимает только в одной точке множества X.
Теорема: Если функция y=f(x) монотонна на множестве X , то она обратима.
Доказательство:
- Пусть функция y=f(x) возрастает на Х и пусть х 1 ≠х 2 — две точки множества Х .
- Для определенности пусть х 1 х 2
.
Тогда из того, что х 1 х 2 следует, что f(х 1) f(х 2) . - Таким образом, разным значениям
аргумента соответствуют разные значения
функции, т.
 е. функция обратима.
е. функция обратима.
(По ходу доказательства теоремы учитель маркером делает все необходимые пояснения на чертеже)
Перед тем как сформулировать определение обратной функции учитель просит учащихся определить, какая из предложенных функций обратима? На интерактивной доске показаны графики функций и записаны несколько аналитически заданных функций:
Б)
Г) y = 2x + 5
Д) y = -x 2 + 7
Учитель вводит определение обратной функции.
Определение 2: Пусть обратимая функция y=f(x) определена на множестве Х и Е(f)=Y . Поставим в соответствие каждому y из Y то единственное значение х , при котором f(x)=y. Тогда получим функцию, которая определена на Y , а Х – область значений функции
Эту функцию обозначают x=f -1 (y) и называют обратной по отношению к функции y=f(x) .
Учащимся предлагается сделать вывод о
связи между областью определения и
множеством значений обратных функций.
Для рассмотрения вопроса о способах нахождения функции обратной данной, учитель привлек двух учащихся. Ребята накануне получили задание у учителя самостоятельно разобрать аналитический и графический способы нахождения функции обратной данной. Учитель выступил в роли консультанта при подготовке учащихся к уроку.
Сообщение первого ученика.
Замечание: монотонность функции, является достаточным условием существования обратной функции. Но оно не является необходимым условием.
Учащийся привел примеры различных ситуаций, когда функция не монотонна, но обратима, когда функция не монотонна и не обратима, когда монотонна и обратима
Затем ученик знакомит учащихся со способом нахождения обратной функции, заданной аналитически.
Алгоритм нахождения
- Убедиться, что функция монотонна.
- Выразить переменную х через у.
- Переобозначить переменные. Вместо х=f -1 (y) пишут y=f -1 (x)
Затем решает два примера на нахождение
функции обратной данной.
Пример 1: Показать, что для функции y=5x-3 существует обратная функция, и найти ее аналитическое выражение.
Решение. Линейная функция y=5x-3 определена на R, возрастает на R и область ее значений есть R. Значит, обратная функция существует на R. Чтобы найти ее аналитическое выражение, решим уравнение y=5x-3 относительно х; получим Это и есть искомая обратная функция. Она определена и возрастает на R.
Пример 2: Показать, что для функции y=x 2 , х≤0 существует обратная функция, и найти ее аналитическое выражение.
Функция непрерывна, монотонна в своей области определения, следовательно, она обратима. Проанализировав области определения и множества значений функции, делается соответствующий вывод об аналитическом выражении для обратной функции.
Второй ученик выступает с сообщением о графическом способе нахождения обратной функции. В ходе своего объяснения ученик использует возможности интерактивной доски.
Чтобы получить график функции y=f -1 (x),
обратной по отношению к функции y=f(x),
надо график функции y=f(x)преобразовать
симметрично относительно прямой y=x.
Во время объяснения на интерактивной доске выполняется следующее задание:
Построить в одной системе координат график функции и график обратной ей функции. Запишите аналитическое выражение обратной функции.
4. Первичное закрепление нового материала.
Цель – установить правильность и осознанность понимания изученного материала, выявить пробелы первичного осмысления материала, провести их коррекцию.
Учащиеся делятся на пары. Им раздаются листы с заданиями, в которых они и выполняют работу в парах. Время на выполнение работы ограничено (5-7 мин). Одна пара учащихся работает на компьютере, проектор на это время выключается и остальным ребятам не видно, как работают учащиеся на компьютере.
По окончании времени (предполагается, что
с работой справилось большинство учащихся)
на интерактивной доске (вновь включается
проектор) показывается работа учащихся, где
и выясняется в ходе проверки правильность
выполнения задания в паре. При
необходимости учителем проводится
коррекционная, разъясняющая работа.
Самостоятельная работа в парах Приложение 2 >
5. Итог урока. По вопросам, которые были заданы перед началом лекции. Объявление оценок за урок.
Домашнее задание §10. №№ 10.6(а,в) 10.8-10.9(б) 10.12 (б)
Алгебра и начала анализа. 10 класс В 2-х частях для общеобразовательных учреждений (профильный уровень) /А.Г.Мордкович, Л.О.Денищева, Т.А.Корешкова и др.; под ред. А.Г.Мордковича, М: Мнемозина, 2007 год
Взаимно обратные функции.
Пусть функция строго монотонная (возрастающая или убывающая) и непрерывная на области определения, область значений этой функции, тогда на интервале определена непрерывная строго монотонная функция с областью значений, которая является обратной для .
Другими словами, об обратной функции для функции на конкретном промежутке имеет смысл говорить, если на этом интервале либо возрастает, либо убывает.
Функции f и g называют взаимно обратными.
Зачем вообще рассматривать понятие обратных функций?
Это вызвано задачей решения уравнений. Решения как раз и записываются через обратные функции.
Рассмотрим несколько примеров нахождения обратных функций .
Начнём с линейных взаимно обратных функций.
Найти функцию, обратную для.
Эта функция линейная, её графиком является прямая. Значит, функция монотонна на всей области определения. Поэтому, искать обратную ей функцию будем на всей области определения.
.
Выразим x через y (другими словами, решим уравнение относительно x ).
— это и есть обратная функция, правда здесь y – аргумент, а x – функция этого аргумента. Чтобы не нарушать привычки в обозначениях (это не имеет принципиального значения), переставив буквы x и y , будем писать .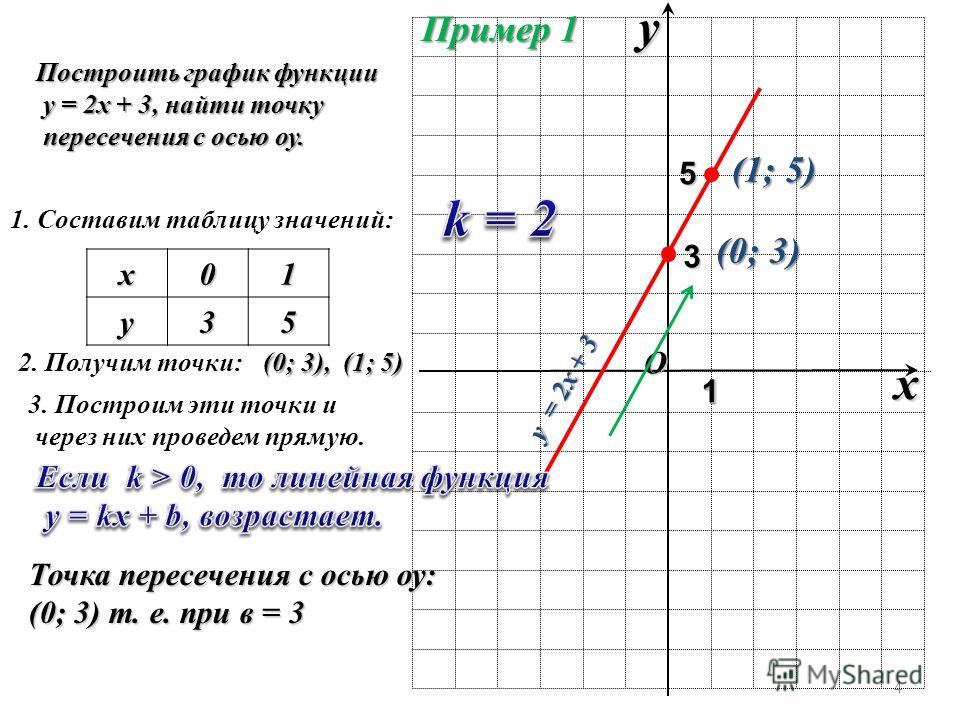
Таким образом, и — взаимно обратные функции.
Приведём графическую иллюстрацию взаимно обратных линейных функций.
Очевидно, что графики симметричны относительно прямой (биссектрисы первой и третьей четверти). Это одно из свойств взаимно обратных функций, о которых речь пойдёт ниже.
Найти функцию, обратную.
Эта функция квадратная, графиком является парабола с вершиной в точке.
.
Функция возрастает при и убывает при. Значит, искать обратную функцию для заданной можно на одном из двух промежутков.
Пусть, тогда, и, меняя местами х и у, получаем обратную функцию на заданном промежутке: .
Найти функцию, обратную.
Эта функция кубическая, графиком является кубическая парабола с вершиной в точке.
.
Функция возрастает при. Значит, искать обратную функцию для заданной можно на всей области определения.
, и, меняя местами х и у, получаем обратную функцию.
Проиллюстрируем это на графике.
Перечислим свойства взаимно обратных функций и.
и.
Из первого свойства видно, что область определения функции совпадает с областью значений функции и наоборот.
Графики взаимно обратных функций симметричны относительно прямой.
Если возрастает, то и возрастает, если убывает, то и убывает.
Найдите область значений каждой из взаимно обратных функций и, если указаны их области определения:
Найдите функцию, обратную данной.
Является ли данная функция обратной по отношению к самой себе: Задайте функцию, обратную данной и постройте её график: Постройте на одной системе координат графики этих взаимно обратных функций:
Постройте на одной системе координат графики этих взаимно обратных функций:
Для заданной функции найдите обратную функцию:
Для заданной функции найдите обратную и постройте графики заданной и обратной функции: Выясните, существует ли обратная функция для заданной функции. Если да, то задайте обратную функцию аналитически, постройте график заданной и обратной функции: Найдите область определения и область значений функции, обратной для функции, если:Являются ли функции взаимно обратными, если:
Взаимно обратные функции, основные определения, свойства, графики
Понятие обратной функции
Допустим, что у нас есть некая функция y=f(x), которая является строго монотонной (убывающей или возрастающей) и непрерывной на области определения x∈a; b; область ее значений y∈c; d, а на интервале c; d при этом у нас будет определена функция x=g(y) с областью значений a; b. Вторая функция также будет непрерывной и строго монотонной. По отношению к y=f(x) она будет обратной функцией. То есть мы можем говорить об обратной функции x=g(y) тогда, когда y=f(x) на заданном интервале будет либо убывать, либо возрастать.
Две этих функции, f и g, будут взаимно обратными.
Для чего вообще нам нужно понятие обратных функций?
Это нужно нам для решения уравнений y=f(x), которые записываются как раз с помощью этих выражений.
Нахождение взаимно обратных функций
Допустим, нам нужно найти решение уравнения cos(x)=13. Его решениями будут все точки: x=±arсcos13+2π·k, k∈Z
Обратными по отношению друг к другу будут, например, функции арккосинуса и косинуса.
Разберем несколько задач на нахождение функций, обратных заданным.
Пример 1Условие: какая функция будет обратной для y=3x+2?
Решение
Область определений и область значений функции, заданной в условии, – это множество всех действительных чисел. Попробуем решить данное уравнение через x, то есть выразив x через y.
Мы получим x=13y-23. Это и есть нужная нам обратная функция, но y здесь будет аргументом, а x — функцией. Переставим их, чтобы получить более привычную форму записи:
y=13x-23
Ответ: функция y=13x-23 будет обратной для y=3x+2.
Обе взаимно обратные функции можно отобразить на графике следующим образом:
Мы видим симметричность обоих графиков относительно y=x. Эта прямая является биссектрисой первого и третьего квадрантов. Получилось доказательство одного из свойств взаимно обратных функций, о котором мы поговорим далее.
Эта прямая является биссектрисой первого и третьего квадрантов. Получилось доказательство одного из свойств взаимно обратных функций, о котором мы поговорим далее.
Возьмем пример, в котором нужно найти логарифмическую функцию, обратную заданной показательной.
Пример 2Условие: определите, какая функция будет обратной для y=2x.
Решение
Для заданной функции областью определения являются все действительные числа. Область значений лежит в интервале 0; +∞. Теперь нам нужно выразить x через y, то есть решить указанное уравнение через x. Мы получаем x=log2y. Переставим переменные и получим y=log2x.
В итоге у нас вышли показательная и логарифмическая функции, которые будут взаимно обратными друг другу на всей области определения.
Ответ: y=log2x.
На графике обе функции будут выглядеть так:
Основные свойства взаимно обратных функций
В этом пункте мы перечислим основные свойства функций y=f(x) и x=g(y), являющихся взаимно обратными.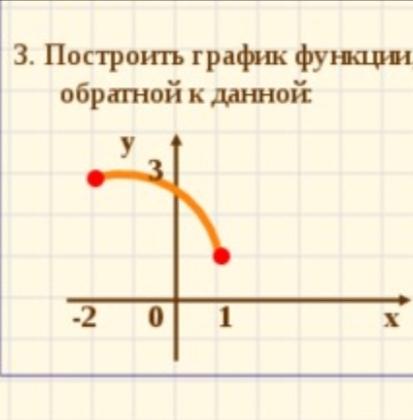
- Первое свойство мы уже вывели ранее: y=f(g(y)) и x=g(f(x)).
- Второе свойство вытекает из первого: область определения y=f(x) будет совпадать с областью значений обратной функции x=g(y), и наоборот.
- Графики функций, являющихся обратными, будут симметричными относительно y=x.
- Если y=f(x) является возрастающей, то и x=g(y) будет возрастать, а если y=f(x) убывает, то убывает и x=g(y).
Советуем внимательно отнестись к понятиям области определения и области значения функций и никогда их не путать. Допустим, что у нас есть две взаимно обратные функции y=f(x)=ax и x=g(y)=logay. Согласно первому свойству, y=f(g(y))=alogay. Данное равенство будет верным только в случае положительных значений y, а для отрицательных логарифм не определен, поэтому не спешите записывать, что alogay=y. Обязательно проверьте и добавьте, что это верно только при положительном y.
А вот равенство x=f(g(x))=logaax=x будет верным при любых действительных значениях x.
Не забывайте про этот момент, особенно если приходится работать с тригонометрическими и обратными тригонометрическими функциями. Так, arcsinsin7π3≠7π3, потому что область значений арксинуса -π2; π2 и 7π3 в нее не входит. Верной будет запись
arcsinsin7π3=arcsinsin2π+π3==по формулепривидения=arcsinsinπ3=π3
А вот sinarcsin13=13 – верное равенство, т.е. sin(arcsin x)=x при x∈-1; 1 и arcsin(sin x)=x при x∈-π2; π2. Всегда будьте внимательны с областью значений и областью определений обратных функций!
Графики взаимно обратных функций
- Основные взаимно обратные функции: степенные
Если у нас есть степенная функция y=xa, то при x>0 степенная функция x=y1a также будет обратной ей. Заменим буквы и получим соответственно y=xa и x=y1a.
На графике они будут выглядеть следующим образом (случаи с положительным и отрицательным коэффициентом a):
- Основные взаимно обратные функции: показательные и логарифмические
Возьмем a,которое будет положительным числом, не равным 1.
Графики для функций с a>1 и a<1 будут выглядеть так:
- Основные взаимно обратные функции: тригонометрические и обратные тригонометрические
Если нам нужно построить график главной ветви синуса и арксинуса, он будет выглядеть следующим образом (показан выделенной светлой областью):
График главной ветви косинуса и арккосинуса выглядит так:
График главной ветви арктангенса и тангенса:
График главной ветви арккотангенса и котангенса будет таким:
Если же вам требуется построить обратные ветви, отличные от главных, то обратную тригонометрическую функцию при этом мы сдвигаем вдоль оси Oy на нужное число периодов. Так, если требуется обратная функция для ветви тангенса на π2; 3π2, то мы можем сдвинуть ее на величину π вдоль оси абсцисс. График будет представлять собой ветвь арктангенса, которая сдвинута на π вдоль оси ординат.
Это все свойства обратных функций, о которых мы хотели бы вам рассказать.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Постройте график функции y=x^2-2x-3 Найдите: а) наименьшее значение функции; б) значения х, при которых значение функции равно 5; в) значения х, при которых функция принимает положительные
чему равны индуктивность и энергия магнитного поля соленоида , если при силе тока, равной 4А, магнитный поток через соленоид и равен 0,4 вб
Катя с мамой собирали грибы. 2. За какое время он пройдёт 1 км пути?
2. За какое время он пройдёт 1 км пути?
Пользуйтесь нашим приложением
Алгебра — Обратные функции
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 3-7: Обратные функции
В последнем примере из предыдущего раздела мы рассмотрели две функции \(f\left( x \right) = 3x — 2\) и \(g\left( x \ справа) = \frac{x}{3} + \frac{2}{3}\) и увидел, что
\[\left( {f \circ g} \right)\left( x \right) = \left( {g \circ f} \right)\left( x \right) = x\]
и, как отмечалось в этом разделе, это означает, что это очень специальные функции. Давайте посмотрим, что делает их такими особенными. Рассмотрим следующие оценки.
\[\require{color} \begin{align*}f\left( {\color{ProcessBlue} — 1} \right) & = 3\left({- 1} \right) — 2 = {\color{Red } — 5} & \hspace{0.25in} \Rightarrow \hspace{0.25in}g\left( {\color{Red} — 5} \right) & = \frac{{ — 5}}{3} + \ frac{2}{3} = \ frac{{ — 3}}{3} = {\color{ProcessBlue} — 1}\\ & & \\ g\left ({\color{ProcessBlue} 2} \right) & = \frac{2}{3} + \frac{2}{3} = { \color{Red}\frac{4}{3}} & \hspace{0,25 дюйма} \Rightarrow \hspace{0,25 дюйма} f \ влево ( {\ color {Red} \ frac {4} {3}} \ right) & = 3 \ left ( {\ frac {4} {3}} \ right) — 2 = 4 — 2 = {\ цвет{ProcessBlue} 2 }\end{align*}\]
В первом случае мы подставили \(x = — 1\) в \(f\left( x \right)\) и получили значение -5. Затем мы развернулись и подставили \(x = — 5\) к \(g\left( x \right)\) и получили значение -1, число, с которого мы начали.
Затем мы развернулись и подставили \(x = — 5\) к \(g\left( x \right)\) и получили значение -1, число, с которого мы начали.
Во втором случае мы сделали нечто подобное. Здесь мы подставили \(x = 2\) к \(g\left( x \right)\) и получили значение \(\frac{4}{3}\), мы развернулись и подставили это к \( f\left( x \right)\) и получил значение 2, которое снова является числом, с которого мы начали.
Обратите внимание, что здесь мы действительно выполняем композицию функций. Первый случай действительно
\[\left( {g \circ f} \right)\left( { — 1} \right) = g\left[ {f\left( { — 1} \right)} \right] = g\left[ {- 5} \справа] = — 1\]
и действительно второй случай,
\[\ влево ( {е \ circ g} \ вправо) \ влево ( 2 \ вправо) = е \ влево [ {г \ влево ( 2 \ вправо)} \ вправо] = е \ влево [ {\ гидроразрыва {4} {3}} \справа] = 2\]
Обратите также внимание, что они оба согласуются с формулой для композиций, которую мы нашли в предыдущем разделе. Мы получаем обратно из вычисления функции число, которое мы изначально вставили в композицию.
Мы получаем обратно из вычисления функции число, которое мы изначально вставили в композицию.
Итак, что здесь происходит? В некотором смысле мы можем думать об этих двух функциях как об отмене того, что другая сделала с числом. В первом случае мы подставили \(x = — 1\) в \(f\left( x \right)\), а затем подставили результат этой функции обратно в \(g\left( x \right)\) и каким-то образом \(g\left( x \right)\) отменил то, что \(f\left( x \right)\) сделал с \(x = — 1\), и вернул нам исходный \(x \), с которого мы начали.
Пары функций, демонстрирующие такое поведение, называются обратными функциями . Прежде чем формально определить обратные функции и обозначения, которые мы собираемся использовать для них, нам нужно получить определение.
Функция называется однозначной , если никакие два значения \(x\) не дают одинаковых \(y\). Это довольно простое определение однозначности, но для демонстрации того, что это означает, нужен пример функции, которая не является взаимно однозначной. Прежде чем сделать это, однако, мы должны отметить, что это определение один к одному на самом деле не является математически правильным определением один к одному. Оно идентично математически правильному определению, просто не использует все обозначения из формального определения. 92}\) во взаимно однозначную функцию, если мы ограничимся \(0 \le x < \infty \). Иногда это можно сделать с помощью функций.
Прежде чем сделать это, однако, мы должны отметить, что это определение один к одному на самом деле не является математически правильным определением один к одному. Оно идентично математически правильному определению, просто не использует все обозначения из формального определения. 92}\) во взаимно однозначную функцию, если мы ограничимся \(0 \le x < \infty \). Иногда это можно сделать с помощью функций.
Демонстрация однозначности функции часто является утомительным и трудным процессом. По большей части мы будем предполагать, что функции, с которыми мы будем иметь дело в этом разделе, являются взаимно однозначными. Однако нам нужно было поговорить о функциях «один к одному», поскольку только функции «один к одному» могут быть обратными функциями.
Теперь давайте формально определим, что такое обратные функции.
Обратные функции
Даны две взаимно однозначные функции \(f\left( x \right)\) и \(g\left( x \right)\), если
\[\left( {f \circ g} \right)\left( x \right) = x\hspace{0,25 дюйма}\hspace{0,25 дюйма}{\mbox{AND}}\hspace{0,25 дюйма}\hspace {0,25 дюйма}\влево({г\оборот f}\вправо)\влево(х\вправо) = х\]
, тогда мы говорим, что \(f\left( x \right)\) и \(g\left( x \right)\) являются обратными друг другу. { — 1}}\left( х \справа)\). 9{ — 1}} \circ f} \right)\left( x \right) = x\) верны. Для всех функций, которые мы будем рассматривать в этом разделе, если одна из них истинна, то и другая тоже будет истинна. Однако существуют функции (однако они выходят далеко за рамки этого курса), для которых возможно, что только одно из них будет истинным. Это связано с тем, что во всех задачах здесь мы будем проверять только одну из них. Нам просто нужно всегда помнить, что технически мы должны проверять оба.
{ — 1}}\left( х \справа)\). 9{ — 1}} \circ f} \right)\left( x \right) = x\) верны. Для всех функций, которые мы будем рассматривать в этом разделе, если одна из них истинна, то и другая тоже будет истинна. Однако существуют функции (однако они выходят далеко за рамки этого курса), для которых возможно, что только одно из них будет истинным. Это связано с тем, что во всех задачах здесь мы будем проверять только одну из них. Нам просто нужно всегда помнить, что технически мы должны проверять оба.
Давайте рассмотрим несколько примеров. 9{ — 1}}\влево( х \вправо)\).
Показать решение
Теперь мы уже знаем, что является обратной для этой функции, так как мы уже немного поработали с ней. Тем не менее, было бы неплохо начать с этого, поскольку мы знаем, что мы должны получить. Это будет хорошей проверкой процесса.
Итак, приступим. Сначала мы заменим \(f\left( x \right)\) на \(y\).
\[у = 3x — 2\]
9{ — 1}}\left( x \right)\), \(x \ge 0\).
Показать решение
Тот факт, что теперь мы используем \(g\left( x \right)\) вместо \(f\left( x \right)\), не меняет того, как работает процесс. Вот первые несколько шагов.
\[\begin{align*}y & = \sqrt {x — 3} \\ x & = \sqrt {y — 3} \end{align*}\]
Теперь, чтобы найти \(y\), нам нужно сначала возвести в квадрат обе стороны, а затем действовать как обычно. 9{ — 1}}\влево( х \вправо)\).
Показать решение
Первые несколько шагов почти такие же, как и в предыдущих примерах, так что вот они,
\[\begin{align*}y & = \frac{{x + 4}}{{2x — 5}}\\ x & = \frac{{y + 4}}{{2y — 5}}\end {выровнять*}\]
Будьте осторожны с шагом решения. В такой задаче очень легко ошибиться.
9{ — 1}}} \right)\left( x \right) & = \frac{{2x — 1}}{{2x — 1}}\,\,\frac{{\frac{{4 + 5x} }{{2x — 1}} + 4}}{{2\left( {\frac{{4 + 5x}}{{2x — 1}}} \right) — 5}}\\ & = \frac{ {\ влево ( {2x — 1} \ вправо) \ влево ( {\ гидроразрыва {{4 + 5x}} {{2x — 1}} + 4} \ вправо)}} {{\ влево ( {2x — 1} \right)\left( {2\left( {\frac{{4 + 5x}}{{2x — 1}}} \right) — 5} \right)}}\\ & = \frac{{4 + 5x + 4\влево( {2x — 1} \вправо)}}{{2\влево( {4 + 5x} \вправо) — 5\влево( {2x — 1} \вправо)}}\\ & = \ frac{{4 + 5x + 8x — 4}}{{8 + 10x — 10x + 5}}\\ & = \frac{{13x}}{{13}}\\ & = x\end{align*} \] Вау. Было много работы, но в итоге все получилось. Мы сделали всю нашу работу правильно, и на самом деле мы имеем обратное.
Было много работы, но в итоге все получилось. Мы сделали всю нашу работу правильно, и на самом деле мы имеем обратное.
Есть еще одна последняя тема, которую нам нужно быстро обсудить, прежде чем мы покинем этот раздел. Существует интересная связь между графиком функции и ее обратной.
Вот график функции и обратной из первых двух примеров. Мы не будем рассматривать последний пример, так как это функция, график которой мы еще не обсуждали.
В обоих случаях мы видим, что график обратной функции является отражением фактической функции относительно линии \(y = x\). Это всегда будет иметь место с графиками функции и ее обратной.
Полное руководство — Mashup Math
Следующее пошаговое руководство покажет вам, как найти обратную функцию! (алгебра)Добро пожаловать в это бесплатное пособие, которое прилагается к этому учебному пособию «Поиск обратной функции», в котором вы узнаете ответы на следующие ключевые вопросы и информацию:
Что является обратной функцией?
Как выглядит график обратной функции?
Как алгебраически найти обратную функцию?
Как графически найти обратную функцию?
Полное руководство по поиску обратной функции включает несколько примеров, пошаговое руководство и анимированное видеоруководство.
*Это руководство к уроку сопровождает наше анимированное видео «Как найти обратную функцию за 3 простых шага».
Хотите больше бесплатных уроков математики и видео? Подпишитесь на наш канал бесплатно!
Прежде чем приступить к поиску обратной функции, давайте кратко рассмотрим важную информацию:
Обозначение: Следующие обозначения используются для обозначения функции (слева) и ее обратной функции (справа). Обратите внимание, что использование -1 для обозначения обратной функции равно не показатель степени.
Что такое функция?
По определению, функция — это отношение, которое отображает X в Y.
А что является обратной функцией?
Обратная функция — это отношение, которое отображает Y в X.
Обратите внимание на переключатель?
Вы можете думать о связи между функцией и обратной как о ситуации, когда значения x и y меняются местами. 93 и наоборот.
93 и наоборот.
Посмотрите на таблицу исходной функции и обратной. Обратите внимание, как поменялись местами столбцы x и y!
Определение: Обратной функцией является ее отражение по линии y=x.
Помните об этом соотношении, когда мы рассмотрим пример того, как алгебраически найти обратную функцию.
Мы будем использовать следующий трехэтапный процесс, который можно использовать для нахождения обратной любой функции:
ШАГ ПЕРВЫЙ: Перепишите f(x)= как y=
Если функция, обратную которой вы хотите найти, еще не выражена в форме y=, просто замените f(x)= на y= следующим образом ( поскольку f(x) и y означают одно и то же: результат функции):
ШАГ ПЕРВЫЙ: Поменяйте местами X и Y
Теперь, когда у вас есть функция в форме y=, следующим шагом будет переписать новая функция, использующая старую функцию, где вы меняете местами x и y следующим образом:
Исходная функция
Новая обратная функция!
Эта новая функция с поменявшимися местами X и Y является обратной функцией, но есть еще один шаг!
ШАГ ТРЕТИЙ: Решите для y (получите его сам!)
Последний шаг состоит в том, чтобы изменить функцию, чтобы изолировать y (получить его сам по себе), используя алгебру следующим образом: 9-1(х)=(х+4)/7
Помните, ранее мы говорили, что график обратной функции — это график исходной функции, отраженный по линии y=x? Давайте еще раз посмотрим, что это означает, на последнем примере:
Ниже на рисунке 1 представлен график исходной функции y=7x-4, а на рисунке 2 — график обратной функции y=(x+4)/7.
Рисунок 1
Рисунок 2
Теперь давайте посмотрим на обе линии на одном графике. Обратите внимание, что исходная функция на этот раз синего цвета, а обратная — красного (рис. 3), а затем добавьте линию y=x к тому же графику (рис. 4).
Рисунок 3
Рисунок 4
Вы видите отражение над линией y=x?
Это отношение применимо к любой функции, оно обратное, и оно должно помочь вам понять, почему трехэтапный процесс, который вы использовали ранее, работает для нахождения обратной любой функции!
Посмотрите этот анимированный видеоурок о том, как найти обратную функцию!
Ознакомьтесь со следующими бесплатными ресурсами:Бесплатный учебник
Есть мысли? Поделитесь своими мыслями в разделе комментариев ниже!
(Никогда не пропустите блог Mashup Math — нажмите здесь, чтобы получать нашу еженедельную рассылку!)
Автор: Энтони Персико Вы часто можете увидеть, как я с радостью разрабатываю анимированные уроки математики, которыми я делюсь на моем канале YouTube . Или проводить слишком много времени в тренажерном зале или играть на своем телефоне.
Или проводить слишком много времени в тренажерном зале или играть на своем телефоне.
Комментарий
Обратная функция – объяснение и примеры
Что такое обратная функция?
В математике обратная функция — это функция, которая отменяет действие другой функции.
Например, , сложение и умножение обратны вычитанию и делению соответственно.
Обратную функцию можно рассматривать как отражение исходной функции по линии y = x. Проще говоря, обратная функция получается заменой (x, y) исходной функции на (y, x).
Мы используем символ f − 1 для обозначения обратной функции. Например, если f (x) и g (x) обратны друг другу, то мы можем символически представить это утверждение как:
g(x) = f − 1 (x) или f(x) = g −1 (x)
Об обратной функции следует отметить, что обратная функция не совпадает с обратной, т. е. f – 1 (х) ≠ 1/f(х). В этой статье мы обсудим, как найти обратную функцию.
е. f – 1 (х) ≠ 1/f(х). В этой статье мы обсудим, как найти обратную функцию.
Поскольку не все функции имеют обратную функцию, важно проверить, есть ли у функции обратная функция, прежде чем приступать к определению ее обратной.
Мы проверяем, есть ли у функции обратная функция, чтобы не тратить время на поиск чего-то несуществующего.
Взаимно-однозначные функции
Как же доказать, что данная функция имеет обратную? Функции, имеющие обратную функцию, называются взаимно однозначными.
Функция называется взаимно однозначной, если для каждого числа y в диапазоне f существует ровно одно число x в области определения f такое, что f (x) = y.
Другими словами, область определения и область взаимно однозначной функции имеют следующие отношения: Например, чтобы проверить, является ли f(x) = 3x + 5 заданной функцией один к одному, f(a) = 3a + 5 и f(b) = 3b + 5, ⟹ 3а + 5 = 3б + 5 ⟹ 3а = 3б ⟹ а = б. Следовательно, f (x) является взаимно однозначной функцией, поскольку a = b. Рассмотрим другой случай, когда функция f задается выражением f = {(7, 3), (8, –5), (–2, 11), (–6, 4)}. Эта функция является взаимно однозначной, поскольку ни одно из ее значений y не встречается более одного раза. А как насчет этой другой функции h = {(–3, 8), (–11, –9), (5, 4), (6, –9)}? Функция h не является взаимно однозначной, поскольку значение y, равное –9, появляется более одного раза. Вы также можете графически проверить функцию «один к одному», проведя вертикальную и горизонтальную линии через график функции. Функция является взаимно однозначной, если и горизонтальная, и вертикальная линии проходят через график один раз. Поиск обратной функции — простой процесс, хотя нам действительно нужно быть осторожным с парой шагов. В этой статье мы предполагаем, что все функции, с которыми мы будем иметь дело, являются один к одному. Вот процедура нахождения обратной функции f(x): ⟹ (f ∘ f −1 ) (x) = x ⟹ (f −1 ∘ f) (x) = x Давайте рассмотрим пару примеров. Пример 1 Зная функцию f (x) = 3x − 2, найти ее обратную. Решение f(x) = 3x − 2 Замените f(x) на y. ⟹ y = 3x − 2 Поменять x на y ⟹ x = 3y − 2 Найти y x + 2 = 3y Разделить на 3, чтобы получить; 1/3(х + 2) = у x/3 + 2/3 = y Наконец, замените y на f −1 (x). (x) = x f [f −1 (x)] = f (x/3 + 2/3) ⟹ 3(x/3 + 2/3) – 2 ⟹ x + 2 – 2 = x Следовательно, f −1 (x) = x/3 + 2/3 — правильный ответ. Пример 2 Учитывая f(x) = 2x + 3, найдите f −1 (х). Решение F (x) = y = 2x + 3 2x + 3 = y Swap x и y ⟹2y + 3 = x Теперь решайте Y ⟹2y = x. – 3 ⟹ y = x/2 – 3/2 Наконец, замените y на f −1 (x) ⟹ f −1 (x) = (x– 3)/2 Пример 3 Задайте функцию f (x) = log 10 (x), найдите f −1 (x). Решение F (x) = log₁₀ (x) заменен F (x) на Y ⟹ y = log 10 (x) ⟹ 10 y = x Теперь SWAP x с Y с Y с Y с Y с Y с Y с Y с Y с Y с Y с Y с Y с Y с Y с Y с Y с Y с Y с y с y. получить; ⟹ y = 10 x Наконец, замените y на f −1 (x). f -1 (x) = 10 x Следовательно, обратное выражение f(x) = log 10 (x) равно f -1 (x) = 10 90 391 x Пример 4 Найдите обратную следующую функцию g(x) = (x + 4)/ (2x -5) Решение g(x) = (x + 4)/ (2x -5) ⟹ y = (x + 4)/ (2x -5) Поменять местами y с x и наоборот y = (x + 4)/ (2x -5) ⟹ x = (y + 4)/ (2y — 5) ⟹ x(2y−5) = y + 4 ⟹ 2xy − 5x = y + 4 ⟹ 2xy – y = 4 + 5x ⟹ (2x − 1) y = 4 + 03x 9000 Разделите обе части уравнения на (2x — 1). ⟹ у = (4 + 5х) / (2х — 1) Заменить y на g – 1 (x) = g – 1 (x) = (4 + 5x)/ (2x − 1) Доказательство: (g ∘ g 1 −1 9 ) (x) = g [g −1 (x)] = g [(4 + 5x)/ (2x − 1)] = [(4 + 5x)/ (2x − 1) + 4 ]/ [2(4 + 5x)/ (2x − 1) − 5] Умножить числитель и знаменатель на (2x − 1). ⟹ (2x — 1) [(4 + 5x)/ (2x — 1) + 4]/ [2(4 + 5x)/ (2x — 1) — 5] (2x — 1). ⟹ [4 + 5x + 4(2x — 1)]/ [ 2(4 + 5x) — 5(2x — 1)] ⟹ [4 + 5x + 8x−4]/ [8 + 10x − 10x + 5] ⟹13x/13 = x Пример 5 Определите обратную следующую функцию f(x) = 2x – 5 Решение Замените f(x) на y. f(x) = 2x – 5⟹ y = 2x – 5 Поменяйте местами x и y, чтобы получить; ⟹ x = 2y – 5 Изолировать переменную y. 2 года = х + 5 ⟹ y = x/2 + 5/2 Измените y обратно на f –1 (x). ⟹ f –1 (x) = (x + 5)/2 Пример 6. Решение Измените h (x) на y, чтобы получить; h(x) = (x – 2) 3 ⟹ y = (x – 2) 3 Поменять местами x и y ⟹ x = (y – 2) 3 Изолировать г 3 = x + 2 3 Найдите кубический корень из обеих частей уравнения. 3 √y 3 = 3 √x 3 + 3 √2 3 y = 3 √ (2 
Как найти обратную функцию?


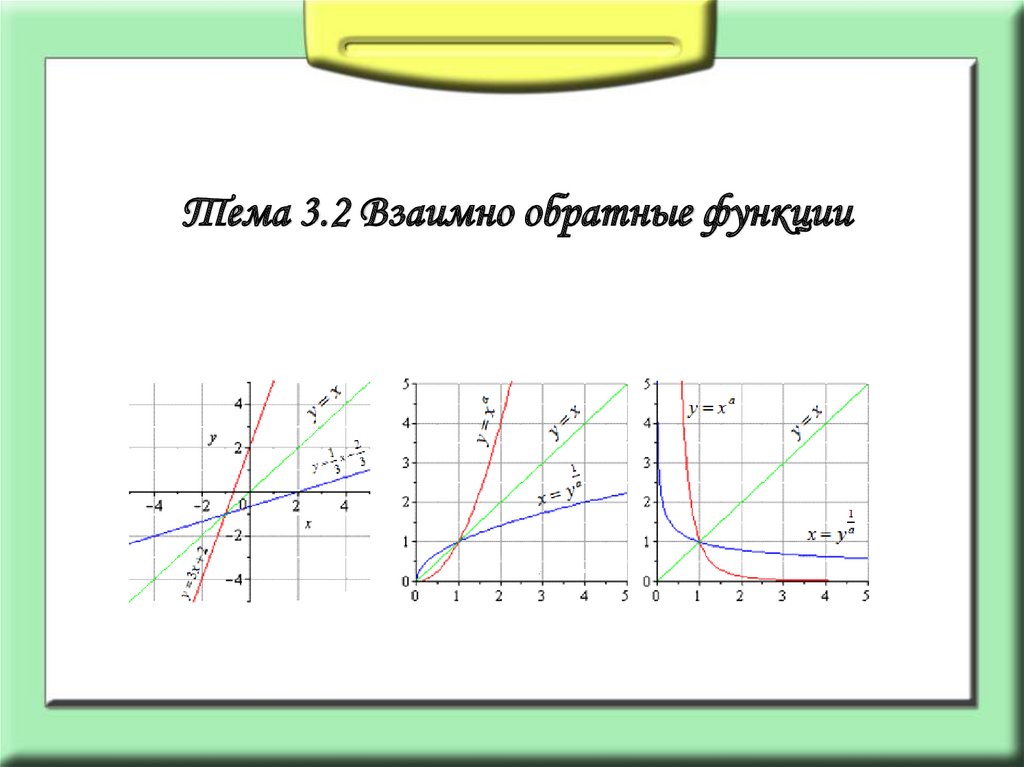
Следовательно, g – 1 (x) = (4 + 5x)/ (2x − 1)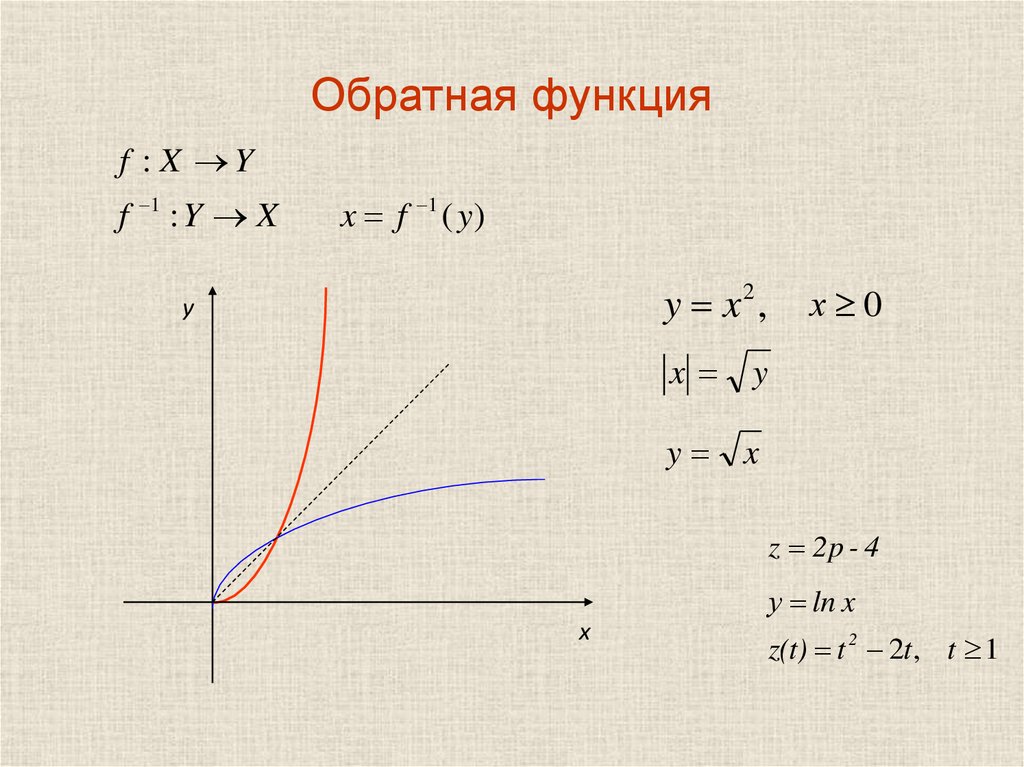
H — 1 (x) = 3 √ (2 3 ) + 2
Пример 7
Найдите конверсие h (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = (x) = 4x + 3)/(2x + 5)
Решение
Замените h (x) на y.
h (x) = (4x+3)/(2x+5) ⟹ y = (4x + 3)/(2x + 5)
Поменять местами x и y.
⟹ х = (4у + 3)/ (2у + 5).
Найдите y в приведенном выше уравнении следующим образом:
⟹ x = (4y + 3)/ (2y + 5)
Умножьте обе части на (2y + 5)
⟹ x (2y + 5) = 4y + 3
Распределить x
⟹ 2xy + 5x = 4y + 3
Изолировать y.
⟹ 2xy – 4y = 3 – 5x
⟹ y (2x – 4) = 3 – 5x
Разделите на 2x – 4, чтобы получить;
⟹ y = (3 – 5x)/ (2x – 4)
Наконец, замените y на h – 1 (x).
⟹ h – 1 (x) = (3 – 5x)/ (2x – 4)
Обратная функция – определение, формула, график, примеры
LearnPracticeDownload
Обратная функция представлена f -1 относительно исходной функции f и область определения исходной функции становится областью значений обратной функции, а область значений данной функции становится областью значений обратной функции. График обратной функции получается заменой (x, y) на (y, x) относительно прямой y = x.
Давайте узнаем больше об обратной функции, шагах по нахождению обратной функции и графике обратной функции.
| 1. | Что такое обратная функция? |
| 2. | шагов для нахождения обратной функции |
| 3. | График обратной функции |
| 4. | Примеры обратной функции |
| 5. | Практические вопросы по обратной функции |
| 6. | Часто задаваемые вопросы об обратной функции |
Что такое обратная функция?
Обратная функция f обозначается как f -1 и существует только тогда, когда f является одновременно и однозначной, и функциональной. Обратите внимание, что f -1 НЕ является обратной величиной f. Композиция функции f и обратной функции f -1 дает значение домена x.
(f -1 ) (x) = (f -1 o f) (x) = x
Для того чтобы функция ‘f’ считалась обратной функцией, каждый элемент в диапазоне y ∈ Y имеет было отображено из некоторого элемента x ∈ X в множестве доменов, и такое отношение называется отношением один-один или отношением предписания. Кроме того, обратная функция f -1 данной функции имеет область определения y ∈ Y, связанную с отдельным элементом x ∈ X в наборе доменов кодов, и такого рода отношения по отношению к данной функции ‘f’ являются онтофункцией или функция сюръекции. Таким образом, обратная функция, являющаяся инъюнктивной и сюръективной функцией, называется биективной функцией.
Кроме того, обратная функция f -1 данной функции имеет область определения y ∈ Y, связанную с отдельным элементом x ∈ X в наборе доменов кодов, и такого рода отношения по отношению к данной функции ‘f’ являются онтофункцией или функция сюръекции. Таким образом, обратная функция, являющаяся инъюнктивной и сюръективной функцией, называется биективной функцией.
Рассмотрим функцию f, областью определения которой является множество X, а областью значений является множество Y. Функция f обратима, если существует другая функция g, областью определения которой является Y, а областью значений является X. Эти две функции можно представить в виде f(x) = Y и g(y) = X. Для этой ситуации, если функция f(x) обратная, то ее обратная функция g(x) единственна.
Если композиция двух функций f(x) и g(x) дает тождественную функцию f(g(x))=x, то говорят, что эти две функции обратны друг другу. Если применение функции к x в качестве входных данных дает n выходных данных y, то применение другой функции g к y должно возвращать значение x. Следовательно, обратная функция обращает функцию. Область определения данной функции становится областью значений обратной функции, а область значений данной функции становится областью значений обратной функции.
Следовательно, обратная функция обращает функцию. Область определения данной функции становится областью значений обратной функции, а область значений данной функции становится областью значений обратной функции.
шагов, чтобы найти обратную функцию
Следующая последовательность шагов поможет удобно найти обратную функцию. Здесь мы рассматриваем функцию f(x) = ax + b и стремимся найти обратную эту функцию, выполнив следующие шаги.
- Для заданной функции f(x) = ax + b заменить f(x) = y, чтобы получить y = ax + b.
- Поменяйте местами x на y и y на x в функции y = ax + b, чтобы получить x = ay + b.
- Здесь решите выражение x = ay + b для y. И получаем y = (x — b/a
- Наконец, заменим y = f -1 (x), и мы получим f -1 (x) = (x — b)/a.
График обратной функции
Инъективная функция является отражением исходной функции относительно линии y = x и получается путем замены (x, y) на (y, x).
Если даны графики двух функций, мы можем определить, являются ли они обратными друг другу. Если графики обеих функций симметричны относительно прямой y = x, то говорят, что эти две функции обратны друг другу. Это связано с тем, что если (x, y) лежит на функции, то (y, x) лежит на обратной ей функции.
Связанные темы
Следующие темы помогают лучше понять обратную функцию.
- Биективная функция
- Инъекционная функция
- Периодическая функция
- Непрерывная функция
- Сигнум Функция
- Отношения и функции
Примеры обратной функции
Пример 1: Определите, являются ли функции f(x) = 2x + 3 и g(x) = (x — 3)/2 обратными друг другу, используя формулу обратной функции.
Решение:
Проверим, является ли (fo g)(x) = (g o f)(x) = x.
(f o g)(x) = f (g(x))
= f ((x-3)/2)
= 2 ((x-3)/) + 3
= x — 3 + 3
= x
(g o f)(x) = g (f(x))
= g (2x + 3)
= (2x + 3 — 3)/2
= 2x/2
= x
Мы доказали, что (fo g)(x) = (g o f)(x) = x.

По формуле обратной функции f и g обратны друг другу.
Ответ: Мы доказали, что f = g -1 и g = f -1 .
- Пример 2 : Найдите обратную функцию для заданной функции f(x) = \( \dfrac{4x+1}{3x-2}\).
Решение:
Мы будем использовать формулу обратной функции (или шаги для нахождения обратной функции).
Данная функция:
y = \( \dfrac{4x+1}{3x — 2}\)
Поменять местами x и y.
x = \( \dfrac{4y+1}{3y — 2}\)
Теперь мы решим это для y.
Умножение обеих частей на (3x — 2),
x (3y — 2) = 4y + 1
3xy — 2x = 4y + 1
3xy — 4y = 2x + 1
y (3x — 4) = 2x + 1
y = \(\dfrac{2x + 1}{3x-4}\)
Замените y на f -1 (x).
f -1 (x) = \(\dfrac{2x + 1}{3x-4}\)
Ответ: f -1 (x) = \(\dfrac{2x + 1}{3x-4}\).
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила.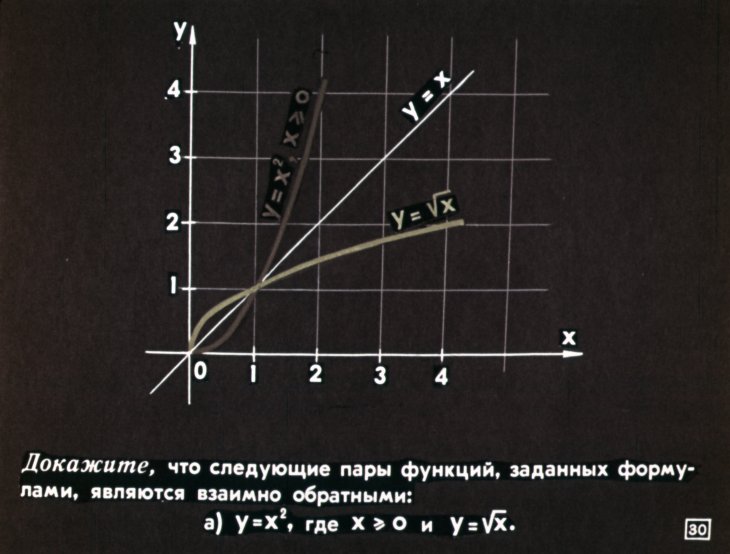 Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Запишитесь на бесплатный пробный урок
Практические вопросы по обратной функции
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об обратной функции
Что такое обратная функция?
Обратная функция f обозначается f -1 , и она существует только тогда, когда f является одновременно и однозначной, и функциональной. Обратите внимание, что f -1 НЕ является обратной величиной f. Композиция функции f и обратной функции f -1 дает значение домена x.
(f -1 ) (x) = (f -1 o f) (x) = x
Как найти обратную функцию?
Следующая последовательность шагов помогает найти обратную функцию. Здесь мы рассматриваем функцию f(x) = ax + b.
- Для заданной функции f(x) = ax + b заменить f(x) = y, чтобы получить y = ax + b.
- Поменяйте местами x на y и y на x в функции y = ax + b, чтобы получить x = ay + b.

- Здесь решите выражение x = ay + b для y. И получаем y = (x — b/a
- Наконец, заменим y = f -1 (x), и мы получим f -1 (х) = (х — б)/а.
Что является примером обратной функции?
Примером обратной функции является функция f(x) = 2x + 3, а ее обратной функцией является f -1 (x) = (x — 3)/2.
Как найти обратную функцию тригонометрических функций?
Обратная функция тригонометрической функции аналогична нахождению обратной нормальной функции с помощью алгебраических выражений.
Что такое область определения и область значений обратной функции?
Область определения и область значений обратной функции получаются путем замены области значений и области значений заданной функции. Область определения данной функции становится областью значений обратной функции, а область значений данной функции становится областью значений обратной функции.
Рабочие листы по математике и визуальный учебный план
Композиция и обратные функции
Композиция функций
В математике часто бывает так, что результат одной функции оценивается путем применения второй функции. Например, рассмотрим функции, определенные как f(x)=x2 и g(x)=2x+5. Первый, g оценивается, где x=-1, а затем результат возводится в квадрат с использованием второй функции, f .
Например, рассмотрим функции, определенные как f(x)=x2 и g(x)=2x+5. Первый, g оценивается, где x=-1, а затем результат возводится в квадрат с использованием второй функции, f .
Это последовательное вычисление дает 9. Мы можем упростить этот процесс, создав новую функцию, определяемую f(g(x)), которая явно получается путем подстановки g(x) в f(x).
f(g(x))=f(2x+5)=(2x+5)2=4×2+20x+25
Следовательно, f(g(x))=4×2+20x+25 и мы можем проверить что при x=−1 результатом будет 9.
f(g(−1))=4(−1)2+20(−1)+25=4−20+25=9
Вышеприведенный расчет описывает состав функцийПрименение функции к результатам другой функции., что указывается с помощью оператора композиции. Открытая точка, используемая для обозначения состава функции (f○g)(x)=f(g(x)) . (○). Если заданы функции f и g ,
(f○g)(x)=f(g(x)) Композиция Функций
Обозначение f○g7, состоящее из g0
8 f
». Эта операция определена только для значений, x , в области g , так что g(x) находится в области f .
Пример 1
Учитывая f(x)=x2−x+3 и g(x)=2x−1 вычислить:
- (f○g)(x).
- (г○ф)(х).
Решение:
Замените g на f .
(f○g)(x)=f(g(x))=f(2x−1)=(2x−1)2−(2x−1)+3=4×2−4x+1−2x+1+ 3=4×2−6x+5
Замените f на g .
(g○f)(x)=g(f(x))=g(x2−x+3)=2(x2−x+3)−1=2×2−2x+6−1=2×2−2x+ 5
Ответ:
- (f○g)(x)=4×2−6x+5
- (г○f)(x)=2×2−2x+5
Предыдущий пример показывает, что композиция функций не обязательно коммутативна.
Пример 2
Для заданных f(x)=x3+1 и g(x)=3x−13 найти (f○g)(4).
Решение:
Начните с нахождения (f○g)(x).
(f○g)(x)=f(g(x))=f(3x−13)=(3x−13)3+1=3x−1+1=3x
Затем подставьте 4 дюйма вместо х .
(f○g)(x)=3x(f○g)(4)=3(4)=12
Ответ: (f○g)(4)=12
Функции могут быть составлены сами с собой.
Пример 3
По заданному f(x)=x2−2 найти (f○f)(x).
Решение:
(f○f)(x)=f(f(x))=f(x2−2)=(x2−2)2−2=x4−4×2+4−2=x4−4×2 +2
Ответ: (f○f)(x)=x4−4×2+2
Попробуйте! Для заданных f(x)=2x+3 и g(x)=x−1 найдите (f○g)(5).
Ответ: 7
(нажмите, чтобы посмотреть видео)
Обратные функции
Рассмотрим функцию, которая переводит градусы Фаренгейта в градусы Цельсия: C(x)=59(x−32). Мы можем использовать эту функцию для преобразования 77°F в градусы Цельсия следующим образом.
C(77)=59(77−32)=59(45)=25
Следовательно, 77°F эквивалентно 25°C. Если мы хотим преобразовать 25°C обратно в градусы Фаренгейта, мы будем использовать формулу: F(x)=95х+32.
F(25)=95(25)+32=45+32=77
Обратите внимание, что две функции C и F обращают действие друг на друга.
Описывает обратную зависимость. В общем, f и g являются обратными функциями , если )(x)=g(f(x))=x для всех x в области f.
В этом примере
C(F(25))=C(77)=25F(C(77))=F(25)=77
Пример 4
Алгебраически проверьте, что функции, заданные формулами f(x)=12x−5 и g(x)=2x+10, являются обратными.
Решение:
Скомпонуйте функции в обоих направлениях и убедитесь, что результат равен x .
Ответ: Оба (f○g)(x)=(g○f)(x)=x; следовательно, они инверсны.
Далее мы исследуем геометрию, связанную с обратными функциями. Графики обеих функций в предыдущем примере представлены на одном и том же наборе осей ниже.
Обратите внимание, что существует симметрия относительно линии y=x; графики f и g являются зеркальным отображением этой линии. Также обратите внимание, что точка (20, 5) находится на графике f , а точка (5, 20) — на графике g . Оба этих наблюдения в целом верны, и мы имеем следующие свойства обратных функций:
Оба этих наблюдения в целом верны, и мы имеем следующие свойства обратных функций:
- Графики обратных функций симметричны относительно прямой y=x.
- Если (a,b) находится на графике функции, то (b,a) находится на графике обратной функции.
Кроме того, если g обратно f , мы используем обозначение g=f−1. Здесь f−1 читается как « f обратное», и его не следует путать с отрицательными показателями степени. Другими словами, f−1(x)≠1f(x), и мы имеем
(f○f−1)(x)=f(f−1(x))=x и(f−1○f )(x)=f−1(f(x))=x
Пример 5
Алгебраически проверить, что функции, определяемые формулами f(x)=1x−2 и f−1(x)=1x+2, являются обратными .
Решение:
Скомпонуйте функции в обоих направлениях, чтобы убедиться, что результат равен х .
Ответ: Поскольку (f○f−1)(x)=(f−1○f)(x)=x, они обратны.
Напомним, что функция — это отношение, в котором каждый элемент домена соответствует ровно одному элементу диапазона. Мы используем тест вертикальной линии, чтобы определить, представляет ли график функцию или нет. Функции могут быть дополнительно классифицированы с использованием обратной зависимости. Функции «один к одному» — функции, в которых каждое значение в диапазоне соответствует ровно одному значению в домене. — это функции, в которых каждое значение в диапазоне соответствует ровно одному элементу домена. Тест горизонтальной линии Если горизонтальная линия пересекает график функции более одного раза, то она не является взаимно однозначной. используется для определения того, представляет ли график функцию взаимно однозначного соответствия. Если горизонтальная линия пересекает график более одного раза, то она не представляет однозначной функции.
Мы используем тест вертикальной линии, чтобы определить, представляет ли график функцию или нет. Функции могут быть дополнительно классифицированы с использованием обратной зависимости. Функции «один к одному» — функции, в которых каждое значение в диапазоне соответствует ровно одному значению в домене. — это функции, в которых каждое значение в диапазоне соответствует ровно одному элементу домена. Тест горизонтальной линии Если горизонтальная линия пересекает график функции более одного раза, то она не является взаимно однозначной. используется для определения того, представляет ли график функцию взаимно однозначного соответствия. Если горизонтальная линия пересекает график более одного раза, то она не представляет однозначной функции.
Горизонтальная линия представляет значение в диапазоне, а количество пересечений с графиком представляет количество значений, которым она соответствует в домене. Функция, определяемая выражением f(x)=x3, является взаимно однозначной, а функция, определяемая выражением f(x)=|x| не является. Определение того, является ли функция взаимно однозначной, важно, потому что функция имеет обратную тогда и только тогда, когда она взаимно однозначна. Другими словами, функция имеет обратную, если она проходит тест горизонтальной линии.
Определение того, является ли функция взаимно однозначной, важно, потому что функция имеет обратную тогда и только тогда, когда она взаимно однозначна. Другими словами, функция имеет обратную, если она проходит тест горизонтальной линии.
Примечание : В этом тексте, когда мы говорим « функция имеет обратную», мы имеем в виду, что существует другая функция, f−1, такая, что (f○f−1)(x)=(f−1○f )(х)=х.
Пример 6
Определить, является ли заданная функция взаимно однозначной.
Решение:
Ответ: Данная функция проходит тест горизонтальной линии и, таким образом, является однозначной.
На самом деле, любая линейная функция вида f(x)=mx+b, где m≠0, является взаимно однозначной и, следовательно, имеет обратную. Шаги для нахождения обратной однозначной функции описаны в следующем примере.
Пример 7
Найдите обратную функцию f(x)=32x−5.
Решение:
Прежде чем начать этот процесс, вы должны убедиться, что функция является взаимно однозначной. В этом случае у нас есть линейная функция, где m ≠ 0, и, следовательно, она взаимно однозначна.
В этом случае у нас есть линейная функция, где m ≠ 0, и, следовательно, она взаимно однозначна.
Шаг 1: Замените обозначение функции f(x) на y .
f(x)=32x−5y=32x−5
Шаг 2: Обмен x и y . Мы используем тот факт, что если (x,y) — точка на графике функции, то (y,x) — точка на графике обратной функции.
х=32у-5
Шаг 3: Найдите y .
х=32у-5х+5=32у23⋅(х+5)=23⋅32у23х+103=у
Шаг 4: Полученная функция является обратной f . Замените y на f−1(x).
f−1(x)=23x+103
Шаг 5: Проверка.

Ответ: f−1(x)=23x+103
Если функция не является взаимно однозначной, часто бывает так, что мы можем ограничить область определения таким образом, чтобы результирующий граф был взаимно однозначным. -один. Например, рассмотрим функцию возведения в квадрат, сдвинутую вверх на одну единицу, g(x)=x2+1. Обратите внимание, что он не проходит тест горизонтальной линии и, следовательно, не является однозначным. Однако если мы ограничим область определения неотрицательными значениями, x≥0, то график действительно пройдет тест горизонтальной линии.
В ограниченном домене g взаимно однозначно, и мы можем найти его обратное.
Пример 8
Найдите обратную функцию, определяемую выражением g(x)=x2+1, где x≥0.
Решение:
Начните с замены обозначения функции g(x) на y .
g(x)=x2+1y=x2+1 где x≥0
Обмен x и y .
x=y2+1 где y≥0
Найдите y .
х=у2+1х-1=у2±х-1=у
Поскольку y≥0, мы рассматриваем только положительный результат.
y=x−1g−1(x)=x−1
Ответ: g−1(x)=x−1. Чек остается читателю.
Графики в предыдущем примере показаны на том же наборе осей, что и ниже. Обратите внимание на симметрию относительно линии y=x.
Пример 9
Найдите обратную функцию f(x)=2x+1x−3.
Решение:
Используйте графическую утилиту, чтобы убедиться, что эта функция является однозначной. Начните с замены обозначения функции f(x) на и .
f(x)=2x+1x−3y=2x+1x−3
Обмен x и y .
x=2y+1y−3
Найдите y .
x=2y+1y−3x(y−3)=2y+1xy−3x=2y+1
Получите все члены с переменной y с одной стороны уравнения и все остальные с другой. Это позволит нам рассматривать и как GCF.
xy−3x=2y+1xy−2y=3x+1y(x−2)=3x+1y=3x+1x−2
Ответ: f−1(x)=3x+1x−2. Чек остается читателю.
Попробуйте! Найдите обратную функцию f(x)=x+13−3.
Ответ: f−1(x)=(x+3)3−1
(нажмите, чтобы посмотреть видео)
Ключевые выводы
- Оператор композиции (○) указывает, что мы должны заменить одну функцию на другую. Другими словами, (f○g)(x)=f(g(x)) означает, что мы подставляем g(x) в f(x).
- Если две функции являются обратными, то каждая из них обратит действие другой. Используя обозначения, (f○g)(x)=f(g(x))=x и (g○f)(x)=g(f(x))=x.
- Обратные функции имеют специальные обозначения. Если g является обратным значением f, то мы можем написать g(x)=f−1(x). Это обозначение часто путают с отрицательными показателями, и оно не равно делению на f(x).
- Графики инверсий симметричны относительно прямой y=x. Если (a,b) — точка на графике функции, то (b,a) — точка на графике обратной функции.
- Если каждая точка в диапазоне функции соответствует ровно одному значению в домене, то функция является взаимно однозначной.
 Используйте тест горизонтальной линии, чтобы определить, является ли функция однозначной.
Используйте тест горизонтальной линии, чтобы определить, является ли функция однозначной. - У однозначной функции есть обратная функция, которую часто можно найти, поменяв местами x и y и найдя y . Эта новая функция является обратной исходной функции.
Тематические упражнения
f(x)=4x−1, g(x)=3x
f(x)=−2x+5, g(x)=2x
f(x)=3x−5, g(x)=x−4
f(x)=5x+1, g(x)=2x−3
f(x)=x2−x+1, g(x)=2x−1
f(x)=x2−3x−2, g(x)=x−2
f(x)=x2+3, g(x)=x2−5
f(x)=2×2, g(x)=x2−x
f(x)=8×3+5, g(x)=x−53
f(x)=27×3−1, g(x)=x+13
f(x)=1x+5, g(x)=1x
f(x)=1x−3, g(x)=3x+3
f(x)=5x, g(x)=3x−2
f(x)=2x, g(x)=4x+1
f(x)=12x, g(x)=x2+8
f(x)=2x−1, g(x)=1x+1
f(x)=1−x2x, g(x)=12x+1
f(x)=2xx+1, g(x)=x+1x
(ф○г)(2)
(г○f)(−1)
(г○ф)(0)
(ф○г)(0)
(ф○ч)(3)
(г○ч)(16)
(ч○г)(35)
(ч○ф)(−3)
(ф○г)(1)
(г○ж)(−2)
(г○ф)(0)
(ф○г)(−2)
(ф○ч)(−1)
(ч○г)(−12)
(ч○ф)(24)
(г○ч)(0)
f(x)=3x−1
f(x)=25x+1
f(x)=x2+5
f(x)=x2−x+6
f(x)=x3+2
f(x)=x3−x
f(x)=1x+1
f(x)=x+12x
Часть A: Состав функций
Для заданных функций f и g найдите (f○g)(x) и (g○f)(x).
Для заданных функций f(x)=3×2−2, g(x)=5x+1 и h(x)=x вычислить следующее.
Для заданных функций f(x)=x+33, g(x)=8×3−3 и h(x)=2x−1 вычислите следующее.
Зная функцию, определить (f○f)(x).
ф(х)=х+1
г(х)=х2+1
ч(х)=|х|+1
г(х)=х3+1
ф(х)=х+1
г(х)=3
f(x)=3x−4, f−1(x)=x+43
f(x)=−5x+1, f−1(x)=1−x5
f(x)=-23x+1, f-1(x)=-32x+32
f(x)=4x−13, f−1(x)=14x+112
f(x)=x−8, f−1(x)=x2+8, x≥0
f(x)=6×3−3, f−1(x)=(x+3)36
f(x)=xx+1, f−1(x)=x1−x
f(x)=x−33x, f−1(x)=31−3x
f(x)=2(x−1)3+3, f−1(x)=1+x−323
f(x)=5x−13+4, f−1(x)=(x−4)3+15
f(x)=5x
f(x)=12x
f(x)=2x+5
f(x)=−4x+3
f(x)=−23x+13
f(x)=−12x+34
г(х)=х2+5, х≥0
г(х)=х2-7, х≥0
f(x)=(x−5)2, x≥5
f(x)=(x+1)2, x≥−1
ч(х)=3х3+5
ч(х)=2×3−1
f(x)=(2x−3)3
f(x)=(x+4)3−1
г(х)=2×3+1
г(х)=1×3−2
f(x)=5x+1
f(x)=12x−9
f(x)=x+5x−5
f(x)=3x−42x−1
ч(х)=х-510х
ч(х)=9х+13х
г(х)=5х+23
г(х)=4х-33
f(x)=x−63−4
f(x)=2x+23+5
ч(х)=х+15−3
ч(х)=х-85+1
f(x)=mx+b, m≠0
f(x)=ax2+c, x≥0
f(x)=ax3+d
f(x)=a(x−h)2+k, x≥h
ф(х)=х+2
f(x)=23x−4
f(x)=−2x+2
f(x)=−13x+4
г(х)=х2-2, х≥0
г(х)=(х-2)2, х≥2
ч(х)=х3+1
ч(х)=(х+2)3−2
f(x)=2−x
f(x)=−x+1
Часть B: Обратные функции
Данные функции взаимно однозначны? Объяснять.
По заданному графику однозначной функции постройте график ее обратной функции.
Алгебраически проверьте, что две заданные функции являются обратными. Другими словами, покажите, что (f○f−1)(x)=x и (f−1○f)(x)=x.
Найдите инверсию следующих функций.
Постройте график функции и ее обратной функции на одном наборе осей.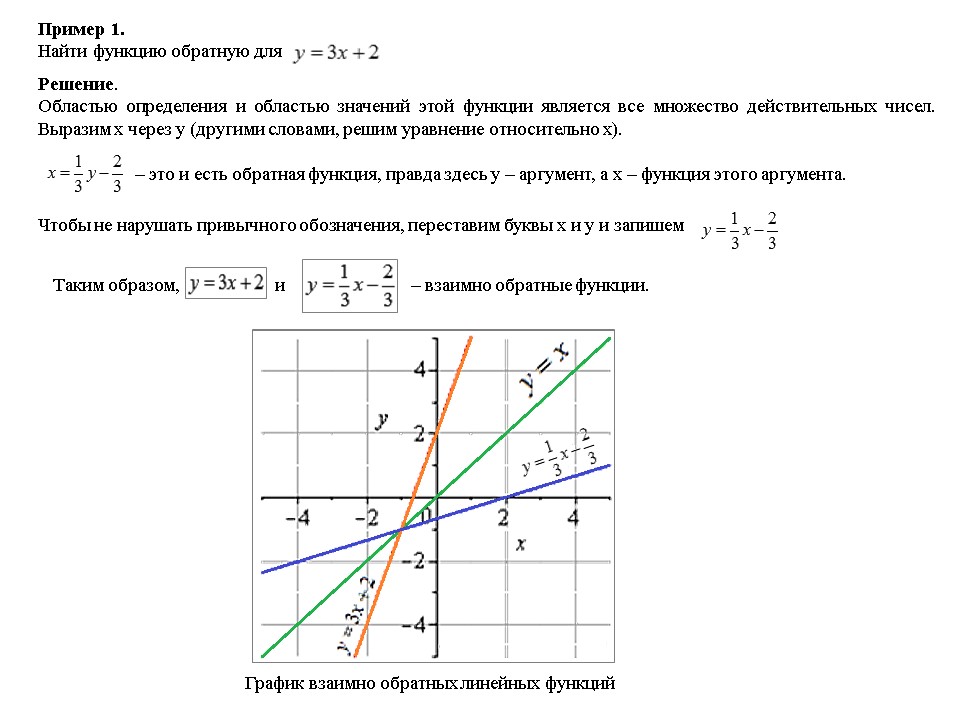
Является ли композиция функций ассоциативной? Объяснять.

Объясните, почему C(x)=59(x−32) и F(x)=95x+32 определяют обратные функции. Докажите это алгебраически.
Представляют ли графики всех прямых линий взаимно однозначные функции? Объяснять.
Если графики обратных функций пересекаются, то как найти точку пересечения? Объяснять.
Часть C: Дискуссионная доска
Ответы
(ф○г)(х)=12х-1; (g○f)(x)=12x−3
(f○g)(x)=3x−17; (g○f)(x)=3x−9
(f○g)(x)=4×2−6x+3; (g○f)(x)=2×2−2x+1
(f○g)(x)=x4−10×2+28; (g○f)(x)=x4+6×2+4
(f○g)(x)=8x−35; (g○f)(x)=2x
(f○g)(x)=x5x+1; (г○f)(х)=х+5
(f○g)(x)=53x−2; (g○f)(x)=15x−2
(f○g)(x)=12×2+16;(g○f)(x)=1+32x24x2
(ф○г)(х)=х; (г○f)(х)=х
361
−9
7
2
2
21
0
5
(f○f)(x)=9x−4
(f○f)(x)=x4+10×2+30
(f○f)(x)=x9+6×6+12×3+10
(ф○ф)(х)=х+1х+2
Нет, не работает HLT
Да, проходит HLT
Да, его граф проходит HLT.

Нет, его график не соответствует HLT.
Да, его граф проходит HLT.
Доказательство
Доказательство
Доказательство
Доказательство
Доказательство
f−1(x)=x5
f−1(x)=12x−52
f−1(x)=−32x+12
г-1(х)=х-5
f−1(x)=x+5
ч-1(х)=х-533
f−1(x)=x3+32
г-1(х)=2-xx3
f−1(x)=5−xx
f−1(x)=5(x+1)x−1
ч-1(х)=-510х-1
г-1(х)=х3-25
f−1(x)=(x+4)3+6
ч-1(х)=(х+3)5-1
f−1(x)=x−bm
f−1(x)=x−da3
Ответ может отличаться
Ответ может отличаться
Найти обратную функцию
Найти обратную функцию — предварительный расчет—>
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительное исчисление
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский диалект
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочее
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Мы открыты в субботу и воскресенье!
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все ресурсы Precalculus
12 диагностических тестов 380 практических тестов Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 3 4 Следующая →
Precalculus Help » Функции » Обратные функции » Найти обратную функцию
Найти обратную заданной функции:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти обратную функцию, мы хотим поменять местами значения домена в диапазоне. Другими словами, поменяйте местами переменные и в функции:
Другими словами, поменяйте местами переменные и в функции:
Отчет о ошибке
Найдите обратную функцию следующей функции:
Возможные ответы:
Правильный ответ:
. Объяснение:
Чтобы найти обратную, просто поменяйте местами f(x) и x, а затем найдите f(x). Таким образом, обратная функция:
Сообщить об ошибке
Найдите обратную следующей функции:
Возможные ответы:
Правильный ответ:
Объяснение:
Обратную функцию можно найти, «обратив» операции, выполняемые над , то есть вычитая из окончательного решения, а затем находя третий корень этого числа, или, говоря математическим языком,
Сообщить об ошибке
Найдите обратную функцию .
Возможные ответы:
Ни один из других ответов.
Правильный ответ:
Объяснение:
Чтобы найти обратную, вы должны поменять местами переменные и найти y.
Обратный переменные:
Решение для Y:
Отчет о ошибке
эти две функции инверны? а также .
Возможные ответы:
Не могу сказать
Да
G(x) не имеет обратного.
F(x) не имеет обратного.
Нет
Правильный ответ:
Да
Пояснение:
Можно установить, есть ли у двух функций обратные, найдя по очереди композицию обеих функций. Каждая композиция должна равняться x, если функции действительно обратны друг другу.
Каждая композиция должна равняться x, если функции действительно обратны друг другу.
Функции обратны друг другу.
Сообщить об ошибке
Найдите обратное уравнение:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти обратную функцию, замените x на любую позицию y:
Исходное уравнение:
Обратное уравнение:
Теперь найдите обратное значение y.
Отчет о ошибке
Найдите обратное из следующего уравнения:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти обратную функцию, замените x на любую позицию y:
Исходное уравнение:
Обратное уравнение:
Теперь найдите обратное значение y.
Отчет о ошибке
Найдите обратное из следующего уравнения:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти обратную функцию, замените x на любую позицию y:
Исходное уравнение:
Обратное уравнение:
Теперь найдите обратное значение y.
Отчет о ошибке
Определить обратную функцию, приведенный
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти обратную функцию, мы
- меняем местами переменные и
- найти новую переменную
Для функции
.

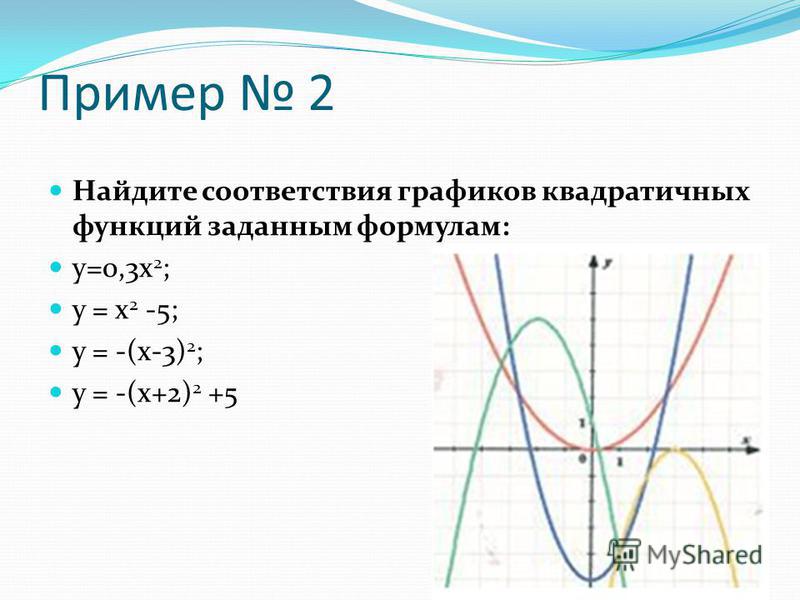 рис. 18.8 слева.
Пусть y∗∈(max(f(a),f(x2)),f(x1)). По теореме о
промежуточном значении на [a,x1]
найдётся такая точка c1, что f(c1)=y∗. По той же теореме на
[x1,x2] найдётся такая точка c2, что f(c2)=y∗.
Противоречие с обратимостью.
рис. 18.8 слева.
Пусть y∗∈(max(f(a),f(x2)),f(x1)). По теореме о
промежуточном значении на [a,x1]
найдётся такая точка c1, что f(c1)=y∗. По той же теореме на
[x1,x2] найдётся такая точка c2, что f(c2)=y∗.
Противоречие с обратимостью. е. функция обратима.
е. функция обратима. Постройте на одной системе координат графики этих взаимно обратных функций:
Постройте на одной системе координат графики этих взаимно обратных функций: 09.18
09.18


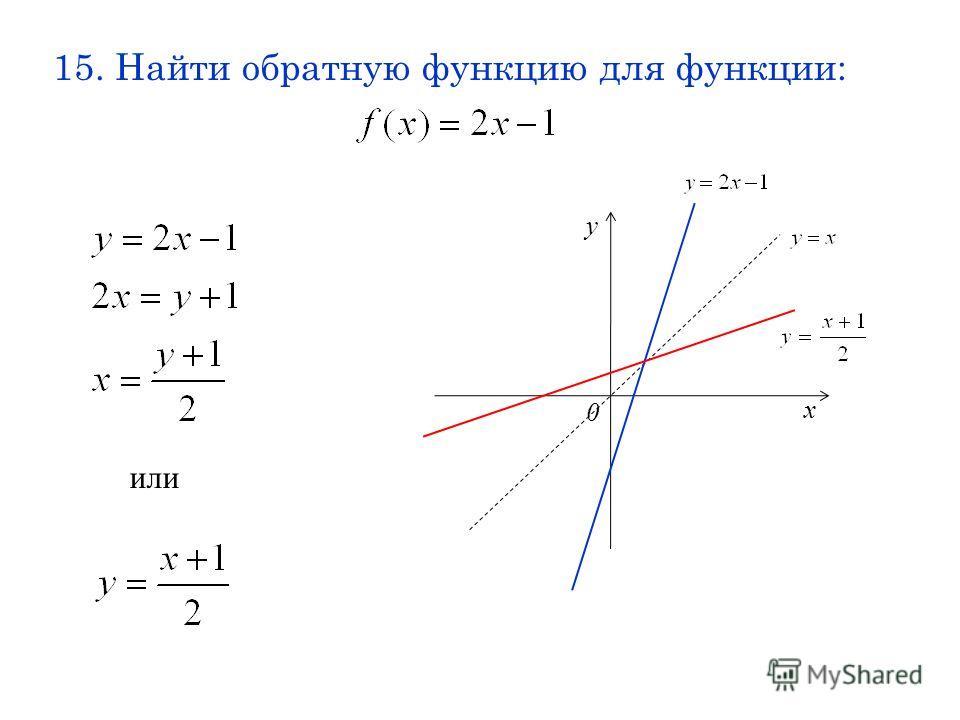 Используйте тест горизонтальной линии, чтобы определить, является ли функция однозначной.
Используйте тест горизонтальной линии, чтобы определить, является ли функция однозначной.
